Prawitasari, Elyine R. 2014
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT MENGGUNAKAN METODE MEHAR
Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY
TRANSSHIPMENT MENGGUNAKAN METODE MEHAR
SKRIPSI
Diajukan untuk Memenuhi Sebagian dari Syarat Memperoleh Gelar Sarjana
Program Studi Matematika Konsentrasi Terapan
Oleh
ELTINE REGIENA PRAWITASARI
1006658
JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
Prawitasari, Elyine R. 2014
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT MENGGUNAKAN METODE MEHAR
Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
Prawitasari, Elyine R. 2014
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT MENGGUNAKAN METODE MEHAR
Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
PENERAPAN MODEL PEMBELAJARAN KOOPERATIF TIPE COURSE
REVIEW HORAY UNTUK MENINGKATKAN HASIL BELAJAR SISWA
PADA MATERI PENJUMLAHAN DAN PENGURANGAN PECAHAN (Penelitian Tindakan Kelas pada Siswa Kelas IV SDN 1 Suntenjaya Tahun Ajaran
2013/2014 Kecamatan Lembang Kabupaten Bandung Barat)
ABSTRAK
Penelitian ini dilatarbelakangi oleh rendahnya hasil belajar siswa pada materi Penjumlahan dan Pengurangan Pecahan yang disebabkan oleh kurangnya kemampuan siswa dalam mengkali bilangan serta kurangnya ketelitian dan kerjasama siswa. Penelitian ini bertujuan untuk mendeskripsikan kondisi awal
pembelajaran, mendeskripsikan proses pembelajaran serta mengetahui
Prawitasari, Elyine R. 2014
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT MENGGUNAKAN METODE MEHAR
Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
Prawitasari, Elyine R. 2014
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT MENGGUNAKAN METODE MEHAR
Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
LEMBAR PERNYATAAN ... i
ABSTRAK ... ii
KATA PENGANTAR ... iv
DAFTAR ISI ... . vi
DAFTAR TABEL ... ... viii
DAFTAR GAMBAR ... x
DAFTAR LAMPIRAN ... xii
BAB I PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Rumusan Masalah ... 4
1.3 Batasan Masalah ... 5
1.4 Tujuan Penelitian ... 5
1.5 Manfaat Penelitian ... 5
1.6 Metode Penelitian ... 5
1.7 Sistematika Pembahasan ... 6
BAB II LANDASAN TEORI ... 8
2.1 Pemrograman Linier ... 8
2.2 Masalah Transshipment ... 9
2.3 Keseimbangan Model Transshipment... 10
2.4 Solusi Masalah Transshipment ... 11
2.4.1 Menentukan Solusi Fisibel Awal... 12
2.4.2 Teknik Mengecek Optimalitas ... 18
2.5 Bilangan Fuzzy ... 25
2.5.1 Himpunan Fuzzy ... 25
2.5.2 Fungsi Keanggotaan ... 25
2.5.3 Bilangan Fuzzy Trapesium ... 27
2.5.4 Operasi Aritmatika ... 28
2.6 Masalah Fuzzy Transshipment ... 28
BAB III SOLUSI OPTIMAL MASALAH FUZZY TRANSSHIPMENT 34
3.1 Metode Mehar ... 34
3.2 Studi Kasus Masalah Fuzzy Transshipment ... 39
3.2.1 Analisa Kasus ... 39
3.2.2 Penyelesaian ... 43
BAB IV PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT ... 71
4.1 Perancangan Program ... 71
4.4.1 Diagram Alur Program Aplikasi ... 71
4.4.2 Rancangan Desain Antarmuka ... 71
4.2 Implementasi Program ... 76
4.2.1 Perangkat Lunak Pendukung ... 76
4.2.2 Perangkat Keras Pendukung ... 76
4.2.3 Implementasi Antarmuka ... 76
4.3 Pengujian Program ... 79
4.3.1 Pengujian Jendela Input Data ... 79
4.3.2 Pengujian Jendela Model Fuzzy ... 81
4.3.3 Pengujian Jendela Model Crisp ... 84
4.3.4 Pengujian Jendela Solusi ... 87
BAB V PENUTUP... 90
5.1 Kesimpulan ... 90
5.2 Saran ... 91
DAFTAR PUSTAKA ... 92
Prawitasari, Elyine R. 2014
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT MENGGUNAKAN METODE MEHAR
Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
BAB I PENDAHULUAN
1.1 LATAR BELAKANG
Pada dunia bisnis, manajemen rantai suplai merupakan strategi klasik yang
banyak digunakan oleh industri atau perusahaan dalam mengembangkan
usahanya. Salah satu tingkat taktisnya adalah strategi transportasi, termasuk
frekuensi komoditi dan rute distribusinya. Komoditi yang terbatas membuat
industri perlu melakukan perencanaan yang matang dalam pendistribusiannya ke
daerah penerima, tergantung pada jumlah permintaan. Hal tersebut juga tak lepas
dari biaya distribusi pengiriman komoditi. Pengalokasian sumber daya yang
terbatas sehingga dapat memenuhi permintaan yang ada patut diperhitungkan
secara matang agar biaya distribusi yang dikeluarkan seminimal mungkin.
Para ahli menyelesaikan masalah pendistribusian ini dengan pendekatan
matematika. Solusi dari masalah alokasi sumber daya yang terbatas adalah dengan
pendekatan pemrograman linier. Pemrograman linier menerjemahkan
permasalahan yang ada ke dalam model matematika.
Mencari � , � , … , � yang memaksimumkan (atau meminimumkan) � =
� + � + ⋯ + � dengan memenuhi kendala sebagai berikut :
� + � + ⋯ + � , =, � + � + ⋯ + � , =,
� + � + ⋯ + � , =,
� 0, � 0, … , � 0
Formula di atas merupakan suatu permasalahan pemrograman linier. Program
linier atau linear programming berasal dari kata programa dan linier. Programa
adalah sinonim untuk perencanaan sedangkan linier berarti bahwa model yang
linier pertama kali dicetuskan L. V. Kantorovich dengan metode penyelesaian
yang masih terbatas. Kemudian George B. Dantzig mengembangkan dan
menemukan cara memecahkan pemrograman linier tersebut dengan menggunakan
“metode simpleks”. Menurut Dimyati dan Dimyati (1992 : 17), pemrograman linier mampu mengatasi berbagai permasalahan industri seperti persoalan
pengalokasian fasilitas produksi, persoalan pengalokasian sumber daya nasional
untuk kebutuhan domestik, penjadwalan produksi, solusi permainan, dan
pemilihan pola pendistribusian (shipping).
Hitchcock memodifikasi metode simpleks dengan memperhatikan pola
khusus dari nilai koefisien pada fungsi kendalanya untuk menyelesaikan persoalan
distribusi komoditas ini, biasa disebut masalah transportasi. Kemudian Charness
dan Cooper memperkenalkan metode stepping stone sebagai alternatif lain untuk
mengecek optimalitas dari solusi fisibel awal. Solusi fisibel awal bagi masalah
transportasi sendiri dapat diperoleh dengan menggunakan metode pojok kiri atas,
ongkos terendah atau pendekatan Vogel (Kumar, et al., 2011 : 164).
Masalah transportasi berkaitan dengan pendistribusian sembarang komoditi
dari sembarang kelompok pusat pemasok, yang disebut sumber, ke sembarang
kelompok pusat penerima, yang disebut tujuan, sedemikian rupa sehingga
meminimumkan biaya distribusi total. Sasarannya adalah mencari pola
pendistribusian dan banyaknya komoditas yang diangkut dari masing-masing
sumber ke masing-masing tujuan yang meminimalkan ongkos angkut secara
keseluruhan, dengan kendala-kendala yang ada. Masalah transportasi
mengasumsikan sumber hanya berfungsi sebagai daerah pemasok dan tujuan
hanya berfungsi sebagai daerah penerima. Hal Ini berarti total biaya distribusi
minimum pada permasalahan transportasi didapat dengan pendistribusian
langsung dari sumber ke tujuan yang ditunjuk. Namun faktanya, total biaya
distribusi minimum bisa saja diperoleh dari pendistribusian komoditi melewati
sumber atau tujuan yang lain sebelum akhirnya sampai di tujuan yang ditunjuk.
Jadi, pada kenyataannya sumber maupun tujuan dapat berfungsi sebagai daerah
Metode penyelesaian masalah transshipment yang ada selama ini
membutuhkan parameter yang bernilai pasti. Parameter tersebut antara lain biaya
distribusi per unit, jumlah komoditi yang tersedia di sumber dan jumlah
permintaan terhadap komoditi tersebut. Namun pada kenyataannya, parameter
tersebut mungkin tidak diketahui secara pasti karena faktor-faktor yang tak
terkendali sehingga nilainya menjadi samar. Umumnya nilai dari parameter
tersebut ditentukan secara subjektif karena ketidaktersediaan data lampau. Hal
tersebut akan mempengaruhi keakuratan optimasi terlebih untuk perencanaan
distribusi di masa yang akan datang. Kesamaran nilai tersebut dapat diwakili oleh
bilangan fuzzy yang diperkenalkan oleh Zadeh ( 1965 : 339 ). Sehingga yang
dibutuhkan adalah metode pengambilan keputusan bilangan samar (fuzzy).
Pemrograman linier fuzzy pertama kali diperkenalkan oleh H. J. Zimmerman.
Selanjutnya, pemrograman linier fuzzy tersebut dikembangkan untuk
menyelesaikan masalah transportasi. Kumar, et al. ( 2011 : 167 ) dalam jurnalnya
yang berjudul “Fuzzy Linear Programming Approach for Solving Fuzzy
Transportation Problems with Transshipment” memperkenalkan metode Mehar
untuk mencari solusi optimal dari masalah transshipment dengan pola pengiriman
sebagai berikut :
1. Dari sumber ke sumber lainnya
2. Dari tujuan ke tujuan lainnya
3. Dari tujuan ke sembarang sumber
Metode tersebut selalu menghasilkan solusi optimal yang nilainya no-negatif dan
sesuai dengan situasi nyata dimana jumlah komoditi yang tersedia, banyak
permintaan, dan biaya distribusi per unit komoditi tidak dapat diprediksi secara
pasti. Selain itu, metode tersebut dapat merubah masalah fuzzy transshipment
yang tak seimbang menjadi seimbang dengan lebih mudah, tanpa menggunakan
teknik �-cut.
Prinsip dasar dari metode Mehar adalah dengan mengkonversi fungsi tujuan
dan fungsi kendala fuzzy pada masalah pemrograman linier fuzzy ke bentuk
crisp menggunakan metode yang sudah ada. Nilai yang diperoleh selanjutnya
disubstitusikan ke variabel fuzzy, sehingga diperolehlah variabel keputusan fuzzy
yang diinginkan. Dengan prinsip yang sama, metode Mehar juga dapat diterapkan
untuk menyelesaikan persoalan pemrograman linier yang lain, tidak hanya untuk
masalah fuzzy transshipment. Kajian yang telah dilakukan sampai saat ini antara
lain untuk masalah analisa sensitivitas sistem manufaktur dan mencari solusi
optimal dari masalah transportasi fuzzy multi-objektif.
Perhitungan pemrograman linier fuzzy cenderung melelahkan bila dilakukan
secara manual karena memerlukan ketelitian yang cukup tinggi dan variabel yang
digunakan sangat banyak. Adanya aplikasi komputer (software) tentu akan sangat
membantu agar penyelesaiannya lebih efektif, akurat dan cepat. Aktivitas
perusahaan yang kini tak lepas dari komputer juga menjadi faktor pendukung
perlunya aplikasi praktis untuk menyelesaikan masalah fuzzy transshipment di
atas.
Lebih jauhnya mengenai penyelesaian masalah fuzzy transshipment tersebut
tersusun dalam skripsi penulis dengan judul, “Program Aplikasi Penyelesaian Masalah Fuzzy Transshipment Menggunakan Metode Mehar”. Penelitian dilakukan dengan mengkaji jurnal dari Kumar, et al. ( 2011 : 163 ). Kontribusi
penulis adalah menjabarkan metode optimasi pemrograman linier crisp dari
pemrograman linier fuzzy yang telah dikonversi sebelumnya dan membuat
program aplikasi penyelesaian masalah transshipment fuzzy dengan menggunakan
Delphi 7.
1.2 RUMUSAN MASALAH
Atas dasar latar belakang di atas, maka diambillah perumusan masalah
sebagai berikut :
1. Bagaimana cara mencari solusi optimal dari masalah fuzzy transshipment
dengan menggunakan metode Mehar ?
2. Bagaimana cara membuat aplikasi penyelesaian masalah fuzzy
3. Bagaimana hasil uji coba aplikasi penyelesaian masalah transshipment
fuzzy tersebut ?
1.3 BATASAN MASALAH
Untuk mempermudah penyusunan algoritma program maka variabel yang
digunakan untuk fungsi tujuan pada program aplikasi terbatas sebanyak 2 variabel
untuk supply dan 2 variabel untuk demand.
1.4 TUJUAN PENELITIAN
Berdasarkan rumusan masalah di atas, tujuan dari penelitian ini adalah
sebagai berikut :
1. Mengetahui cara mencari solusi optimal masalah transshipment dengan
menggunakan metode Mehar.
2. Mengetahui cara membuat aplikasi penyelesaian masalah fuzzy
transshipment menggunakan Delphi 7.
3. Mengetahui hasil uji coba aplikasi penyelesaian masalah fuzzy
transshipment tersebut.
1.5 MANFAAT PENELITIAN
Adapun manfaat dari penelitian ini yaitu :
1. Bagi penulis
Mengetahui cara menyelesaikan masalah transshipment fuzzy
menggunakan metode Mehar dan memanfaatkan teori yang telah didapat
selama menuntut ilmu di FPMIPA UPI serta mengembangkan diri dalam
membuat aplikasi komputer.
2. Bagi Jurusan Pendidikan Matematika
Menambah khasanah pengetahuan matematika pada topik kajian fuzzy
transshipment.
Metode penelitian dibutuhkan untuk mengetahui dengan cara apa penelitian
tersebut dilakukan agar tujuan yang diinginkan dapat tercapai. Adapun metode
yang digunakan dalam penelitian ini antara lain :
1. Studi Literatur.
Melakukan pendekatan kepustakaan melalui buku-buku, jurnal, dan artikel
yang berkaitan dengan penelitian yang dibahas.
2. Perancangan aplikasi.
Perencanaan dan perancangan desain antarmuka dan algoritma yang
dibutuhkan untuk membuat program aplikasi.
3. Pembuatan aplikasi.
Pembuatan program aplikasi dengan menggunakan algoritma-algoritma yang
telah dirancang dalam bahasa pemrograman Delphi 7.
4. Pengujian aplikasi.
Pengujian hasil pembuatan program aplikasi yang telah dibuat untuk melihat
ada tidaknya kesalahan untuk kemudian dapat diperbaiki.
1.7 SISTEMATIKA PEMBAHASAN
Penelitian ini disusun dalam sebuah skripsi yang terangkum dalam lima bab,
yaitu sebagai berikut :
BAB I PENDAHULUAN
Mengemukakan latar belakang masalah, antara lain tentang pentingnya
perencanaan distribusi komoditi suatu industri, solusi untuk
menyelesaikan permasalahan distribusi komoditi terbatas, perbedaan
masalah transportasi dengan masalah transshipment, perkembangan
metode yang digunakan untuk optimasi yang diinginkan, dan
kesesuaian penggunaan bilangan fuzzy untuk menerjemahkan
permasalahan sebenarnya. Dijabarkan pula tujuan dari diadakannya
penelitian, manfaat yang diharapkan dari pengadaan penelitian, metode
BAB II LANDASAN TEORI
Menjabarkan dasar-dasar teori yang menunjang penelitian, seperti
definisi bilangan fuzzy beserta operasinya, metode penyelesaian
masalah transportasi, dan algoritma pemrograman dasar yang
digunakan untuk membuat program aplikasi.
BAB III SOLUSI OPTIMAL MASALAH FUZZY TRANSSHIPMENT
Penjabaran metode Mehar dan studi kasus untuk mengetahui bagaimana
cara mengaplikasikan metode Mehar pada masalah transshipment yang
ada.
BAB IV PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY
TRANSSHIPMENT
Merancang desain tampilan program aplikasi dan algoritma dasar untuk
pembuatan program, juga menampilkan hasil implementasi dari
program aplikasi yang telah dibuat beserta hasil uji coba program.
BAB V KESIMPULAN
Menyimpulkan hasil dari penelitian yang telah dilakukan dengan
Prawitasari, Elyine R. 2014
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT MENGGUNAKAN METODE MEHAR
Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
BAB III
SOLUSI OPTIMAL MASALAH FUZZY TRANSSHIPMENT
3.1 METODE MEHAR
Pada tahun 2011, Kumar, et al. dalam jurnalnya yang berjudul “Fuzzy Linear
Programming Approach for Solving Fuzzy Transportation Problems with
Transshipment” memperkenalkan metode Mehar untuk menyelesaikan
permasalahan transshipment dengan pola pengiriman sebagai berikut :
a. Dari sumber ke sumber lainnya
b. Dari tujuan ke tujuan lainnya
c. Dari tujuan ke sembarang sumber
Pada metode Mehar, biaya distribusi, jumlah komoditi yang tersedia, dan jumlah
permintaan terhadap komoditi direpresentasikan oleh bilangan fuzzy trapesium.
Metode Mehar sangat mudah dipahami dan diterapkan untuk mencari solusi
optimal dari masalah fuzzy transshipment yang sesuai dengan kondisi sebenarnya
karena berdasarkan pada konsep metode transportasi klasik. Keunggulan dari
metode Mehar ini adalah selalu menghasilkan solusi optimal yang non negatif.
Misalkan permasalahan transshipment seperti yang disajikan pada Tabel 2.14.
Berikut adalah algoritma dari metode Mehar untuk menyelesaikan permasalahan
fuzzy transshipment ( Kumar et al., 2011 : 168 ) :
1. Hitung total ketersediaan ∑= ̃ dan total permintaan ∑ = ++ ̃ . Misalkan ∑= ̃ = , , , dan ∑ = ++ ̃ = ′, ′, ′, ′ . = banyaknnya
sumber dan = banyaknya tujuan.
a. Jika ∑= ̃ = ∑ = ++ ̃, maka permasalahan transshipment tersebut
sudah seimbang, lanjut ke langkah 2.
b. Jika ∑= ̃ ≠ ∑ = ++ ̃ , maka permasalahan transshipment tersebut
seimbang menjadi permasalahan transshipment yang seimbang dengan
cara berikut :
i) Jika ′, − ′− ′, − ′− ′, dan − ′− ′,
maka tambahkan sebuah sumber semu � + dengan ketersediaan fuzzy ′− , ′− , ′− , ′− pada sumber semu � + dan tidak ada permintaan fuzzy (−) di tujuan semu � + . Tujuan semu � + secara otomatis muncul karena sumber semu � + telah
ditambahkan sebelumnya.
Asumsikan bahwa :
Ongkos distribusi per unit produk dari sumber semu � + ke semua tujuan sebagai bilangan fuzzy trapesium nol.
Ongkos distribusi per unit produk dari semua sumber ke tujuan semu � + (kecuali dari sumber semu � + ) sebagai bilangan fuzzy trapesium yang sangat besar, �, �, �, � .
ii) Jika ′, − ′− ′, − ′− ′, dan − ′− ′
maka tambahkan sebuah tujuan semu � + dengan permintaan fuzzy − ′, − ′, − ′, − ′ pada tujuan semu � + dan tidak ada permintaan fuzzy (−) di sumber semu � + . Sumber semu � + secara otomatis muncul karena tujuan semu � + telah ditambahkan sebelumnya.
Asumsikan bahwa :
Ongkos distribusi per unit produk dari semua sumber ke tujuan semu � + sebagai bilangan fuzzy trapesium nol.
Ongkos distribusi per unit produk dari sumber semu � + (kecuali dari sumber semu � + ) ke semua tujuan sebagai bilangan fuzzy trapesium yang sangat besar, �, �, �, � .
iii) Jika tidak memenuhi (i) atau (ii) maka tambahkan sumber semu � + dan tujuan semu � + dengan ketersediaan fuzzy (maksimum {0,
}, maksimum {0, ’ − } + maksimum { , ’ − ’ − − } +
maksimum { , ’ − ’ − − }, maksimum {0, ’ − } +
maksimum { , ’ − ’ − − } + maksimum { , ’ − ’ −
− } + maksimum { , ’ − ’ − − }) pada sumber semu
� + dan tidak ada permintaan (−) pada sumber semu � + .
Permintaan fuzzy sebesar (maksimum {0, − ′}, maksimum {0,
− ′} + maksimum {0, − − ′ − ′ }, maksimum {0,
− ′} + maksimum { , − − ′ − ′ } + maksimum
{ , − − ′ − ′ }, maksimum {0, − ′} + maksimum
{ , − − ′ − ′ } + maksimum { , − − ′ − ′ } +
maksimum { , − − ′ − ′ }) di tujuan semu � + dan tidak
ada permintaan di tujuan semu � + . Tujuan semu � + dan sumber semu � + secara otomatis muncul karena sumber semu � + dan tujuan semu � + telah ditambahkan sebelumnya.
Asumsikan bahwa :
Ongkos distribusi per unit produk dari sumber semu � + ke semua tujuan dan dari semua sumber ke tujuan semu � + sebagai bilangan fuzzy trapesium nol.
Ongkos distribusi per unit produk dari semua sumber ke tujuan semu � + (kecuali dari sumber semu � + ) dan dari sumber semu � + (kecuali dari sumber semu � + ) ke semua tujuan sebagai bilangan fuzzy trapesium yang sangat besar,
�, �, �, � .
2. Masalah transshipment yang seimbang memiliki + sumber dan +
tujuan, = atau + dan = atau + .
3. Tambahkan stok sementara �̃ = ∑= ̃ atau ∑ = ++ ̃ pada masing-
Tabel 3.1 Penambahan Stok pada Fuzzy Transshipment
�
� � … � � … � Ketersediaan
� 0 … ̃ ̃ + … ̃ + ̃ �̃
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
� ̃ … 0 ̃ + … ̃ + ̃ �̃
� ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ �̃
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
� ̃ + … ̃ + … … 0 �̃
Permintaan �̃ … �̃ ̃ + �̃ … ̃ + �̃ ∑ ̃
∑ ̃
4. Berdasarkan permasalahan transshipment pada Tabel 3.1, selesaikanlah
permasalahan pemograman linier berikut :
Minimumkan ℜ(∑=+ ∑ =+ ̃ �̃ )
dengan kendala : ∑ =+ �̃ = ̃ �̃ = , , …
∑ + �̃
= = �̃ = + , … +
∑ + �̃
= = �̃ = , , …
∑ + �̃
= = ̃ �̃ = + , … +
�̃ adalah bilangan fuzzy trapesium yang non negatif
Misalkan ∑=+ ∑ =+ ̃ �̃ = , , , , maka masalah
pemrograman linier fuzzy di atas dapat ditulis sebagai berikut :
Minimumkan ℜ , , ,
dengan kendala : ∑ +
= , ∑ =+ , ∑ =+ , ∑ =+ = , , , ,
= , , … ∑ +
= , ∑ =+ , ∑ =+ , ∑ =+ = , , , ,
∑ + = , ∑=+ , ∑ =+ , ∑ =+ = , , , , = , , … (∑ + = , ∑=+ , ∑=+ , ∑=+ ) = ′ , ′ , ′ , ′ , = + , … +
, , , adalah bilangan fuzzy trapesium yang non negatif.
5. Konversi pemrograman linier fuzzy di atas ke dalam pemograman linier crisp,
denga cara berikut :
Minimumkan , , ,
6. Carilah solusi optimal , , , dengan cara menyelesaikan
pemograman linier crisp di poin 5.
7. Temukan solusi optimal fuzzy �̃ dengan mensubstitusi nilai dari
, , , ke �̃ = , , , .
8. Temukan total ongkos fuzzy minimum dengan mensubstitusikan nilai dari �̃
ke ∑=+ ∑ =+ ̃ �̃ .
3.2 STUDI KASUS MASALAH FUZZY TRANSSHIPMENT
3.2.1 Analisa Kasus
Dari jurnal yang berjudul “Fuzzy Linear Programming Approach for Solving Fuzzy Transportation Problem with Transshipment“, Kumar et al.
(2011 : 174) memberikan suatu permasalahan transshipment dengan dua buah
sumber dan dua buah tujuan. Ketersediaan fuzzy di sumber � dan �
masing-masing adalah ̃ = (10,20,30,40) dan ̃ = (0,4,8,10). Permintaan fuzzy di
tujuan � dan � masing-masing adalah ̃ = (6,8,10,20) dan ̃ =
(10,16,18,20). Ongkos distribusi fuzzy untuk masalah transshipment tersebut adalah sebagai berikut :
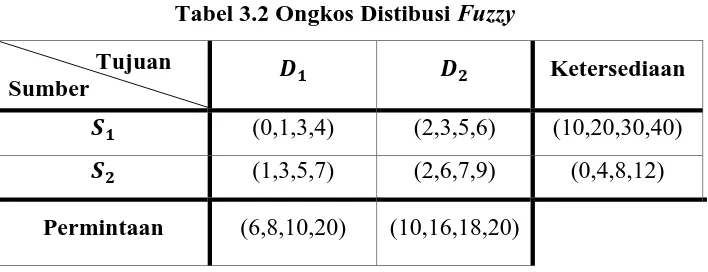
Tabel 3.2 Ongkos Distibusi Fuzzy Tujuan
Sumber � � Ketersediaan
� (0,1,3,4) (2,3,5,6) (10,20,30,40)
� (1,3,5,7) (2,6,7,9) (0,4,8,12)
Permintaan (6,8,10,20) (10,16,18,20)
Adapun pola pengiriman yang terjadi adalah sebagai berikut :
a. Dari sumber ke sumber lainnya
b. Dari tujuan ke tujuan lainnya
c. Dari tujuan ke sembarang sumber
Berdasarkan pola pengiriman di atas, maka distribusi ke daerah tujuan
tujuan yang lain terlebih dahulu. Artinya, daerah sumber dapat melakukan
pengiriman ke daerah sumber lainnya dan daerah tujuan dapat melakukan
pengiriman ke daerah tujuan lainnya. Biaya distribusi ke daerah transit
disajikan pada Tabel 3.3.
Tabel 3.3 Ongkos Distribusi ke Daerah Transit
Sumber Tujuan Ongkos
� � (1,1,1,1)
� � (0,1,3,4)
Pendistribusian pun dapat terjadi dari tujuan ke sembarang sumber dan tidak
ada perbedaan ongkos ditribusi dari tujuan ke sumber, artinya ongkos
distribusi dari � ke � sama dengan ongkos distribusi dari � ke �.
Permasalahan transshipment di atas digambarkan oleh tablo transshipment
berikut :
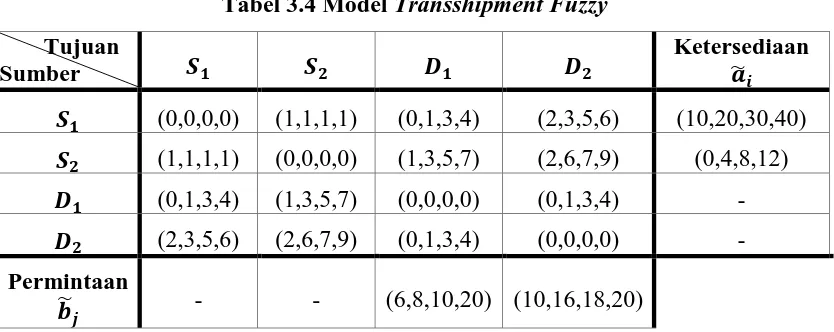
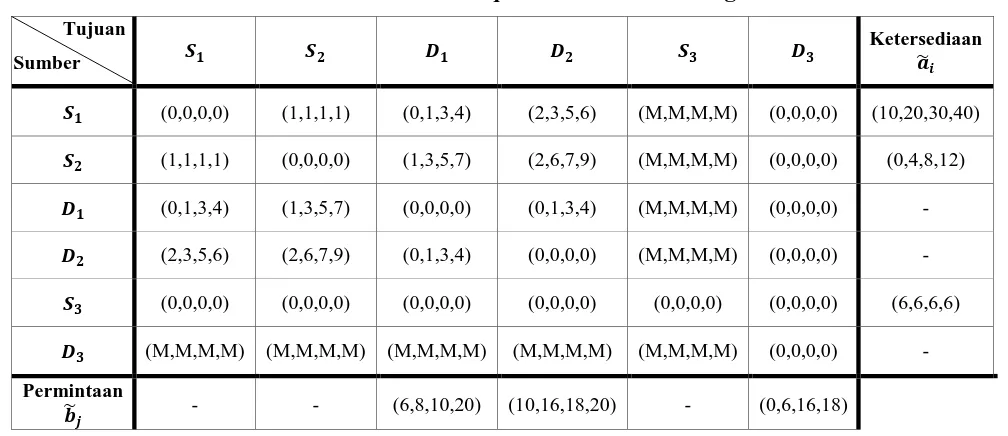
Tabel 3.4 Model Transshipment Fuzzy Tujuan
Sumber � � � �
Ketersediaan ̃
� (0,0,0,0) (1,1,1,1) (0,1,3,4) (2,3,5,6) (10,20,30,40)
� (1,1,1,1) (0,0,0,0) (1,3,5,7) (2,6,7,9) (0,4,8,12)
� (0,1,3,4) (1,3,5,7) (0,0,0,0) (0,1,3,4) -
� (2,3,5,6) (2,6,7,9) (0,1,3,4) (0,0,0,0) -
Permintaan
̃ - - (6,8,10,20) (10,16,18,20)
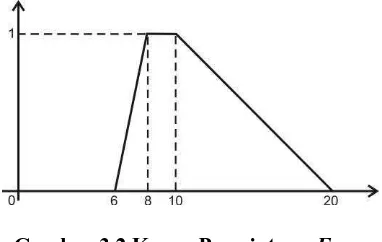
Ketersediaan fuzzy di daerah sumber � = (10,20,30,40) merupakan
bilangan fuzzy trapesium dengan kurva sebagai berikut :
Kurva pada Gambar 3.1 merepresentasikan ketersediaan minimum di sumber
� adalah 10 unit dan maksimum 40 unit, sedangkan rata-rata jumlah komoditas yang selalu tersedia di � adalah antara 20-30 unit. Dengan
interpretasi yang sama, ketersediaan komoditas minimum di � adalah 0 unit,
artinya tidak ada komoditas yang tersedia di � , dan maksimum 12 unit,
sedangkan rata-rata jumlah komoditas yang selalu tersedia di � antara 2-8
unit.
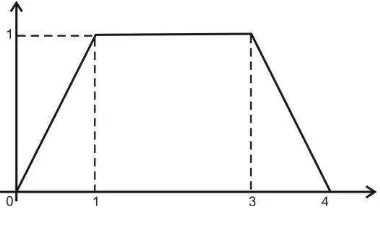
Permintaan fuzzy di daerah tujuan � = (6,8,10,20) merupakan bilangan
fuzzy trapesium dengan kurva sebagai berikut :
Gambar 3.2 Kurva Permintaan Fuzzy
Kurva pada Gambar 3.2 merepresentasikan permintaan minimum di
tujuan � adalah 6 unit dan maksimum 20 unit, sedangkan rata-rata jumlah
komoditas yang dibutuhkan oleh daerah tujuan � adalah antara 8-10 unit.
Dengan interpretasi yang sama, ketersediaan komoditas minimum di �
adalah 10 unit dan maksimum 20 unit, sedangkan rata-rata jumlah komoditas
yang dibutuhkan oleh daerah tujuan � antara 16-18 unit.
Ongkos fuzzy untuk distribusi komoditas dari sumber � ke � =
(0,1,3,4) merupakan bilangan fuzzy trapesium dengan kurva seperti yang
Gambar 3.3 Kurva Permintaan Fuzzy
Kurva pada Gambar 3.3 merepresentasikan ongkos minimum untuk mengirim
per unit komoditas dari sumber � ke tujuan � adalah 0 satuan harga, artinya
tidak ada biaya pengiriman yang harus dikeluarkan, dan maksimum 4 satuan
harga, sedangkan rata-rata ongkos pengiriman yang harus dikeluarkan
adaalah antara 1-3 satuan harga. Dengan interpretasi yang sama, ongkos
minimum untuk mengirim per unit komoditas dari sumber � ke tujuan �
adalah 2 satuan harga dan maksimum 6 satuan harga, sedangkan rata-rata
ongkos pengiriman yang harus dikeluarkan adaalah antara 2-3 satuan harga.
Ongkos minimum untuk mengirim per unit komoditas dari sumber � ke
tujuan � adalah 1 satuan harga dan maksimum 7 satuan harga, sedangkan
rata-rata ongkos pengiriman yang harus dikeluarkan adaalah antara 3-5 satuan
harga. Ongkos minimum untuk mengirim per unit komoditas dari sumber �
ke tujuan � adalah 2 satuan harga dan maksimum 9 satuan harga, sedangkan
rata-rata ongkos pengiriman yang harus dikeluarkan adaalah antara 6-7 satuan
harga. Ongkos minimum untuk mengirim per unit komoditas dari sumber �
ke sumber � adalah 1 satuan harga. Ongkos minimum untuk mengirim per
unit komoditas dari sumber � ke tujuan � adalah 0 satuan harga, artinya
tidak ada biaya pengiriman yang harus dikeluarkan, dan maksimum 4 satuan
harga, sedangkan rata-rata ongkos pengiriman yang harus dikeluarkan
3.2.2 Penyelesaian
Permasalahan transshipment di atas akan diselesaikan menggunakan
metode Mehar melalui langkah-langkah berikut :
Langkah 1
Cek keseimbangan model.
∑= ̃ = , , , , , ,
= + , + , + , +
= , , ,
∑ = ̃ = , , , , , ,
= + , + , + , +
= , , ,
∑ ̃ ≠ ∑ ̃, maka masalah transshipment tersebut tidak seimbang.
Misal ∑ ̃ = , , , dan ∑ ̃ = , , ,
− = − dan − = −
= =
Karena − = = − dan = = , maka harus
ditambahkan variabel semu � dan � .
̃ = [ { , − }, { , − } + { , − −
− }, { , − } + { , − − − } +
{ , − − − }, { , − } +
{ , − − − } + { , − −
− } + { , − − − }]
= [ , + , + + , + + + ]
= [ , , , ]
̃ = [ { , − }, { , − } + { , − −
− }, { , − } + { , − − − } +
{ , − − − }, { , − } +
{ , − − − } + { , − −
= [ , + , + + , + + + ]
= [ , , , ]
∑= ̃ = ∑= ̃ ̃
= , , , , , ,
= + , + , + , +
= , , , ∑ = ̃ = ∑ = ̃ ̃
= , , , , , ,
= + , + , + , +
= , , ,
∑ ̃ = , , , = ∑ ̃ .
Sekarang, model sudah seimbang. (Lihat Tabel 3.5)
Langkah 2
Menambahkan stok sementara.
�̃ = ∑ ̃ ( ∑ ̃ ) = , , , ̃� = ̃ �̃ = , , , , , ,
= + , + , + , +
= , , ,
̃� = ̃ �̃ = , , , , , ,
= + , + , + , +
= , , ,
̃� = ̃ �̃ = , , , , , ,
= + , + , + , +
= , , , ̃� = �̃ = , , ,
̃� = �̃ = , , ,
̃� = �̃ = , , , ̃� = �̃ = , , , ̃� = �̃ = , , ,
̃� = ̃ �̃= , , , , , ,
= + , + , + , +
= , , ,
̃� = ̃ �̃= , , , , , ,
= + , + , + , +
= , , ,
̃� = ̃ �̃= , , , , , ,
= + , + , + , +
= , , ,
Sehingga, model transshipment sekarang seperti terlihat pada Tabel 3.6.
Langkah 3
Bentuk pemrograman linier fuzzy dari model transshipment pada tabel 3.6
adalah sebagai berikut :
� ∶
, , , �̃ , , , �̃ , , , �̃ , , , �̃ �, �, �, � �̃ , , , �̃ , , , �̃ , , , �̃ , , , �̃ , , , �̃ �, �, �, � �̃
, , , �̃ , , , �̃ , , , �̃ , , , �̃ , , , �̃ �, �, �, � �̃ , , , �̃ , , , �̃ , , , �̃ , , , �̃ , , , �̃ �, �, �, � �̃ , , , �̃ , , , �̃ , , , �̃ , , , �̃ , , , �̃ , , , �̃ , , , �̃ �, �, �, � �̃ �, �, �, � �̃ �, �, �, � �̃ �, �, �, � �̃
� ∶
�̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ �̃ �̃ �̃ �̃ �̃ = , , , �̃ , ∀ ,
Konversikan ke bentuk pemrograman linier crisp menggunakan fungsi
ranking, sehingga permasalahan tersebut menjadi seperti berikut :
� ∶
+ + + + + + + + + +
+ � + � + � + � + + + + + +
+ + + + + + + � + � +
� + � + + + + + + + + +
+ + +� + � + � + � + + + +
+ + + + + + + + � +
� + � + � + � + � + � + � + � + � +
� + � + � + � + � + � + � + � + � +
� + � + � + � + � � ∶
+ + + + + =
Prawitasari, Elyine R. 2014
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT MENGGUNAKAN METODE MEHAR Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
+ + + + + = + + + + + = + + + + + =
+ + + + + = + + + + + = + + + + + =
+ + + + + = + + + + + = + + + + + =
+ + + + + = + + + + + = + + + + + =
+ + + + + = + + + + + = + + + + + =
+ + + + + = + + + + + = + + + + + =
+ + + + + = + + + + + = + + + + + =
+ + + + + = + + + + + = + + + + + =
+ + + + + = + + + + + =
+ + + + + = + + + + + = − , − ,
+ + + + + = + + + + + = − , ∀ ,
+ + + + + = + + + + + =
+ + + + + = + + + + + =
+ + + + + = + + + + + =
+ + + + + = + + + + + =
+ + + + + = + + + + + =
+ + + + + = + + + + + =
Tabel 3.5 Model Transshipment Sudah Seimbang
Tujuan
Sumber � � � � � �
Ketersediaan ̃
� (0,0,0,0) (1,1,1,1) (0,1,3,4) (2,3,5,6) (M,M,M,M) (0,0,0,0) (10,20,30,40)
� (1,1,1,1) (0,0,0,0) (1,3,5,7) (2,6,7,9) (M,M,M,M) (0,0,0,0) (0,4,8,12)
� (0,1,3,4) (1,3,5,7) (0,0,0,0) (0,1,3,4) (M,M,M,M) (0,0,0,0) -
� (2,3,5,6) (2,6,7,9) (0,1,3,4) (0,0,0,0) (M,M,M,M) (0,0,0,0) -
� (0,0,0,0) (0,0,0,0) (0,0,0,0) (0,0,0,0) (0,0,0,0) (0,0,0,0) (6,6,6,6)
� (M,M,M,M) (M,M,M,M) (M,M,M,M) (M,M,M,M) (M,M,M,M) (0,0,0,0) -
Permintaan
̃ - - (6,8,10,20) (10,16,18,20) - (0,6,16,18)
Tabel 3.6 Model Transshipment Ditambah Stok Sementara
Tujuan
Sumber � � � � � �
Ketersediaan ̃
� (0,0,0,0) (1,1,1,1) (0,1,3,4) (2,3,5,6) (M,M,M,M) (0,0,0,0) (26,50,74,98)
� (1,1,1,1) (0,0,0,0) (1,3,5,7) (2,6,7,9) (M,M,M,M) (0,0,0,0) (16,34,52,70)
� (0,1,3,4) (1,3,5,7) (0,0,0,0) (0,1,3,4) (M,M,M,M) (0,0,0,0) (16,30,44,58)
� (2,3,5,6) (2,6,7,9) (0,1,3,4) (0,0,0,0) (M,M,M,M) (0,0,0,0) (16,30,44,58)
� (0,0,0,0) (0,0,0,0) (0,0,0,0) (0,0,0,0) (0,0,0,0) (0,0,0,0) (22,36,50,64)
� (M,M,M,M) (M,M,M,M) (M,M,M,M) (M,M,M,M) (M,M,M,M) (0,0,0,0) (16,30,44,58)
Permintaan
Langkah 4
Menyelesaikan pemrograman linier crisp.
a. � ∶
+ + � + + + + � + + � +
+ + � + � + � + � + � + �
� ∶
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
Permasalahan di atas digambarkan pada Tabel 3.7
Masalah transshipment tersebut akan diselesaikan dengan
menggunakan metode Least Cost. Pemilihan sel basis harus sangat
hati-hati karena cukup banyak ongkos distribusi yang bernilai 0. Oleh
karena itu, akan lebih baik bila mengutamakan sel diagonal (entri baris
dan kolom sama, i=j). Hal tersebut dilakukan agar bisa mengeliminasi
stok sementara yang ditambahkan sebelumnya. Misalkan yang pertama
dipilih adalah sel .
Alokasikan � = min ketersediaan , permintaan
Tabel 3.7 Ongkos Distribusi Bilangan Fuzzy
Keterse-diaan
� 26
� 16
0 0 0 � 0 16
� 16
0 0 0 0 0 0 22
� � � � � 16
Permin
-taan
16 16 22 26 16 16
Selanjutnya kurangi ketersediaan dan permintaan dengan � ,
akibatnya kolom 1 tidak terpilih lagi (Lihat Tabel 3.8). Lakukan hal yang
serupa untuk seluruh sel diagonal (i=j). Hasilnya seperti yang terlihat
pada Tabel 3.9.
Tabel 3.8 Penyelesaian Ongkos Distribusi Bilangan Fuzzy Menggunakan Metode Least Cost, Peraga 1
Ketersediaan
� � � � �
� 10
� � � � � �
� 16
� 0 � � 0 � 0 � � � 0 16
� � � � � � � 16
� 0 � 0 � 0 � 0 � 0 � 0 22
� � � � � � � � � � � 16
[image:31.595.124.531.483.751.2]Pada Tabel 3.9 terlihat bahwa = = = adalah ongkos
terkecil, pilih salah satu diantara ketiga sel tersebut untuk dijadikan
variabel basis selanjutnya. Misal , maka � = min , = ,
[image:32.595.122.530.230.504.2]ketersediaan = − = , permintaan = − = . Selanjutnya kolom 3 tidak dapat dipilih kembali.
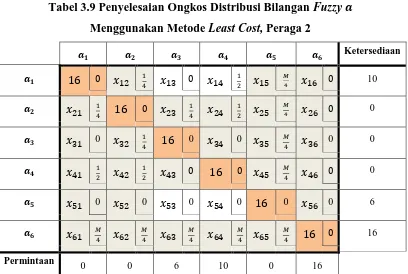
Tabel 3.9 Penyelesaian Ongkos Distribusi Bilangan Fuzzy Menggunakan Metode Least Cost, Peraga 2
Ketersediaan
� � � � � � 10
� � � � � � 0
� 0 � 0 � 0 � � � 0 0
� � � � � � 0
� 0 � 0 � 0 � 0 0 � 0 6
� � � � � � � � � � 16
Permintaan 0 0 6 10 0 16
Selanjutnya dari Tabel 3.10 diketahui bahwa = adalah ongkos
terkecil, maka sel tersebut merupakan variabel basis selanjutnya. � = min , = , ketersediaan = − = , permintaan =
Tabel 3.10 Penyelesaian Ongkos Distribusi Bilangan Fuzzy Menggunakan Metode Least Cost, Peraga 3
Ketersediaan
� � � � � 4
� � � � �
� 0
� 0 � 0 � 0 � � � 0 0
� � � � � � 0
� 0 � 0 � 0 � 0 0 � 0 6
� � � � � � � � � � 16
Permintaan 0 0 0 10 0 16
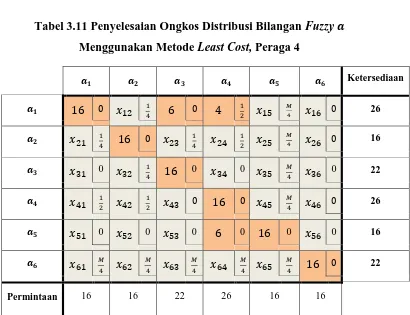
Tabel 3.11 Penyelesaian Ongkos Distribusi Bilangan Fuzzy Menggunakan Metode Least Cost, Peraga 4
Ketersediaan
� � �
� 26
� � � � � � 16
16
� 0 � 0 � 0 � � � 0 22
� � � � � � 26
16
� 0 � 0 � 0 0 0 � 0 16
� � � � � � � � � � 22
[image:33.595.133.543.425.740.2]Selanjutnya adalah memeriksa apakah solusi fisibel awal yang
diperoleh pada Tabel 3.11 memang sudah optimal atau belum
mengunakan metode MODI. Langkah pertama, yaitu menentukan
multiplier dan dengan pedoman = untuk seluruh variabel
basis, sehingga = + . Variabel-variabel basisnya adalah
� , � , � � , � , � , � ,� dan � . Sisanya non basis.
Variabel basis terbanyak berada pada baris ke-1 dan kolom ke-4.
Pilih salah satu, misalkan baris ke-1, sehingga didefinisikan sebagai
0. Nilai multiplier yang lain sebagai berikut :
= + = + = = + = + = = + = + = = + = − + = = + = + = = + = + = − = + = + = −
Kemudian, nilai opportunity cost akan menentukan sel yang akan
menjadi variabel masuk. Nilai tersebut didapat melalui persamaan
= ( + ) − .
Opportunity cost pada seluruh variabel non basis adalah sebagai
= + − = (− + ) − = − = + − = (− + ) − = −
Opportunity cost sel 34 bernilai positif, artinya kemungkinan solusi
fisibel awal belum optimal sehingga perlu dilakukan realokasi dengan
menggunakan loop yang berawal dari sel 34. Diperoleh loop �+ → �− → �+ → �−. Loop tersebut melibatkan sel 33 dengan tanda (-), itu
artinya jika realokasi dilakukan maka akan mengakibatkan stok di sel 33
kurang dari stok semu �̃ = yang ditambahkan sebelumnya. Selain itu, realokasi juga akan mengakibatkan pemindahan beban sebanyak
min(�−, �− = , = dari sel 33 ke sel 13. Hal ini tidak mungkin dilakukan karena stok bersifat semu atausebenarnya tidak ada. Karena
tidak terdapat loop lain yang bisa dibuat dari sel 34 tanpa melibatkan sel
33, maka solusi fisibel yang diperoleh pada Tabel 3.11 sudah optimal.
b. � ∶
+ + + � + + + + � + +
+ + � + + + + � + � +
� + � + � + � � ∶
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
Permasalahan tersebut ditransformasikan pada Tabel 3.12.
Tabel 3.12 Ongkos Distribusi Bilangan Fuzzy
Ketesediaan
� 50
� 34
0 � 0 30
� 30
0 0 0 0 0 0 36
� � � � � 30
Permintaan
30 30 38 46 30 36
Masalah transshipment tersebut diselesaikan menggunakan metode Least
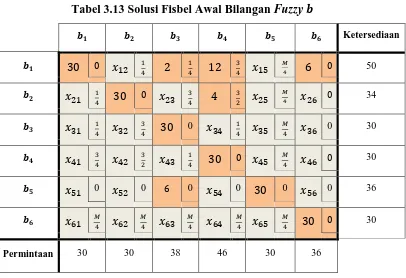
Cost dengan solusi fisibel awal seperti yang terlihat pada Tabel 3.13.
Tabel 3.13 Solusi Fisbel Awal Bilangan Fuzzy
Ketersediaan
� � � 50
� � � � � 34
� � 0 � � � � 0 30
� � � � � � 30
� 0 � 0 0 � 0 0 � 0 36
� � � � � � � � � � 30
[image:36.595.123.529.442.720.2]Iterasi 1
Langkah pertama, yaitu menentukan multiplier dan . Dari Tabel
3.13 diperoleh 11 variabel basis, yaitu � , � , � , � , � , � , � ,
� , � ,� dan � . Sisanya non basis.
Karena variabel basis terbanyak berada pada baris ke-1 maka
dimisalkan sebagai 0. Adapun Nilai multiplier yang diperoleh adalah
sebagai berikut :
= , = , = − , = − , = − , =
= , = − , = , = , = , =
Opportunity cost pada seluruh variabel non basis adalah sebagai
berikut :
= − , = −�− , = , = , = −�− ,
= , =− , =− , = , =−�,
= − , = − , =− , = − , = −�+ ,
= − , =− , = − , = , =− ,
= −�, = −�+ , =−�− , =−�− , = −�−
Terdapat opportunity cost yang non negatif, yaitu sel 21, 23, 26, 34, dan
54. Opportunity cost terbesar ada pada sel 26, maka realokasi terjadi pada
loop yang berawal dari sel 34. Diperoleh loop �+ → �− → �+ → �− (Lihat Tabel 3.14).
Pada Tabel 3.14 Nilai � terkecil dari variabel bertanda (-) adalah
4 pada sel 26. Alokasikan sebanyak 4 unit pada loop tersebut. Sehingga,
� = + = � = + =
� = − = � = − =
Variabel basisnya kini adalah � = , � = , � = , � = ,
� = , � = , � = , � = , � = ,� = dan � =
Tabel 3.14 Loop Iterasi 1 Least Cost, Bilangan Fuzzy
� + � � − 0
� � − � � �+
� � 0 � � � � 0 −
� � � � � �
−
� 0 � 0 0 � 0 0 � 0 −
� � � � � � � � � � 0
0 − 0
Iterasi 2
Variabel basis terbanyak dari hasil iterasi 1 berada pada baris ke-1, maka
dimisalkan sebagai 0. Dari sini bisa diperoleh nilai multiplier yang
lainnya (Lihat Tabel 3.15).
Tabel 3.15 Solusi Fisibel Iterasi 1 Least Cost, Bilangan Fuzzy
30 0 � � � 0
� 30 0 � � � � 4
� � 30 0 � � � � 0 −
� � � 30 0 � � � −
� 0 � 0 0 � 0 30 0 � 0 −
� � � � � � � � � � 30 0 0
[image:38.595.137.544.479.748.2]Nilai opportunity cost dari variabel non basisnya sebagai berikut :
= − , =−�− , = − , =− , = − ,
= −�− , = − , = − , = , = −�,
=− , = − , = −9, =− , =−�+ ,
=− , = − , =− , = , = − ,
=−�, = −�, = −�− , =−�− , =−�−
Opportunity cost yang paling positif ada pada sel 54. Loop yang dapat
dibuat adalah �+ → �− → �+ → �− . Realokasikan sebanyak
min �−, �− = min , = . Sehingga,
� = + = � = + =
� = − = � = − =
Variabel basisnya kini adalah � = , � = , � = , � = ,
� = , � = , � = , � = , � = ,� = dan � =
.
Iterasi 3
Variabel basis terbanyak dari hasil iterasi 2 berada pada baris ke-1, maka
dimisalkan sebagai 0. Dari sini bisa diperoleh nilai multiplier yang
lainnya (Lihat Tabel 3.16).
Dengan menggunakan nilai multiplier yang ada pada Tabel 3.16
diperoleh nilai opportunity cost dari variabel non basis, yaitu sebagai
berikut :
= − , =−�− , = − , =− , = − ,
= −�− , = − , = − , = , =−�− ,
=− , = − , = −9, =− , = −�,
=− , = − , =− , = , = − ,
Tabel 3.16 Solusi Fisibel Iterasi 2 Least Cost, Bilangan Fuzzy
30 0 � � �
� 30 0 � � � � 4
� � 30 0 � � � � 0
−
� � � 30 0 � � � −
� 0 � 0 � 0 0 0 � 0 −
� � � � � � � � � �
0 0
Opportunity cost yang non negatif ada pada sel 34. Loop yang dapat
dibuat adalah �+ → �− → �+ → �−. Loop tersebut melibatkan sel 33 dengan tanda (-), itu artinya jika realokasi dilakukan maka akan
mengakibatkan stok di sel 33 kurang dari stok semu �̃ = yang ditambahkan sebelumnya. Selain itu, realokasi juga akan mengakibatkan
pemindahan beban sebanyak min(�−, �− = , = dari sel 33 ke
sel 13. Hal ini tidak mungkin dilakukan karena stok yang dipindahkan
tersebut bersifat semu atau sebenarnya tidak ada. Oleh karena tidak
terdapat loop lain yang bisa dibuat dari sel 34 tanpa melibatkan sel 33,
maka solusi fisibel yang diperoleh pada Tabel 3.16 sudah optimal.
c. � ∶
+ + + � + + + + � + +
+ + � + + + + � + � + � +
� + � + � � ∶
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
[image:41.595.161.394.331.590.2]Permasalahan di atas digambarkan pada Tabel 3.17.
Tabel 3.17 Ongkos Distribusi Bilangan Fuzzy
Keterse-diaan
� 74
� 52
0 � 0 44
� 44
0 0 0 0 0 0 50
� � � � � 44
Permin
-taan
44 44 54 62 44 60
Masalah transshipment tersebut diselesaikan menggunakan metode Least
Cost dengan solusi fisibel awal seperti yang terlihat pada Tabel 3.18.
Selanjutnya adalah memeriksa apakah solusi fisibel awal yang
diperoleh pada Tabel 3.18 memang sudah optimal atau belum
Tabel 3.18 Solusi Fisbel Awal Bilangan Fuzzy
Ketersediaan
� � � 74
� � � � � 52
� � 0 � � � � 0 44
� � � � � � 44
� 0 � 0 0 � 0 0 � 0 50
� � � � � � � � � � 44
Permintaan 44 44 54 62 44 60
Iterasi 1
Menentukan multiplier dan . Dari Tabel 3.18 diperoleh 11 variabel
basis, yaitu � , � , � , � , � , � , � , � , � ,� dan � .
Sisanya non basis.
Karena variabel basis terbanyak berada pada baris ke-1 maka
dimisalkan sebagai 0. Adapun Nilai multiplier yang diperoleh adalah
sebagai berikut :
= , = , = − , = − , = − , =
= , = , = , = , = , =
Opportunity cost pada seluruh variabel non basis adalah sebagai
berikut :
= − , = −�− , = − , = − , =− ,
=−�− , =− , = − , = − , =−�,
= − , = − , = − , = − , = −�+ ,
= −�, = −�, =−�− , = −�− , = −�−
Terdapat opportunity cost yang non negatif, yaitu sel 54. Diperoleh loop
�+ → �− → �+ → �−. Realokasikan sebanyak min �−, �− =
min , = . Sehingga,
� = + = � = + =
� = − = � = − =
Variabel basisnya kini adalah � = , � = , � = , � = ,
� = , � = , � = , � = , � = , � = dan � = .
Iterasi 2
Variabel basis terbanyak dari hasil iterasi 1 berada pada baris ke-1, maka
dimisalkan sebagai 0. Dari sini bisa diperoleh nilai multiplier yang
[image:43.595.130.536.416.679.2]lainnya (Lihat Tabel 3.19).
Tabel 3.19 Solusi Fisibel Iterasi 1 Least Cost, Bilangan Fuzzy
� � � 0
� � � � �
� � 0 � � � � 0 −
� � � � � �
−
� 0 � 0 � 0 0 0 � 0 −
� � � � � � � � � � 0
Nilai opportunity cost dari variabel non basisnya sebagai berikut :
= − , = −�− , = − , = − , =− ,
= −�− , =− , = − , = − , = −�− ,
=− , = − , = − , = − , =−�,
=− , =− , = − , = − , =− ,
= −�, =−�, =−�− , = −�− , = −�−
Semua nilai opportunity cost bernilai non negatif, artinya solusi fisibel
pada Tabel 3.19 sudah optimal.
d. � ∶
+ + + + � + + + + � +
+ + + � + + + + � +
� + � + � + � + � � ∶
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
+ + + + + =
Permasalahan di atas digambarkan pada Tabel 3.20.
Masalah transshipment tersebut diselesaikan menggunakan metode
3.21. Selanjutnya adalah memeriksa apakah solusi fisibel awal yang
diperoleh pada Tabel 3.21 memang sudah optimal atau belum
[image:45.595.216.448.189.428.2]mengunakan metode MODI.
Tabel 3.20 Ongkos Distribusi Bilangan Fuzzy
Keterse-diaan
� 98
9 � 70
0 � 0 58
9 � 58
0 0 0 0 0 0 64
� � � � � 58
Permin
-taan
58 58 78 78 58 76
Tabel 3.21 Solusi Fisbel Awal Bilangan Fuzzy
Ketersediaan
� 20 � � 6 98
� � � 9 � � 12 70
� � 0 � � � � 0 58
� � 9 � � � � 58
� 0 � 0 0 � 0 0 � 0 64
� � � � � � � � � � 58
[image:45.595.129.537.437.717.2]Iterasi 1
Menentukan multiplier dan . Dari Tabel 3.21 diperoleh 11 variabel
basis, yaitu � , � , � , � , � , � , � , � , � ,� dan � .
Sisanya non basis.
Karena variabel basis terbanyak berada pada baris ke-1 maka
dimisalkan sebagai 0. Adapun Nilai multiplier yang diperoleh adalah
sebagai berikut :
= , = , = − , = − , = − , =
= , = , = , = , = , =
Opportunity cost pada seluruh variabel non basis adalah sebagai
berikut :
= − , = −�− , =− , = − , = − ,
=−�− , = − , = − , = − , = −�,
= − , = − , =− , = − , =−�+ ,
= − , = − , = − , = , = − ,
= −�, =−�, = −�− , =−�− , =−�− .
Terdapat opportunity cost yang non negatif, yaitu sel 54. Diperoleh
loop �+ → �− → �+ → �−. Realokasikan sebanyak min �− , �− = min , = . Sehingga,
� = + = � = + =
� = − = � = − =
Variabel basisnya kini adalah � = , � = , � = , � = ,
� = , � = , � = , � = , � = , � = dan
� = .
Iterasi 2
Variabel basis terbanyak dari hasil iterasi 1 berada pada baris ke-1,
maka dimisalkan sebagai 0. Dari sini bisa diperoleh nilai
Tabel 3.22 Solusi Fisibel Iterasi 1 Least Cost, Bilangan Fuzzy
� 20 14 � � 6 0
� � � 9 � � 12 0
� � 0 � � � � 0 −
� � 9 � � � �
−
� 0 � 0 � 0 0 0 � 0 −
� � � � � � � � � � 0
0 0 1 1 0
Nilai opportunity cost dari variabel non basisnya sebagai berikut :
= − , = −�− , =− , = − , = − ,
=−�− , = − , =− , = − , =−�− ,
= − , = − , =− , = − , = −�,
=− , =− , =− , = − , = − ,
=−�, = −�, = −�− , =−�− , =−�− .
Semua nilai opportunity cost bernilai non negatif, artinya solusi fisibel
pada Tabel 3.22 sudah optimal.
Selanjutnya adalah mengecek apakah variabel keputusan dari
masing-masing bilangan fuzzy , , , dan sudah memenuhi syarat :
− , − , −
Dari hasil perhitungan sebelumnya, seluruh variabel keputusan yang telah
Tabel 3.23 Seluruh Variabel Keputusan Pemrograman Linier Crisp
Sel − − −
11 16 30 44 58 14 14 14
13 6 8 10 20 2 2 10
14 4 10 12 14 6 2 2
16 0 2 8 6 2 6 -2
22 16 30 44 58 14 14 14
26 0 4 8 12 4 4 4
33 16 30 44 58 14 14 14
44 16 30 44 58 14 14 14
54 6 6 6 6 0 0 0
55 16 30 44 58 14 14 14
66 16 30 44 58 14 14 14
Variabel lain bernilai 0
Pada Tabel 3.23 terlihat bahwa − = − , artinya sel 16 tidak
memenuhi syarat bahwa − haruslah bernilai non negatif. Oleh karena
itu perlu dilakukan pemindahan beban untuk menambah beban pada agar
dapat memenuhi − . Jadi, pada sekurang-kurangnya harus
diberi tambahan beban sebanyak 2 unit. Perlu dicari terlebih dahulu loop yang
bisa memberikan beban tambahan ke . Loop tersebut dapat dilihat pada
Tabel 3.24.
Semua nilai pemindahan beban dari loop pada Tabel 3.24 berharga
positif. Itu artinya realokasi akan mengakibatkan kenaikan pada total ongkos
distribusi. Oleh karena itu loop yang harus dipilih adalah loop dengan nilai
pemindahan beban paling kecil agar kenaikan total ongkos distribusi
seminimum mungkin. Jadi, loop yang terpilih adalah loop dengan variabel
masuk � . Alokasikan sebanyak 2 unit ke dalam loop tersebut sehingga,
� = + = � = + =
Tabel 3.24 Loop yang Memberikan Penambahan Beban pada
Variabel
Masuk Loop
Nilai Pemindahan Beban
� �+ → �− → �+ → �− → �+ − + − =
� �+7 → �− → �+ → �− → �+7 − + − =
� �+9 → �− → �+ → �− → �+7 9− + − =
� �
+�
→ �− → �+ → �− → �+
→ �− → �+�
�
− + − + − =�−
� �+� → �− → �+ → �− → �+� �− + − =�
� �+�
→ �− → �+ → �− → �+� �− + − =�−
� �+� → �− → �+ → �− → �+� �− + − =�−
Tabel 3.25 Variabel Keputusan Hasil Pengecekan
Sel − − −
11 16 30 44 56 14 14 12
13 6 8 10 20 2 2 10
14 4 10 12 14 6 2 2
16 0 2 8 8 2 6 0
21 0 0 0 2 0 0 2
22 16 30 44 58 14 14 14
26 0 4 8 10 4 4 2
33 16 30 44 58 14 14 14
44 16 30 44 58 14 14 14
54 6 6 6 6 0 0 0
55 16 30 44 58 14 14 14
66 16 30 44 58 14 14 14
[image:49.595.148.522.443.749.2]Langkah 5
Substitusikan variabel keputusan crisp yang diperoleh ke variabel fuzzy
�̃ = , , ,
�̃ = , , , , �̃ = , , , , �̃ = , , , , �̃ = , , , , �̃ = , , , , �̃ = , , , , �̃ = , , , , �̃ = , , , , �̃ = , , , , �̃ = , , , , �̃ = , , , , �̃ = , , , .
Langkah 6
Menentukan total ongkos fuzzy minimum dengan mensubstitusikan nilai dari
�̃ ke ∑=+ ∑ =+ ̃ �̃ .
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
̃ �̃ = , , , , , , = , , ,
, , , Dari hasil yang diperoleh, maka pengiriman yang terjadi antara lain :
a. Dari � ke � dikirim sebanyak �̃ = , , ,
b. Dari � ke � dikirim sebanyak �̃ = , , ,
Dengan total ongkos pengiriman fuzzy sebesar , , , . Dengan kata
lain, total ongkos pengiriman minimum sebesar 8, maksimum 166, rata-rata
Prawitasari, Elyine R. 2014
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT MENGGUNAKAN METODE MEHAR
Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
BAB V PENUTUP
5.1 KESIMPULAN
Dari hasil penelitian di Bab IV dan penyelesaian studi kasus di Bab III dapat
ditarik kesimpulan sebagai berikut :
1. Cara mencari solusi optimal masalah fuzzy transshipment menggunakan
metode Mehar antara lain dengan mengkonversi model fuzzy dari masalah
tersebut ke model crisp dengan memanfaatkan fungsi rangking, kemudian
menyelesaikan model crisp yang diperoleh dengan menggunakan metode
penyelesaian masalah transportasi yang sudah ada, dalam penelitian ini
diselesaikan mengunakan metode Least Cost dan MODI. Metode Mehar
sendiri merupakan metode baru yang diperkenalkan oleh Amit Kumar dkk
untuk menyelesaikan masalah Fuzzy Transshipment, fungsi tujuan dan
syaratnya bervariabel fuzzy, melalui pendekatan pemrograman linier tanpa
menggunakan teknik � − � (Chanas, 1996). Metode ini mudah dipahami
karena pengerjaannya memanfaatkan metode pemecahan masalah
transshipment yang sudah ada dan variabel keputusan yang diperoleh pun
selalu bernilai positif sehingga mudah untuk diinterpretasikan.
2. Pembuatan program aplikasi penyelesaian masalah transshipment dilakukan
dengan menerjemahkan langkah-langkah pada metode Mehar ke dalam bahasa
pemrograman Delphi7. Sebelumnya dirancang terlebih dahulu tampilan dari
program aplikasi yang akan dibuat sehingga dapat ditentukkan prosedur apa
saja yang diperlukan.
3. Membandingkan hasil penyelesaian masalah fuzzy transshipment yang
dikerjakan secara manual dan dikerjakan menggunakan program aplikasi, dapat
disimpulkan bahwa program aplikasi yang dibuat dapat berjalan dengan baik
dan apa yang diharapkan dari pembuatan program tersebut, yaitu kecepatan
5.2 SARAN
Untuk lebih mengoptimalkan hasil dari penelitian ini, beberapa hal yang
dapat dikembangkan antara lain :
1. Cara pengoperasian program dipermudah lagi agar pengguna dapat
mengoperasikannya dengan lebih mudah.
2. Algoritma program untuk mencari solusi dan model crisp yang telah dibentuk
akan lebih baik bila menggunakan metode simpleks yang telah direvisi. Penulis
menilai hal ini akan lebih memudahkan pengguna untuk mengoperasikan
program.
3. Dapat dilakukan pengembangan program untuk masalah Fuzzy Transshipment
dengan lebih dari 2 sumber dan 2 tujuan.
4. Dapat dilakukan penerapan Metode Mehar pada masalah Fuzzy Transshipment
yang terjadi di kehidupan sehari-hari, menggunakan data lapangan dari studi
Prawitasari, Elyine R. 2014
PROGRAM APLIKASI PENYELESAIAN MASALAH FUZZY TRANSSHIPMENT MENGGUNAKAN METODE MEHAR
Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
DAFTAR PUSTAKA
Dimyati T.T. dan Dimyati A. 1992. Operation Research : Model-model Pengambilan Keputusan, CV. Sinar Baru Bandung : Bandung.
Kumar, A, Kaur, A. dan Gupta, A. 2011. Fuzzy Linear Programming Approach for Solving Fuzzy Transportation Problems with Transshipment. J. Math. Model Algor. 10, 163-180.
Kusumadewi S. dan Hari P. 2010 Aplikasi Logika Fuzzy untuk Pendukung Keputusan. Graha Ilmu : Yogyakarta.
Kadir, A. 2001. Dasar Pemrograman Delphi 5.0 Jilid 1. ANDI : Yogyakarta.
Munir, R. 2011. Algoritma dan Pemrograman dalam Bahasa Pascal dan C Edisi Revisi. Informatika : Bandung.
Siswanto. 2007. Operation Research Jilid 1. Erlangga : Jakarta.
Suarga. 2006. Algoritma dan Pemrograman. Penerbit ANDI : Yogyakarta.
Taha, H.A. 1996. Riset Operasi Jilid 1. Binarupa Aksara : Jakarta.