Estimasi Parameter Model Regresi Spline

(1)

Estimasi Parameter Model Regresi Spline

Estimation of Parameter Spline Regression Model

M. Fathurahman

Program Studi Statistika FMIPA Universitas Mulawarman

e-mail : mailfathur@yahoo.com

Abstract

Regression analysis is frequently used to knowledge influence of explanatory variables on the response variable. There are two approaches in regression, parametric and nonparametric approach. If the information of regression curve is not available, the nonparametric regression approach can be applied. This approach does not depend on any regression curve assumption. Spline regression model is more flexible and one of the models with nonparametric approach, which is a modification from polynomial segment function. The research objective was to determine estimator of parameter spline regression model using least square method and applied to case of the effect tryout score on UNAS score of SMKN 1 Samarinda students.

The results showed estimator of parameter spline regression model with least squares method is



x~



x~

y~

x~

f

~

T 1 T     





and spline regression model to knowledge influence of tryout score on UNAS

score of SMKN 1 Samarinda students is,









1,996275

0,7930463

2 ,

09659

(

7 ,

30 )

_

ˆ

x

y

2,657039

(

x



7 ,

58 )

_



0,8548267

(

x



8 ,

19 )

_

Based on this model, the effect of tryout score on UNAS score of SMKN 1 Samarinda students is 80.12 percent with mean square error, 7.23 percent.

Keywords : Regression, spline, nonparametric approach, score of tryout and UNAS.

PENDAHULUAN

Analisis regresi merupakan salah satu teknik analisis data dalam statistika yang paling banyak digunakan untuk mengetahui hubungan antara variabel-variabel prediktor dengan variabel responnya (Kutner, Nachtsheim dan Neter, 2004). Untuk menjelaskan hubungan antara variabel prediktor dengan variabel respon digunakan sebuah kurva, yang disebut dengan kurva regresi. Kurva ini dapat diperoleh dengan dua pendekatan, yaitu pendekatan regresi parametrik dan regresi nonparametrik. Pendekatan regresi parametrik digunakan jika bentuk kurva regresi diketahui. Kemudian kurva regresi secara matematis diwakili oleh suatu bentuk model. Model dengan pendekatan parametrik mempunyai keterbatasan untuk

mengestimasi perubahan pola data yang tidak diharapkan. Jika asumsi pemodelan dengan pendekatan parametrik tidak terpenuhi, maka kurva regresi dapat diestimasi menggunakan pendekatan nonparametrik.

Salah satu model regresi dengan pendekatan nonparametrik yang sangat sering digunakan untuk melakukan estimasi terhadap kurva regresi adalah regresi spline. Beberapa kelebihan dari regresi spline diantaranya adalah dapat menyesuaikan diri secara efektif terhadap karakteristik lokal dari data (Budiantara dan Subanar, 1997), dapat menggambarkan perubahan (piecewise) pola perilaku dari fungsi pada sub interval tertentu (Eubank,1988) dan dapat digunakan untuk

mengatasi pola data yang menunjukkan naik/turun yang tajam dengan bantuan titik-titik knot, serta kurva yang dihasilkan relatif mulus (Hardle, 1990).

Berdasarkan uraian di atas, maka penelitian ini mengkaji estimasi parameter model regresi spline yang difokuskan pada knot dan orde, yang penyelesaiannya dengan menggunakan optimasi

least square. Kemudian penelitian ini dibatasi

pada estimasi parameter model regresi spline linier untuk satu variabel prediktor dengan satu titik knot, dua titik knot dan tiga titik knot. Kemudian untuk memilih model regresi spline terbaik adalah menggunakan kriteria nilai generalized cross

validation (GCV) terkecil.

ANALISIS REGRESI

Istilah “regresi” pertama kali dikemukakan oleh Sir Francis Galton (1822-1911), seorang antropolog dan ahli meteorologi terkenal dari Inggris. Dalam makalahnya yang berjudul “Regression towards

mediocrity in hereditary stature”, yang dimuat

dalam Journal of the Anthropological Institute, volume 15, halaman 246 sampai dengan 263, tahun 1885. Galton menjelaskan bahwa biji keturunan tidak cenderung menyerupai biji induknya dalam hal besarnya, namun lebih medioker (lebih mendekati rata-rata) lebih kecil daripada induknya kalau induknya besar dan lebih besar daripada

(2)

induknya kalau induknya sangat kecil (Draper dan Smith, 1972).

Dalam analisis regresi, diperlukan suatu model yang digunakan untuk mengetahui hubungan antara variabel tidak bebas (respon) dengan satu atau lebih variabel bebas (prediktor) dan untuk melakukan peramalan terhadap variabel respon. Model regresi dapat diperoleh dengan melakukan estimasi terhadap parameter-parameternya menggunakan metode tertentu. Adapun metode yang dapat digunakan untuk mengestimasi parameter model regresi, khususnya parameter model regresi linier (sederhana dan berganda) adalah dengan metode kuadrat terkecil (least square) dan metode kemungkinan maksimum (maximum likelihood) (Kutner et.al, 2004).

Regresi Nonparametrik

Regresi nonparametrik merupakan suatu teknik analisis data dalam statistika yang dapat menjelaskan hubungan antara variabel prediktor dengan variabel respon yang tidak diketahui bentuk fungsinya karena sebelumnya tidak ada informasi tentang bentuk fungsi tersebut dan hanya diasumsikan mulus (smooth) dalam arti termuat dalam suatu ruang fungsi tertentu sehingga regresi nonparametrik sangat mempertahankan fleksibilitasnya (Eubank, 1988).

Secara umum bentuk model regresi nonparametrik dapat ditulis seperti pada persamaan (1) berikut ((Eubank 1988) dan (Wahba 1990)).







f

(x

)

y

(1) dengan:

y

= Variabel respon.

)

(x

f

= Fungsi regresi nonparametrik yang memuat variabel prediktor.



= Faktor gangguan yang tidak dapat dijelaskan oleh model yang disebut dengan error, yang diasumsikan sebagai variabel random dengan mean nol, variansi

σ

2.

Regresi Spline

Potongan polinomial memainkan peranan penting dalam teori statistika. Potongan polinomial mempunyai sifat fleksibel dan efektif untuk menangani sifat lokal atau data (Eubank, 1988). Salah satu potongan polinomial yang penting adalah polinomial spline. Spline yang didasarkan pada suatu persoalan optimasi dikembangkan oleh Wahba (1990). Spline muncul sebagai suatu solusi dari persoalan regresi polinomial yang belum mampu menangani suatu fungsi yang smooth. Berdasarkan hal ini maka muncul modifikasi polinomial menjadi polinomial spline.

Bentuk model regresi spline berorde m adalah seperti pada persamaan (2) berikut (Eubank, 1988).

i p j m jk j m r s k k m j r j r j i

X

K

y

j





_



















 



        1 1 1 1 1 ) 1 .( . 0

(

)

Untuk i = 1, 2, …, n; j = 1, 2, …, p dan k = 1, 2, …,

s

_j

dengan fungsi truncated ,



















   jk j jk j m jk j m jk j

_X

_K

K

X

K

X

K

X

;

0 ;

)

(

)

(

1 1 0



,



_j._r,



_j_.(_m_₁_)._k = Parameter model yang akan diestimasi, dan

0



= Intersep

r j.



= Slope pada variabel

X

_j dengan

orde ke-r

k m j.( 1).



= Slope pada variabel

X

_j

truncated knot ke-k pada spline

berorde m

j

X

= Variabel prediktor ke-j

jk

K

= Knot ke-k pada variabel

X

_j

j = 1, 2, …, p dan k = 1, 2, …,

s

_j

j

s

= Banyaknya knot dalam variabel prediktor ke-j

Jika j = 1, maka dari persamaan (2) diperoleh bentuk umum model regresi spline berorde m untuk satu variabel prediktor, yaitu seperti pada persamaan (3) berikut (Eubank 1988).

i m r s k m k k m r r i j

K

X

y

























      1 1 1 1 ) 1 ( 0

(

)

Estimasi Parameter

Jika dalam suatu masalah parameter

θ

tidak diketahui, maka harus mengestimasinya dengan menggunakan data sampel, hal ini dapat dilakukan melalui statistik, atau dapat dikatakan statistik adalah kuantitas yang dihitung dari pengamatan sampel. Untuk menentukan statistik mana yang paling sesuai perlu dipertimbangkan sifat-sifat baik suatu estimator antara lain: tak bias, efisien, konsisten dan cukup (Hogg dan Craig, 1978). Metode Kuadrat Terkecil

Metode kuadrat terkecil (Least Square) adalah salah satu metode yang paling sering digunakan dalam melakukan estimasi terhadap parameter model regresi. Prinsip dari metode kuadrat terkecil adalah meminimumkan error yang dihasilkan oleh

(3)

model sehingga diharapkan model regresi menjelaskan data dengan baik. Mengingat error yang dihasilkan model regresi pada tiap amatan dapat bernilai negatif dan positif, maka untuk menghindari penjumlahan yang bernilai negatif, dicari jumlah dari kuadrat nilai error (Draper dan Smith, 1992).

Parameter Penghalus

Ada beberapa metode yang sangat populer untuk memilih parameter penghalus

λ

optimal antara

lain adalah metode Generalized Cross Validation (GCV). Dalam pemilihan

λ

_optimal, kriteria GCV dapat dihitung berdasarkan persamaan (4) berikut

((Wahba, 1985, Eubank 1988))



₁



2

)

H

~

I

~

(

tr

n

)

(

MSE

)

(

GCV

 

_







(4) dengan

tr

(

H

~

_

)



n

dan,

I

~

= Matriks Identitas 

H

~

=

X

~

_

(

X

~

T_

X

~

_

)

1

X

~

T_ 

X

~

= Matriks disain dari model yang membentuk penduga

~

f

_ dengan



yang optimal. n = ukuran sampel

Berdasarkan metode GCV, maka dapat dipilih model regresi spline terbaik, yaitu model yang memiliki nilai GCV (λ) terkecil (Eubank 1988). Nilai Ujian Nasional Sekolah Menengah Kejuruan

Nilai Ujian Nasional (UNAS) Sekolah Menengah Kejuruan (SMK) adalah nilai yang diperoleh siswa setelah melakukan kegiatan pembelajaran selama tiga tahun di jenjang SMK diselenggarakan secara nasional yang meliputi tiga mata uji, yaitu Matematika, Bahasa Inggris dan Bahasa Indonesia. Salah satu faktor yang diduga berpengaruh terhadap nilai UNAS SMK adalah Nilai Tryout (Sutarsi, 2008). Nilai tryout adalah penilaian yang dilaksanakan secara terpadu dengan kegiatan pembelajaran atau terpisah. Penilaian jenis ini diharapkan mampu meningkatkan standar mengajar, semangat belajar, dan akuntabilitas. Hasil penilaian ini dapat digunakan sebagai umpan balik bagi peserta didik untuk mengetahui tingkat penguasaan materi sehingga memotivasi untuk memperbaiki hasilnya, masukan bagi guru dalam memperbaiki strategi pembelajarannya, dan acuan dalam menentukan peserta didik mencapai kompetensi dengan kecepatan belajar yang berbeda-beda meliputi tiga mata pelajaran yaitu Matematika, Bahasa Inggris dan Bahasa Indonesia.

METODE

Data yang digunakan dalam penelitian ini adalah diperoleh dari hasil penelitian (Sahrul, 2009). Kemudian variabel-variabel yang digunakan adalah rata-rata nilai tryout sebagai variabel prediktor (X) dan rata-rata nilai UNAS sebagai variabel respon (Y).

Adapun langkah-langkah analisis data dalam penelitian ini adalah sebagai berikut:

1. Mengidentifikasi pola hubungan antara variabel prediktor dengan variabel respon menggunakan

scatter plot.

2. Melakukan estimasi parameter model regresi spline linier (orde 2) untuk 1 knot, 2 knot dan 3 knot.

3. Menghitung nilai GCV (λ) untuk masing-masing model regresi spline yang diperoleh dari langkah 2.

4. Memilih model regresi spline terbaik berdasarkan titik knot optimal menggunakan kriteria GCV (λ) minimum.

5. Menghitung nilai koefisien determinasi (R2_{) dan}

Rata-rata kuadrat error (MSE) untuk model regresi spline terbaik

6. Menarik kesimpulan.

Dalam melakukan analisis dan pengolahan data pada penelitian ini, menggunakan bantuan software statistika Minitab 16 dan S-Plus 2000 (Venables dan Ripley, 1994).

HASIL DAN PEMBAHASAN

Identifikasi Pola Hubungan antara Variabel Prediktor dengan Variabel Prediktor

Untuk mengetahui hubungan antara variabel prediktor (nilai tryout) dengan variabel respon (nilai UNAS) secara visual dapat dilihat seperti pada Gambar 1 berikut.

TRYOUT U N A S S M K 10 9 8 7 6 5 9,5 9,0 8,5 8,0 7,5 7,0 6,5 6,0

Plot Nilai Tryout Terhadap Nilai UNAS SMK

Gambar 1. Plot hubungan antara nilai tryout dengan nilai UNAS

Berdasarkan Gambar 1, terlihat bahwa tidak ada kecenderungan dari nilai tryout terhadap nilai UNAS SMK membentuk pola tertentu dan ada

(4)

indikasi perubahan pola perilaku dari nilai tryout pada sub-sub interval tertentu. Oleh karena itu sulit digunakan model pendekatan regresi parametrik. Selanjutnya pola data akan didekati dengan menggunakan regresi nonparametrik spline. Estimasi Parameter Model Regresi Spline

Hasil estimasi parameter model regresi spline linier dengan satu variabel prediktor menggunakan metode least square adalah seperti diuraikan berikut ini.

Langkah pertama adalah menulis persamaan (3) dalam notasi vektor dan matriks seperti pada persamaan (5) berikut.

Y

~

=

X

~

1 ~

₁+

 

X

~

K

~

₂ +

~

(5)

[ n x 1] [ n x z ] [ z x 1 ] [ n x s ] [ s x 1 ] [ n x 1 ]

z = [ 1+(m-1) ] m=orde splines = Banyaknya knot dengan:

Y

~

             n y y y  2 1 ;

X

~

1 















   1 2 1 2 2 2 2 1 1 2 1 1

1

m n n n m m

x











; 1

~

                 1 2 1 0 m      ;

~

             n     2 1 ;

~

₂                   n m m m ). 1 ( 2 ). 1 ( 1 ). 1 (



 ;

 

X

~

K

















         1 1 2 1 1 1 2 1 2 2 1 1 2 1 1 1 2 1 1 1 1

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

m s n m n m n m s m m m s m m

k

x

k

x

k

x

k

x

k

x

k

x

k

x

k

x

k

x











Kemudian persamaan matriks (5) dapat ditulis seperti persamaan (6) berikut.









X

~

Y

~

(6) dengan

X

~

=



X

~

1

 

X

~

K



dan



















2 1

~

. Berdasarkan persamaan (6) diperoleh









y~

x~

~

_, _untuk

_Y

~ 

_y~

_dan

_X

~ 

_x~

_.

Kemudian sesuai dengan metode least square, diperoleh,







 











~

y~

x~

~

y~

x~

~

_T T















y~

T

y~

T

x~

~

T

x~

T

y~

~

T

x~

T

x~

~

Karena keempat struktur pembentuk matriks

~

 ~

T



adalah dalam skalar, maka suatu matriks akan

bernilai sama dengan matriks kebalikannya. Sehingga diperoleh,













~

y~

2 ~

x~

y~

~

x~

~

T T T T T T

Untuk mendapatkan nilai terkecil dari fungsi

~

 ~

T



yang bersifat kuadratik, maka turunan pertamanya terhadap parameter yang diduga (



~

) disamakan dengan nol, yaitu:

 

₀

~

T T











0 ~

x~

2 y~

x~

2

T

_

T

_

_



y~

x~

~

x~

T

_

_

T

Apabila

x~

T

x~

bersifat nonsingular, yaitu mempunyai matriks invers, maka;

 

x~

y~

~

ˆ

b

~

_

_

_

T 1 T ₍₇₎

Dalam hubungannya dengan estimator kurva mulus

)

(x

f

, yang mempunyai



optimal, maka untuk memilih estimator

f

(x

)

yang terbaik diantara kelas estimator dengan menggunakan model regresi spline sebagai penduga kurva mulus

f

_, dilakukan penyesuaian persamaan (7) menjadi persamaan (8) berikut.



x~



x~

y~

~

ˆ

b

~

T 1 T      







(8)

dengan

x~

_adalah matriks disain dari model yang membentuk estimator

~

f

_ dengan



yang optimal. Fungsi estimatornya, adalah :

  



b

~

x~

f

~



x~



x~

y~

x~

f

~

T 1 T      



(9)

Persamaan (9) dapat juga ditulis seperti persamaan (10) berikut.

Y

~

H

~

f

~

 



(10)

dengan

H

~

_matriks yang bersifat simetris, definit non-negatif dan idempoten.

Berdasarkan estimasi parameter model regresi spline menggunakan metode least square, diperoleh estimator

f

~

_



x~

_



x~

_T

x~

_



1

x~

_T

y~

.

Aplikasi Estimasi Model Regresi Spline Pada Kasus Nilai UNAS

Setelah dilakukan estimasi parameter model regresi spline yang menyatakan hubungan nilai

tryout dengan nilai UNAS dengan metode kuadrat

(5)

Tabel 1. Hasil estimasi parameter model regresi spline untuk satu titik knot

Parameter Estimasi 0



3,689801 1



0,5312931 2



0,1627495

Berdasarkan Tabel 1, diperoleh model regresi spline dengan satu titik knot (K = 7,82) adalah seperti pada persamaan (11) berikut.

     3,689801 0,5312931 0,1627495 ( 7,82) ˆ x x y

Tabel 2. Hasil estimasi parameter model regresi spline untuk dua titik knot



1,982151 1



0,7952671 2



-4,474847 3



4,437148

Berdasarkan Tabel 2, diperoleh model regresi spline dengan dua titik knot (K1 = 7,35

dan K2= 7,44) adalah seperti pada persamaan (12)

berikut.         ) 44 , 7 ( 437148 , 4 ) 35 , 7 ( 474847 , 4 7952671 , 0 982151 , 1 ˆ x x x y

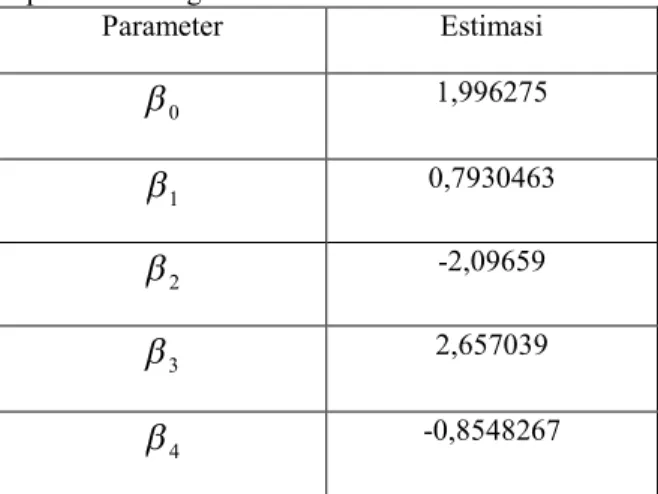
Tabel 3. Hasil estimasi parameter model regresi spline untuk tiga titik knot



1,996275 1



0,7930463 2



-2,09659 3



2,657039 4



-0,8548267

Berdasarkan Tabel 3, diperoleh model regresi spline dengan tiga titik knot (K1= 7,30, K2= 7,58

dan K3= 8,19) adalah seperti pada persamaan (13)

berikut.









1,996275

0,7930463

2 ,

09659

(

7 ,

30 )

_

ˆ

x

y

 





2,657039

(

x

7 ,

58 )

0,8548267

(

x

8 ,

19 )

Setelah diperoleh model regresi spline pada persamaan (11), (12) dan (13), maka selanjutnya dilakukan pemilihan model terbaik dari ketiga model tersebut menggunakan nilai GCV (λ) terkecil. Hasil yang diperoleh adalah seperti pada Tabel 4 berikut.

Tabel 4. Nilai GCV (λ) model regresi spline Jumlah

knots (K)

Letak titik knots (K) Nilai GCV 1 2 3 Linier 1 7,82 - - 0,0936 2 7,35 7,44 - 0,08344 3 7,30 7,58 8,19 0,0801

Berdasarkan Tabel 4, nilai GCV (λ) terkecil adalah sebesar 0,08010432 berkaitan dengan model regresi spline dengan tiga titik knot berada pada titik-titik knot K1= 7,30, K2= 7,58 dan K3= 8,19.

Model regresi spline ini diberikan oleh persamaan (14) berikut.     1,996275 0,7930463 2,09659( 7,30)_ ˆ x x y  





2,657039

(

x

7 ,

58 )

0,8548267

(

x

8 ,

19 )

Selanjutnya persamaan (14) dapat juga ditulis dalam bentuk seperti persamaan (15) berikut.

                  19 , 8 , 498669 , 0 162057 , 4 19 , 8 58 , 7 , 353495 , 1 2,83897 -58 , 7 30 , 7 , 30354 , 1 30138 , 17 30 , 7 , 0,7930463 1,996275 ˆ x x x x x x x x y

Berdasarkan persamaan (14) dan (15), diperoleh nilai koefisien determinasi (R2_{) sebesar 0,8012 atau}

80,12% dan MSE sebesar 0,0723. Hal ini menunjukkan bahwa nilai tryout mampu menerangkan sebesar 80,12% terhadap nilai UNAS atau dapat dikatakan bahwa pengaruh nilai tryout terhadap nilai UNAS siswa SMKN 1 Samarinda adalah sebesar 80,12%. Kemudian nilai MSE minimum menunjukkan bahwa nilai taksiran mendekati nilai sebenarnya.

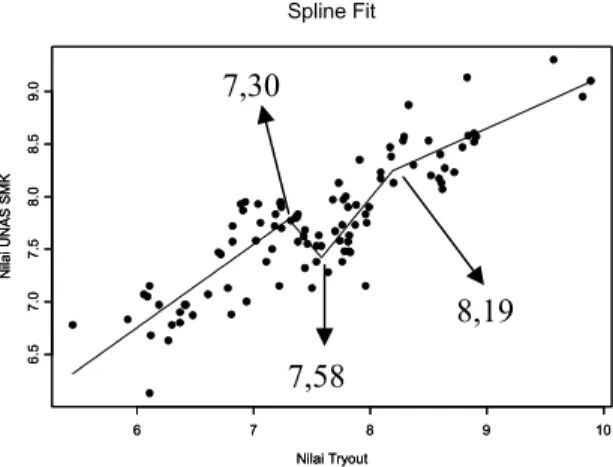
Bentuk kurva regresi spline berdasarkan persamaan (14) dan (15) adalah seperti pada Gambar 2 berikut.

(6)

Nilai Tryout N ila iU N A S S M K 6 7 8 9 10 6 .5 7 .0 7 .5 8 .0 8 .5 9 .0 Spline Fit Nilai Tryout N ila iU N A S S M K 6 7 8 9 10 6 .5 7 .0 7 .5 8 .0 8 .5 9 .0

Gambar 2. Kurva regresi spline yang menyatakan hubungan antara nilai tryout dengan nilai UNAS

KESIMPULAN

Berdasarkan hasil dan pembahasan, maka dapat disimpulkan bahwa model regresi nonparametrik spline yang menyatakan hubungan antara nilai

tryout dengan nilai UNAS siswa SMKN 1

Samarinda adalah:









1,996275

0,7930463

2 ,

09659

(

7 ,

30 )

_

ˆ

x

y

 





2,657039

(

x

7 ,

58 )

0,8548267

(

x

8 ,

19 )

Dari model regresi spline ini dapat diketahui bahwa pengaruh nilai tryout terhadap nilai UNAS siswa SMKN 1 Samarinda adalah sebesar 80,12%.

DAFTAR PUSTAKA

Budiantara, I.N. dan Subanar, 1997, Regresi Spline dan Permasalahannya, Berkala Penelitian Pascasarjana Universitas Gadjah Mada Yogyakarta, 10, 111-127.

Draper and Smith, 1992, Analisis Regresi Terapan, PT Gramedia Pustaka Utama, Jakarta.

Eubank,R., 1988, Spline Smoothing and

Nonparametric Regression, Marcel Dekler,

New York.

Hardle, W. 1990. Applied Nonparametric

Regression. Cambridge, University Press.

Hogg, R.V. and Craig, A.T., 1978, Introduction to

Mathematical Statistics, Macmilan Publishing

Co., Inc, New York.

Kutner, M.H., Nachtsheim, C.J. dan Neter, J. 2004.

Applied Linear Regression Models. New York:

McGraw-Hill/Irwin.

Sahrul. 2009. Pendekatan Regresi Spline untuk Memodelkan dan Mengetahui Faktor-faktor yang Mempengaruhi Nilai Ujian Nasional Siswa Sekolah Menengah Kejuruan Negeri 1 Samarinda. Skripsi. Program Studi Statistika FMIPA Universitas Mulawarman, Samarinda. Sutarsi, Sri. 2008. “Pendekatan Regresi Spline

Untuk Memodelkan Nilai UNAS Siswa SMK Negeri 3 Buduran Sidoarjo”. Tesis. Mahasiswa Jurusan Statistika FMIPA ITS, Surabaya. Venables, W.N. dan Ripley, B.D., 1994, Modern

Applied Statistics with S-Plus, Spinger-Verlag,

New York.

Wahba, G., 1985, A Comparation of GCV and GML for Choosing the Smoothing Parameter in The Generalized Smoothing Problem, The

Annals of Statistics, 13, 1378-1402.

Wahba, G., 1990, Spline Models for Observational

Data, SIAM, Philadelphia.

7,30

7,58