BAB 2
LANDASAN TEORI
2.1 Penjadwalan Iklan
Penjadwalan adalah proses penyusunan menentukan jadwal yang tepat terhadap suatu pekerjaan untuk mencapai suatu tujuan tertentu terhadap sumber daya yang tersedia sesuai dengan constraint yang harus dipenuhi (Soraya, 2007). Penjadwalan iklan adalah masalah menempatkan waktu dan ruangan kepada sejumlah iklan pada sela-sela waktu acara dengan memperhatikan sejumlah aturan yang berhubungan dengan kapasitas dan lokasi dari ruang yang tersedia, waktu bebas yang diperlukan dan sejumlah aturan lain yang berkaitan dengan toleransi untuk pemasang iklan.
Periklanan merupakan alat komunikasi untuk menyampaikan pesan mengenai barang-barang, jasa atau ide-ide yang ditujukan kepada khalayak ramai yang merupakan calon pembeli dari produk atau jasa tersebut. Periklanan dapat mempengaruhi konsumen sehingga timbul rasa untuk melakukan pembelian. Jadi periklanan mempunyai peranan penting dalam meningkatkan volume penjualan. Banyak pengertian mengenai periklanan yang dikemukakan oleh para ahli dan kebanyakan orang percaya bahwa periklanan bekerja dengan mengirimkan suatu pesan lewat suatu media cetak maupun elektronika akan diperoleh jumlah konsumen yang cukup besar dalam waktu yang tidak begitu lama. Namun dalam masyarakat yang komunikatif, pesan yang disampaikan oleh media promosi terbentur oleh kesadaran, pengertian dan tindakan konsumen untuk melakukan pembelian. Sehingga perusahaan melaksanakan kegiatan periklanan karena mempunyai peranan yang cukup besar bagi kegiatan penjualan.
wilayah yang luas. Radio merupakan sarana handal untuk menjangkau orang yang mungkin tidak mempunyai akses media yang lain, radio dapat menjangkau orang-orang yang buta huruf yang tidak dapat membaca surat kabar, dan radio merupakan media yang dapat menjangkau hingga kepelosok daerah. Radio berfungsi sebagai sarana informasi, komunikasi, pengetahuan dan pendidikan serta hiburan yang mempunyai peran cukup penting dalam menyampaikan berita tentang perkembangan nasional maupun internasional.
Terkait dengan pangsa pasar dan basis konsumen, merek dengan pangsa pasar yang tinggi pada umumnya membutuhkan anggaran biaya periklanan yang lebih rendah guna mempertahankan posisinya. Itulah kenapa banyak perusahaan atau instansi beriklan melalui media radio, karena radio adalah media auditif yang lebih mudah untuk mengingat apa yang didengar pada setiap kesempatan.
Radio Suara Medan 94.7 hadir sebagai salah satu media di kota Medan yang memanjakan stakeholder dalam pemenuhan kebutuhan beriklan dan berpromosi, secara umum gambaran singkat tentang Radio Medan dapat dijelaskan dalam uraian singkat berupa karakteristik radio, yaitu: Efficient Value.
Radio adalah media beriklan yang ekonomis dari sisi pembiayaan dan efektif.
Flexibility Value. Radio adalah media yang bersifat mobile, karena bisa didengar
dalam setiap kesempatan, kapanpun dan di manapun. Real Time Value. Radio adalah media yang paling unggul dalam kecepatan penyampaian informasi, baik dalam penyampaian hiburan dan komersial. Customize Value. Radio adalah media yang mudah untuk mengemas suatu penyampaian pesan dalam bentuk siaran yang variatif dan kreatif sesuai keinginan dan kebutuhan pemasang iklan. Ada beberapa produk iklan yang disajikan oleh Radio Medan dalam memanjakan pemasang iklan, yaitu dalam bentuk:
a. Loose Spot, adalah produk iklan yang dibuat dengan merekam suara orang
yang membaca pesan tertentu yang ingin disampaikan dan diperindah lagi dengan musik atau sound effect lainnya, di mana pesan yang disampaikan antara lain adalah jadwal kegiatan, jenis produk yang ditawarkan, info harga hingga bagaimana dan di mana produk tersebut bisa dibeli atau didapatkan oleh konsumen.
permainan atau games yang terkait erat dengan produk yang dipromosikan, dengan jaminan mendapatkan hadiah-hadiah tertentu, dengan keterlibatan ini pemasang iklan jenis ini berharap agar brand-nya diposisikan disekitar nilai-nilai dan kebutuhan sosial.
c. Lalu Time Signal, merupakan jenis iklan tanda waktu pada waktu atau jam tertentu yang dianggap strategis.
Ada pula sponsor program / Talk Show, dalam penerapannya di radio, praktisi radio menamakan program ini sebagai blocking time program, artinya adalah pembelian jam siaran dengan durasi tertentu, untuk diisi dengan program khusus yang dimiliki untuk tujuan kegiatan pemasaran. Jenis produk berupa Live Reportase, jenis produk ini adalah perpaduan antara siaran On-Air maupun Off-Air, di mana pemasang iklan menginginkan produknya lebih dikenal dimasyarakat dalam bentuk event tertentu yang disiarkan secara langsung melalui radio.
Dan yang terakhir adalah Adlibs Radio Program (ARP), merupakan iklan radio berupa teks tertulis (script) dibacakan dan diimprovisasi oleh penyiar radio dalam pola penyampaiannya. Pemasang iklan dimanjakan dengan pilihan waktu tayang iklan yang relatif menguntungkan dengan asumsi bahwa dalam jam tertentu merupakan capaian pendengar dalam jumlah banyak, dan berikut
2.2 Algoritma Genetika
Algoritma genetika pertama kali ditemukan oleh John Holland, itu dapat dilihat dalam bukunya yang berjudul Adaption in Natural and Artificial Systems pada tahun 1960-an d1960-an kemudi1960-an dikemb1960-angk1960-an bersama murid d1960-an rek1960-an kerj1960-anya di Universitas Michigan pada tahun 1960-an sampai 1970-an. Tujuan Holland mengembangkan Algoritma Genetika saat itu bukan untuk mendesain suatu algoritma yang dapat memecahkan suatu masalah, namun lebih mengarah ke studi mengenai fenomena adaptasi di alam dan mencoba menerapkan mekanisme adaptasi alam tersebut ke dalam sistem komputer (Fariza, 2006).
Algoritma Genetika sebagai cabang dari Algoritma Evolusi merupakan metode yang digunakan untuk memecahkan suatu pencarian nilai dalam sebuah masalah optimasi yaitu permasalahan-permasalahan yang tak linier (Mitsuo & Runwei, 2000).
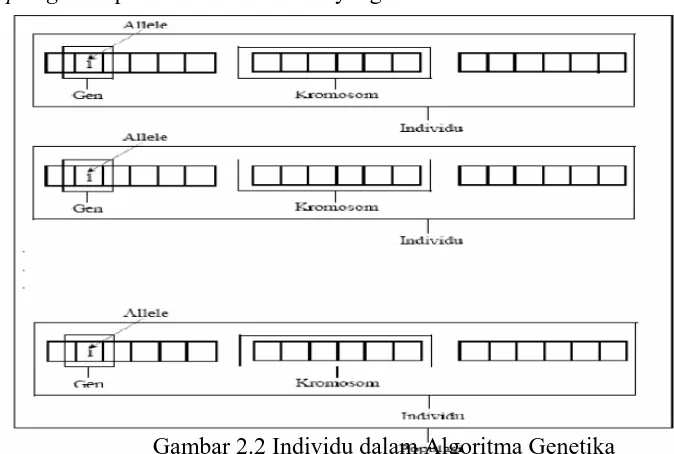
mekanisme seleksi alam dan ilmu genetik sehingga istilah-istilah pada Algoritma Genetik akan bersesuaian dengan istilah-istilah pada seleksi alam dan ilmu genetik. Sebuah solusi yang dibangkitkan dalam algoritma genetika disebut sebagai kromosom, sedangkan kumpulan kromosom-kromosom tersebut disebut sebagai populasi. Sebuah kromosom dibentuk dari komponen-komponen penyusun yang disebut sebagai gen dan nilainya dapat berupa bilangan numerik, biner, simbol ataupun karakter tergantung dari permasalahan yang ingin diselesaikan. Kromosom-kromosom tersebut akan berevolusi secara berkelanjutan yang disebut dengan generasi. Dalam tiap generasi kromosom-kromosom tersebut dievaluasi tingkat keberhasilan nilai solusinya terhadap masalah yang ingin diselesaikan (fungsi_objektif) menggunakan ukuran yang disebut dengan Fitness.
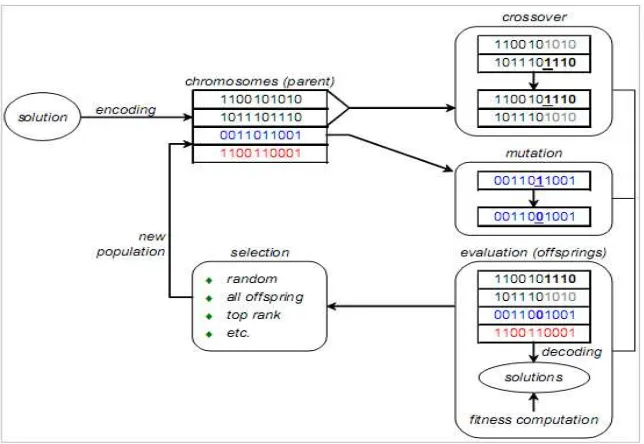
Secara umum tahapan proses dari algoritma genetika diperlihatkan pada Gambar 2.1. Seperti terlihat pada gambar kromosom merupakan representasi dari solusi. Operator genetika yang terdiri dari crossover dan mutasi dapat dilakukan kedua-duanya atau hanya salah satu saja yang selanjutnya operator evolusi dilakukan melalui proses seleksi kromosom dari parent (generasi induk) dan dari offspring (generasi turunan) untuk membentuk generasi baru (new population) yang diharapkan akan lebih baik dalam memperkirakan solusi optimum, proses iterasi kemudian berlanjut sesuai dengan jumlah generasi yang telah ditetapkan.
2.3 Struktur Umum Algoritma Genetika
Secara umum struktur dari suatu algoritma genetika dapat didefenisikan dengan langkah-langkah sebagai berikut:
1. Mulai
Proses algoritma genetika dimulai dengan membangun populasi random sebanyak n kromosom (sesuai dengan masalahnya).
2. Populasi Awal
Populasi awal ini dibangkitkan secara random sehingga didapatkan solusi awal. Populasi itu sendiri terdiri atas sejumlah kromosom yang merepresentasikan solusi yang diinginkan.
3. Evaluasi Fitness
Pada setiap generasi kromosom-kromosom akan dievaluasi berdasarkan tingkat keberhasilan nilai solusinya terhadap masalah yang ingin diselesaikan dengan menggunakan evaluasi Fitness. Proses evaluasi Fitness adalah melakukan evaluasi setiap Fitness f(x) dari setiap kromosom x pada populasi.
4. Pembentukan Generasi Baru
Proses ini dilakukan secara berulang sehingga didapatkan jumlah kromosom yang cukup untuk membentuk generasi baru (offspring) di mana generasi baru merupakan representasi dari solusi baru.
5. Seleksi
Untuk memilih kromosom yang akan tetap dipertahankan untuk generasi selanjutnya maka dilakukan proses seleksi. Proses seleksi dilakukan dengan memilih 2 kromosom
parent dari populasi berdasarkan Fitnessnya (semakin besar Fitnessnya, maka
semakin besar kemungkinannya untuk terpilih). 6. Crossover
Proses selanjutnya melakukan perkawinan silang sesuai dengan besarnya kemungkinan
perkawinan silang, orang tua (parent) yang terpilih disilangkan untuk membentuk anak
(offspring). Jika tidak ada crossover, maka anak merupakan salinan dari orang tuanya.
Jumlah kromosom dalam populasi yang mengalami perkawinan silang (crossover)
ditentukan oleh parameter yang disebut dengan probabilitas perkawinan silang (crossover
7. Mutasi
Proses mutasi dilakukan sesuai dengan besarnya kemungkinan mutasi yang telah ditentukan, anak dimutasi pada setiap lokus (posisi pada kromosom). Jumlah gen dalam populasi yang mengalami mutasi ditentukan oleh parameter yang disebut dengan probabilitas mutasi (mutationr probabilit, Pm). Setelah beberapa generasi akan dihasilkan, kromosom-kromosom yang nilai gennya konvergen ke suatu nilai tertentu merupakan solusi optimum yang dihasilkan oleh algoritma genetika terhadap permasalahan yang ingin diselesaikan.
8. Memenuhi syarat regenerasi
Apabila generasi baru memenuhi syarat regenerasi, maka proses akan selesai. Namun, apabila generasi baru tidak memenuhi syarat regenerasi, maka proses akan kembali ke evaluasi Fitness.
Parameter yang digunakan dalam algoritma genetika adalah:
1. Fungsi Fitness untuk menentukan tingkat kesesuaian individu tersebut. 2. Populasi jumlah individu pada setiap generasi.
3. Probabilitas terjadinya crossover pada setiap generasi. 4. Probabitas terjadinya mutasi pada setiap generasi. 5. Jumlah generasi yang akan dibentuk.
Golberg (1989) mengemukakan bahwa algoritma genetika mempunyai karakteristik-karakteristik yang perlu diketahui sehingga dapat dibedakan dari prosedur pencarian atau optimasi yang lain, yaitu:
1. Algoritma genetika dengan pengkodean dari himpunan solusi permasalahan berdasarkan parameter yang telah ditetapkan bukan parameter itu sendiri.
2. Algoritma genetika pencarian pada sebuah solusi dari sejumlah individu-individu yang merupakan solusi permasalahan bukan hanya dari sebuah individu.
3. Algoritma genetika informasi fungsi objektif (Fitness), sebagai cara untuk mengevaluasi individu yang mempunyai solusi terbaik, bukan turunan dari suatu fungsi.
4. Algoritma genetika menggunakan aturan transisi peluang, bukan aturan-aturan deterministik.
a. Gen
Gen merupakan nilai yang menyatakan satuan dasar yang membentuk suatu arti tertentu dalam satu kesatuan gen yang dinamakan kromosom.
b. Kromosom / Individu
Kromosom merupakan gabungan dari gen-gen yang membentuk nilai tertentu dan menyatakan solusi yang mungkin dari suatu permasalahan.
c. Populasi
Populasi merupakan sekumpulan individu yang akan diproses bersama dalam satu satuan siklus evolusi.
d. Fitness
Fitness menyatakan seberapa baik nilai dari suatu individu yang didapatkan.
e. Seleksi
Seleksi merupakan proses untuk mendapatkan calon induk yang baik.
f. Crossover
Crossover merupakan proses pertukaran atau kawin silang gen-gen dari dua induk
tertentu. g. Mutasi
Mutasi merupakan proses pergantian salah satu gen yang terpilih dengan nilai tertentu. h. Generasi
Generasi merupakan urutan iterasi di mana beberapa kromosom bergabung. i. Offspring
Offspring merupakan kromosom baru yang dihasilkan.
2.4 Teknik Pengkodean
Pengkodean adalah suatu teknik untuk menyatakan populasi awal sebagai calon solusi suatu masalah ke dalam suatu kromosom sebagai suatu kunci pokok persoalan ketika menggunakan algoritma genetika (Desiani, 2005). Agar dapat diproses melalui algoritma genetika, maka harus dikodekan terlebih dahulu ke dalam bentuk kromosom. Kromosom akan berisi informasi sejumlah gen yang mengkodekan informasi.
Ada beberapa jenis pengkodean yang dapat digunakan dalam algoritma genetika yaitu pengkodean biner (binary encoding), pengkodean nilai (value
encoding), pengkodean permutasi (permutation enocding), pengkodean pohon (tree
encoding).
2.4.1 Pengkodean Biner
Pengkodean ini merupakan pengkodean yang sering digunakan dan paling sederhana. Pada pengkodean biner setiap kromosom direpresentasikan dalam barisan bit 0 atau 1, seperti dapat dilihat pada tabel 2.1 berikut ini:
Tabel 2.1 Contoh Pengkodean Biner
Kromosom A 10101011010
Kromosom B 11000010111
Pengkodean biner memberikan banyak kemungkinan untuk kromosom walaupun dengan jumlah nilai-nilai yang mungkin terjadi dalam suatu gen sedikit (0 atau 1). Pengkodean ini sering tidak sesuai untuk beberapa masalah terkadang harus dilakukan pengkoreksian setelah operasi crossover dan mutasi.
2.4.2 Pengkodean Nilai
Tabel 2.2 Contoh Pengkodean Nilai
Kromosom A 1.345, 4.534, 7.654, 8.789
Kromosom B ABC, ADC, CBC, BCA
Kromosom C 1, 3, 4, 7, 5
Kromosom D Forward, backward, right, left
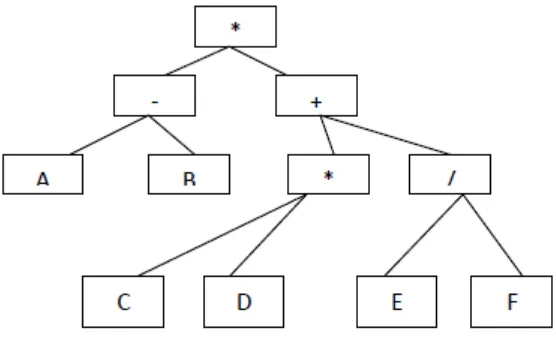
2.4.3 Pengkodean Pohon
Pengkodean pohon digunakan untuk menyusun program atau ekspresi didalam algoritma genetika. Dalam pengkodean pohon ini, setiap kromosom dinyatakan sebagai sebuah pohon dari setiap objek, seperti fungsi atau perintah dalam bahasa pemograman. Pengkodean pohon sangat baik dalam pembangunan sebuah program. Bahasa pemrograman LISP biasanya sering menggunakan pengkodean pohon, karena program didalamnya dapat direpresentasikan ke dalam bentuk ini, dan dapat dengan mudah di parse menjadi sebuah pohon, sehingga crossover dan mutasi dapat dilakukan dengan lebih mudah. Contoh pengkodean pohon dapat dilihat pada gambar dibawah ini: (*(-(ab))(+(*(CD))(/(EF))))
Gambar 2.3 Pengkodean Pohon
2.4.4 Pengkodean Permutasi
kromosom harus dilakukan untuk menjaga konsistensi representasi kromosom setelah proses crossover dan mutasi. Sebagai contoh, dapat dilihat pada tabel 2.3 berikut ini:
Tabel 2.3 Contoh Pengkodean Permutasi
Kromosom A 2 6 7 5 1 3 4 9 8 10
Kromosom B 10 5 4 9 7 1 3 2 6 8
2.5 Membangkitkan Populasi Awal dan Kromosom
Membangkitkan populasi awal adalah proses membangkitkan sejumlah individu atau kromosom secara acak atau melalui prosedur tertentu. Ukuran untuk populasi tergantung pada masalah yang akan diselesaikan dan jenis operator genetika yang akan diimplementasikan. Setelah ukuran populasi ditentukan, kemudian dilakukan pembangkitan populasi awal. Apabila ukuran populasi yang dipilih terlalu kecil, maka tingkat eksplorasi atas ruang pencarian global akan terbatas, walaupun arah menuju konvergensi lebih cepat. Apabila ukuran populasi terlalu besar, maka waktu akan banyak terbuang karena berkaitan dengan besarnya jumlah data yang dibutuhkan dan waktu ke arah konvergensi akan lebih lama (Goldberg, 1989).
2.6 Evaluasi Fitness
Suatu individu dievaluasi berdasarkan suatu fungsi tertentu sebagai ukuran performansinya. Didalam evolusi alam, individu yang bernilai Fitness tinggi yang akan bertahan hidup. Sedangkan individu yang bernilai Fitness rendah akan mati.
2.7 Seleksi
2.7.1 Seleksi Roda Roulette (Roulete Wheel Selection)
Metode seleksi roda roulette merupakan metode seleksi yang paling sederhana. Metode ini juga sering dikenal dengan nama stochastic sampling with replacement. Pada metode ini cara kerja seleksi berdasarkan nilai Fitness dari tiap individu, jadi individu yang memiliki nilai Fitness terbaik mempunyai kesempatan lebih besar untuk terpilih sebagai orang tua.
Langkah-langkah seleksi roulette wheel:
1. Dihitung nilai Fitness masing-masing individu (fi di mana i adalah individu ke 1 s/d ke-n )
2. Dihitung total Fitness semua individu ,
3. Dihitung Fitness relatif masing-masing individu
4. Dari Fitness relatif tersebut, dihitung Fitness kumulatifnya. 5. Dibangkitkan nilai random
6. Dari bilangan random yang dihasilkan, ditentukan individu mana yang terpilih dalam proses seleksi
2.7.2 Seleksi Ranking (Rank-based Fitness)
Seleksi ranking merupakan metode seleksi alternatif yang bertujuan untuk menghindari terjadinya hasil konvergen yang terlalu cepat dari proses seleksi orangtua. Pada metode seleksi ini, individu-indiviu pada tiap populasi diurutkan berdasarkan nilai Fitnessnya sehingga nilai yang diharapkan dari tiap individu bergantung kepada urutannya bukan hanya kepada nilai Fitnessnya.
2.7.3 Seleksi Turnamen (Turnament Selection)
Seleksi turnamen merupakan variasi dari seleksi roda roulette dan seleksi ranking. Pada metode seleksi ini, kromosom dipilih secara acak, kemudian diranking untuk diambil nilai Fitness terbaiknya.
2.8 Crossover
Crossover (pindah silang) adalah proses pemilihan posisi string secara acak dan
menghasilkan kromosom anak dari kombinasi materi-materi gen dua kromosom induk. Probabilitas crossover (Pc) ditentukan untuk mengendalikan frekuensi
crossover.
2.8.1 One Point Crossover
Pada crossover dilakukan dengan memisahkan suatu string menjadi dua bagian dan selanjutnya salah satu bagian dipertukarkan dengan salah satu bagian dari string yang lain yang telah dipisahkan dengan cara yang sama. Proses yang demikian dinamakan operator crossover satu titik.
Contoh:
Induk 1: 11001 | 010 Induk 2: 00100 | 111 Diperoleh:
Anak 1: 11001 | 111 Anak 2: 00100 | 010
2.8.2 Two Point Crossover
Proses crossover ini dilakukan dengan memilih dua titik crossover. Kromosom keturunan kemudian dibentuk dengan barisan bit dari awal kromosom sampai titik
crossover pertama disalin dari orangtua pertama, bagian dari titik crossover pertama
dan kedua disalin dari orangtua kedua, kemudian selebihnya disalin dari orangtua pertama lagi.
Contoh:
Induk 1: 110 | 010 | 10 Induk 2: 001 | 001 | 11 Diperoleh:
Anak 1: 110 | 001 | 10 Anak 2: 001 | 010 | 11
2.8.3 Uniform Crossover
Crossover seragam manghasilkan kromosom keturunan dengan menyalin bit-bit
Contoh:
11001011 + 11011101 = 11011111
2.8.4 Partially Mapped Crossover (PMX)
PMX diciptakan oleh Goldberg dan Lingle. PMX merupakan rumusan modifikasi dari pindah silang dua-poin. Hal yang penting dari PMX adalah pindah silang dua poin ditambah dengan beberapa prosedur tambahan.
Contoh:
Pilih posisi untuk menentukan substring secara acak Induk 1: 1 2 3 | 4 5 6 | 7 8
Induk 2: 3 7 5 | 1 6 8 | 2 4 Diperoleh:
Anak 1 : 4 2 3 | 1 6 8 | 7 5 Anak 2 : 3 7 8 | 4 5 6 | 2 1
2.9 Mutasi
Operator mutasi dioperasikan sebagai cara untuk mengembalikan materi genetic yang hilang. Melalui mutasi, individu baru dapat diciptakan dengan melakukan modifikasi terhadap satu atau lebih nilai gen pada individu yang sama. Mutasi mencegah kehilangan total materi genetika setelah reproduksi dan pindah silang. Mutasi ini berperan utuk menggantikan gen yang hilang dari populasi akibat seleksi yang memungkinkan munculnya kembali gen yang tidak muncul pada inisialisasi populasi.
2.9.1 Mutasi Pengkodean Biner
Tabel 2.4 Contoh Mutasi Pengkodean Biner
Keadaan Kromosom Proses Mutasi
Kromosom sebelum mutasi 1000 1111 1011 0110 Kromosom sesudah mutasi 10011 1011 0110
2.9.2 Mutasi Pengkodean Nilai
Mutasi pengkodean nilai adalah proses yang terjadi pada saat pengkodean nilai. Proses mutasi dalam pengkodean nilai dapat dilakukan dengan cara memilih sembarang posisi gen pada kromosom, dan nilai yang ada kemudian ditambahkan atau dikurangkan dengan suatu nilai kecil tertentu yang diambil secara acak. Sebagai contoh, dapat dilihat pada tabel berikut ini, yaitu nilai riil ditambahkan dan dikurangkan dengan nilai 0 dan 1.
Tabel 2.5 Contoh Mutasi Pengkodean Nilai
Keadaan Kromosom Proses Mutasi
Kromosom sebelum mutasi 1,45 2,67 1,87 2,56 Kromosom sesudah mutasi 1,55 2,67 1,77 2,56
2.9.3 Mutasi Pengkodean Permutasi
Proses mutasi pengkodean permutasi tidak sama halnya dengan proses mutasi yang dilakukan pada pengkodean biner dengan mengubah langsung bit-bit pada kromosom. Salah satu cara yang dapat dilakukan adalah dengan memilih dua posisi (locus) dari kromosom dan kemudian nilainya saling dipertukarkan. Orangtua yang berada dibawah titik crossover dipertukarkan untuk menghasilkan anak baru. Contoh Mutasi pada pengkodean permutasi, dapat dilihat pada tabel di berikut ini:
Tabel 2.6 Contoh Mutasi Pengkodean Permutasi
Keadaan Kromosom Proses Mutasi
Kromosom sebelum mutasi 1 2 3 4 5 6 7 8 9 Kromosom sesudah mutasi 1 2 7 4 6 5 8 3 9
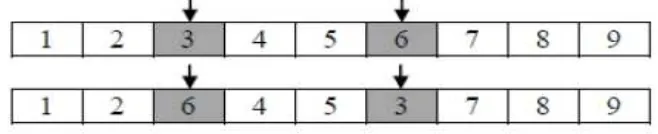
a. Inversion Mutation
Inversion mutation dilakukan dengan cara memilih substring secara acak kemudian
substring yang terpilih dibalik dan penempatan substring pada posisi yang sama. Penyisipan tersebut posisi acak. Contoh ilustrasi operasi mutasi ini, dapat dilihat pada gambar 2.4 berikut ini:
Gambar 2.4 Contoh Inversion Mutation
b. Insertion Mutation
Insertion Mutation dilakukan dengan cara memilih salah satu gen secara acak
kemudian gen yang terpilih disisipkan ke posisi yang lain. Penyisipan tersebut pada posisi acak. Contoh ilustrasi operasi mutasi ini, dapat dilihat pada gambar 2.5 berikut ini:
Gambar 2.5 Contoh Exchange Mutation
2.9.4 Mutasi Pengkodean Pohon
Tabel 2.7 Contoh Mutasi Pengkodean Pohon
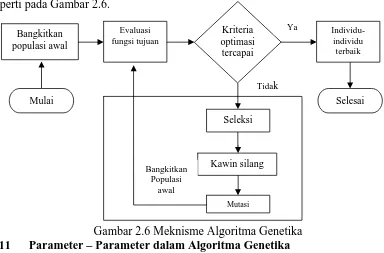
2.10 Meknisme Algoritma Genetika
Algoritma genetika dimulai dengan pembentukan sejumlah solusi yang dilakukan secara acak. Sebuah solusi yang dibangkitkan dalam algoritma genetika disebut sebagai kromosom, sedangkan kumpulan kromosom tersebut disebut sebagai populasi. Sebuah kromosom dibentuk dari komponen penyusun disebut dengan gen dan nilainya dapat berupa bilangan numerik, biner, simbol ataupun karakter tergantung dari permasalahan yang ingin diselesaikan.
Secara umum blok diagram dari mekanisme kerja algoritma genetika adalah seperti pada Gambar 2.6.
Gambar 2.6 Meknisme Algoritma Genetika 2.11 Parameter – Parameter dalam Algoritma Genetika
Bangkitkan populasi awal
Evaluasi fungsi tujuan
Kriteria optimasi
tercapai
Individu-individu terbaik
Selesai Mulai
Seleksi
Kawin silang
Mutasi
Bangkitkan Populasi
awal
Ya
Parameter-parameter genetika berperan dalam pengendalian operator-operator genetika yang digunakan dalam optimasi algoritma genetika menggunakan algoritma genetika. (Davis, 1991; Sundhararajan, 1994; Sastry, 2004). Parameter genetika yang sering digunakan meliputi ukuran populasi (N), probabilitas pindah silang (Pc), dan probabilitas mutasi (Pm). Pemilihan ukuran populasi yang digunakan tergantung pada masalah yang akan diselesaikan. Untuk masalah yang lebih kompleks biasanya diperlukan ukuran populasi yang lebih besar guna mencegah konvergensi prematur (yang menghasilkan optimum lokal).
Pada tiap generasi, sebanyak Pc * N individu dalam populasi mengalami pindah silang. Makin besar nilai Pc yang diberikan maka makin cepat struktur individu baru yang diperkenalkan ke dalam populasi. Jika nilai Pc yang diberikan terlalu besar, individu yang merupakan kandidat solusi terbaik dapat hilang lebih cepat dibanding seleksi untuk peningkatan kerja. Sebaliknya nilai Pc yang rendah dapat mengakibatkan stagnasi karena rendahnya angka eksplorasi.
Probabilitas mutasi adalah probabilitas di mana setiap posisi bit pada tia string dalam populasi baru mengalami perubahan secara acak setelah proses seleksi. Dalam satu generasi dengan L panjang struktur, kemungkinan terjadi mutasi sebanyak Pm*N*L.
2.12 Parameter Genetik
Pengoperasian algoritma genetika dibutuhkan 3 parameter (Juniawati, 2003) yaitu: 1. Probabilitas Persilangan (Crossover Probability)
Menunjukkan kemungkinan crossover terjadi antara 2 kromosom. Jika tidak terjadi crossover maka keturunannya akan sama persis dengan kromosom orangtua, tetapi tidak berarti generasi yang baru akan sama persis dengan generasi yang lama. Jika probabilitas crossover 100% maka semua keturunannya dihasilkan dari crossover. Crossover dilakukan dengan harapan bahwa kromosom yang baru akan lebih baik.
2. Probabilitas Mutasi (Mutation Probability)
Menunjukkan kemungkinan mutasi terjadi pada gen-gen yag menyusun sebuah kromosom. Jika tidak terjadi mutasi maka keturunan yang dihasilkan setelah
probabilitas 100%, semua kromosom dimutasi. Jika probabilitasnya 0%, tidak ada yang mengalami mutasi.
3. Ukuran Populasi
Menunjukkan jumlah kromosom yang terdapat dalam populasi. Jika hanya sedikit kromosom dalam populasi maka algoritma genetika akan mempunyai sedikit variasi kemungkinan untuk melakukan crossover. Sebaliknya jika terlalu banyak maka algoritma genetika akan berjalan lambat dalam menemukan solusi.
Ada beberapa rekomendasi parameter yang bisa digunakan, yaitu:
a. Untuk permasalahan yang memilki kawasan solusi cukup besar, De Jong merekomendasikan untuk nilai parameter kontrol: (popsize; pc; pm) = (50;0,6;0,001).
b. Bila rata-rata Fitness setiap generasi digunakan sebagai indikator, maka Grenfenstette merekomendasikan: (popsize;pc;pm) = (30;0,95;0,01)
c. Bila Fitness dari individu terbaik dipantau pada setiap generasi, maka usulannya adalah: (popsize;pc;pm) = (80;0,45;0.01).
Ukuran populasi sebaiknya tidak lebih kecil dari 30, untuk sembarang jenis permasalahan.
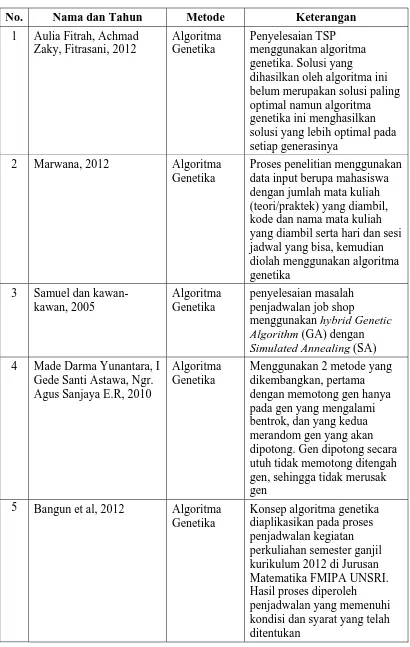
2.13 Penelitian Terdahulu
Penelitian Aulia Fitrah, Achmad Zaky, Fitrasani, 2012 yang berjudul Penerapan algoritma genetika pada persoalan pedagang keliling (TSP). Pada penelitian ini dilakukan penyelesaian TSP menggunakan algoritma genetika. Solusi yang dihasilkan oleh algoritma ini belum merupakan solusi paling optimal namun algoritma genetika ini menghasilkan solusi yang lebih optimal pada setiap generasinya.
solusi penjadwalan pada waktu yang dapat digunakan baik oleh mahasiswa dan ruangan yang terlibat dalam suatu mata kuliah.
Penelitian Samuel dan kawan-kawan, 2005 yang berjudul Penerapan algoritma genetika untuk Traveling Salesman Problem dengan menggunakan metode order
crossover dan Insertion Mutation. Pada penelitian ini membahas bagaimana algoritma
genetik menyelesaikan TSP dengan menggunakan order crossover sebagai teknik rekombinasi dan insertion mutation sebagai teknik mutasi yang digunakan pada algoritma genetik menunjukkan bahwa algoritma genetika dapat digunakan untuk menyelesaikan masalah optimasi yang kompleks seperti mencari rute paling optimum, menggunakan beberapa metode seleksi yaitu roulette wheel, elitism dan gabungan antara metode roulette wheel dan elitism. Ada dua jenis crossover yang digunakan yaitu one cut point crossover dan two cut point crossover; (Tamilarsi & Kumar 2010) menemukan sebuah metode baru dalam penyelesaian masalah penjadwalan job shop menggunakan hybrid Genetic Algorithm (GA) dengan Simulated Annealing (SA); (Nasution, 2012) analisis penyelesaian TSP menggunakan partially mapped crossover dengan menentukan nilai probabilitas crossover 20%, 40%, 60%, 80% dan 99%. (Kusum Deep & Hadush Mebrahtu, 2012) membuat variasi pada partially mapped
crossover dengan menentukan letak kromosom dalam posisi acak. (Alfonsas &,
Bronislovas, 2005). membandingkan 10 operator crossover pada Quadratic Assignment Problem di mana hasil yang diperoleh menunjukkan bahwa crossover MPX mampu mendapakan solusi yang lebih baik dibandingkan operator lain yang telah diuji. (Kusum Deep & Hadush Mebrahtu, 2011) menggabungkan 2 operator mutasi untuk meningkatkan kerja algoritma genetika untuk meminimumkan cost pada travelling salesman problem (TSP).
mencapai nilai terbaik atau mendekati 1 daripada metode yang hanya merandom gen saja. Dari nilai akhir juga terlihat bahwa metode yang memotong gen pada gen yang bentrok memiliki nilai akhir lebih baik. Selain itu kedua metode ini mampu meminimalisir kerusakan pada kromosom hasil dari crossover.
Penelitian Bangun et al, 2012 yang berjudul Penerapan Konsep Algoritma Genetika untuk Penjadwalan Kegiatan Perkuliahan Semester Ganjil Kurikulum 2012 di Jurusan Matematika FMIPA UNSRI. Pada penelitian ini, konsep algoritma genetika diaplikasikan pada proses penjadwalan kegiatan perkuliahan semester ganjil kurikulum 2012 di Jurusan Matematika FMIPA UNSRI. Hasil proses diperoleh penjadwalan yang memenuhi kondisi dan syarat yang telah ditentukan. Jadwal yang telah dihasilkan merupakan jadwal yang diperoleh dari kromosom 5 generasi ke-19.
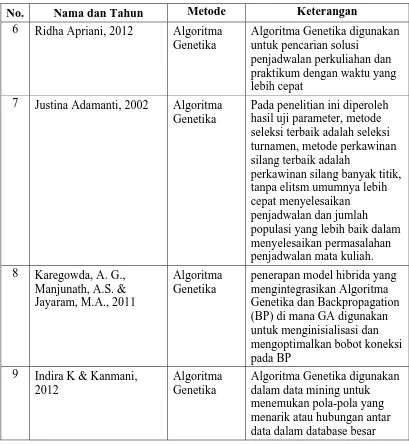
Penelitian Ridha Apriani, 2012 yang berjudul Algoritma genetika untuk menyelesaikan permasalahan penjadwalan perkuliahan dan praktikum. Pada penelitian ini
pencarian solusi penjadwalan perkuliahan dan praktikum dengan waktu yang lebih cepat. Hasil pengujian dengan input nilai parameter yang sama atau berbeda, proses penjadwalan menghasilkan hasil generasi dan iterasi yang berbeda – beda.
Penelitian Justina Adamanti, 2002 yang berjudul Penyelesaian masalah penjadwalan mata kuliah di Fakultas Matematika Dan Ilmu Pengetahuan Alam Universitas Gadjah Mada dengan menggunakan algoritma genetika. Pada penelitian ini diperoleh hasil uji parameter, metode seleksi terbaik adalah seleksi turnamen, metode perkawinan silang terbaik adalah perkawinan silang banyak titik, tanpa elitsm umumnya lebih cepat menyelesaikan penjadwalan dan jumlah populasi yang lebih baik untuk model kromosom masalah penjadwalan mata kuliah yang memiliki sekitar 300 gen adalah sekitar 100 individu, tetapi tidak lebih cepat dalam waktu dibandingkan dengan jumlah populasi yang lebih sedikit.
Pada penelitian Karegowda, A. G., Manjunath, A.S. & Jayaram, M.A., 2011 yang berjudul Application of genetic algorithm Optimized neural network Connection
weights for medical Diagnosis of pima Indians diabetes. Pada penelitian ini dilakukan
variabel input yang relevan dan pemilihan koneksi optimal bobot. Makalah ini menyajikan penerapan model hibrida yang mengintegrasikan Algoritma Genetika dan Backpropagation (BP) di mana GA digunakan untuk menginisialisasi dan mengoptimalkan bobot koneksi pada BP. Fitur signifikan diidentifikasi dengan menggunakan dua metode Pohon Keputusan. Metode GA CFS digunakan sebagai masukan untuk model hibrida untuk diagnosa diabetes mellitus. Hasilnya membuktikan bahwa, GA dioptimalkan dengan algoritma BP dapat mengungguli pendekatan BP tanpa GAi. Selain hybrid GA-BPN dengan input yang relevan menyebabkan lebih improvisasi akurasi kategorisasi dibandingkan dengan hasil yang dihasilkan oleh GA-BPN sendiri dengan beberapa masukan yang berlebihan.
Pada penelitian Indira K & Kanmani, 2012 yang berjudul Performance
Analysis of Genetic Algorithm for Mining Association Rules. Pada penelitian ini aturan
Tabel 2.8 Penelitian Terdahulu
No. Nama dan Tahun Metode Keterangan
1 Aulia Fitrah, Achmad Zaky, Fitrasani, 2012
dihasilkan oleh algoritma ini belum merupakan solusi paling optimal namun algoritma genetika ini menghasilkan solusi yang lebih optimal pada setiap generasinya
2 Marwana, 2012 Algoritma Genetika
Proses penelitian menggunakan data input berupa mahasiswa dengan jumlah mata kuliah (teori/praktek) yang diambil, kode dan nama mata kuliah yang diambil serta hari dan sesi jadwal yang bisa, kemudian diolah menggunakan algoritma genetika
3 Samuel dan kawan-kawan, 2005 Gede Santi Astawa, Ngr. Agus Sanjaya E.R, 2010
Algoritma Genetika
Tabel 2.9 Penelitian Terdahulu (Lanjutan)
No. Nama dan Tahun Metode Keterangan
6 Ridha Apriani, 2012 Algoritma Genetika
Algoritma Genetika digunakan untuk pencarian solusi
penjadwalan perkuliahan dan praktikum dengan waktu yang lebih cepat
7 Justina Adamanti, 2002 Algoritma Genetika
Pada penelitian ini diperoleh hasil uji parameter, metode seleksi terbaik adalah seleksi turnamen, metode perkawinan silang terbaik adalah
perkawinan silang banyak titik, tanpa elitsm umumnya lebih cepat menyelesaikan
penjadwalan dan jumlah populasi yang lebih baik dalam menyelesaikan permasalahan