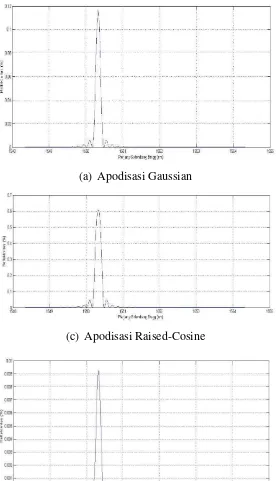
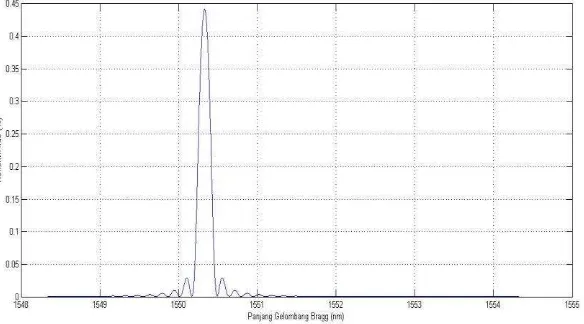
(a)
Apodisasi Gaussian
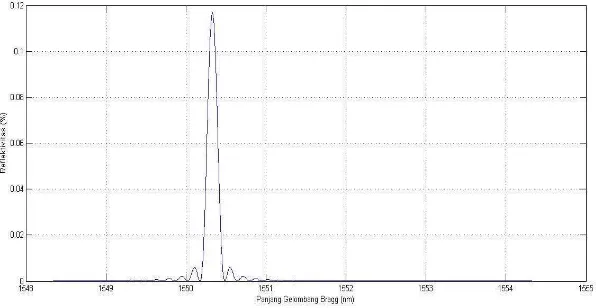
(b)
(c)
Apodisasi Raised-Cosine
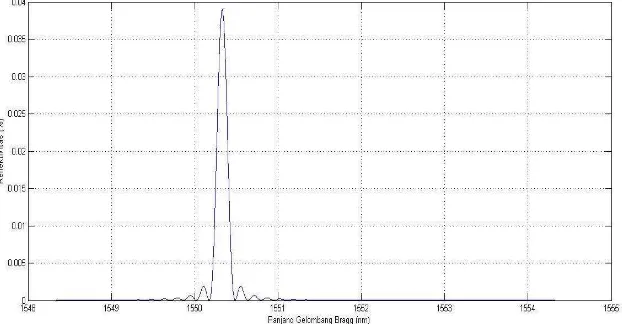
(d)
(e)
Apodisasi Synchronous
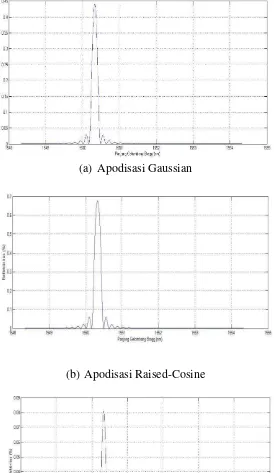
(a)
Apodisasi Gaussian
(b)
Apodisasi Raised-Cosine
(c)
Apodisasi Synchronous
(a)
Apodisasi Gaussian
(b)
Apodisasi Raised-Cosine
(c)
Apodisasi Synchronous
(a)
Apodisasi Gaussian
(b)
Apodisasi Raised-Cosine
(c)
Apodisasi Synchronous
(a)
Apodisasi Gaussian
(b)
Apodisasi Raised-Cosine
(c)
Apodisasi Synchronous
(a)
Apodisasi Gaussian
(b)
Apodisasi Raised-Cosine
(c)
Apodisasi Synchronous
(a)
Apodisasi Gaussian
(b)
Apodisasi Raised-cosine
(c)
Apodisasi Synchronous
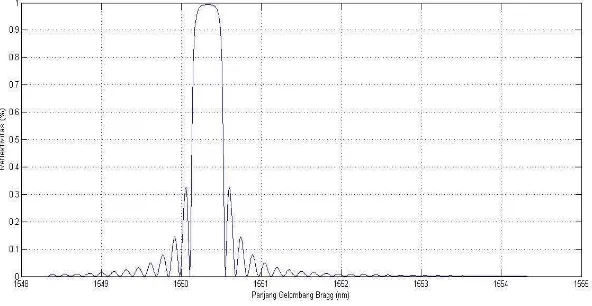
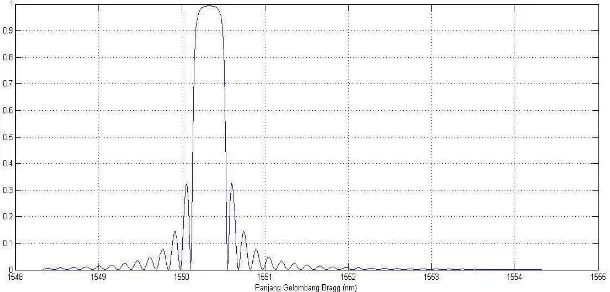
%spektrum reflektansi filter %refleksi lamda2
n=1;
for lamda = 1550.34:0.01:1556.32; n1=1.47;
n2=1.457; lb2=1553.33; r=10000;
%untuk lamda 2
v2 = (2*pi*r./lb2)*sqrt(n1^2 - n2^2);neff2 = sqrt (n2^2 + (lb2 .^2.*(1.1428.*v2 - 0.996).^2./(4*pi^2*r^2)));
per2 = lb2./(2.*neff2); N=10000;
l2=N*per2; delta_n=0.0003;
koe_koplinPout = (pi.*delta_n/lamda) k2 = (2*pi*neff2)/lamda;
delta_k2 = k2 - (pi./per2);
s2 = sqrt (koe_koplinPout.^2 - delta_k2.^2);
T11 = (cosh (s2*l2))-1i*(delta_k2./s2)*sinh(s2*l2); T12 = 1i *(koe_koplinPout/s2)*sinh(s2*l2);
T21= -1i*(koe_koplinPout/s2)*sinh(s2*l2);
T22=(cosh(s2*l2)) + 1i *((delta_k2/s2)*sinh(s2*l2)); T = [T11 T12; T21 T22];
Tout = T;
refl (n) = abs (Tout (2,1)./Tout (1,1)).^2; n=n+1;
end
l2=N*per2; delta_n=0.0001;
z=1; %1≤z≤10
L=10;
koe_koplinPout = (pi.*delta_n/lamda).*exp(-log (2*((0.5*z-2.5).^2)));
k2 = (2*pi*neff2)/lamda; delta_k2 = k2 - (pi./per2);
s2 = sqrt (koe_koplinPout.^2 - delta_k2.^2);
T11 = (cosh (s2*l2))-1i*(delta_k2./s2)*sinh(s2*l2); T12 = 1i *(koe_koplinPout/s2)*sinh(s2*l2);
T21= -1i*(koe_koplinPout/s2)*sinh(s2*l2);
T22=(cosh(s2*l2)) + 1i *((delta_k2/s2)*sinh(s2*l2)); T = [T11 T12; T21 T22];
Tout = T;
refl (n) = abs (Tout (2,1)./Tout (1,1)).^2; n=n+1;
end
per2 = lb2./(2.*neff2);
koe_koplinPout = (pi.*delta_n/lamda).*0.5.*(1+cos (3.14*(0.05*z-0.5)));
k2 = (2*pi*neff2)/lamda; delta_k2 = k2 - (pi./per2);
s2 = sqrt (koe_koplinPout.^2 - delta_k2.^2);
T11 = (cosh (s2*l2))-1i*(delta_k2./s2)*sinh(s2*l2); T12 = 1i *(koe_koplinPout/s2)*sinh(s2*l2);
T21= -1i*(koe_koplinPout/s2)*sinh(s2*l2);
T22=(cosh(s2*l2)) + 1i *((delta_k2/s2)*sinh(s2*l2)); T = [T11 T12; T21 T22];
Tout = T;
refl (n) = abs (Tout (2,1)./Tout (1,1)).^2; n=n+1;
end
l2=N*per2; delta_n=0.0001; z=1;
%1≤z≤10
L=10;
koe_koplinPout = (pi.*delta_n/lamda).*sinc(0.628*z-3.14); k2 = (2*pi*neff2)/lamda;
delta_k2 = k2 - (pi./per2);
s2 = sqrt (koe_koplinPout.^2 - delta_k2.^2);
T11 = (cosh (s2*l2))-1i*(delta_k2./s2)*sinh(s2*l2); T12 = 1i *(koe_koplinPout/s2)*sinh(s2*l2);
T21= -1i*(koe_koplinPout/s2)*sinh(s2*l2);
T22=(cosh(s2*l2)) + 1i *((delta_k2/s2)*sinh(s2*l2)); T = [T11 T12; T21 T22];
Tout = T;
refl (n) = abs (Tout (2,1)./Tout (1,1)).^2; n=n+1;
end