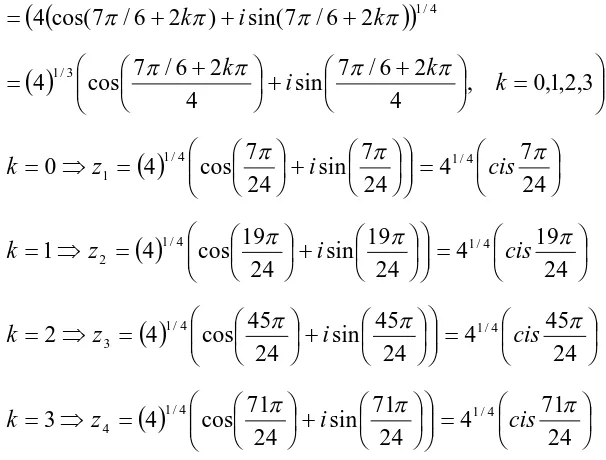modul analisis variabel komplek 19 08 2015

(1)

M O D U L

ANALI SI S VARI ABEL KOMPLEK

O l e h

Dwi Purnomo

PROGRAM STUDI PENDIDIKAN MATEMATIKA

IKIP BUDI UTOMO MALANG

TAHUN 2014

X

Y

 x

y r



cos,isin



r

X

Y





cos,isin



r

r y

x





cos,isin



r

X X

Y

x x



y

 _r r _ _y



cos,isin



r

(2)

Analisis Variabel Komplek: Dwi Purnomo ii

DAFTAR ISI

Halaman

Halaman Sampul ... I

Daftar Isi ... ii

Kata Pengantar ... iii

1.1 Pendahuluan ... 1

1.2 Representasi Grafik Bilangan Real ... ... 2

1.3 Sistem Bilangan Komplek ... 20

1.4 Operasi Dasar Bilangan Komplek ... 22

1.5 Nilai Mutlak ... 26

1.6 Pembangun Aksioma Sistem Bilangan Komplek ... 30

1.7 Representasi Grafik Bilangan Komplek ... 34

1.8 Bentuk Polar Bilangan Komplek ... 38

1.9 Teorema de Moivre ... 43

1.10 Akar-akar Bilangan Komplek ... 53

1.11 Rumus Euler ... 61

1.12 Persamaan Polinomial ... 66

1.13 Akar-akar ke-n dari Satuan ... 69

1.14 Interpretasi Vektor dari Bilangan Komplek ... 70

1.15 Representasi Spherical Bilangan Komplek ... 74

1.16 Hasil Kali Titik dan Silang ... 75

1.17 Koordinat-koordinat Konjugate Bilangan Komplek ... 78

1.18 Himpunan-himpunan Titik ... 80

1.19 Soal-soal ... 82

(3)

Analisis Variabel Komplek: Dwi Purnomo iii

KATA PENGANTAR

Puji dan syukur penulis panjatkan kehadirat Allah swt. atas semua limpahan rahmat dan karunia-Nya, sehingga penulisan modul Analisis Variabel Komplek dapat diselesaikan sesuai dengan rencana sebelumnya. Namun demikian mengingat kekurangan dan sifat “manusiawi” penulis sehingga materi dalam modul yang telah disusun belum sesuai dengan harapan pembaca.

Penulisan modul Analisis Variabel Komplek dimaksudkan untuk menjelaskan beberapa konsep yang berkaitan dengan sistem bilangan komplek, operasi dan representasinya dalam grafik maupun vektor. Modul ini menjelaskan pokok bahasan bilangan real representasinya secara grafis, sistem bilangan komplek, operasi-operasi dasar, bilangan real, nilai mutlak, pembangun aksioma sistem bilangan komplek, representasi grafis bilangan kompek, bentuk polar bilangan komplek, teorema de Moivre, akar-akar bilangan komplek, rumus Euler, persamaan polinomial, akar-akar

n

ke bilangan komplek, interpretasi vektor bilangan komplek, representasi spherical bilangan komplek, hasil kali titik dan silang, koordinat-koordinat konjugate komplek, himpunan-himpunan titik.

Penyusunan modul Analisis Variabel Komplek mulai awal hingga akhir sangat dibantu oleh teman dan kolega, khususnya teman satu profesi di Program Studi Pendidikan Matematika Institut Keguruan dan Ilmu Pendidikan Budi Utomo Malang, lebih-lebih para mahasiswa matematika, antara lain matematika angkatan 2009 A/B, 2010 A/B dan khususnya angkatan 2011 B (Maria Susanti N. dkk.) yang menjadi sumber inspirasi dan bantuan motivasi kepada penulis untuk segera menyelesaikan bahan ajar. Harapan penulis semoga konsep teori, pembahasan soal, dan soal-soal latihan yang disajikan dapat berguna dan membantu mahasiswa. Kekurangan dan kekhilafan disana sini Insya’allah diperbaiki dikemudian hari.

Malang, 1 Agustus 2014 Penulis

(4)

(5)

Analisis Variabel Komplek: Dwi Purnomo- 5

Untuk yang tercinta

(6)

BILANGAN KOMPLEK

1.1 Pendahuluan

Sistem bilangan seperti yang kita kenal hingga saat ini merupakan hasil dari pengembangan secara bertahap seperti yang ditunjukkan dalam daftar berikut.

1. Bilangan asli 1, 2, 3, 4,. . , juga disebut bilangan bulat positip, pertama kali digunakan dalam menghitung. Simbol bervariasi dengan waktu, misalnya yang digunakan bangsa Romawi I, II, III, IV. . ., jika a dan b adalah bilangan asli,

jumlah ab dan perkalian a.b,(a)(b)atau ab juga disebut bilangan asli. Untuk

alasan ini himpunan bilangan asli dikatakan tertutup di bawah operasi penjumlahan dan perkalian atau memenuhi sifat tertutup (closure) terhadap operasi ini.

2. Bilangan bulat negatip dan nol, dilambangkan dengan - 1, - 2, - 3. . . dan 0 masing-masing, muncul untuk memungkinkan solusi dari persamaan seperti

xba, dimana a dan b adalah setiap bilangan asli. Hal ini mengarah pada

operasi pengurangan, atau invers penjumlahan, dan kita tulis dengan xab himpunan bilangan bulat positip, negatip dan nol disebut himpunan bilangan bulat dan tertutup di bawah operasi-operasi penjumlahan, perkalian, dan pengurangan.

3. Bilangan rasional dan pecahan seperti ,... 4 13 , 5 6 , 7 1 , 4 3



 muncul sebagai bagian yang memungkinkan selesaian persamaan berbentuk bxa untuk semua bilangan bulat a dan b di mana b0._{Hal ini mengarah ke operasi pembagian atau invers} perkalian, dan ditulis dengan

b a

x yang disebut hasil bagi a dan b , di mana a

adalah pembilang dan b adalah penyebut.

Himpunan bilangan bulat adalah himpunan bagian atau subset dari bilangan

rasional, karena bilangan bulat sesuai dengan bilangan rasional

b a

(7)

4. Bilangan irasional seperti √2 =1.41423. . . dan π = 3. 14159. . . adalah bilangan

yang tidak rasional, yang tidak dapat dinyatakan dengan

b a

dimana a dan b

adalah bilangan bulat dan b0.

Himpunan bilangan rasional dan irasional di sebut dengan himpunan bilangan real. Diasumsikan bahwa siswa sudah mengetahui dengan berbagai operasi pada bilangan real.

1.2 Representasi Grafis Bilangan Real

Sebelum penulis menguraikan konsep sistem bilangan real (R), terlebih dahulu marilah kita ingat kembali konsep himpunan (set). Himpunan mempunyai peranan sangat penting dalam memahami sistem bilangan real. Secara eksplisit himpunan didefinisikan sebagai sekumpulan objek, unsur atau sesuatu yang mempunyai ciri-ciri, kriteria dan syarat yang tertentu serta terdefinisi dengan jelas. Objek atau unsur sesuatu himpunan A dinamakan anggota atau elemen. Anggota suatu himpunan dinyatakan dengan a,b,c,d,.... atau 1,2,3,4,.... sedangkan nama himpunan dinyatakan dengan huruf kapital A,B,C,D, dan seterusnya. Misal kita mendefinisikan suatu himpunan A dengan menyatakan secara jelas anggota-anggotanya yang terdiri dari a,b,c,d,e, himpunan A tersebut dapat ditulis dalam bentuk A{a,b,c,d,e} dengan masing-masing anggota himpunan A dipisahkan oleh tanda baca koma dan terdapat dua tanda kurung { }. Jika himpunan A mempunyai anggota banyaknya tak hingga maka unsur-unsurnya tidak ditulis semuanya akan tetapi cukup dituliskan beberapa anggotanya dan titik-titik sebanyak 3 atau 5 , Jika a adalah anggota himpunan A maka pernyataan tersebut ditulis dengan notasi aA dan dibaca a anggota A. Jika a bukan anggota himpunan A, maka dituliskan aAdan dibaca “a bukan anggota A. Jika suatu himpunan A tidak memiliki anggota, maka A disebut himpunan kosong, dan dinyatakan dengan notasi  atau { }.

(8)

Contoh:

1) A{yybilangan prima kurang dari10}

2) B{xx faktor ganjildari21} 3) C {xx2 1,xbilanganprima}

4) D{xx faktor genapdari21}

5) E {xx2 3x40} 6) F {xx2 3x40} 7) G{xx42} 8) H {(x,y)x2 y2 4}

9) V {himpunankuasadari{1,2,3}}

Metode perincian dilakukan dengan cara mendaftar seluruh anggota himpunan yang memenuhi syarat dan ketentuan yang diberikan dalam suatu himpunan.

Contoh

1) A{1,2,3,4,5,...}

2) B{senin,selasa,rabu,kamis, jum'at,sabtu}

3) C{2,3,5,7,11,13,17,19,...}

4) D{merah,kuning,hijau}

5) E {0}

6) F {}

7) G { x1, }

8) H {(1,2),(2,3),(3,4),...}

9) V {,{1},{2},{1,2}}

(9)

Selanjutnya untuk memudahkan para pembaca dalam memahami konsep sistem bilangan real berikut ini diberikan beberapa bilangan dan himpunan bilangan yang pada bab-bab selanjutnya dalam buku ini sering ditemukan. Bilangan dan himpunan bilangan tersebut adalah:

1. Himpunan bilangan asli (Natural)

Himpunan bilangan asli biasanya dinotasikan dengan N dan anggota-anggota

bilangan asli adalah 1, 2, 3, 4, 5, 6, ... sehingga N{1,2,3,4,5,6,...}

Bilangan asli tertutup terhadap operasi penjumlahan dan perkalian, artinya untuk setiap a,b bilangan asli maka (ab)dan ( ba. )bilangan asli. Oleh karena itu, himpunan semua bilangan asli membentuk suatu sistem sistem bilangan asli.

2. Bilangan cacah (whole)

Bilangan cacah biasanya dinotasikan dengan W dan anggota-anggota bilangan cacah adalah 0, 1, 2, 3, 4, 5, 6, ..., sehingga W{0,1,2,3,4,5,6,...}. Bilangan cacah tertutup terhadap operasi penjumlahan dan perkalian, artinya untuk setiap a,b bilangan cacah maka (ab)dan ( ba. ) bilangan cacah.

3. Sistem bilangan asli bersama-sama dengan bilangan nol dan lawan dari bilangan-bilangan asli membentuk sistem bilangan-bilangan bulat, Bilangan bulat biasanya dinotasikan dengan Z yang anggota-anggotanya adalah ...-3, -2, -,1, 0, 1, 2, 3, ..., sehingga Z{...3,2,2,0,1,2,3,...}.

4. Bilangan pecahan atau bilangan rasional (quotient) biasanya dinyatakan dengan Q. Bilangan rasional adalah bilangan yang secara umum dinyatakan dengan

0 , ,

.  

 a b Z b

b a Q

Contoh

1)

3 1 

p

2)

11 2  

q

3)

7 22 

r

(10)

1) 0,33333333...

3 1

 

p

2) 0,285714285714285714...

11 2

   

q

3) 3,142857142857148...

7 22

 

r

Jika kita cermati lebih mendetail, bilangan-bilangan desimal sebagai mana tersebut di atas selalu berulang angka-angkanya, sehingga bilangan rasional juga disebut bilangan desimal berulang. Sebaliknya bilangan desimal berulang dapat dinyatakan sebagai bilangan rasional. Untuk menyatakan bentuk desimal menjadi bilangan rasioan adalah dengan cara melihat angka yang berulang pada bilangan tersrsebut. Jika terdapat 1 angka yang berulang maka kalikan bilangan dimaksud dengan 101. Jika terdapat 2 angka yang berulang maka kalikan bilangan tersebut dengan 102. dan seterusnya. Selanjutnya cari selisih bilangan semula dengan bilangan yang baru. Dengan metode perhitungan sederhana akhirnya diperoleh bilangan rasional yang dimaksud. Untuk lebih jelasnya perhatikan contoh-contoh berikut ini.

Contoh:

Ubahlah bilangan desimal berikut ini menjadi bentuk rasional  .a,bZ,b0

b a Q

1. Tentukan bentuk rasional bilangan 0,12121212... Jawab

Bilangan 0,12121212...adalah bilangan desimal dengan 2 angka berulang yaitu angka 1 dan 2.

Karena banyaknya angka yang berulang pada bilangan 0,1,212121212... adalah 2 angka, kalikan bilangan 0,12121212... dengan bilangan 2

10 . Misal x0,12121212..., sehingga diperoleh

... 212121212 ,

1 , 12 100x

Akibatnya 100xx(12,121212.12...)(0,12121212...)12 ...)

12121212 ,

0 ( ...) 12 . 121212 ,

12 (

10xx 

99 12

12 99

 

(11)

Sehingga bentuk rasional dari bilangan 0,12121212... adalah

99 12

2. Tentukan bentuk rasional bilangan 1,412333333...

Jawab

Bilangan 1,412333333...adalah bilangan desimal dengan 1 angka berulang yaitu angka 3.

Karena banyaknya angka yang berulang pada bilangan 1,412333333...adalah 1 angka, kalikan bilangan 1,412333333...dengan bilangan 1

10 . Misal x1,4123333333..., sehingga diperoleh

... 12333333 ,

14 10x

Akibatnya 10xx(14,123333333...)(1,412333333...)

900 1271 9

71 , 12

71 , 12 9

 



x x

900 1271

3. Tentukan bentuk rasional bilangan 0,9826273273273...

Jawab

Bilangan 0,9826273273273...adalah bilangan desimal dengan 3 angka berulang yaitu angka 2,7, dan 3.

Karena banyaknya angka yang berulang pada bilangan 0,9826273273273...

adalah 3 angka, kalikan bilangan 0,9826273273273...dengan bilangan 3

10 . Misal

x0,9826273273273... ... 3 5627327327 ,

982 1000x

Akibatnya 1000xx(982,56273273273...)(0,98256273273273...)

99900 98158017 999

58017 , 981

58017 , 981 999

  

  

x x

Sehingga bentuk rasional dari bilangan 0,9826273273273... adalah

(12)

4. Tentukan bentuk rasional bilangan 0,0543125431254312...

Jawab

Bilangan 0,0543154315431... adalah bilangan desimal dengan 4 angka berulang yaitu angka 5, 4, 3, dan 1.

Karena banyaknya angka yang berulang pada bilangan 0,0543154315431...

adalah 4 angka, kalikan bilangan 0,0543154315431...dengan bilangan 4

10 . Misal

x0,0543154315431..., sehingga diperoleh

.... 154315431 ,

543 10000x

Akibatnya 10000xx(543,154315431...)(0,0543154315431...)

99990 5421 9999

1 , 542

1 , 542 9999

 



x x

99990 5421

5. Bilangan Irasional (

_

Q ) atau disebut juga bilangan tidak rasional yaitu bilangan yang

tidak dapat dinyatakan dalam bentuk  .a,bZ,b0

b a

Q . Karena bilangan

rasional dapat dinyatakan dengan bilangan desimal yang angka-angkanya berulang, maka bilangan irasional adalah bilangan desimal yang angka-angkanya tidak ada yang berulang. Bilangan irasional juga disebut dengan bilangan bentuk akar.

Persoalan dalam kehidupan sehari-hari sering dijumpai adanya bilangan-bilangan irasional. Contoh bilangan-bilangan irasional antara lain adalah 2 dan . Bilangan

(13)

Gambar 1.1

Sedangkan bilangan  merupakan hasil bagi antara keliling sebarang lingkaran dengan panjang garis tengah lingkaran tersebut. Perhatikan gambar berikut ini.

Gambar 1.2 Contoh

1) 2 = 1,41421356237... 2) 3 = 1,73205080756... 3) 11 = 3,316625790355... 4) π = 3.14159265358979….

5) e = 2,71828 18284 59045 23536 02874 71352…

Berdasarkan contoh di atas, tampak bilangan-bilangan dalam bentuk akar umumnya adalah bilangan desimal yang angka-angkanya tidak ada yang berulang. Sehingga bilangan akar juga disebut bilangan irasional. Dengan demikian apa yang

1

d d₂

1

l

2

l



 

2 2 1 1

d l d

l

2 1

(14)

selama ini dianggap sama yaitu

7 22

=  tidaklah selalu benar. Karena

7 22

adalah

bilangan rasional, sedangkan  adalah bilangan irasional.

6. Himpunan semua bilangan irasional bersama-sama dengan bilangan rasional membentuk himpunan semua bilangan real (R), sehingga RNWZQQ Seperti telah diketahui, untuk menyatakan sebarang bilangan real seringkali digunakan cara desimal.

Contoh

Bilangan-bilangan

66 7 dan , 3 5 , 4 3

masing-masing dapat dinyatakan dalam desimal

sebagai

  

0,75, 1,666...



,dan 0,1060606.... Dapat ditunjukkan bahwa bentuk desimal bilangan-bilangan rasional adalah salah satu dari 2 tipe berikut:

i. berhenti ( dst. 8 1 , 2 5 , 4 3

), atau

ii. berulang beraturan ( ,dst. 66

7 , 3 5

).

Sifat-sifat Sistem Bilangan Real

Untuk sebarang a,b,c, d bilangan real berlaku sifat-sifat sebagai berikut: 1) Sifat komutatif

(i). abba (ii).a.bb.a 2) Sifat asosiatif



 



   

bc ab c abc a

c b a c b a c b a

. . . . . . ). ii (

). i (

 

       

3) Sifat distibutif perkalian terhadap penjumlahan a.(bc)(a.b)(a.c)

4) (i).  .1, b0

b a b a

(ii). , 0, 0

. ) . ( ) . (

  



 b d

d b

c b d a d c b a

(iii). , 0, 0

. .

.  b d 

d b

c a d

c b a

(15)

(ii). (a).(b)a.b (iii). (a)a

6) (i). 0 0

a , untuk setiap bilangan a0. (ii).

0

a

tak terdefinisikan.

(iii). 1

a a

, untuk setiap bilangan a0. 7) Hukum kanselasi

(i). Jika a.c b.c dan c0 maka ab. (ii). Jika b,c0 maka

b a c b

c a

 . .

.

8) Sifat pembagi nol

Jika a.b0 maka a0 atau b0.

Bilangan real dapat direpresentasikan oleh titik-titik pada garis yang disebut sumbu real, seperti ditunjukkan pada gambar 1.1 di bawah ini. Titik yang sesuai dengan nol disebut titik asal.

Gambar 1.3

Sebaliknya untuk setiap titik pada baris ada satu dan hanya satu bilangan real. Jika suatu titik A sesuai dengan bilangan real _{a yang terletak di sebelah kanan titik} Bsesuai dengan b bilangan real, kita katakan bahwa a lebih besar dari b atau kurang dari a

dan ditulis secara berurutan dengan ab atau ba.

Himpunan dari nilai-nilai x termasuk a < x <b disebut interval terbuka pada sumbu real bila axb, yang mana didalamnya terdapat titik awal a dan titik akhir

,

b disebut interval tertutup. Lambang x, yang mana dapat berdiri untuk semua susunan dari nilai–nilai asli, yang disebut variabel asli.

4

  3 2 1 0 1 2 3 ₄

3 2



2 3 

4 3



(16)

Nilai mutlak dari sebuah bilangan real a , dinotasikan dengan a , adalah a jika

0



a , –a untuk a < 0 dan 0 jika a = 0. Jarak antara dua titik a dan b pada sumbu real

adalah | − |. Atau dengan kata lain:

   

 

  

0 ,

0

0 ,

a jika a

a jika

a jika a a

Sifat-sifat terurut bilangan Real

Prinsip adalah aturan atau sifat yang digunakan sebagai dasar atau landasan dalam uraian yang berkaitan dengan bukti sesuatu. Prinsip dapat diambil dari definisi, aksioma, atau dalil-dalil yang “dimunculkan” kembali untuk digunakan pada bagian lain suatu konsep yang memerlukan. Diantara prinsip dalam matematika adalah prinsip urutan (well ordering principle).

Prinsip urutan berkaitan dengan kepositipan dan ketaksamaan antara bilangan-bilangan real. Cara yang dapat dilakukan untuk melakukan sifat keterurutan adalah mengidentifikasi suatu subset khusus dari R dengan menggunakan gagasan “kepositipan”.

Definisi

Misalkan P himpunan bagian R dan P. Untuk selanjutnya P disebut bilangan real positip kuat, maka berlaku sifat-sifat berikut ini:

(1) Jika a,bP maka (ab)P (2) Jika a,bP maka (a.b)P

(3) Jika aR, maka tepat dari salah satu yang berikut dipenuhi aP,a 0,aP

Dua sifat yang pertama menjamin kesesuaian dari urutan dengan operasi penjumlahan dan perkalian secara berurutan. Sifat (3) biasanya disebut sifat trikotomi karena membagi R menjadi 3 jenis unsur yang berbeda. Dinyatakan bahwa {aaP} dari bilangan real negatip tidak mempunyai unsur persekutuan dengan P, dan selanjutnya himpunan R merupakan gabungan dari tiga himpunan yang saling asing.

(17)

1) Jika aP, kita mengatakan bahwa a adalah suatu bilangan real positip kuat

(strictly positip) dan dituliskan dengan a0, Jika aP{0} , maka a disebut

bilangan real tidak negatip dan dituliskan dalam bentuk a0.

2) Jika aP, kita mengatakan bahwa a adalah suatu bilangan real negatip kuat

(strictly negatip) dan dituliskan dalam bentuk a0, Jika aP{0}, maka a

disebut bilangan real tidak positip dan dituliskan dalam bentuk a0.

3) Jika a,bRdan jika abP maka dituliskan dalam bentuk ab atau ba. 4) ika a,bRdan jika abP{0} maka dituliskan dalam bentuk ab atau

a

b .

Untuk kesepakatan bersama kita akan menuliskan abcyang berarti abdan

c

b . Demikian juga jika abc yang berarti ab maka bc dan seterusnya. Berikut ini diberikan beberapa teorema yang berkaitan dengan prinsip keterurutan

Teorema 1

Misalkan a,b,cR

1. Jika ab dan bc maka ac.

2. Tepat dari salah satu pernyataan berikut ini dipenuhi ab,ab,ab

3. Jika ab dan ab maka ab

Bukti

1) abmaka menurut definisi ab0atau a  b  P

c

b maka menurut definisi bc0 atau b  c  P

Karena a  b  P dan b  c  P maka menurut definisi diperoleh (a  b)  (b  c) P

sehingga a  c  P atau a  c

2) Dengan sifat trikotomi dalam definisi, maka tepat salah satu dari yang berikut mungkin terjadi

0



 b

(18)

3) Jika a  b , maka a  b  0 , sehingga dari bukti (b) kita dapatkan a  b  P atau b  c  P yakni a  b atau b  a . Dalam kasus lainnya salah satu dari hipotesisi tersebut kontradiksi. Jadi haruslah a  b

Teorema 2

1. Jika a  R dan a  0 maka a2  0. 2. 1  0

3. Jika

n



N

maka n  0

Bukti

1. Dengan sifat trikotomi jika a  0 , maka a  P atau aP. Jika a  P maka dengan definisi kita mempunyai a2 a.a, untuk a  P . Dengan cara yang sama Jika -a  P maka dengan definisi sebelumnya diperoleh bentuk

P a a

a    

 ) ( )( )

( 2 . Berdasarkan teorema sebelumnya berakibat bahwa:







2

) 1 )( 1 ( ) 1 ( ) 1 ( ) )(

(a a   a  a    a . Akibatnya bahwa a2  P _{. Jadi kita} simpulkan bahwa jika aP, maka a2 0.

2. Karena 2

) 1 (

1 , menurut bukti di atas akan menyebabkan bahwa 1 > 0.

3. Kita dapat menggunakan induksi matematika untuk membuktikan pernyataan ini. Pernyataan tersebut benar untuk n1 yakni 1 > 0. Selanjutnya kita anggap benar untuk nk , dengan k bilangan asli.

Karena 1 > 0 dan 1P, maka k1P, sehingga pernyataan di atas benar adanya dengan menggunakan definisi sebelumnya.

Teorema 3

Misalkan a,b,cR

1. Jika ab, maka acbc

2. Jika ab, dan bc maka acbd

3. Jika ab, c0 maka acbc

4. Jika ab, c0maka acbc

5. Jika a0maka 1 0

(19)

6. Jika a0 maka 1 0

a

Bukti teorema di atas dapat dijelaskan sebagai berikut:

1. Karena ab berarti menurut definisi sebelumnya ab0. Karena ab0 sehingga abP.

) ( ) ( )

(ab  ab  cc

) ( ) ( ) ( )

(ab  cc  ac  bc

Sehingga (ac)(bc)P. Dengan kata lain (ac)(bc)0

Karena (ac)(bc)0berarti (ac)(bc)

2. Karena ab dan c d berarti ab0dan cd 0. Hal ini berarti abP dan cdP.

Menurut definisi bilangan real positip kuat (1) diperoleh P

d c b

a )(  )

( . Dengan kata lain (ab)(cd)0, atau

0 ) ( )

(ab  cd  sehingga berlaku (ab)(cd)

3. Karena ab dan c d berarti ab0dan cd 0. Hal ini berarti abP dan cdP.

c b a ) 

( . Dengan kata lain (acbc)P, atau

0 )

(acbc  sehingga berlaku acbc

4. Karena ab dan c0 berarti ab0dan c0atau (c)0. Hal ini berarti abP dan cP.

c b

a )( )

( . Dengan kata lain (bcac)P, atau P

ac bc )

( sehingga berlaku bcac

5. Jika a0 maka a0(berdasarkan sifat trikotomi). Karena a0, berdasarkan sifat sebelumnya maka berlaku 1 0,

a Jika 0

1 

a , berdasarkan teorema sebelumnya

diperoleh 1 10      

a

a .

Hal ini bertentangan dengan kenyataan bahwa 1 < 0. Jadi haruslah

0 1



(20)

6. Jika a0, maka a0 (berdasarkan sifat trikotomi). Karena a0, berdasarkan sifat sebelumnya maka maka berlaku 1 0,

a Jika

1 0

a , berdasarkan teorema sebelumnya diperoleh 0

1

1 

     

a a

Hal ini bertentangan dengan kenyataan bahwa 1 < 0. Jadi haruslah

1 0

a

Teorema 4

Jika a,bR, maka a



ab



b

2 1

Bukti.

Karena ab, maka dapat diperoleh aa abatau 2aab Demikian pula abmaka dapat diperoleh ab bbatau ab2b Dari ketaksamaan 2aabdan ab2bdidapatkan

b b a

a  2

b b b

a a

a    

 (2 )

2 1 ) ( 2 1 ) 2 ( 2 1

b b a

a  

 ( )

2 1

Akibat dari teorema di atas adalah:

jika aR dan a0 maka a (ab)b

2 1

Contoh

Tentukan selesaian persamaan dan pertidaksamaan di bawah ini. 1) 2x43

Jawab 3 4 2x 

2 7 2 7 2 2

7 2

4 3 4 4 2

  

     

(21)

Jadi selesaian persamaan 2x43adalah

Pertidaksamaan tipe lain mungkin lebih sulit diselesaikan dibandingkan pertidaksamaan-pertidaksamaan seperti pada contoh di atas.

Beberapa contoh diberikan sebagai berikut. 1) Tentukan selesaian x2 5x60

Jawab

Dengan memfaktorkan ruas kiri pertidaksamaan, maka diperoleh:

  

x2 x3 0

Telah diketahui bahwa hasil kali 2 bilangan real positif apabila ke dua faktor positif atau ke dua faktor negatif. Oleh karena itu,

(22)

Sehingga diperoleh: x3.

(ii).Jika ke dua faktor negatif, maka:

3 dan 2

0 3 dan 0 2

 



  



x x

Diperoleh: x2.

Jadi, selesaian persamaan x2 5x60 adalah x2atau x3.

Selesaian pertidaksamaan di atas dapat pula diterangkan sebagai berikut: Ruas kiri pertidaksamaan bernilai nol jika x2atau x3. Selanjutnya, ke dua bilangan ini membagi garis bilangan menjadi 3 bagian: x2, 2x3, dan x3.

     

Gambar 1.4

Pada bagian x2, nilai (x2) dan (x3) keduanya negatif, sehingga hasil kali keduanya positif. Pada segmen 2 x3, (x2) bernilai positif sedangkan (x3)

bernilai negatif. Akibatnya, hasil kali keduanya bernilai negatif. Terakhir, pada bagian 3



x , (x2) dan (x3) masing-masing bernilai positif sehingga hasil kali keduanya juga positif. Rangkuman uraian di atas dapat dilihat pada Tabel berikut.

Tanda nilai

Kesimpulan 2



x x3 (x2)(x3)

2



x - - + Pertidaksamaan dipenuhi

3

2x + - - Pertidaksamaan tidak dipenuhi 3



x + + + Pertidaksaman dipenuhi

Jadi, selesaian pertidaksamaan adalah x2 atau x3.

Metode penyelesaian seperti pada contoh 1 di atas dapat pula diterapkan pada bentuk-bentuk pertidaksamaan yang memuat lebih dari 2 faktor maupun bentuk-bentuk pecahan.

x<2 2<x<3 x>3

(23)

2) x3 2x2 x11. Jawab

Apabila ke dua ruas pada pertidaksamaan di atas ditambah 1, maka diperoleh:

0 ) 2 )( 1 )( 1 (

0 2 2 2

3

    

   

x x x

Jika (x1)(x1)(x2)0, maka diperoleh: x1, x1, atau x2. Selanjutnya, perhatikan table berikut:

Nilai-nilai peubah x1,x1,x2 disebut titik kritis. Tanda nilai/nilai

Kesimpulan 1



x x1 x2 (x1)(x1)(x2)

1

 

x - - - - Pertidaksamaan dipenuhi

1 1 

 x + - - + Pertidaksamaan tidak dipenuhi

2

1x + + - - Pertidaksamaan dipenuhi

2



x + + + + Pertidaksamaan tidak dipenuhi

1

 

x 0 -2 -3 0 Pertidaksamaan dipenuhi

1



x 2 0 -1 0 Pertidaksamaan dipenuhi

2



x 3 1 0 0 Pertidaksamaan dipenuhi

Jadi, selesaian pertidaksamaanx3 2x2 x11 x  1 atau 1  x2. Cara lain untuk menentukan selesaian pertidaksamaan x3 2x2 x11. adalah dengan menggunakan garis bilangan

2 ,

1 ,

1

, 0 ) 2 )( 1 )( 1 (

0 1 1 2

1 1 2

2 3

 

 

    

     

    

x dan x

x

adalah maan

pertidaksa kritis

titik Sehingga

x x x

Dengan memilih satu titik sebarang disetiap interval diatas diperoleh: - - - + + + + + + + - - - + + + + + + +

1

(24)

Berdasarkan garis bilangan di atas selesaian pertidaksamaan adalah x 1 atau 1 x2.

3) 1

2 8 2

 

 x

x x

.

Penyelesaian

Apabila pada ke dua ruas ditambahkan (x1) maka diperoleh:

0 2

) 2 )( 5 (

0 2

10 3

0 2

2 8

2 0 ) 1 ( 2

8 2

2



 

 



 

 



  

      

x x x

x x x x

x x

x

Nilai nol pembilang adalah 2dan 5, sedangkan nilai nol penyebut adalah 2.

Sekarang, untuk mendapatkan nilai x sehingga 0 2

) 2 )( 5 (



 



x x x

diperhatikan tabel

berikut:

Tanda nilai/nilai

Kesimpulan 2



x x2 x5

2 ) 5 )( 2 (

 



x x x

2

 

x - - - - Pertidaksamaan tidak

dipenuhi 2

2 

 x + - - + Pertidaksamaan

dipenuhi 5

2 x + + - - Pertidaksamaan tidak

dipenuhi 5



x + + + + Pertidaksamaan

dipenuhi 2

 

x 0 -4 -7 0 Pertidaksamaan

dipenuhi 2



x 4 0 -3 Tidak

terdefinisi

Pertidaksamaan tidak dipenuhi

5



x 7 3 0 0 Pertidaksamaan

dipenuhi

(25)

Soal-soal

1) Misalkana,b,c,d  R buktikan pernyataan berikut: a. Jika ab,bcmaka adbcacbd

b. Jika ab dan cd maka acbd

c. a2  b2  0 jika dan hanya jika a = 0 atau b = 0

2) Carilah bilangan a,b,c,d  R yang memenuhi 0ab dan ad 0 dan berlaku

a) acbd b) acbd.

3) Tentukan bilangan real x , sedemikian sehingga:

a) x2 3x4

b) 1x2 4

c) x2 3x40

d) 0

6 2

1   

x x

e) 0

1 2 2

  

x x

f) 5

1 2 1

  

x x

g)

x

x 3

4

1 

h) x

x 

1

i) 7

2 1



x

j) 3

2 1

 

x

1.3 Sistem Bilangan Komplek

(26)

dengana,b,creal. Nilai peubah x yang memenuhi persamaan kuadrat dinamakan

selesaian. Selesaian suatu persamaan yang juga disebut dengan akar-akar persamaan kuadrat dapat berupa bilangan real atau tidak real. Misal x2 10 adalah sebarang persamaan kuadrat, maka persamaan tersebut akar-akarnya tidak real atau dengan kata lain tidak ada bilangan real yang memenuhi persamaan x2 10_{, hal ini dikarenakan}

. 1

2 

x _{Pernyataan ini adalah sesuatu yang tidak mungkin karena tidak ada kuadrat} suatu bilangan real yang hasilnya 1._{Untuk itu perlu diperkenalkan bilangan komplek}

yaitu suatu bilangan yang mempunyai bentuk umum abi dimana a,breal_dan 1

 

i .

Bilangan komplek didefinisikan sebagai pasangan berurutan dari bilangan real b

a, yang memenuhi sifat-sifat tertentu yang secara umum dituliskan sebagaizabi.

Kita dapat mengangap sebuah bilangan komplek mempunyai sifat 2 1.

i _{. Untuk} selanjutnya dalam bilangan komplek zabi. a disebut bagian real dari dari z dan b disebut bagian bilangan imajiner dari z, secara berturut-turut keduanya dilambangkan dengan aRe{z}_danbIm{z}. Variable yang berlaku pada bilangan komplek disebut sebagai variabel komplek.

Dua bilangan komplek z₁ abi dan z₂ cdiadalah sama jika dan hanya jika ac dan bd. Kita dapat mengangap bilangan asli sebagai sebuah bagian dari

susunan bilangan komplek dengan b = 0. Bilangan komplek 0 + 0i dan -3 +0i kembali ditunjukan bilangan asli 0 dan -3 berturut-turut. Jika a = 0 ,bilangan komplek 0 + bi atau disebut bilangan imajiner sejati.

Konjugate komplek atau secara singkat konjugate, suatu bilangan komplek bi

a adalah abi. Konjugate bilangan bilangan komplek z sering diindikasikan oleh atau z*.

Contoh:

1) 23i23i

2) i i i

4 5 4 1 4

5 1 4

5 1

    

3) (3i)(22i)(66i2i2i2)(66i2i2)84i84i

(27)

Maka

a) Re{z₁z₂}1 b) Re{z1z2}2 c) Re{z₁z₂}2

d) Im



6 3 4



/7

3 2

1  

     

z z z

e) Im



z₁ z₂ z₃



1 3 Soal-soal

1. Tunjukkan bahwa z1 1i,z2 1i adalah akar-akar dari persamaan kuadrat

0 2 2

2   

z z

2. Tunjukkan bahwa

2 2 1 ,

2 2 1

2 1

i z

i

z       adalah akar-akar dari persamaan

kuadrat z2 z10

3. _Tentukan

a.

 

32i 2 53i



b.

    

  

i i

3 2

4 2 3

1.4 Operasi dasar pada bilangan Komplek

Operasi yang ditunjukan pada bilangan komplek juga berlaku seperti pada Aljabar. Operasi pada bilangan komplek meliputi penjumlahan, pengurangan, perkalian, dan pembagian. Pada operasi bilangan komplek kita dapat memprosesnya seperti aljabar dari bilangan-bilang asli dan mengganti dengan -1 sehingga diperoleh hasil sebagai operasinya.

Misal z1 abi dan z2 cdi hasil operasinya dapat dijelaskan sebagai berikut:

1. Penjumlahan

i d b c a di c bi a di c bi a z

z₁ ₂ (  )(  )    (  )(  )

Contoh

(28)

b. _\2(14i)2(42i)(28i)(84i)(28)(8i4i)104i

c.

  

2i  37i

 

 22i



2i37i22i76i

2. Pengurangan

i

Contoh

a) 3(14i)2(7i)(312i)(142i)(314)(12i2i)1714i b) 3(14i)2(1i)(312i)(22i)(32)(12i2i)110i

c) 2(4i)(2i)(23i)



82i2i23i

 

 8222ii3i



44i

3. Perkalian

i

Contoh

(29)

Contoh

1. Selesaikanlah a. (32i)(7i)

b. (7i)(32i)

c. (86i)(2i7)

(30)

e.



(53i)(12i)



(75i) f. (23i)(42i)

g. (42i)(23i)

h. (2i)



(32i)(54i)



i.



(2i)(32i)



(54i) j. (12i)



(75i)(34i)



k.

i i

 1

2 3

l.

i i

i

3 4

20 4

3 5 5

   

m.

1 2 310 19

 

i i i

n.

2

3 3 2 1

    

  



 i

o.

3 2

1 1 2 1

1

3 

    

        

 

i i i

i

p. ₅ ₁₀ ₁₅

16 9 4

2 i i i

i i i

    

q.

3

7 5 2

   

 

 

i i

r.

2 7 2 3

 

 i

i i

i

s.

) 2 )( 1 (

3

i i

i

 

t.



32i



2 u.

   

1i 2 2i 2

2. Jika = 2 + , = 3−2 = − + √ ,

Tentukan nilai masing-masing berikut ini. a. 3z₁ 4z₂

(31)

c.

 

z₃ 4

1.5 Nilai Mutlak

Nilai Mutlak atau modulus dari suatu bilangan komplek zabi dinotasikan dengan z dan didefinisikan sebagai z  abi  a2 b2

Contoh

a) 2 3 2 ( 3) 4 9 13

2

2      

(32)

b) 4 2 ( 4) 2 16 4 20 2 5

2

2     

  

 i

c) 2 3 2 3 4 9 13

2

2     

 i

d) 4 5 ( 4) ( 5) 16 25 41

2

2      

 

 i

e)

13 6 1 9 1 4 1 3

1 2

1 3

1 2

1 2 2

                

 i

Jika z₁,z₂,z₃,...z_m adalah bilangan komplek, berlaku sifat-sifat berikut

1. z₁z₂  z₁ z₂ atau z₁z₂ ...z_m  z₁ z₂ ... z_m

Bukti

Misal z1 abi, z2 cdi



a bi



c di

 

ac bd

 

ad bc



i z

z₁ ₂       

 z₁z₂  (acbd)2 (adbc)2`

 (a2c2 2acbdb2d2)(a2d2 abcdb2c2`

 (a2c2 b2d2 a2d2`

 (a2 b2)(c2 d2)`

 2 2 2 2

d c b

a  

 ( 2 2)( 2 2)`

d c b

a  

 z1 z2

2. ,

2 1 2 1

z z z z

 jika z2 0

Bukti

Dari operasi pembagian dua bilangan komplek diperoleh:





2 2 2

1 ( )

d c

i ad bc bd ac di c

bi a z z

 

   

(33)





Dilain pihak

Sehingga dapat

disimpulakn bahwa ,

2 (a). Penyelesaian

Misal z₁  x₁ iy₁,z₂  x₂ iy₂ dan kita harus menunjukkan bahwa

Contoh soal

(34)

1) Jika z i z i z i

Sehingga diperoleh dua persamaan

(35)

Dengan menggunakan metode substitusi diperoleh x1,y2

(36)

Tentukan nilai masing-masing berikut ini. a) 3z₁ 4z₂

b) z₁3 3z₁2 4z₁8 c)

 

z3 4

d)

2

1 3

3 2

5 2

i z

z

i z

z

 

  



e) z₁2 3z₁2z₁4 f) 3z₁ 4z₂

3. Tentukan z dari:

a.

2 3 2

1 i

z  

b. (1 )

2 2

i

z  

c. z(4i)(i1)(7i2)

d. z 33i 3 e. z2

 

i 3

1.6 Pembangun-pembangun Aksiomatis dari Sistem Bilangan Komplek

Dari suatu segi pandangan yang logis dapat digambarkan angka-angka complex sebagai pasangan ( ba, )dari bilangan real a dan b menunjuk pada yang definisi yang

beragam ternyata sama dengan definisi diatas. Semua definisi yang digambarkan ini, dimana semua angka menggantikan bilangan-bilangan real.

a. Persamaan (a,b)(c,d) jika dan hanya jika ac,bd b. Penjumlahan (a,b)(c,d)(ac,bd)

c. Produk (a,b)(c,d)(acbd,ad bc) dan m(a,b)(ma,mb)

Dari ini kita dapat menunjukkan bahwa (a,b)a(1,0)b(0,1) dan kita berhubungan dengan ini abi di mana lambang untuk (0,1) dan mempunyai

) 0 , 1 ( ) 1 , 0 )( 1 , 0 (

2   

(37)

jadilah setara dengan bilangan real 1. Pasangan yang diinginkan (0,0)sesuai dengan bilangan real 0.

Dari pernyataan di atas kita dapat membuktikan bahwa jika z1,z2,z3bagian dari

Hukum Komutatif Penjumlahan

3. z₁(z₂ z₃)(z₁z₂)z₃

Hukum Asosiatif Penjumlahan

4.

Hukum komutatif Perkalian

(38)







Hukum Distributif Perkalian terhadap Penjumlahan

7.

0 disebut identintas penjumlahan 1 disebut identintas perkalian

8. Untuk suatu bilangan komplek z ada satu bilangan ₁ zS

yang tunggal sedemikian sehingga z1 z zz1 0. Untuk selanjutnya zdisebut invers (balikan) penjumlahan dari z dan dilambangkan dengan ₁ z₁.

(39)

disebut inver perkalian dari z dan dilambangkan dengan ₁

1 1



z atau

1

z

Secara umum suatu himpuan sedemikian sehingga seperti pada S yang

anggota-anggotanya memenuhi sifat di atas disebut dengan field (lapangan). Contoh

1. Gunakan defenisi dari sebuah bilangan kompleks sebagai pasangan orderdari bilangan real dan defenisi pada halaman tiga untuk membuktikan bahwa (a,b)=a(1,0),b(0,1)dimana (0,1),(0,1)=(-1,0)=(a,c) + (c,b)=(a,b)

Dari defenisi jumlah dan produk atau hasil di halaman 3, kita mendapatkan ( , ) = ( , 0) + ( 0, ) = ( 1,0) + ( 1,0) dimana

( 0,1) ( 0,1) = ( 0∗0−1∗1,0∗1 + 1∗0) = (−1,0) Dari identifikasi ( 1,0) dengan 1 dan ( 0,1) dengan , kita melihat bahwa ( , ) = +

2. Jika = ( , ) , = ( , ) dan = ( , ), membuktikan hukum

persamaan distribusi z₁(z₂ z₃)z₁z₂ z₁z₃

Kita mendapatkan

, = ( , ) { ( , ) + ( , ) } = ( , ) ( , ) + ( , )

= { ( + )− ( , ) , ( , ) + ( + ) }

= − + − , + + +

= ( − , + ) + ( − , + )

= ( , ) ( , ) + ( , ) ( , ) = , + ,

1.7 Representasi secara Grafis Bilangan Komplek

(40)

Gambar 1.4

Selanjutnya kita dapat meletakkan sebarang titik pada bidang dengan cara menarik garis yang sejajar masing-masing dan kedua garus dapat b ertemu di satu titik, titik tersebut dinamakan koordinat tegak lurus dan dinotasikan dengan (x,y).Pada gambar di atas dipilih titik P(3,5).

Karena suatu bilangan komplek z xyi dapat dipandang sebagai pasangan berurutan bilangan real sehingga kita dapat merepresentasikan bilang komplek dengan suatu titik pada bidang xy. Bidangxy sebagai representasi bilangan komplek dinamakan bidang komplek atau argand. Bilangan komplek yang ditunjukkan titik

) 5 , 3 (

P seperti pada gambar 1.2 dapat dipandang sebagai 35i. Setiap bilangan komplek berkorepondesni satu dan hanya satu dengan setiap titik pada bidang, sebaliknya setiap satu titik pada bidang berkorespondensi dengan satu dan hanya satu bilangan komplek. Karena hal ini sering dan biasa kita menyatakan bilang komplek z,

sebagai titik z .

Kadang-kadang kita dapat menyatakan sumbu x dan sumbu y sebagai sumbu real dan sumbu imajiner secara berturut-turut dan bidangnya dinamakan bidang z Jarak . antara dua titik z₁ x₁ y₁i dan z₂  x₂ y₂ipada bidang komplek diberikan oleh

2 2 1 2 2 1 2

1 z (x x ) (y y )

z     

Contoh soal

(41)

a)



23i



(45i) Secara analitis

Secara grafis

Gambar 1.5

b) 3(1 + 2i) – 2(2 – 3i) Secara analitis

i i

i

i) 2(2 3) (3 6 ) (4 6 ) (3 4) (6 6) 1 12 2

1 (

3             

Secara grafis

gambar 1.6

c) (7 + i) – (4 – 2i)

d) 3(1 + i) + 2(4 – 3i) – (2 + 5i)

e) ( 4−3 ) + ( 5 + 2 )

X Y

i

6 3

i

6 4 

i

12 1 

i

3 2

i

5 4

i

2 6

X Y

(42)

Contoh 1.c,d dan e ditinggalkan penulis sebagai latihan bagi pembaca.

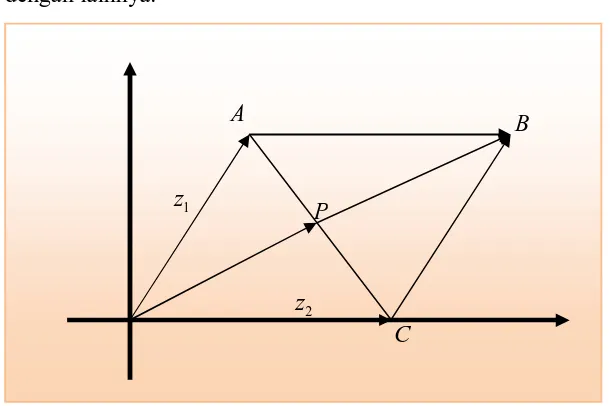
2. Jika z₁,z₂dan z3merupakan vektor yang ditunjukan dalam gambar 1.7, buatlah

grafik : (a). 2z₁ + z₃ (c). z₁+ (z₂+ z₃) (e). ₂ ₁ ₃ 3 2 4 3 3 1

z z

z  

(b). (z₁+ z₂) + z₃ (d). 3z₁- 2z₂+ 5z₃

Gambar 1.7

3. Jika z₁= 4 – 3i dan z₂= -1 + 2i, buatlah grafik dan analitik:

(a). z1z2 (b). z1z2

(b). z₁z₂ (d). 2z13z22

4. Letak vektor dari titik A,Bdan C dari segitiga ABC masing-masing diberi

1

z = 1 + 2i, z₂= 4 - 2i dan z₃ = 1 – 6i. Buktikan bahwa ABC merupakan segitiga

samakaki dan hitunglah panjang sisinya.

5. Misalkan z₁,z₂,z₃,z₄,letak vektor tegak lurus untuk segi empat ABCD . Buktikan

bahwa ABCD adalah sebuah jajaran genjang jika dan hanya jika

.` 0

4 3 2

1 z z z 

z

6. Jika diagonal sebuah segi empat saling membagi dua,buktikan bahwa segi empat merupakan sebuah jajaran genjang.

X Y

1

z

2

z

3

(43)

7. Buktikan bahwa median dari sebuah segitiga dihubungkan dalam satu titik.

8. Misalkan segi empat ABCD dan E,F,G,Htitik tengah dari sisinya. Buktikan bahwa EFGH adalah sebuah jajaran genjang.

9. Dalam jajar genjang ABCD , titik E membagi dua sisi AD. Buktikan bahwa dimana titik BE dihubungkan dengan titik AC membagi AC .

10.Letak vektor dari titik A,B berturut-turut adalah 2 + i dan 3 – 2i. (a). carilah sebuah persamaan garis AB. (b). carilah sebuah persamaan garis yang tegak lurus ke AB pada titik tengahnya.

11.Gambar dan grafik bentuk manakah yang ditunjukan di bawah ini:

(a). zi 2, (b). z2i  x2i 6, (c). z3 z3 4,(d). z(z2)3,(e).

 

4. Imz2 

12.Carilah sebuah persamaan (a). sebuah lingkaran jari-jarinya 2 dengan titik pusat (-3,4) , (b). panjang lingkaran dengan titik pusat pada (0,2) dan (0,-2) yang mana sumbu utama mempunyai panjang 10.

1.8 Bentuk Polar Bilangan Komplek

Jika P adalah titik pada bidang komplek yang berkorepondensi dengan bilangan komplek (x,y) atau xyi_{maka berdasarkan gambar 1.8 kita dapat melihat}

(44)

Gambar 1.8

Karena r x2  y2  x yi adalah modulus atau nilai mutlak dari bilangan komplek

1

iy x

z   (dinotasikan dengan mod zatau z ); dan _{disebut amplitude atau}

argument dari zxiy(dinotasikan dengan arg z), adalah sudut yang dibuat oleh garis

OP dengan sumbu x positif.

Oleh karena itu, zxy r(cos isin)

Yang disebut bentuk polar dari bilangan komplek, r dan θ disebut koordinat polar. Kadang-kadang dengan mudah untuk menulis dan menyebut sebagai singkatan cis

untuk cosisin.

Untuk suatu bilangan kompleks z 0 terdapat korespondensi satu dan hanya satu terdapat hanya satu nilai yang sesuai dengan  untuk 0 ≦ < 2π. Namun, interval lain dari panjang 2π, misalnya - π < θ ≦ π, dapat digunakan. Setiap pilihan utama, diputuskan terlebih dahulu, disebut jarak utama, dan nilai θ disebut nilai utamanya.

Contoh

1. Nyatakan setiap titik dalam koordinat tegak lurus berikut dalam bentuk polar a. 22i

) , (x y P

X Y



y

x r

(45)

Gambar 1.9

Karena z22i maka z r  22 (2)2  8 2 2

Karena titiknya terletak pada kuadran ke-4 maka 335 7 /4 2

2

cos   o   Sehingga z22i2 2



cos7/4isin7/4



2 2cis



7 /4



b. 1 i 3

Gambar 1.10

Karena zii 3 maka z r (1)2 ( 3)2  4 2

Karena titiknya terletak pada kuadran ke-2 maka 120 2 /3 2

3

sin   o  

Sehingga z 1i 32



cos2 /3isin2 /3



2cis



2 /3



c. 2 22 2i

X Y

3 1 i



3 / 2

X Y

i

2 2

2 

2

4

(46)

Gambar 1.11

2 2 2

2 i

z  maka z r  (2 2)2(2 2)2  16 4

Karena titiknya terletak pada kuadran ke-1 maka 45 /4 2

2 4

2 2

cos    o 

Sehingga z2 22i 24



cos/4isin/4



4cis

 

 /4

d. i

Gambar 1.12

i

z maka z r  (0)2(1)2  11

Karena titiknya terletak pada sumbu -Y maka 0 270 3 /2 1

0

cos    



 o

Sehingga zi1



cos3 /2isin3/2



cis



3/2



e. -4

X Y

i



X Y

2 2 2

(47)

Gambar 1.13

4  

z maka z r (4)2(0)2  144

Karena titiknya terletak pada sumbu -X maka   1180o  4

4 cos

Sehingga z44



cos isin



4cis

 



f. 2 32i

Gambar 1.14

i

z2 32 maka z r  (2 3)2(2)2  16 4 Karena titiknya terletak pada kuadran 3 maka 210o

4 2 cos    Sehingga z2 32i4



cos210oisin210o



g. Buktikan bahwa

) 2 / 1 (tan 1

5

2i ei  X Y

i

2 3

2 



(48)

Gambar 1.15

i

z2 maka z r (2)2 (1)2  5 Karena titiknya terletak pada kuadran 1 maka

2 1 tan 

Diperoleh 

    

2 1 arctan



Sehingga z2i 5



cos(arctan(1/2)isin(arctan(1/2)



 5eiarctan(1/2)  5eitan1(1/2)

2. Nyatakanlah bentuk polar berikut dalam koordinat tegak lurus a. 6(cos135oisin135o)

Karena  135o 3/4 berarti x0,y0

dan diperoleh

2 3 ) 2 2 / 1 ( 6 135 cos

6   

 o

x

2 3 ) 2 2 / 1 ( 6 135 sin

6  

 o

y

Sehingga 6(cos135o isin135o)6cis135o (3 2,3 2)

Catatan

4 / 3

6 ) 135 sin 135

(cos

6 oi o  e i

b. o

cis 90

12

Karena  90o /2 berarti x0,y0

dan diperoleh

Y



i

 2

(49)

0

dan diperoleh

2

dan diperoleh

3

dan diperoleh

3

Soal-soal

(50)

b. 12i

c. 3i 3 d. 22 3i

e. 55i

f.  6i 2 g. 3i

h. 5

2. Buatlah grafik untuk titik yang dinyatakan oleh a. 6cos(240o isin240o)

b.

4 2cis

c. 

  

 

4 7 2

2 cis 

d. 3 /5

4e i e. 2ei/4

3. Seseorang menempuh perjalalan wisata 12 km dalam arah timur laut (northeast), dilanjutkan 20 km dalam arah o

30 disebelah barat dari utara kemudian 18 km o

60

disebelah selatan dari barat. Tentukan secara analitis dan grafis jarak yang ditempuh dan bagaimana arah yang ditempuh dari titik awal.

1.9 Teorema de Moivre

Jikaz₁ x₁iy₁r₁(cos₁ isin₁)danz₂ x₂ iy₂ r₂(cos₂ isin₂)_kita dapat menunjukkan bahwa:

) sin (cos

) sin

(cos 1 1 2 2 2

1 2

1z r  i  r  i 

z   



1 2



2 2 1 2

1 2

1r cos cos icos sin isin cos i sin sin

r   





i



r

r₁ ₂ (cos₁cos₂sin₁sin₂)(sin₁cos₂cos₁sin₂) 



cos( 1 2) sin( 1 2)



... (2)

2

1r i

r     



 2 1

z z

) sin (cos

2 2

2

1 1

1



 i 

r

i r

 