Metode branch-and-cut untuk menyelesaikan permasalahan rute kendaraan berkapasitas - USD Repository

i

METODE BRANCH-AND-CUT UNTUK MENYELESAIKAN

PERMASALAHAN RUTE KENDARAAN BERKAPASITAS

Skripsi

Diajukan untuk Memenuhi Salah

Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun Oleh :

Victor

NIM : 063114001

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

ii

BRANCH AND CUT METHOD TO SOLVE CAPACITATED VEHICLE

ROUTING PROBLEMS

Thesis

Presented as Partial Fulfillment of the Requirements

To Obtain The Sarjana Sains

In Mathematics

By :

Victor

Student Number : 063114001

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT

SCIENCE AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY

YOGYAKARTA

vi

HALAMAN PERSEMBAHAN

Kupersembahkan untuk

Papa

dan

mama

viii ABSTRAK

ix ABSTRACT

x

KATA PENGANTAR

Segala puji dan syukur, penulis panjatkan kepada Tuhan Yesus Kristus, sang Juru Selamat, sehingga karena kasih dan karunia-Nya skripsi ini dapat terselesaikan tepat waktu.

Dalam penyusunan skripsi ini penulis membutuhkan bantuan dari berbagai pihak. Oleh karena itu, pada kesempatan ini ingin mengucapakan terima kasih atas segala segala bimbingan, bantuan, dorongan dan kerjasama yang telah diberikan sehingga skripsi ini dapat terselesaikan dengan baik, kepada:

1. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen pembimbing dan Kaprodi Matematika FST-USD yang dengan rendah hati mau meluangkan banyak waktu luang dan penuh kesabaran telah membimbing selama penyusunan skripsi ini dari awal hingga akhir.

2. Ibu Ch. Enny Murwaningtyas, S.Si., M.Si., selaku dosen penguji yang telah memberikan saran dan kritik dalam skripsi ini.

3. Bapak St. Eko Hari Parmadi, S.Si., M.Kom., selaku dosen penguji yang telah memberikan saran dan kritik dalam skripsi ini.

4. Papa, mama, kakak-kakakku, dan keluargaku atas kasih sanyang, doa, semangat, dan dukungannya.

5. Sahabat-sahabatku seperjuangan angkatan 2006, terima kasih atas semangat dan dukungannya.

xi

7. Semua pihak yang telah membantu penulisan skripsi ini yang tidak dapat penulis sebutkan satu persatu.

Tak ada gading yang tak retak, penulis menyadari kekurangan dalam skripsi ini, untuk itu saran serta kritik sangat diharapkan dalam peningkatan kualitas skripsi ini, dan akhirnya penulis berharap semoga skripsi ini dapat bermanfaat bagi semua pihak.

Yogyakarta, Juni 2010

Penulis

xii DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

HALAMAN PERSEMBAHAN ... vi

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ... vii

ABSTRAK ... viii

ABSTRACT ... ix

KATA PENGANTAR ... x

DAFTAR ISI ... xii

DAFTAR GAMBAR ... xiv

BAB I. PENDAHULUAN ... 1

A. Latar Belakang Masalah ... 1

B. Perumusan Masalah ... 3

C. Batasan Masalah ... 3

D. Tujuan Penulisan ... 4

E. Metode Penulisan ... 4

F. Manfaat Penulisan ... 4

xiii

BAB II. METODE BRANCH-AND-BOUND DAN CUTTING PLANE ... 6

A. Matriks dan Operasi Baris Elementer ... 6

B. Program Linear... 8

C. Metode Simpleks yang Diperbaharui ... 16

D. Metode Branch-and-bound ... 22

E. Metode Cutting plane ... 36

BAB III. METODE BRANCH-AND-CUT PADA PERMASALAHAN RUTE KENDARAAN BERKAPASITAS ... 47

A. Permasalahan Rute Kendaraan Berkapasitas (Capacitated Vehicle Routing Problems - CVRP) ... 47

B. Metode Branch-and-cut ... 54

C. Perbandingan Metode Branc- and-Cut, Cutting plane, dan Branc-and-Bound. ... 66

BAB IV. APLIPAKSI METODE BRANCH-AND-CUT DALAM MASALAH PENDISTRIBUSIAN BUSA PADA PABRIK “Sari Guna” ... 84

BAB V. PENUTUP A. Kesimpulan ... 101

B. Saran ... 102

DAFTAR PUSTAKA ... 103

xiv

DAFTAR GAMBAR

Halaman

Gambar 2.4.1. Algoritma Metode Branch-and-bound ... 26

Gambar 2.5.1 Algoritma Metode Cutting plane ... 39

Gambar 3.2.1. Algoritma Metode Branch-and-cut ... 57

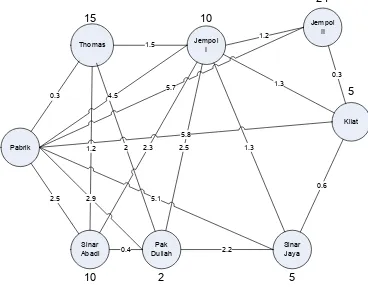
Gambar 4.1.1. Graf permasalahan distribusi di pabrik busa “Sari Guna” ... 85

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Berkembangnya sebuah perusahaan yang memproduksi barang dapat menyebabkan perusahaan perlu melakukan perluasan bidang usaha. Dengan adanya perluasan bidang usaha, perusahaan dituntut untuk dapat memenuhi kebutuhan konsumen yang ada. Hal ini mengakibatkan biaya operasi perusahaan semakin besar, terutama pada bidang pengiriman barang. Oleh sebab itu, belakangan ini banyak terlihat peningkatan kegunaan dari pengoptimalan pengiriman barang yang berbasis pada riset operasi dan pemograman matematika. Banyak perusahaan-perusahaan menggunakan pengoptimalan untuk masalah perencanaan pengiriman barang dan dapat menghemat antara 5% sampai 20% dari total biaya pengiriman itu sendiri (Paolo T, 2002). Permasalahan seperti pengiriman barang dari produsen kepada konsumen seperti ini secara umum disebut permasalahan rute kendaraan (Vehicle Routing Problem).

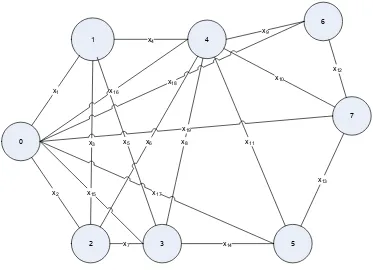
Dengan menggunakan metode jaringan yang ada pada riset operasi, pengiriman barang biasanya digambarkan menggunakan graf dengan anak panah dan simpul. Anak panah menggambarkan jalan atau rute yang dapat dilewati. Tidak semua anak panah dapat langsung dilewati begitu saja menuju konsumen, ini semua tergantung dari apakah rute tersebut hanya dapat dilewati satu arah saja atau dapat dilewati dua arah. Setiap anak panah mempunyai nilainya masing-masing yang mungkin dapat diartikan sebagai ongkos atau secara umum sering dianggap sebagai panjang atau waktu tempuh rute tersebut. Simpul menggambarkan tempat-tempat yang dilewati sewaktu mengirimkan barang dan simpul terakhir biasanya diartikan sebagai konsumen atau tempat terakhir pengiriman barang tersebut.

konsumen dapat dilayani yang dikarenakan konsumen sedang tidak ada ditempat, adanya batasan waktu yang diberikan konsumen untuk memenuhi permintaannya, dan banyaknya kendaraan yang bisa dipakai untuk melayani konsumen. Terkadang setiap permintaan konsumen tidak dapat dipenuhi seutuhnya atau tidak sama sekali. Untuk menghadapi hal seperti ini prioritas atau pinalti yang berhubungan dengan keterbatasan pengiriman dapat diberikan kepada konsumen.

Permintaan-permintaan konsumen dilayani oleh perusahaan menggunakan kendaraan. Kendaraan disini mempunyai karakteristik yang berbeda-beda bergantung pada keperluan konsumen. Beberapa karakteristik dari kendaraan tersebut adalah sumber (home depot) dan kemungkinan berakhir ditempat lain setelah menyelesaikan masalah, kapasitas kendaraan yang mengekspresikan berat atau volum atau banyaknya barang yang dapat dibawa sebuah kendaraan, jenis barang yang dapat diangkut oleh sebuah kendaraan, jalan yang mana yang bisa dilalui oleh sebuah kendaraan, dan biaya yang dikenakan pada kendaraan (jarak, waktu, jalan, dll).

Melihat adanya berbagai macam permintaan dari konsumen dan karakteristik yang ada pada kendaraan, maka ada banyak masalah pengoptimalan yang timbul yaitu permasalahan rute kendaraan berkapasitas (Capacitated Vehicle Routing Problems), yang merupakan bentuk paling dasar dari permasalahan pada VRP, distance-constained VRP, VRP dengan Time Windows, VRP dengan Backhauls dan VRP dengan Pickup and Delivery. Dalam penulisan ini hanya akan dibahas pada permasalahan rute kendaraan berkapasitas (Capacitated Vehicle Routing Problems).

Permasalahan rute kendaraan berkapasitas adalah masalah pengoptimalan yang hanya berbasis pada satu tempat awal, permintaan konsumen yang pasti, semua kendaraan yang dipakai adalah identik, dan terdapat batasan kapasitas pada kendaraan. Tujuan dari masalah pengoptimalan di atas adalah untuk meminimumkan total biaya untuk melayani semua komnsumen yang ada.

yang melambangkan biaya yang diperlukan dari simpul awal menuju simpul tujuan. Secara umum perjalanan dari suatu simpul menuju simpul yang sama tidak diperbolehkan. Untuk menghindari hal ini didefinisikan biaya perjalanan tersebut adalah ∞. Setiap konsumen mempunyai suatu bilangan nonnegatife yang menyatakan permintaan yang harus dikirimkan ke konsumen tersebut, sedangkan permintaan untuk sumber adalah 0. Pengiriman barang dilakukan dengan sejumlah kendaraan di sumber yang masing-masing mempunyai kapasitas yang sama. Untuk menjamin adanya daerah yang memenuhi, perlu diasumsikan bahwa setaiap permintaan konsumen tidak lebih dari kapasitas kendaraan

Dari graf tersebut, Capacitated Vehicle Routing Problem dapat dirumuskan sebagai permasalahan program linear bilangan bulat. Untuk menyelesaikan permasalahan tersebut, dapat menggunakan metode Cutting plane, metode Branch-and-bound, metode Branch-and-cut, metode Set Covering, metode Classical Heuristics, metode Metaheuristics, metode implicit enumeration, dan lain sebagainya. Namun, dalam penulisan ini akan dipaparkan metode Branch-and-cut untuk menyelesaikan masalah Capacitated Vehicle Routing Problem.

B. Perumusan Masalah

Berdasarkan latar belakang masalah di atas dapat dirumuskan permasalahan sebagai berikut:

1. Bagaimana cara menentukan solusi optimal Capacitated Vehicle Routing Problem dengan menggunakan metode Branch-and-cut.

2. Bagaimana algoritma metode Branch-and-cut dan implementasinya menggunakan bahasa pemrogaman MATLAB.

C. Batasan Masalah

D. Tujuan Penulisan

Tujuan penulisannya adalah untuk menyelesaikan permasalahan rute kendaraan berkapasitas dengan menggunakan metode Branch-and-cut dan untuk menyusun algoritma Branch-and-cut menggunakan bahasa pemrograman MATLAB.

E. Metode Penulisan

Metode penulisan ini menggunakan metode studi pustaka, yaitu dengan menggunakan buku-buku pendukung yang berkitan dengan metode Branch-and-cut dan menuliskan programnya dengan bahasa pemrograman MATLAB.

F. Manfaat Penulisan

Manfaat penulisan ini adalah untuk memperoleh pengetahuan tentang metode Branch-and-cut dalam menyelesaikan permasalahan rute kendaraan berkapasitas serta pemrogramannya dengan bahasa pemrograman MATLAB.

G. Sistematika Penulisan

BAB I PENDAHULUAN

A. Latar Belakang Masalah B. Perumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Metode Penulisan F. Manfaat Penulisan G. Sistematika Penulisan

BAB II METODE BRANCH-AND-BOUND DAN CUTTING PLANE

A. Matriks dan Operasi Baris Elementer B. Program Linear

D. Metode Branch-and-bound E. Metode Cutting plane

BAB III METODE BRANCH-AND-CUT PADA PERMASALAHAN RUTE

KENDARAAN BERKAPASITAS

A. Permasalahan Rute Kendaraan Berkapasitas (Capacitated Vehicle Routing Problems - CVRP)

B. Metode Branch-and-cut

C. Perbandingan Metode bound, Cutting plane, dan Branch-and-cut.

BAB IV APLIPAKSI METODE BRANCH-AND-CUT DALAM MASALAH

PENDISTRIBUSIAN BUSA PADA PABRIK “Sari Guna”

BAB V PENUTUP

BAB II

METODE BRANCH-AND-BOUND DAN CUTTING PLANE

A. Matriks dan Operasi Baris Elementer

Definisi 2.1.1

Matriks bujur sangkar A berukuran n×n mempunyai invers jika ada matriks B sehingga AB=BA=I_n. Matriks B disebut matriks invers dari A.

Teorema 2.1.2

Jika matriks A berukuran n×n mempunyai invers, maka untuk sebarang matriks kolom b berukuran n×1, sistem persamaan Ax=b mempunyai penyelesaian tunggal, yaitu x=A−1b berukuran n×1.

Bukti:

Karena A mempunyai invers, maka

b A x

b A Ix

b A Ax

A

b Ax

1 1 1 1

− − − −

= = = =

2 1

1 2

1 2

1 2 1 1

1 2

1 2 2 1

x x

x x

ο

) x I(x

ο

) x A(x A

ο

A

) x A(x

ο

Ax Ax

ο

Ax Ax

= − =

− =

− =

− =

− =

=

− −

■

Definisi 2.1.3

Matriks yang mempunyai invers disebut matriks tak singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.

Definisi 2.1.4

Operasi baris elementer pada suatu matriks adalah salah satu operasi: 1. Menukar letak dari dua baris tersebut.

2. Mengalikan suatu baris dengan konstanta tak nol.

3. Menganti suatu baris dengan hasil penjumlahan baris tersebut dan kelipatan baris lain.

Definisi 2.1.5

Sebuah sistem persamaan Ax=b terdiri dari tiga matriks, yaitu matriks koefisien, A, matriks variabel, x, dan matriks ruas kanan, b. Matriks lengkap adalah matriks yang terdiri dari matriks koefisien dan matriks ruas kanan, yakni

B. Program Linear

Program linear (Linear Programming - LP) adalah sebuah alat untuk menyelesaikan permasalahan optimisasi. Pada tahun 1947, George Dantzig mengembangkan sebuah metode yang efisien, yaitu metode algoritma simpleks untuk menyelesaikan permasalahan program linear. Sejak pengembangan dari algoritma simpleks, program linear telah banyak dipakai dalam permasalahan optimisasi di dalam berbagai industri yang berbeda-beda, seperti pada perbankan, bidang pendidikan, ilmu kehutanan, bidang perminyakan, dan transportasi.

Dalam sebuah program linear terdiri dari enam faktor, yang pertama adalah variabel keputusan (decision variable). Dalam program linear, variabel keputusan haruslah dapat menggambarkan secara utuh keputusan apa saja yang harus dibuat. Sebagai contoh, yaitu banyaknya kendaraan yang harus dioperasikan setiap minggunya atau banyaknya pasukan yang diperlukan setiap minggunya.

Faktor kedua adalah fungsi objektif (objective function). Dalam setiap program linear, keputusan yang dibuat biasanya ingin memaksimalkan (untung) atau meminimalkan (biaya) sebuah fungsi dari variabel keputusan. Fungsi seperti inilah yang disebut sebagai fungsi objektif.

Faktor ketiga adalah kendala (constraints). Kendala adalah batasan-batasan yang diberikan pada variabel keputusan yang dapat berupa persamaan atau pertidaksamaan dalam variabel keputusan.

mencerminkan teknologi yang dipakai untuk menghasilkan hasil yang berbeda. Sedangkan konstanta yang berada pada ruas kanan persamaan atau pertidaksamaan di dalam kendala yang fungsinya adalah memperlihatkan banyaknya sumber daya yang tersedia disebut RHS (Right Hand Side), dan ini merupakan faktor kelima dalam program linear.

Faktor keenam adalah tanda batasan (sign restrictions). Fungsi dari tanda batasan ini adalah untuk membatasi apakah variabel keputusan dapat bernilai positif atau negatif, atau variabel keputusan hanya boleh bernilai nonnegatif. Jika variabel keputusan dapat bernilai positif atau negatif, maka dapat dikatakan bahwa variabel keputusan tersebut tidak ada batasan tanda (Unrestricted Sign - sering disingkat dengan urs).

Dari keenam faktor di atas secara umum sebuah program linear dirumuskan

Maksimumkan/minimumkan

∑

=

= n

j j jx c z

1

m n

j j mj n

j j j

b x

a

b x

a

≥ = ≤

≥ = ≤

∑

∑

= =

1

1 1

1 Kendala

M

dengan z adalah fungsi objektif, x_j adalah variabel keputusan,

(

i m j n

)

Definisi 2.2.1

Sebuah fungsi f

(

x₁,x₂,K,x_n

)

disebut fungsi linear jika dan hanya jika untuk sembarang konstanta a₁,a₂,K,a_n

(

x x xn

)

a x a x anxn f ₁, ₂,K, = _{1 1}+ _{2 2} +L+

Definisi 2.2.2

Untuk sembarang fungsi linear f

(

x₁,x₂,K,x_n

)

dan sembarang bilangan b, pertidaksamaan f

(

x₁,x₂,K,x_n

)

≤ b atau f

(

x₁,x₂,K,x_n

)

≥ b disebut pertidaksamaan linear.

Definisi 2.2.3

Sebuah permasalahan program linear adalah permasalahan pengoptimalan di mana:

1. bertujuan mengoptimalkan (memaksimalkan atau meminimalkan) fungsi objektif.

2. nilai dari variabel keputusan harus memenuhi setiap kendala yang ada. Setiap kendala harus merupakan persamaan linear atau pertidaksamaan linear.

Definisi 2.2.4

Suatu program linear dikatakan mempunyai penyelesaian jika ada titik yang memenuhi semua kendala yang ada.

Definisi 2.2.5

Daerah penyelesaian atau daerah layak sebuah program linear adalah himpunan dari semua titik-titik yang memenuhi semua kendala atau batasan yang ada pada program linear.

Definisi 2.2.6

Untuk permasalahan pemaksimalan (peminimalan), sebuah penyelesaian optimal untuk program linear adalah titik yang berada pada daerah layak yang jika substitusikan pada fungsi objektif menghasilkan nilai yang paling besar (kecil).

Ada beberapa metode untuk menyelesaikan permasalahan program linear. Metode yang paling sering dipakai adalah metode simpleks. Terdapat beberapa definisi sebelum mengetahui algoritma dari metode simpleks

Definisi 2.2.7

Variabel dasar (Basic Variable – BV) adalah variabel dimana kolom yang

variabel dimana kolom yang bersesuaian pada tabel optimum mempunyai lebih dari satu elemen tak nol.

Definisi 2.2.8

Sebuah penyelesaian dasar untuk Ax=b didapat dengan mengatur n−m variabel non dasar (Bukan Variabel Dasar – NBV) = 0 dan mencari nilai m variabel dasar (BV) yang tersisa.

Metode Simpleks

Agar sebuah permasalahan program linear dapat diselesaikan menggunakan metode simpleks, permasalahan tersebut haruslah dirubah menjadi bentuk standar. Yaitu dengan cara:

1. Ubah fungsi objektif menjadi 0 1

= −

∑

=

n

i i ix c

z .

2. Mengalikan -1 pada kendala dimana b_i <0.

3. Ubah setiap pertidaksamaan linear

(

)

j n

j x x x b

f ₁, ₂,K, ≤ menjadi

(

n

)

j _j

j x x x s b

f ₁, ₂,K, + = , dengan s_j adalah variabel pengetat.

4. Ubah setiap pertidaksamaan linear

(

)

j n

j x x x b

f ₁, ₂,K, ≥ menjadi

(

n

)

j _j

j x x x e b

f ₁, ₂,K, − = , dengan e_j adalah variabel surplus.

5. Tambahkan tanda batasan e_j,s_j ≥0 ( j=1,2,Km).

(

n

)

j _j

j x x x e b

f ₁, ₂,K, − = dan mungkin terdapat baris yang tidak mempunyai

variabel dasar, yaitu pada persamaan

(

)

j n

j x x x b

f ₁, ₂,K, = . Untuk mengatasi

masalah ini, tambahkan variabel semu a_j pada setiap persamaan di atas. Tetapi, setelah menambahkan variabel semu pada persamaan tersebut muncul permasalahan baru yaitu dengan mengambil a_j dan s_j sebagai variabel dasar menyebabkan x_i =e_j =0. Dan jika memasukkan nilai x_i =0, tidak akan memenuhi kendala awal,

(

n

)

_j j

j x x x b b

f ₁, ₂,K, ≥ → 0≥

dan

(

)

_j

j n

j x x x b b

f ₁, ₂,K, = →0= .

Untuk menyelesaikan masalah tersebut, pada permasalahan peminimalan ditambahkan bilangan yang sangat besar M pada fungsi objektif sebagai koefisien dari a_j, dan pada permasalahan pemaksimalan ditambahkan bilangan

M

− pada fungsi objektif sebagai koefisien dari a_j. Hal ini dimaksudkan agar

variabel a_j keluar dari variabel dasar menjadi variabel non dasar. Selanjutnya dibentuk matriks lengkapnya sebagai berikut:

Setelah mengubah program linear menjadi bentuk standar, lalu dilakukan uji optimalitas, dengan melihat koefisien pada baris ke-0 (baris paling bawah pada matriks lengkap yang merupakan koefisien di fungsi objektif). Pada permasalahan pemaksimalan (peminimalan), jika semua koefisien NBV pada baris ke-0 tak negatif (tak positif), maka bfs yang didapat adalah nilai optimal. Hal ini disebabkan jika salah satu NBV masuk menjadi BV hanya akan mengurangi (menambahkan) nilai z.

Jika terdapat NBV, x_j, yang mempunyai koefisien negatif (positif), pilih NBV yang koefisiennya paling kecil (besar). Dengan memilih koefisien yang

paling kecil (besar) diharapkan dapat memaksimalkan (meminimalkan) nilai z paling banyak. Untuk menentukan BV mana yang akan keluar, dilakukan uji rasio

yaitu dengan menghitung

    

  

>0 ,

min _ij

ij i _a a b

. Dipilihnya a_ij >0 adalah agar NBV

yang akan masuk bernilai positif dan diambil yang paling minimum agar saat membentuk variabel dasar yang baru, yaitu dengan melakukan operasi baris elementer berhingga kali, tidak membuat nilai variabel dasar yang lain menjadi

negatif. Dengan dipilihnya kj k a

b

yang paling minimum, maka _≥0

  

  

−

kj k

ij i

a b a

b

.

Secara umum algoritma metode simpleks untuk permasalahan pemaksimalan (peminimalan) adalah

3. Menentukan variabel dasar mana yang akan keluar dan variabel non dasar mana yang akan masuk lalu kembali ke langkah ke-2.

Contoh 2.2.1

Maksimalkan

2

1 4

5x x z= + Kendala

45 6

10

5 2

1 2 1

≤ +

≤ +

x x

x x

Penyelesaian

Iterasi 1

Langkah 1

Ubah menjadi bentuk standar Maksimalkan

0 0 0 4

5 ₁− ₂ − ₁− ₂ =

− x x s s

z

Kendala

45 6

10

5 2

2 1

1 2 1

= + +

= + +

s x x

s x x

Dengan tabel awalnya adalah

0 0 0 4 5

45 1 0 6 10

5 0 1 1 1

2 1 2 1

− −

RHS s

Langkah 2

Dapat dilihat bahwa z=0,s₁ =5,s₂ =45 merupakan penyelesaian dasar. Dipilih NBV=x₁ karena x₁ mempunyai koefisien negatif yang paling kecil.

Rasio x₁ yang paling kecil adalah pada baris kendala ke-2, sehingga dengan menggunakan operasi baris elementer didapat

5 . 22 5 . 0 0 1 0

5 . 4 1 . 0 0 6 . 0 1

5 . 0 1 . 0 1 4 . 0 0

2 1 2 1

−

−

RHS s

s x x

Karena masih terdapat NBV yang negatif, lanjutkan ke langkah ke-2. Iterasi 2

Langkah 2

Dipilih NBV=x₂ karena x₂ mempunyai koefisien negatif yang paling kecil. Rasio x₂ yang paling kecil adalah pada baris ke-1, dengan menggunakan operasi baris elementer didapat

75 . 23 25 . 0 5 . 2 0 0

75 . 3 15 . 0 5 . 1 0 1

25 . 1 25 . 0 5 . 2 1 0

2 1

2 1

− −

RHS s

s x x

Iterasi 3

Langkah 2

C. Metode Simpleks yang Diperbaharui

Sebuah program linear dapat juga diselesaikan dengan metode simpleks yang sudah diperbaharui, yaitu dengan mengubahnya menjadi bentuk matriks. Perumusan secara umum program linear dalam bentuk matriks adalah

Maksimumkan/minimumkan z=cx

b

Ax=

Kendala

dengan c=

[

c1 c2 L c_n

]

,

   

 

   

  =

n x x x

M

2 1

x ,

   

 

   

  =

mn m

m

n n

a a

a

a a

a

a a

a

L M M

M

L L

2 1

2 22

21

1 12

11

A , dan

   

 

   

  =

m b

b b

M

2 1

b

Misalkan N adalah matrik yang bersesuaian dengan koefisien variabel non dasar, B adalah matriks yang bersesuain dengan koefisien variabel dasar, x_N adalah vektor dari variabel non dasar, x_B adalah vektor dari variabel dasar, c_N adalah vektor koefisien variabel non dasar pada fungsi objektif, dan c_B adalah vektor koefisien veariabel dasar pada fungsi objektif. Dengan mengubah matriks A menjadi A=

[

NMB

]

, vektor c menjadi c=

[

c_N M c_B

]

, dan vektor x menjadi

          =

B N

x x

[

]

N N B B B

N

B N

z c x c x

x x

c

c = +

    

    

= M L (2.3.1)

dan Nx_N +Bx_B =b (2.3.2) Dari persamaan (2.3.2) dapat dicari nilai dari x_B, yaitu

N

B B b B Nx

x = −1 − −1 (2.3.3) Dengan mensubstitusikan persamaan (2.3.3) ke persamaan (2.3.1) akan didapat

N B

B N N

z=c x +c B−1b−c B−1Nx Atau

N B

N B

z=c B−1b+(c −c B−1N)x (2.3.4) Dengan mensubstitusikan nilai variabel-variabel maka akan didapat penyelesaian sementara, yaitu

B B z c x)

)₌

, dengan x)_B =B−1b

Misalkan c)_j adalah elemen dari vektor )c=(c_N −c_BB−1N) yang bersesuaian dengan x_j∈x_N, maka

N z

z= )+c)x (2.3.5)

Teorema 2.3.1

Pada permasalahan pemaksimalan (peminimuman), penyelesaian sementara

B B

z)=c x) , dengan x)_B =B−1b dikatakan optimal jika ∀c_j∈)c, c_j ≤0 (∀c_j∈c), c_j ≥0)

Bukti

Perhatikan persamaan (2.3.5), z= z)+c)x_N. Karena diketahui ∀c_j∈c), c_j ≤0 (∀c_j∈c), c_j ≥0) dan x_N ≥0, maka cˆx_N ≤0 (cˆx_N ≥0). Akibatnya z≤ zˆ

(z≥ zˆ). Dengan kata lain nilai z baru akan tidak lebih besar (kecil) dari nilai z

sebelumnya.

■

Jika 0∃c_j∈c), c_j ≥ (∃c_j ∈c), c_j ≤0) maka dipilih c_j yang paling besar (kecil) dan x_j akan masuk sebagai variabel dasar selanjutnya. Hal ini diharapkan menambah (mengurangi) nilai z paling banyak.

Perhatikan persamaan (2.3.3), x_B =B−1b−B−1Nx_N. Jika ˆ ∈ −1 ≥0 N B

ij

c ,

maka nilai

( )

x_{B i} akan berkurang seiring dengan bertambahnya nilai

( )

x_{N i}. Jika

( )

x ,ˆ B 1b ˆ

ˆ

−

∈

= _i

ij i i

N b

c b

, maka

( )

x_{B i} =0. Jika ˆ ∈ −1 ≤0 N B

ij

c , maka nilai

( )

x_{B i} bertambah seiring dengan bertambahnya nilai

( )

x_{N i}. Karena terdapat batasan

0

≥

B

( )

x min : 0 , ∈B−1b, ∈B−1N

    

  

>

= _{ij i ij}

ij i i

B c b c

c

b ) ) )

) )

Secara umum algoritma metode simpleks berbasis matriks untuk menyelesaikan permasalahan pemaksimalan (peminimalan) dapat ditulis menjadi langkah-langkah berikut:

1. Uji program linear, yaitu apakah sebuah program linear mempunyai penyelesaian atau tidak. Jika B merupakan matriks singular, maka program linear tersebut tidak mempunyai penyelesaian. Jika B merupakan matriks tak singular lanjut ke langkah ke-2.

2. Uji optimalitas, yaitu dengan mencari )c=(c_N −c_BB−1N).

Jika 0∀c_j∈c), c_j ≤ (∀c_j∈)c, c_j ≥0), maka penyelesaian sementara sudah optimal, jika tidak lanjut ke langkah berikutnya.

3. Pilih elemen c) yang mempunyai nilai positif (negatif) terbesar, lalu hitung

N B b

B 1 , 1

, 0 :

min ∈ − ∈ −

    

  

>

= ij i ij

ij i

j c b c

c b

x ₎ ) ) )

)

untuk masuk sebagai

variabel dasar baru.

4. Baharui matriks B, x_B, x_N, c_B, dan c_N, dengan menukar variabel dasar baru dengan variabel non dasar yang baru. Kembali ke langkah pertama.

Secara umum algoritma metode dual simpleks berbasis matriks untuk menyelesaikan permasalahan program linear dapat ditulis menjadi langkah-langkah berikut:

1. Jika setiap elemen b bernilai positif, maka penyelesaian sementara sudah optimal. Jika terdapat elemen b yang bernilai negatif, maka lanjut ke langkah selanjutnya.

2. Pilih elemen b yang mempunyai nilai negatif terbesar, agar lalu hitung

N B c

c

c ₁

ˆ , , 0 ˆ : ˆ

min ∈ ∈ −

    

  

<

= ij j ij

ij j

j c c

c

x ) )

)

untuk masuk sebagai variabel

dasar yang baru.

3. Jika terdapat kendala dimana mempunyai RHS bernilai negatif dan setiap koefisien variabel pada kendala tersebut bernilai positif, maka permasalahan program linear tersebut tidak mempunyai daerah penyelesaian karena untuk sembarang variabel non dasar yang akan masuk menjadi variabel dasar akan selalu bernilai negatif, dan ini melanggar batasan bahwa setiap variabel dasar harus bernilai positif.

Pada umumnya metode dual simpleks serting digunakan dalam situasi: 1. Mencari penyelesaian optimal baru setelah menambah kendala baru pada

program linear.

3. Menyelesaikan permasalahan peminimalan yang setiap kendalanya mempunyai tanda ≥.

Definisi 2.2.11

Program linear bilangan bulat adalah permasalahan program linear yang

mengharuskan semua nilai variabelnya bernilai bulat.

Definisi 2.2.12

Program linear yang didapat dengan menghilangkan kendala bilangan bulat pada variabel disebut Program Linear Relaxation dari pemrogramman linear bilangan bulat.

Banyak cara yang dapat digunakan untuk menyelesaikan sebuah program linear bilangan bulat, yaitu dengan menggunakan metode branch-and-bound, metode cutting plane, metode implicit enumeration, dan metode heuristics. Dalam bab

selanjutnya hanya akan dibahas pada penggunaan metode branch-and-bound dan metode cutting plane.

D. Metode Branch-and-bound

permasalahan pemrograman linear bilangan bulat. Salah satu contohnya adalah algoritma additive, dimana komputasi algoritma ini sangat sederhana sehingga dipercaya dapat memberikan solusi permasalahan pemrograman linear bilangan bulat secara umum.

Kata Branch pada algoritma Branch-and-bound menandakan adanya percabangan, yaitu dengan membuang nilai variabel yang tidak bulat dan memecah permasalahan sebelumnya menjadi dua dan menambahkan kendala pada permasalahan yang baru. Kendala yang baru ini adalah batasan untuk variabel agar nilai yang didapat adalah bilangan bulat.

Sedangkan kata Bound pada algoritma Branch-and-bound menandakan adanya batasan yang harus dipenuhi agar penyelesaian yang didapat dari permasalahan-permasalahan baru yang dihasilkan pada percabangan adalah penyelesaian optimal untuk permasalah awal.

Cara kerja dari algoritma Branch-and-bound adalah menyelesaikan dahulu permasalahan linear awal dan melihat daerah layaknya (LP₀), lalu mengambil salah satu nilai variabel yang tidak bulat (x_i) dan membuat dua permasalahan linear baru dengan menambahkan batasan pada daerah layaknya. Maka permasalahan linear baru yang pertama adalah permasalahan linear awal dengan tambahan batasan pada daerah layaknya, yaitu LP₁ = LP₀ +

(

x_i ≤

 

x_i

)

dimana

 

x_i adalah bilangan bulat terbesar yang kurang dari atau sama dengan

i

dimana

 

x_i adalah bilangan bulat terkecil yang lebih besar atau sama dengan x_i. Setelah itu setiap permasalahan baru tersebut ditentukan penyelesaiannya.

Terdapat tiga kemungkinan yang dapat terjadi pada saat menyelesaikan permasalahan yang baru, yaitu:

1. tidak mempunyai penyelesaian.

2. mempunyai penyelesaian tetapi bukan penyelesaian bilangan bulat. 3. mempunyai penyelesaian bilangan bulat.

Jika kemungkinan pertama terjadi, maka percabangan tidak akan dilanjutkan pada permasalahan tersebut. Jika kemungkinan kedua terjadi, maka akan dibentuk dua permasalahan yang baru dengan menambahkan batasan pada daerah layaknya,

 

(

i i

)

l

k LP x x

LP₊₁ = + ≤ dan LP_k+2 =LP_l +

(

x_i ≥

 

x_i

)

, l=1,2,3,K, k=2,4,6K

dan menyelesaikan permasalahan yang baru lagi. Jika kemungkinan ketiga yang terjadi, maka percabangan tidak akan dilakukan dan mengganti batasan untuk permasalahan pemaksimalan jika z< z_l dan z>z_l untuk permasalahan peminimalan dimana z bernilai +∞ untuk permasalahan pemaksimalan dan −∞ untuk permasalahan peminimalan dan z_l adalah penyelesaian bilangan bulat untuk permasalahan ke-l lalu menyelesaikan permasalahan yang tersisa.

Secara umum algoritma Branch-and-bound dapat ditulis dalam langkah-langkah berikut:

1. Atur l=0,z=−∞,k=0

i. Jika semua variabel bilangan bulat dan z_l ≥z, maka ubah 1

, = +

=z l l

z _l dan lanjutkan ke langkah ke-5

ii. Jika ada variabel yang bukan bilangan bulat lanjutkan ke langkah ke-3 iii. Jika LP_l tidak mempunyai daerah layak atau mempunyai penyelesaian

bilangan bulat dengan z_l ≤ z, maka ubah l=l+1 dan lanjutkan ke langkah ke-5

3. Ambil salah satu variabel x_i yang bukan bilangan bulat dan bentuk permasalahan linear baru lainnya dengan daerah layaknya adalah LPk+1 dan LPk+2 dimana

 

(

)

 

(

i i

)

l k

i i l k

x x LP LP

x x LP LP

≥ + =

≤ + =

+ +

2 1

4. Ubah l=l+1 dan k=k+2

5. Jika l>k perhitungan berhenti, jika tidak kembali ke langkah ke-2.

Langkah-langkah di atas digunakan khususnya untuk permasalahan pemaksimalan pemrograman linear bilangan bulat. Untuk permasalahan peminimalan pemrograman linear bilangan bulat, cukup mengganti nilai awal

,

+∞ =

z dan pada langkah ke-2 diubah menjadi:

2. Selesaikan permasalahan dengan menggunakan LP_l, yaitu daerah layak permasalahan ke-l

i. Jika semua variabel bilangan bulat dan z_l ≤z, maka ubah 1

, = +

= z l l

ii. Jika ada variabel yang bukan bilangan bulat lanjutkan ke langkah ke-3

iii. Jika LP_l tidak mempunyai daerah penyelesaian atau mempunyai penyelesaian bilangan bulat dengan z_l ≥z , maka ubah 1l=l+ dan lanjutkan ke langkah ke-5

−∞ = = =

z k l

0 0

   i i l k

i i l k

x x LP LP

x x LP LP

≥ + =

≤ + =

+ + 2 1

2 1 + =

+ =

k k

l l

1 + =l l

z zl>

k l>

1 + =

=

l l

z

z l

l LP

Berikut diberikan contoh penerapan metode branch-and-bound pada permasalahan pemrograman linear adalah

Contoh 2.4.1

Maksimalkan

2

1 4

5x x z= + Kendala

+

Ζ ∈ ≤ +

≤ +

2 1 2 1

2 1

,

45 6

10

5

x x x x

x x

Penyelesaian:

Iterasi 1

Langkah 1

Atur

0 , ,

0 =−∞ =

= z k

l

Langkah 2

Selesaikan permasalahan linear awal dengan daerah layak permasalahan ke-0, yaitu LP₀

Bentuk standarnya adalah Maksimalkan

0 0 0 4

5 ₁− ₂ − ₁− ₂ =

− x x s s

Kendala 45 6 10 5 2 2 1 1 2 1 = + + = + + s x x s x x

Dengan tabel awalnya adalah

0 0 0 4 5 45 1 0 6 10 5 0 1 1 1 2 1 2 1 − − RHS s s x x

Dengan menggunakan metode simpleks pada bagian B maka diperoleh penyelesaian optimal untuk masalah di atas adalah:

25 . 1 75 . 3 75 . 23 2 1 0 = = = x x z 75 . 23 25 . 0 5 . 2 0 0 75 . 3 15 . 0 5 . 1 0 1 25 . 1 25 . 0 5 . 2 1 0 2 1 2 1 − − RHS s s x x

Karena terdapat nilai variabel yang tidak bulat maka lanjut ke langkah ke-3 Langkah 3

Ambil variabel yang bukan bilangan bulat yaitu x₁, lalu bentuk permasalahan linear baru lainnya dengan daerah layaknya adalah:

4 3 1 0 2 1 0 1 ≥ + = ≤ + = x LP LP x LP LP Langkah 4 Ubah 2 1 = = k l Langkah 5

Iterasi 2

Langkah 2

Selesaikan permasalahan linear awal dengan daerah layak permasalahan ke-1, yaitu LP₁ Bentuk standarnya adalah

Bentuk standarnya adalah Maksimalkan

0 0 0 0 4

5 ₁− ₂ − ₁− ₂ − ₃ =

− x x s s s

z

Kendala

3 45 6

10

5

3 1

2 2 1

1 2 1

= +

= + +

= + +

s x

s x x

s x x

Dengan tabel awalnya adalah

0 0 0 0 4 5

3 1 0 0 0 1

45 0 1 0 6 10

5 0 0 1 1 1

3 2 1 2 1

− −

RHS s

s s x x

Dengan menggunakan metode simpleks pada bagian A maka diperoleh penyelesaian optimal untuk masalah di atas adalah:

2 3 23

2 1 1

= = =

x x z

23 1 0 4 0 0

3 1 0 0 0 1

3 4 1 6 0 0

2 1 0 1 1 0

3 2 1 2 1

− −

−

RHS s

s s x x

Karena semua nilai variabel bilangan bulat dan z₁> z maka ubah z=23, l =2

Langkah 5

Karena l≤k, maka kembali ke langkah ke-2

Iterasi 3

Langkah 2

Selesaikan permasalahan linear awal dengan daerah layak permasalahan ke-2, yaitu LP₂

Bentuk standarnya adalah Maksimalkan

0 0 0 0 4

5 ₁− ₂ − ₁− ₂ − ₃ =

− x x s s s

z

Kendala

4 45 6

10

5

3 1

2 2 1

1 2 1

− = + −

= + +

= + +

s x

s x x

s x x

Dengan tabel awalnya adalah

0 0 0 0 4 5

4 1 0 0 0 1

45 0 1 0 6 10

5 0 0 1 1 1

3 2 1 2 1

− −

− −

RHS s

s s x x

83 . 0

4 33 . 23

2 1 2

= = =

x x z

33 . 23 667 . 1 667 . 0 0 0 0

4 1

0 0

0 1

833 . 0 667 . 1 167 . 0 0 1 0

167 . 0 667 . 0 167 . 0 1 0 0

3 2

1 2 1

− −

− − −

RHS s

s s

x x

Karena terdapat nilai variabel yang tidak bulat maka lanjut ke langkah ke-3 Langkah 3

Ambil variabel yang bukan bilangan bulat yaitu x₂, lalu bentuk permasalahan linear baru lainnya dengan daerah layaknya adalah:

1 0 2 2 4

2 2 3

≥ + =

≤ + =

x LP LP

x LP LP

Langkah 4

Ubah

4 3

= =

k l

Langkah 5

Karena l≤k, maka kembali ke langkah ke-2

Iterasi 4

Langkah 2

Selesaikan permasalahan linear awal dengan daerah layak permasalahan ke-3, yaitu LP₃

Bentuk standarnya adalah Maksimalkan

0 0 0 0 0 4

5 ₁− ₂ − ₁− ₂ − ₃ − ₄ =

− x x s s s s

Kendala 0 4 45 6 10 5 4 2 3 1 2 2 1 1 2 1 = + − = + − = + + = + + s x s x s x x s x x

Dengan tabel awalnya adalah

0 0 0 0 0 4 5 0 1 0 0 0 1 0 4 0 1 0 0 0 1 45 0 0 1 0 6 10 5 0 0 0 1 1 1 4 3 2 1 2 1 − − − − RHS s s s s x x

Dengan menggunakan metode dual simpleks pada bagian C maka diperoleh penyelesaian optimal untuk masalah di atas adalah:

0 5 . 4 5 . 22 2 1 3 = = = x x z 5 . 22 1 0 5 . 0 0 0 0 0 1 0 0 0 0 0 5 . 4 6 . 0 0 1 . 0 0 0 1 5 . 0 6 . 0 1 1 . 0 0 0 0 5 . 0 4 . 0 0 1 . 0 1 0 0 4 3 2 1 2 1 − − − − − − RHS s s s s x x

Karena terdapat nilai variabel yang tidak bulat maka lanjut ke langkah ke-3 Langkah 3

Ambil variabel yang bukan bilangan bulat yaitu x₁, lalu bentuk permasalahan linear baru lainnya dengan daerah layaknya adalah:

6 4

= =

k l

Langkah 5

Karena l≤k, maka kembali ke langkah ke-2 Iterasi 5

Langkah 2

Selesaikan permasalahan linear awal dengan daerah layak permasalahan ke-4, yaitu LP₄

Bentuk standarnya adalah Maksimalkan

0 0 0 0 0 4

5 ₁− ₂ − ₁− ₂ − ₃ − ₄ =

− x x s s s s

z

Kendala

1 4 45 6

10

5

4 2

3 1

2 2 1

1 2 1

− = + −

− = + −

= + +

= + +

s x

s x

s x x

s x x

Dengan tabel awalnya adalah

0 0 0 0 0 4 5

1 1 0 0 0 1 0

4 0 1 0 0 0 1

45 0 0 1 0 6 10

5 0 0 0 1 1 1

4 3 2 1 2 1

− −

− −

− −

RHS s

s s s x x

Langkah 5

Karena l≤k, maka kembali ke langkah ke-2

Iterasi 6

Langkah 2

Selesaikan permasalahan linear awal dengan daerah layak permasalahan ke-5, yaitu LP₅

Bentuk standarnya adalah Maksimalkan

0 0 0 0 0 0 4

5 ₁− ₂ − ₁− ₂ − ₃ − ₄ − ₅ =

− x x s s s s s

z

Kendala

4 0 4 45 6

10

5

5 1

4 2

3 1

2 2 1

1 2 1

= −

= +

− = + −

= + +

= + +

s x

s x

s x

s x x

s x x

Dengan tabel awalnya adalah

0 0 0 0 0 0 4 5

4 1 0 0 0 0 0 1

0 0 1 0 0 0 1 0

4 0 0 1 0 0 0 1

45 0 0 0 1 0 6 10

5 0 0 0 0 1 1 1

5 4 3 2 1 2 1

− −

− −

RHS s

s s s s x x

0 4 20 2 1 5 = = = x x z 20 5 4 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 1 0 4 1 0 0 0 0 0 1 5 10 6 0 1 0 0 0 1 4 1 0 0 1 0 0 5 4 3 2 1 2 1 − − − − − − RHS s s s s s x x

Karena mempunyai solusi bilangan bulat dengan z₅ <23, maka ubah l=6 dan lanjut ke langkah ke-5

Langkah 5

Karena l≤k, maka kembali ke langkah ke-2

Iterasi 7

Langkah 2

Selesaikan permasalahan linear awal dengan LP₆, yaitu daerah layak permasalahan ke-6

Bentuk standarnya adalah Maksimalkan 0 0 0 0 0 0 4

5 ₁− ₂ − ₁− ₂ − ₃ − ₄ − ₅ =

− x x s s s s s

Dengan tabel awalnya adalah

0 0 0 0 0 0 4 5

5 1 0 0 0 0 0 1

0 0 1 0 0 0 1 0

4 0 0 1 0 0 0 1

45 0 0 0 1 0 6 10

5 0 0 0 0 1 1 1

5 4 3 2 1 2 1

− −

− −

− −

RHS s

s s s s x x

Karena untuk nilai minimum x₁ =5 tidak memenuhi kendala kedua, maka permasalahan ke-6 tidak mempunyai penyelesaian, maka ubah l=7 dan lanjut ke langkah ke-5

Langkah 5

Karena l>k, maka perhitungan dihentikan dan nilai optimum untuk permasalahan linear (2.4.1) adalah z=23 dengan x₁=3 dan x₂ =2.

E. Metode Cutting plane

Pada bab sebelumnya telah dijelaskan bagaimana menyelesaikan sebuah program linear bilangan bulat dengan menggunakan metode branch-and-bound. Selain menggunakan metode branch-and-bound, dapat juga menggunakan metode cutting plane. Sama seperti dengan metode branch-and-bound, metode cutting

plane juga berawal dari penyelesaian optimal program linear. Sebuah kendala

Cara kerja dari metode cutting plane adalah dengan mencari penyelesaian optimal dari program linear dalam bentuk standar dengan daerah layak awal (LP₀) dan melihat apakah terdapat variabel yang bukan bilangan bulat. Jika terdapat variabel yang bukan bilangan bulat, maka akan dibentuk sebuah program linear dengan daerah layak baru (LP₁), yaitu dengan menambahkan sebuah kendala baru (cuts). Lalu mencari penyelesaian optimal program linear baru ini.

Definisi 2.5.1

Kendala cuts adalah kendala yang dibentuk dengan memisahkan semua koefisien

fraksional pada salah satu baris di tabel optimal yang RHS bukan bilangan di ruas kanan dan koefisien bulat di ruas kiri persamaan dan mememenuhi dua syarat, yaitu

1. sembarang titik penyelesaian untuk program linear bilangan bulat memenuhi kendala baru.

Kendala cuts yang baru merupakan bagian fraksional dari sebuah kendala pada

tabel optimal yang berbentuk

∑

   

∑

= =

− =

− n

i i ji j

j n

i

i

ji x b f f x

a

1 1

. Untuk sembarang

penyelesaian bilangan bulat, ruas kanan akan selau bernilai bulat dan karena 0

,

1 ≥

< i

j x

f , maka ruas kanan pada persamaan di atas haruslah bilangan bulat

yang lebih kecil dari 1, yaitu 0 1

≤ −

∑

=

n

i i ji

j f x

f .

Karena kendala cuts ini dibentuk dari sebuah baris pada tabel optimal dan pada satu baris hanya terdapat satu variabel dasar, maka ∀x_i, x_i adalah variabel non-dasar yang nilainya adalah 0. maka jika penyelesaian optimal yang didapat dimasukkan pada kendala cuts,

0 0 0 1

≤ ≤ −

∑

=

j n

i ji j

f f f

Hal ini bertentangan dengan 0≤ f_j <1, maka penyelesaian optimal yang didapat sebelumnya tidak akan memenuhi kendala cuts ini.

Secara umum algoritma cutting plane dapat ditulis dalam langkah-langkah berikut ini:

1. Atur k =0

2. Selesaikan permasalahan dengan menggunakan LP_k, yaitu daerah layak permasalahan ke-k

i. Jika semua variabel bernilai bulat, maka didapat penyelesaian optimal untuk program linear awal.

ii. Jika terdapat variabel yang bukan bilangan bulat, maka lanjut ke langkah berikutnya.

3. Ambil sembarang kendala, kendala ke-j pada tabel optimal LP_k yang RHS-nya bukan bilangan bulat.

(

 

)

 

_{j j} n

i

i ji

ji f x b f

a + = +

∑

=1

(2.5.1)

dimana 0≤ fj,fji <1, i=1,2,K

5. Bentuk persamaan pada langkah ke-4 menjadi

   

∑

∑

= =

− =

− n

i i ji j

j n

i

i

ji x b f f x

a

1 1

.

6. Bentuk kendala baru (cuts), yaitu 0 1

≤ −

∑

=

n

i i ji

j f x

f .

7. Ubah k =k+1 dan kembali ke langkah ke-2.

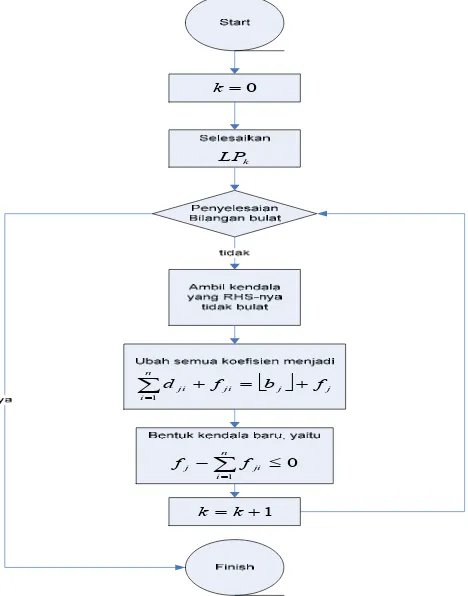
Algoritma tersebut dapat digambarkan dalam flow chart berikut.

0

=

k

 j j n

i

ji

ji f b f

d + = +

∑

=1

0

1

≤

−_∑

=

n

i ji

j f

f

1

+ =k k

k

LP

Berikut diberikan contoh penerapan metode cutting plane pada permasalahan pemrograman linear adalah

Contoh 2.5.1

Maksimalkan

2

1 4

5x x z= + Kendala

+

Ζ ∈ ≤ +

≤ +

2 1 2 1

2 1

,

45 6

10

5

x x x x

x x

Penyelesaian

Iterasi 1

Langkah 1

Atur k =0 Langkah 2

Selesaikan permasalahan linear awal dengan daerah layak permasalahan ke-0, yaitu LP₀

Bentuk standarnya adalah Maksimalkan

0 0 0 4

5 ₁− ₂ − ₁− ₂ =

− x x s s

z

Kendala

45 6

10

5 2

2 1

1 2 1

= + +

= + +

s x x

Dengan tabel awalnya adalah

0 0 0 4 5

45 1 0 6 10

5 0 1 1 1

2 1 2 1

− −

RHS s

s x x

Dengan menggunakan metode simpleks pada bagian A maka diperoleh untuk masalah di atas adalah:

25 . 1

75 . 3

75 . 23

2 1 0

= = =

x x z

75 . 23 25 . 0 5 . 2 0 0

75 . 3 15 . 0 5 . 1 0 1

25 . 1 25 . 0 5 . 2 1 0

2 1

2 1

− −

RHS s

s x x

Langkah 3

Ambil kendala yang tidak bulat, yaitu kendala ke-1. Langkah 4

Ubah kendala ke-1 menjadi

25 0 1 75 0 5

0

2 _{1 1 2 2}

2+ s + . s −s + . s = + .

x

Langkah 5

Bentuk persamaan pada langkah ke-4 menjadi

2 1

2 1

2 2s s 1 025 05s 075s

x + − − = . − . − . Langkah 6

Bentuk kendala baru yaitu 0 75 0 5 0 25

0. − . s₁− . s₂ ≤ Langkah 7

Iterasi 2

Langkah 2

Selesaikan permasalahan linear awal dengan daerah layak permasalahan ke-1, yaitu LP₁

Bentuk standarnya adalah Maksimalkan 0 0 0 0 4

5 ₁− ₂ − ₁− ₂ − ₃ =

− x x s s s

z Kendala 25 . 0 75 . 0 5 . 0 45 6 10 5 3 2 1 2 2 1 1 2 1 − = + − − = + + = + + s s s s x x s x x

Dengan tabel awalnya adalah

0 0 0 0 4 5 25 . 0 1 75 . 0 5 . 0 0 0 45 0 1 0 6 10 5 0 0 1 1 1 3 2 1 2 1 − − − − − RHS s s s x x

Dengan menggunakan metode dual simpleks pada bagian C maka diperoleh untuk masalah di atas adalah:

3333 1 6667 3 6667 23 2 1 0 . . . = = = x x z 667 . 23 333 . 0 0 333 . 2 0 0 333 . 1 333 . 0 0 667 . 2 1 0 667 . 3 333 . 0 0 667 . 1 0 1 333 . 0 333 . 1 1 667 . 0 0 0 3 2 1 2 1 − − − RHS s s s x x Langkah 3

Langkah 4

Ubah kendala ke-1 menjadi

3333 0 6667 0 2 6667

0. s₁+s₂ − s₃+ . s₃ = . Langkah 5

Bentuk persamaan pada langkah ke-4 menjadi

3 1

3

2 2s 03333 06667s 06667s

s − = . − . − .

Langkah 6

Bentuk kendala baru yaitu 0 6667 0 6667 0 3333

0. − . s₁− . s₃ ≤ Langkah 7

Ubah k =2.

Iterasi 3

Langkah 2

Selesaikan permasalahan linear awal dengan daerah layak permasalahan ke-2, yaitu LP₂

Bentuk standarnya adalah Maksimalkan

0 0 0 0 0 4

5 ₁− ₂ − ₁− ₂ − ₃ − ₄ =

− x x s s s s

Kendala 333 . 0 667 . 0 667 . 0 25 . 0 75 . 0 5 . 0 45 6 10 5 4 3 1 3 2 1 2 2 1 1 2 1 − = + − − − = + − − = + + = + + s s s s s s s x x s x x

Dengan tabel awalnya adalah

0 0 0 0 0 4 5 333 . 0 1 667 . 0 0 667 . 0 0 0 25 . 0 0 1 75 . 0 5 . 0 0 0 45 0 0 1 0 6 10 5 0 0 0 1 1 1 4 3 2 1 2 1 − − − − − − − − RHS s s s s x x

Dengan menggunakan metode dual simpleks pada bagian C maka diperoleh untuk masalah di atas adalah:

5 1 5 3 5 23 2 1 0 . . . = = = x x z 5 . 23 5 . 0 0 0 2 0 0 1 2 0 1 2 0 0 5 . 1 5 . 0 0 0 3 1 0 5 . 3 5 . 0 0 0 2 0 1 5 . 0 5 . 1 1 0 1 0 0 4 3 2 1 2 1 − − − − RHS s s s s x x Langkah 3

Ambil kendala yang tidak bulat, yaitu kendala ke-1. Langkah 4

Ubah kendala ke-1 menjadi 5 0 5 0

2 _{4 4}

3

1+s − s + . s = .

s

Langkah 5

4 4

3

1 s 2s 05 05s

s + − = . − . Langkah 6

Bentuk kendala baru yaitu 0

5 0 5

0. − . s₄ ≤ Langkah 7

Ubah k =3.

Iterasi 4

Langkah 2

Selesaikan permasalahan linear awal dengan daerah layak permasalahan ke-3, yaitu LP₃

Bentuk standarnya adalah Maksimalkan

0 0 0 0 0 0 4

5 ₁− ₂ − ₁− ₂ − ₃ − ₄ − ₅ =

− x x s s s s s

z

Kendala

5 . 0 5

. 0

333 . 0 667

. 0 667 . 0

25 . 0 75

. 0 5 . 0

45 6

10

5

5 4

4 3 1

3 2 1

2 2 1

1 2 1

− = + −

− = + −

−

− = + −

−

= + +

= + +

s s

s s s

s s s

s x x

Dengan tabel awalnya adalah 0 0 0 0 0 0 4 5 5 . 0 1 5 . 0 0 0 0 0 0 333 . 0 0 1 667 . 0 0 667 . 0 0 0 25 . 0 0 0 1 75 . 0 5 . 0 0 0 45 0 0 0 1 0 6 10 5 0 0 0 0 1 1 1 5 4 3 2 1 2 1 − − − − − − − − − − RHS s s s s s x x

Dengan menggunakan metode dual simpleks pada bagian C maka diperoleh untuk masalah di atas adalah:

2 3 23 2 1 0 = = = x x z 23 1 0 0 0 2 0 0 3 1 0 0 0 2 0 1 1 2 1 0 0 0 0 0 2 3 0 1 0 1 0 0 3 4 0 0 1 2 0 0 2 1 0 0 0 3 1 0 5 4 3 2 1 2 1 − − − − − RHS s s s s s x x

BAB III

METODE BRANCH-AND-CUT PADA PERMASALAHAN RUTE

KENDARAAN BERKAPASITAS

A. Permasalahan Rute Kendaraan Berkapasitas (Capacitated Vehicle

Routing Problems - CVRP)

Terdapat banyak kegunaan dari penggunaan riset operasi dalam kehidupan sehari-hari, dan yang sering dipakai oleh perusahaan-perusahaan adalah permasalahan pengoptimalan. Pengoptimalan yang berbasis pada program linear dengan permasalahan perencanaan pengiriman dari produsen kepada konsumen inilah yang disebut Permasalahan Rute Kendaraan (Vehicle Routing Problem – VRP). Permasalahan rute kendaraan mempunyai beberapa bentuk dasar

permasalahan, yaitu permasalahan rute kendaraan berkapasitas (Capacitated VRP – CVRP), yang merupakan bentuk paling dasar dari permasalahan pada VRP, distance-constained VRP, VRP dengan Time Windows, VRP dengan Backhauls

dan VRP dengan Pickup and Delivery.

Capacitated VRP adalah sebuah bentuk dasar permasalahan rute

Definisi 3.1.1

Graf adalah sebuah jaringan yang terdiri dari himpunan simpul-simpul dan himpunan busur-busur.

Definisi 3.1.2

Graf berarah adalah graf yang busur-busurnya mempunyai arah, dengan kata

lain busur

( )

i,j , yaitu busur yang menghubungkan simpul i dengan simpul j, tidak sama dengan busur

( )

j,i .

Definisi 3.1.3

Rute dari simpul i ke simpul j adalah suatu urutan simpul i,K,j bersama-sama dengan himpunan busur yang menghubungkan simpul pertama dengan simpul kedua, simpul kedua dengan simpul ketiga, sampai dengan simpul terakhir.

Secara umum CVRP dapat digambarkan dengan menggunakan graf, dengan G=

(

V,A

)

, dimana V =

{

0,L,n

}

adalah himpunan simpul-simpul dan A

+∞ =

i i

c untuk semua i∈V. Jika G merupakan graf berarah, maka c_ij ≠c_ji. Sebaliknya jika c_ij =c_ji untuk semua (i, j)∈A, maka secara umum himpunan A digantikan dengan himpunan busur-busur tak berarah, E. Banyaknya jumlah anggota himpunan E dinyatakan dengan notasi E .

Sebanyak K kendaraan identik yang masing-masing berkapasitas C dipakai untuk memenuhi setiap permintaan konsumen, d_i,(i=1,K,n), dimana

C d_i ≤

<

0 . Setiap konsumen hanya dilayani oleh satu kendaaran saja dan sebuah kendaaran tidak dapat melayani beberapa konsumen yang total permintaannya melebihi kapasitas kendaraan.

Untuk sembarang himpunan S ⊆V₀, didefinisikan: 1) d(S) adalah jumlah semua permintaan pada S,

( )

∑

∈

=

S i

i d S

d ,

2) δ

( )

S adalah himpunan busur-busur di E yang tepat satu salah satu titik ujungnya berada di S,

3) E

( )

S adalah himpunan busur-busur di E yang kedua titik ujungnya berada di S,

4) r

( )

S adalah banyaknya kendaraan minimum yang dipakai untuk melayani semua konsumen di S, r

( ) ( )

S =d S _C.

Secara umum CVRP dapat dirumuskan menjadi:

( )

( )

( )

(

)

( )

(

)

( )

{

}

(

( )

)

{ }

0,1

(

\

( )

0

)

0 2

, 1 , 0

) (

2 2 0

, , 2 , 1 2

0

δ δ δ

δ δ

E e x

e x

V S S

r S

x

K x

n i

i x Kendala

x c Min

e e E

e e e

∈ ∈

∈ ∈

⊆ ≥

=

= =

∑

∈

K

(

3.1.5

)

) 4 . 1 . 3 (

) 3 . 1 . 3 (

) 2 . 1 . 3 (

) 1 . 1 . 3 (

Kendala (3.1.3) pada umumnya disebut dengan pertidaksamaan kapasitas (capacity inequalities) dan kendala (3.1.1), sering disebut sebagai persamaan derajat (degree equations) dan menjamin bahwa setiap konsumen dilayani tepat satu kali. Kendala (3.1.2) memastikan bahwa tepat memakai K kendaraan. Kendala (3.1.3) dan (3.1.4) merupakan syarat bilangan bulat. Pada kendala (3.1.4)

e

x mungkin bernilai 2 jika terdapat rute yang langsung menghubungkan depot dan konsumen. Dengan menggunakan rumusan di atas, permasalahan CVRP mempunyai 2n + E kendala.

Definisi 3.1.4

Misalkan himpunan S mempunyai nelemen. Banyaknya himpunan bagian S yang terdiri dari r,

(

r≤n

)

, disebut kombinasi n objek yang diambil sebanyak r objek sekaligus. Disimbolkan _

    

r n

, C

( )

n,r , atau _nC_r. Banyaknya kombinasi yang dimaksud dapat dinyatakan dalam persamaan

(

)

! !

! r n r

n r

n

Teorema 3.1.5       +       − =       + r n r n r n 1 1 n r r < ≤

∀ ,0

Bukti:

(

)

(

(

)

)

(

)

(

) (

(

)

)

(

) (

)

(

) (

(

)

)(

)

(

) (

)

(

)

(

)

(

) (

(

)

)(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

      + = − + + = + − + = + − + = + − + − + = − + − − + − + = − − + − + − − = − − + + − − = − + − − − =       +       − r n r n r n r