Metodologi Penelitian

(1)

MODUL PERKULIAHAN VIII

Metodologi

Penelitian

ANALISA REGRESI

Fakultas Program Studi Tatap Muka Kode MK Disusun Oleh

Pasca Sarjana Magister Teknik Elektro

08

54001 (3) Dr. Hamzah Hilal

Abstract

Kompetensi

Kuliah keempat ini memuat materi tentang analisis prediksi dengan menggunakan metode kuadrat terkecil: regresi linier Linier, regresi nonlinier, regresi polinomial

Pengetahuan dan pemahaman mengenai analisis prediksi dengan menggunakan metode kuadrat terkecil: regresi linier Linier, regresi nonlinier, regresi polinomial

(2)

Pembahasan

8.1 UMUM

Dalam analisis data sering dilakukan pembuatan suatu kurva yang dapat mewakili suatu rangkaian data yang diberikan dalam sistem koordinat x-y. Data tersebut dapat berupa hasil percobaan di laboratorium atau pengamatan di lapangan seperti pertumbuhan pemakaian

handphone di suatu daerah dari tahun ke tahun dan lain-lain.

Karena adanya kesalahan atau ketidakpastian dalam pengujian, pengukuran atau variasi perubahan data dari waktu ke waktu, maka titik-titik data tersebar dalam koordinat x-y. Sebagai contoh, volume barang atau jumlah penumpang yang dilayani oleh suatu pelabuhan tidak selalu sama setiap hari, bulan atau tahun. Kondisi tersebut menyebabkan penyebaran data hubungan antara volume barang/penumpang dan tahun pengamatan.

Dalam analisis regresi akan dibuat kurva atau fungsi berdasarkan sebaran titik data. Kurva yang terbentuk diharapkan dapat mewakili titik-titik data tersebut. Seringkali, setelah kurva terbentuk, dilakukan pula ekstrapolasi untuk mendapatkan nilai y yang berkaitan dengan nilai x yang berada di luar rangkaian data yang ada. Misalnya dalam melakukan prediksi jumlah barang, atau penumpang yang akan dilayani suatu pelabuhan pada tahun-tahun yang akan datang (prediksi 5, 10, 15, ….n tahun yang akan datang). Metode yang digunakan untuk membuat kurva tersebut adalah metode kuadrat terkecil (least square method). Metode tersebut memungkinkan untuk membuat kurva yang paling mendekati titik-titik data.

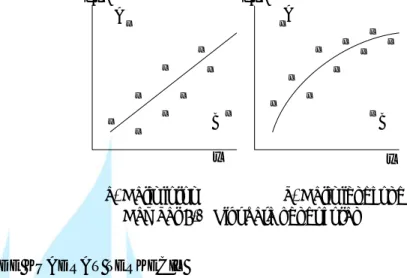
Gambar 8.1 adalah penyebaran titik-titik data hasil dari suatu percobaan pada sistem koordinat x-y. Penetapan bentuk kurva, apakah kurva linier (garis lurus) atau lengkung (logaritmik atau berpangkat), tergantung pada kecenderungan (trend) dari penyebaran titik data, seperti ditunjukkan pada gambar 8.1.a. dan 8.1.b. Seringkali dijumpai adanya beberapa data yang mempunyai kesalahan sangat besar seperti titik A dan B pada gambar 8.1. Pembuatan kurva dengan menggunakan titik A dan B akan menghasilkan nilai yang juga mempunyai kesalahan. Oleh karena itu data A dan B dapat dihilangkan.

x x x x x x x x x x x x x x x x x x x x x f(x) f(x) x x A B A B

a. Garis lurus b. Garis lengkung Gambar 8.1 Plot data pengukuran

8.2 METODE KUADRAT TERKECIL

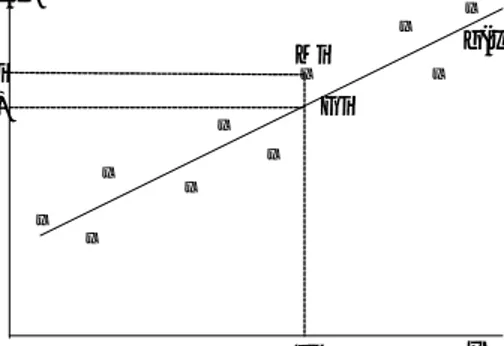
Gambar 8.2 adalah sebaran titik-titik data dari hasil pengukuran pada bidang x-y. Akan dicari suatu kurva g(x) yang dapat mewakili titik percobaan tersebut. Cara termudah adalah

(3)

membuat kurva secara visual (dengan perasaan) yang merupakan fungsi terbaik g(x) yang digambarkan oleh titik-titik data. Tetapi cara ini tidak bisa memberikan hasil yang memuaskan, terutama apabila penyebaran titik data cukup besar. Diinginkan suatu metode yang lebih pasti untuk mendapatkan kurva tersebut; yaitu dengan membuat kurva yang meminimumkan perbedaan (selisih) antara titik-titik data dan kurva. Teknik untuk mendapatkan kurva tersebut dikenal dengan regresi kuadrat terkecil.

x x x x x x x x x x f(x) x xi g(xi) g(xi) yi Gi Mi

Gambar 8.2 Kurva mewakili titik-titik data Teknik tersebut dilakukan dengan prosedur berikut ini.

a. Titik-titik percobaan digambar pada suatu sistem koordinat. Dari gambar sebaran titik data tersebut dapat diketahui trend (pola) secara umum dari kumpulan titik data, sehingga dapat ditentukan apakah kurva yang mewakili berupa garis lurus (linier) atau lengkung.

b. Dipilih suatu fungsi g(x) yang dianggap bisa mewakili f (x) yang mempunyai bentuk umum berikut ini.

g(x) = a0 + a1 x + a2x2+ ………. + arxr (8.1)

Fungsi tersebut tergantung pada parameter a0, a1, ………., ar

c. Ditentukan parameter a0, a1 ………. ar sedemikian rupa sehingga g(xi ; ao, aI

………., ar) melalui sedekat mungkin titik-titik data. Bentuk g(xi ; ao, aI ………., ar)

mempunyai arti fungsi g(xi) dengan parameter ao, aI ………., ar.

d. Apabila koordinat dari titik-titik percobaan adalah M(xi , yi), dengan i = 1,2,3,…n maka selisih ordinat antara titik-titik tersebut dengan fungsi g(xi ; ao, aI ……., ar) adalah:

Ei = Mi Gi = yi – g(xi ; ao, aI ………., ar)

= yi – (a0 + a1xi + a2x_i2a3x_i3...a_r x_ir)

e. Dipilih suatu fungsi g(x) yang mempunyai kesalahan Ei terkecil. Dalam metode ini jumlah

kuadrat dari kesalahan adalah terkecil.

D2₌







    n i n i i yi g xi E 1 2 1 2 ) ( (8.2)

f. Dicari parameter a0, a1 , …., ar sedemikian sehingga D2 adalah minimum. Nilai D2 akan

minimum apabila turunan pertamanya terhadap a0, a1 , …., ar adalah nol, sehingga :

0 0 2    a D 0 1 2    a D (8.3)

(4)

0 2    r a D

g. Penyelesaian persamaan (8.3) akan memberikan hasil parameter ao,aI a2 ….ar. Dengan

demikian persamaan kurva terbaik yang mewakili titik-titik data telah diperoleh.

8.3 METODE KUADRAT TERKECIL UNTUK KURVA LINIER

Bentuk paling sederhana dari regresi kuadrat terkecil adalah apabila kurva yang mewakili titik-titik data merupakan garis lurus, sehingga persamaannya adalah:

g(x) = a + bx (8.4)

dimana dalam hal ini, a0 = a dan a1 = b.

Jumlah kuadrat dari kesalahan dihitung sesuai dengan persamaan (8.2):

D2 ₌





2 1 1 2 )



     n i n i i i i y a bx E (8.5)

Agar nilai D2_{adalah minimum, maka persamaan (8.5) diturunkan terhadap parameter}

a dan b, dan kemudian disamadengankan nol.

Turunan pertama terhadap parameter a adalah :

0 2    a D



      n i i i a bx y a 1 2 0 ) (



     n i i i a bx y 1 0 ) ( 2 ∑ yi - ∑ a - ∑ b xi = 0 (8.6)

Turunan pertama terhadap parameter b adalah

0 2    b D



      n i i i a bx y b 1 2 0 ) {



     n i i i i a bx x y 1 0 ] ) [( 2 0 2   



yixi



axi



bxi (8.7)

Penjumlahan masing-masing suku pada persamaan (8.6) dan (8.7) adalah dari 1 sampai n. Persamaan (8.6) dan (8.7) dapat ditulis dalam bentuk:

(5)

∑xi a + x_i2bx_i y_i (8.9)

dengan ∑ a = n a

Selanjutnya persamaan (8.8) dapat ditulis menjadi :

na = ∑yi - ∑xi b





xb n y n b x y n a 1  _i  _i  1



_i1



_i (8.10) atau x b y a  (8.11)

Interpolasi persamaan (8.10) ke dalam persamaan (8.9) menghasilkan:

i i i i i i y xb x b x y n x      2 ) ( 1 i i i i i i y x b n x b n x y x         2 2 ) ) ( i i i i i i x n x y x y x n b[  2  ( )2]     atau 2 2 ₍ ₎ i i i i i i x x n y x y x n b         (8.12)

Dengan menggunakan persamaan (8.11) dan (8.12) untuk menghitung koefisien a dan

b, maka fungsi g(x) dapat dicari.

Persamaan garis lain, selain persamaan (8.4) memberikan jumlah kuadrat kesalahan yang lebih besar. Dengan demikian persamaan (8.4) adalah perkiraan terbaik dari data. Untuk mengetahui derajat kesesuaian dari persamaan yang didapat, dihitung nilai koefisien korelasi yang berbentuk : 2 2 2 t t D D D r  (8.13)

dengan r adalah koefisien, sedang 2

D dan D_t2 diberikan oleh bentuk :



   n i t yi y D 1 2 2 ) (



    n i ii a ax y D 1 2 1 0 2 ) (

Nilai r bervariasi antara 0 dan 1. Untuk perkiraan yang sempurna nilai r =1. Apabila

r=0 perkiraan suatu fungsi sangat jelek. Koefisien korelasi ini juga dapat digunakan untuk

memilih suatu persamaan dari beberapa alternatif yang ada, terutama di dalam regresi garis tidak lurus. Kurva lengkung dapat didekati dengan beberapa tipe persamaan, misalnya bentuk

y = axb_{, y = a e}b_{, y = a}₀_{+ a}₁_{x + a}₂_x2_{, atau persamaan lain. Dari beberapa alternatif tersebut}

(6)

Contoh 8.1: Tentukan persamaan garis yang mewakili data seperti pada tabel 8.1berikut. Tabel 8.1 Table data x dan y

x 4 6 8 10 14 16 20 22 24 28

y 30 18 22 28 14 22 16 8 20 8

Dari hitungan dalam tabel 8.1, nilai rerata dari xdan y adalah :

2 , 15 10 152     n x x 6 , 18 10 186     n y y

Persamaan garis yang mewakili titik-titik data adalah :

y = a + bx

Tabel 8.2. Hitungan regresi linier No xi yi xi yi xi2 1 4 30 120 16 2 6 18 108 36 3 8 22 176 64 4 10 28 280 100 5 14 14 196 196 6 16 22 352 256 7 20 16 320 400 8 22 8 176 484 9 24 20 480 576 10 28 8 224 784 ∑ 152 186 2432 2912 dengan : 2 2 ₍ ₎ i i i i i i x x n y x y x n b         0,6569 6016 3952 ) 152 ( 2912 10 186 152 2432 10 2      x x x

x

b

y

a





=18,6 + 0,6569 x 15,2 = 28,5849 Jadi persamaan garis adalah :

(7)

8.4 ANALISA REGRESI NONLINIER

Dalam praktek sering dijumpai bahwa sebaran titik-titik pada sistem koordinat mempunyai kecenderungan (trend) yang berupa kurva lengkung (non-liier), sehingga persamaan (10.4) tidak bisa langsung digunakan. Gambar 8.3 menunjukkan sebaran data pada sistem koordinat

x-y. Pada gambar 8.3a. titik data diwakili oleh kurva linier, sedang gambar 8.3b diwakili oleh

kurva lengkung. Terlihat bahwa pendekatan dengan kurva lengkung memberikan hasil yang lebih baik dari pada garis lurus (kurva linier). Agar persamaan regresi linier dapat digunakan untuk mempresentasikan kurva lengkung, maka perlu dilakukan transformasi koordinat sedemikian sehingga sebaran titik data bisa dipresentasikan dalam kurva linier.

Berikut ini diberikan dua fungsi transformasi data yang biasa digunakan, yaitu fungsi eksponensial dan tungsi berpangkat.

x b a x y x y x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x

Gambar 8.3 Titik data didekati dengan garis lurus dan lengkung

8.4.1 Persamaan Berpangkat

Persamaan berpangkat diberikan dalam bentuk berikut ini: 2 2 b x a y (8.14)

dengan a2 dan b2 adalah koefisien konstan.

Persamaan tersebut dapat dilinierkan dengan menggunakan fungsi logaritmik sehingga didapat:

2 2log log

logyb x a (8.15)

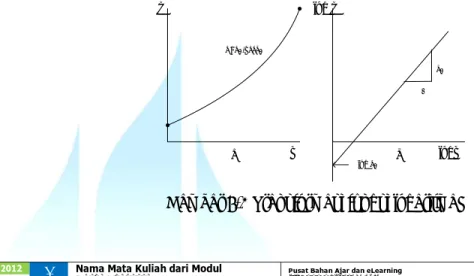
yang merupakan hubungan log-log antara log y dan log x. Persamaan tersebut mempunyai bentuk garis lurus dengan kemiringan b2 dan memotong sumbu y pada log a2. Gambar 8.4

menunjukkan transformasi dari fungsi asli menjadi fungsi logaritmik.

b a logx log y x y Y=a2.x^^b2 log a2 1 b2

(8)

8.4.2 Fungsi Exponensial

Contoh lain dari kurva tak linier adalah fungsi eksponensial seperti diberikan oleh bentuk berikut: x b e a y 1 1  (8.16)

dengan a1 dan b1 adalah konstanta.

Persamaan tersebut dapat dilinierkan dengan menggunakan logaritma natural sehingga menjadi : e x b a y ln ln ln  ₁ ₁

Oleh karena 1n e = 1, maka : x

b a y ln ₁ ₁

ln   (8.17)

Persamaan (8.17) merupakan hubungan semi logaritmik antara 1n y dan x. Persamaan tersebut mempunyai bentuk garis lurus dengan kemiringan b1 dan memotong

sumbu 1n y pada 1n a1. Gambar 8.5 menunjukkan transformasi fungsi asli menjadi fungsi

semi logaritmik. b a x ln y x y Y=a1.e^^b1.x ln a1 1 b1

Gambar 8.5 Transformasi fungsi eksponensial

Contoh 8.2: Tentukan persamaan kurva lengkung (non-linier) yang mewakili data berikut ini. x 1 2 3 4 5

y 0,5 1,7 3,4 5,7 8,4

Penyelesaian: Gambar 8.6 menunjukkan sebaran titik data pada sistem koordinat x-y. Dicoba untuk mencari kurva dengan menggunakan dua bentuk transformasi, yaitu transformasi log dan ln. x x x x y x f(x)

Gambar 8.6 Sebaran data dan kurva lengkung a. Transformasi log

Misalkan persamaan kurva yang dicari adalah:

b

ax y

(9)

Transformasi dengan menggunakan fungsi log, sehingga:

x

b

a

y

log





Dilakukan transformasi berikut:

p = log y B = b

A= log a q = log x

Sehingga persamaan di atas dapat ditulis dalam bentuk:

p =A + B q

Hitungan dilakukan dengan menggunakan tabel 8.3. Dari hitungan dalam tabel 8.3 didapat beberapa parameter berikut ini.

4158 , 0 5 0791 , 2 log     n x q i 42822 , 0 5 1411 , 2 log _ _   n y p i

Tabel 8.3 Hitungan regresi linier dengan transformasi log

No xi yi qi = log xi pi = log yi qi pi 2 i q 1 1 0,5 0 -0,3010 0 0 2 2 1,7 0,3010 0,2304 0,0693 0,0906 3 3 3,4 0,4771 0,5315 0,2536 0,2276 4 4 5,7 0,6020 0,7559 0,4550 0,3624 5 5 8,4 0,6990 0,9243 0,6461 0,4886  15 19,7 2,0791 2,1411 1,4240 1,1692

Koefisien A dan B dihitung dengan persamaan (8.11) dan (8.12)

2 2 ) ( _i i i i i i q q n p q p q n B         1,7572 5233 , 1 6684 , 2 0791 , 2 0791 , 2 1692 , 1 5 ) 1411 , 2 ( ) 0791 , 2 ( ) 4240 , 1 ( 5 _ _    x x

Setelah nilai B didapat kemudian dicari nilai A: q

B p

A  = 0,42822 - 1,7572 x 0,4158 = - 0,3024

Dengan demikian persamaan transformasi adalah:

p = -0,3024 + 1,7572 q

Mengingat:

A = log a  -0,3024 = log a  a =0,4984 B = b  b = 1,7572

(10)

7572 , 1 4984 , 0 x y b. Transfomasi ln

Misalkan persamaan kurva mempunyai bentuk:

bx

ae

y

Transformasi dengan menggunakan fungsi 1n, sehingga persamaan di atas menjadi: 1n y = 1n a ebx_{= 1n a + 1n e}bx

1n y = 1n a + bx

Dilakukan transformasi berikut:

p = 1n y A = 1n a q = x B = b

Sehingga persamaan di atas dapat ditulis dalam bentuk:

p = A + B q

Hitungan dilakukan dengan menggunakan tabel 8.4. Dari hitungan pada tabel 8.4 didapat beberapa parameter berikut ini:

3 5 15     n q q i 986 , 0 5 93 , 4 _    n p p i

Tabel 8.4 Hitungan regresi linier dengan transformasi 1n

No xi = qi yi qi2 = xi2 pi = 1n yi qi pi 1 1 0,5 1 -0,6931 -0,6931 2 2 1,7 4 0,5306 1,0612 3 3 3,4 9 1,2238 3,6714 4 4 5,7 16 1,7405 6,962 5 5 8,4 25 2,1282 10,641  15 19,7 55 4,93 21,6425

Koefisien A dan B dihitung dengan persamaan (8.11) dan (8.12).

2 2 ) ( _i i i i i i q q n p q p q n B         0,68525 50 26525 , 34 ) 15 ( 55 5 93 , 4 15 6425 , 21 5 2      x x x

Setelah nilai B didapat kemudian dicari nilai A, yaitu q

B p

A  = 0,986 - 0,68525 x 3,0 = -1,06975 Dengan demikian persamaan transformasi adalah:

(11)

Mengingat:

A = 1n a  -1,06575 = 1n a  a = 0,3431

B = b  b = 0,68525

maka persamaan yang dicari adalah:

x

e

y₀_,₃₄₃₁ 0,68525

Untuk memilih salah satu dari kedua hasil terbaik, dihitung nilai koefisien korelasi. Koefisien korelasi dihitung dengan menggunakan persamaan (8.13) :

₂ 2 2 t t D D D r  dengan



   n i i t yi y D 1 2 2 ) (



    n i i t yi a ax D 1 2 1 0 2 ) (

Hitungan dilakukan dengan menggunakan tabel 8.5.

Dengan menggunakan hitungan yang diberikan dalam tabel 8.5, dihitung nilai koefisien korelasi berikut ini:

Nilai r untuk transformasi log:

99997 , 0 132 , 40 00238 , 0 132 , 40 2 2 2      t t D D D r

Nilai r untuk transformasi 1n :

92751 , 0 132 , 40 60746 , 5 132 , 40 2 2 2      t t D D D r

Dari kedua nilai tersebut, koefisien korelasi r untuk transformasi log adalah lebih besar dari transformasi 1n, sehingga dapat disimpulkan bahwa persamaan yang didapat dari transformasi log adalah lebih baik.

Tabel 8.5. Hitungan koefisien korelasi

No xi yi

Transformasi log Transformasi 1n g(xi) D2 2 t D g(xi) D2 2 t D 1 2 3 4 5 1 2 3 4 5 0,5 1,7 3,4 5,7 8,4 0,4984 1,6848 3,4354 5,6953 8,4296 0,000003 0,000231 0,00125 0,000022 0,000876 11,8336 5,0176 0,2916 3,0976 19,8916 0,6835 1,3563 2,6912 5,3401 10,5963 0,03367 0,11813 0,50240 0,12953 4,82373 11,8336 5,0176 0,2916 3,0976 19,8916  0,00238 40,132  5,60746 40,132

(12)

8.4.3 Regresi Polinomial

Di dalam pertemuan sebelumnya telah dijelaskan penurunan persamaan dengan menggunakan metode kuadrat terkecil. Untuk kurva lengkung persamaannya dapat diturunkan dengan melakukan transformasi data asli ke dalam bentuk lain yang sesuai. Selain dengan transformasi persamaan kurva lengkung juga dapat diturunkan dengan menggunakan regresi polinomial. Penurunan persamaan dilakukan dengan menggunakan metode kuadrat terkecil.

Persamaan polinomial order r mempunyai bentuk:

r rx a x a x a a y ₀ ₁  ₂ 2... Jumlah kuadrat dari kesalahan adalah:



       n i r i r i i i a ax a x a x y D 1 2 2 2 1 0 2 )) ... ( (

Dengan cara seperti terdahulu, persamaan di atas diturunkan terhadap tiap koefisien dari polinomial dan kemudian disamadengankan nol, sehingga diperoleh:

0 )) ... ( ( 2 ₁ ₂ 2 1 0 0 2          



 r i r i i n i i a a x a x a x y a D 0 )) ... ( ( 2 ₁ ₂ 2 1 0 1 2          

_

 r i r i i n i i i y a a x a x a x x a D 0 )) ... ( ( 2 2 2 1 1 0 2 2 2          

_

 r i r i i n i i i y a a x a x a x x a D (8.18) 0 )) ... ( ( 2 ₁ ₂ 2 1 0 2          



 r i r i i n i i r i r x a x a x a a y x a D

Persamaan (8.18) dapat ditulis dalam bentuk:

                                                                                               i r i i i i i i r r r i r i r i r i r i i i i r i i i i r i i i y x y x y x y a a a a x x x x x x x x x x x x x x x n . . . . . . ... . . . . . . . . . . . . ... ... ... 2 2 1 0 2 1 2 4 3 2 1 3 2 2 (8.19 )

Dimana i = 1 sampai n. Dari r+1 persamaan tersebut akan dicari bilangan tak diketahui

a0, a1, a2, …, ar dengan metode yang telah dibicarakan pada pertemuan sebelumnya.

Koefisien matrik dari persamaan tersebut biasanya sangat padat (sangat sedikit koefisien nul) dan masing-masing koefisien sangat berbeda. Namun demikian biasanya nilai r adalah kecil sehingga sistem persamaan tersebut masih mudah diselesaikan.

(13)

Contoh 8.3: Cari persamaan kurva polinomial order dua yang mewakili data berikut: x 0 1 2 3 4 5 y 2,1 7,7 13,6 27,2 40,9 61,1 Penyelesaian: Persamaan polinomial order 2 mempunyai bentuk:

g (x) = a0 + a1x + a2x2 (8.20)

Ei = yi – g (x)

Ei2 =  (yi – a0 – a1x – a2x2)2

D2₌__E_i2

Untuk polinomial order dua, diferensial dari D2_{terhadap tiap koefisien dari polinomial}

dan kemudian disamadengankan nol menghasilkan bentuk:

                                          i i i i i i i i i i i i i y x y x y a a a x x x x x x x x n 2 2 1 0 4 3 2 3 2 2 (8.21)

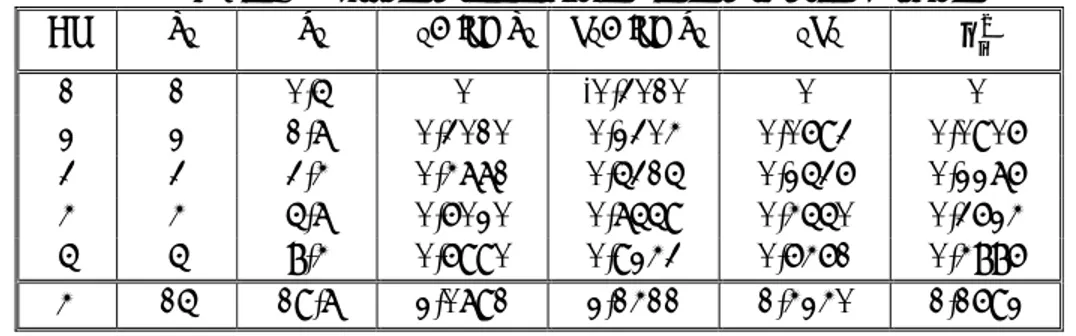
Hitungan dilakukan dengan menggunakan tabel 8.6. Tabel 8.6 Hitungan regresi polinomial order dua

No xi yi xi2 xi3 xi4 xi yi xi2yi 1 0 2,1 0 0 0 0 0 2 1 7,7 1 1 1 7,7 7,7 3 2 13,6 4 8 16 27,2 54,4 4 3 27,2 9 27 81 81,6 244,8 5 4 40,9 16 64 256 163,6 654,4 6 5 61,1 25 125 625 305,5 1527,5 15 397,4 55 175 979 585,6 2488,8

Dengan melakukan hitungan dalam tabel 8.6, maka sistem persamaan (8.21) menjadi: 6 , 152 55 15 6a₀ a₁ a₂  6 , 585 225 55 15a₀ a₁ a₂  8 , 2488 275 225 55a₀ a₁ a₂ 

Penyelesaian dari persamaan di atas adalah a₂ 1,860714; a₁2,359286; dan 478571

, 2

0 

a .

Dengan demikian persamaan kurva adalah:

2 8607 , 1 359286 , 2 478571 , 2 x x y  

(14)

Daftar Pustaka

1. Nazir, Moh., ”Metode Penelitian”, Ghalia Indonesia, 2011.

2. Noor, J., ”Metodologi Penelitian: Skripsi, Tesis, Disertasi, dan Karya Ilmiah”, Prenadamedia Group, 2011.

3. Wijanto, SH., ”Metode Penelitian: Menggunakan Structural Equation Modelling Dengan LISREL 9”, Lembaga Penerbit Fakultas Ekonomi UI, Jakarta, 2015.

4. Sugiyono, ”Metode Penelitian dan Pengembangan”, ALFABETA, 2015. 5. Taha, H.A., Riset operasi, Binarupa Aksara, 2009.

6. Beightler, C.S., et al, Foundation of optimization, Prentice Hall of India, 2010.