DIMENSI METRIK GRAF COMMUTING DAN NON COMMUTING DARI GRUP DIHEDRAL SKRIPSI OLEH MOH. AFIFUDDIN NIM

(1)

DIMENSI METRIK GRAF COMMUTING DAN NON COMMUTING DARI GRUP DIHEDRAL

SKRIPSI

OLEH

MOH. AFIFUDDIN NIM. 11610070

JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS ISLAM NEGERI MAULANA MALIK IBRAHIM MALANG

2016

(2)

GRUP DIHEDRAL

SKRIPSI

Diajukan Kepada Fakultas Sains dan Teknologi

Universitas Islam Negeri Maulana Malik Ibrahim Malang untuk Memenuhi Salah Satu Persyaratan dalam

Memperoleh Gelar Sarjana Sains (S.Si)

Oleh Moh. Afifuddin NIM. 11610070

JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS ISLAM NEGERI MAULANA MALIK IBRAHIM MALANG

2016

(3)

(4)

(5)

(6)

MOTO































“Dan hendaklah takut kepada Allah orang-orang yang seandainya meninggalkan di belakang mereka anak-anak yang lemah, yang mereka khawatir terhadap (kesejahteraan) mereka. Oleh sebab itu hendaklah mereka bertakwa kepada Allah

dan hendaklah mereka mengucapkan perkataan yang benar” (QS. an-Nisaa: 09).

(7)

PERSEMBAHAN

Karya kecil ini penulis persembahkan untuk orang-orang yang turut mewarnai hidup penulis.

Kedua Orang Tua Penulis.

Rama Achmad Zarnuji dan Ibu Arifatun.

Yang telah mencurahkan kasing sayangnya tanpa mengenal batas waktu.

Membimbing, mendo’akan, memotivasi, serta menginspirasi penulis untuk menjadi manusia yang lebih baik.

Adik-adik Penulis.

Ach. Taqiyuddin, alm. Muhyiddin, Hasbiyallah dan Mutawally.

Terima kasih atas segala kasih sayang, motivasi, dan dukungan yang telah diberikan.

Seluruh Keluarga Besar Penulis.

(8)

viii

Alhamdulillah puji syukur penulis panjatkan ke hadirat Allah Swt. yang telah melimpahkan rahmat, taufiq, hidayah, serta inayah-Nya kepada penulis sehingga penulisan skripsi ini dapat diselesaikan. Shalawat serta salam semoga tetap tercurahkan kepada Nabi Muhammad Saw. yang telah membimbing manusia dari jalan kegelapan menuju jalan yang terang benderang yaitu agama Islam di mana ilmu pengetahuan sudah berkembang pesat seperti sekarang ini.

Suatu kebahagiaan dan kebanggaan tersendiri bagi penulis karena telah dapat menyelesaikan penulisan skripsi yang berjudul “Dimensi Metrik Graf Commuting dan Non Commuting dari Grup Dihedral” dengan baik. Penulis menyadari bahwa dalam penulisan skripsi ini tidak terlepas dari bimbingan, arahan, dan bantuan dari berbagai pihak. Oleh karena itu, dalam kesempatan ini penulis ingin menyampaikan ucapan terima kasih yang sebesar-besarnya serta penghargaan yang setinggi-tingginya kepada:

1. Prof. Dr. H. Mudjia Rahardjo, M.Si., selaku rektor Universitas Islam Negeri (UIN) Maulana Malik Ibrahim Malang.

2. Dr. drh. Bayyinatul Muchtaromah, M.Si., selaku dekan Fakultas Sains dan Teknologi UIN Maulana Malik Ibrahim Malang.

3. Dr. Abdussakir, M.Pd., selaku ketua Jurusan Matematika Fakultas Sains dan Teknologi UIN Maulana Malik Ibrahim Malang sekaligus dosen pembimbing yang senantiasa dengan sabar memberikan arahan dan bimbingan dalam penulisan skripsi ini.

(9)

ix

4. Dr. H. Imam Sujarwo, M.Pd., selaku dosen pembimbing keagamaan yang telah mamberikan sumbangsih dalam penulisan skripsi ini.

5. Seluruh dosen UIN Maulana Malik Ibrahim Malang khususnya para dosen matematika yang telah memberikan banyak pengalaman dan ilmu serta senantiasa membimbing dan memberikan motivasi kepada penulis agar dapat menyelesaikan studi dengan baik.

6. Rama Achmad Zarnuji dan Ibu Arifatun tercinta yang telah mencurahkan kasih sayangnya, senantiasa mendoakan, membimbing, serta memotivasi penulis untuk dapat menyelesaikan penulisan skripsi ini dengan baik.

7. Dr. Hj. Mufidah Ch, M.Ag selaku ketua LP2M beserta teman relawan yang menjadi rumah inspirasi penulis di UIN Maulana Malik Ibrahim Malang

8. Seluruh teman-teman mahasiswa Jurusan Matematika angkatan 2011 dan semua pihak yang tidak dapat penulis sebutkan satu persatu, yang telah memberikan bantuan baik moril, materiil, maupun spiritual bagi penulis sehingga dapat menyelesaikan skripsi dengan baik.

Penulis berharap semoga skripsi ini dapat bermanfaat khususnya bagi penulis dan bagi pembaca pada umumnya.

Malang, Mei 2016

Penulis

(10)

x DAFTAR ISI

HALAMAN JUDUL HALAMAN PENGAJUAN HALAMAN PERSETUJUAN HALAMAN PENGESAHAN

HALAMAN PERNYATAAN KEASLIAN TULISAN HALAMAN MOTO

HAMALAN PERSEMBAHAN

KATA PENGANTAR ... viii

DAFTAR ISI ... x

DAFTAR TABEL ... xii

DAFTAR GAMBAR ... xiii

ABSTRAK ... xiv

ABSTRACT ... xv

خلم ص

... xvi

BAB I PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Rumusan Masalah ... 4

1.3 Tujuan Penelitian ... 4

1.4 Manfaat Penelitian ... 5

1.5 Metode Penelitian ... 5

1.6 Sistematika Penulisan ... 5

BAB II KAJIAN PUSTAKA 2.1 Graf ... 7

2.2 Derajat titik ... 8

2.3 Graf Terhubung ... 11

2.4 Radius dan Diameter Graf ... 13

2.5 Dimensi Metrik ... 14

2.6 Grup Dihedral ... 16

2.7 Graf Commuting ... 18

2.8 Graf Non Commuting ... 19

2.9 Jarak dalam Al-Quran ... 21

BAB III PEMBAHASAN 3.1 Dimensi Metrik Graf Commuting dari Grup Dihedral ... 23

(11)

xi

3.1.1 Dimensi Metrik Graf Commuting dari Grup Dihedral ... 23

3.2 Dimensi Metrik Graf Non Commuting dari Grup Dihedral ... 39

3.2.1 Dimensi Metrik Graf Non Commuting dari Grup Dihedral . 39 3.2.2 Dimensi Metrik Graf Non Commuting dari Grup Dihedral . 41 3.2.3 Dimensi Metrik Graf Non Commuting dari Grup Dihedral 42

3.2.4 Dimensi Metrik Graf Non Commuting dari Grup Dihedral 44

3.3 Interpretasi Dimensi Metrik dalam Pandangan Agama ... 54

BAB IV PENUTUP 4.1 Kesimpulan ... 59

4.2 Saran ... 59

DAFTAR PUSTAKA ... 60 RIWAYAT HIDUP

(12)

xii

DAFTAR TABEL

Tabel 2.1 Tabel Cayley dari ... 18

Tabel 3.6 Tabel Cayley dari .... ... 33

Tabel 3.7 Dimensi Metrik Graf Commuting dari Grup Dihedral ... 34

Tabel 3.14 Dimensi Metrik Graf Non Commuting dari Grup Dihedral ... 50

(13)

xiii

DAFTAR GAMBAR

Gambar 2.1 Graf Lintasan Tiga Titik ... 14

Gambar 2.2 Graf Bintang ... 15

Gambar 2.3 Graf Commuting dari ... 19

Gambar 2.4 Graf Non Commuting dari ... 20

(14)

xiv ABSTRAK

Afifuddin, Moh. 2016. Dimensi Metrik Graf Commuting dan Non Commuting dari Grup Dihedral. Skripsi. Jurusan Matematika Fakultas Sains dan Teknologi Universitas Islam Negeri Maulana Malik Ibrahim Malang.

Pembimbing: (I) Dr. Abdussakir, M.Pd. (II) Dr. H. Imam Sujarwo, M.Pd.

Kata kunci: dimensi metrik, graf commuting, graf non commuting, grup dihedral.

Beberapa penelitian tentang penerapan graf pada grup dihedral telah banyak dilakukan. Dengan demikian perlu adanya penelitian secara berkelanjutan mengenai graf commuting dan graf non commuting dari grup dihedral. Sehingga pada penulisan skripsi ini akan diteliti mengenai dimensi metrik graf commuting dan graf non commuting dari grup dihedral.

Metode yang digunakan dalam penulisan skripsi ini adalah kajian pustaka, dengan menggunakan rujukan beberapa buku dan jurnal. Sedangkan analisis yang dilakukan adalah dengan mengamati pola berdasarkan beberapa contoh. Dari pola yang dihasilkan, kemudian dicari rumus umumnya yang selanjutnya dinyatakan sebagai teorema.

Berdasarkan hasil pembahasan dalam penelitian ini, diperoleh suatu teorema. Teorema yang dihasilkan adalah dimensi metrik graf commuting dan non commuting dari grup dihedral.

1. Dimensi metrik graf commuting dari grup dihedral , adalah untuk n ganjil, dan untuk n genap.

2. Dimensi metrik graf non commuting dari grup dihedral , adalah untuk n ganjil dan untuk n genap.

3. Interpretasi dimensi metrik dalam penelitian ini fokus pada jarak. Jarak sangat menentukan terhadap kedisiplinan dan akan berdampak pada masa depan.

Dalam penulisan skripsi ini, penulis hanya memfokuskan pada pembahasan dimensi metrik graf commuting dan non commuting dari grup dihedral. Dengan demikian untuk penelitian selanjutnya, penulis menyarankan kepada pembaca untuk meneliti dimensi metrik pada graf lainnya.

(15)

xv ABSTRACT

Afifuddin, Moh. 2016. Metric Dimension of Commuting and Non Commuting Graph of Dihedral Group. Thesis. Department of Mathematics, Faculty of Science and Technology, State Islamic University of Maulana Malik Ibrahim Malang. Advisors: (I) Dr. Abdussakir, M.Pd. (II) Dr. H. Imam Sujarwo, M.Pd.

Keywords: metric dimension, commuting graph, non commuting graph, dihedral group.

Several researches have been done to investigate the application of dihedral group. Thus the research on the commuting and non commuting graph of dihedral group is necessary. So metric dimensions that this thesis will examine the commuting and non commuting graph of dihedral group.

The method used in this thesis is library research using some references such as books and journals. As for the analysis, the pattern based on some examples will be observed. From the obtained pattern, the general formula will be gained and will be stated as lemma or theorem.

Based of the result of this thesis, a theorem about metric dimension of commuting and non commuting graph of dihedral group can be stated as follows:

1. Metric dimension of commuting graph of dihedral group , is – for n odd, and for n even

2. Metric dimension of non commuting graph of dihedral group , is – for n odd, and for n even

3. Metric dimensions interpretation in this study focus on the distance. The distance determines the discipline and will have inpact in the future.

The focus of this thesis is only on metric dimension of commuting and non commuting graph of dihedral group. Thus for further research, the author suggests to the reader to examine other dimensions on graph metrics.

(16)

xvi

صخلم

نيدلا فيفع دممح .

6102 مجح .

Metrik

ططخمل

Commuting

و

Non Commuting

عمجم نع

Dihedral

. .يعمالجا ثحبلا ةيضايرلا ةبعش

ةيجولونكتلا و مولعلا ةيلك

لجا ةيموكحكا ةيماملإسا ةعما ميهاربإ كلام انلاوم

( :فرشلما .جنلاام 0

دبع روتكدلا )

( يرتسجالما ركشلا 6

) حكا روتكدلا اورجول مامإ جا

.يرتسج الما

لا تاملكلا ةيسيئر

: مجح

metrik

، ططخلم

commuting

، ططخلم

non commuting

،

عوممج .

^dihedral

قيبطت نع ثوحبلا تلعف ططخلما

عوممج فى .

^dihedral

رارمتللاا ثحبلا جاتتح كلاذلف

نع مجح

metrik

ططخلم

commuting

و

non commuting

عوممج نم

dihedral

كلاذلف .

نع يعمالجا ثحبلا ثحابلا بتك مجح

metric

ططخلم

commuting

و

non commuting

عوممج نم .

^dihedral

ةقيرطلا مدختسلما

ة وه ثحبلاذه فى لما

رااإساك ةلمجلا و بتكلا مادختلاب ةيبتكلما ججن

اعلا زمرلا ثحبت ثم .ةلثملأا نم طمنلا ةضحامبم وه مدختسلما ليلتح امأ و .ىرظنلا ىذلا طنم نم م

ىمست ثم هيف دجوت

lemma

و ةيرظن .

دجوت ثحبلاذه فى تانايبلا ليلتح نم لصحكا ةيرظن

لا اميل . تى لصح اجيلع وه ثبلاذه فى مجح

metric

ططخلم

commuting

و

non commuting

عوممج نم

dihedral

.

1 مجح .

metric

ططخلم

commuting

عوممج نم

dihedral

،

وه

لى

و ، ذاش ددع لى

.يوسي ددع

2 مجح .

metric

ططخلم

commuting

عوممج نم

dihedral

،

وه

لى

و ، ذاش ددع

لى ددع .يوسي

3 تايرسفتلا . مجح

metric

ىذلا طابضنلاا ىلع سايقلما يرثؤت .سايقلما في زكرت ثحبلاذه في

لبقتسلما فى رثؤيل .اضيا

نع ثحبلا ثحابلا دديح ثحبلاذه فى مجح

metric

ططخلم

commuting

و

^non

commuting

عوممج نم .

^dihedral

ءادلأ ئراقلا لىإ ثحابلا حترقي لبقتسلما ثحبلل كلاذلف

نع ثحبلا مجح

metric

في

ططخلم

.رخلآلا

(17)

1 BAB I PENDAHULUAN

1.1 Latar Belakang

Era globalisasi ini semua aspek keilmuan mengalami berkembangan yang sangat pesat, khususnya dalam bidang sains dan teknologi. Sebagai bagian dari sains, matematika berkembang dengan pesat di berbagai bidang di dalamnya.

Bidang aljabar yang merupakan salah satu bidang dalam ilmu matematika cukup mengalami perkembangan yang saat pesat. Salah satu cabang aljabar yang banyak diteliti adalah graf, dengan banyaknya penelitian graf yang sudah berhasil selalu memunculkan masalah baru yang sangat menarik untuk diteliti lebih lanjut.

Perkembangan dalam bidang aljabar mulai dari pengembangan konsep yang sudah ada hingga kolaborasi antar konsep seperti penerapan graf pada grup dihedral.

Graf G adalah pasangan (V(G), E(G)) dengan V(G) himpunan tidak kosong dan berhingga dari objek-objek yang disebut titik, dan E(G) adalah himpunan (mungkin kosong) pasangan takberurutan dari titik-titik berbeda di V(G) yang disebut sisi. Banyaknya unsur di V(G) disebut order dari G dan dilambangkan dengan p(G), dan banyaknya unsur di E(G) disebut ukuran dari G dan dilambangkan dengan q(G). Jika graf yang dibicarakan hanya graf G, maka order dan ukuran dari G masing-masing cukup ditulis p dan q. Graf dengan order p dan ukuran q dapat disebut graf-(p, q) (Chartrand & Lesniak, 1986).

Sisi e = (u, v) dikatakan menghubungkan titik u dan v. Jika e = (u, v) adalah sisi di graf G, maka u dan v disebut terhubung langsung (adjacent), v dan e

(18)

serta u dan e disebut terkait langsung (incident), dan titik u dan v disebut ujung dari e. Untuk selanjutnya, sisi e = (u, v) akan ditulis e = uv. Derajat dari titik v di graf G, ditulis degG(v), adalah banyaknya sisi di G yang terkait langsung dengan v. Dalam konteks pembicaraan hanya terdapat satu graf G, maka tulisan degG(v) disingkat menjadi deg(v) (Chartrand & Lesniak, 1986).

Perkembangan terbaru teori graf juga membahas graf yang dibangun dari grup. Misal G grup berhingga dan X adalah subset dari G. Graf commuting C(G,X) adalah graf yang memiliki himpunan titik X dan dua titik berbeda akan terhubung langsung jika saling komutatif di G. Jadi, titik x dan y akan terhubung langsung di C(G, X) jika dan hanya jika xy = yx di G (Vahidi & Talebi, 2010:123). Terkait penelitian mengenai graf commuting, Vahidi & Talebi (2010) membahas tentang bilangan bebas, bilangan clique, dan bilangan cover minimum. Chelvam, dkk (2011) meneliti tentang bilangan kromatik dan bilangan clique pada graf commuting yang diperoleh dari grup dihedral. Abdussakir, dkk. (2013) meneliti tentang spectrum dari graf commuting yang diperoleh dari grup dihedral.

Misalkan grup tidak komutatif dan adalah center dari . Graf non commuting adalah graf yang memiliki himpunan titik dan dua titik akan terhubung langsung di jika (Abdollahi, dkk., 2006). Atau graf non commuting dari didefinisikan sebagai graf yang himpunan titiknya adalah bukan anggota center dari dan dua titik saling terhubung jika dan hanya jika tidak komutatif (Abdollahi, dkk, 2010).

Misalkan subset dari barisan himpunan titik dan v adalah sebuah titik yang menghubungkan graf G. Representasi dari v terhadap S adalah barisan berurut n elemen, | , dimana

(19)

3 menggambarkan jarak antara titik x dan titik y. Himpunan S merupakan himpunan pemisah pada graf G jika untuk setiap titik pada graf G mempunyai representasi jarak yang berbeda terhadap S. Dimensi metrik pada graf G adalah jumlah anggota minimum pada himpunan pemisah, dilambangkan dengan dim(G).

Himpunan pemisah yang memuat jumlah anggota minimum dinamakan basis dari graf G. Dengan demikian dim(G) adalah kardinalitas basis dari graf G.

Membahas dimensi metrik pada graf maka tidak terlepas dari beberapa penelitian yang sudah ada. Terkait dimensi metrik graf, Mudjiati (2011) membahas dimensi metrik graf kincir dengan daun bervariasi. Saputro (2012) membahas dimensi metrik graf regular dan graf komposisi.

Mendalami dan mangkaji ilmu pengetahuan merupakan keharusan yang harus dilakukan sacara berkelanjutan dengan tujuan selalu mengagungkan ciptaan Allah Swt. dalam kondisi apapun. Keharusan tersebut selaras dengan firman Allah Swt. dalam surat Ali Imron ayat 191,













































“(Yaitu) orang-orang yang mengingat Allah sambil berdiri atau duduk atau dalam keadaan berbaring dan mereka memikirkan tentang penciptaan langit dan bumi (seraya berkata): "Ya Tuhan Kami, Tiadalah Engkau menciptakan ini dengan sia-sia, Maha suci Engkau, Maka peliharalah kami dari siksa neraka”(QS. Ali Imron: 191)

Berdasarkan ayat di atas, jelas bahwa semua ciptaan Allah harus selalu direnungkan dan dikembangkan dengan menggunakan akal pikiran manusia guna semakin mengetahui kekuasaan dan keagungan-Nya termasuk dalam hal ini adalah ilmu pengetahun.

(20)

Berdasarkan uraian di atas, sampai saat ini belum ada yang mengkaji secara paralel tentang dimensi metrik graf commuting dan non commuting grup dihedral. Pada penelitian ini, dikaji lebih dalam salah satu sifat pada graf commuting dan non commuting dari grup dihedral. Penelitian diarahkan pada dimensi metrik graf commuting dan non commuting dari grup dihedral serta dikaji bagaimana interpretasinya dalam pandangan agama berdasarkan ayat-ayat al- Quran.

1.2 Rumusan Masalah

Rumusan masalah dalam penelitian ini dengan berdasarkan latar belakang di atas antara lain:

1. Bagaimana bentuk umum dimensi metrik graf commuting dari grup dihedral?

2. Bagaimana bentuk umum dimensi metrik graf non commuting grup dihedral?

3. Bagaimana interpretasi dimensi metrik dalam pandangan agama?

1.3 Tujuan Penelitian

Sesuai dengan rumusan masalah di atas maka tujuan penelitian ini antara lain:

1. Mendeskripsikan bentuk umum dimensi metrik graf commuting dari grup dihedral

2. Mendeskripsikan bentuk umum dimensi metrik graf non commuting grup dihedral

3. Mendeskripsikan interpretasi dimensi metrik dalam pandangan agama

(21)

5 1.4 Manfaat Penelitian

Penelitian ini diharapkan mampu menambah wawasan peneliti dalam melakukan penelitian serta menambah wawasan peneliti dalam memahami teori graf yang sekaligus menjadi sumbangsih pengembangan teori graf. Penelitian ini diharapkan menjadi landasan dasar untuk penelitian selanjutnya.

1.5 Metode Penelitian

Metode yang digunakan dalam penulisan skripsi ini menggunakan studi literatur yaitu penelitian yang dilakukan dengan cara mengumpulkan data dan informasi dengan bantuan materi yang terdapat di perpustakaan. Adapun langkah- langkah dalam penelitian ini sebagai berikut:

1. Menentukan grup dihedral dari D6, D8, D10, D12, D14, D16.

2. Menggambarkan tabel Cayley dari grup dihedral D6, D8, D10, D12, D14, D16.

3. Menggambarkan graf commuting dan non commuting dari grup dihedral D₆, D8, D10, D12, D14, D16.

4. Menentukan dimensi metrik dari masing-masing graf yang terbentuk.

5. Menentukan pola dimensi metrik yang terbentuk pada graf commuting dan non commuting, dan dinyatakan sebagai teorema.

6. Membuktikan teorema yang diperoleh.

1.6 Sistematika Penulisan

Sistematika penulisan dimaksudkan untuk mempermudah dalam memahami intisari dari penulisan skripsi ini. Sistematika pada skripsi sebagai berikut:

(22)

Bab I Pendahuluan

Pada bab ini membahas tentang latar belakang masalah, rumusan masalah, tujuan penelitian, manfaat penelitian, metode penelitian dan sistematika penulisan.

Bab II Kajian Pustaka

Pada bab ini menyajikan tentang penjabaran materi graf dan grup dihedral.

Bab III Pembahasan

Bab ini membahas tentang dimensi metrik graf commuting dan non commuting dari grup dihedral.

Bab IV Penutup

Bab ini berisi tentang kesimpulan dari hasil pembahasan dan saran.

(23)

7 BAB II KAJIAN PUSTAKA

2.1 Graf

Graf merupakan salah satu banyak cabang ilmu matematika yang aplikasinya banyak digunakan dalam kehidupan kita, namun dalam teori graf masih banyak sekali kajian di dalamnya. Graf terdiri atas himpunan yang tidak kosong dari elemen-elemen yang disebut titik (vertex) dalam penulisan ini disimbolkan dengan , sedangkan himpunan sisi (edge) disimbolkan dengan dan seterusnya menggunakan istilah titik dan sisi.

Graf G adalah pasangan himpunan (V, E) dengan V adalah himpunan tidak kosong dan berhingga dari obyek-obyek yang disebut sebagai titik dan E adalah himpunan (mungkin kosong) pasangan tak berurutan dari titik-titik berbeda di V yang disebut sebagai sisi. Himpunan titik di G dinotasikan dengan V(G) dan himpunan sisi dinotasikan dengan E(G). Sedangkan banyaknya unsur di V disebut order dari G dan dilambangkan dengan p(G) dan banyaknya unsur di E disebut ukuran dari G dan dilambangkan dengan q(G). Jika graf yang dibicarakan hanya graf G, maka order dan ukuran dari G tersebut cukup ditulis dengan p dan q. Graf dengan order p dan ukuran q dapat disebut graf(p,q) (Chartrand dan Lesniak, 1986).

Sisi dikatakan menghubungkan titik u dan v. Jika adalah sisi di graf G, maka u dan v disebut terhubung langsung (adjacent), v dan e serta u dan e disebut terkait langsung (incident), dan titik u dan v disebut ujung dari e. Dua sisi berbeda dan disebut terhubung langsung (adjacent), jika

(24)

terkait langsung pada satu titik yang sama. Untuk selanjutnya, sisi akan ditulis (Chartrand dan Lesniak, 1986:4).

2.2 Derajat Titik

Jika v adalah titik pada graf G, maka himpunan semua titik di G yang terhubung langsung dengan v disebut lingkungan dari v dan ditulis NG(v). Derajat dari titik v di graf G, ditulis degG(v), adalah banyaknya sisi di G yang terkait langsung dengan v. Dalam konteks pembicaraan hanya terdapat satu graf G, maka tulisan degG(v) disingkat menjadi deg(v) dan NG(v) disingkat menjadi N(v). Jika dikaitkan dengan konsep lingkungan, derajat titik v di graf G adalah banyaknya anggota dalam N(v). Jadi,

| |

Titik yang berderajat 0 disebut titik terasing atau titik terisolasi. Titik yang berderajat 1 disebut titik ujung atau titik akhir. Titik yang berderajat genap disebut titik genap dan titik yang berderajat ganjil disebut titik ganjil. Derajat maksimum titik di G dilambangkan dengan (G) dan derajat minimum titik di G dilambangkan dengan (G).

Hubungan antara jumlah derajat semua titik dalam suatu graf G dengan banyak sisi, yaitu q adalah

∑

disebut sebagai “Teorema Pertama dalam Teori Graf” yang dinyatakan dalam teorema berikut.

(25)

9 Teorema 1

Jika G graf dengan order p dan ukuran q, dengan , maka



 p 

i

i q

v

1

G( ) 2

deg (Chartrand dan

Lesniak, 1986).

Bukti

Setiap menghitung derajat suatu titik di G, maka suatu sisi dihitung 1 kali.

Karena setiap sisi menghubungkan dua titik berbeda maka ketika menghitung derajat semua titik, sisi akan terhitung dua kali. Dengan demikian diperoleh bahwa jumlah semua derajat titik di G sama dengan 2 kali jumlah sisi di G. Terbukti bahwa

∑

Berdasarkan hubungan tersebut, maka banyak titik ganjil dalam suatu graf selalu genap. Hal ini dinyatakan dalam teorema berikut.

Teorema 2

Banyaknya titik ganjil dalam suatu graf selalu genap.

Bukti

Misalkan G graf. Misalkan X adalah himpunan titik genap di G dan Y adalah himpunan titik ganjil di G. Maka

∑ ∑ ∑

Karena X adalah himpunan titik genap maka ∑ adalah genap.

Karena 2q adalah bilangan genap dan ∑ juga genap maka

∑ haruslah bilangan genap.

(26)

Karena Y himpunan titik ganjil dan ∑ adalah bilangan genap, maka banyak titik di Y haruslah genap, sebab jika banyak titik di Y ganjil maka ∑ adalah ganjil.

Terbukti bahwa banyaknya titik ganjil di G adalah genap.

Graf G dikatakan beraturan-r atau beraturan dengan derajat r jika masing- masing titik v di G, maka , untuk bilangan bulat taknegatif r. Suatu graf disebut beraturan jika graf tersebut beraturan-r untuk suatu bilangan bulat taknegatif r. Graf beraturan-3 biasa juga disebut dengan graf kubik.

Graf G dikatakan komplit jika setiap dua titik yang berbeda saling terhubung langsung (adjacent). Graf komplit dengan order n dinyatakan dengan . Dengan demikian, maka graf merupakan graf beraturan-(n – 1) dengan order dan ukuran

( ).

Graf G dikatakan bipartisi jika himpunan titik pada G dapat dipartisi menjadi dua himpunan tak kosong dan sehingga masing-masing sisi pada graf G tersebut menghubungkan satu titik di dengan satu titik di . Jika G adalah graf bipartisi beraturan-r, dengan , maka | | | |. Graf G dikatakan partisi-n jika himpunan titiknya dapat dipartisi menjadi sebanyak n himpunan tak kosong , sehingga masing-masing sisi pada graf G menghubungkan titik pada dengan titik pada , untuk . Jika , graf partisi-n disebut graf tripartisi.

Suatu graf G disebut bipartisi komplit jika G adalah graf bipartisi dan masing-masing titik pada suatu partisi terhubung langsung dengan semua titik pada partisi yang lain. Graf bipartisi komplit dengan m titik pada salah satu partisi dan n titik pada partisi yang lain ditulis . Graf bipartisi komplit disebut

(27)

11 graf bintang (star) dan dinotasikan dengan . Jadi, mempunyai order dan ukuran n.

Graf G dikatakan partisi-n komplit jika G adalah graf partisi-n dengan himpunan partisi , sehingga jika dan , , maka . Jika | | , maka graf ini dinotasikan dengan . Urutan tidak begitu diperhatikan. Graf partisi-n komplit merupakan graf komplit jika dan hanya jika untuk semua i. Jika untuk semua i, , maka graf partisi-n komplit ini merupakan graf beraturan dan dinotasikan dengan . Jadi, tidak lain adalah .

2.3 Graf Terhubung

Misalkan G graf. Misalkan u dan v adalah titik di G (yang tidak harus berbeda). Jalan u-v pada graf G adalah barisan berhingga yang berselang-seling

antara titik dan sisi, yang dimulai dari titik dan diakhiri dengan titik, dengan

adalah sisi di G. disebut titik awal, disebut titik akhir, titik disebut titik internal, dan n menyatakan panjang dari W. Jika , maka W disebut jalan terbuka. Jika , maka W disebut jalan tertutup. Jalan yang tidak mempunyai sisi disebut jalan trivial. Karena dalam graf dua titik hanya akan dihubungkan oleh tepat satu sisi, maka jalan u-v

dapat ditulis menjadi

(28)

Jalan W yang semua sisinya berbeda disebut trail. Jalan terbuka yang semua titiknya berbeda disebut lintasan. Dengan demikian setiap lintasan pasti merupakan trail, tetapi tidak semua trail merupakan lintasan.

Teorema 3

Setiap jalan u-v pada suatu graf selalu memuat lintasan u-v (Chartrand dan Lesniak, 1996: 17).

Bukti

Misalkan W adalah jalan u-v di graf G. Jika W tertutup, maka jelas W memuat lintasan trivial di G. Misalkan

adalah jalan u-v terbuka. Jika tidak ada titik yang berulang di W, maka W adalah lintasan u-v. Jika ada titik yang berulang di W, misakan i dan j adalah bilangan bulat positif berbeda dengan sehingga . Maka, suku dihapus dari W. Hasilnya sebut , yakni jalan u-v baru yang panjangnya kurang dari panjang W. Jika pada tidak ada titik yang berulang, maka adalah lintasan u-v. Jika pada ada titik yang berulang, maka lakukan proses penghapusan seperti sebelumnya, sampai akhirnya diperoleh jalan u-v yang merupakan lintasan u-v.

Graf berbentuk lintasan dengan titik sebanyak n dinamakan graf lintasan order n dan ditulis Pn. Jalan tertutup W tak trivial yang semua sisinya berbeda disebut sirkuit. Dengan kata lain, sirkuit adalah trail tertutup tak trivial. Jalan tertutup tak trivial yang semua titiknya berbeda disebut sikel. Dengan demikian setiap sikel pasti merupakan sirkuit, tetapi tidak semua sirkuit merupakan sikel.

Jika dicarikan hubungan antara sirkuit dan sikel diperoleh bahwa: trail tertutup

(29)

13 dan tak trivial pada graf G disebut sirkuit di G. Sirkuit dengan dengan berbeda disebut sikel. Sikel dengan panjang k disebut sikel-k. Sikel-k disebut genap atau ganjil bergantung pada k genap atau ganjil.

Sebuah sirkuit di graf G yang memuat semua sisi G disebuat sirkuit Euler.

Sebuah graf yang memuat sirkuit Euler disebut graf Euler. Sikel yang memuat semua titik pada graf disebut sikel Hamilton. Graf yang memuat sikel Hamilton disebut graf Hamilton (Budayasa, 2007:6).

Misalkan u dan v titik berbeda pada graf G. Titik u dan v dikatakan terhubung (connected), jika terdapat lintasan u-v di G. Suatu graf G dikatakan terhubung (connected), jika untuk setiap titik u dan v yang berbeda di G terhubung. Dengan kata lain, suatu graf G dikatakan terhubung (connected), jika untuk setiap titik u dan v di G terdapat lintasan u-v di G. Sebaliknya, jika ada dua titik u dan v di G, tetapi tidak ada lintasan u-v di G, maka G dikatakan tak terhubung (disconnected).

2.4 Radius dan Diameter Graf

Untuk suatu graf terhubung G, maka jarak antara dua titik u dan v di G adalah panjang lintasan terpendek yang menghubungkan u dan v di G. Jika tidak ada lintasan dari titik u ke v, maka didefinisikan jarak . Eksentrisitas dari suatu titik v pada graf terhubung G adalah jarak terjauh (maksimal lintasan terpendek) dari titik v ke setiap titik di G dapat dituliskan . Titik v dikatakan titik eksentrik dari u jika jarak dari u ke v sama dengan eksentrisitas dari u atau . Radius dari G

(30)

adalah eksentrisitas minimum pada setiap titik di G, dapat dituliskan . Sedangkan diameter dari G, dinotasikan diam G adalah eksentrisitas maksimum pada setiap titik di G, dapat dituliskan (Chartrand dan Lesniak, 1986:29).

2.5 Dimensi Metrik

Misalkan subset dari barisan himpunan titik dan v adalah sebuah titik yang menghubungkan graf G. Representasi dari v terhadap S adalah barisan berurut n elemen, | , dimana menggambarkan jarak antara titik x dan titik y. Himpunan S merupakan himpunan pemisah pada graf G jika untuk setiap titik pada graf G mempunyai representasi jarak yang berbeda terhadap S. Dimensi metrik pada graf G adalah jumlah anggota pada himpunan pemisah, dilambangkan dengan . Sebuah himpunan pemisah yang mengandung jumlah anggota minimum dinamakan basis dari graf G.

Contoh:

Gambar 2.1 Graf Lintasan Tiga Titik

Misal diambil , maka representasinya adalah:

| | |

karena masih terdapat nilai representasi yang sama yaitu | dan | , maka , bukan merupakan himpunan pemisah, selanjutnya akan diambil S lainnya, misal diambil , maka representasinya adalah:

x1 x2 x3

(31)

15 | | | ,

karena semua titik pada graf tersebut mempunyai representasi yang berbeda terhadap , maka merupakan salah satu himpunan pemisah.

Begitu juga apabila diambil , representasinya adalah sebagaimana berikut:

| | | ,

Karena dan merupakan himpunan pemisah dari graf di atas, dan disebut sebagai himpunan pemisah yang mempunyai jumlah anggota minimum (basis) sehingga . Untuk selanjutnya apabila ada dua basis metrik maka akan diambil satu basis metrik untuk mempercepat penghitungan dimensi metriknya.

Contoh:

Gambar 2.2 Graf Bintang

Ambil , maka representasinya adalah:

| | | | , karena masih terdapat representasi yang sama yaitu | dan | maka bukan merupakan himpunan pemisah. Oleh sebab itu dicoba untuk mengambil dua titik. Ambil , maka representasi semua titik terhadap S untuk himpunan S yang memiliki lebih dari satu anggota dihitung mulai dari representasi jarak anggota pertama diikuti representasi

x22

x12

x1

x32

(32)

anggota kedua dan seterusnya. Keterangan lebih jelas, dapat diamati pada representasi berikut.

Representasi semua titik terhadap adalah:

| | | | , Karena mempunyai representasi yang berbeda dan mempunyai jumlah anggota minimum yaitu 2, maka adalah basis graf , maka dimensi metrik adalah dua, dim( ) = 2.

2.6 Grup Dihedral

Grup adalah suatu struktur aljabar yang dinyatakan sebagai dengan G adalah himpunan tidak kosong dan  adalah operasi biner di G yang memenuhi sifat-sifat berikut:

1. , (yaitu assosiatif ).

2. Ada suatu elemen e di G sehingga , (e disebut identitas di G).

3. Untuk setiap ada suatu element di G sehingga ( disebut invers dari a)

Sebagai tambahan, grup disebut abelian (grup komutatif) jika , (Raisinghania dan Aggarwal, 1980:31 dan Dummit dan Foote, 1991:13-14). Himpunan bilangan bulat Z dengan operasi jumlah memenuhi aksioma grup, yakni adalah grup abelian.

Grup dihedral adalah grup dari himpunan simetri-simetri dari segi-n beraturan, dinotasikan , untuk setiap n bilangan bulat positif dan .

(33)

17 Dalam buku lain ada yang menuliskan grup dihedral dengan (Dummit dan Foote, 1991:24-25).

Misalkan suatu grup yang didefinisikan oleh untuk yang diperoleh dari simetri (simetri sebagai fungsi pada segi-n, sehingga adalah fungsi komposisi). Jika akibat permutasi titik berturut-turut , maka akibat dari . Operasi biner pada adalah assosiatif karena fungsi komposisi adalah assosiatif. Identitas dari adalah identitas dari simetri (yang meninggalkan semua titik tetap), dinotasikan dengan 1, dan invers dari adalah kebalikan semua putaran dari simetri s (jadi jika s akibat permutasi pada titik akibat dari ) (Dummit dan Foote, 1991:24-25).

Karena grup dihedral akan digunakan secara ektensif, maka perlu beberapa notasi dan beberapa hitungan yang dapat menyederhanakan perhitungan selanjutnya dan membantu mengamati , yaitu:

1. , 2. | | ,

3. , ,

4. , dengan . Jadi

, yaitu setiap elemen dapat

dituliskan secara tunggal dalam bentuk untuk dan ,

5. ,

6. untuk semua (Dummit dan Foote, 1991:26).

Sebagai contoh adalah grup dihendral yang memuat semua simetri (rotasi dan refleksi) pada bangun segitiga sehingga .

(34)

2.7 Graf Commuting

Misal G adalah grup berhingga dan X adalah subset dari G , graf commuting adalah graf dengan X sebagai himpunan titik dan dua elemen berbeda di X terhubung langsung jika keduanya adalah elemen yang saling komutatif di G (Nawawi, dkk, 2012).

Sebagai contoh pada grup dihedral order 6 yaitu terhadap operasi fungsi komposisi. Diambil maka akan ditentukan unsur yang saling komutatif melalui tabel berikut.

Tabel 2.1 Tabel Cayley dari

Dari Tabel 2.1 terlihat bahwa:

1. 1 komutatif dengan setiap elemen (sifat elemen identitas) sehingga 1 terhubung langsung dengan setiap elemen di .

2. merupakan elemen-elemen yang komutatif sehingga terhubung langsung di .

3. Untuk elemen-elemen yang tidak komutatif maka elemen-elemen tersebut tidak terhubung langsung di .

(35)

19 Secara geometri, graf commuting pada dapat disajikan sebagai berikut.

Gambar 2.3 Graf Commuting dari

2.8 Graf Non Commuting

Misal G adalah sebuah grup, maka himpunan Z dikatakan center dari grup G, dituliskan

(Raisinghania dan Aggarwal, 1980: 229).

Misal G grup non abelian dan adalah center dari G. Graf non commuting adalah sebuah graf yang mana titik-titiknya merupakan himpunan dari dan dua titik x dan y terhubung langsung jika dan hanya jika (Abdollahi, dkk, 2006).

Sebagai contoh pada grup dihedral order 6 yaitu terhadap operasi fungsi komposisi. Dihedral dibangun dari elemen-elemen , hasil operasi komposisi pada setiap elemen grup dihedral berbentuk tabel Cayley yang menunjukkan unsur-unsur yang tidak komutatif pada

sebagai berikut:

(36)

Tabel 2.2 Tabel Cayley D6

1 r r² s sr sr² 1 1 r r² s sr sr² r r r² 1 sr² s sr r² r² 1 r sr sr² s s s sr sr² 1 r r² sr sr sr² s r² 1 r sr² sr² s sr r r² 1

Dari Tabel 2.2, center atau yaitu {1} yang ditunjukkan pada Tabel dengan warna biru, dan elemen-elemen pada yang tidak komutatif ditunjukkan pada tabel dengan warna kuning. Sehingga graf non commuting dari grup memiliki himpunan titik-titiknya . Dari hasil tersebut akan digambarkan ke dalam bentuk graf non commuting sebagai berikut:

Gambar 2.4 Graf Non Commuting dari D6

(37)

21 2.9 Jarak dalam Al-Quran

Jarak adalah panjang lintasan antara satu titik terhadap titik yang lain.

Menyinggung tentang jarak, dalam al-Quran disebutkan beberapa istilah jarak antara lain:































































“Dan Kami (tundukkan) angin bagi Sulaiman, yang perjalanannya di waktu pagi sama dengan perjalanan sebulan dan perjalanannya di waktu sore sama dengan perjalanan sebulan (pula) dan Kami alirkan cairan tembaga baginya. Dan sebahagian dari jin ada yang bekerja di hadapannya (di bawah kekuasaannya) dengan izin Tuhannya. Dan siapa yang menyimpang di antara mereka dari perintah Kami, Kami rasakan kepadanya adzab neraka yang apinya menyala- nyala” (QS. Saba’: 12)

Maksud dari ayat di atas ialah bila Nabi Sulaiman melakukan perjalanan dari pagi sampai tengah hari, maka jarak yang ditempuhnya sama dengan jarak perjalanan unta yang cepat dalam sebulan. Begitu pula bila ia melakukan perjalanan dari tengah hari sampai sore, maka kecepatannya sama dengan perjalanan sebulan.







































“Dan Kami jadikan antara mereka dan antara negeri-negeri yang Kami limpahkan berkat kepadanya, beberapa negeri yang berdekatan dan Kami tetapkan antara negeri-negeri itu (jarak-jarak) perjalanan. Berjalanlah kamu di kota-kota itu pada malam hari dan siang hari dengan dengan aman” (QS. Saba’:

18 )

Dari ayat di atas, yang dimaksud dengan negeri yang Kami limpahkan berkat kepadanya ialah negeri yang berada di Syam karena kesuburannya, dan negeri-negeri yang berdekatan ialah negeri-negeri antara Yaman dan Syam, sehingga orang-orang dapat berjalan dengan aman siang dan malam tanpa

(38)

terpaksa berhenti di padang pasir dan tanpa mendapat kesulitan sebab jarak antara negeri yang satu dengan lainnya cukup ideal untuk melakukan perjalanan.













“Maka jadilah Dia dekat (pada Muhammad sejarak) dua ujung busur panah atau lebih dekat (lagi)” (QS. An-Najm: 9 ).

Berdasarkan ayat-ayat al-Quran di atas terlihat ada dua istilah jarak yang berbeda.

Pada ayat yang berkenaan pada peristiwa perjalanan nabi Sulaiman jarak yang dimaksud adalah jarak dengan bobot waktunya, sedangkan pada ayat yang menjelaskan kesuburan negeri-negeri yang berada di Syam jarak yang dimaksud adalah jarak dengan bobot panjang, begitu pula pada ayat yang terakhir adalah jarak dengan bobot panjang.

(39)

23 BAB III PEMBAHASAN

Pada bab ini dibahas tentang dimensi metrik graf commuting dan non commuting yang dibentuk dari grup dihedral D2n berdasarkan pada tabel Cayley.

3.1 Dimensi Metrik Graf Commuting dari Grup Dihedral 3.1.1 Dimensi Metrik Graf Commuting dari Grup Dihedral D6

Elemen-elemen pembangun dari grup dihedral yaitu { }. Berdasarkan elemen-elemen pembangunnya tersebut, maka diperoleh tabel Cayley dari sebagai berikut:

Tabel 3. 1 Tabel Cayley dari D6

1 r r² S sr sr² 1 1 r r² S sr sr²

r r r² 1 sr² s Sr

r² r² 1 r Sr sr² S

s s Sr sr² 1 s r²

sr sr sr² s r² 1 R

sr² sr² s sr S r² 1

Berdasarkan tabel Cayley di atas dapat diketahui elemen-elemen komutatif dari dengan operasi . Elemen-elemen yang memenuhi sifat komutatif dengan operasi pada ditunjukkan dengan warna yang berbeda.

Sehingga didapatkan graf commuting sebagai berikut:



(40)

Gambar 3.1 Graf Commuting dari D6

Berdasarkan graf pada Gambar 3.1 akan diuraikan representasi masing- masing himpunan bagian S pada graf commuting dari dengan anggota 3 elemen.

representasi S | |

| | |

|

representasi S | |

| | |

|

representasi S | |

| | |

|

representasi S | |

| | |

|

representasi S | |

| | |

|

representasi S | |

| | |

|

(41)

25

representasi S | |

| | |

|

representasi S | |

| | |

|

representasi S | |

| | |

|

Berdasarkan uraian di atas merupakan salah satu himpunan pemisah yang anggotanya paling sedikit, sehingga diperoleh dimensi metrik adalah 3. Selanjutnya akan ditunjukkan bahwa S dengan 2 elemen memiliki representasi yang sama sebagai berikut:

1. dengan representasi sama | dan |

3.1.2 Dimensi Metrik Graf Commuting dari Grup Dihedral

Elemen-elemen pembangun dari grup dihedral yaitu { }. Berdasarkan elemen-elemen pembangunnya tersebut, maka diperoleh tabel Cayley dari sebagai berikut:

(42)

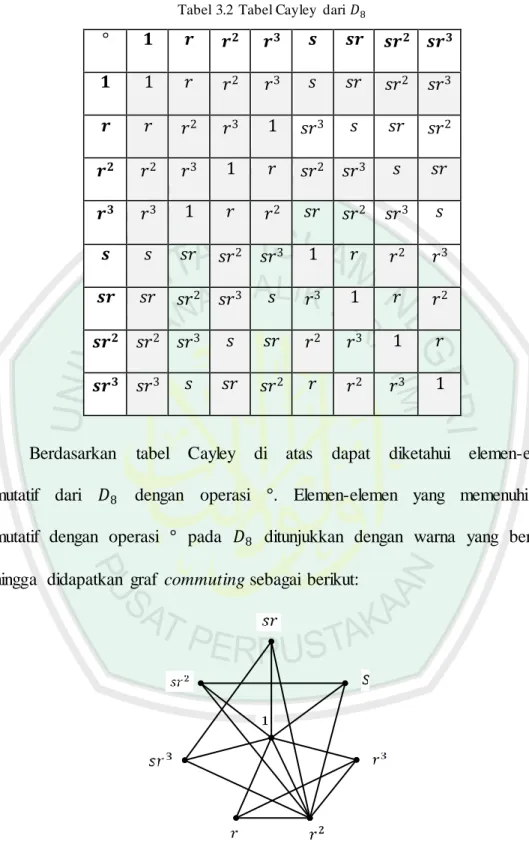
Tabel 3.2 Tabel Cayley dari

Gambar 3.2 Graf Commuting dari D8

Berdasarkan graf pada Gambar 3.2 diperoleh dimensi metrik adalah 4, dengan . Selanjutnya ditunjukkan bahwa S dengan 3 elemen

(43)

27 memiliki representasi yang sama sebagai berikut:

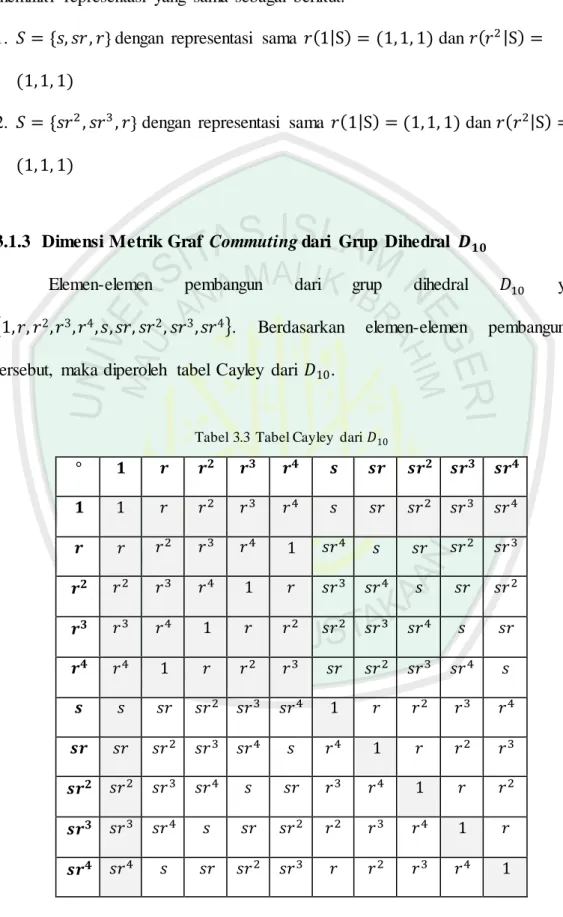
Elemen-elemen pembangun dari grup dihedral yaitu { }. Berdasarkan elemen-elemen pembangunnya tersebut, maka diperoleh tabel Cayley dari .

Berdasarkan tabel Cayley di atas dapat diketahui elemen-elemen komutatif dari dengan operasi . Elemen-elemen yang memenuhi sifat

(44)

komutatif dengan operasi pada ditunjukkan dengan warna yang berbeda.

Berdasarkan graf pada Gambar 3.3 diperoleh dimensi metrik adalah 7, dengan S = { }. Selanjutnya ditunjukkan bahwa S dengan 6 elemen memiliki representasi yang sama sebagai berikut:

Elemen-elemen pembangun dari grup dihedral yaitu { }. Berdasarkan elemen-elemen pembangunnya tersebut, maka diperoleh tabel Cayley dari .

(45)

29

(46)

Berdasarkan graf pada Gambar 3.4 diperoleh dimensi metrik adalah 7, dengan . Selanjutnya akan ditunjukkan bahwa S dengan 6 elemen memiliki representasi yang sama sebagai berikut:

Elemen-elemen pembangun dari grup dihedral yaitu { }. Berdasarkan elemen-elemen pembangunnya tersebut, maka diperoleh tabel Cayley dari .

r r ²

r ³ r ⁴

r ⁵ s sr

sr ² sr ³

sr ⁴

sr ⁵

(47)

31

(48)

Berdasarkan graf pada Gambar 3.5 diperoleh dimensi metrik adalah 11, dengan . Selanjutnya ditunjukkan bahwa S dengan 10 elemen memiliki representasi yang sama sebagai berikut:

Elemen-elemen pembangun dari grup dihedral yaitu { ^}. Berdasarkan elemen- elemen pembangunnya tersebut, maka diperoleh tabel Cayley dari .