EKSISTENSI BIFURKASI MUNDUR DAN
KENDALI OPTIMAL PADA MODEL PENYAKIT VEKTOR-BORNE YANG DISEBABKAN NYAMUK CHARISMA JUNI KUMALASARI
NRP 1211 100 032 Dosen Pembimbing: Subchan, M.Sc, Ph.D Drs. M. Setijo Winarko,M.Si JURUSAN MATEMATIKA
Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Sepuluh Nopember
EXISTENCE OF BACKWARD BIFURCATION AND OPTIMAL CONTROL VECTOR-BORNE DISEASE MODELS ON CAUSED MOSQUITO
CHARISMA JUNI KUMALASARI NRP 1211 100 032
Supervisors:
Subchan, M.Sc, Ph.D Drs. M. Setijo Winarko,M.Si
DEPARTMENT OF MATHEMATICS
Faculty of Mathematics and Natural Sciences Sepuluh Nopember Institute of Technology Surabaya 2015
KENDALI OPTIMAL PADA MODEL PENYAKIT VEKTOR-BORNE YANG
DISEBABKAN NYAMUK Nama Mahasiswa : Charisma Juni Kumalasari
NRP : 1211 100 032
Jurusan : Matematika FMIPA-ITS Pembimbing : 1. Subchan, M.Sc, Ph.D
2. Drs. M. Setijo Winarko,M.Si
Abstrak
Penyakit vector-borne merupakan penyakit yang terjadi pada manusia yang penularannya melalui vektor (perantara) seperti serangga. Contoh penyakit vector-borne seperti demam berdarah, virus West Nile, virus encephalitis dan malaria [1]. Model yang digunakan merupakan kombinasi dari dua model non linear dari populasi individu dan vektor [1]. Populasi individu dikelompokkan menjadi susceptible, infected, dan recovered, sedangkan vektor dikelompokkan menjadi susceptible dan infected. Dalam Tugas Akhir ini membahas tentang analisa pada model penyakit vector-borne dengan menyelidiki adanya bifurkasi mundur, menentukan basic reproduction number, kestabilan dari setiap titik kesetimbangan, kendali optimal, dan solusi numerik dari model interaksi dinamis yang disimulasikan dengan menggunakan MATLAB, sehingga didapatkan hasil untuk meminimalkan jumlah host (inang) yang terinfeksi serta jumlah populasi vektor.
Kata-kunci: Model epidemik, Bifurkasi Mundur, Kendali Optimal, Prinsip Minimum Pontriagyn (PMP)
AND OPTIMAL CONTROL VECTOR-BORNE DISEASE MODELS ON CAUSED MOSQUITO
Name : Charisma Juni Kumalasari
NRP : 1211 100 032
Department : Mathematics FMIPA-ITS Supervisors : 1. Subchan, M.Sc, Ph.D
2. Drs. M. Setijo Winarko,M.Si
Abstract
Vector-borne diseases are diseases that occur in humans are transmitted through a vector (intermediaries) such as insects. Examples of vector-borne diseases such as dengue fever, West Nile virus, encephalitis virus and malaria [1]. The model is used a combination of two non-linear models of the individual and vector population [1]. The population of individuals is classified into susceptible, infected, and recovered, while the vectors classified into susceptible and infected. In this final project is about the analysis on the model of vector-borne diseases to investigate the existence of backward bifurcation, determine the basic reproduction number, the stability of each equilibrium point, optimal control, and the numerical solution of the dynamic interaction models are simulated using MATLAB, so we get the results to minimize the number of hosts (host) and the number of infected vector population.
Key-words: Epidemic model, Backward bifurcation, Optimal control, Pontryagins Minimum Principle (PMP)
Assalamu’alaikum Wr. Wb.
Alhamdulillaahirobbil’aalamiin, segala puji dan syukur penulis panjatkan ke hadirat Allah SWT yang telah memberikan limpahan rahmat, petunjuk serta hidayah-Nya, sehingga penulis dapat menyelesaikan Tugas Akhir yang berjudul
”EKSISTENSI BIFURKASI MUNDUR DAN KENDALI OPTIMAL PADA MODEL PENYAKIT
VEKTOR-BORNE YANG DISEBABKAN NYAMUK”
sebagai salah satu syarat kelulusan Program Sarjana Jurusan Matematika FMIPA Institut Teknologi Sepuluh Nopember (ITS) Surabaya.
Tugas Akhir ini dapat terselesaikan dengan baik berkat bantuan dan dukungan dari berbagai pihak. Oleh karena itu, penulis menyampaikan ucapan terima kasih dan penghargaan kepada:
1. Ibu Dr. Erna Apriliani, M.Si selaku Ketua Jurusan Matematika FMIPA ITS.
2. Bapak Drs. M. Setijo Winarko, M.Si dan Bapak Subchan, M.Sc, Ph.D selaku dosen pembimbing atas segala bimbingan dan motivasinya kepada penulis dalam mengerjakan Tugas Akhir ini sehingga dapat terselesaikan dengan baik.
3. Bapak Dr. Hariyanto, M.Si, Drs. Iis Herisman, M.Si dan Drs. Daryono Budi Utomo, M.Si selaku dosen
perbaikan Tugas Akhir ini.
4. Bapak Drs. Chairul Imron, MI.Komp selaku Ketua Prodi S-1 Jurusan Matematika FMIPA ITS.
5. Bapak Drs. Soetrisno, MI.Komp selaku dosen wali yang telah memberikan arahan akademik selama penulis menempuh pendidikan di Jurusan Matematika FMIPA ITS.
6. Bapak dan Ibu dosen serta seluruhstaff Tata Usaha dan Laboratorium Jurusan Matematika FMIPA ITS. 7. Teman teman angkatan 2011 Jurusan Matematika atas
dukungan yang telah diberikan kepada penulis.
Penulis juga menyadari bahwa dalam Tugas Akhir ini masih terdapat kekurangan. Oleh sebab itu, kritik dan saran yang bersifat membangun sangat penulis harapkan demi kesempurnaan Tugas Akhir ini. Akhirnya, penulis berharap semoga Tugas Akhir ini dapat bermanfaat bagi banyak pihak.
Surabaya, Januari 2015
Penulis
Keberhasilan penulisan Tugas Akhir ini tidak lepas dari orang-orang terdekat penulis. Oleh sebab itu, penulis mengucapkan terima kasih kepada :
1. Allah SWT yang telah memberi rahmat, petunjuk, kekuatan, dan kesabaran dalam setiap langkah kehidupan penulis serta kepada Nabi Muhammad SAW yang telah membimbing umat-Nya dari zaman jahiliyah menuju zaman yang penuh ilmu.
2. Mbok e, Mama, dan Ayah yang tercinta, terima kasih atas segala doanya, juga kasih sayang dan pendidikan yang selalu dicurahkan kepada penulis selama ini. 3. Kakak-kakak yang sangat ku sayangi, mas Gatot, mas
Gepri, dan mas Rizky. Terima kasih banyak atas segala doa, dukungan, motivasi, dan nasihat-nasihatnya kepada penulis.
4. Mas Tony, Mas Ipin, Mas Fahim, Mas Danang, Mbak Fahmi, Mbak Irma, dan Mbak Firdha atas semua bantuan yang diberikan dalam pengerjaan Tugas Akhir ini.
5. Teh Gita, Mb Fia, Veda, Mila dan teman satu atap lainnya yang selalu memberikan semangat serta saran-saran kepada penulis. Terima kasih juga anak-anak lab lainnya dan mas Tux yang telah membantu dan menyemangati penulis. Makasih banyak ya semuanya.. 6. Teman-teman seperjuangan Tugas Akhir, Nilam, Ka
Marmel, Mas Lulu, Mas Romi, Mb Nadia, Muna, Zamroji, Andika, dan lain-lain yang saling mendukung dan memotivasi satu sama lain.
dukungan kalian selama ini. Kalian merupakan keluarga baru ku disini.
8. Seluruh keluarga besar HIMATIKA ITS dan UKM Taekwondo ITS atas dukungan dan semangat yang diberikan kepada penulis.
9. Semua pihak yang tak bisa penulis sebutkan satu-persatu, terima kasih telah membantu sampai terselesaikannya Tugas Akhir ini.
HALAMAN JUDUL i LEMBAR PENGESAHAN vi ABSTRAK vii ABSTRACT ix KATA PENGANTAR xi DAFTAR ISI xv
DAFTAR GAMBAR xix
DAFTAR TABEL xxi
DAFTAR SIMBOL xxiii
DAFTAR SIMBOL xxv BAB I PENDAHULUAN 1 1.1 Latar Belakang . . . 1 1.2 Rumusan Masalah . . . 2 1.3 Batasan Masalah . . . 2 1.4 Tujuan . . . 3 1.5 Manfaat . . . 3 1.6 Sistematika Penulisan . . . 3
BAB II TINJAUAN PUSTAKA 5 2.1 Penyakit Vector-Borne . . . 5
2.2 Sistem Kompartemen . . . 6
2.3 Bilangan Reproduksi Dasar (R0) . . . 6
2.4 Kestabilan Titik Tetap . . . 9
2.5 Stabil Asimtotik Lokal . . . 9 xv
2.7 Teori Kendali Optimal . . . 11
2.8 Prinsip Minimum Pontryagin . . . 12
2.9 Metode Beda Hingga . . . 15
BAB III METODE PENELITIAN 19 3.1 Studi Literatur . . . 19
3.2 Mengkaji Model Interaksi Dinamis . . . 19
3.3 Mencari Titik Kesetimbangan, Menentukan Bilangan Reproduksi Dasar dari Model, dan Bifurkasi . . . 19
3.4 Menentukan Formulasi Masalah Kendali Optimal . . . 20
3.5 Menentukan Penyelesaian Kendali Optimal . . 20
3.6 Membuat Simulasi . . . 20
3.7 Kesimpulan dan Saran . . . 20
BAB IV ANALISIS DAN PEMBAHASAN 21 4.1 Deskripsi Model dan Asumsi . . . 21
4.2 Daerah Penyelesaian Model . . . 26
4.3 Titik Kesetimbangan Bebas Penyakit . . . 31
4.4 Menentukan Bilangan Reproduksi Dasar . . . . 33
4.5 Titik Kesetimbangan Endemik . . . 38
4.6 Kestabilan Lokal Model Interaksi Dinamis . . 44
4.6.1 Kestabilan Lokal Titik Setimbang Bebas Penyakit . . . 53
4.6.2 Kestabilan Lokal Titik Setimbang Endemik . . . 57
4.7 Analisa Bifurkasi . . . 66
4.8 Model Kendali Optimal . . . 71
4.9 Penyelesaian Kendali Optimal . . . 76
4.10 Solusi Numerik . . . 83 xvi
5.1 Kesimpulan . . . 91 5.2 Saran . . . 93
DAFTAR PUSTAKA 95
LAMPIRAN A Kurva Bifurkasi Mundur 97
LAMPIRAN B Kurva Bifurkasi Maju 99
LAMPIRAN C Simulasi dari populasi individu yang terinfeksi dan Simulasi dari jumlah populasi
vektor dengan kendali 101
LAMPIRAN D Biodata Penulis 107
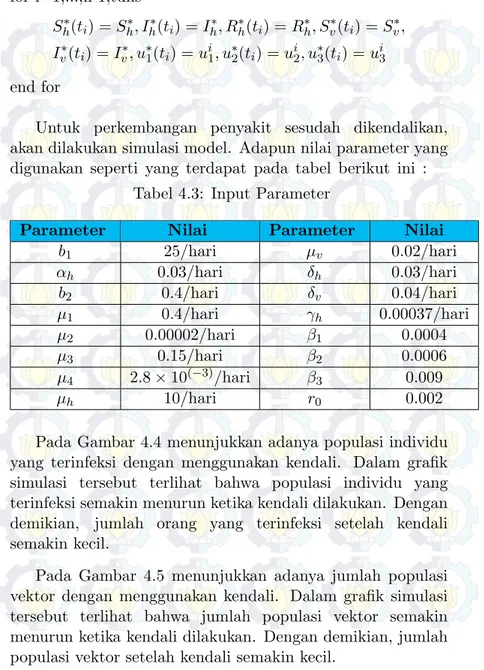
Tabel 4.1 Input Parameter . . . 68 Tabel 4.2 Input Parameter . . . 70 Tabel 4.3 Input Parameter . . . 88
Gambar 2.1 Bifurkasi Maju . . . 10 Gambar 2.2 Bifurkasi Mundur . . . 10 Gambar 4.1 Diagram Kompartemen Dari Model
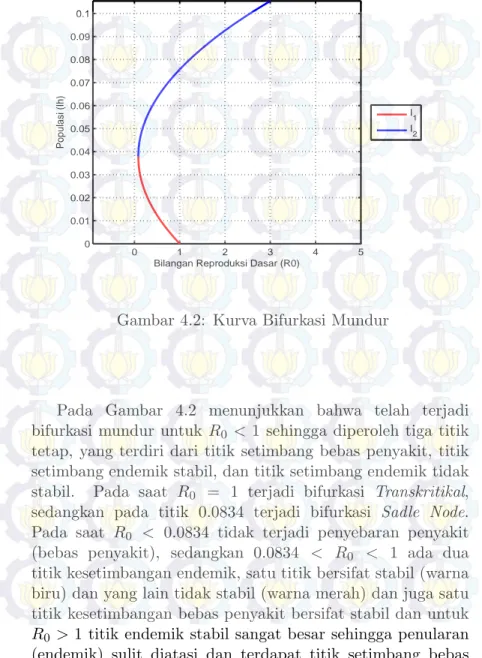
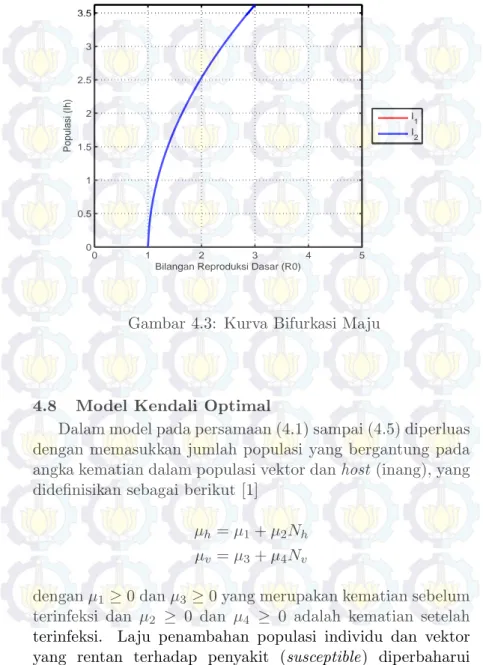
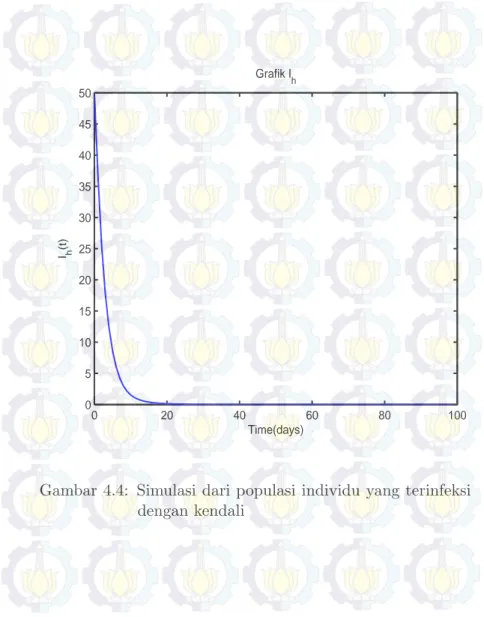
Interaksi Dinamis . . . 23 Gambar 4.2 Kurva Bifurkasi Mundur . . . 69 Gambar 4.3 Kurva Bifurkasi Maju . . . 71 Gambar 4.4 Simulasi dari populasi individu yang
terinfeksi dengan kendali . . . 89 Gambar 4.5 Simulasi dari jumlah populasi vektor
dengan kendali . . . 90
Sh(t) Individu yang rentan terhadap penyakit
pada waktu t.
Ih(t) Individu yang telah terinfeksi penyakit
pada waktu t.
Rh(t) Individu yang telah sembuh dari penyakit
pada waktu t.
Sv(t) Vektor yang rentan terhadap penyakit
pada waktu t.
Iv(t) Vektor yang telah terinfeksi penyakit
pada waktu t.
Nh(t) Jumlah populasi individu pada waktu t.
Nv(t) Jumlah populasi vektor pada waktu t.
b1 angka kelahiran populasi individu yang rentan.
b2 angka kelahiran populasi vektor yang rentan.
β1 angka kejadian penularan melalui kontak
langsung dengan individu yang terinfeksi. β2 angka kejadian penularan melalui kontak
dengan vektor yang terinfeksi.
β3 angka individu yang terinfeksi menjadikan
vektor rentan terinfeksi.
µh angka kematian natural dari populasi individu.
µv angka kematian natural dari populasi vektor.
γh angka kesembuhan pada populasi individu
yang terinfeksi.
δh angka kematian individu yang disebabkan
penyakit.
δv angka kematian dari vektor yang terinfeksi
yang disebabkan penyakit. R0 Bilangan reproduksi dasar.
Ef Titik kesetimbangan bebas penyakit.
E1 Titik kesetimbangan endemik.
J Matrik Jacobian.
λ Nilai eigen.
H Fungsi Hamiltonian.
J(u1, u2, u3) Fungsi Objektif.
I = [t0, tf] Periode waktu yang direncanakan.
λ1, λ2, λ3 Variabel ko-keadaan (costate).
λ4, λ5
u1, u2, u3 Variabel pengendali.
δ Variasi.
PENDAHULUAN
Pada bab ini dijelaskan hal-hal yang melatarbelakangi munculnya permasalahan yang dibahas dalam Tugas Akhir ini. Kemudian permasalahan tersebut disusun kedalam suatu rumusan masalah. Selanjutnya dijabarkan juga batasan masalah untuk mendapatkan tujuan yang diinginkan serta manfaat yang dapat diperoleh. Adapun sistematika penulisan Tugas Akhir diuraikan pada bagian akhir bab ini.
1.1 Latar Belakang
Penularan penyakit dapat terjadi pada manusia melalui vektor (perantara) seperti serangga dikenal sebagai ”arthropod borne disease” atau kadang-kadang disebut juga dengan ”vector borne disease”. Penyakit yang tergolong ”arthropod borne disease” merupakan penyakit yang bersifat berbahaya dan dapat bersifat endemis serta dapat menimbulkan wabah dengan ancaman kematian [3].
Penyakit vektor-borne seperti demam berdarah, virus
West Nile, virus encephalitis dan malaria merupakan infeksi menular ke manusia dan hewan lain yang disebabkan oleh arthropoda pemakan-darah. Arthropoda (serangga atau
arakhnida) yang kebanyakan menyediakan vektor termasuk serangga pengisap darah seperti, nyamuk, kutu, dan lalat penggigit. Mayoritas penyakit bawaan vektor bertahan di alam dengan memanfaatkan hewan sebagai host (inang) vertebratanya, dan zoonosis. Untuk sejumlah kecil zoonosis, seperti malaria dan demam berdarah, manusia adalah host
(inang) utama. Vektor pembawa patogen dari host (inang) 1
yang terinfeksi dan mengirimkannya untuk host (inang) perantara atau langsung kehost (inang) manusia [1].
Penyakit vector-borne penting bagi WHO (World Health Organization) khususnya wilayah asia bagian selatan-timur. Penyakitvector-borne adalah ancaman serius bagi kesehatan, yang mempengaruhi populasi yang paling rentan secara ekonomi. Dengue adalah salah satu penyakit menular yang paling cepat menyebar dari abad kedua puluh satu. Penyebarannya berubah ketika bergerak dari kota ke daerah pedesaan dan wilayah geografis baru akibat perubahan iklim. Lebih dari 1,3 miliar orang di kawasan ini beresiko malaria, seperti lebih dari 75% penduduk tinggal di daerah rawan malaria [5].
Dalam Tugas Akhir ini akan dilakukan analisa pada model penyakit vector-borne dengan menyelidiki adanya bifurkasi mundur. Selain itu, digunakan kendali optimal untuk meminimalkan jumlah host (inang) yang terinfeksi serta jumlah populasi vektor. Selanjutnya, akan ditentukan solusi yang optimal dari model tersebut.
1.2 Rumusan Masalah
Permasalahan dalam Tugas Akhir ini adalah :
1. Bagaimana menentukan basic reproduction number, kestabilan dari setiap titik kesetimbangan, dan bifurkasi mundur ?
2. Bagaimana menentukan solusi yang optimal dari model tersebut ?
3. Bagaimana interpretasi hasil analisa dari model tersebut beserta simulasinya ?
1.3 Batasan Masalah
Batasan masalah yang digunakan dalam Tugas Akhir ini antara lain:
1. Menerapkan Prinsip Minimum Pontryagin dalam penyelesaian yang optimal.
2. Model interaksi dinamik antara populasi manusia dan populasi vektor nyamuk adalah kombinasi dari dua model non linear dari populasi individu dan vektor [1].
1.4 Tujuan
Tujuan yang dicapai dari penulisan Tugas Akhir ini antara lain:
1. Menentukan basic reproduction number, kestabilan dari setiap titik kesetimbangan, dan bifurkasi mundur. 2. Menentukan solusi yang optimal dari model tersebut. 3. Mengintrepetasikan hasil analisa dari model tersebut
beserta simulasinya.
1.5 Manfaat
Manfaat dari Tugas Akhir ini antara lain:
1. Membantu mempelajari dampak dari ditentukannya
basic reproduction number, kestabilan dari setiap titik kesetimbangan, dan bifurkasi mundur pada model penyakit vektor-borne.
2. Membantu menentukan cara yang efektif untuk mengendalikan pencegahan penyakit vektor-borne.
1.6 Sistematika Penulisan
Penulisan Tugas Akhir ini disusun dalam lima bab, yaitu: 1. BAB I PENDAHULUAN
Pada bab ini berisi tentang gambaran umum dari penulisan Tugas Akhir yang meliputi latar belakang, rumusan masalah, batasan masalah, tujuan, manfaat, dan sistematika penulisan.
2. BAB II TINJAUAN PUSTAKA
Pada bab ini berisi tentang materi-materi yang mendukung Tugas Akhir ini, antara lain penyakit
vektor-borne, sistem kompartemen, bilangan reproduksi dasar, kestabilan titik tetap, bifurkasi, teori kendali optimal, prinsip minimum pontryagin, dan metode beda hingga.
3. BAB III METODE PENELITIAN
Pada bab ini dibahas tentang langkah langkah dan metode yang digunakan untuk menyelesaikan tugas akhir ini.
4. BAB IV ANALISIS DAN PEMBAHASAN
Pada bab ini akan menguraikan bagaimana memperoleh daerah penyelesaian model, kestabilan lokal di setiap titik kesetimbangan, analisa bifurkasi berdasarkan bilangan reproduksi dasar, penerapan prinsip minimum pontryagin dan hamiltonian untuk mencari kendali optimal, mencari solusi numerik dengan menggunakan metode beda hingga dan simulasi dari model tersebut 5. BAB V PENUTUP
Bab ini berisi kesimpulan akhir yang diperoleh dari Tugas Akhir serta saran untuk pengembangan penelitian selanjutnya.
TINJAUAN PUSTAKA
Pada bab ini akan dijelaskan mengenai tinjauan pustaka yang menjadi dasar materi dalam penyusunan tugas akhir serta menunjang metode metode yang digunakan dalam pembahasan tugas akhir ini.
2.1 Penyakit Vector-Borne
Vektor adalah organisme yang mengirimkan patogen dan parasit dari satu orang yang terinfeksi (atau hewan) yang lain, menyebabkan penyakit serius pada populasi manusia [5].
Penyakit vector-borne adalah penyakit yang disebabkan oleh patogen dan parasit pada populasi manusia yang paling sering ditemukan di daerah tropis dan tempat di mana akses terhadap air minum dan sanitasi yang sehat terhambat. Penyakitvector-borne paling mematikan adalah malaria yang menyebabkan sekitar 660.000 kematian pada tahun 2010, sebagian besar adalah anak-anak Afrika. Namun, penyakit
vector-borne paling cepat berkembang di dunia adalah demam berdarah, dengan peningkatan 30 kali lipat dalam kejadian penyakit selama 50 tahun terakhir [4].
Terjadinya penyebaran penyakit vektor-borne adalah melalui kontak langsung yaitu Artropoda secara langsung memindahkan penyakit atau investasi dari satu orang ke orang lain melalui kontak langsung, melalui transmisi secara mekanis yaitu Artropoda sebagai vektor mekanis yang membawa agen penyakit dari manusia yang berasal dari tinja, darah,
ulkus superficial, atau eksudat, serta melalui transmisi secara biologis yaitu agen penyakit mengalami perubahan siklus
dengan atau tanpa multiplikasi di dalam tubuh artropoda. Penyakit yang ditularkan oleh vektor (nyamuk) adalah Malaria, filarial, yellow fever, ensefalitis, dan DHF. Vektor (nyamuk) dapat mudah berkembang pesat jika kondisi lingkungan mendukung. Beberapa kondisi yang mengakibatkan vektor (nyamuk) dapat berkembang pesat sebagai berikut [11]:
a. Perubahan lingkungan fisik seperti pertambangan, industri dan pembangunan perumahan yang mengakibatkan berkembangbiaknya vektor(nyamuk) penyakit.
b. Sistemdrainase permukiman dan perkotaan yang tidak memenuhi syarat sehingga menjadi tempat perindukan vektor.
c. Sistem pengelolaan sampah yang belum memenuhi syarat sehingga sampah menjadi sarang vektor(nyamuk).
2.2 Sistem Kompartemen
Sistem kompartemen merupakan sebuah susunan kerja atau proses yang menunjukkan aliran individu dari satu kompartemen ke kompartemen lainnya seperti saat individu tersebut sehat, tertular penyakit atau sembuh dari penyakit [2].
2.3 Bilangan Reproduksi Dasar (R0)
Bilangan reproduksi dasar (Basic Reproduction Number)
atau biasa disebut R0 adalah suatu parameter yang
digunakan untuk mengetahui tingkat penyebaran suatu penyakit. Bilangan reproduksi dasar adalah bilangan yang menunjukkan jumlah individu rentan yang dapat menderita penyakit disebabkan oleh satu individu infeksi. Namun
adapula yang mengartikan bilangan yang menyatakan banyaknya rata-rata individu infected sekunder akibat tertular individu infected primer yang berlangsung dalam populasi individu rentan penyakit.
Untuk menentukan bilangan reproduksi dasar, digunakan metode Driessche dan Watmough [12]. Dengan mengasumsikan bahwa populasi dapat dikelompokkan ke dalam n kompartemen. Diberikan x = (x1, ..., xn)t, dengan
xi ≥ 0 adalah bilangan dari individu pada masing-masing
kompartemen sehingga kompartemen m < n pertama sesuai dengan individu terinfeksi. Diberikan Xs adalah himpunan
dari semua titik kesetimbangan bebas penyakit. Didefinisikan Xs={x≥0|xi= 0, i= 1, ..., m}
Selanjutnya untuk menghitung R0, penting untuk
membedakan infeksi baru dari semua perubahan dalam populasi. Untuk itu didefinisikan Fi(x) adalah laju dari
kemunculan infeksi baru pada kompartemen i,Vi−(x) adalah laju dari perpindahan individu keluar dari kompartemen i, dan Vi+(x) adalah laju dari perpindahan individu masuk ke kompartemen i. Model penyebaran penyakit terdiri dari kondisi awal non-negatif dengan persamaan sistem berikut:
˙
xi=fi =Fi(x)− Vi(x), i= 1, ..., n, denganVi =Vi−− Vi+
dan memenuhi asumsi-asumsi berikut:
a. Jika x ≥ 0, maka Fi,Vi−,Vi+ ≥ 0 untuk i=1,...,n.
Karena masing-masing merepresentasikan perpindahan langsung dari individu, maka semua non-negatif. b. Jika xi = 0, maka Vi−= 0. Secara khusus, jika x ∈Xs,
makaVi−= 0 untuk i=1,...,n. Hal ini berarti jika sebuah kompartemen kosong, maka tidak ada perpindahan dari
individu yang keluar dari kompartemen dikarenakan kematian atau infeksi.
c. Fi = 0 jika i > m. Hal ini mengakibatkan timbulnya penyakit adalah nol.
d. Jika x∈Xs, maka Fi = 0 danVi+= 0 untuk i=1,...,m.
Jika populasi bebas dari penyakit, maka populasi akan tetap bebas dari penyakit (tidak ada infeksi).
e. Jika F(x) menuju ke nol, maka semua nilai eigen dari Df(x0) mempunyai bagian real negatif. Hal ini
berdasarkan turunan darifdi dekat titik kesetimbangan bebas penyakit (DFE), didefinisikan DFE darif adalah penyelesaian kestabilan lokal dari titik kesetimbangan bebas penyakit, denganf terbatas keXs. Jika populasi
ada di sekitar DFE, maka populasi akan kembali ke DFE menurut linearisasi sistem :
˙ x=Df(x0)(x−x0), dengan Dfi(x0) = ∂fi ∂xi x=0
adalah matriks Jacobian yang dihitung di sekitar x = x0. Oleh karena itu, asumsi ini mengakibatkan DFE
stabil.
DidefinisikanK=F V−1sebagainext generation matriks dan R0=ρ(F V−1) dengan F = ∂Fi(x0) ∂xi , V = ∂Vi(x0) ∂xi , 1≤i, j ≤m,
dan ρ(A) adalah nilai eigen yang dominan dari matriks A [6]. Jika model hanya mempunyai dua titik kesetimbangan yaitu titik kesetimbangan bebas penyakit dan titik kesetimbangan endemik, maka tidak terjadi endemik jika R0 ≤1 dan terjadi endemik jika R0 ≥1 [9].
2.4 Kestabilan Titik Tetap
Pandang persamaan diferensial sebagai berikut : dx
dt =f(x, y) dy
dt =g(x, y) (2.1) Sebuah titik (x0, y0) merupakan titik kesetimbangan dari
persamaan (2.1) jika memenuhi f(x0, y0) = 0 dang(x0, y0) =
0. Karena turunan suatu konstanta sama dengan nol, maka sepasang fungsi konstan [6].
x(t)≡x0 dan y(t)≡y0
adalah penyelesaian kesetimbangan dari persamaan (2.1) untuk semua t.
2.5 Stabil Asimtotik Lokal
Kestabilan asimtotis lokal pada titik keseimbangan ditentukan oleh tanda pada bagian real dari akar-akar karakteristik sistem.
Teorema 2.1
Titik setimbang (x0, y0) stabil asimtotis jika dan hanya jika
nilai karakteristik dari
M atriks J = ∂f ∂x(x0, y0) ∂f ∂y(x0, y0) ∂g ∂x(x0, y0) ∂g ∂y(x0, y0)
mempunyai tanda negatif pada bagian realnya dan tidak stabil jika sedikitnya satu dari nilai karakteristik mempunyai tanda positif pada bagian realnya.
Analisis kestabilan dilakukan untuk mengetahui laju penyebaran suatu penyakit. Analisis ini dilakukan pada titik setimbang bebas penyakit(Disease Free Equilibrium)dan titik setimbang endemik (Endemic Equilibrium).
2.6 Bifurkasi
Pada sistem dinamiknon linearsering dijumpai kestabilan di sekitar titik kesetimbangan suatu sistem persamaan yang menunjukkan fenomena bifurkasi. Bifurkasi secara umum adalah perubahan kualitatif yang meliputi perubahan stabilitas dan perubahan banyaknya titik kesetimbangan karena perubahan nilai-nilai parameter. Dalam epidemiologi, fenomena bifurkasi berhubungan dengan parameter ambang batas, yang sering disebut bilangan reproduksi dasar dan biasanya disimbolkan dengan R0 [7].
Ada dua jenis bifurkasi dalam model penyebaran penyakit menular yaitu bifurkasi maju dan bifurkasi mundur. Eksistensi bifurkasi maju dan mundur pada model penyebaran penyakit ditunjukkan oleh diagram bifurkasi pada Gambar 2.1 dan Gambar 2.2 dengan merupakan parameter bifurkasi dan merupakan populasi individu yang terinfeksi penyakit.
Fenomena bifurkasi maju terjadi pada saatR0 >1 dimana
hanya ada satu titik kesetimbangan endemik. Sedangkan fenomena bifurkasi mundur terjadi pada saat R0 < 1
mempunyai dua titik kesetimbangan endemik [7].
2.7 Teori Kendali Optimal
Pada prinsipnya, tujuan dari pengendali optimal adalah menentukan signal atau kendali yang akan diproses dalam sistem dinamik dan memenuhi beberapa konstrain, dengan tujuan memaksimumkan atau meminimumkan fungsi tujuan (J) yang sesuai [10]. Adapun formulasi masalah kendali optimal terdiri dari:
a. Mendiskripsikan secara matematis suatu sistem (model).
b. Menentukan fungsi objektif (performance index). c. Menentukan kendala dan kondisi batas yang harus
dipenuhi.
Secara umum, masalah kendali optimal diformulasikan sebagai berikut: misalkan suatu sistem dinamik diberikan oleh persamaan:
˙
x =f (x(t),u(t), t) (2.2) dengan keadaan awal x(t0) = x0 dan keadaan akhir x(tf) =
xf serta u(t) yang menyatakan pengendali keadaan pada
waktu t. Dalam hal ini, masalah kendali optimal adalah mencari pengendali optimal u∗(t) yang memenuhi persamaan keadaan (state) dengan syarat nilaiJ berikut ini:
J =S(x(tf), tf) + Z tf
t0
V(x(t),u(t), t) (2.3)
adalah minimum atau maksimum. Bentuk umum persamaan J di atas disebut fungsi tujuan bentuk Bolza dengan S adalah bentuk Mayer dan V adalah bentuk Lagrange. Dengan kondisi sistem yaitu waktu akhir tetap atau bebas dan keadaan(state)
2.8 Prinsip Minimum Pontryagin
Prinsip Minimum Pontryagin merupakan salah satu cara dalam menyelesaikan masalah kendali optimal dengan kendala yang terbatas. Metode tersebut digunakan untuk memperoleh kendali terbaik pada sistem dinamik dari state
awal hingga akhir, yaitu dengan memininumkan fungsi objektif yang ingin dicapai. Hal ini dikembangkan oleh L. S. Pontryagin pada tahun 1950. Oleh karena itu, prinsip ini disebut sebagai Prinsip Minimum Pontryagin. Prinsip ini menyatakan secara informal bahwa persamaan Hamiltonian akan diminimumkan sepanjang U yang merupakan himpunan dari semua kendali [13]. Hasilnya juga dapat dinamakan Prinsip Maksimum Pontryagin yaitu dengan mengalikan (-1) padaperformance index.
Penyelesaian masalah kendali optimal dengan menggunakan metode tidak langsung dilakukan dengan menyelesaikan kondisi perlu kendali optimal. Berdasarkan Prinsip Minimum Pontryagin, kondisi perlu dari masalah kendali optimal yang harus diselesaikan adalah persamaan
stasioner, persamaan state, dan persamaan costate serta kondisi transversality [9].
Dengan memperhatikan persamaan keadaan dan fungsi tujuan yang telah diberikan pada persamaan (2.2) dan (2.3), langkah dalam menyelesaikan masalah kendali optimal adalah sebagai berikut [8] :
a. Langkah 1
Bentuk fungsi Hamiltonian yang disimbolkan denganH, yaitu:
H =H(x(t),u(t),λ(t), t)
=V(x(t),u(t), t) + λ0(t) f(x(t),u(t), t) dengan tanda ”0” menyatakan suatu transpose.
b. Langkah 2
MemaksimumkanH terhadapu(t) dengan cara: ∂H
∂u(t) =0
sehingga diperoleh kondisi stasioner u∗(t). c. Langkah 3
Dengan menggunakan u∗(t) yang telah dihasilkan pada langkah 2, akan didapatkan fungsi Hamiltonian baru yang optimal, H∗, yaitu:
H∗ =H(x∗(t),u∗(t),λ∗(t), t)≤H(x∗(t),u(t),λ∗(t), t) d. Langkah 4
Selesaikan 2n persamaan, dengan n adalah jumlah variabel keadaan:
˙
x∗(t) = ∂H ∗ ∂λ
dan persamaancostate yaitu: ˙
λ∗(t) =−∂H ∗ ∂x
Dengan kondisi batas diberikan oleh keadaan awal dan keadaan akhir yang disebut kondisitransversality. Kondisi batas secara umum yaitu:
H∗+ ∂S ∂t tf δtf+ ∂S ∂x ∗ −λ∗ 0 tf δxf = 0
Dengan S adalah bentuk Mayer dari fungsi objektif, H adalah persamaan Hamiltonian, δ menunjukkan variasi dan tanda ∗ menunjukkan keadaan saat variabel pengendalinyastasioner.
e. Langkah 5
Substitusi hasil-hasil yang diperoleh pada langkah 4 ke dalam persamaan u∗(t) pada langkah 2 untuk mendapatkan kendali optimal yang dicari.
Dalam menentukan kondisi transversality yang sesuai, terdapat macam-macam kondisi batas, yaitu [8]:
a. Fixed-final time and Fixed-final state system
Artinya waktu akhir dan state saat waktu akhir telah ditentukan/diketahui.
x(t0) =x0,x(tf) =xf
b. Free-final time and Fixed-final state system
Artinya waktu akhir belum ditentukan/tidak diketahui dan state saat waktu akhir telah ditentukan/diketahui.
x(t0) =x0,x(tf) =xf, H∗+∂S ∂t tf = 0 c. Fixed-final time and Free-final state system
Artinya waktu akhir telah ditentukan/diketahui sedangkanstate saat waktu akhir belum diketahui/tidak ditentukan. x(t0) =x0,λ∗(tf) = ∂S ∂x ∗tf
d. Free-final time and dependent free-final state system
Artinya waktu akhir belum ditentukan/tidak diketahui dan state saat akhir belum ditentukan/tidak diketahui dan nilainya bergantung pada sesuatu.
x(t0) =x0,x(tf) =θf, H+∂S ∂t ∗ + ∂S ∂x−λ ∗(t) 0 ∗ ˙ θ(t) tf = 0
e. Free-final time and independent free-final state system
Artinya waktu akhir belum ditentukan/tidak diketahui dan state saat akhir belum ditentukan/tidak diketahui dan nilainya tidak bergantung pada sesuatu.
δx(t0) =x0 H+∂S ∂t ∗tf = 0, ∂S ∂x −λ ∗ (t) ∗tf = 0
2.9 Metode Beda Hingga
Jika u = u(x) maka turunan pertama dari u terhadap x didefinisikan
du dx = limh→0
u(x+h)−u(x) h
dengan mensubtitusikan nilaix=x−h, maka du
dx = limh→0
u(x)−u(x−h) h
dengan mensubtitusikan nilaix=x+h2, maka du
dx = limh→0
u(x+h2)−u(x−h2) h
Jika u = u(x) diekspansikan menurut deret taylor, maka diperoleh
1. Persamaan persamaan beda hingga maju adalah sebagai berikut:
u(x+h) =u(x) + hdu 1!dx(x) +
h2 2!
d2u
dx2(x) +... (2.4)
u(x+h)−u(x) = hdu
dx (x) +o(h 2) u(x+h)−u(x) h ≈ du dx
2. Persamaan persamaan beda hingga mundur adalah sebagai berikut:
u(x−h) =u(x)− hdu 1!dx(x) +
h2 2!
d2u
dx2(x) +... (2.5)
u(x)−u(x−h) = hdu
dx (x) +o(h 2) u(x)−u(x−h) h ≈ du dx
3. Persamaan persamaan beda hingga tengah jika persamaan (2.4) dikurangkan dengan persamaan (2.5), maka u(x+h)−u(x−h) = 2hdu dx+... u(x+h)−u(x−h) = 2hdu dx+o(h 2) u(x+h)−u(x−h) 2h ≈ du dx
Dengan tiga syarat batas, yaitu:
1. Syarat batas Diriclet, contoh: u(0) = 100
2. Syarat batas Neumann, contoh : du
dx(1) = 0
3. Syarat batas Robbins, contoh: u(0) + du
dx(0) = 3
Selain itu persamaan beda dapat dituliskan dalam bentuk lain yaitu sebagai berikut:
du dx =
ui+1−ui
h adalah beda maju du
dx =
ui−ui−1
h adalah beda mundur du
dx =
ui+1−ui−1
METODE PENELITIAN
Bab ini menguraikan metode yang akan digunakan dalam penelitian secara rinci. Metodologi penelitian yang digunakan berguna sebagai acuan sehingga penelitian ini dapat disusun secara sistematis.
3.1 Studi Literatur
Tahap ini merupakan tahap untuk melakukan identifikasi permasalahan, yaitu mencari referensi yang menunjang penelitian. Referensi bisa berupa tugas akhir, jurnal, buku, maupun artikel terkait.
3.2 Mengkaji Model Interaksi Dinamis
Untuk memahami model interaksi dinamik disusun asumsi-asumsi tertentu sehingga dapat dibuat model kompartemen dengan susceptible, infected, dan recovered
untuk populasi manusia dan susceptible dan infected untuk populasi nyamuk.
3.3 Mencari Titik Kesetimbangan, Menentukan
Bilangan Reproduksi Dasar dari Model, dan Bifurkasi
Dari model interaksi dinamis akan dicari titik kesetimbangan bebas penyakit (I = 0) dan titik kesetimbang -an endemik (I 6= 0) melalui substitusi persamaan model. Kemudian menentukan nilai bilangan reproduksi dasar (R0)
dan selanjutnya menentukan kurva bifurkasi melalui nilaiR0.
3.4 Menentukan Formulasi Masalah Kendali Optimal
Pada tahapan ini, ditentukan formulasi masalah kendali optimal yang meliputi menentukan model kendali optimal, fungsi objektif, dan kondisi syarat batas yang harus dipenuhi.
3.5 Menentukan Penyelesaian Kendali Optimal
Pada tahap ini, dilakukan penyelesaian kendali optimal yang telah diformulasikan pada tahapan sebelumnya. Metode yang digunakan dalam penyelesaian masalah tersebut adalah Prinsip Minimum Pontryagin. Langkah-langkah yang dilakukan dalam tahap ini antara lain:
1. Membentuk fungsi Hamiltonian,
2. Menentukan persamaan state dancostate, 3. Menentukan kondisi batas yang harus dipenuhi, 4. Menentukan pengendali optimal.
3.6 Membuat Simulasi
Dari Bifurkasi yang diperoleh akan dibuat simulasinya dan pada kendali optimal diselesaikan dengan menggunakan metode beda hingga semi implisit. Langkah-langkahnya adalah menyelesaikan model sistem dengan menggunakan metode beda hingga maju, dan fungsi adjoin yang diperoleh diselesaikan dengan menggunakan metode beda hingga mundur karena adanya kondisi transversality. Selanjutnya, dapat diperoleh penyelesaian model sistem secara numerik.
3.7 Kesimpulan dan Saran
Setelah dilakukan analisis dan pembahasan maka dapat ditarik suatu kesimpulan dan saran sebagai masukan untuk pengembangan penelitian lebih lanjut.
ANALISIS DAN PEMBAHASAN
Pada bab ini, akan dibahas tentang daerah penyelesaian model, titik kesetimbangan bebas penyakit,titik kesetimbangan endemik, kemudian akan dicari kestabilan lokal dari setiap titik kesetimbangan tersebut, dan bilangan reproduksi dasar, kemudian menentukan bifurkasinya (bifurkasi mundur) berdasarkan nilai bilangan reproduksi dasar, dan menentukan solusi yang optimal dari model dengan menerapkan Prinsip Minimum Pontryagin. Selanjutnya akan ditentukan penyelesaian solusi numerik dari model dan mensimulasikannya dengan menggunakanMATLAB.
4.1 Deskripsi Model dan Asumsi
Model interaksi dinamis yang akan dibahas pada Tugas Akhir ini memiliki asumsi sebagai berikut:
1. Individu dikelompokkan menjadi tiga kelompok, yaitu
susceptible (Sh(t)) yaitu individu yang rentan terhadap
penyakit pada saat t , infected (Ih(t)) adalah individu
yang terinfeksi penyakit pada saat t, dan recovered
(Rh(t)) adalah individu yang sembuh dari penyakit pada
saat t sedangkan untuk vektor (nyamuk) dikelompokkan menjadi dua kelompok, yaitu susceptible (Sv(t)) adalah
vektor yang rentan terhadap penyakit pada saat t , dan
infected (Iv(t)) adalah vektor yang terinfeksi penyakit
pada saat t. Vektor yang sembuh akan langsung mati, sehingga tidak terjadi penularan. Jumlah populasi individu dinyatakan sebagai Nh(t) dengan Nh(t) =
Sh(t) +Ih(t) +Rh(t), sedangkan untuk jumlah populasi
vektor dinyatakan sebagaiNv(t) =Sv(t) +Iv(t).
2. Model mendiskripsikan interaksi antara individu (rentan) yang berkaitan dengan kematian yang disebabkan karena kontak dengan penyakit maupun vektor yang terifeksi penyakit. Individu (rentan) terhadap penyakit dapat terinfeksi melalui dua cara, yaitu melakukan kontak langsung dengan penyakit β1
dan melakukan kontak dengan vektor yang terinfeksi β2.
3. Berikut merupakan definisi parameter-parameter yang terdapat dalam model dinamik, yaitu
a. b1 menyatakan angka kelahiran populasi individu
yang rentan dan b2 menyatakan angka kelahiran
populasi vektor yang rentan.
b. β3 menyatakan angka individu yang terinfeksi
menjadikan vektor rentan terinfeksi.
c. µh menyatakan angka kematian natural dari
populasi individu dan µv menyatakan angka
kematian natural dari populasi vektor.
d. γh menyatakan angka kesembuhan pada populasi
individu yang terinfeksi, δh menyatakan angka
kematian individu yang disebabkan penyakit, dan δv menyatakan angka kematian dari vektor yang
terinfeksi yang disebabkan penyakit.
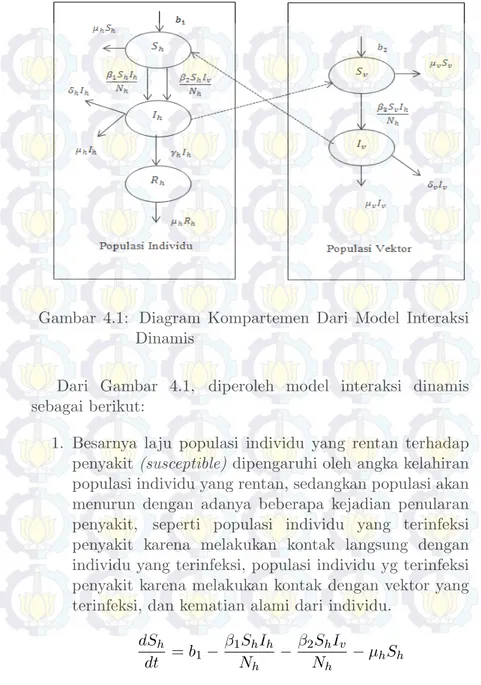
Dari asumsi di atas, dapat digambarkan diagram kompartemen dari model interaksi dinamis sebagai berikut:
Gambar 4.1: Diagram Kompartemen Dari Model Interaksi Dinamis
Dari Gambar 4.1, diperoleh model interaksi dinamis sebagai berikut:
1. Besarnya laju populasi individu yang rentan terhadap penyakit (susceptible)dipengaruhi oleh angka kelahiran populasi individu yang rentan, sedangkan populasi akan menurun dengan adanya beberapa kejadian penularan penyakit, seperti populasi individu yang terinfeksi penyakit karena melakukan kontak langsung dengan individu yang terinfeksi, populasi individu yg terinfeksi penyakit karena melakukan kontak dengan vektor yang terinfeksi, dan kematian alami dari individu.
dSh dt =b1− β1ShIh Nh −β2ShIv Nh −µhSh
2. Besarnya laju populasi individu yang terinfeksi penyakit
(infected) akan bertambah saat terdapat populasi individu yang terinfeksi penyakit akibat kontak langsung dengan individu yang terinfeksi maupun dengan vektor yang terinfeksi dan populasi akan menurun dengan adanya kejadian individu yang terinfeksi namun telah sembuh dan juga menurun karena kematian yang disebabkan karena terinfeksi penyakit maupun secara alami.
dIh dt = β1ShIh Nh +β2ShIv Nh −γhIh−δhIh−µhIh
3. Besarnya laju populasi individu yang sembuh dari penyakit (recovered) bergantung pada jumlah individu yang terinfeksi namun telah sembuh dan populasi akan berkurang saat terdapat kejadian kematian individu yang sembuh.
dRh
dt =γhIh−µhRh
4. Besarnya laju populasi vektor yang rentan terhadap penyakit(susceptible) bergantung pada angka kelahiran populasi vektor yang rentan dan populasi akan berkurang saat angka populasi individu yang terinfeksi yang menjadikan vektor rentan terinfeksi dan kematian populasi vektor. dSv dt =b2− β3SvIh Nh −µvSv
5. Besarnya laju populasi vektor yang terinfeksi penyakit
(infected) bergantung pada angka populasi individu yang terinfeksi yang menjadikan vektor rentan terinfeksi
dan populasi akan berkurang akibat angka kematian dari vektor yang terinfeksi yang disebabkan penyakit dan kematian alami yang terinfeksi.
dIv
dt =
β3SvIh
Nh
−δvIv−µvIv
Dari penjelasan diatas, maka sistem persamaan dapat ditulis sebagai berikut [1]:
dSh dt = b1− β1ShIh Nh −β2ShIv Nh −µhSh (4.1) dIh dt = β1ShIh Nh +β2ShIv Nh −γhIh−δhIh−µhIh (4.2) dRh dt = γhIh−µhRh (4.3) dSv dt = b2− β3SvIh Nh −µvSv (4.4) dIv dt = β3SvIh Nh −δvIv−µvIv (4.5)
dengan kondisi awal:
Sh(0)>0, Ih(0)>0, Rh(0)>0, Sv(0)>0, Iv(0)>0
Diketahui bahwa jumlah populasi individu dinyatakan sebagai Nh(t) dengan Nh(t) =Sh(t) +Ih(t) +Rh(t) sehingga
dapat dituliskan Rh(t) = Nh(t) − Sh(t) − Ih(t). Supaya
memudahkan perhitungan analisis selanjutnya, persamaan (4.3) digantikan oleh persamaan dNh
dt = b1 − µhNh − δhIh
tersebut terhadap t, sehingga: Nh0(t) =Sh0(t) +Ih0(t) +R0h(t) = b1− β1ShIh Nh −β2ShIv Nh −µhSh + β1ShIh Nh +β2ShIv Nh −γhIh−δhIh−µhIh + (γhIh−µhRh) =b1−µhSh−δhIh−µhIh−µhRh =b1−µhSh−δhIh−µhIh−µh(Nh−Sh−Ih) =b1−µhSh−δhIh−µhIh−µhNh+µhSh +µhIh =b1−µhNh−δhIh (4.6)
Maka sistem persamaan baru dari model menjadi : dSh dt = b1− β1ShIh Nh −β2ShIv Nh −µhSh (4.7) dIh dt = β1ShIh Nh +β2ShIv Nh −γhIh−δhIh−µhIh (4.8) dNh dt = b1−µhNh−δhIh (4.9) dSv dt = b2− β3SvIh Nh −µvSv (4.10) dIv dt = β3SvIh Nh −δvIv−µvIv (4.11)
Dengan kondisi awal:
Sh(0)>0, Ih(0)>0, Nh(0)>0, Sv(0)>0, Iv(0)>0 (4.12)
4.2 Daerah Penyelesaian Model
Dalam sistem persamaan baru dari model, diketahui bahwa dNh
sama akan dicari nilai dNv
dt . Karena diketahui bahwa Nv =
Sv +Iv Kemudian turunkan persamaan tersebut terhadap t,
diperoleh : Nv0(t) =Sv0(t) +Iv0(t) = b2− β3SvIh Nh −µvSv + β3SvIh Nh −δvIv−µvIv =b2−µvSv−δvIv−µvIv selanjutnya substitusikan Sv =Nv−Iv Nv0(t) =b2−µv(Nv−Iv)−δvIv−µvIv =b2−µvNv+µvIv−δvIv−µvIv =b2−µvNv−δvIv (4.13)
Selanjutnya akan dicari nilai Nh(t) dan Nv(t) melalui
persamaan (4.6) dan (4.13) dNh
dt =b1−µhNh−δhIh ≤b1−µhNh
Sehingga persamaan diferensialnya dapat dituliskan dNh
dt =b1−µhNh
Maka dapat diselesaikan dengan menggunakan persamaan diferensial peubah terpisah.
dNh
dt =b1−µhNh dNh
b1−µhNh
=dt (4.14)
Selanjutnya persamaan (4.14) akan diintegralkan di kedua ruasnya
Z dN h b1−µhNh = Z dt Misal: u=b1−µhNh (4.15) makadNh=−µduh, sehingga Z − du uµh = Z dt ⇔ − 1 µh ln|u|=t−ln|c|µh1 ⇔ln|u|=−µht+µhln|c| 1 µh ⇔ln|u| −µhln|c| 1 µh =−µht ⇔ln |u| |c| 1 µhµh =−µht ⇔ln|u| |c| =−µht ⇔ u c =e −µht ⇔u=ce−µht
Selanjutnya substitusikan nilai u ke persamaan (4.15), sehingga b1−µhNh =ce−µht µhNh =b1−ce−µht Nh(t) = b1−ce−µht µh lim t→∞Nh(t) = limt→∞ b1−ce−µht µh = b1 µh
Karena itu, maka 0< Nh(t)≤ b1 µh Sedangkan dNv dt =b2−µvNv−δvIv ≤b2−µvNv
Sehingga persamaan diferensialnya dapat dituliskan dNv
dt =b2−µvNv
Maka dapat diselesaikan dengan menggunakan persamaan diferensial peubah terpisah.
dNv
dt =b2−µvNv dNv
b2−µvNv
=dt (4.16)
Selanjutnya persamaan (4.16) akan diintegralkan di kedua ruasnya Z dN v b2−µvNv = Z dt Misal: u=b2−µvNv (4.17) maka dNv =− du µv
sehingga Z − du uµv = Z dt ⇔ − 1 µv ln|u|=t−ln|c|µv1 ⇔ln|u|=−µvt+µvln|c| 1 µv ⇔ln|u| −µvln|c| 1 µv =−µvt ⇔ln |u| |c|µv1 µv =−µvt ⇔ln|u| |c| =−µvt ⇔ u c =e −µvt ⇔u=ce−µvt
Selanjutnya substitusikan nilai u ke persamaan (4.17) sehingga b2−µvNv =ce−µvt µvNv =b2−ce−µvt Nv(t) = b2−ce−µvt µv lim t→∞Nv(t) = limt→∞ b2−ce−µvt µv = b2 µv Sehingga 0< Nv(t)≤ µb2v
Jadi daerah yang mungkin untuk sistem persamaan (4.7) sampai (4.11) adalah Ω =
(Sh, Ih, Nh, Sv, Iv)∈R5+,(Nh ≤ µb1h, Nv ≤ µb2v)
dikarenakan kondisi awal pada persamaan (4.12) bernilai positif dan pada
R5
+, maka Ω merupakan invarian positif. Selain itu, dN hdt dan dN v
dt ≤ 0 memenuhi Ω yang merupakan invarian positif dan
t→ ∞, sehingga dapat ditulis 0<(Nh, Nv)≤(µb1h,µb2v).
4.3 Titik Kesetimbangan Bebas Penyakit
Titik kesetimbang bebas penyakit adalah suatu keadaan tidak terjadi penyebaran penyakit menular dalam suatu populasi sehingga I = 0.
Untuk memperoleh titik kesetimbangan bebas penyakit dengan menyatakan ruas kiri pada persamaan (4.7) sampai (4.11) bernilai nol kemudian mensubstitusikannya untuk memperoleh titik Ef = Sh0, Ih0, Nh0, Sv0, Iv0
.
Karena pada kondisi tidak ada penyebaran penyakit menular, maka Ih0 = Iv0 = 0. Selanjutnya akan dicari nilai Sh0, Nh0 danSv0 melalui persamaan (4.7),(4.9), dan (4.10) yang ruas kanannya bernilai nol kemudian mensubstitusikannya dengan Ih0 =Iv0= 0. Menentukan nilai S0 h dSh dt = 0 ⇔b1− β1ShIh Nh −β2ShIv Nh −µhSh = 0 ⇔b1−0−0−µhSh = 0 ⇔b1−µhSh = 0 ⇔µhSh =b1 ⇔Sh = b1 µh ,maka Sh0= b1 µh (4.18)
Menentukan nilai N0 h dNh dt = 0 ⇔b1−µhNh−δhIh= 0 ⇔b1−µhNh−0 = 0 ⇔b1−µhNh = 0 ⇔µhNh=b1 ⇔Nh = b1 µh ,maka Nh0 = b1 µh (4.19) Menentukan nilai Sv0 dSv dt = 0 ⇔b2− β3SvIh Nh −µvSv = 0 ⇔b2−0−µvSv = 0 ⇔b2−µvSv = 0 ⇔µvSv =b2 ⇔Sv = b2 µv ,maka Sv0= b2 µv (4.20)
Berdasarkan persamaan (4.18),(4.19),dan (4.20), diketahui bahwaIh0 =Iv0= 0, maka diperoleh titik kesetimbangan bebas penyakit Ef = Sh0, Ih0, Nh0, Sv0, Iv0 = b1 µh ,0, b1 µh , b2 µv ,0 .
4.4 Menentukan Bilangan Reproduksi Dasar
Dalam model epidemiologi, bilangan reproduksi dasar yang dilambangkan dengan R0 adalah konsep kunci dan
didefinisikan sebagai jumlah rata-rata infeksi sekunder yang timbul dari individu yang terinfeksi primer yang masuk ke kelassusceptible selama periode infeksisusceptible[2].
Dengan menggunakan metode Driessche dan Watmough
[12] akan ditentukan bilangan reproduksi dasar untuk itu didefinisikan sebagai berikut :
dIh dt = β1ShIh Nh +β2ShIv Nh −(γh+δh+µh)Ih dIv dt = β3SvIh Nh −(δv+µv)Iv dNh dt =b1−µhNh−δhIh (4.21) dSh dt =b1− β1ShIh Nh −β2ShIv Nh −µhSh dSv dt =b2− β3SvIh Nh −µvSv
Fi adalah laju kemunculan infeksi baru pada kompartemen i, Vi− adalah laju dari perpindahan individu keluar dari kompartemen i,
Vi+ adalah laju dari perpindahan individu masuk ke dalam kompartemen i
Vi=Vi−− Vi+
F = β1ShIh Nh β3SvIh Nh 0 0 0 dan V = −β2ShIv Nh + (γh+δh+µh)Ih (δv+µv)Iv −b1+µhNh+δhIh −b1+ β1NShIh h + β2ShIv Nh +µhSh −b2+ β3NSvhIh +µvSv
Kompartemen yang terinfeksi adalah Ih ke Iv, sehingga
perhatikan Ih dan Iv dengan mensubtitusikan nilai titik
kesetimbangan bebas penyakitEf = b1 µh ,0, b1 µh , b2 µv ,0 . F = β1Ih β3b2µh µvb1 Ih 0 0 0 dan V = −β2Iv+ (γh+δh+µh)Ih (δv+µv)Iv −b1+µhNh+δhIh −b1+β1NShIh h + β2ShIv Nh +µhSh −b2+β3NSvhIh +µvSv Sehingga diperoleh, F = β1Ih β3b2µh µvb1 Ih dan V = −β2Iv+ (γh+δh+µh)Ih (δv+µv)Iv
Selanjutnya akan dicari matriks F dan V yang didapat dariF dan V dengan cara berikut sebagai berikut:
F = ∂FIh Ih ∂FIh Iv ∂FIv Ih ∂FIv Iv dan V = ∂VIh Ih ∂VIh Iv ∂VIv Ih ∂VIv Iv
maka akan didapatkan matriks sebagai berikut [12]
F = β1 0 β3b2µh µvb1 0 dan V = γh+δh+µh −β2 0 δv+µv
dari F tersebut dapat dituliskan sebagai berikut
F = β1 0 0 0 + 0 0 β3b2µh µvb1 0
Selanjutnya dicari V−1, sehingga diperoleh V−1 = 1 (δv+µv)(γh+δh+µh) δv+µv β2 0 γh+δh+µh V−1 = 1 (γh+δh+µh) β2 (δv+µv)(γh+δh+µh) 0 1 (δv+µv)
Selanjutnya mencari nilai R0 yaituR0=ρ(F V−1) sehingga
a. untuk F = β1 0 0 0
maka F V−1= β1 0 0 0 1 (γh+δh+µh) β2 (δv+µv)(γh+δh+µh) 0 1 (δv+µv) = β1 (γh+δh+µh) β1β2 (δv+µv)(γh+δh+µh) 0 0
Jadi nilai eigen dari matriks next generation diperoleh dengan menyelesaikan det (F V−1 −λI) = 0, sehingga didapat det β1 (γh+δh+µh) −λ β1β2 (δv+µv)(γh+δh+µh) 0 −λ = 0 β1 (γh+δh+µh) −λ (−λ) = 0 − β1 (γh+δh+µh) λ+λ2 = 0 λ − β1 (γh+δh+µh) +λ = 0
Dari perhitungan diatas bisa didapatkan nilai eigen untukλ= 0 dan didapat
λ= β1 (γh+δh+µh)
b. Untuk F = 0 0 β3b2µh µvb1 0 maka F V−1 = 0 0 β3b2µh µv b1 0 1 (γh+δh+µh) β2 (δv+µv)(γh+δh+µh) 0 1 (δv+µv) = " 0 0 β3b2µh (µvb1)(γh+δh+µh) β2β3b2µh (µvb1)(δv+µv)(γh+δh+µh) #
Jadi nilai eigen dari matriks next generation diperoleh dengan menyelesaikan det (F V−1 −λI) = 0, sehingga didapat det 0−λ 0 β3b2µh (µvb1)(γh+δh+µh) β2β3b2µh (µvb1)(δv+µv)(γh+δh+µh) −λ = 0 β2β3b2µh (µvb1)(δv+µv)(γh+δh+µh) −λ (−λ) = 0 − β2β3b2µh (µvb1)(δv+µv)(γh+δh+µh) λ+λ2= 0 λ − β2β3b2µh (µvb1)(δv+µv)(γh+δh+µh) +λ = 0 Dari perhitungan diatas bisa didapatkan nilai eigen untukλ= 0 dan didapat
λ= β2β3b2µh
(µvb1)(δv+µv)(γh+δh+µh)
(4.23) Berdasarkan perolehan nilai eigen dari persamaan (4.22) dan (4.23), makaR0 diperoleh sebagai berikut
R0=
β2β3b2µh
(µvb1)(δv+µv)(γh+δh+µh)
+ β1
4.5 Titik Kesetimbangan Endemik
Titik Kesetimbangan Endemik digunakan untuk menunjukkan adanya penyebaran penyakit pada suatu populasi sehingga Ih∗ 6=Iv∗ 6= 0.
Untuk memperoleh titik kesetimbangan endemik dengan menyatakan ruas kiri bernilai nol pada persamaan (4.7) sampai (4.11), sehingga dSh dt = 0, dIh dt = 0, dNh dt = 0, dSv dt = 0, dan dIv
dt = 0. Kemudian mensubstitusikannya untuk
memperoleh titikE1 = (Sh∗, Ih∗, Nh∗, Sv∗, Iv∗).
Pertama-tama akan dicari nilai Nh∗ sehingga dNh dt = 0 ⇔b1−µhNh−δhIh = 0 ⇔µhNh=b1−δhIh Nh∗= b1−δhI ∗ h µh (4.24) Selanjutnya akan dicari nilai Sh∗ dengan cara berikut
dIh dt = 0 ⇔ β1ShIh Nh +β2ShIv Nh −γhIh−δhIh−µhIh = 0 ⇔Sh β1Ih+β2Iv Nh = (γh+δh+µh)Ih (4.25) Selanjutnya dSh dt = 0 ⇔b1− β1ShIh Nh − β2ShIv Nh −µhSh = 0 ⇔b1−µhSh =Sh β1Ih+β2Iv Nh (4.26)
Dengan mensubtitusikan persamaan (4.25) ke persamaan (4.26) , sehingga b1−µhSh = (γh+δh+µh)Ih b1−(γh+δh+µh)Ih = µhSh Sh∗ = b1−(γh+δh+µh)I ∗ h µh (4.27)
Selanjutnya akan dicari nilai Sv∗ dengan cara berikut dSv dt =b2− β3SvIh Nh −µvSv = 0 ⇔ β3SvIh Nh =b2−µvSv ⇔ β3SvIh Nh +µvSv =b2 ⇔Sv β3Ih+µvNh Nh =b2 Sv∗ = b2N ∗ h β3Ih∗+µvNh∗ (4.28)
Dengan mensubtitusikan persamaan (4.24) ke persamaan (4.28), sehingga Sv∗ = b2 b 1−δhIh∗ µh β3Ih∗+µv b1−δ hIh∗ µh = b2b1−b2δhIh∗ µh µh β3Ih∗µh+µv(b1−δhIh∗) = b2(b1−δhI ∗ h) β3Ih∗µh+µv(b1−δhIh∗)
Selanjutnya akan dicari nilai Iv∗, sehingga dIv dt = 0 ⇔ β3SvIh Nh −δvIv−µvIv = 0 ⇔ β3SvIh Nh =Iv(δv+µv) ⇔ β3 b2(b1−δhIh) β3Ihµh+µv(b1−δhIh) Ih b1−δhIh µh =Iv(δv+µv) ⇔ β3b2Ih(b1−δhIh) µhβ3Ih+µv(b1−δhIh) µh b1−δhIh =Iv(δv+µv) Iv∗ = β3b2I ∗ hµh (δv+µv) µhβ3Ih∗+µv(b1−δhIh∗) (4.29)
Misalkan K1 = (γh+δh+µh) dan K2 = (δv+µv), sehingga
persamaan (4.27) menjadi Sh∗ = b1−K1I ∗ h µh (4.30)
dan persamaan (4.29) menjadi
Iv∗ = β3b2I ∗
hµh
K2 µhβ3Ih∗+µv(b1−δhIh∗)
(4.31)
Karena Nilai Ih∗ 6= 0, maka selanjutnya akan dicari nilai g(Ih) dengan cara mensubtitusikan nilai Sh∗ , N
∗
h , S
∗
v , dan
dengankan nol, sehingga dIh dt = β1ShIh Nh +β2ShIv Nh −γhIh−δhIh−µhIh ⇔0 = β1S ∗ hI ∗ h Nh∗ + β2Sh∗Iv∗ Nh∗ −(γh+δh+µh)I ∗ h ⇔0 = β1 b 1−K1Ih∗ µh Ih∗ b 1−δhIh∗ µh + β2 b1−K 1Ih∗ µh β 3b2Ih∗µh K2(µhβ3Ih∗+µv(b1−δhIh∗)) b 1−δhIh∗ µh −K1I ∗ h ⇔0 = β1(b1−K1I ∗ h)I ∗ h (b1−δhIh∗) + β2(b1−K1Ih∗) (b1−δhIh∗) (β3b2Ih∗µh) K2 µhβ3Ih∗+µv(b1−δhIh∗) ! −K1Ih∗ ⇔0 = β1(b1−K1I ∗ h)I ∗ h(K2(µhβ3I ∗ h+µv(b1−δhI ∗ h))) (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) + β2(b1−K1I ∗ h)β3b2Ih∗µh (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) − K1I ∗ h(b1−δhI ∗ h) (K2(µhβ3I ∗ h +µv(b1−δhI ∗ h))) (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) ⇔0 = (β1b1I ∗ h−β1K1I ∗2 h ) (K2(µhβ3I ∗ h+µv(b1−δhI ∗ h))) (K2b1−K2δhIh∗) µhβ3Ih∗+µv(b1−δhIh∗) + (β2β3b1b2µhI ∗ h−β2β3b1b2K1µhIh∗2) (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) − (K1b1I ∗ h−K1δhI ∗ h) (K2(µhβ3I ∗ h +µv(b1−δhI ∗ h))) (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗)
⇔0 = β1b1K2µhβ3I ∗2 h +K2µvb21β1Ih∗ (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) −K2µvb1β1δhIh∗2−β1K1K2µhβ3Ih∗3 (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) −β1K1K2µvb1Ih∗2+β1K1K2µvδhIh∗3 (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) +β2b1β3b2µhIh∗−β2K1µhb2β3Ih∗2 (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) −K1K2b1µhβ3Ih∗2−K1K2b21µvIh∗ (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) +K1K2b1µvδhIh∗2+K1K2µhδhβ3Ih∗3 (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) +K1K2µvδhb1Ih∗2−K1K2µvδ2hIh∗3 (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗)
Selanjutnya pembilang dan penyebut dibagi dengan −Ih∗, sehingga 0 = −β1b1K2µhβ3I ∗ h−K2µvb21β1+K2µvb1β1δhIh∗ 1 −I∗ h (b1−δhIh∗) K2(µhβ3Ih∗+µv(b1−δhIh∗)) + β1K1K2µhβ3I ∗2 h +β1K1K2µvb1I ∗ h−β1K1K2µvδhI ∗2 h 1 −I∗h (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) − β2b1β3b2µh−β2K1µhb2β3I ∗ h−K1K2b1µhβ3Ih∗ 1 −I∗ h (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) + K1K2b 2 1µv−K1K2b1µvδhIh∗−K1K2µhδhβ3Ih∗2 1 −Ih∗ (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) − K1K2µvδhb1I ∗ h−K1K2µvδh2I ∗2 h 1 −Ih∗ (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗)
0 = (−β1K1K2µvδh+β1K1K2µhβ3)I ∗2 h 1 −Ih∗ (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) + (−K1K2µhδhβ3+K1K2µvδ 2 h)I ∗2 h 1 −Ih∗ (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) − (β1b1K2µhβ3−β1b1K2µvδh)I ∗ h 1 −Ih∗ (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) − (β1b1K2µhβ3−β1b1K2µvδh)I ∗ h 1 −Ih∗ (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) − (−β1K1K2µvb1−β2K1µhb2β3)I ∗ h 1 −Ih∗ (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) − (−β3K1K2µhb1+b1K1K2µvδh+b1K1K2µvδh)I ∗ h 1 −Ih∗ (b1−δhIh∗) K2 µhβ3Ih∗+µv(b1−δhIh∗) − β1b 2 1K2µv−β2β3µhb1b2+K1K2µvb21 1 −Ih∗ (b1−δhIh∗) K2(µhβ3Ih∗+µv(b1−δhIh∗)) Sehingga diperoleh g(Ih) = (K1K2µhβ1β3−K1K2µhβ3δh+K1K2µvδ2h K1K2β1µvδh)Ih∗2+ (K1K2µvb1β1 −2K1K2µvb1δh+K1K2µhb1β3+K2b1β1µvδh −K2b1β1µhβ3+K1µhb2β2β3)Ih∗+µvb21K1K2 −µvb21K1K2 µhb2β2β3 µvb1K1K2 −µvb21K1K2 β1 K1
= (K1K2(µhβ3(β1−δh) +µvδh(δh−β1)))Ih∗2 + (K1K2(µvb1β1−2µvb1δh+µhb1β3))Ih∗ + (K2b1β1(µvδh−µhβ3) +K1µhb2β2β3)Ih∗ +µvb21K1K2 1− µhb2β2β3 µvb1K1K2 + β1 K1 = (K1K2(µhβ3(β1−δh) +µvδh(δh−β1)))Ih∗2 + (K1K2(µvb1β1−2µvb1δh+µhb1β3)) + (K2b1β1(µvδh−µhβ3) +K1µhb2β2β3)Ih∗ +µvb21K1K2(1−R0)
Sehingga diperoleh persamaan g(Ih) sebagai berikut
g(Ih) =AIh∗2+BI ∗ h+C = 0 dengan A=K1K2(µhβ3(β1−δh) +µvδh(δh−β1)), B =K1K2(µvb1β1−2µvb1δh+µhb1β3) +K2b1β1(µvδh−µhβ3) +K1µhb2β2β3, C=µvb21K1K2(1−R0), R0 = µhb2β2β3 µvb1K1K2 + β1 K1
4.6 Kestabilan Lokal Model Interaksi Dinamis
Setelah diperoleh titik kesetimbangan maka dilakukan analisis kestabilan. Analisis kestabilan dilakukan untuk mengetahui laju penyebaran suatu penyakit. Analisis ini dilakukan pada titik setimbang bebas penyakit (Disease Free Equilibrium) dan titik setimbang endemik (Endemic Equilibrium).
Model interaksi dinamis merupakan model persamaan yang tak linier, sehingga perlu dilakukan linierisasi terlebih
dahulu sebelum melakukan analisis kestabilan. Untuk melakukan linierisasi digunakan ekspansi deret Taylor, pada persamaan (4.7) sampai (4.11) sehingga dapat dituliskan sebagai berikut. dSh dt =A(Sh, Ih, Nh, Sv, Iv) =b1− β1ShIh Nh −β2ShIv Nh −µhSh dIh dt =B(Sh, Ih, Nh, Sv, Iv) = β1ShIh Nh +β2ShIv Nh −γhIh−δhIh−µhIh dNh dt =C(Sh, Ih, Nh, Sv, Iv) (4.32) =b1−µhNh−δhIh dSv dt =D(Sh, Ih, Nh, Sv, Iv) =b2− β3SvIh Nh −µvSv dIv dt =E(Sh, Ih, Nh, Sv, Iv) = β3SvIh Nh −δvIv−µvIv
Dengan titik tetap (S0h, Ih0, Nh0, Sv0, Iv0), maka dSh dt =A(S 0 h, Ih0, Nh0, Sv0, Iv0) = 0 dIh dt =B(S 0 h, Ih0, Nh0, Sv0, Iv0) = 0 dNh dt =C(S 0 h, Ih0, Nh0, Sv0, Iv0) = 0 (4.33) dSv dt =D(S 0 h, Ih0, Nh0, Sv0, Iv0) = 0
dIv dt =E(S 0 h, Ih0, Nh0, Sv0, Iv0) = 0 Misalkan: Sh−Sh0 = u⇒S˙h = ˙u Ih−Ih0 = v⇒I˙h= ˙v Nh−Nh0 = x⇒N˙h = ˙x (4.34) Sv−Sv0 = y ⇒S˙v = ˙y Iv−Iv0 = z⇒I˙v = ˙z
Deret Taylor dari sistem (4.32) disekitar titik tetap (Sh0, Ih0, Nh0, Sv0, Iv0) adalah dSh dt =A(S 0 h, Ih0, Nh0, Sv0, Iv0) + (Sh−Sh0) ∂A ∂Sh + (Ih−Ih0) ∂A ∂Ih + (Nh−Nh0) ∂A ∂Nh + (Sv−Sv0) ∂A ∂Sv + (Iv−Iv0) ∂A ∂Iv +· · · dIh dt =B(S 0 h, Ih0, Nh0, Sv0, Iv0) + (Sh−Sh0) ∂B ∂Sh + (Ih−Ih0) ∂B ∂Ih + (Nh−Nh0) ∂B ∂Nh + (Sv−Sv0) ∂B ∂Sv + (Iv−Iv0) ∂B ∂Iv +· · · dNh dt =C(S 0 h, Ih0, Nh0, Sv0, Iv0) + (Sh−Sh0) ∂C ∂Sh + (Ih−Ih0) ∂C ∂Ih + (Nh−Nh0) ∂C ∂Nh + (Sv−Sv0) ∂C ∂Sv + (Iv−Iv0) ∂C ∂Iv +· · ·
dSv dt =D(S 0 h, Ih0, Nh0, Sv0, Iv0) + (Sh−S0h) ∂D ∂Sh + (Ih−Ih0) ∂D ∂Ih + (Nh−Nh0) ∂D ∂Nh + (Sv−Sv0) ∂D ∂Sv + (Iv−Iv0) ∂D ∂Iv +· · · dIv dt =E(S 0 h, Ih0, Nh0, Sv0, Iv0) + (Sh−Sh0) ∂E ∂Sh + (Ih−Ih0) ∂E ∂Ih + (Nh−Nh0) ∂E ∂Nh + (Sv−Sv0) ∂E ∂Sv + (Iv−Iv0) ∂E ∂Iv +· · ·
Berdasarkan persamaan (4.33), maka linearisasi dari sistem (4.32) adalah dSh dt = (Sh−S 0 h) ∂A ∂Sh + (Ih−Ih0) ∂A ∂Ih + (Nh−Nh0) ∂A ∂Nh + (Sv−Sv0) ∂A ∂Sv + (Iv−Iv0) ∂A ∂Iv dIh dt = (Sh−S 0 h) ∂B ∂Sh + (Ih−Ih0) ∂B ∂Ih + (Nh−Nh0) ∂B ∂Nh + (Sv−Sv0) ∂B ∂Sv + (Iv−Iv0) ∂B ∂Iv dNh dt = (Sh−S 0 h) ∂C ∂Sh + (Ih−Ih0) ∂C ∂Ih + (Nh−Nh0) ∂C ∂Nh + (Sv−Sv0) ∂C ∂Sv +
(Iv−Iv0) ∂C ∂Iv dSv dt = (Sh−S 0 h) ∂D ∂Sh + (Ih−Ih0) ∂D ∂Ih + (Nh−Nh0) ∂D ∂Nh + (Sv−Sv0) ∂D ∂Sv + (Iv−Iv0) ∂D ∂Iv dIv dt = (Sh−S 0 h) ∂E ∂Sh + (Ih−Ih0) ∂E ∂Ih + (Nh−Nh0) ∂E ∂Nh + (Sv−Sv0) ∂E ∂Sv + (Iv−Iv0) ∂E ∂Iv
Dengan menggunakan permisalan (4.34), maka hasil linearisasi dari sistem (4.32) seperti yang tertulis tersebut menjadi: dSh dt =u ∂A ∂Sh +v∂A ∂Ih +x ∂A ∂Nh +y∂A ∂Sv +z∂A ∂Iv dIh dt =u ∂B ∂Sh +v∂B ∂Ih +x ∂B ∂Nh +y∂B ∂Sv +z∂B ∂Iv dNh dt =u ∂C ∂Sh +v∂C ∂Ih +x ∂C ∂Nh +y∂C ∂Sv +z∂C ∂Iv (4.35) dSv dt =u ∂D ∂Sh +v∂D ∂Ih +x ∂D ∂Nh +y∂D ∂Sv +z∂D ∂Iv dIv dt =u ∂E ∂Sh +v∂E ∂Ih +x ∂E ∂Nh +y∂E ∂Sv +z∂E ∂Iv
Persamaan (4.35) dapat ditulis dalam bentuk matriks sebagai berikut:
dSh dt dIh dt dNh dt dSv dt dIv dt = ∂A ∂Sh ∂A ∂Ih ∂A ∂Nh ∂A ∂Sv ∂A ∂Iv ∂B ∂Sh ∂B ∂Ih ∂B ∂Nh ∂B ∂Sv ∂B ∂Iv ∂C ∂Sh ∂C ∂Ih ∂C ∂Nh ∂C ∂Sv ∂C ∂Iv ∂D ∂Sh ∂D ∂Ih ∂D ∂Nh ∂D ∂Sv ∂D ∂Iv ∂E ∂Sh ∂E ∂Ih ∂E ∂Nh ∂E ∂Sv ∂E ∂Iv " u v x y z #
Matriks Jacobian dari matriks tersebut adalah
J = ∂A ∂Sh ∂A ∂Ih ∂A ∂Nh ∂A ∂Sv ∂A ∂Iv ∂B ∂Sh ∂B ∂Ih ∂B ∂Nh ∂B ∂Sv ∂B ∂Iv ∂C ∂Sh ∂C ∂Ih ∂C ∂Nh ∂C ∂Sv ∂C ∂Iv ∂D ∂Sh ∂D ∂Ih ∂D ∂Nh ∂D ∂Sv ∂D ∂Iv ∂E ∂Sh ∂E ∂Ih ∂E ∂Nh ∂E ∂Sv ∂E ∂Iv
Selanjutnya akan dicari matriks Jacobian dari sistem (4.32) dengan mendiferensialkannya sebagai berikut
∂A ∂Sh = ∂ ∂Sh b1− β1ShIh Nh −β2ShIv Nh −µhSh = −β1Ih Nh − β2Iv Nh −µh (4.36) ∂A ∂Ih = ∂ ∂Ih b1− β1ShIh Nh −β2ShIv Nh −µhSh = −β1Sh Nh (4.37) ∂A ∂Nh = ∂ ∂Nh b1− β1ShIh Nh −β2ShIv Nh −µhSh = β1ShIh (Nh)2 +β2ShIv (Nh)2 (4.38)
∂A ∂Sv = ∂ ∂Sv b1− β1ShIh Nh −β2ShIv Nh −µhSh = 0 (4.39) ∂A ∂Iv = ∂ ∂Iv b1− β1Sh Nh −β2ShIv Nh −µhSh = −β2Sh Nh (4.40) ∂B ∂Sh = ∂ ∂Sh β1ShIh Nh + β2ShIv Nh + ∂ ∂Sh (−γhIh−δhIh−µhIh) = β1Ih Nh +β2Iv Nh (4.41) ∂B ∂Ih = ∂ ∂Ih β1ShIh Nh +β2ShIv Nh + ∂ ∂Ih (−γhIh−δhIh−µhIh) = β1Sh Nh −γh−δh−µh (4.42) ∂B ∂Nh = ∂ ∂Nh β1ShIh Nh +β2ShIv Nh + ∂ ∂Nh (−γhIh−δhIh−µhIh) = −β1ShIh (Nh)2 −β2ShIv (Nh)2 (4.43) ∂B ∂Sv = ∂ ∂Sv β1ShIh Nh +β2ShIv Nh + ∂ ∂Sv (−γhIh−δhIh−µhIh) = 0 (4.44)
∂B ∂Iv = ∂ ∂Iv β1ShIh Nh +β2ShIv Nh + ∂ ∂Iv (−γhIh−δhIh−µhIh) = β2Sh Nh (4.45) ∂C ∂Sh = ∂ ∂Sh (b1−µhNh−δhIh) = 0 (4.46) ∂C ∂Ih = ∂ ∂Ih (b1−µhNh−δhIh) = −δh (4.47) ∂C ∂Nh = ∂ ∂Nh (b1−µhNh−δhIh) = −µh (4.48) ∂C ∂Sv = ∂ ∂Sv (b1−µhNh−δhIh) = 0 (4.49) ∂C ∂Iv = ∂ ∂Iv (b1−µhNh−δhIh) = 0 (4.50) ∂D ∂Sh = ∂ ∂Sh b2− β3SvIh Nh −µvSv = 0 (4.51) ∂D ∂Ih = ∂ ∂Ih b2− β3SvIh Nh −µvSv = −β3Sv Nh (4.52) ∂D ∂Nh = ∂ ∂Nh b2− β3SvIh Nh −µvSv = β3SvIh (Nh)2 (4.53)
∂D ∂Sv = ∂ ∂Sv b2− β3SvIh Nh −µvSv = −β3Ih Nh −µv (4.54) ∂D ∂Iv = ∂ ∂Sv b2− β3SvIh Nh −µvSv = 0 (4.55) ∂E ∂Sh = ∂ ∂Sh β3SvIh Nh −δvIv−µvIv = 0 (4.56) ∂E ∂Ih = ∂ ∂Ih β3SvIh Nh −δvIv−µvIv = β3Sv Nh (4.57) ∂E ∂Nh = ∂ ∂Nh β3SvIh Nh −δvIv−µvIv = −β3SvIh (Nh)2 (4.58) ∂E ∂Sv = ∂ ∂Sv β3SvIh Nh −δvIv−µvIv = β3Ih Nh (4.59) ∂E ∂Iv = ∂ ∂Iv β3SvIh Nh −δvIv−µvIv = −δv−µv (4.60)
Dari hasil turunan persamaan (4.36) sampai (4.60), dapat ditulis dalam bentuk matriks Jacobian sebagai berikut:
J = −β1Ih Nh −β2Iv Nh −µh − β1Sh Nh β1ShIh (Nh)2 +β2ShIv (Nh)2 β1Ih Nh + β2Iv Nh β1Sh Nh −γh−δh−µh − β1ShIh (Nh)2 − β2ShIv (Nh)2 0 −δh −µh 0 −β3Sv Nh − β3SvIh (Nh)2 0 β3Sv Nh −β3SvIh (Nh)2 0 −β2Sh Nh 0 β2Sh Nh 0 0 −β3Ih Nh −µv 0 β3Ih Nh −δv−µv
4.6.1 Kestabilan Lokal Titik Setimbang Bebas Penyakit
Telah diketahui sebelumnya bahwa titik setimbang bebas penyakit adalah Ef = (Sh0, Ih0, Nh0, Sv0, Iv0) = b1 µh ,0, b1 µh , b2 µv ,0 , maka J(Ef) = −µh −β1 0 0 −β2 0 β1−(γh+δh+µh) 0 0 β2 0 −δh −µh 0 0 0 −β3b2µh b1µv 0 −µv 0 0 β3b2µh b1µv 0 0 −(δv+µv)
Untuk mempermudah mencari persamaan
bentuk matriks segitiga atas dengan cara OBE sebagai berikut. J(Ef) = −µh −β1 0 0 −β2 0 β1−(γh+δh+µh) 0 0 β2 0 −δh −µh 0 0 0 −β3b2µh b1µv 0 −µv 0 0 β3b2µh b1µv 0 0 −(δv+µv) ∼B3+ δh (β1−(γh+δh+µh)) B2 ∼B4+ β3b2µh b1µv (β1−(γh+δh+µh)) B2 ∼B5− β3b2µh b1µv (β1−(γh+δh+µh)) B2 J(Ef) = " −µh −β1 0 0 β1−(γh+δh+µh) 0 0 0 −µh 0 0 0 0 0 0 0 −β2 0 β2 0 0 −µv 0 0 −(δv+µv)(β1−(γh+δh+µh))b1µv−β2β3b2µh b1µv(β1−(γh+δh+µh))
Selanjutnya dicari persamaan karakteristik dari matriks Jacobian tersebut dengan menggunakan
Sehingga " −µh −β1 0 0 0 β1−(γh+δh+µh) 0 0 0 0 −µh 0 0 0 0 −µv 0 0 0 0 −β2 β2 0 0 −(δv+µv)(β1−(γh+δh+µh))b1µv−β2β3b2µh b1µv(β1−(γh+δh+µh)) −λ " 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 # = 0 Maka −µh−λ −β1 0 0 β1−(γh+δh+µh)−λ 0 0 0 −µh−λ 0 0 0 0 0 0 0 −β2 0 β2 0 0 −µv−λ 0 0 −(δv+µv)(β1−(γh+δh+µh))b1µv−β2β3b2µh b1µv(β1−(γh+δh+µh))−λ = 0
Dari matriks Jacobian tersebut maka akan diperoleh persamaan karakteristik sebagai berikut.
(−µh−λ) (β1−(γh+δh+µh)−λ) (−µh−λ)(−µv−λ) −(δv+µv)(β1−(γh+δh+µh)b1µv)−β2β3b2µh b1µv(β1−(γh+δh+µh)) −λ = 0 Sehingga akan diperoleh nilai eigen dari akar karakteristiknya sebagai berikut.
λ1 = −µh<0 λ2 = β1−(γh+δh+µh) = (γh+δh+µh)( β1 (γh+δh+µh) −1) untuk β1 (γh+δh+µh) <1 maka λ2 = β1−(γh+δh+µh)<0
λ3 = −µh<0 λ4 = −µv <0 λ5 = −(δv+µv) (β1−(γh+δh+µh))b1µv−β2β3b2µh b1µv(β1−(γh+δh+µh)) = −(δv+µv) (β1−(γh+δh+µh))b1µv−β2β3b2µh b1µv(β1−(γh+δh+µh)) = − β2β3b2µh+b1µv(δv+µv) (β1−(γh+δh+µh)) b1µv(β1−(γh+δh+µh)) = − β2β3b2µh b1µv(β1−(γh+δh+µh)) −(δv+µv) = (δv+µv) − β2β3b2µh b1µv(δv+µv)(β1−(γh+δh+µh)) −1 = (δv+µv) (− β2β3b2µh b1µv(δv+µv)(γh+δh+µh) β1 (γh+δh+µh) −1 − β1 (γh+δh+µh)−1 β1 (γh+δh+µh)−1 ) = (δv+µv) β1 (γh+δh+µh)−1 − β2β3b2µh b1µv(δv+µv)(γh+δh+µh) − β1 (γh+δh+µh) −1 = − (δv+µv) β1 (γh+δh+µh)−1 β2β3b2µh b1µv(δv+µv)(γh+δh+µh) + β1 (γh+δh+µh) −1 = − (δv+µv) β1 (γh+δh+µh)−1 β2β3b2µh b1µv(δv+µv)(γh+δh+µh) + β1 (γh+δh+µh) −1
untuk R0 = β2β3b2µh b1µv(δv+µv)(γh+δh+µh)+ β1 (γh+δh+µh) <1 maka λ5 = −(δv+µv) (β1−(γh+δh+µh))b1µv−β2β3b2µh b1µv(β1−(γh+δh+µh)) <0
Karena nilai eigen (λ1, λ2, λ3, λ4, dan λ5) bernilai negatif
pada bagian realnya maka berdasarkan akar akar karakteristik (nilai eigen λ) maka titik setimbang Ef =
b1 µh ,0, b1 µh ,b2 µv ,0
stabil lokal asimtotis dan titik kesetimbangan bebas penyakit bersifat stabil untukR0 <1.
4.6.2 Kestabilan Lokal Titik Setimbang Endemik
Telah diketahui sebelumnya bahwa titik setimbang endemik E1 = (Sh∗, Ih∗, Nh∗, Sv∗, Iv∗), dalam hal ini Ih∗ selalu
positif dengan Sh∗ = b1−(γh+δh+µh)I ∗ h µh Sv∗ = b2(b1−δhI ∗ h) µhβ3Ih∗+µv(b1−δhIh∗) Iv∗ = µhb2β3I ∗ h (µv+δv)(µhβ3Ih∗+µv(b1−δhIh∗)) Nh∗ = b1−δhI ∗ h µh
Pada titik setimbang E1 = (Sh∗, Ih∗, Nh∗, Sv∗, Iv∗) matrik
Jacobiannya adalah J(E1) = −β1I ∗ h Nh∗ − β2Iv∗ Nh∗ −µh − β1Sh∗ Nh∗ β1S∗hIh∗ (N∗h)2 + β2S∗hIv∗ (Nh∗)2 β1Ih∗ Nh∗ + β2I∗v Nh∗ β1Sh∗ Nh∗ −γh−δh−µh − β1S∗hI∗h (Nh∗)2 − β2S∗hI∗v (Nh∗)2 0 −δh −µh 0 −β3Sv∗ Nh∗ − β3Sv I∗h∗ (Nh∗)2 0 β3Sv∗ Nh∗ − β3Sv I∗h∗ (Nh∗)2