SOLUSI EKSAK DAN KESTABILAN SISTEM BANDUL GANDA

(1)

J. Sains MIPA, Edisi Khusus Tahun 2008, Vol. 14, No. 1, Hal.: 23 - 32 ISSN 1978-1873

SOLUSI EKSAK DAN KESTABILAN SISTEM BANDUL GANDA

**Amanto* dan La Zakaria**

Jurusan Matematika FMIPA Universitas Lampung Jl. S. Brojonegoro No.1, Bandar Lampung 35145 Indonesia Alamat untuk surat menyurat e-mail : Otnama1@yahoo.co.id

Diterima 28 Agustus 2007, perbaikan 10 Desember 2007, disetujui untuk diterbitkan 27 Desember 2007

ABSTRACT

Simple double pendulum system is a system consisting of two objects and two pieces of strong strand of metal but light. The system sway vertical with influenced by earth gravitation. On the happening of transfer of position of silent situation, the pendulum could sway by stabilizing or unstable. This article will present stable or unstable situation of the double pendulum system that concerned using the stability condition evaluated from eigen value of the system.

Keywords: stability, simple double pendulum, stable-unstable condition, eigen value

1. PENDAHULUAN

Suatu fenomena alam dapat dinyatakan dalam suatu model matematis, yang berupa sistem persamaan diferensial. Teori sistem merupakan cabang ilmu matematika yang berfokus pada kajian kontrol input dan output. Teori ini telah banyak diterapkan pada bidang teknik, fisika, biologi, dan bidang ilmu lain dan telah dikembangkan secara intensif oleh para ahli teknik teoritis, terutama teori sistem linear atas bilangan real 1) _{. Kestabilan merupakan konsep dasar yang penting dalam}

teori sistem matematis, disamping konsep keterkendalian dan keterobservasian2) _.

Model-model dalam aplikasi matematika pada ilmu rekayasa, fisika, biologi dan lain sebagainya, banyak yang berbentuk sistem persamaan diferensial biasa. Perilaku solusi dari sistem seperti itu adalah contoh permasalahan yang dibahas dalam sistem dinamik. Sistem kerja pada Tim SAR (Search and Rescue) dan suplai makanan atau amunisi ke barak

menggunakan pesawat helikopter merupakan dua contoh sistem kerja yang identik dengan sistem kerja pendulum.

2 m2

m

1 1 m1 B2 B1 L1 L2 m2 m2 l2 l1 l = l1 + l2

(2)

Amanto dan La Zakaria Solusi Eksak dan Kestabilan

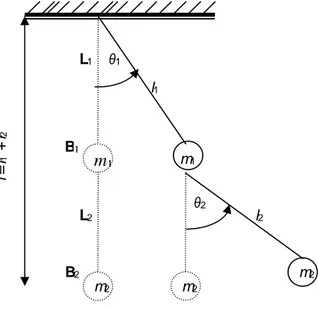
Sistem dinamik yang cukup realistis adalah sistem bandul ganda sederhana. Sistem bandul ini dapat merepresentasikan sistem kerja tim SAR (Search and Rescue) yang sedang mengupayakan penyelamatan dengan membawa perlengkapan penyelamatan atau korban bencana alam atau kecelakaan dengan menggunakan helikopter. Sistem bandul ganda sederhana adalah sistem yang terdiri dari dua benda B1 dan B2 dengan massa masing-masing benda adalah

m

₁ dan

2

m

. Selain itu benda tersebut masing-masing dihubungkan dengan dua helai kawat yang kuat tapi ringan L1 dan L2

dengan panjang masing-masing kawat adalah

l

₁dan

l

₂. Benda B1 terpasang pada ujung kawat L1 (ujung kawat L1

lainnya terpasang mantap pada sebuah bidang). Sementara itu benda B2 terpasang pada ujung kawat L2, di bawah

pengaruh gravitasi 3) _{(ujung kawat L}₂_{lainnya terpasang mantap pada benda pertama) (lihat Gambar 1).}

Dari Gambar 1. sistem bandul ganda memiliki 4 (empat) parameter yakni l1, l2, m1, dan m2. Dengan Dipengaruhi oleh

grafitasi bandul gandaberosilasi pada bidang vertikal dengan sudut perpindahan untuk suatu waktu adalah ₁

t

dan

2

t

. Model matematika untuk sistem bandul ganda yang diilustrasikan dalam Gambar 1. adalah sebagai berikut 4) :

, 0 ) ( ) (m₁ m₂ l₁2 ₁ m₂l₁l₂ ₂ m₁ m₂ l₁g ₁ 0 2 2 2 2 2 2 2 1 2 1 2ll ml ml g m (1)

dengan g adalah kecepatan gravitasi.

Untuk dua dekade terakhir, sejumlah matematikawan telah dan sedang menyelidiki tentang sifat-sifat struktur kualitatif pada sistem persamaan diferensial biasa. Dalam artikel ini akan paparkan hasil kajian kestabilan dari sistem bandul ganda untuk suatu waktu tertentu. Suatu sistem persamaan diferensial dapat diketahui kestabilannya dengan melakukan penyelidikan terhadap solusinya melalui pemberian nilai awal yang terletak pada persekitaran titik kesetimbangannya. Titik kesetimbangan adalah titik yang menyebabkan setiap persamaan penyusun sistem berniali nol6) _{. Suatu sistem dikatakan}

stabil jika diberikan suatu nilai awal yang dekat dengan titik kesetimbangan, maka solusinya juga cukup dekat dengan titik kesetimbangan tersebut. Sebaliknya, jika solusi sistem persamaan diferensial jauh dari titik kesetimbangan, maka sistem tersebut dikatakan tak stabil. Pada beberapa kasus sistem menuju titik kesetimbangannya. Jika terjadi demikian, maka sistem tersebut dikatakan stabil asimtotis. Dengan diketahui (kapan dan dimana) sistem tersebut stabil, maka akan diketahui pula prilaku sistem dan sifat-sifat nya. Sifat kualitatif yang dimaksud antara lain : kestabilan, keterkendalian dan keterobservasian6)_.

2. METODE PENELITIAN

Metode yang digunakan dalam penelitian ini adalah studi pustaka/literatur. Adapun langkah-langkah yang ditempuh adalah:

1. Mengubah bentuk persamaan sistem bandul ganda (1) (sistem PDB orde dua) menjadi bentuk sistem linear (sistem PDB orde satu) dengan mengambil permisalan yang sudah baku1) _.

2. Menentukan matriks koefisien untuk sistem linear yang terbentuk oleh langkah 1.

3. Menetukan nilai- eigen matriks koefisien sistem linear untuk kemudian dikaji kestabilan sistem dengan menggunakan teorema kestabilan sistem linear.

4. Menentukan solusi umum dari sistem pendulum ganda yang selanjutnya digambar potret fasenya berdasarkan solusi khususnya.

3. HASIL DAN PEMBAHASAN

Tinjau sistem bandul ganda yang direpresentasikan oleh model matematika sistem persamaan diferensial biasa orde dua (1). Misalkan

a

(m1 m2)l1g

b

(m1 m2)l12

j

m₂ l₁l₂

h

m2 l2g (2)

j

m2 l1l2

(3)

J. Sains MIPA, Edisi Khusus Tahun 2008, Vol. 14, No. 1

dengan a, b, j, h, dan k > 0

Oleh karena itu sistem persamaan (1) menjadi b 1 j 2 a 1

j 1 k 2 h 2 (3) Misalkan x₁ ₁,

x

₂ ₁ , x₂ ₁ , x₃ ₂, x₄ ₂ , dan x₄ ₂ . Persamaan (3) menjadi x1 1 x2 2 1 2 1 2 2 2 1 2 x3 bk j jh x bk j ak bk j jh bk j ak x 4 2 3 x x (4) 3 2 1 2 2 2 1 2 2 4 x bk j bh x bk j aj bk j bh bk j aj x

Dalam bentuk matriks sistem persamaan (4) menjadi:

2 2 1 1 1 1 2 2 2 2 1 2 3 4 3 3 3 2 2 4 4 4

0

1

0

0 ,

,

0

1

0

T T T

ak

aj

x

j

bk

x

j

bk

x

jh

x

bh

j

bk

j

bk

x

3 4 T

x

atau x Ax

(5) dengan 4 3 2 1 x x x x x , 0 0 1 0 0 0 0 0 0 0 1 0 2 2 2 2 bk j bh bk j aj bk j jh bk j ak A , dan 4 3 2 1 x x x x x .

Untuk menyelidiki kestabilan sistem (5) , digunakan teorema uji kestabilan berikut ini. Teorema Kesetabilan7)

Jika diberikan sebuah sistem linear (5) dengan A adalah matriks konstan berukuran nxn dengan nilai eigen-nilai eigen

n

,...,

,

₂

1 yang berbeda dan

k

n

, maka berlaku pernyataan berikut:

1. Sistem (5) stabil jika Re _i < 0, untuk i = 1,2, ,k. Kemudian untuk setiap nilai eigen _i dengan Re _i = 0 memiliki vektor eigen-vektor eigen yang bebas linier, maka sistem (5) stabil netral. Jika tidak demikian maka sistem (5) tak stabil.

2. Sistem (5) tak stabil jika terdapat _i sedemikian hingga Re _i > 0 untuk i = 1,2, ,k.

3. Sistem (5) stabil asimtotis jika dan hanya jika Re _i < 0, untuk i = 1,2, ,k.

(4)

Tabel 1. Hasil dari Teorema Kestabilan

Nilai eigen Tipe titik kesetimbangan Jenis kestabilan A. Real

1. Berbeda dan positif 2. Berbeda dan negatif 3. Berlawanan tanda 4. Sama dan positif 5. Sama dan negatif

Simpul improper Simpul improper Titik sadel Simpul proper/improper Simpul proper/improper Tak stabil Stabil asimtotis Tak stabil Tak stabil Stabil asimtotis B. Kompleks ( = a + ib) 1. a < 0 2. a = 0 3. a > 0 Titik spiral Fokus Titik spiral Stabil asimtotis Stabil netral Tak stabil Adapun nilai eigen A untuk sistem (5) adalah

2 ) ( 4 ) ( 2 2 2 1 bk j bk j ah ak bh ak bh

(6) 2 ) ( 4 ) ( 2 2 2 2 bk j bk j ah ak bh ak bh

(9)

Mengacu pada teorema kestabilan maka sistem persamaan (5), akan menjadi suatu sistem yang stabil netral untuk nilai eigen _i kompleks dengan Re _i 0. Dengan demikian ₁ sampai dengan ₄ pada persamaan (6 9) akan ditunjukkan bahwa hanya memiliki nilai yang imajiner.

Tinjau persamaan (6) berikut:

2 ) ( 4 ) ( 2 2 2 1 bk j bk j ah ak bh ak bh

Dengan menggunakan sifat

2

b a

ab atau (a b) 2 ab

untuk a, b > 0. persamaan (6) disederhanakan menjadi bk j bk j ah ak bh ak bh 2 2 2 ) ( 4 ) 2 ( 2 2 1 bk j j ah ak bh ak bh ak bh 2 2 4 4 4 2 2 1

(5)

bk j j ah ak bh 2 2 4 2 2 1 bk j j ah ak bh 2 2 2 2 2 1 bk j j ah ak bh 2 2 2 2 1 bk j j ah ak bh 2 2 2 2 1 bk j j ah ak bh 2 2 1 (10) Suku bk j j ah ak bh 2 2

bernilai imajiner dengan ba2h2j2k

bernilai positif dan

j

2

bk

bernilai negatif.

Substitusikan (2) ke (10) diperoleh )] ( [ ) ( ) )( )( ( ) )( ( 1 ₂ 2 2 2 1 2 2 1 1 2 2 2 1 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 1 2 1 1 2 1 2 2 1 1 l m l m l m l l m l m l l m g l m g l m g l m l m l m 2 2 2 1 2 2 2 2 1 2 1 2 2 2 1 2 2 2 6 2 2 1 5 2 2 4 1 3 2 2 4 1 2 2 1 2 4 1 2 2 1 2 4 1 3 1 3 3 ) ( ) ( 1 l l m l l m m l l m g l l m g l m g l m m g l m m g l m 2 2 2 1 2 1 4 6 2 6 1 8 2 4 6 2 6 1 7 2 1 4 6 2 6 1 6 2 2 1 4 6 2 6 1 5 2 3 1 3 3 1 l l m m g l l m g l l m m g l l m m g l l m m Karena 6 4 2 6 1 8 2 4 6 2 6 1 7 2 1 4 6 2 6 1 6 2 2 1 4 6 2 6 1 5 2 3 1m l l g 3m m l l g 3mm l l g m l l g

m bernilai positif dan 2

2 2 1 2 1ml l m bernilai negatif, maka 2 2 2 1 2 1 4 6 2 6 1 8 2 4 6 2 6 1 7 2 1 4 6 2 6 1 6 2 2 1 4 6 2 6 1 5 2 3 1 3 3 l l m m g l l m g l l m m g l l m m g l l m m bernilai imajiner. Oleh karena itu (6) hanya memiliki nilai imajiner, tanpa adanya suku bernilai real (Re 1 0).

Untuk pembuktian ₂ sampai ₄ dapat dilakukan dengan cara yang sama seperti ₁.

Dengan menggunakan metode matriks, maka sistem persamaan (4) dapat dicari penyelesaian umumnya. Adapun persamaan karakteristik dari sistem (4) adalah

2 2 2 2

0

1

0

1

0

i i i i

ak

jh

j

bk

j

bk

aj

bh

j

bk

j

bk

(11)

(6)

Konstanta-konstanta A₁,A₂,A₃,A₄ dari penyelesian (5) memenuhi sistem (a₁₁ _i)A₁ a₁₂A₂ a₁₃ A₃ a₁₄ A₄ 0 a₂₁A₁ (a₂₂ _i)A₂ a₂₃A₃ a₂₄A₄ 0

(12) a₃₁A₁ a₃₂ A₂ (a₃₃ _i)A₃ a₃₄A₄ 0 a₄₁A₁ a₄₂ A₂ a₄₃A₃ (a₄₄ _i)A₄ 0 dengan

4 ,

3 ,

2 ,

1 i

, , 0 , , 0 , 0 , 1 , 0 ₁₂ ₁₃ ₁₄ ₂₁ ₂ ₂₂ ₂₃ ₂ 11 bk j jh a a bk j ak a a a a a 0 , , 0 , , 1 , 0 , 0 , 0 , 0 ₃₁ ₃₂ ₃₃ ₃₄ ₄₁ ₂ ₄₂ ₄₃ ₂ ₄₄ 24 a bk j bh a a bk j aj a a a a a a . Misalkan, bk j bh bk j aj bk j jh bk j ak 2 2 2 1 2 1 2 1 , , , .

Kemudian substitusikan nilai-nilai

a

₁₁

,

a

₁₂

,

a

₁₃

,

...

,

a

₄₄ ke (12), diperoleh

d₁( _i) bilangan real 2 2 1 1 2 ) ( ) ( ) ( i i i d d

i i i i d d 2 2 1 1 3 ) ( ) ( ) (

(13) i i i i i d d 1 2 2 2 2 1 1 4 ) ( ) ( ) ( ) ( .

)

,

(

_i _i j

d

adalah eigen vektor kolom, dengan i = j = 1, 2, 3, 4 Sehingga penyelesaian umum dari sistem persamaan (4) berbentuk

t t t t t t t t t t t t t t t t e d e d e d e d C e d e d e d e d C e d e d e d e d C e d e d e d e d C x x x x 4 4 4 4 3 3 3 3 2 2 2 2 1 1 1 1 ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 4 4 4 3 4 2 4 1 4 3 3 3 3 3 2 3 1 3 2 4 2 3 2 2 2 1 2 1 4 1 3 1 2 1 1 1 4 3 2 1

dengan C1,C2,C3,C4 konstanta-konstanta sebarang. Contoh Kasus

Untuk mengetahui kestabilan pada sistem bandul ganda, diberikan contoh sebagai berikut. Diketahui m1 937.5slugs,m2 312.5slugs, l1 16kaki,l2 16kaki, g 32ft_sec2 dan

sec 0 . 2 ) 0 ( , sec 0 . 1 ) 0 ( , 0 . 1 ) 0 ( , 5 . 0 ) 0 ( 2 1 2

1 rad rad rad rad . Dengan mensubstitusikan nilai-nilai

yang diketahui ke (2) didapatkan a = 64 , b = 32 , j = 8 , h = 16 , j = 8 , dan k = 8. Dari nilai-nilai tersebut dapat dicari solusi ₁ dan ₂ dengan cara sebagai berikut.

Aturan Crammer memberlakukan

k j j b k h j a 2 1 1 = 8 8 8 32 8 16 8 64 2 1 = ₁ 192 512 + ₂ 192 128

(7)

atau 1 = 2 1 3 192 128 192 512 x x x .

Selain itu, aturan Crammer juga memberlakukan

k j j b h j a b 2 1 2 1 2 1 2

32

64

8

16

512

512 32 8

192

8

atau 3 1 4 2 192 512 192 512 x x x .

Dengan notasi matriks persamaan ₁ dan ₂ dapat ditulis sebagai berikut:

0 192 152 0 192 512 , 1 0 0 0 , 0 192 128 0 192 512 , 0 0 1 0 4 3 2 1 x x x x . Sehingga 0 192 512 0 192 512 1 0 0 0 0 192 128 0 192 512 0 0 1 0 A

Nilai eigen A diperoleh dari perhitungan

3 2 , 3 2 , 2 , 2 0 ) 3 2 ( ) 3 2 ( ) 2 ( ) 2 ( 0 ) ( det 4 3 2 1 i dan i i i i i i i I A

Karena Re

i

0

, maka berdasarkan teorema kestabilan dapat disimpulkan kasus (1) stabil netral.

Dengan mengunakan metode matriks, maka kasus di atas dapat dicari penyelesian umumnya. Adapun persamaan karakteristiknya adalah i i i i 0 192 512 0 192 512 1 0 0 0 0 192 128 0 192 512 0 0 1 0

dan akar-akar karakteristiknya adalah

3 2 , 3 2 , 2 , 2 ₂ ₃ ₄ 1 i dan i i

i . Konstanta-konstanta A1 ,A2,A3,A4 dari penyelesian di atas memenuhi sistem (12), dengan

a

11

0 ,

a

12

1 ,

a

13

0 ,

a

14

0 ,

(8)

Amanto dan La Zakaria Solusi Eksak dan Kestabilan , 192 512 , 1 , 0 , 0 , 0 , 0 , 192 128 , 0 , 192 512 41 34 33 32 31 24 23 22 21 a a a a a a a a a 0 , 192 512 , 0 ₄₃ ₄₄ 42 a a

a . Substitusikan nilai-nilai

a

₁₁

,

a

₁₂

,

a

₁₃

,

...

,

a

₄₄ ke (12). Kemudian pilih

8

1 )

(

,

8

1 )

(

,

8

1 )

(

,

8

1 )

(

₁ ₁ ₂ ₁ ₃ ₁ ₄ 1

d

lalu disubstitusikan ke (13) diperoleh penyelesaian

umumnya 3 2 3 2 3 2 3 2 4 3 2 3 2 3 2 3 2 3 2 2 2 2 2 2 2 2 2 1 4 3 2 1 3 16 3 8 4 1 8 1 3 16 3 8 4 1 8 1 16 8 4 1 8 1 16 8 4 1 8 1 it it it it it it it it t i t i t i t i t i t i t i t i e i e i e e C e i e i e e C e i e i e e C e i e i e e C x x x x 2 2 2 2 2 1 2 2 2 2 1

16

8

4

1

8

1

16

8

4

1

8

1 ]

[

t

e

i

e

i

e

C

e

i

e

i

e

C

x

it it it it it it it it 4 3 2 3 2 3 2 3 2 3 3 2 3 2 3 2 3 2 3 16 3 8 4 1 8 1 3 16 3 8 4 1 8 1 C e i e i e e C e i e i e e it it it it it it it it

Untuk

x

₃ dengan menggunakan MATHEMATICA dan memilih

4

1 )

(

)

(

)

(

)

(

1 1 2 1 3 1 4 1

d

, lalu

disubstitusikan ke (10) diperoleh penyelesaian umumnya

2 2 2 2 2 1 2 2 2 2 3 8 4 2 1 4 1 8 4 2 1 4 1 ] [t e e ie ie C e e ie ie C x i t it it it it it it it 4 3 2 3 2 3 2 3 2 3 3 2 3 2 3 2 3 2 3 8 3 4 2 1 4 1 3 8 3 4 2 1 4 1 C e i e i e e C e i e i e e it it it it it it it it

dengan

C

₁

,

C

₂

,

C

₃

,

C

₄ konstanta-konstanta sebarang.

Karena pada (4) x₁ ₁ dan x₃ ₂ maka

x

₁ dan

x

₃ adalah solusi dari ₁ dan ₂. Gambar 2 berikut merupakan visualisasi kestabilan pada ₁

Gambar 9. Kondisi Kestabilan pada ₁

Gambar 2. menunjukkan bahwa ₁ < 0.5 sistem menuju titik kestabilan pada titik 0.2 ,dan pada 0.5 < ₁ < 3 sistem menuju titik kestabilan pada titik 2.

0 0.5 1 1.5 2 2.5 3 0 0.5 1 1.5 2 2.5 3

(9)

Gambar 3 berikut merupakan visualisasi kestabilan pada ₂

Gambar 3. Kondisi kestabilan pada ₂

Gambar 3 menunjukkan bahwa 0 < ₂ < 2 Sistem menuju titik kestabilan pada titik 0.4 , sedangkan ₂ > 2 Sistem menjauhi titik kestabilan. Kestabilan antara ₁ dan ₂ , dapat dilihat dari gambar berikut:

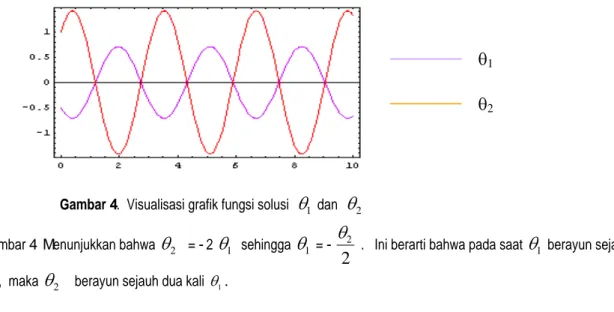
Gambar 4. Visualisasi grafik fungsi solusi ₁ dan ₂ Gambar 4 Menunjukkan bahwa ₂ = - 2 ₁ sehingga ₁ = -

2

. Ini berarti bahwa pada saat ₁ berayun sejauh 0.5, maka ₂ berayun sejauh dua kali 1.

4. KESIMPULAN

Sifat kestabilan sistem bandul ganda dapat diketahui melalui nilai eigen dari matriks sistem PDB linear yang terbentuk dengan menggunakan teorema uji kestabilan sistem. Sistem bandul ganda yang dapat merepresentasikan sistem kerja Tim SAR dan suplai makanan atau amunisi ke barak menggunakan Helikopter merupakan sistem yang stabil netral, sebab nilai eigennya berupa bilangan kompleks dengan bagian real bernilai nol . Hal ini berarti sistem bandul ganda pada suatu waktu tertentu akan mendekati titik kesetimbangannya.

UCAPAN TERIMAKASIH

Penelitian ini dapat dilaksananakan dengan baik berdasarkan bantuan dana dari Hibah Penelitian (Research Grant) yang diprogramkan Program Hibah Kompetisi (PHK) A2 Jurusan Matematika FMIPA Universitas Lampung. Oleh karena itu, penulis mengucapkan terima kasih yang sebesar-besarnya kepada pengelola PHK A2 Jurusan Matematika atas segala bantuan yang telah diberikan.

DAFTAR PUSTAKA

1. Amanto, 2005. Analisis Keterobservasian Sistem Gerak Kereta Sederhana Dengan Dua Pendulum Terbalik. Jurnal

Sains dan Teknologi 11(2) : 101 104.

1 2 0 0 . 5 1 1 . 5 2 2 . 5 3 0 0 . 5 1 1 . 5 2 2 . 5 3

(10)

2. Cobb, J.D. 1984. Controllability, observability and duality in singular syastem. IEEE Trans Aut. Control, AC-29 (12) : 1076 1082.

3. Shinbrot, 1992. Chaos in a double pendulum. Am. J. Phys. 6 (60) : 491 499.

4. iordano dan Weir. 1994. Differential Equations A Modeling Approach. Addison-Wesley, Publishing Company. 5. Amanto, La Zakaria dan Saidi, S. 2003. Uji kestabilan sistem perang gerilya. Prosiding Seminar Nasional Hasil

Penelitian MIPA dan Pendidikan MIPA, Universitas Negeri Yogyakarta : 107 111.

6. Olsder, G.J. 1994. Mathematical Systems Theory First Edition. Delftse Uitgevers Maatschappij, Delft, Netherlands. 7. Braun, M. 1983. Diffrential Equation And Their applications. Third Edition. Springer-Verlag, New York.