i UJI KUASA (UMP-TEST) UNTUK PARAMETER DISTRIBUSI
DALAM KELUARGA EKSPONENSIAL SKRIPSI
Diajukan Untuk Memenuhi Sebagian Persyaratan Mencapai Derajat Sarjana S-1
OLEH HIJRAWATI
F1A1 11 051
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS HALU OLEO
KENDARI 2016
iii KATA PENGANTAR
Alhamdulillah, puji dan syukur penulis panjatkan kehadirat Allah Subhanahu Wa Ta’ala sehingga penyusunan tugas akhir ini yang berjudul “Uji Kuasa (UMP-TEST) Untuk Parameter Distribusi Dalam Keluarga Eksponensial” dapat terselesaikan dan tersusun sebagaimana mestinya. Tugas akhir ini merupakan sebagian persyaratan dalam penyelesaian tahap pendidikan sarjana S-1 pada jurusan Matematika Fakultas MIPA Universitas Haluoleo.
Penulis menyadari bahwa dalam penulisan tugas akhir ini tidak dapat terselesaikan tanpa bimbingan dan arahan dari berbagai pihak. Oleh karena itu, penulis mengucapkan terimah kasih dan penghargaan yg setinggi-tingginya kepada Bapak Dr.rer.nat Wayan Somayasa, S.Si., M.Si selaku pembimbing I dan Ibu Rahmaliah Sahupala, S.Si., M.Sc selaku pembimbing II yang telah banyak meluangkan waktunya untuk membimbing dan mengarahkan serta memberikan dorongan dan motivasi kepada penulis sejak dari perencanaan hingga terselesaikannya tugas akhir ini.
Melalui hasil karya ini secara khusus dan dengan hati yang tulus penulis persembahkan untuk ayahanda tersayang ABDUL RAHMAN dan ibunda tercinta NURBAETI yang telah mendukung dan memberikan restu, motivasi serta doa yang tak pernah putus, tulus dan ikhlas demi kesuksesan penulis, saudara-saudaraku k’niar (mamanya ai), Trialviani (via), dan Asmaul Husna (ika)serta
iv saudari iparku k’anto(bapakya ai) yang selalu memberikan dukungan semangat untuk menyelesaikan tugas akhir ini.
Ucapan terima kasih juga penulis haturkan kepada berbagai pihak yang secara langsung membantu penulis selama menjalani perkuliahan dan dalam penyusunan tugas akhir inikhususnya kepada:
1. Rektor Universitas Halu Oleo Kendari, Bapak Prof. Dr. Ir. H. UsmanRianse, M.S.
2. Dekan F-MIPA Universitas Halu Oleo, Bapak Dr. Muh. Zamrun F., S.Si., M.Si., M.Sc.
3. Ketua Jurusan Matematika dan sekretaris jurusan F-MIPA Universitas Halu Oleo, Bapak La Gubu, S.Si., M.Si., dan Bapak Rasas Raya, S.Si., M.Si. 4. Kepala Laboratorium Matematika F-MIPA Universitas Halu Oleo, Ibu
Norma Muchtar, S.Si., M.Si.
5. Ibu Norma Muchtar, S.Si., M.Si. selaku penasehat akademik yang telah memberikan pengarahan dan bimbingan dalam memprogramkan mata kuliah. 6. La Gubu, S.Si., M.Si., Drs. Asrul Sani, M.Sc., Ph.D dan Dr. Ruslan, S.Si.,
M.Si., selaku dewan penguji.
7. Bapak dan Ibu Dosen Jurusan Matematika serta seluruh staf lingkungan F-MIPA UHO..
8. Rekan-rekan seperjuanganku di “Somayasa Divisi”, Riska Juliani, Ridayani, Cakra Pusnawati, Mega puspita sari, Sartika, Peni saputra, Nini Karlis Kartini.F, dan Wayan Eka Murtiawan, atas kebersamaan dan saling mendukung satu sama lain.
v 9. Teman-temanMath 011: Kalvin, Rahmat, Edi, Ion, Raful, Anty, Nining, Cici, Ririn,Wahyu, Ayu, Naim, Lia, Paulina, Takim, Arif, Nisfa, Tendri, linda, Phepez, dan lain-lain yang telah memberikan dorongan moral dan spiritual serta kebersamaan yang tidak terlupakan.
10. Sepupu-sepupuku yang cantik Uni (ndut), lili , mamanya Naya, Waone, serta seluruh keluarga besarku atas dukungan dan motifasinya.
11. Kakak-kakak Senior Math-09 dan Math-10, terima kasih atas bantuan dan saranya selama ini.
12. Junior Matematika Angkatan 2012 dan 2013 semuanya yang tidak dapat disebutkan satu persatu.
13. Teman-teman KKN didesa LAKALAMBA, MUNA BARAT: Nisa, Inda, K’gina, Mahrum, Haris, k’yuspin, Saslin dan Saslin Serta seluruh keluarga besar Desa Lakalamba Kec. Sawerigadi Kab. Muna Barat.
14. Terspesial buat Ayamin Musri Suriyamin (kak AMS) terimakasih atas dukungan dan motivasinya selama ini, dan juga menjadi salah satu sumber inspirasiku.
vi Selanjutnya penulis menyadari bahwa penulisan tugas akhir ini masi jauh dari kata kesempurnaan. Sehingga dengan senang hati dan segala kerendahan hati penulis menerima segala saran yang sifatnya membangun demi pentempurnaanya. Akhir kata penulis berharab semoga tugas akhir ini dapat bermanfaat bagi semua pihak yang membutuhkan.
Kendari, Maret 2016
vii DAFTAR ISI
Halaman
HALAMAN JUDUL ... i
KATA PENGESAHAN ... ii
KATA PENGANTAR ... iii
DAFTAR ISI ... vii
ABSTRAK ... ix ABSTRACT ... x BAB I PENDAHULAN 1.1 Latar Belakang... 1 1.2 Rumusan Masalah ... 4 1.3 Tujuan Penelitian ... 4 1.4 Manfaat Penelitian ... 4
BAB II LANDASAN TEORI 2.1 Variabel Acak ... 5
2.2 Fungsi Distribusi Peluang... 6
2.1.2 Pengertian Fungsi Distribusi Peluang ... 6
2.3 Distribusi Keluarga Eksponensial ... 6
2.4 Uji Hipotesis ... 9
2 4.1 Langkah-Langkah Pengujian Hipotesis ... 10
2 4.2 Kesalahan Tipe I dan Kesalahan Tipe II ... 10
2 4.3 Konsep Umum Dari Pengujian Hipotesis... 12
2 4.4 Tes UMP untuk Hipotesis Sederhana ... 13
2 4.5 Tes UMP untuk Hipotesis Komposit ... 14
BAB III METODOLOGI PENELITIAN 3.1 Waktu dan Tempat Penelitian ... 16
3.2 Metode Penelitian ... 16 3.3 Prosedur Penelitian ... 16 BAB IV PEMBAHASAN 4.1 Distribusi Binomial ... 18 4.2 Distribusi Poisson ... 19 4.3 Distribusi Normal... 19
viii
4.4 Distribusi Gamma ... 20
4.5 Tes UMP untuk Hipotesis Sederhana ... 21
4.6 Tes UMP untuk Hipotesis Komposit ... 24
4.7 Keluarga Monotone Likelihood Ratio ... 25
4.8 Tes UMP Terhadap Model Distribusi Keluarga Eksponensial30 4.9 Informasi Data ... 34
BAB V PENUTUP 5.1 Kesimpulan ... 40
5.2 Saran ... 40
ix UJI KUASA (UMP-TEST) UNTUK PARAMETER DISTRIBUSI DALAM
KELUARGA EKSPONENSIAL
Oleh
HIJRAWATI F1A1 11 051
ABSTRAK
Penelitian ini membahas tentang Uji Kuasa Seragam untuk Parameter Distribusi dalam Keluarga Eksponensial. Uji Kuasa Seragam(Uniformaly Most Powerfull-Test) disingkat (UMP-Test) digunakan untuk melakukan pengujian terhadap hipotesis H0 pada tingkat signifikansi α=5% apakah akan diterima atau ditolak. Ada 2 macam hipotesis yaitu hipotesis H0dan H1. Sehubungan dengan perumusan hipotesis ini dapat dirumuskan 2 kekeliruan yaitu : menolak hipotesis yang seharusnya diterima disebut kesalahan alfa(α), dan menerima hipotesis yang seharusnya ditolak disebut kesalahan beta(β). Selanjutnya Uji Kuasa UMP-Test diterapkan pada data sekunder yang diperoleh dari nilai ujian mata kuliah Statistika Matematika II dari Populasi Mahasiswa Jurusan Matematika. Dengan menggunakan uji hipotesis H0: dan H1 : dengan α sebesar 5%, maka diperoleh kuasa uji untuk sebesar ̅ . Dari nilai yang diperoleh tersebut dapat disimpulkan bahwa H0 ditolak.
Kata Kunci :Uji Kuasa Seragam (UMP-Test), Keluarga Eksponensial, Keluarga Monoton Likelihood Ratio, Hipotesis.
x UNIFORMLY MOST POWERFUL TEST FOR SOME DISTRIBUTION
PARAMETERS IN EXPONENTIAL FAMILY
By
HIJRAWATI F1A1 11 051
Abstract
This research discusses about uniformly most powerful test ( UMP-Test) for some parameters of distribution in exponential family, ump-test Is used to test the hypotheses a level of significance α=5% whether it will be accepted or not, there are two kind of hypotheses and . Correspondingly there two types of errors caused by the rejection of the hypotheses. That is type I error appears by the rejection of the two and type II error appears when we attempt to apply the ump test procedure to a data presenting two score of student for the lecture mathematical statistic II. Considniy the hypotheses H0: vs H1 : whit α=5% we obtain that ̅ which leads to the rejection of .
Keywords: Uniformly Most Powerful Test(UMP-Test), exponential family, the monotonous likelihood ratio,hypotheses.
1 BAB I
PENDAHULUAN 1.1 Latar Belakang
Statistika merupakan pengetahuan yang berhubungan dengan teknik pengumpulan data, pengolahan atau penganalisanya dan penarikan kesimpulan berdasarkan kumpulan data dan penganalisa yang dilakukan (Sudjana, 1996).
Statistika dibagi menjadi dua yakni statistika deskriptif dan statistika inferensial. Statistika deskriptif merupakan metode-metode yang berkaitan dengan pengumpulan dan penyajian sekumpulan data, sehingga dapat memberikan informasi yang berguna. Statistika inferensial merupakan cabang statistika yang berkenaan dengan cara penarikan kesimpulan berdasarkan data yang diperoleh dari sampel untuk menggambarkan karakteristik atau ciri dari suatu populasi (Supranto, 1985). Statistika inferensial dapat dibedakan menjadi dua yaitu estimasi parameter dan uji hipotesis. Estimasi parameter dibedakan menjadi dua yaitu estimasi parameter titik dan estimasi parameter interval(Walpole dan Myers, 1995).
Masalah pada estimasi titik adalah mendapatkan suatu harga dugaan dari suatu parameter. Pada beberapa situasi sering dihadapkan dengan masalah memilih satu tindakan diantara dua pilihan. Sebagai contoh, perusahaan obat menganggap bahwa pasar obat produk baru untuk menyembuhkan penyakit dibandingkan obat yang telah ada mempunyai tingkat penyembuhan sebesar 60%. Berdasarkan pada percobaan terbatas, divisi penelitian mengklaim bahwa obat baru lebih efektif. Jikaobat tersebut gagal lebih efektif atau mempunyaiefek
2 samping yang membahayakan, maka akan kehilangan pelanggan yang disebabkan oleh kekunoan produk akan lebih kecil pengaruhnya dibandingkan dengan kegagalan yang diakibatkan oleh ketidak-efektifan obat yang baru. Dalam hal ini diperlukan suatu uji yang cermat, pemilihan keputusan seperti ini diperlukan teori uji hipotesis(Widiharih, 2009).
Hipotesis adalah asumsi atau dugaan mengenai sesuatu hal yang dibuat untuk menjelaskan hal itu yang sering dituntut untuk melakukan pengecekan. Jika asumsi atau dugaan itu dikhususkan mengenai populasi, umumnya mengenai nilai-nilai parameter populasi, maka hipotesis itu disebut hipotesis statistik. Setiap hipotesis bisa benar atau tidak benar dan karenanya perlu diadakan penelitian sebelum hipotesis itu diterima atau ditolak. Langkah atau prosedur untuk menentukan apakah menerima atau menolak hipotesis dinamakan pengujian hipotesis (Sudjana, 1996).Tujuan dari uji hipotesis adalah memutuskan berdasarkan sampel dari populasi, dimana dari dua hipotesis yang saling asing yang benar, yaitu hipotesis nol dinotasikan dan hipotesis alternatif dinotasikan
(Widiharih, 2009).
Pada setiap eksperimen yang melibatkan pengamatan pasti ada kesalahan yang berimbas pada proses pengambilan keputusan terhadap , yaitu kesalahan
tipe I (menolak padahal benar) dan kesalahan tipe II (tidak menolak padahal salah) (Somayasa, 2008). Sayangnya, dengan ukuran sampel yang
tetap, maka hal ini tidak dapat dilakukan. Hal yang dapat dilakukan adalah memilih ukuran tertentu untuk tingkat keberartian yang diperlukan biasanya α diambil0,005;0,001; 0,05; 0,01 dan mencari uji yang memaksimumkan kuasa.
3 Untuk uji tingkat α yang memaksimumkan kuasa uji diantara semua uji tingkat α dikatakan uji paling kuasa seragam (Uniformaly Most Powerfull Test = UMP-Tes).(Setiawan, 2006).
Ada beberapa macam metode penentuan kriteria uji tergantung dari bentuk hipotesis yang diambil. Dalam hal ini akan dibahas tentang uji paling kuasa seragam (Uniformaly Most Powerfull Test = UMP-Tes) untuk parameter dalam keluarga eksponensial. Cara untuk menentukan uji paling kuasa seragam ini pertama-tama menentukan rasio seperti pada uji Pearson. Uji Neyman-Pearson merupakan suatu metode untuk menentukan uji paling kuasa seragam, kadang-kadang juga merupakan uji paling kuasa seragam bila hipotesis alternatifnya berbentuk komposit satu sisi dengan harga sebarang dan kemudian ditunjukkan bahwa uji tidak bergantung pada harga hipotesis alternatif yang spesifik (Widiharih, 2009).
4 1.2 Rumusan Masalah
Dalam penulisan tugas akhir ini, rumusan masalah berdasarkan latar belakang diatas yaitu bagaimana cara merumuskan prosedur uji paling kuasa untuk parameter distribusi dalam keluarga Eksponensial khususnya distribusi Normal. 1.3 Tujuan Penelitian
Adapun tujuan dari penelitian ini berdasarkan rumusan masalah diatas adalah memperoleh metode UMP-Test dengan menggunakan model distribusi dalam keluarga Ekspoensial.
1.4 Manfaat Penelitian.
Adapun manfaat dari penelitian ini diharapkan dapat memberikan kontribusi bagi pembaca dalam menyelesaikan masalah-masalah yang berkaitan dengan statistika khususnya metode UMP-Test untuk distribusi dalam keluarga Eksponensial.
5 BAB II
TINJAUAN PUSTAKA 2.1 Variabel Acak
Definisi 1:
Variabel acak dilambangkan dengan huruf besar misalnya X,Y, dan Z. Misalkan S merupakan suatu ruang sampel dari suatu percobaan statistika maka variabel acak didefinisikan sebagai fungsi yang memetakan setiap anggota dari S ke himpunan bilangan real dengan kata lain, variabel acak adalah suatu cara mengangkakan setiap anggota dari ruang sampel S.
Variabel acak dibedakan menjadi dua jenis, yaitu varibel acak diskrit dan variabel acak kontinu.Variabel acak diskrit adalah variabel acak yang mempunyai nilai-nilai terhitung (countable). Jadi, variabel acak diskrit dapat bernilai . Sedangkan variabel acak kontinu adalah variabel acak yang nilai-nilainya tak terhitung (uncountable). Jadi nilai-nilai vaiabel acak kontinu dapat merupakan semua nilai dalam satu interval terhingga, yaitu , dimana banyaknya bilangan yang terkandung pada interval tersebut adalah tak terhingga atau tak terbilang (Walpole dan Myers, 1995).
6 2.2 Fungsi Distribusi Peluang
2.2.1 Pengertian Fungsi Distribusi Peluang Definisi 2 :
Himpunan pasangan terurut * ( )+ merupakan fungsi peluang atau distribusi peluang variabel acak diskrit jika untuk setiap kemungkinan hasil memenuhi:
1. ( )
2. ∑ ( )
3. ( ) ( )
Definisi 3 :
Jika X adalah suatu variabel acak kontinu, maka ( ) disebut fungsi padatan peluang dari peubah acak X, jika memenuhi :
1. ( ) untuk semua . 2. ∫ ( )
3. ( ) ∫ ( )
Untuk menghitung peluang bahwa nilai amatan variabel acak akan lebih kecil atau sama dengan suatu bilangan real . Bila ( ) ( ) untuk setiap bilangan real , maka ( ) disebut sebagai fungsi distribusi (kumulatif) variabel acak (Walpole dan Myers, 1995).
2.3 Distribusi Keluarga Eksponensial
Suatu variabel acak Y dengan fungsi kepadatan peluang ( ) dan parameter dikatakan menjadi anggota distribusi keluarga eksponensial jika dapat
7 dinyatakandalam bentuk umum distribusi keluarga eksponensial. Penentuan statistic cukup bagi suatu parameter dapat dilakukan dengan menggunakan keluarga eksponensial.
1. Suatu fkp dengan satu parameter dikatakan termasuk dalam keluarga eksponensial. Jika fkp tersebut dapat diuraikan dalam bentuk:
( ) ( ) , ( ) ( )- ( )
2. Jika merupakan sampel acak yang berasal dari distribusi dengan fkp gabunganya dinotasikan dengan ( ) maka ( ) dikatakan termasuk dalam keluarga eksponensial.
Teorema 1:
misalkan variabel random saling bebas dan berdistribusi identik dengan fungsi kepadatan probabilitas merupakan anggota keluarga eksponensial 1 parameter.
1. Statistik ∑ ( ) merupakan statistic cukub untuk θ. 2. Fungsi kepadatan probabilitas dari selalu berbentuk
( ) , ( )- , ( ) - ( )
Dengan h(t) tidak bergantung pada θ asalkan variabel random distrit. 3. Jika variabel random kontinu maka fungsi kepadatan probabilitasnya dapat
8 Teorema 2:
Keluarga * ( ) + lengkap asalkan mengandung interval non degenerate. Dalam hal * ( ) dengan ( ) adalah keluarga fungsi dengan kepadatan probabilitas dari statistic cukup
Definisi 4:
Keluarga densitas disebut keluarga eksponensial k parameter bila densitas tersebut dapat dinyatakan dalam bentuk:
( ) ( ) ( ) (∑ ( ) ( )
)
Keterangan;
Dengan ( ) untuk dan
( )
( ) dan ( ) untuk himpunan nilai positif dari ( ) yang saling bebas teerhadap dimana
( )= fungsi non negatif dari x ( )= fungsi berharga nyata dari x ( ) = fungsi non negatif dari θ
9 Pada table 1 akan ditampilkan distribusi keluarga eksponensial dengan
parameternya. (Jong & Heller, 2008)
Distribusi ( ) ( ) ( ) ( ) Binomial, ( ) ( ) 1 ( ) Poisson, ( ) 1 Normal, ( ) 1 Gamma, ( ) ( ) 2.4 Uji Hipotesis
Untuk menguji hipotesis, digunakan data yang dikumpulkan dari sampel, sehingga merupakan data perkiraan (estimate). Itulah sebabnya, keputusan yang dibuat dalam menolak/tidak menolak hipotesis mengandung ketidakpastian (uncertainty), maksudnya keputusan bisa benar bisa juga salah. Adanya unsur ketidakpastian menyebabkan risiko bagi pembuat keputusan.
Dalam “menerima” atau “menolak” suatu hipotesis yang kita uji, ada satu hal yang harus dipahami, bahwa penolakan suatu hipotesis berarti menyimpulkan bahwa hipotesis itu salah, sedangkan menerima suatu hipotesis semata-mata
10 mengimplikasikan bahwa kita tidak mempunyai bukti untuk mempercayai sebaliknya (Supranto, 2001).
2.4.1 langkah-langkah pengujian hipotesis prosedur umum pengujian hipotesis:
1. Nyatakan hipotesis nol ( ) dan alternatifnya ( )
2. Menentukan statistik, hal ini tergantung pada asumsi tentang bentuk sebarang dan bentuk hipotesisnya.
3. Menentukan daerah kritis (daerah penolakan )
4. Mengambil kesimpulan, jika statistik yang dihitung terletak pada daerah penolakan maka tolak atau sebaliknya (Somayasa, 2008).
Definisi 5 :
Dua hipotesis yang saling asing dalam persoalan uji hipotesis tersebut, hipotesis nol dinotasikan dan hipotesis alternative dinotasikan .Bila menyatakan parameter populasi, menyatakan ruang parameter, format umum dari hipotesis nol dan hipotesis alternative adalah dan dengan komplemen dari jika hanya memuat satu harga yaitu * + maka hipotesis nol ( ) disebut hipotesis sederhana (simple hypothesis) dan selain itu disebut hipotesis komposit(Widiharih, 2009).
2.4.2 Kesalahan tipe I dan kesalahan tipe II
Setiap proses pengambilan keputusan tentang apakah kita menerima atau menolak suatu hipotesis, kita selalu dihadapkan pada 2 macam kesalahan pengambilan keputusan yang berbeda. Kesalahan menolak dinamakan
11 P(kesalahan tipe I) atau kesalahan ( ) sedangkan kesalahan menerima dinamakan P(kesalahan tipe II) atau kesalahan ( ) Untuk lebih jelasnya perhatikan ilustrasi berikut:
Keputusan
Hipotesis nol ( )
Benar Salah
Menolak Kesalahan tipe I ( ) Keputusan benar
Menerima Keputusan benar Kesalahan tipe II ( )
Definisi 6 :
Suatu tes untuk hipotesis adalah suatu fungsi * +, sedemikian hingga ( ) ,
( ) { ( ( ) )
Jadi merupakan fungsi penolakan dari , dimana akan ditolak jika dan tidak ditolak jika .
Definisi 7:
Fungsi power dari tes adalah suatu fungsi , - yang diberikan oleh ( ) ( | ) ( ) untuk . Selanjutnya , ukuran (size) dari adalah ( ) . Untuk suatu bilangan ( ) , tes dikatakan tes dengan signifikansi jika ( ) . Karena untuk setiap , ( ) ( ) , maka setiap tes adalah tes dengan tingkat signifikansi yang diberikan oleh ukurannya. (Lehman, 1986)
12 Definisi 8 :
Suatu hipotesis yang berbentuk untuk suatu , disebut hipotesis sederhana. Sedangkan hipotesis yang menyatakan bahwa berada pada suatu interval disebut hipotesis komposit. Jadi hipotesis yang terbentuk untuk suatu adalah hipotesis komposit. (George dan Beryer, 1990).
2.4.3 Konsep umum dari pengujian hipotesis Neyman-Pearson
J.Neyman dan E.S Pearson mengemukakan teori pengujian hipotesis pada tahun 1936 dan 1938.Suatu pernyataan berkenan dengan parameter seperti uji random atau statistik untuk pengujian hipotesis adalah fungsi terukur yang didefinisikan pada * + dan mempunyai interpretasi.disebut N-P test berukuran α untuk hipotesis sederhana jika:
Ψ ( ) {
( ) ( ) ( )
( )
untuk suatu konstanta yang memenuhi persamaan ( ) . Definisi 9 :
Misalkan ( ) , - sehingga
( ) , -
Dengan hal ini berarti bahwa ( ) dengan adalah probabilitas untuk menolak dibawah anggapan benar. untuk , ( ) adalah probabilitas tipe I berlaku ( ) dengan adalah probabilitas menerima yang dihitung dibawah anggapan salah. Jadi untuk ( ) menyatakan
13 probablitas kesalahan tipe II. Jelas bahwa, α merupakan batas atas terkecil dari probabilitas kesalahan tipe I.(Setiawan, 2006).
2.4.4 Tes UMP untuk hipotesis sederhana
Dalam kasus ini, ruang parameter hanya terdiri dari 2 titik yang dapat dituliskan sebagai dan yaitu:
* + Teorema 3 :
Misalkan variabel random salinf bebas dengan fungsi
kepadatan probabilitas ( ) * + akan diuji hipotesis pada level ( ). Misalkan
( ) ( ) ( ) ( ) ( ) ( ) ( ) dan uji yang didefenisikan sehingga
( ) {
( ) ( ) ( )
(1.1)
dengan konstan ( ) dan ditentukan sehingga
, ( )- (1.2)
Untuk menguji hipotesis melawan pada tingkat α digunakan uji seperti (1.1) dan (1.2) merupakan uji UMP.
14 Teorema 4 :
Test Neyman Pearson berukuran untuk hipotesis merupakan UMP-Test.
Tes-NP untuk hipotesis sederhana pada tingkat adalah: Ψ ( ) { ( ) ( ) ( ) ( )
2.4.5 Tes UMP untuk hipotesis komposit
Konsep dari uji paling kuasa diperluas untuk untuk kasus hipotesis alternative berbentuk komposit. Metode yang ditempuh adalah dengan mendefenisikan tes N-P berukuran untuk hipotesis sederhana . Sifat momotone likelihood ratio (MLR) yang sangat berguna untuk menentukan uji paling kuasa .
Definisi 10 :
Densitas bersama ( | ) dikatakan mempunyai sifat momotone likelihood ratio (MLR) dalam statistik ( ) jika dua harga parameter
rasio ( | ) ( | ) tergantung X hanya melalui ( ) dan rasio merupakan fungsi tidak turun dari ( ).
Teorema 5 :
Jika densitas bersama ( | ) mempunyai sifat MLR dalam statistik ( ) maka uji paling kuasa ukuran untuk adalah:
15 ( ( ) | )
dengan mengingat sifat baik dari keluarga eksponensial diantaranya sifat MLR. Teorema 6:
Jika ( ) merupakan anggota dari keluarga MLR dalam ( ) maka tes UMP berukuran untuk hipotesis
adalah :
( ) { ( ( ) )
dimana k adalah konstanta yang ditentukan dari persamaan * ( ) | +
jika nilai k yang memenuhi persamaan ini adalah , maka daerah kritik dari tes ini adalah *( ) ( ) +.
16 BAB III
METODE PENELITIAN
3.1 Waktu dan Tempat Penelitian
Penelitian ini berlangsung dari bulan januari sampai dengan maret 2016. Penelitian ini berlokasi di Laboratorium Statistika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Halu Oleo.
3.2 Materi Penelitian
Materi yang digunakan dalam penelitian ini adalah terbaik secara seragam (Uniformaly Most Power Full Test) atau tes UMP untuk parameter beberapa distribusi dalam keluarga eksponensial.
3.3 Metode dan Prosedur Penelitian
Metode yang diterapkan dalam penyelesaian penelitian ini yaitu metode kepustakaan. Metode ini digunakan peneliti untuk menyelesaikan teori-teori yang dapat mendukung pokok permasalahan yang dimunculkan pada penelitian ini, agar pembahasanya dapat diselesaikan secara tuntas. Teori-teori pendukung tersebut telah dibahas pada Bab II. Adapun langkah-langkah yang dilakukan dalam penelitian ini adalah sebagai berikut:
1. Melakukan simulasi data.
2. Menaksir parameter-parameter dalam distribusi keluarga eksponensial khususnya distribusi Normal.
17 4. Menentukan prosedur uji UMP-Test untuk parameter distribusi
dalam keluarga eksponensial hususnya distribusi normal. 5. Menarik kesimpulan.
18 BAB IV
PEMBAHASAN
Metode yang digunakan untuk memperoleh nilai uji kuasa pada distribusi keluarga eksponensial adalah metode UMP, pada penulisan ini yang akan dibahas adalah cara merumuskan uji UMP dan contoh penerapan kasusnya. Kemudian dalam teori peluang, terdapat macam-macam distribusi diantaranya distribusi binomial, poisson, normal, dan gamma. Keempat distribusi ini merupakan anggota dari keluarga eksponensial untuk menguji kebenaranya maka digunakan bentuk umum dari Teorema 1.
4.1 Distribusi Binomial
Jika adalah sampel random binomial ( ) maka ∑ ( ) . Keluarga densitas disebut keluarga eksponensial bila fungsi densitas tersebut dapat dinyatakan dalam bentuk :
( ) ( ) ( ) (∑ ( ) ( )
)
Jika ∑ ( ), maka dentitasnya adalah:
( ) . / ( ) ( )
. / ( ) ( )
. / ( ) {
19 hal ini berarti bahwa ( ) ( ) ( ) ( ) dan ( ) Maka berdasarkan bentuk umum keluarga eksponensial terbukti bahwa distribusi binomial merupakan kelurga eksponensial.
4.2 Distribusi poisson
Karna X berdistribusi poisson ( ) maka fungsi probabilitas dari X adalah:
( )
untuk sehingga ( ) dapat dinyatakan sebagai
( )
* +
hal ini berarti bahwa ( ) ( ) ( ) ( ) ( ) akibatnya distribusi poisson ( ) merupakan anggota dari keluarga eksponensial.
4.3 Distribusi Normal
Misalkan variabel random X berdistribusi ( ) fungsi kepadatan probabilitas dari Xdapat dinyatakan sebagai:
( ) √ { . / } √ { ( )} √ { } * + ( )
20 dengan ( )
√ ( ) dan ( ) . Ini berarti distribusi normal merupakan anggota keluarga eksponensial.
4.4 Distribusi Gamma
Karena berdistribusi gamma ( ) dengan maka fungsi kepadatan probabilitas dari X adalah:
( )
( )
untuk sehingga ( ) dapat dinyatakan sebagai
( )
( ) ( )
hal ini berarti bahwa ( ) ( ) ( ) ( ) ( ) akibatnya distribusi ( ) dengan diketahui merupakan anggota dari kelurga eksponensial.
21 4.5 Tes UMP untuk hipotesis sederhana
Misalkan merupakan n variabel random dengan fungsi dentitas
bersama ( ) suatu tes * + untuk hipotesis dengan disebut tes
Neyman-Pearson (tes N-P) berukuran α, jika:
( ) { ( ) ( ) ( ) ( )
Untuk setiap titik ( ) dimana , ) merupakan sembarang konstanta yang akan ditentukan dari persamaan ( ) pada definisi ini diasumsikan ( )
Teorema 4.5.1: tes diatas adalah tes UMP berukuran α
Bukti: misalkan merupakan sembarang tes berukuran α untuk hipotesis sederhana yaitu ( ) misalkan:
*( ) ( ) ( )+
*( ) ( ) ( )+
Jika ( ) , maka ( ) ini berakibat ( ) ( ) sebaliknya, jika ( ) , maka ( ) ini berakibat ( ) ( ). Maka
22 ( ) ( ) ( ) ∫( (( ) ( )) ( ) = ∫ ( (( ) ( )) ( ) + ∫ ( (( ) ( )) ( ) ∫ ( (( ) ( )) ( ) ∫( (( ) ( )) ( ) ∫( (( ) ( )) ( ) . ( ) ( )/ ( ) Jadi ( ) ( ). Contoh 4.5.2
Misalkan merupakan sampel random dari populasi berdistribusi ( ) Akan dirumuskan tes N-P berukuran α untuk hipotesis
, dimana diasumsikan . Karna
( )
23 ∑ dimana (
)
Maka daerah penolakan berukuran α diturunkan dari persamaan:
{∑
} { ∑ }
Karena ∑ berdistribusi ( )
Maka
( )jadi tes N-P berukuran α akan menolak jika ∑
( ) atau ∑ ( ) /2, untuk .
Contoh 4.5.3
Misalkan merupakan sampel random dari populasi berdistribusi ( ) . Akan dirumuskan tes N-P berukuran α untuk menguji hipotesis dimana diasumsikan Karna ( )
( ) . / {∑ . /}
∑ dimana ( )
Konstanta ditentukan dari persamaan
{∑
} {∑ ( )
24 Karna ∑ . / berdistribusi ( ) maka tes N-P berukuran akan menolak
jika ∑ . / ( ) atau ∑ ( )
Contoh 4.5.4
Misalkan merupakan sampel random dari populasi berdistribusi ( ) selanjutnya dirumuskan tes N-P berukuran α untuk menguji hipotesis dimana dirumuskan karena
( )
( ) * ( )+( ) ∑ ∑
Dimana * ( )+ ( ) perubahan “ menjadi “ karna asumsi sehingga ( ) misalkan ∑ maka dibawah berdistribusi ( )
4.6 Tes UMP untuk hipotesis komposit
Misalkan * + merupakan tes untuk hipotesis komposit untuk sembarang dengan dimana
( ) ( ) { ( ) ( ) ( ) ( )
25
Tes UMP berukuran α untuk hipotesis ini akan menolak jika ̅ ( ) tes ini tidak akan berubah selama jadi
merupakan tes N-P berukuran α yang tidak bergantung pada selama maka adalah tes UMP berukuran α untuk hipotesis . Fungsi power dari adalah :
( ) { ̅ ( ) } { ̅ ( ) }
{ ̅ ( ) } ( ). ( ) /
dimana
( )( ) adalah fungsi distribusi komulatif dari variabel ( ) .karna
( ) merupakan fungsi turun dari maka ( ) merupakan fungsi monoton naik dari sehingga berlaku ( ) ( ) .
juga merupakan tes UMP berukuran untuk hipotesis komposit .
4.7 Keluarga monotone likelihood ratio (MLR)
Misalkan mempunyai fungsi dentitas bersama ( ) dengan . Misalkan merupakan statistic. Maka ( )dikatakan dikatakan dari kelurga monotone likelihood ratio (MLR) dengan T, jika terdapat suatu fungsi non negatif ( ) sedemikian sehingga dan
26 ( )
( ) ( ( ) )
Dengan ( ( ) ) monoton naik dalam ( ).
Contoh 4.7.1
Misalkan merupakan sampel random dari ( ) dengan maka untuk berlaku :
(
)
(
)
( )
(
)
∑Misalkan ( ) ∑ karena maka ruas kanan dari persamaan diatas merupakan fungsi monoton naik dari ( ) jadi fungsi
dentitas bersama ( ) ∑ ∏ ( ) adalah dari keluarga MLR dalam ( ) ∑
Teorema 4.7.2 :
Misalkan mempunyai fungsi densitas:
( ) * ( ) ( ) ( ) ( )+
dimana h merupakan fungsi hanya dari ( ) sedangkan c dan q adalah fungsi-fungsi dari . Jika q merupakan fungsi monoton naik tegas, maka ( )merupakan anggota keluarga MLR dalam ( )
27 Bukti :
Jika maka
( )
( ) *( ( ) ( )) ( ) ( ) ( )+
Karena q merupakan fungsi monoton naik secara tegas dari , maka ruas kanan dari persamaan diatas merupakan fungsi monoton dari ( ) . Jadi ( ) merupakan anggota MLR dari T.
Contoh 4.7.3
Jika merupakan sampel random dari populasi ( ) dengan maka berlaku: ( ) √ { ∑( ) } { ̅ ∑ ( ( √ ))} = * ( ) ( ) ( ) ( )+
28 Dengan ( ) ( ) ∑ ( ) ( √ ) dengan ( ) ̅ q merupakan fungsi fungsi monoton naik tegas dari , sehingga dapat disimpulkan ( ) dari kelurga MLR dalam ̅
Teorema 4.7.4:
Jika ( ), merupakan anggota dari keluarga MLR dalam ( ) maka tes UMP berukuran α untuk hipotesis
adalah :
( ) { ( ( ) )
Dimana k adalah konstanta yang ditentukan dari persamaan * ( ) | +
Jika nilai k yang memenuhi persamaan ini adalah nilai k*, maka daerah kritisnya adalah:
*( ) ( ) k*}
Bukti:
1. merupakan tes N-P berukuran α untuk hipotesis sederhana untuk sebarang dengan , dan
29 2. Fungsi power ( ) merupakan fungsi monoton naik dari . Karena
( ) merupakan fungsi naik dari t , maka berlaku:
( ) ( ( ) ) ( )
Dimana
( )jadi tes equivalen dengan
( ) { ( ) ( ) ( ) ( ) Selanjutnya, * ( ) | + { ( ) ( ) } Jadi adalah tes N-P berukuran α untuk hipotesis . Tes tersebut tidak bergantung pada pemilihan , asalkan sehingga adalah tes UMP berukuran α untuk hipotesis bahwa fungsi power ( ) monoton naik pada . Akibat dari kemonoton dari ( ), berlaku ( ) ( ) . Jadi adalah tes UMP berukuran untuk hipotesis .
30 4.8 Test UMP Terhadap Model Distribusi Dalam Keluarga Eksponensial 4.8.1 Kasus Binomial
Misalkan sampel acak dari populasi berdistribusi ( ) dimana ( ) akan diuji hipotesis , . Berdasarkan konsep umun dari pengujian hipotesis Neyman-Pearson maka diperoleh: ( ) ( ) ( ) ∏ ( ) ∏ ( ) ∑ ( ) ∑ ∑ ( ) ∑ ( ) ∑ ( ) ∑ ∑ ( ) ∑ ( ) ∑ ( ) ∑ ∑ ( ) ∑ ( ) ∑ ( ) ∑ ∑ . ∑ / ( ) ∑ ( ) ∑ ( )
31 ∑ ( ( ) ( )) ∑ ( ( )) Karena dan sehingga Maka ∑ ( . /) mengakibatkan: ∑ . / jika benar, maka:
∑ ( )
sehingga Test UMP akan menolak pada tingkat signifikansi jika ∑ ( )( )
4.8.2 Kasus Poisson
Misalkan sampel random dari populasi yang berdistribusi Poisson ( ). Berdasarkan sampel tersebut akan diuji hipotesis
32 ( ) ( ) ( ) ∑ ∏ ∑ ∏ ( ) ∑ ( ) sehingga, ( ) ∑ ( ) karena ( ) maka ( ) sehingga,
∑ ( ) ( ) ∑ ( ) ( ) ∑ ( ) [ ( ( ))]
karena maka sehinga Akibatnya
∑ [ ( ( ))] . / atau ∑ dengan [ ( ( ))] . /
maka test UMP dapat didefenisikan sebagai ( ) { ∑ ∑ dan ∑ ( )
33 4.8.3 Kasus Normal
Misalkan merupakan sampel random dari populasi ( ) diasumsikan tidak diketahui. Maka tes UMP berukuran untuk hipotesis
dan adalah:
( ) { ̅ ̅
Dengan { ̅ } . Jika merupakan nilai sebenarnya dari , maka daerah kritis dari adalah:
{( ) √ ( ̅ ) }
{( ) ̅ √ }
4.8.4 Kasus Gamma ( )
Misalkan k diketahui, maka akan diuji hipotesis dengan anggapan diperoleh:
( ) ( ) ( ) . ( ) / (∏ ) ∑ . ( ) / (∏ ) ∑ ( ( ) ( ) ) ∑ . / ∑ . /
34 dengan ( ( ) ( ) ) ∑ ( ) ∑ jika maka ∑ ( )
jadi ditolak pada tingkat signifikansi jika ∑
( )
4.9 Informasi Data.
Data yang digunakan dalam tugas akhir ini merupakan data skunder yang diperoleh dari nilai ujian matakuli ah Statistik Matematika II dari populasi mahasiswa jurusan Matematika. Misalkan diambil data berukuran 20 mahasiswa dari populasi nilai ujian Statistik Matematika II yaitu :
81,10 73,25 85,15 74,95 73,80 81,55 84,10 72,60 79,40 72,60 75,65 75,45 81,15 79,05 84,50 70,12 83,56 72,14 71,34 80,13
35 Selanjutnya akan dilakukan uji Kolmogorov-Smirnov untuk 20 sampel data mahasiswa, adapun langkah-langkah untuk uji Kolmogorov-Smirnov adalah: 1. Hipotesis
= data sampel berdistribusi normal = data sampel tidak berdistribusi normal 2. Statistik uji
| ( ) ( )|
3. Kesimpulan
ditolak pada tingkat signifikansi α jika dan hanya jika Dari data tabel diperoleh sebagai berikut:
̅ ∑ √ ∑( ̅)
Ilustrasi uji kolmogorof untuk data pertama : ̅ ( ) ( ) ( ) | ( ) ( )| | |
36 Selajutnya lihat tabel berikut:
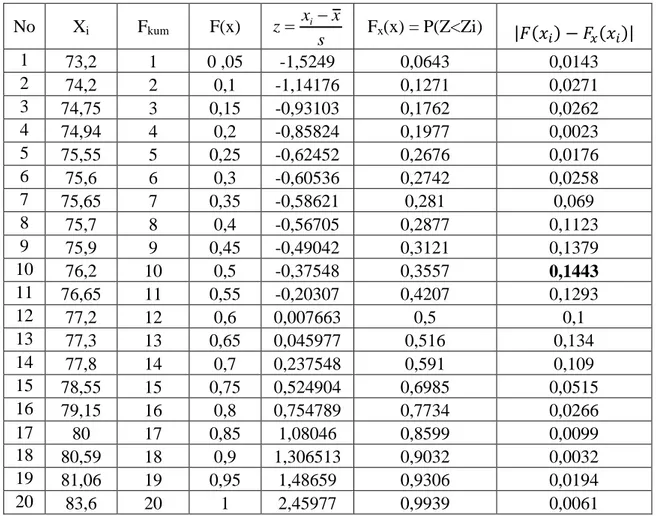
Tabel 4.1Analisis Data nilai ujian setelah diurutkan
No Xi Fkum F(x) s x x z i Fx(x) = P(Z<Zi) | ( ) ( )| 1 73,2 1 0 ,05 -1,5249 0,0643 0,0143 2 74,2 2 0,1 -1,14176 0,1271 0,0271 3 74,75 3 0,15 -0,93103 0,1762 0,0262 4 74,94 4 0,2 -0,85824 0,1977 0,0023 5 75,55 5 0,25 -0,62452 0,2676 0,0176 6 75,6 6 0,3 -0,60536 0,2742 0,0258 7 75,65 7 0,35 -0,58621 0,281 0,069 8 75,7 8 0,4 -0,56705 0,2877 0,1123 9 75,9 9 0,45 -0,49042 0,3121 0,1379 10 76,2 10 0,5 -0,37548 0,3557 0,1443 11 76,65 11 0,55 -0,20307 0,4207 0,1293 12 77,2 12 0,6 0,007663 0,5 0,1 13 77,3 13 0,65 0,045977 0,516 0,134 14 77,8 14 0,7 0,237548 0,591 0,109 15 78,55 15 0,75 0,524904 0,6985 0,0515 16 79,15 16 0,8 0,754789 0,7734 0,0266 17 80 17 0,85 1,08046 0,8599 0,0099 18 80,59 18 0,9 1,306513 0,9032 0,0032 19 81,06 19 0,95 1,48659 0,9306 0,0194 20 83,6 20 1 2,45977 0,9939 0,0061
Berdasarkan perhitungan pada Tabel 4.1 ternyata selisih maksimum terlihat pada interval (76,2 ; 75,9) dengan nilai sebagai berikut;
| ( ) ( )|
Sehingga Ho tidak ditolak pada tingkat signifikansi α = 5 %, karena nilai yaitu maka data nilai ujian mahasiswa Matematika tersebut merupakan distribusi normal.
37 Berdasarkan konsep umum dari pengujian Hipotesis Neyman-Pearson maka dimisalkan sampel random dari populasi yang berdistribusi ( ) berdasarkan sampel tersebut akan diuji hipotesis
pada level dengan anggapan maka diperoleh:
( ) ̅ ̅
dimana k ditentukan , karena hipotesisnya merupakan hipotesis sederhana, tes atau daerah kritik berukuran α sehingga
( ) ( ̅ )
sekarang dimisalkan ingin dilakukan pengujian pada tingkat signifikasi α=5% maka akan dilakukan pengambilan keputusan apakah diterima atau ditolak. Berdasarkan teorema 4.3.4 dan sebagai gambaran berdasarkan sampel dari nilai ujian matakuliah
Statistik Matematika II yang berdistribusi normal maka akan diuji hipotesis . Untuk menguji hipotesis digunakan uji UMP yang dinyatakan dengan:
( ) ̅ ̅
maka untuk memutuskan apakah ditolak atau diterima jika
|
( ̅
)
√
|
Karna kesalahan tipe I dan tipe II tidak bisa dihindari maka penentuan daerah kritis dengan tingkat signifikasi α ditentukan dengan cara menentukan nilai (kesalahan tipe I) = α dimana α bilangan kecil seperti 5%, 1%, dan 0,05%.
38 Karena hipotesisnya merupakan hipotesis sederhana, maka tes atau daerah kritik berukuran adalah : ( ) { ̅ } { ̅
√
√ } (
√ ) Ini berakibat ( ) ( ) ( ) ( ) (kesalahan tipe I) = { } * ̅ + { ̅ } * + * +
39 Daerah kritis dengan tingkat signifikasi
{( ) ̅
} atau
jadi daerah kritisnya adalah :
*( ) ̅ +
Ini berarti dengan menggunakan tingkat signifikasi sebesar diperoleh ̅ maka dapat ditarik kesimpulan bahwa akan ditolak
40 BAB V
PENUTUP 5.1 Kesimpulan
Dari hasil yang diperoleh dalam penulisan tugas akhir ini, dapat disimpulkan bahwa uji terbaik dalam menguji hipotesis adalah uji paling kuasa seragam (Uniformly Most Powerful test) disingkat UMP-test dengan menggunakan metode uji Neyman Pearson. Untuk ukuran sampel yang dihitung dengan menguji hipotesis sederhana vs dimana adalah berdistribusi normal. Sehingga, pada tingkat signifikansi maka akan ditolak.
5.2 Saran
Pada tugas akhir ini digunakan metode Neyman Pearson untuk merumuskan prosedur uji kuasa (UMP-Test). Maka untuk penelitian selanjutnya disarankan untuk menggunakan metode yang lain untuk merumuskan tes yang terbaik .
41 DAFTAR PUSTAKA
Bain, L.J and Engelhardt, M. 1992. Introduction to probability and mathematical statistic (second edition). Duxbury press: California.
Casella, G dan Roger L.B. 1990. Statistical Inference. Duxbury Press, Belmont, California.
Lehman, E.L. 1986. Testing Statistical Hypotheses (second edition). John Wiley & sons, New York.
Mustafid. 2003. Statistika Elementer. Semarang: Universitas Diponegoro.
Nasoetion, M.H. 2003. Diktat Kuliah Statistika. Semarang: Universitas Diponegoro.
Setiawan, A. 2006. Diktat Kuliah Statistik Matematika. Salatiga: Universitas Kristen Satya Wacana.
Somayasa, W. 2001. Statistika Elementer. Kendari: Universitas Halu Oleo.
Somayasa, W. 2008. Diktat Kuliah Statistika Matematika I. Kendari: Universitas Halu Oleo.
Sudjana. 1996. Metode Statistik Edisi ke-6. Bandung : Tarsiro. Supranto, J. 2001. Statistik Edisi ke-6. Jakarta
Walpole, R .E dan Myers, R. H. 1995. Ilmu Peluang dan Statistika untuk Insinyur dan Ilmuwa Edisi ke - 4. Alih bahasa oleh Sembiring, R.K. Penerbit ITB; andung.
Widiharih, T. 2009. Buku Ajar Statistika Matematika II. Semarang : UNDIP Semarang.