PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis Konstruksi Algoritme Aritmetik (5 ) Dengan Operasi Dibangkitkan Dari Sifat Grup siklik adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis.

Bogor, Agustus 2009 Ahmadi NRP G551070691

ABSTRACT

AHMADI. The Construction of Arithmetic Algorithms _{( ) Generated by} Cyclic Group Properties. Supervised by SUGI GURITMAN and NUR ALIATININGTYAS.

To construct a cryptographic algorithm, many arithmetic concepts are needed. ElGamal encryption for example, can be defined over cyclic group ∗, the usual arithmetic concepts. If the use of this arithmetic is associated with security aspect, then it requires large computational work. This thesis aims to construct arithmetic algorithm as an alternative arithmetic that can be applied to any cryptographic scheme, especially public key scheme. This algorithm is imposed from finite field _{(5). Thus, the procedures to construct arithmetic algorithm} are as follows. The first step is to choose primitive polynomial _{( ) [ ]of} lower degree. The second step is to find primitive root _{M(α) = 0 , thus the} equation _{( ) = 0 has a root α in (5). The resulted arithmetic algorithms} are computational procedures for standard operation in _{(5 ): addition,} multiplication, division, invertion, and exponentiation. It can be concluded that constructed arithmetic algorithms _{(5) are better than standard algorithms} because some operations can be reduced using primitive polynomial or cyclic group properties, and using reduction of zero.

RINGKASAN

AHMADI. Konstruksi Algoritme Aritmetik _{(5 ) Dengan Operasi} Dibangkitkan Dari Sifat Grup siklik. Dibimbing oleh SUGI GURITMAN dan NUR ALIATININGTYAS.

Masalah keamanan merupakan salah satu aspek penting dari sebuah sistem informasi. Untuk menjamin keamanan sebuah informasi yang bersifat rahasia diperlukan suatu teknik pengamanan baik secara fisik maupun non fisik. Salah satu teknik pengamanan secara non fisik yaitu dengan mengenkripsi informasi rahasia menggunakan teknik kriptografi.

Kriptografi secara terminologi dasarnya terdiri dari dua tipe yaitu kriptografi simetrik dan kriptografi asimetrik atau sering disebut sebagai kriptografi kunci publik. Kunci simetris adalah jenis kriptografi yang paling umum digunakan. Kunci untuk membuat pesan yang disandikan sama dengan kunci untuk membuka pesan yang disandikan itu. Kunci asimetris merupakan pasangan kunci kriptografi yang salah satunya digunakan untuk proses enkripsi dan yang satu lagi untuk dekripsi. Contoh algoritme terkenal yang menggunakan kunci asimetrik adalah skema yang ditemukan oleh ElGamal pada tahun 1985. Skema ini didasarkan pada pemecahan problem logaritma diskret. Keamanan algoritme ini sangat tergantung pada pemilihan bilangan prima p. Semakin besar p maka algoritme ini akan semakin aman, akan tetapi semakin besar pula beban komputasi yang digunakan. Oleh karena itu pada masa sekarang, orang sudah mulai mencari alternatif lain untuk menggantikan aritmetik modular diantaranya aritmetik yang dibangkitkan struktur finite field _{( ), kurva eliptik kriptografi,} dan hipereliptik kriptografi.

Sebenarnya sudah banyak sekali penelitian tentang _{( ) yang pernah} dilakukan, diantaranya adalah paper berjudul ”Montgomery Multiplication in GF(2k_{)” menunjukkan operasi perkalian = . . dalam field GF(2}k_{) dimana r} adalah unsur tetap dari field dapat diimplementasikan lebih cepat dalam perangkat lunak dibandingkan dengan operasi perkalian standar (Koc, 1998), paper berjudul ”Analysis and Construction of Galois Field for Efficient Storage Reliability” juga menganalisis adanya implementasi berdasarkan tabel dan teknik optimasi operasi perkalian dan pembagian dalam _{(2) (Greenan, 2007), dan} thesis berjudul ”Konstruksi Algoritme Aritmetik _{(2) Dengan Operasi} Perkalian Dibangkitkan Dari Sifat Grup Siklik” menyebutkan bahwa algoritme aritmetik hasil konstruksi cukup cepat dalam perhitungan komputasinya (Rosdiana, 2009).

Dalam thesis ini peneliti mencoba mengkonstruksi aritmetik yang berbeda dari sebelumnya yaitu aritmetik _{(5) dan dengan pendekatan yang sama dari} konstruksi yang telah dilakukan oleh Ibu Sri Rosdiana (2009) yaitu mendefinisikan sekaligus mengkonstruksi _{(5) didasarkan pada sifat bahwa} (5 )∗_{merupakan grup siklik yang dibangkitkan dari akar primitif. Penelitian} ini bertujuan mengkonstruksi finite field _{(5) dengan memperhatikan segi} kecepatan dan kapasitas memori yang digunakan.

Untuk mengkonstruksi aritmetik _{(5) dalam penelitian ini langkah} pertama adalah dengan memilih polinomial primitif berderajat m atas Z5, misal

( ) ∈ [ ] dimana ( ) = + + ⋯ . Langkah kedua tentukan unsur primitifnya misal α sehingga M(α) = 0. Lalu tentukan basisnya di _{(5 )} sebagai ruang vektor atas Z5. Adapun basis dari polinomial

primitifnya yaitu {1, α1, α2, …, αm-1}. Sehingga

(5 ) = { . 1 + + ⋯ | , , … , ∈ (5)} . Kemudian

semua unsur dari _{(5 ) direpresentasikan ke dalam bentuk ruang vektor} berdimensi m atas . Algoritme hasil konstruksi terdiri atas Algoritme Penjumlahan, Algoritme Perkalian, Algoritme Invers, Algoritme Pembagian, dan Algoritme Eksponensial.

Dari hasil penelitian yang telah dilakukan diperoleh kesimpulan : 1) Finite field _{(5) dikonstruksi dari polinomial primitif. Untuk mengkonstruksi} algoritme aritmetik _{(5) dipilih polinomial primitif yang bersuku terkecil, hal} ini akan mengakibatkan proses komputasi yang dijalankan lebih cepat dibandingkan dengan menggunakan polinomial primitif biasa. 2) Algoritme Reduksi Nol digunakan untuk mengurangi jumlah operasi pada sebuah algoritme. Algoritme ini digunakan pada Algoritme Penjumlahan, Algoritme Penjumlahan digunakan dalam Algoritme Perkalian, Algoritme Penjumlahan dan Algoritme Perkalian digunakan dalam Algoritme Invers, dan seterusnya. 3) Algoritme Geser Satu mampu mempercepat proses kerja suatu algoritme, karena pada algoritme ini hanya mengubah strukturnya saja dan menggeser bersifat konstan. Algoritme ini digunakan pada Algoritme Perkalian, Algoritme Perkalian digunakan dalam Algoritme Invers, dan seterusnya. 4) Algoritme aritmetik hasil konstruksi tidak membutuhkan ruang yang besar sehingga cukup cepat dalam komputasinya karena yang dipakai sebagai modulo digunakan polinomial primitif bersuku terkecil, melakukan reduksi nol yang berfungsi mengurangi jumlah operasi dalam algoritme, dan operasi geser satu.

Kata kunci : algoritme, grup siklik, _{(5 ), akar primitif, polinomial primitif,} kriptografi.

©Hak cipta milik IPB, tahun 2009

Hak cipta dilindungi Undang-undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebut sumber.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah.

b. Pengutipan tidak merugikan kepentingan yang wajar IPB.

2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis dalam bentuk apapun tanpa izin IPB.

KONSTRUKSI ALGORITME ARITMETIK

_{( )}

DENGAN OPERASI DIBANGKITKAN

DARI SIFAT GRUP SIKLIK

AHMADI

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Departemen Matematika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2009

Judul Tesis : Konstruksi Algoritme Aritmetik _{(5 ) Dengan Operasi} Dibangkitkan Dari Sifat Grup siklik

Nama : Ahmadi NRP : G551070691

Disetujui Komisi Pembimbing

Dr.Sugi Guritman. Dra. Nur Aliatiningtyas, M.Si

Ketua Anggota

Diketahui

Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.

PRAKATA

Segala puji dan syukur penulis panjatkan kehadirat Allah SWT yang telah memberikan segala rahmat dan karunia-Nya, sehingga penulis dapat menyelesaikan tesis yang berjudul “Konstruksi Algoritme Aritmetik _{(5 )} Dengan Operasi Yang Dibangkitkan Dari Sifat Grup siklik”.

Penulis menyadari bahwa dalam penyusunan tesis ini masih banyak terdapat kekurangan, hal ini karena peengetahuan yang dimiliki oleh penulis sangat terbatas.

Dalam kesempatan ini penulis mengucapkan terimakasih yang sebesar-besarnya kepada yang terhormat

1. Bapak Dr. Sugi Guritman dan Ibu Dra. Nur Aliatiningtyas, MS selaku pembimbing, pendidik dan pengajar yang dengan penuh kesabaran memberikan bimbingan, arahan, nasehat serta motivasi kepada penulis.

2. Bapak Drs. Prapto Tri Supriyo, M.Kom. selaku penguji, pendidik dan pengajar yang telah memberikan saran dan kritikannya kepada penulis.

3. Departemaen Agama RI yang telah memberikan beasiswa kepada penulis untuk melanjutkan Sekolah Pascasarjana pada Institut Pertanian Bogor periode 2007 s.d 2009.

4. Ketua Departemen, ketua Program Studi, dan seluruh staf pengajar serta staf administrasi Fakultas Matematika dan Ilmu Pengetahuan Alam yang turut membantu proses penyelesaian tesis.

5. Kepala sekolah dan seluruh staf pengajar MTs At-Taqwa Gembongdadi yang turut mendoakan dan memotivasi penulis dalam menyelesaikan tesis ini. 6. Istri dan kedua orang tua yang senantiasa mendoakan penulis disetiap waktu

dalam menyelesaikan tesis.

7. Seluruh teman-teman yang turut membantu penyelesaian tesis.

Penulis doakan semoga segala bantuan, bimbingan dan pengarahan yang diberikan mendapat ganjaran yang berlipat ganda dari Allah SWT, dan semoga tesis ini bermanfaat bagi kita semua. Amin.

Bogor, Agustus 2009 Ahmadi

RIWAYAT HIDUP

Penulis dilahirkan di Tegal pada tanggal 09 Januari 1980 dari ayah Kholil dan ibu Muninggar. Penulis merupakan putra kelima dari delapan bersaudara.

Pendidikan dasar ditempuh di SD Negeri Karangjati 01 – Tarub - Tegal lulus tahun 1993, MTs. Hasyim Ay’ari Tarub lulus tahun 1996. Pendidikan atas ditempuh di SMA Hasyim Ay’ari Tarub lulus tahun 1999. Pendidikan sarjana ditempuh di Jurusan Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan Universitas Pancasakti Tegal lulus tahun 2005.

Setelah lulus pendidikan sarjana, penulis menjadi staf pengajar di MTs. At-Taqwa Gembongdadi sebagai guru honorer sampai dengan sekarang.

Pada tahun 2007 penulis mendapat kesempatan untuk melanjutkan sekolah ke jenjang yang lebih tinggi yakni Program Magister. Penulis melanjutkan belajar Program Magister pada program studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor melalui beasiswa BUD Departemen Agama Republik Indonesia.

DAFTAR ISI

DAFTAR TABEL ………... xii

DAFTAR GAMBAR ………...…… xiii

DAFTAR ALGORITME ………. xiv

DAFTAR LAMPIRAN ……… xv

BAB I PENDAHULUAN ……….. 1

1.1 Latar Belakang ……….. 1

1.2 Tujuan Penelitian ……….. 3

1.3 Manfaat Penelitian ……… 3

BAB II TINJAUAN PUSTAKA ………... 4

2.1 Teori Grup ……….. 4

2.2 Grup Siklik ………. 6

2.3 Grup Homomorfisme Dan Isomorphisme ………. 6

2.4 Ring ……….……….. 7

2.5 Ring Polinomial …………..………... 9

2.6 Perluasan Field ……….. 10

BAB III PEMBAHASAN TEOREMA DAN LEMMA YANG DIBUTUHKAN DALAM KONSTRUKSI ARITMETIK GF(5m_{) ……….. 14}

3.1 Polinomial Minimum ………….……… 18

BAB IV KONSTRUKSI ALGORITME ARITMETIK GF(5m) ………... 25

4.1 Penjumlahan Polinomial ……….……….. 28

4.2 Perkalian Polinomial ……….……… 30

4.3 Invers Polinomial …..………. 33

4.4 Pembagian Polinomial ……….. 36

4.5 Eksponen Polinomial ……… 37

BAB V KESIMPULAN DAN SARAN ………. 39

5.1 Kesimpulan ………..….……… 39

5.2 Saran ………..……….. 39

DAFTAR PUSTAKA ……….. 40

DAFTAR TABEL

Halaman

1. Finite Field _{(5)……….………..} 17

DAFTAR ALGORITME

Halaman

4.1 Pengetesan Polinomial Irredusibel 27

4.2 Pengetesan Polinomial Primitif 28

4.3 Penjumlahan Polinomial 29 4.4 Reduksi Nol 30 4.5 Kelipatan Vektor 30 4.6 Geser Satu 31 4.7 Perkalian Polinomial 32 4.8 Negasi Vektor 33

4.9 Pembagian Polinomial Tanpa Modulo m 34

4.10 Invers Polinomial 35

4.11 Pembagian Polinomial 37

4.12 Eksponen Polinomial 37

DAFTAR GAMBAR

Halaman

1. Perluasan Field F 11

DAFTAR LAMPIRAN

BAB I

PENDAHULUAN

1.1 Latar Belakang

Masalah keamanan merupakan salah satu aspek penting dari sebuah sistem informasi. Untuk menjamin keamanan sebuah informasi yang bersifat rahasia diperlukan suatu teknik pengamanan baik secara fisik maupun non fisik. Salah satu teknik pengamanan secara non fisik yaitu dengan mengenkripsi informasi rahasia menggunakan teknik kriptografi.

Kriptografi secara terminologi dasarnya terdiri dari dua tipe yaitu kriptografi simetrik dan kriptografi asimetrik atau sering disebut sebagai kriptografi kunci publik. Kunci simetris adalah jenis kriptografi yang paling umum digunakan. Kunci untuk membuat pesan yang disandikan sama dengan kunci untuk membuka pesan yang disandikan itu. Jadi pembuat pesan dan penerimanya harus memiliki kunci yang sama persis. Siapapun yang memiliki kunci tersebut termasuk pihak-pihak yang tidak diinginkan dapat membuat dan membongkar rahasia ciphertext. Contoh algoritme kunci simetris yang terkenal adalah DES (Data Encryption Standard). Karya ini menjadi alat keamanan komersial elektronik di banyak institusi keuangan di seluruh dunia hingga pertengahan tahun 1990-an. DES secara DES tak aman sejak juli 1998. Walaupun demikian DES telah melandasi prinsip-prinsip sandi simetrik modern yang dewasa ini muncul produk-produk penggantinya seperti : AES (Advanced Encryption Standard), Blowfish, 3DES, RC5, dan lain sebagainya.

Kunci asimetrik merupakan pasangan kunci kriptografi yang salah satunya digunakan untuk proses enkripsi dan yang satu lagi untuk dekripsi. Semua orang yang mendapatkan kunci publik dapat menggunakannya untuk mengenkripsikan suatu pesan,data ataupun informasi, sedangkan hanya satu orang saja yang memiliki rahasia tertentu dalam hal ini kunci privat untuk melakukan pembongkaran terhadap sandi yang dikirim untuknya. Pada algoritme kunci publik ini, semua orang dapat mengenkripsi data dengan memakai kunci publik penerima yang telah diketahui secara umum. Akan tetapi data yang telah terenkripsi tersebut hanya dapat didekripsi dengan menggunakan kunci privat

2 yang hanya diketahui oleh penerima. Contoh algoritme terkenal yang menggunakan kunci asimetrik adalah skema RSA yang ditemukan oleh Rivest, Shamir, dan Adleman pada tahun 1978. Skema ini didasarkan pada problem matematika yang sulit, yaitu pemecahan masalah faktorisasi integer besar. Bentuk praktis skema kunci publik lainnya ditemukan oleh ElGamal pada tahun 1985. Skema ini didasarkan pada pemecahan problem logaritma diskret. Keamanan algoritme ini sangat tergantung pada pemilihan bilangan prima p. Semakin besar p maka algoritme ini akan semakin aman, akan tetapi semakin besar pula beban komputasi yang digunakan. Oleh karena itu pada masa sekarang, orang sudah mulai mencari alternatif lain untuk menggantikan aritmetik modular diantaranya aritmetik yang dibangkitkan struktur finite field , kurva eliptik kriptografi, dan hipereliptik kriptografi.

Teori finite field mulai diperkenalkan pada abad ke tujuh dan abad ke delapan, dengan tokoh matematikanya Pierre de Fermat (1601-1665) dan Leonhard Euler (1707-1783) dengan kontribusinya pada khusus teori struktur finite field. Teori secara umum tentang finite field mulai dikerjakan oleh Carl Friedrich Gauss (1777-1855) dan Evariste Galois (1811-1832), teori ini banyak dikembangkan dalam dunia aplikasi matematika, komputer, dan teori komunikasi.

Sebenarnya sudah banyak sekali penelitian tentang yang pernah dilakukan, diantaranya adalah paper berjudul ”Montgomery Multiplication in GF(2k)” menunjukkan operasi perkalian dalam field GF(2k) dimana r adalah unsur tetap dari field dapat diimplementasikan lebih cepat dalam perangkat lunak dibandingkan dengan operasi perkalian standar (Koc, 1998), paper berjudul ”Analysis and Construction of Galois Field for Efficient Storage Reliability” juga menganalisis adanya implementasi berdasarkan tabel dan teknik optimasi operasi perkalian dan pembagian dalam (Greenan, 2007), dan thesis berjudul ”Konstruksi Algoritme Aritmetik Dengan Operasi Perkalian Dibangkitkan Dari Sifat Grup Siklik” menyebutkan bahwa algoritme aritmetik hasil konstruksi cukup cepat dalam perhitungan komputasinya (Rosdiana, 2009).

3 Dalam thesis ini peneliti mencoba mengkonstruksi aritmetik yang berbeda dari sebelumnya yaitu aritmetik dan dengan pendekatan yang sama dari konstruksi yang telah dilakukan oleh Sri Rosdiana (2009) yaitu mendefinisikan sekaligus mengkonstruksi didasarkan pada sifat bahwa

merupakan grup siklik yang dibangkitkan dari akar primitif.

1.2 Tujuan Penelitian

Penelitian ini bertujuan mengkonstruksi finite field dengan memperhatikan segi kecepatan yang didasarkan pada sifat-sifat grup siklik.

1.3. Manfaat Penelitian

Manfaat dari penelitian ini adalah sebagai algoritme aritmetik alternatif yang dapat digunakan pada algoritme-algoritme kriptografi yang selanjutnya dapat digunakan secara luas pada bidang teknologi informasi.

4

BAB II

TINJAUAN PUSTAKA

Untuk mencapai tujuan penulisan penelitian diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam subbab ini akan diberikan beberapa teori berupa definisi, lemma, dan teorema yang berkaitan dengan pembahasan.

2.1. Teori Grup

Definisi 2.1. Struktur aljabar tertutup terhadap operasi biner  disebut grup jika memenuhi aksioma-aksioma berikut:

a) Operasi biner bersifat asosiatif: a b c  



 

a b c 



, untuk setiap

, ,

a b c G .

b) Terdapat unsur identitas e G , untuk * pada G sehingga berlaku a e e a a    untuk setiap a G .

c) Untuk setiap a G ada unsur _a1_{G sehingga a a} 1_a1_{ a e. ( a}-1 disebut invers a terhadap operasi *).

Grup G disebut grup komutatif atau grup abelian jika operasi * bersifat komutatif yaitu: a b b a   , untuk semua a b G,  .

Grup berhingga yaitu grup yang kardinalitasnya berhingga. Dalam hal ini kardinalitas suatu grup G disebut dengan order dari G, dinotasikan ord G

 

atau

 

O G atau G .

Definisi 2.2. Jika H himpunan bagian atas grup G adalah grup di bawah operasi G, maka H subgrup dari G.

Teorema 2.3. (Uji satu langkah) Misalkan G grup dan H himpunan bagian yang tak kosong atas G. Maka H adalah subgrup atas G jika H tertutup di bawah operasi pembagian; yaitu jika bilamana

5 Teorema 2.4. (Uji dua langkah) Misalkan G grup dan H himpunan bagian tak kosong atas G. Maka, H disebut subgrup dari G jika bilamana

(tertutup terhadap perkalian), dan bilamana (tertutup terhadap invers)

Sebagai contoh, Z dan Q merupakan subgrup dari R terhadap operasi +. Tentu saja ZQR dan masing-masing merupakan grup terhadap operasi yang sama yaitu +.

Misal G sembarang grup, a G , dan n bilangan bulat positif, maka:  kali : ... n n a aa a, 1 1 1 kali : ... n n a a a  a  , = (an)-1 dan _a0_:e.

Jika ada bilangan bulat tidak nol m sedemikian sehingga _am_{e, maka order}

dari unsur a, notasi O a

 

, didefinisikan sebagai bilangan bulat positif terkecil n sedemikian sehingga _an _{e. Jika tidak ada bilangan bulat tidak nol n sedemikian}

sehingga _an _{e, maka dikatakan a mempunyai order di tak hingga (infinity).}

Ringkasan 2.5. Berikut ini 3 sifat dasar yang berkaitan dengan pengertian order.

1. Jika O a

 

n, maka ada tepat n kuasa dari a (power of a) yang masing-masing berbeda, yaitu _a0 _{e a a, , ,...,}2 _an1_.

2. Jika O a

 

tak hingga, maka semua kuasa dari a berbeda. Artinya, jika r dan s yaitu dua bilangan bulat yang berbeda, maka _ar _as_.

3. Misalkan a yaitu unsur dari grup G dan O a

 

n. Maka _at _{e jika dan}

hanya jika t yaitu kelipatan dari n (t kelipatan n artinya ada bilangan bulat q sehingga t=nq).

Definisi 2.6. Misalkan H subgrup dari grup G. Himpunan bagian atas G disebut koset kiri atas H memuat . Sedangkan himpunan bagian atas G disebut koset kanan atas H memuat .

6 Teorema 2.7. (Teorema Lagrange) Misalkan H subgrup dari grup berhingga G. Maka order dari H adalah pembagi dari order G.

Teorema 2.8. Order dari unsur grup berhingga G membagi order G.

Jika H merupakan subgrup dari grup G, indeks dari H di dalam G diartikan sebagai jumlah koset dari H di dalam G, notasinya



G H:



. sedangkan



G H:



G

H 

2.2. Grup Siklik

Grup G disebut siklik jika dan hanya jika ada unsur a G (a disebut generator) sehingga



n



G a  a n Z .

Dalam kasus G grup aditif, dapat ditulis





G a  na n Z .

Ringkasan 2.9. (Sifat-sifat Grup Siklik)

1. Jika grup G berorder n, maka G siklik jika dan hanya jika ada a G sehingga

 

O a n.

2. Setiap grup siklik yaitu abelian.

3. Setiap subgrup dari grup siklik adalah siklik. 4. Jika G a dan b G , maka O b O a .

   

5. Jika G yaitu grup siklik berorder n dan suatu bilangan bulat k n, maka ada b G sehingga O b

 

k.

6. Misalkan G yaitu grup abelian berorder mn dengan m dan n prima relatif. Jika G mempunyai suatu unsur a dengan O a

 

m dan b dengan O b

 

n, maka G yaitu grup siklik dengan G ab .

7. _ar _{yaitu generator dari G a dengan G n jika dan hanya jika r dan n}

prima relatif.

7 Misal G dan H grup. Suatu homomorfisma (grup) dari G ke H yaitu suatu fungsi f G: H sedemikian sehingga untuk sembarang a dan b di dalam G,

 

   

f ab  f a f b .

Bayangan (Imej) dari f, dinotasikan Im f

 

, yaitu

 

 



 



Im f  f G  f x x G . Kernel dari f, dinotasikan ker f

 

, yaitu

 



 



ker f  x G f x e (secara implisit e yaitu unsur identitas dari f).

Sifat-sifat dasar homomorfisma dinyatakan dalam Ringkasan berikut ini.

Ringkasan 2.10. (Sifat-sifat Dasar Homomorfisma) Misalkan G dan H yaitu

grup, f G: H homomorfisma, maka sifat-sifat berikut dipenuhi. 1. f e

 

e.

2. untuk setiap a G .

3. Im f

 

merupakan subgrup dari H. 4. ker f

 

merupakan subgrup dari G.

Jika homomorfisme yang bijektif, maka f disebut isomorfisme.

2.4. Ring

Struktur aljabar dengan dua operasi biner yang paling umum yaitu Ring. Definisi 2.11. Ring R adalah himpunan dengan dua operasi + dan x (disebut dengan penjumlahan dan perkalian) yang memenuhi aksioma-aksioma berikut: a. R, adalah grup abelian

b. Operasi adalah asosiatif : untuk setiap a b c R, ,  . c. Berlaku hukum distributif atas R : Untuk setiap a b c R, ,  memenuhi

8 Ring R disebut komutatif jika perkaliannya bersifat komutatif. Ring R disebut mempunyai unsur kesatuan jika terdapat unsur dengan

Definisi 2.12. Unsur bukan nol dari Ring komutatif R disebut pembagi nol jika ada unsur bukan nol sehingga

Definisi 2.13. Ring komutatif dengan unsur kesatuan disebut daerah integral jika tidak memuat pembagi nol

Definisi 2.14. Karakteristik Ring R adalah sekurang-kurangnya integer positif sehingga untuk setiap . Jika tidak ada, R disebut berkarakteristik 0. Teorema 2.15. Karakteristik daerah integral adalah 0 atau prima.

Teorema 2.16. Di dalam sembarang Daerah Integral D dengan karakteristik p,



_{a b}



p _ap_bp _{untuk semua unsur a b D,  .}

Definisi 2.17. Field adalah suatu Ring komutatif, ada unsur kesatuan 1 dan setiap unsur tak nolnya mempunyai invers (multiplikatif)

Teorema 2.18. Daerah integral yang berhingga adalah field.

Akibat 2.19. Untuk setiap bilangan prima p, Ring Zp integer modulo p, adalah

field

Definisi 2.20. SubRing A dari Ring R disebut ideal dari R jika untuk setiap dan setiap , dan .

Teorema 2.21. Misal R Ring, I , I tidak kosong. Himpunan bagian I disebut R ideal jika memenuhi:

a.

b. dan dan .

Untuk setiap Ring R, {0} dan R adalah ideal atas R. Ideal {0} disebut ideal trivial. Misalkan R Ring komutatif dengan unsur kesatuan 1 dan . Suatu himpunan

merupakan ideal. Ideal yang demikian disebut ideal utama yang dibangun oleh .

9 Definisi 2.22. Suatu ideal I atas Ring komutatif R disebut ideal prima atas R jika

dan sehingga dan . Suatu ideal B atas Ring komutatif R disebut ideal maksimal atas R jika B adalah ideal atas R dan maka B = A atau B = R.

Misalkan Ring R dan I merupakan ideal dari R. Karena R merupakan grup terhadap penjumlahan dan I subgrup dari R, maka Ring faktor dapat ditulis

sebagai .

Teorema 2.23. Misal R Ring komutatif dengan unsur kesatuan 1. I ideal maksimal dari R. Maka R I adalah field jika dan hanya jika I ideal maksimal. Definisi 2.24. Suatu homomorfisma dari Ring R ke Ring _R' _{yaitu suatu fungsi}

'

:

f RR yang memenuhi, berlaku : a. f a b







 f a

 

 f b

 

, dan

b. f ab

 

 f a f b

   

.

Jika f surjektif, maka _{R disebut bayangan homomorfik dari R.}'

Kernel dari f diDefinisikan

 



 



ker f  x R f x 0 , dan range dari f diDefinisikan

 



 



ran f  f x x R .

Jika f homomorfisma yang bijektif, maka f disebut isomorfisma. Dalam hal ini R dan _R' _{dikatakan isomorfik, dinotasikan}

Teorema 2.25. Misal _{f R: R}' _{Ring homomorfisma. Maka}

 



 



ker f  x R f x 0 merupakan ideal dari R.

Teorema 2.26. R I merupakan bayangan homomorfik dari R.

Teorema 2.27. (Teorema dasar homomorfisme) Misalkan _{f R: R}'

10

2.5. Ring Polinomial

Misalkan R Ring komutatif dengan unsur kesatuan, dan x simbol yang tak

tetap. Setiap ekspresi berbentuk disebut

polinomial dalam x dengan . Polinomial dalam x dapat ditulis dengan

dan lain-lain. Misal

merupakan sembarang polinomial, derajat dari polinomial yaitu bilangan terbesar n sehingga koefisien dari bukan nol dan dinotasikan dengan deg .

Polinomial yang semua koefisiennya nol

disebut polinomial nol, dan dinotasikan dengan Jika polinomial maka berderajat nol dan disebut polinomial konstan. Misalkan

dan

. Operasi penjumlahan dan perkalian polinomial didefinisikan sebagai berikut :

Dimana

Dimana, , untuk k = 0, …, m+n

Jika R Ring, maka menotasikan himpunan semua polinomial dalam x yang koefisiennya ada di R dengan operasi penjumlahan dan perkalian seperti yang didefinisikan sebelumnya.

Teorema 2.28. Misal R Ring komutatif dengan unsur kesatuan 1. Maka R[x] merupakan Ring komutatif dengan unsur kesatuan 1.

11 Definisi 2.30. Suatu polinomial irredusibel atas F bila f(x) tidak dapat

dinyatakan sebagai perkalian dimana keduanya

berderajat lebih rendah dari f(x).

Teorema 2.31. Misal F field dan Ring polinomial F x

 

. Jika f x g x

 

, ( )F x

 

dengan g x

 

0, maka ada polinomial unik q x r x

 

, ( )F x

 

sehingga

     

( )

f x q x g x r x dengan r x

 

0 atau derajat r x

 

derajat g x

 

. Teorema 2.32. Misal F field, I ideal tak nol di F[x], dan unsur Ideal

jika dan hanya jika merupakan polinomial tak nol berderajat terendah di I.

Teorema 2.33. Semua ideal dari merupakan ideal utama

Teorema 2.34. Misal F field dan . ideal maksimal jika dan hanya jika irredusibel atas F.

Teorema 2.35. ideal maksimal jika dan hanya jika field.

2.6. Perluasan Field

Definisi 2.36. Jika E field yang memuat subfield F, maka E disebut perluasan field dari F.

Definisi 2.37. Misal E perluasan field dari field F dan c E . c disebut algebraic atas F jika f c

 

0 untuk f x

 

F x

 

yang tak nol.

Gambar 1. Perluasan Field F

Definisi 2.38. Misal E perluasan field dari field F dan c E algebraic atas F. Polinomial monik p x

 

merupakan polinomial irredusibel dengan akar c atas F

E

c



12 dinotasikan dengan irr ,



c F



dan derajat dari polinomial irredusibel dengan akar c atas F dinotasikan dengan deg ,



c F



Teorema 2.39. Misal F subfield dari field E, c E dan x tak tentu (indeterminate). Pemetaan c:F x

 

E yang diDefinisikan dengan

 





 

c f x f c   dimana

 

0 1 ... n n f x a a x a x , f x

 

F x

 

merupakan homomorfisma. Homomorfisma c disebut homomorfisma evaluasi dan berlaku

 

c x c

  sertac

 

a a, a F .

Kernel atas homomorfisma merupakan himpunan semua polinomial sehingga . Jadi, kernel berisi semua polinomial

sehingga c merupakan akar dari . Misalkan kernel dinotasikan sebagai , menurut Teorema 2.25 kernel untuk setiap homomorfisma merupakan ideal, sehingga merupakan ideal dari F[x]. Menurut Teorema 2.33 setiap ideal dari F[x] merupakan ideal utama. Karena merupakan ideal utama dan berdasarkan Teorema 2.32, ,

dengan polinomial berderajat terendah. Dengan Definisi 2.30 mudah untuk membuktikan bahwa merupakan polinomial irredusibel. Misalkan

Sehingga ,

dimana . Hal ini tidaklah mungkin, karena merupakan polinomial berderajat terendah di dalam . Sehingga merupakan polinomial berderajat lebih tinggi dari Maka menurut Definisi 2.30, merupakan polinomial irredusibel. Karena setiap konstanta pengali dari ada di maka monik. Sehingga dapat disimpulkan bahwa merupakan polinomial minimum dari c atas F.

13 Range

Dari penjelasan di atas diperoleh merupakan epimorfisme, dengan polinomial irredusibel. Dengan menggunakan Teorema dasar homomorfisme, maka . Menurut Teorema 2.34, jika

polinomial irredusibel maka merupakan ideal maksimal. Dan berdasarkan Teorema 2.35 dapat disimpulkan bahwa merupakan field. Karena maka juga merupakan field.

Teorema 2.40. Misal F field dan p x

 

polinomial tak konstan di F x

 

. Ada suatu perluasan field E dari F dan unsur c di E sehingga c akar dari p x

 

. Definisi 2.41 V himpunan, F field, operasi di V yaitu penjumlahan dan perkalian skalar. V disebut ruang vektor atas F jika memenuhi aksioma berikut:

1. Untuk setiap ,a b V  terdapat tunggal c V sehingga tertutup terhadap penjumlahan: a b c  .

2. Untuk setiap , ,a b c V   bersifat asosiatif:



a b



  c a 

 

b c .

3. Terdapat tunggal identitas 0 V , untuk setiap a V sehingga

0 0

a     a a .

4. Untuk setiap a V terdapat tunggal invers b V sehingga

0

a b b a      , b a.

5. Untuk setiap ,a b V  bersifat komutatif: a b b a    .

6. Untuk setiap k F dan setiap a V terdapat tunggal b V sehingga tertutup terhadap perkalian: ka b .

7. Untuk setiap k F dan setiap ,a b V  , k a b







ka kb . 8. Untuk setiap ,k l F dan setiap a V ,



k l a ka la



  . 9. Untuk setiap ,k l F dan setiap a V ,

 

kl a k la

 

 .

14 10. Untuk setiap a V , 1a a ; 1 unsur identitas di F, .

Definisi 2.42. Misal E perluasan field dari field F. Jika E ruang vektor atas F berdimensi hingga n, maka E disebut perluasan hingga berderajat n atas F. Derajat E atas F sama dengan n dinotasikan



E F:



n.

Definisi 2.43. Jika field E dibangun oleh unsur satu c atas field F: E F c

 

, maka E disebut perluasan tunggal dari F dan unsur c disebut unsur primitif atau akar primitif untuk perluasan.

Teorema 2.44. Misal E F c

 

dengan c E algebraic atas F, dan





deg ,c F n, n . Setiap unsur 1  dari E F c

 

dapat dinyatakan secara unik

dalam bentuk 1 1 0 1 ... n 1 n b b c b c        , dimana b_iF x

 

.

Teorema 2.45. Derajat dari atas F sama dengan derajat dari polinomial minimum dari c atas F.

Sebagai contoh, i merupakan akar dari polinomial irredusibel atas R[x]. mempunyai derajat 2, menurut Teorema 2.44, dengan basisnya {1, i}. Setiap unsur dalam R[i] merupakan kombinasi linear dari 1 dan i yang berbentuk dimana dan dinotasikan dengan

.

Teorema 2.46. Misalkan merupakan polinomial irredusibel berderajat m, maka adalah finite field berderajat . Operasi penjumlahan polinomial dan operasi perkalian polinomial dilakukan dalam modulo .

Teorema 2.47. Misal E perluasan field dari field F dan c E algebraic atas F. Jika deg ,



c F



n, maka F c

 

ruang vektor atas F berdimensi-n dengan basis

15 Lemma 2.48. Misal basis dari ruang vektor K atas F dan

basis dari ruang vektor E atas K. Maka himpunan perkalian merupakan basis dari ruang vektor E atas field F.

BAB III

PEMBAHASAN TEOREMA DAN LEMMA YANG DIBUTUHKAN DALAM KONSTRUKSI ARITMETIK GF(5m)

Teori finite field mulai diperkenalkan pada abad ke tujuh dan abad ke delapan, dengan tokoh matematikanya Pierre de Fermat (1601-1665) dan Leonhard Euler (1707-1783) dengan kontribusinya pada khusus teori struktur finite field. Teori secara umum tentang finite field mulai dikerjakan oleh Carl Friedrich Gauss (1777-1855) dan Evariste Galois (1811-1832), teori ini banyak dikembangkan dalam dunia aplikasi matematika, komputer, dan teori komunikasi.

Dalam melakukan konstruksi finite field _{(5), langkah pertama yang} dilakukan adalah dengan memilih polinomial irredusibel berderajat 5 atas _{Z ,} misalkan _{( ) ϵ Z[x]. Kenapa kita memilih polinomial irredusibel f(x) ? karena} dengan memilih polinomial irredusibel f(x), menurut Teorema 2.35 _{[ ]/} 〈 ( )〉merupakan field. Menurut Teorema 2.39 [ ]/〈 ( )〉 ≃ ( ), sehingga menurut Teorema 2.44 _{[ ]/〈 ( )〉} dapat ditulis sebagai

{ + + ⋯ + | , , … , }. Langkah selanjutnya

mengetes apakah polinomial irredusibel f(x) tersebut mempunyai akar atau tidak. Hasilnya dipergunakan untuk mengkonstruksi perluasan field F. Teorema berikut menjelaskan bahwa _{[ ]/〈 ( )〉 ≃ ( ) ≃ (5).}

Teorema 3.1. Misal p x

 

yaitu polinomial irredusibel berderajat n atas Z_p.

( ) = + + ⋯ + , , … , merupakan field.

Bukti:

Diketahui p x

 

yaitu polinomial irredusibel berderajat m atas Z_p. Misalkan : [ ] → () yaitu fungsi yang didefinisikan ( ) = ( ) ( ). Fungsi f dibawah operasi  dan  merupakan homomorfisma karena

( ( ) + ( )) = ( ( ) + ( )) ( )

= ( ( ) ( )) + (( ) ( )) = ( ( )) + ( ( ))

15

( ( ). ( )) = ( ( ). ( )) ( )

= ( ( ) ( )). (( ) ( )) = ( ( )). ( ( ))

Fungsi f surjektif karena ambil _{( ) ( ) ) terdapat ( ) [ ](} sedemikian hingga _{( ( )) = ( ) ( )}

Kernel dari f yaitu

( ) = ( ) [ ] ( ) = 0

_{= { ( ) [ }| ( ) ( ) = 0} = 〈 ( )〉}

Karena fungsi f homomorfisma dan surjektif maka f epimorfisma. Selanjutnya dengan memandang Teorema Dasar homomorfisma maka _{[ ]/〈 ( )〉 ≅}

( ). Menurut Teorema 2.35 F x

   

p x field maka terbukti _{( ) juga} field.

Akibat dari teorema di atas, maka _{[ ]/〈 ( )〉 ≃ ( ) ≃ (5)} sehingga diperoleh representasi _{(5) sebagai berikut .}

1. field _{(5) = { + + ⋯ +} | , , … , }

2. field _{(5) dapat dipandang sebagai ruang vektor atas} berdimensi m dengan basis standar _{{1, , , … , }.}

3. field GF(5m) dapat dipandang sebagai vektor dengan koordinatnya

{ , , … , }, sehingga kita dapat menulis (5) = {[ , , … , ]| , , … , }.

Misal diberikan field hingga _{(5) dan didefinisikan (5)}∗ yaitu himpunan unsur-unsur _{(5) yang bukan nol dan dinotasikan dengan} (5)\{0}. Dua teorema berikut menjelaskan bahwa (5)∗ _merupakan grup siklik multiplikatif dan mempunyai generator c yang merupakan unsur primitif dari _(5).

Teorema 3.2. _{( )}∗ _{merupakan grup siklik multiplikatif ber order − 1.} Bukti:

Dari Definisi field _{( )}∗ _{merupakan grup multiplikatif. Misal ()}∗ Karena _{( )}∗ _{ber order − 1 maka c mempunyai paling banyak} i _{− 1}

16 r i i c  _c

 

_{c c c}r i i _{c c}i i  





1 r i i c c c   (Sifat Assosiatif) 1 r c   .

Dapat disimpulkan r_{Z minimum sehingga}  _{O c}

 

_r.

Pilih c sehingga r sebesar mungkin. Akan ditunjukkan order l dari sembarang ()∗ _{yaitu membagi r. Untuk sembarang prima}

_

_{, misal r}a_{r' dan}

'

b

l l dimana 'r dan l' tidak dapat dibagi oleh



. Maka ca mempunyai order 'r , _l' _{mempunyai order }b_{, dan} a _l'

c  mempunyai order _b_r'_{. Dari} sini diperoleh b a atau r tidak maksimal. Dapat disimpulkan setiap pangkat prima pembagi dari l juga pembagi dari r dan l r.

Maka setiap ₍₎∗ _{memenuhi persamaan x}r_{  . Artinya 1 0 x}r_{ dapat 1}

dibagi oleh





* F x    



. Karena _{∃ − 1 ()}∗, _{≥ − 1 tetapi} ≤ − 1 maka diperoleh _{= − 1.} Sehingga diperoleh





1 * 1 n p F x x       



dan. _{( )}∗ _{= , , , … , , = 1}

Teorema 3.3. Sembarang _{( ) memuat suatu unsur primitif atau akar} primitif.

Bukti:

Misal _{( ) field berhingga berorder . Ambil c sebagai generator grup} siklik _{( )}∗_{. Dari Definisi 2.43 maka c merupakan unsur primitif atau akar} primitif.

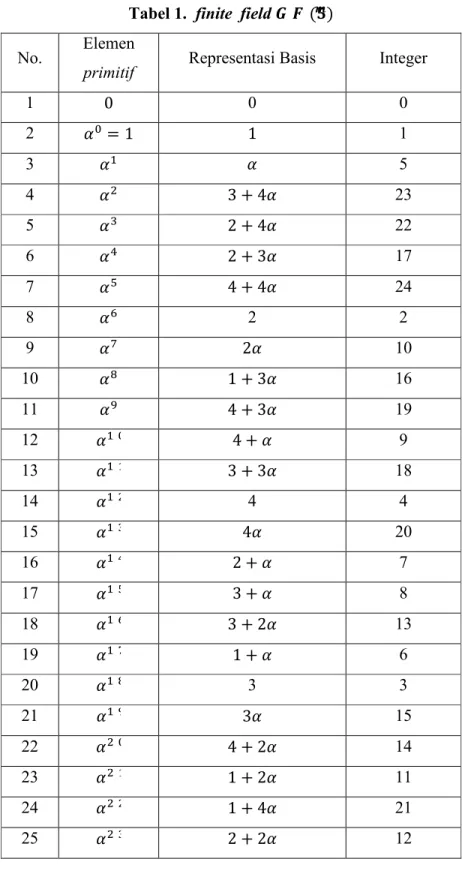
Karena ₍₅₎∗ merupakan grup siklik multiplikatif, maka terdapat (5)∗ _{sehingga (5)}∗_{= 〈 〉 = 1, , , . . . , . Sebagai} akibatnya _{(5) = 0, 1, , , . . . ,} . Tabel berikut ini menunjukkan adanya hubungan antara representasi elemen primitif, representasi basis polinomial, dan representasi integer dalam _{(5) yang dibangun oleh} polinomial primitif _{( ) = + + 2}

17

Tabel 1. finite field _{( )}

No. Elemen

primitif Representasi Basis Integer

1 ₀ 0 0 2 _{= 1 1} 1 3 5 4 _{3 + 4} 23 5 _{2 + 4} 22 6 _{2 + 3} 17 7 _{4 + 4} 24 8 2 2 9 ₂ 10 10 _{1 + 3} 16 11 _{4 + 3} 19 12 _{4 +} 9 13 _{3 + 3} 18 14 4 4 15 ₄ 20 16 _{2 +} 7 17 _{3 +} 8 18 _{3 + 2} 13 19 _{1 +} 6 20 3 3 21 ₃ 15 22 _{4 + 2} 14 23 _{1 + 2} 11 24 _{1 + 4} 21 25 _{2 + 2} 12

18

3.1. Polinomial Minimum

Kenapa kita perlu membahas polinomial minimum ? Karena polinomial minimum menjamin bahwa polinomial tersebut adalah irredusibel dan jika berunsur primitif merupakan polinomial primitif. polinomial primitif inilah yang akan kita gunakan dalam mengkonstruksi algoritme aritmetik _(5).

Definisi 3.4. polinomial minimum M x

 

dari c atas Z merupakan polinomial _p monik berderajat terendah dengan koefisien dari Z sehingga_p M c

 

0.

Teorema 3.5. Misalkan m(x) adalah polinomial minimum dengan unsur α dalam finite field GF(pm_{). Maka}

(i) m(x) irredusibel

(ii) jika α akar dari polinomial f(x) dengan koefisien didalam GF (p), maka m(x) membagi f(x)

(iii) m(x) membagi ₋ (iv) derajat _{( ) ≤}

(v) Polinomial minimum berunsur primitif dari _{( ) yang berderajat m} merupakan polinomial primitif.

Bukti :

(i) Jika m(x) redusibel, maka _{( ) = ( ) ( ).} Sebagai akibatnya ( ) = 0. Karena tidak memuat pembagi nol, maka _{( ) = 0atau} ( ) = 0.Hal ini kontradiksi dengan Definisi 3.4. Sehingga dapat disimpulkan bahwa _{( )polinomial irredusibel.}

(ii) Dengan menggunakan algoritma pembagian, _{( ) = ( ) ( ) + ( )}, dimana derajat dari _{( )lebih rendah daripada derajat ( )}. Karena

( ) = ( ) = 0, ( ) = 0. Dan karena derajat dari _{( )lebih rendah} daripada derajat _{( ), maka ( ) ≈ 0.}

(iii) Dari pembuktian sifat (ii) terbukti m(x) membagi ₋

(iv) Karena _{() dan ( ) ruang vektor berdimensi m atas ( )}. Ada _{+ 1sembarang anggota yaitu {1, , … , } yang tak bebas linear.}

+ + ⋯ + = 0 dan terdapat = {1, 2, … , sehingga } ( ). Maka _∑ merupakan polinomial berderajat _≤ yang mempunyai akar c sehingga derajat _{( ) ≤}

19

(v) Misal _{() unsur primitif. Menurut sifat 1, polinomial minimum} ( )berderajat d merupakan polinomial irredusibel. Dengan Teorema 3.1, gunakan _{( )untuk membangun field F ber order} . Karena F memuat c dan semua unsur dari _{( ), maka ≥ . Selanjutnya} menurut sifat 4, derajat _{( ) ≤ , mengakibatkan =}

Dua teorema berikut menegaskan tentang eksistensi dan ketunggalan dari finite field _(5).

Teorema 3.6. Semua field hingga ber order adalah isomorfik. Bukti:

Misal F dan G field ber order . Misal _{( )polinomial minimum dari}



F

dan _{( )polinomial minimum lain dari}  . Menurut Teorema 3.3, G



F

dan G merupakan unsur primitif atau akar primitif dari F dan dari G, dan dengan Teorema 3.5.5 merupakan polinomial primitif. Dengan Teorema 3.5.3,. ( )| − . Dan dari Teorema 3.5.4, derajat ( ) ≤ sehingga dengan Teorema 3.1, field F dan G dapat dianggap memuat semua polinomial dalam 

dan  berderajat  n 1, yaitu memuat polinomial modulo _{( ). Maka dapat} dikatakan pemetaan   merupakan isomorfima pemetaan FG.

Teorema 3.7. Untuk sembarang p prima dan bilangan bulat _{≥ 1, maka ada} tunggal field ber order yang dinotasikan dengan _{( ).}

Bukti:

Misal _{( ). perluasan field hingga dari ( )}.. Untuk _{= 1,} GF p

 

 Z_p.

Untuk _{> 1bentuk} F1GF p

 

.

Akan dibuktikan _{( ) field yang memuat semua akar dari . −}

Misal f x₁

 

faktor irredusibel berderajat 2 dari _{− atas} F . Menurut ₁ Teorema 3.1 dengan menggunakan p x

 

 f x1

 

dapat diperoleh field baru F .2

Misal f x2

 

faktor irredusibel berderajat 2 dari − atas F . Menurut 2

Teorema 3.1 dengan menggunakan p x

 

 f x2

 

dapat diperoleh field baru F .3

20

Sehingga diperoleh: _{( ) = − = ( ) ( ) … ( )}

Berikut ini merupakan Teorema dan Lemma sub field dari _{( ).}

Lemma 3.8. Jika n, r, s bilangan bulat dengan n1,r1,s , maka 1 _ns_1_nr_1 jika dan hanya jika s r.

Bukti: Misal r Qs R  dimana 0 R s  . 1 1 1 1 1 1 1 1 r Qs R Qs r R s s s s n n n n n n n n n   _  _{ }  _      .

Maka _nQs_{ selalu dapat dibagi dengan} 1 _ns_{ . 1}

Teorema 3.9.

i) _{GF p}

 

r _{memuat sub field (isomorfik dengan ) GF p}

 

s _{jika dan hanya jika}

s r.

ii) Jika _{c GF p}

 

r _{, maka c GF p}

 

s _{jika dan hanya jika c}ps _{ . Untuk c}

sembarang field jika _c2_{ , maka c yaitu 0 atau 1.c}

Bukti:

i)  Misal ) _{c GF p}

 

s _{merupakan unsur primitif maka p}s 1 ₁

c   sehingga

 

s 1

O c  p  Karena _{GF p}

 

s _{sub field GF p}

 

r _{maka c GF p}

 

r

sehingga _pr 1 ₁

c  _{ . Berdasarkan sifat dasar ketiga dalam Ringkasan 2.3, maka}

1 1

s r

p  p  dan selanjutnya dengan Lemma 3.11 mengakibatkan s r.

)

 Misal _{c GF p}

 

s _{merupakan unsur primitif maka p}s 1 ₁

c  _{ sehingga}

 

s 1

O c  p  . Dengan Lemma 3.11, karena s r diperoleh _ps_1 _pr_{ .} 1 Karena _ps_1 _pr_{ dan} 1 _{GF p}

 

s _{sub field GF p}

 

r _{akibatnya p}s 1 ₁

c   sehingga _{c GF p}

 

r _.

21

ii)  Diketahui ) _{c GF p}

 

r _{, maka c GF p}

 

s _{. Dari Teorema Fermat setiap}

unsur _{c GF p}

 

s _{memenuhi c}ps _{ .c}

)

 Misalkan _{c GF p}

 

r _{dan diketahui p}s

c  . Dari i) karena c _{GF p}

 

s _sub

field _{GF p}

 

r _{maka c GF p}

 

s _.

= ↔ − = 0 ↔ ( − 1) = 0. Karena merupakan Daerah Integral dan tidak memuat pembagi nol diperoleh c0 atau. _{− 1 = 0 ↔ = 1}

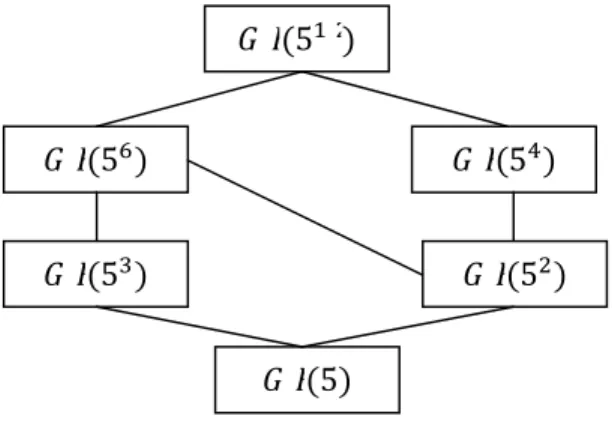
Dari teorema di atas, kita bisa mengetahui bahwa sub field dari _{(5 )} adalah _{(5 ), (5 ), (5 ), (5 ), (5 ), dan (5)}. Secara jelas dapat digambarkan sebagai berikut :

Untuk mencari polinomial monik dan irredusibel dalam _{(5) digunakan} teorema berikut ini.

Teorema 3.10. _{− =perkalian semua polinomial monik, irredusibel atas}

p

Z yang derajatnya membagi m. Bukti:

)

 Misal M x

 

polinomial irredusibel atas Z_p berderajat d, dimana | . Untuk kasus M x

 

x trivial. Asumsi M x

 

x. Gunakan M x

 

untuk membuat field, maka M x

 

merupakan polinomial minimum. Misalkan _{( ) =}

− dan dari Teorema3.5.3: ( )| − . Dengan memandang Lemma (5 ) (5) (5 ) (5 ) (5 ) (5 )

22

3.8, karena | maka _{− 1| − 1 dan} − − ↔ −

1 − 1. Oleh karena itu _{( )}| − . )

 Misal M x

 

pembagi dari _{− , polinomial irredusibel, dan berderajat d.} Akan ditunjukkan _{| . Asumsi. ( ) ≠ → ( )}−1_{− 1. Gunakan M x}

 

untuk membuat field _{GF p}

 

d _{ber order p . Misal} d _{c GF p}

 

d _{akar dari}

 

M x dan _{GF p}

 

d _{merupakan unsur primitif dapat dinyatakan}

2 1 0 1 2 ... 1 d d a a c a c a c         (*) (menurut Teorema 2.44)

Karena c akar dari M x

 

maka _{( ) = 0 ↔ − = 0 ↔ = ↔} . = . ↔ = 1. Dari (*) dan Teorema 2.16:



_{a b}



p _ap_bp

maka diperoleh _{− = 0 ↔ = ↔ = ↔ = 1.}

Berdasarkan sifat dasar ketiga dalam Ringkasan 2.5 maka _pd _1 _pn_{ .} 1 Selanjutnya dengan Lemma 3.8 diperoleh d n.

Dari teorema di atas kita dapat mencari polinomial irredusibel dan polinomial monik dalam _{(5) sebagai berikut :}

 _{Untuk = 1} ( ) = − = + 4 = ( + 4) = ( + 1)( + 4) = ( + 2)( + 3)( + 1)( + 4)  _{Untuk = 2} ( ) = − = + 4 = ( + 4) = ( + 1)( + 4) = ( + 2)( + 3)( + 1)( + 4) = ( + 3)( + 2 + 4)( + 2)( + 3 + 4)( + 2) ( + 3)( + 1)( + 4) = ( + 2)( + 3)( + 1)( + 1)( + 4)( + 3) ( + 2)( + 4 + 1)( + 3 + 4)( + + 1) ( + 2 + 4)( + + 2)( + 4 + 2)  _{Dan seterusnya}

23

Untuk memeriksa bahwa polinomial yang diperoleh merupakan polinomial irredusibel dan polinomial primitif digunakan dua teorema berikut ini.

Teorema 3.11. Jika p adalah prima dan m adalah intejer positif, maka berlaku : 1) Produk dari semua polinomial irredusibel monik dalam Ζp[x] yang derajatnya

membagi m atau faktor dari m sama dengan _{− .}

2) Misalkan f(x) adalah polinomial berderajat m dalam Ζp[x], maka f(x) irredusibel atas Ζp[x] jika dan hanya jika ( ), − = 1, untuk setiap _{1 ≤ ≤}

Bukti :

1) Misalkan f(x) polinomial irredusibel atas Ζpberderajat m, dimana | . Untuk kasus f(x) = x trivial. Asumsi _{( ) ≠ .Gunakan f(x) untuk membuat field} GF(pm_{), maka f(x) merupakan polinomial minimum. Misalkan ( ) = −} dan dari Teorema 3.5.4 maka _{( ) − 1. Dengan memandang} Lemma 3.8 dan karena | maka − 1| − 1 dan − − ↔

− 1 − 1. Dengan demikian ( ) − . Sebaliknya misalkan f(x) pembagi dari _{− , polinomial irredusibel dan berderajat m. Akan} ditunjukkan bahwa _{| . Asumsi ( ) ≠ → ( ) − 1. Gunakan f(x)} untuk membuat field GF(pm_{) ber order p}m_{. Misalkan () adalah akar} dari f(x) dan _{() merupakan unsur primitif maka menurut Teorema} 2.43 dapat dinyatakan sebagai _{= + + ⋯ +} (*). Karena α adalah akar dari f(x), maka _{( ) = 0 ↔ − = 0 ↔ = ↔}

. = . ↔ = 1.

Dari (*) dan Teorema 2.17 maka _{( + )= +} sehingga diperoleh :

− = 0 ↔ = ↔ . = . ↔ = 1

Berdasarkan sifat ketiga pada Ringkasan 2.5 maka _{− 1| − 1.} Selanjutnya berdasarkan Lemma 3.8 maka diperoleh | .

2) Berdasarkan Teorema 3.11 1), bahwa setiap intejer positif _{≥ 1, maka} polinomial _{− adalah produk dari semua irredusibel monik berderajat} membagi k. Jadi _{( − , ( )) adalah pasti produk dari semua faktor} linear f(x). Jika f(x) tidak mempunyai faktor linear maka _{( − , ( ))}

24

adalah pasti produk dari semua faktor irredusibel quadratik dari f(x). Jika f(x) tidak irredusibel maka harus dapat dibagi oleh beberapa polinomial irredusibel berderajat paling banyak _{/2 dan jika g(x) adalah faktor} irredusibel dari f(x) berderajat minimum (misalkan k), maka _{≤ /2}. Jadi ( − , ( )) ≠ 1. Hal ini kontradiksi dengan pengandaian. Sebaliknya jika f(x) adalah irredusibel, maka _{− , ( ) = 1,} untuk setiap _{1 ≤ ≤ . Jadi untuk mengetes f(x) adalah irredusibel, hal ini} cukup dites _{− , ( ) = 1 untuk setiap intejer positif 1 ≤ ≤}

. Dengan demikian dapat disimpulkan bahwa f(x) adalah irredusibel Teorema 3.12. Misalkan p adalah bilangan prima dan misalkan mempunyai faktor-faktor prima yang berbeda dari pm-1 adalah r1, r2, …, rt maka polinomial irredusibel _{( ) ( )[ ] adalah primitif jika dan hanya jika untuk setiap} 1 ≤ ≤ berlaku ≠ 1( ( ))

Bukti :

Misalkan p adalah bilangan prima dan misalkan faktorisasi dari _{− 1 adalah} r1, r2, …, rt, dimana r1, r2, …, rtadalah polinomial irredusibel atas GF(p)[x]. Akan dibuktikan bahwa jika x adalah unsur primitif atas GF(pm)* maka berlaku

≠ 1 ( ) untuk setiap 1 ≤ ≤

Misalkan d dinotasikan order dari x. Kita tahu bahwa d adalah pembagi dari − 1 dan x adalah primitif jika dan hanya jika = − 1.

Pertama, andaikan bahwa _{≡ 1( ( )) untuk beberapa i, maka jelas bahwa} ≤ − 1/ sehingga pasti ≠ − 1. Sebaliknya, andaikan bahwa ≠ 1 ( ) untuk 1 ≤ ≤ dan juga ≠ − 1. Karena d adalah pembagi dari

− 1 dan < − 1 maka terdapat polinomial irredusibel ridimana 1 ≤ ≤

sedemikian sehingga riadalah pembagi dari ( − 1)/ . Tetapi ini berakibat bahwa d

adalah pembagi _{( − 1)/ . Dengan demikian ≡ ≡ 1( ( )). Hal ini} kontradiksi dengan pernyataan bahwa _{≠ 1 ( )}

BAB IV

KONSTRUKSI ALGORITME ARITMETIK _{( )}

Seperti yang telah dijelaskan dalam Bab III, bahwa _{(5) dapat} direpresentasikan ke dalam bentuk polinomial dan vektor. Demi kemudahan komputasi dalam tesis ini digunakan representasi vector. Berikut ini diberikan ilustrasi operasi penjumlahan dengan representasi vektor.

Misalkan diberikan vektor _{=(0, 1, 2, 3) sebagai representasi dari} ( ) = + 2 + 3 dan vektor _{=(2, 2, 3, 1) sebagai reprentasi dari} ( ) = 2 + 2 + 3 + dalam _{(5), maka}

+ =(0, 1, 2, 3) + (2, 2, 3, 1) =

(0 + 2) 5,( 1 + 2) 5,( 2 + 3) 5,( 3 + 1) 5 = (2, 3, 0, 4). Untuk mengkonstruksi aritmetik GF (5m) dalam penelitian ini langkah pertamanya adalah dengan memilih polinomial primitif berderajat m atas Z5,

misal _{( ) ∈ [ ] dimana ( ) = + + ⋯ +} sehingga diperoleh unsur primitif α dengan M(α) = 0. Kemudian, tentukan basis dari GF(5m) sebagai ruang vektor atas Z5, yaitu {1, α1, α2, …, αm-1}. Dengan demikian, diperoleh

himpunan _{(5 ) = { + + ⋯} | , , … , ∈ (5)}.

Kemudian semua unsur dari _{(5 ) direpresentasikan ke dalam bentuk ruang} vektor berdimensi m atas . Tabel berikut ini menunjukkan adanya hubungan antara representasi elemen primitif, representasi basis polinomial, representasi vektor penta, dan representasi integer dalam _{(5 ) yang dibangun oleh polinomial} primitif _{( ) = + + 2}

Tabel 2. Representasi finite field _{( )}

No. Elemen

primitif Representasi Basis Vektor penta Integer

26 2 _{= 1 1} (1, 0) 1 3 (0, 1) 5 4 _{3 + 4} (3, 4) 23 5 _{2 + 4} (2, 4) 22 6 _{2 + 3} (2, 3) 17 7 _{4 + 4} (4, 4) 24 8 2 (2, 0) 2 9 ₂ (0, 2) 10 10 _{1 + 3} (1, 3) 16 11 _{4 + 3} (4, 3) 19 12 _{4 +} (4, 1) 9 13 _{3 + 3} (3, 3) 18 14 4 (4, 0) 4 15 ₄ (0, 4) 20 16 _{2 +} (2, 1) 7 17 _{3 +} (3, 1) 8 18 _{3 + 2} (3, 2) 13 19 _{1 +} (1, 1) 6 20 3 (3, 0) 3 21 ₃ (0, 3) 15 22 _{4 + 2} (4, 2) 14 23 _{1 + 2} (1, 2) 11 24 _{1 + 4} (1, 4) 21 25 _{2 + 2} (2, 2) 12

Bagaimana memilih polinomial primitif? Sebagaimana telah dijelaskan sebelumnya, polynomial primitif adalah polinomial irredusibel yang akarnya adalah generator dari GF(5)*. Oleh karena itu, diperlukan pemilihan polinomial

27

irredusibel terlebih dahulu. Sesuai dengan Teorema 3.14, diperoleh Algoritme pengetesan polinomial irredusibel sebagai berikut :

Algoritme 4.1. Pengetesan polinomial irredusibel

Setelah kita mendapatkan polinomial irredusibel, kemudian memeriksa apakah polinomial irredusibel yang didapatkan tersebut merupakan polinomial primitif atau bukan. Untuk memeriksa polinomial irredusibel adalah primitif, digunakan Algoritme 4.2. Berdasarkan Teorema 3.15 diperoleh Algoritme 4.2 sebagai berikut :

Deskripsi : Mengetes Vektor Apakah Irredusibel atau Redusibel Input : Vektor A

Output : True atau False

1. a = banyaknya unsur A – 1, _{= ( /2)dibulatkan ke bawah} 2. W = [0, 1]

3. Untuk I dari 1 sampai m, lakukan secara berulang : 3.1. W = W pangkat 5 modulo A

3.2. U= Jumlahkan W dengan [0, 4] menggunakan algoritme 4.4

3.3. H = FPB(U,A)

3.4. h = banyaknya unsur H 3.5. jika h > 1, maka return(false) 4. Return (True)

28

Algoritme 4.2. Pengetesan polinomial primitif

Untuk mempercepat komputasi, dipilih polinomial primitif yang bersuku terkecil. Hal ini sangatlah beralasan, sebab operasi pada finite field ₍₅₎ dilakukan dalam modulo f(x), dimana f(x) merupakan polinomial primitif. Dengan memilih polinomial primitif bersuku terkecil akan mengakibatkan proses komputasi yang dijalankan lebih cepat dibandingkan dengan menggunakan polinomial primitif biasa. Adapun polinomial primitif yang sudah diperoleh dapat dilihat di Lampiran I.

4.1 Penjumlahan Polinomial

Seperti telah dijelaskan di atas, solusi yang digunakan di sini dengan menggunakan representasi vektor penta. Misal diberikan dua sembarang fungsi

polinomial _{( ) = + + ⋯} dan _{( ) = + + ⋯}

maka bentuk field penjumlahannya adalah sebagai berikut :

( ) + ( ) = ( + ) + ( + ) + ⋯ +( + )

Fungsi polinomial a(x) direpresentasikan sebagai vektor penta = [ , , … , ], sedangkan fungsi polinomial b(x) sebagai vektor = [ , , … , ]. Operasi penjumlahan yang digunakan di sini yaitu instruksi Deskripsi : Mengetes Vektor Irredusibel Apakah Primitif atau Bukan

Input : Vektor A Output : True atau False

1. m = banyaknya unsur A – 1, h = 5m– 1 2. F = faktorkan h

3. a = banyaknya unsur F

4. Untuk i dari 1 sampai a, lakukan secara berulang 4.1. k = h/i

4.2. H = [0, 1] pangkat k modulo A 4.3. Jika H = [1], maka return(false) 5. Return(True)