Model Generalized Autoregressive Conditional Heteroscedastic (GARCH) - USD Repository

MODEL GENERALIZED AUTOREGRESSIVE CONDITIONAL HETEROSCEDASTIC (GARCH)

S K R I P S I

Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun Oleh : NANIN FERYANTI

NIM : 053114011

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

GENERALIZED AUTOREGRESSIVE CONDITIONAL

HETEROSCEDASTIC (GARCH) MODEL

T H E S I S

Presented as A Partial Fulfillment of The Requirements to Obtain The Sarjana Sains Degree

In Mathematics

By :

NANIN FERYANTI Student Number : 053114011

MATHEMATICS STUDY PROGRAM DEPARTEMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

TEMBIKAR

Terlalu gigih kucoba

Menjalani hidup ini dengan bermegah diri Hingga suatu hari

Hidupku terlepas jatuh dari tanganku dan hancur berantakan di sekelilingku

Hancur

Aku menanti Allah membentakku dengan keras “Sudah Kubilang!”

Namun,

Dia justru menghampiri ke tempat aku terjatuh dan memungut kepingan-kepingan itu

Lalu berkata, “Jangan menangis. Itu hanya tembikar biasa,

Hanya tembikar biasa.”

ABSTRAK

Model Autoregressive Conditional Heteroscedastic (ARCH) merupakan model Autoregresif dengan variansi bersyarat tidak konstan. Variansi ini dipengaruhi oleh data masa lalu. Model Generalized Autoregressive Conditional Heteroscedastic (GARCH) merupakan perumuman dari model ARCH. Variansi dalam model GARCH dipengaruhi oleh data dan variansi masa lalu. Model GARCH yang paling sederhana adalah model GARCH(1,1). Model tersebut diharapkan mampu menggantikan model ARCH dengan orde tinggi sehingga model menjadi lebih sederhana. Penduga parameter dari model ini dapat diperoleh dengan metode kemungkinan maksimum.

ABSTRACT

Autoregressive Conditional Heteroscedastic (ARCH) model is autore-gressive model and its conditional variance is not constant. This variance depend on past observations. Generalized Autoregressive Conditional Heteroscedastic (GARCH) model is generalization of ARCH model. Its variance depend on past observations and past variance. The simplest GARCH model is GARCH (1,1). It might replace a high order ARCH(q) giving a more parsimonious model. Parameters estimator is found by maximum likelihood method.

KATA PENGANTAR

Puji syukur penulis panjatkan pada Allah Bapa di Surga karena telah melimpahkan berkat dan kesehatan sehingga penulis dapat menyelesaikan skripsi ini dengan baik. Skripsi ini ditulis untuk memenuhi salah satu syarat memperoleh gelar Sarjana Sains di Program Studi Matematika Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta.

Dalam pembuatan skripsi ini penulis mendapatkan bantuan baik moril maupun materiil dari berbagai pihak. Oleh karena itu, penulis ingin mengucapkan terima kasih kepada:

1. Enny Murwaningtyas, S.Si., M.Si., selaku dosen pembimbing yang telah meluangkan banyak waktu, membimbing dan mendorong penulis dengan penuh kesabaran.

2. Yosef Agung Cahyanta, S.T., M.T., selaku Dekan Fakultas Sains dan Teknologi.

3. Lusia Krismiyati Budiasih, S.Si, M.Si selaku Ketua Program Studi Matematika.

4. Hongki Julie, S.Si, M.Si selaku dosen penguji yang telah memberikan masukan-masukan dan koreksi.

5. Prof. Dr. Frans Susilo, S.J., selaku dosen pembimbing akademik.

7. Zaerilus Tukija dan Erma Linda Santyas Rahayu yang telah memberikan pelayanan administrasi selama penulis kuliah.

8. Perpustakaan Universitas Sanata Dharma yang memberikan fasilitas dan kemudahan kepada penulis.

9. Kedua orang tua yang selalu mendukung penulis dengan doa, semangat, dan materi.

10. Agustinus Joko Pramudi (adik) dan Yano Kristianto (kemenakan) yang selalu memberikan semangat dan dorongan, serta doa.

11. Herningtyas Kurniawati, Wiwin Kartika Putri, Vincentius Prabowojati Wicaksana, dan Maria Endah Savitri yang selalu memberikan semangat dan dorongan.

12. Semua pihak yang telah ikut membantu penulis dalam menyelesaikan skripsi ini.

Penulis menyadari bahwa skripsi ini masih jauh dari sempurna. Oleh karena itu, penulis sangat mengharapkan kritik dan saran yang dapat membangun dan menyempurnakan skripsi ini. Akhirnya, semoga skripsi ini dapat memberikan wawasan dan pengetahuan bagi pembaca demi perkembangan ilmu pengetehuan, khususnya matematika.

Yogyakarta, 30 September 2009

DAFTAR ISI

HALAMAN JUDUL ………. HALAMAN PERSETUJUAN PEMBIMBING………. HALAMAN PENGESAHAN……… HALAMAN KEASLIAN KARYA………... HALAMAN PERSEMBAHAN………. ABSTRAK………. ABSTRACT………... KATA PENGANTAR……… DAFTAR ISI……….. DAFTAR TABEL……….. DAFTAR GAMBAR……… BAB I. PENDAHULUAN……… A. Latar Belakang Masalah……… B. Perumusan Masalah………... C. Batasan Masalah………

D. Tujuan Penulisan………

E. Manfaat Penulisan……….. F. Metode Penulisan………... G. Sistematika Penulisan……… BAB II. DASAR-DASAR TEORI PROBABILITAS……….. A. Variabel Random dan Distribusi Probabilitasnya………..

1. Variabel Random Diskret dan Kontinu………. 2. Distribusi Probabilitas………... 3. Nilai Harapan dan Variansi………... B. Distribusi Normal……….. C. Distribusi Probabilitas Bersama………. D. Sifat-Sifat Variabel Random -Dimensi………...

1. Nilai Harapan dan Variansi dari Variabel Random -Dimensi…

BAB III. DASAR-DASAR ANALISIS RUNTUN WAKTU DAN DERET WAKTU LINEAR………... A. Stasioneritas………... B. Fungsi Autokorelasi………... C. Deret White Noise……….. D. Deret Waktu Linear………... E. Model Autoregresif (AR)……….. 1. Sifat-sifat Model AR (1)………... 2. Sifat-sifat Model AR (2)………... 3. Sifat-sifat Model AR (p)………... 4. Identifikasi Model AR (p)………. F. Model Moving-Average (MA)………... 1. Sifat-sifat Model MA (1)……….. 2. Sifat-sifat Model MA (2)……….. 3. Sifat-sifat Model MA (q)……….. G. Model Autoregresif Moving-Average (ARMA)……….... 1. Sifat-sifat Model ARMA (1,1)……….. 2. Sifat-sifat Model ARMA (p,q)……….. 3. Peramalan dengan Model ARMA (p,q)……… BAB IV. MODEL HETEROSKEDASTIK BERSYARAT…………. A. Model Autoregressive Conditional Heteroscedastic (ARCH)……..

1. Sifat-sifat Model ARCH (1)………. 2. Sifat-sifat Model ARCH (m)………. 3. Langkah-langkah Menyusun Model ARCH………. a. Menentukan persamaan rata-rata yang sesuai……….. b. Pengujian efek ARCH……….. c. Menentukan orde m………..

(GARCH)………... 1. Sifat-sifat model GARCH (m,s)……… 2. Sifat-sifat model GARCH (1,1)……… 3. Langkah-langkah Menyusun Model GARCH……….. 4. Peramalan dengan menggunakan model GARCH (1,1)………... BAB V. APLIKASI MODEL GARCH PADA DATA HARGA SAHAM MATAHARI PUTRA PRIMA DAN ASTRA AGRO LESTARI INDONESIA……… A. Aplikasi pada Harga Saham Matahari Putra Prima………... B. Aplikasi pada Harga Saham ASTRA Agro Lestari Indonesia…….. BAB VI. PENUTUP……….

A. Kesimpulan………

B. Saran……….. DAFTAR PUSTAKA……… LAMPIRAN

127 128 134 140 142

Tbk dengan Menggunakan Model MA (1)-GARCH(1,1)….. Tabel 5.2. Hasil Peramalan Data Harga Saham ASTRA Agro Lestari

Indonesia Tbk dengan Menggunakan Model AR(1)-GARCH(2,1)………...

156

Gambar 3.1.2. Deret waktu yang tidak stasioner dalam variansi…... Gambar 3.1.3. Deret waktu yang stasioner………. Gambar 3.5.1.1. Grafik ACF dari model AR(1) dengan

φ

₁ >0…… Gambar 3.5.1.2. Grafik ACF dari model AR(1) dengan

φ

1<0…….

Gambar 3.5.2.1. Grafik ACF dengan akar-akar karakteristik berni-lai real……… Gambar 3.5.2.1. Grafik ACF dengan akar-akar karakteristik

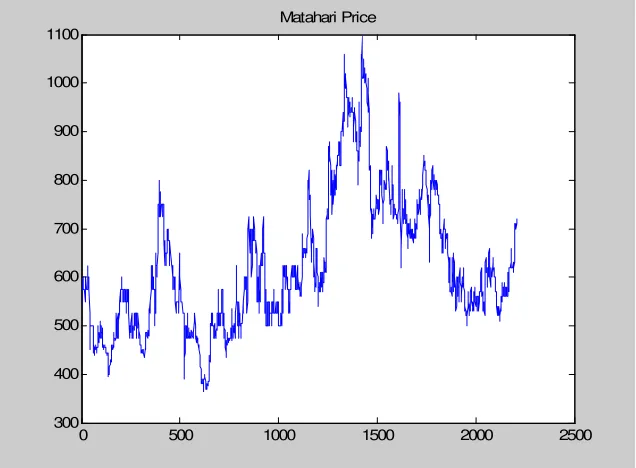
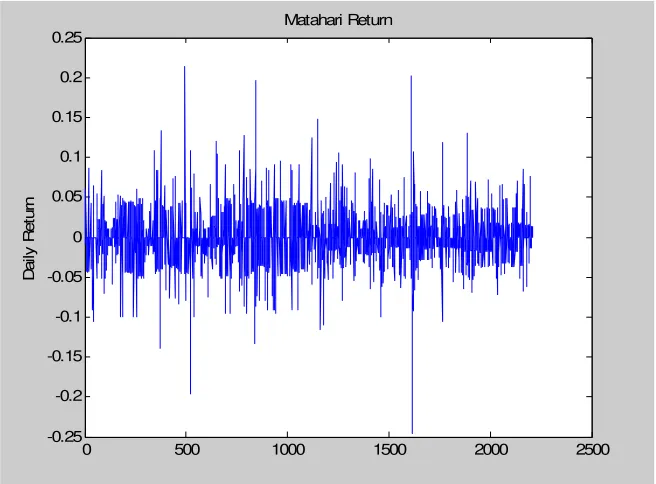
berni-lai kompleks……….. Gambar 5.1.1. Grafik Harga Saham Matahari Putra Prima………… Gambar 5.1.2. Grafik Return dari Harga Saham Matahari Putra

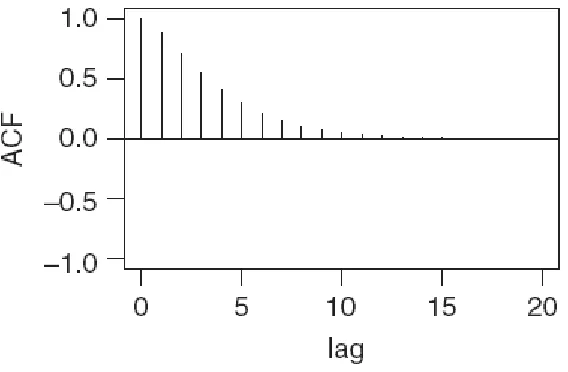
Prima………. Gambar 5.1.3. Grafik ACF Return dari Harga Saham Matahari

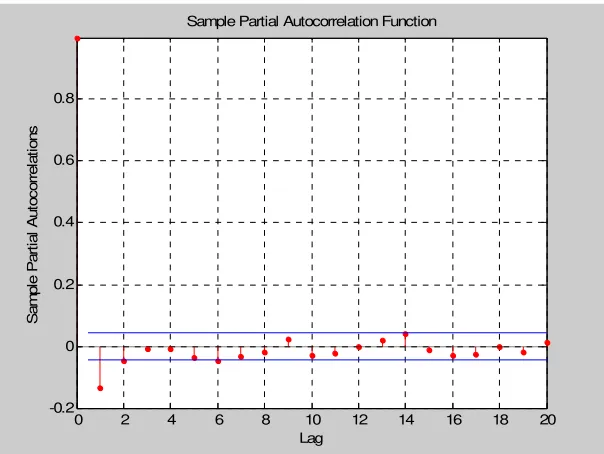
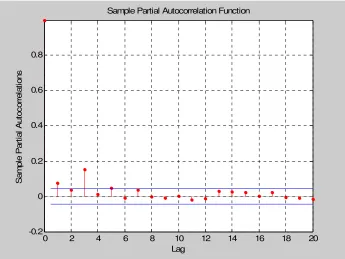
Putra Prima……… Gambar 5.1.4. Grafik PACF Return dari Harga Saham Matahari

Putra Prima……… Gambar 5.1.5. Grafik ACF galat kuadrat dari model ARMA(1,1)… Gambar 5.1.6. Grafik PACF galat kuadrat dari model ARMA(1,1).. Gambar 5.1.7. Grafik ACF galat kuadrat dari model MA(1)………. Gambar 5.1.8. Grafik PACF galat kuadrat dari model MA(1)……... Gambar 5.2.1. Grafik Harga Saham AALI.JK………... Gambar 5.2.2. Grafik Return dari Harga Saham AALI.JK………… Gambar 5.2.3. Grafik ACF Return dari Harga Saham AALI.JK…... Gambar 5.2.4. Grafik PACF Return dari Harga Saham AALI.JK…. Gambar 5.2.5. Grafik ACF galat kuadrat dari model AR(1)……….. Gambar 5.2.6. Grafik PACF galat kuadrat dari model AR(1)……… Gambar 5.2.7. Grafik ACF galat kuadrat dari model MA(1)………. Gambar 5.2.8. Grafik PACF galat kuadrat dari model MA(1)……...

47 48 68 68

74

75 145

146

147

BAB I.

PENDAHULUAN

A. LATAR BELAKANG

Beberapa analis pada sebuah media memaparkan bahwa seorang calon investor (individu yang akan bertransaksi saham pada suatu perusahaan) sangat memerlukan pengetahuan yang luas tentang perusahaan tersebut. Apa nama perusahaan tersebut, bisnis apa yang dijalankan, seberapa besar hutangnya, bagaimana perkembangan perusahaan tersebut adalah informasi-informasi yang seharusnya diketahui. Tak kalah pentingnya perlu diketahui juga informasi tentang pergerakan harga saham perusahaan tersebut dalam beberapa tahun terakhir, 1, 5, sampai 10 tahun yang lalu. Menurut beberapa data di lapangan, harga saham sekarang dipengaruhi oleh harga saham sebelumnya. Untuk selanjutnya, data yang dipengaruhi oleh data sebelumnya disebut data runtun waktu.

Salah satu model yang dikembangkan untuk memodelkan data runtun waktu adalah Autoregresi. Misalkan y1, y2,K, yt adalah data runtun waktu.

Berdasarkan asumsi terhadap variansinya, model autoregresi dibagi menjadi dua kelompok, yaitu:

1. Autoregresi dengan Var

( )

yt =σ2(variansi konstan), contohnya:model

Autoregressive (AR), Moving-Average (MA), Autoregressive Moving-Average (ARMA).

2. Autoregresi dengan

( )

2

t t

y

Var =σ (variansi berubah terhadap waktu) contohnya: model Autoregressive Conditional Heteroscedastic (ARCH) dan Generalized Autoregressive Conditional Heteroscedastic (GARCH).

2 1 2 1 0 2

j t s

j j i

t m

i i t

t t t

a u

a

− = −

=

∑

∑

+

+ = =

σ β α

α σ

σ

dengan

t = indeks waktu

t

a = galat pada waktu ke-t

2

t

σ = variansi pada waktu ke-t

{ }

ut = suatu barisan dari variabel random iid (independent and

identically distributed )

j i β

α

α0, , adalah konstanta

Setelah mendapatkan modelnya, selain dapat melihat pergerakan harga saham (yang diperlihatkan oleh variansi) pada masa lalu, model tersebut juga dapat digunakan untuk memprediksi pergerakan harga saham pada periode berikutnya.

B. RUMUSAN MASALAH

1. Apakah model GARCH itu?

2. Bagaimana cara menguji ada dan tidaknya efek GARCH pada suatu data?

3. Bagaimana cara mendapatkan orde (m,s) yang sesuai?

6. Apakah jika semakin tinggi ordenya, maka semakin tepat peramalan-nya?

C. BATASAN MASALAH

1. Pembahasan masalah hanya akan dibatasi pada model GARCH. 2. Sifat-sifat fungsi Gamma tidak dibuktikan.

3. Statistik -rasio tidak dibuktikan.

4. Pendekatan fungsi kriteria informasi tidak dibahas. 5. Aturan Cramer tidak dijelaskan secara rinci. 6. T-statistic tidak dibuktikan.

7. Statistik Ljung-Box tidak dibuktikan. 8. Statistik uji efek ARCH tidak dibuktikan.

D. TUJUAN PENULISAN

Tujuan yang akan dicapai dalam penulisan ini adalah: 1. Memahami model GARCH.

2. Mengetahui bagaimana cara mendapatkan orde yang sesuai.

3. Mengetahui bagaimana cara mendapatkan koefisien-koefisien dalam model GARCH.

E. MANFAAT PENULISAN

Manfaat yang dapat diambil dari penulisan ini adalah dengan pengetahuan yang ada tentang model GARCH kita dapat meramal pergerakan harga saham pada suatu perusahaan.

F. METODE PENULISAN

Metode yang digunakan adalah studi pustaka, baik dari buku-buku juga dari jurnal-jurnal ilmiah. Data akan diolah dengan software MATLAB.

G. SISTEMATIKA PENULISAN

BAB I : menjelaskan tentang latar belakang masalah, rumusan masalah, batasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan, dan sistematika penulisan.

BAB II : menjelaskan tentang variabel random dan distribusi probabilitasnya, distribui normal, distribusi probabilitas bersama, sifat-sifat variabel random k-dimensi, dan metode kemungkinan maksimum

BABIII : stasioneritas, fungsi autokorelasi (ACF), proses white noise, model Autoregresi (AR), model Moving-Average (MA), dan kombinasi model Autoregresi-Moving Average (ARMA).

BAB V : menjelaskan tentang penerapan model GARCH pada harga saham suatu perusahaan, pengujian efek GARCH, dan penentuan orde dan koefisien-koefisien model GARCH.

BAB II.

DASAR-DASAR TEORI PROBABILITAS

A. VARIABEL RANDOM DAN DISTRIBUSI PROBABILITASNYA

1. Variabel Random Diskret dan Kontinu

Suatu model matematika dari suatu kejadian dalam ruang sampel diekspresikan dalam bentuk nilai-nilai numeris daripada hasil percobaan. Misalnya, dalam sebuah percobaan pelemparan uang logam sebanyak tiga kali, ruang sampel yang dihasilkan dapat dituliskan sebagai berikut

, , , , , , ,

dengan =ruang sampel; =sisi gambar; =sisi angka. Bila yang diperhatikan adalah kemunculan sisi gambar sebagai suatu fungsi, maka setiap titik sampel dapat dipetakan pada bilangan 0,1,2, atau 3.

Definisi 2.1.1.1

Sebuah variabel random merupakan fungsi bernilai real yang didefinisikan pada sebuah ruang sampel.

random dibedakan atas diskret dan kontinu. Berikut adalah definisi dari kedua variabel random.

Definisi 2.1.1.2

Variabel random diskret adalah variabel random yang didefinisikan pada ruang sampel yang berhingga atau tak berhingga terbilang.

Contoh 2.1.1

Jika adalah variabel random yang menyatakan banyaknya pelemparan uang logam yang diperlukan sampai sisi angka muncul, menyatakan sisi gambar, dan

menyatakan sisi angka. Maka ruang sampel dari percobaan pelemparan uang logam berulang-ulang sampai sisi angka muncul adalah

, , , …

Banyaknya titik sampel pada himpunan tersebut tak berhingga, tetapi himpunan tersebut dapat dikorespondesikan satu-satu dengan himpunan bilangan cacah sehingga dapat dikatakan bahwa tak berhingga terbilang. Oleh karena itu, merupakan variabel random diskret.

Definisi 2.1.1.3

Suatu variabel random kontinu adalah variabel random yang didefinisikan pada ruang sampel yang tidak diskret.

2. Distribusi Probabilitas

Definisi 2.1.2.1

Fungsi , , , … yang menyatakan probabilitas untuk semua kemungkinan nilai variabel random diskret disebut fungsi probabilitas diskret.

Fungsi probabilitas tersebut dapat dinyatakan dalam rumus fungsi atau tabel pasangan nilai variabel random berikut dengan peluangnya (disebut distribusi probabilitas).

Sifat 2.1.2.1

Fungsi adalah fungsi probabilitas diskret jika dan hanya jika memenuhi (i) 0, untuk semua

(ii) ∑ 1

Bukti:

(ii) Nilai , 1,2, … merupakan semua kemungkinan nilai , maka kejadian

, 1,2, … merupakan partisi dari ruang sampel  , sehingga

∑ ∑ 1

Definisi 2.1.2.2

Fungsi disebut fungsi probabilitas kontinu (fungsi densitas) bagi variabel random jika dan hanya jika memenuhi syarat:

(i) 0 untuk semua nilai  bernilai real

(ii) ∞ 1

Cara lain untuk menyatakan distribusi probabilitas adalah dengan menyatakannya dalam interval, misalnya ∞, untuk semua bernilai real. Distribusi yang dinyatakan dengan cara demikian disebut fungsi distribusi kumulatif yang dibedakan atas diskret dan kontinu.

Definisi 2.1.2.3

Fungsi distribusi kumulatif suatu variabel random diskret didefinisikan sebagai untuk semua nilai real .

Definisi 2.1.2.4

Fungsi densitas  dapat diperoleh dari fungsi distribusi kumulatif melalui diferensiasi, yaitu

3. Nilai Harapan dan Variansi

Dalam statistika, konsep nilai harapan memegang peranan yang sangat penting. Rata-rata dan variansi adalah contoh yang paling mudah dan keduanya hampir selalu muncul dalam teknik-teknik analisis statistika elementer maupun lanjut. Nilai harapan dapat dinyatakan dalam definisi berikut.

Definisi 2.1.3.1

Andaikan X variabel random, maka nilai harapan dari variabel random X yang dinotasikan dengan didefinisikan sebagai berikut

(i) ∑ , jika X diskrit dengan fungsi probabilitas ,

(ii) , jika X kontinu dengan fungsi densitas .

Sifat 2.1.3.1

Bukti:

Pembuktian untuk variabel random kontinu.

. 1

Pembuktian untuk variabel random diskret dapat dikerjakan secara

analog.

Sifat 2.1.3.2

Jika variabel random dan konstanta, , konstanta. Bukti:

Pembuktian untuk variabel random kontinu.

Pembuktian untuk variabel random diskret dapat dikerjakan secara

Definisi 2.1.3.2

Andaikan X variabel random dan  adalah fungsi dari X, maka nilai harapan dari fungsi variabel random X yang dinotasikan dengan didefinisikan sebagai berikut

(i) ∑ , jika X diskrit dengan fungsi probabilitas .

(ii) , jika X kontinu dengan fungsi densitas .

Sifat 2.1.3.3

Jika adalah variabel random kontinu dengan fungsi densitas , dan merupakan fungsi-fungsi variabel random berharga real, maka

Bukti:

Menurut Definisi 2.3.2 (ii),maka

Definisi 2.1.3.4

Andaikan X variabel random, maka variansi X yang dinotasikan dengan didefinisikan sebagai berikut

(i) ∑ , jika X diskrit dengan fungsi probabilitas ,

(ii) , jika X kontinu dengan fungsi densitas

.

Sifat 2.1.3.4

Jika variabel random, maka .

Bukti:

Pembuktian untuk variabel random kontinu.

Ambil ,

Menurut Definisi 2.1.3.2 (ii), maka

Pembuktian untuk variabel random diskret dapat dikerjakan secara

Sifat 2.1.3.5

Jika variabel random kontinu dan konstanta, maka . Bukti:

Dengan menggunakan Sifat 2.1.3.4 diperoleh

Dengan menggunakan Sifat 2.1.3.2 diperoleh

Definisi 2.1.3.5

Andaikan X variabel random kontinu dan  fungsi densitas dari X . Momen ke-ℓ dari X didefinisikan sebagai berikut

ℓ′ ℓ ℓ

∞

, ℓ 1,2, …

Definisi 2.1.3.6

Andaikan X variabel random kontinu,  fungsi densitas dari X, dan   rata-rata dari X. Momen sentral ke-ℓ dari X didefinisikan sebagai berikut

ℓ   ℓ   ℓ

∞

Momen ke empat digunakan dalam formulasi kurtosis. Kurtosis mengukur keruncingan dari kurva distribusi frekuensi. Secara khusus, kurtosis dapat didefinisikan sebagai berikut.

Definisi 2.1.3.7

Andaikan X variabel random, rata-rata dari X , dan variansi dari X. Kurtosis dari X yang dinotasikan dengan didefinisikan sebagai berikut

 

Kuantitas dari 3 disebut excess kurtosis. Sebuah distribusi dengan

excess kurtosis bernilai positif membentuk kurva distribusi yang sangat runcing,

yang disebut leptokurtik. Dan sebaliknya jika excess kurtosis bernilai negatif membentuk kurva distribusi yang agak mendatar, disebut platikurtik.

B. DISTRIBUSI NORMAL

Distribusi normal ditemukan oleh De Moivre pada tahun 1733. Kemudian Gauss berhasil mendapatkan persamaan kurva normal melalui studi galat dalam pengukuran yang berulang-ulang terhadap benda yang sama. Sehingga distribusi normal sering disebut juga distribusi Gauss.

variabel random normal ini bergantung pada rata-rata dan simpangan bakunya .

Gambar 2.1. Kurva normal

Definisi 2.2.1

Variabel random dikatakan berdistribusi normal dengan rata-rata dan simpangan baku bila fungsi densitasnya berbentuk

; , 1

√2 ,   ∞ ∞

Untuk menunjukkan bahwa distribusi normal memenuhi sifat-sifat fungsi densitas diperlukan definisi dan sifat-sifat fungsi Gamma.

Definisi 2.2.2

Fungsi Gamma yang dinotasikan dengan Γ , untuk semua 0 didefinisikan sebagai berikut

Sifat 2.2.1

Fungsi Gamma memenuhi sifat-sifat berikut:

(i) Γ 1 Γ 1 , 1

(ii) Γ 1 !

(iii) Γ √

Selanjutnya akan diperlihatkan bahwa distribusi normal memenuhi sifat-sifat fungsi densitas. Fungsi densitas untuk variabel random yang berdistribusi normal menurut Definisi 2.2.1 adalah

; , 1

√2

(i) Karena nilai dan selalu positif, maka diperoleh

; , 1

√2 0

Syarat pertama menurut Definisi 2.1.2.2 dipenuhi. (ii) Akan dicari ∞ ; ,

√ ∞

(2.2.1)

Misalkan (2.2.2)

maka (2.2.3)

Dengan mensubstitusikan Persamaan 2.2.2 dan 2.2.3 pada Persamaan 2.2.1, maka diperoleh

1 √

1 √2 ∞

       2.2.4

Misalkan (2.2.5)

maka √2 (2.2.6)

dan √2   (2.2.7)

Dengan mensubstitusikan Persamaan 2.2.5 , 2.2.6 dan 2.2.7 pada Persamaan 2.2.4, maka diperoleh

1 √

1

√2 √2

∞

 

1 √

∞

        2.2.8

Dengan menggunakan Definisi 2.2.2, maka persamaan 2.2.8 menjadi

1

√ Γ

1 2

Dengan menggunakan Sifat 2.2.1(iii), maka persamaan tersebut menjadi

1

√ √ 1

Syarat ke dua menurut Definisi 2.1.2.2 dipenuhi.

Integran yang diperoleh dengan mensubstitusikan memegang

1

√2 ,  ∞ ∞

Berikut akan dicari rata-rata dan variansi serta nilai harapan dari dari variabel random yang berdistribusi normal standar.

(i) Rata-rata dari variabel random yang berdistribusi normal standar

1 √2 ∞

        2.2.9

Misalkan (2.2.10)

maka (2.2.11)

dengan mensubstitusikan Persamaan 2.2.10 dan 2.2.11 ke dalam Persamaan 2.2.9, maka diperoleh

1 √2

∞

1 √2

∞

1 √2

∞

1 √2

∞

1

√2 0       2.2.12

Dengan mensubstitusikan Persamaan 2.1.4.12 ke dalam persamaan tersebut, maka diperoleh

Dengan menggunakan Definisi 2.1.3.5 diperoleh

∞

(2.2.13)

Karena berdistribusi normal, maka

1 √2 ∞

       2.2.14

Misalkan (2.2.15)

maka √2 (2.2.16)

dan (2.2.17)

dengan mensubstitusikan Persamaan 2.2.15, 2.2.16, dan 2.2.17 ke dalam Persamaan 2.2.14, maka diperoleh

1

√2 2 √2  

1

√  

1

√ . 2

Dengan menggunakan Definisi 2.2.2, dapat diperoleh

2

√ Γ

3 2  

Dengan menggunakan Sifat 2.2.1 (i) dan (iii) dapat diperoleh

1

√ √ 1       2.2.18    

(iii) Nilai harapan dari

1 √2 ∞

Misalkan (2.2.19)

Maka     (2.2.20)

dan √2 (2.2.21)

dengan mensubstitusikan Persamaan 2.2.19, 2.2.20, dan 2.2.21 dapat diperoleh

4 1

√2 √2

∞

2 √

∞

2

√ . 2

∞

Dengan menggunakan Definisi 2.2.2 dapat diperoleh

4

√ Γ

5 2

Dengan menggunakan Sifat 2.2.1 (i) diperoleh

4 √

3 2Γ

3 2

6 √

1 2Γ

1 2

3

√ √ 3        2.2.22

Selanjutnya akan diperlihatkan bahwa dan adalah rata-rata dan variansi dari variabel random yang berdistribusi normal.

(i) Akan diperlihatkan bahwa

1 √2 ∞

       2.2.23

Misalkan (2.2.24)

maka (2.2.25) dan          2.2.26 Dengan mensubstitusikan Persamaan 2.2.24, 2.2.25, dan 2.2.26 ke dalam Persamaan 2.2.23 maka diperoleh

1

√2  

∞

 

1 √2 ∞

 

1 √2

∞ ₁

√2 ∞

 

1 √2

∞ ₁

√2 ∞

 

Dengan menggunakan Persamaan 2.2.9 dan sifat fungsi densitas dapat diperoleh

. 1 

. 0 (2.2.27)

(ii) Akan diperlihatkan bahwa

2

Dengan menggunakan Persamaan 2.2.27 dapat diperoleh

2

Dengan menggunakan Sifat 2.1.3.3 dapat diperoleh

2

Dengan menggunakan Sifat 2.1.3.1 dan 2.1.3.2 diperoleh

2

Dengan menggunakan Persamaan 2.2.27 dapat diperoleh

2

(2.2.28)

Akan dicari terlebih dahulu.

∞

Karena berdistribusi normal, maka

1 √2 ∞

        2.2.29

Misalkan (2.2.30)

dengan mensubstitusikan Persamaan 2.2.30, 2.2.31, dan 2.2.32 ke dalam Persamaan 2.2.29 dapat diperoleh

1 √2 ∞

2 1

√2 ∞

1 √2 ∞

2 1

√2 ∞

1 √2 ∞

1 √2 ∞

2 1

√2 ∞

1 √2 ∞

Dengan menggunakan Persamaan 2.2.9 dan 2.2.14 serta sifat fungsi densitas, maka diperoleh

2 . 1

Dengan menggunakan Persamaan 2.2.12 dan 2.2.18 dapat diperoleh

. 1 2 . 0

(2.2.33)

Dengan mensubstitusikan Persamaan 2.2.33 ke dalam Persamaan 2.2.28 dapat diperoleh

Sifat 2.2.2

Kurtosis dari variabel random yang berdistribusi normal bernilai 3. Bukti:

Menurut Definisi 2.2.3, formulasi kurtosis adalah sebagai berikut

       2.2.34

Misalkan , maka Persamaan 2.2.34 menjadi

Dengan menggunakan Persamaan 2.2.22 maka diperoleh

3 (2.2.35)

Excess kurtosis yang bernilai nol akan membentuk kurva distribusi normal

atau kurva mesokurtik.

C. DISTRIBUSI PROBABILITAS BERSAMA

Definisi 2.3.1

Distribusi probabilitas diskret bersama dari variabel random berdimensi ,

X , , … , didefinisikan sebagai

, , … , , , … ,

untuk semua kemungkinan nilai x , , … , dari X .

Definisi 2.3.1 menyatakan bahwa distribusi probabilitas bersama merupakan suatu tabel atau rumus yang mendaftarkan semua kemungkinan vektor nilai x bagi vektor variabel random X beserta dengan probabilitasnya yang sesuai.

Sifat 2.3.1

Fungsi adalah fungsi probabilitas diskret jika dan hanya jika memenuhi

(i) , , … , 0, untuk semua kemungkinan nilai x , , … ,

(ii) ∑ ∑ , , … , 1

Definisi 2.3.2

Jika dan adalah variabel random diskret yang didefinisikan pada ruang probabilitas maka fungsi distribusi bersama dan didefinisikan sebagai berikut

, ,

Definisi 2.3.3

Andaikan , , … , variabel random kontinu dengan fungsi distribusi bersama

, , … , , , … ,

untuk semua kemungkinan nilai x , , … , dari X .Fungsi

, , … , disebut fungsi densitas bersama.

Fungsi densitas bersama dapat diperoleh dari fungsi distribusi kumulatif melalui diferensiasi, yaitu

, , … ,     , , … ,

Sifat 2.3.2

Fungsi , , … , disebut fungsi densitas bersama -variabel random bila dan hanya bila

(i) , , … , 0, untuk semua kemungkinan nilai x , , … ,

(ii) ∞ ∞ ∞ , , … , 1

Definisi 2.3.3

(i) Jika pasangan variabel random diskret , mempunyai fungsi probabilitas bersama , maka fungsi probabilitas marginal dari dan adalah

∑ , dan ∑ ,

, dan ,

Fungsi probabilitas dari variabel random dengan nilai jika diketahui variabel random dengan nilai dilambangkan dengan | jika dan diskret, atau | jika dan kontinu. Fungsi probabilitas ini disebut fungsi probabilitas bersyarat. Fungsi probabilitas bersyarat dibedakan atas diskret dan kontinu.

Definisi 2.3.4

Andaikan dan variabel random diskret dengan fungsi probabilitas bersama

, dan fungsi probabilitas marginal dan secara

berturut-turut.

(i) fungsi probabilitas bersyarat dari dengan diketahui adalah sebagai berikut

| ,

dengan 0.

(ii) fungsi probabilitas bersyarat dari dengan diketahui adalah sebagai berikut

| ,

Definisi 2.3.5

Andaikan dan variabel random kontinu dengan fungsi probabilitas bersama

, dan fungsi probabilitas marginal dan secara berturut-turut.

(i) fungsi probabilitas bersyarat dari dengan diketahui adalah sebagai berikut

| , , 0

0,          

(ii) fungsi probabilitas bersyarat dari  dengan diketahui adalah sebagai berikut

| , , 0 

0,             

Definisi 2.3.6

(i) Andaikan mempunyai fungsi distribusi kumulatif , mempunyai fungsi distribusi kumulatif , dan dan   mempunyai fungsi distribusi kumulatif bersama , , maka dan dikatakan saling bebas jika dan hanya jika

,

untuk setiap pasangan bilangan real , .

(ii) Jika dan diskret dengan fungsi probabilitas bersama , dan fungsi probabilitas marginal dan secara berturut-turut, maka

dan dikatakan saling bebas jika dan hanya jika

untuk setiap pasangan bilangan real , .

(iii) Jika dan diskret dengan fungsi densitas bersama , dan fungsi densitas marginal dan secara berturut-turut, maka dan dikatakan saling bebas jika dan hanya jika

,

untuk setiap pasangan bilangan real , .

D. SIFAT-SIFAT VARIABEL RANDOM -DIMENSI

1. Nilai Harapan dan Variansi dari Variabel Random -Dimensi

Nilai harapan dari fungsi variabel random -dimensi dibedakan atas diskret dan kontinu.

Definisi 2.4.1.1

Andaikan , … , adalah variabel random dan , … , merupakan fungsi dari , … , , maka nilai harapan dari , … , yang dinotasikan dengan

, … , didefinisikan sebagai berikut

(i) , … , ∑ , … , , … , , jika X diskrit dengan

fungsi probabilitas bersama  , … , .

(ii) , … , , … , , … , … , jika X

Sifat 2.4.1.1

Jika , … , adalah variabel random, maka

Bukti:

Pembuktian untuk variabel random kontinu. Misalkan , … , ∑

Maka

, … ,

Dengan menggunakan Definisi 2.4.1.1 (ii) diperoleh

, ,

, ,

, ,

, ,

, ,

 

Pembuktian ∑ untuk variabel random diskret dapat dikerjakan secara

analog.

Sifat 2.4.1.2

Jika dan variabel random yang saling bebas dan  dan adalah fungsi dari dan secara berturut-turut, maka

Bukti:

Pembuktian untuk variabel random kontinu.

,

Pembuktian untuk variabel random diskret dapat dikerjakan

Sifat 2.4.1.2 dapat digunakan untuk lebih dari dua variabel random. Secara khusus, jika , … , variabel random yang saling bebas dan , … ,

merupakan fungsi dari , … , secara berturut-turut, maka

(2.4.1)

Selanjutnya akan diperlihatkan bahwa  ∑ ∑

2 ∑ ∑ , . Untuk memperlihatkan persamaan tersebut dibutuhkan

definisi dari kovariansi dari dua variabel random.

Definisi 2.4.1.2

Kovariansi dari sepasang variabel random  dan didefinisikan sebagai berikut

,

Sifat 2.4.1.3

Andaikan _{dan variabel random. Jika dan saling bebas maka}

(

X,Y

)

=0

Cov

Bukti:

Menurut Definisi 2.4.1.2, diperoleh

(

X Y

)

E

[

(

X x

)

(

Y y

)

]

Cov , = −µ −µ

[

XY xY X y x y

]

E −µ − µ +µ µ =

Dengan menggunakan Sifat 2.4.1.1 diperoleh

(

X Y

)

E

( ) (

XY E xY

)

E

( ) (

X y E x y

)

(

X Y

)

E

( ) ( )

X E Y xE

( )

Y yE

( )

X x y

Cov , = −µ −µ +µ µ

y x x y y x y

xµ µ µ µ µ µ µ

µ − − +

=

0

=

Sifat 2.4.1.4

Jika , … , adalah variabel random, maka

2 ,

Bukti:

Dengan menggunakan Sifat 2.4.1.1 maka diperoleh

Dengan menggunakan sifat 2.1.3.5 maka diperoleh

2

2

2 ,       

Sifat 2.4.1.5

Jika , … , adalah variabel random yang saling bebas, maka

Bukti:

Menurut Sifat 2.4.1.4,

2 ,

Dengan menggunakan Sifat 2.4.1.3, dapat diperoleh

       

2. Nilai Harapan Bersyarat dan Variansi Bersyarat

Definisi 2.4.2.1

Andaikan variabel random dan berdistribusi bersama, maka nilai harapan bersyarat dari jika diketahui dinotasikan dengan | didefinisikan sebagai berikut

(i) | ∑   | , jika X dan diskrit dengan fungsi probabilitas bersyarat   | ,

(ii) |   | , jika X dan kontinu dengan fungsi densitas

bersyarat | .

Sifat 2.4.2

Jika variabel dan berdistribusi bersama, maka

|

Bukti:

Pembuktian untuk variabel random kontinu

| |  

|   ,    

   

Pembuktian | untuk variabel random diskret dapat dikerjakan

secara analog.

Pembuktian | untuk variabel random diskret dapat dikerjakan secara analog.

Definisi 2.4.2.2

Andaikan variabel random dan berdistribusi bersama, maka variansi bersyarat dari jika diketahui dinotasikan dengan | didefinisikan sebagai berikut

| | |

3. Korelasi

Definisi 2.4.3.1

Koefisien korelasi antara dua variabel random  dan didefinisikan sebagai berikut

. ,

dengan rata-rata dari dan rata-rata dari , dan diasumsikan bahwa variansi kedua variabel ada.

Koefisien korelasi ini mengukur hubungan linear antara dan dengan 1

1≤ _, ≤

− ρxy dan ρx,y =ρy,x. Kedua variabel random tidak berkorelasi jika

0 ,y = x

ρ .

Untuk memperlihatkan ρx,y =0 jika dan hanya jika dan saling bebas,

dengan dan berdistribusi normal, diperlukan definisi variabel random dan berdistribusi normal bivariat.

Definisi 2.4.3.2

Sepasang variabel random dan berdistribusi normal bivariat jika fungsi densitas bersamanya sebagai berikut

, 1

2 1

1

2 1 2

Sifat 2.4.3

Andaikan variabel random  dan berdistribusi normal. Maka, ρx,y =0 jika dan

hanya jika dan saling bebas. Bukti:

Jika X dan Y saling bebas, maka ρx,y =0

Dengan menggunakan teorema 3.2.1, maka diperoleh Cov

(

X,Y

)

= 0 Sehingga

(

)

( ) ( )

X VarY Var Y X Cov y x , , = ρ

( ) ( )

0 0

, = = Y Var X Var y x ρ

Jika ρ_x,y =0maka dan saling bebas.

dan berdistribusi normal, sehingga fungsi probabilitas bersamanya adalah

( )

2 , 1 2 1 , ρ σ πσ − = Y X Y

X x y

f

(

)

(

)(

)

_⎪⎭⎪⎬⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + − − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − × 2 2 2 2 1 2 1 exp Y Y Y X Y X X

X x y y

x σ µ σ σ µ µ ρ σ µ

ρ (3.2)

( )

0 1 2 1 , − = Y X y x f σ πσ

(

)

(

)(

)

_⎪⎭⎪⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + − − × − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − × 2 2 0 2 0 1 2 1 exp Y Y Y X Y X X

X x y y

x σ µ σ σ µ µ σ µ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − × = 2 2 2 1 exp 2 1 Y Y X X Y X y x σ µ σ µ σ πσ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − × = 2 2 2 1 2 1 exp 2 1 Y Y X X Y X y x σ µ σ µ σ πσ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − × ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − × = 2 2 2 1 exp 2 1 exp 2 1 Y Y X X Y X y x σ µ σ µ σ πσ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − × × ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − × = 2 2 2 1 exp 2 1 2 1 exp 2 1 Y Y Y X X X y x σ µ σ π σ µ σ π

( ) ( )

x f y f

=

Karena fungsi probabilitas bersama dari dan merupakan hasil kali dari fungsi probabilitas dari dan fungsi probabilitas dari , jadi dapat dikatakan bahwa

dan saling bebas.  

Jika sampel

{

(

x_t,y_t

)

}

T_t=1ada, korelasi dapat diduga dengan

dimana x x T T

t t

∑

=

= 1

dan y y T T

t t

∑

=

= 1

berturut-turut adalah rata-rata sampel dari

dan .

E. METODE MAXIMUMLIKELIHOOD (KEMUNGKINAN MAKSIMUM)

Metode kemungkinan maksimum adalah salah satu metode yang digunakan untuk menduga parameter yang tidak diketahui. Ide dasarnya adalah menggunakan sebuah nilai dalam ruang parameter yang dapat dikorespondensikan dengan kemungkinan terbesar untuk data yang diobservasi sebagai penduga dari parameter yang tidak diketahui.

Definisi 2.5.1

Andaikan , … , adalah variabel random kontinu dan sebuah vektor parameter dari , … , . Fungsi densitas bersama dari , … , dapat ditulis sebagai hasil kali dari fungsi densitas bersyarat sebagai berikut

, … , ; ; | , … , ;

Definisi 2.5.2

Fungsi kemungkinan dari variabel random , … , yang dilambangkan dengan

, … , ;  didefinisikan sebagai fungsi densitas bersama dari variabel

random , … , .

, … , ;   , … , ;

BAB III.

DASAR-DASAR ANALISIS RUNTUN WAKTU DAN

RUNTUN WAKTU LINEAR

Runtun waktu merupakan sebuah kumpulan dari variabel random yang berurutan pada waktu tertentu. Banyak himpunan data yang tampak sebagai runtun waktu, salah satu contohnya adalah data harga saham yang diambil harian. Sebuah ciri khas dari sebuah runtun waktu adalah variabel random yang berdekatan saling bergantung. Ketergantungan ini dapat dilihat dari autokorelasinya yang akan dibahas dalam bab ini. Sebelum menentukan koefisien autokorelasi, sebuah runtun waktu diuji stasioneritasnya. Selain stasioneritas dan fungsi autokorelasi, dalam bab ini juga akan dibahas tentang runtun white noise dan model runtun waktu linear yang stasioner (Autoregresif (AR), Moving-Average (MA), dan kombinasi Autoregresif-Moving Moving-Average (ARMA)).

A. STASIONERITAS

Ada dua definisi runtun waktu yang stasioner, yaitu runtun waktu yang sta-sioner kuat dan runtun waktu yang stasta-sioner lemah.

Definisi 3.1.1

Sebuah runtun waktu

{ }

rt dikatakan stasioner kuat jika distribusi bersama dari

, … , identik dengan , … , untuk semua t, dimana k sembarang

bilangan bulat positif dan

(

t1,K,tk

)

adalah koleksi k bilangan bulat positif.

Dengan kata lain, dalam proses stasioner kuat distribusi bersama dari , … , merupakan invarian dengan pergeseran waktu.

, … ,  , … ,        3.1

Definisi 3.1.2

Sebuah runtun waktu { }rt dikatakan stationer lemah jika rata-rata dari rtdan

autokovarian antara rt dan rt−l tidak bergantung pada t, dimana l sembarang

bilangan bulat. Dengan kata lain

{ }

r_t stasioner lemah jika (i) E

( )

rt =µ , untuk semua t,

(ii) Cov

(

rt,rt−l

)

=γl, untuk semua t, disebut autokovarian dengan selisih waktu l _(lag-l) dari rt.

Autokovarian lag-l dari rt mempunyai dua sifat, yaitu γ0 =Var

( )

rt dan

l

l γ

Sifat 3.1.1

Jika runtun

{ }

rt stasioner lemah, makaγ0 =Var

( )

rt

Bukti:

Dengan menggunakan Definisi 3.1.2 (ii) dapat diperoleh

(

rt rt

)

Cov ,

0 =

γ

= E

[

(

rt −E

( )

rt

)

(

rt −E

( )

rt

)

]

= E

(

rt −E

( )

rt

)

2

Dengan menggunakan Sifat 2.1.3.4 dapat diperoleh

( )

rt

Var =

0

γ

Sifat 3.1.2

Jika runtun

{ }

rt stasioner lemah, makaγ−l =γl.

Bukti:

Dengan menggunakan Definisi 3.1.2 (ii) dapat diperoleh

(

, ( l)

)

l −−

− =Cov rt rt

γ

=Cov

(

rt−(−l),rt

)

=Cov

(

rt+l,rt

)

, ℓ , dengan t1 =t+l

l

γ

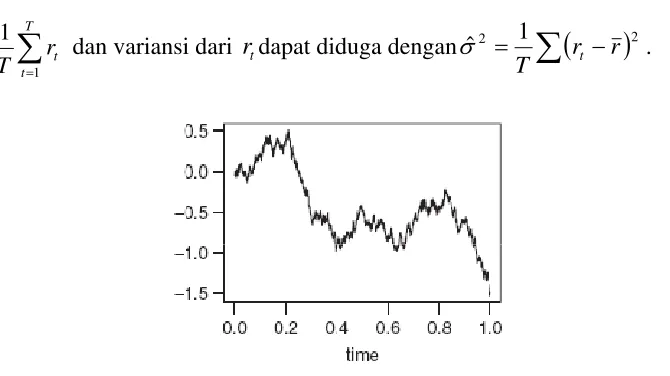
Dalam prakteknya, andaikan tersedia data sebanyak T. Secara tidak langsung stasioneritas lemah menyatakan bahwa grafik data akan menunjukkan bahwa data berfluktuasi dengan variasi yang konstan pada level yang tetap. Dalam aplikasi, stasioneritas lemah memungkinkan data sampel tadi dapat digunakan untuk menarik kesimpulan mengenai data yang akan datang. Oleh karena itu, jika diketahui sampel data sebanyak T, maka rata-rata dari r_t dapat diduga dengan

∑

=

= T

t t

r T r

1 1

dan variansi dari rtdapat diduga dengan =

∑

(

−

)

2

2 1

ˆ r r

T t

σ .

Gambar 3.1.1. Runtun waktu yang tidak stasioner dalam rata-rata

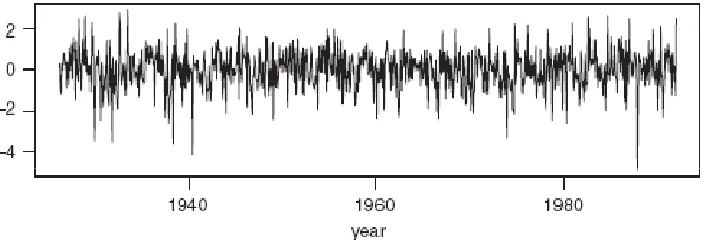
Gambar 3.1.3. Runtun waktu yang stasioner

Secara implisit, dari Definisi 3.1.2 yang menjelaskan bahwa untuk data yang stasioner lemah, autokovarian lag-ltidak bergantung pada t dan Sifat 3.1.1, yaitu autokovarian lag-l dari suatu data dengan l=0 merupakan variansi dari data itu sendiri, dapat dikatakan bahwa ketika data stasioner lemah, rata-rata dan variansi konstan untuk semua t.

Dari kedua definisi di atas, dapat disimpulkan bahwa jika stasioner kuat serta rata-rata, kovariansi tidak bergantung pada waktu t, dan variansinya konstan, maka juga stasioner lemah. Tidak berlaku kebalikannya. Jika runtun waktu

B. FUNGSI AUTOKORELASI

Autokorelasi merupakan korelasi antara suatu variabel r_t dan nilai masa lalunya rt−i,i=1,2,K. Koefisien korelasi antara rtdan rt−ldisebut autokorelasi

lag-ldari r_t dan dinotasikan dengan ρ_l. Pandang sebuah runtun r_t stasioner lemah, maka autokorelasi lag-ladalah sebagai berikut

(

)

( ) ( )

,

( ) ( )

(

,

)

(

( )

,

)

γ₀ γ

ρ l l l

l l

l = = = =

− −

− −

t t t t

t t t t

t t t

r Var

r r Cov r

Var r Var

r r Cov r

Var r Var

r r Cov

(3.2.1)

Autokorelasi lag-lmerupakan fungsi dari l, sehingga dapat disebut juga fungsi autokorelasi (ACF) lag-ldengan −1≤ρl ≤1. Fungsi autokorelasi ini dapat dipergunakan untuk mengidentifikasi model runtun waktu. Dari rumusan tersebut, dapat diperoleh 2 sifat berikut.

Sifat 3.2.1

Jikaruntun rt stasioner lemah, makaρ0 =1.

Bukti:

Dengan mensubstitusikan l=0 pada Persamaan 3.2.1 dapat diperoleh

1 0 0 0 =_γ =

γ ρ

Sifat 3.2.2

Bukti:

Menurut Persamaan 3.2.1,

0

γ γ ρ l

l =

dengan menggunakan Sifat 3.1.2 diperoleh

0 γ γ ρ l l − =

=ρ−l

Sebuah runtun rt yang stasioner lemah tidak berkorelasi secara berturut-turut jika

dan hanya jika ρl =0untuk semua l>0.

Diberikan sampel data

{ }

rt T_t=1. Ambil rrata-rata sampel, r r T

T t t

∑

= = 1 , maka

autokorelasi sampel lag-1 dari rtadalah

(

)(

)

(

)

∑

∑

= = − − − − = _T t t T t t t r r r r r r 1 2 2 1 1 ˆ ρ

Secara umum, autokorelasi sampel lag-ldari rt adalah

(

)(

)

(

)

, 0 1

ˆ

1

2

1 ≤ < −

Contoh 3.2.1

Misalkan menyatakan permintaan terhadap produk A untuk 10 periode waktu yang lalu dan mempunyai nilai yang seperti terlihat pada tabel berikut.

Tabel 3.2

Runtun Waktu dari Permintaan Produk A

t 1 2 3 4 5 6 7 8 9 10

rt 13 8 15 4 4 12 11 7 14 12

Hitunglah koefisien autokorelasi untuk lag 1 (ρˆ₁) dan 2 periode (ρˆ₂) ! Penyelesaian:

Dari data dapat diperoleh 100 10 1 =

∑

= t t r 10 10 100 10 10

1 _{= =}

=

∑

t=

t

r r

a. Mencari ρˆ₁

(

)(

)

(

)

∑

∑

= = − − − − = ₁₀ 1 2 10 2 1 1 ˆ t t t t t r r r r r r ρ

(

) (

2

) (

2

) (

2

) (

2

)

2

(

)

2

1 10 12 10 4 10 4 10 15 10 8 10 13 ) 10 14 )( 10 12 ( ) 10 15 )( 10 4 ( ) 10 8 )( 10 15 ( ) 10 13 )( 10 8 ( ˆ − + + − + − + − + − + − − − + + − − + − − + − − = L L ρ

144 27 ˆ₁ = − ρ

=−0.1875

Ini berarti bahwa nilai-nilai yang berurutan berkaitan satu dengan lainnya de-ngan koefisien korelasi (-)0.1875.

b. Mencari ρˆ₂

(

)(

)

(

)

∑

∑

= = − − − − = ₁₀ 1 2 10 3 2 2 ˆ t t t t t r r r r r r ρ

(

) (

2

) (

2

) (

2

) (

2

)

2

(

)

2

10 12 10 4 10 4 10 15 10 8 10 13 ) 10 7 )( 10 12 ( ) 10 15 )( 10 4 ( ) 10 8 )( 10 4 ( ) 10 13 )( 10 15 ( − + + − + − + − + − + − − − + + − − + − − + − − = L L

( ) ( ) ( ) ( ) ( )

2 2 2 2 2

( )

2 2 6 6 5 2 3 ) 3 )( 2 ( ) 5 )( 6 ( ) 2 )( 6 ( ) 3 )( 5 ( + + − + − + + − + − + + − + − − + = L L 4 36 36 25 4 9 6 30 12 15 + + + + + + − + − + = L L 144 29 − =

=−0.20139

Ini berarti bahwa masing-masing nilai  yang terpisah dua periode saling berkaitan dengan koefisien korelasi (-)0.20139.

apakah koefisien autokorelasi lag-l mendekati nol. Langkah-langkah pengujian ini adalah sebagai berikut:

a. Menentukan hipotesis

Diberikan bilangan bulat positif l. Hipotesis: H0 :ρl =0

0 :

1 ρl ≠

H

b. Menentukan tingkat signifikasi

( )

α c. Menentukan statistik uji

d. Statistik uji yang digunakan adalah

t-rasio

T

i i⎟

⎠ ⎞ ⎜

⎝ ⎛ ₊ =

∑

−

= 1

1 ˆ 2 1

ˆ

l l

ρ ρ

Jika

{ }

rt runtun stasioner Gaussian yang memenuhi ρj =0untuk j>l,

t-rasio secara asimtotik berdistribusi normal standar. e. Menentukan wilayah kritis

0

H ditolak jika |t-rasio|>Zα 2, dimana Zα 2adalah persentil ke 100

(

1−α 2

)

dari distribusi normal standar.

Ketika sampel data kecil, ρˆ merupakan penduga yang bias bagi l ρl. Akan

Contoh 3.2.2

Dengan menggunakan hasil pada Contoh 3.2.1, maka akan diuji apakah ρ₂ =0. Penyelesaian:

Langkah-langkah pengujian: a. Menentukan hipotesis Hipotesis: H₀ :ρ₁ =0 H₁:ρ₁ ≠0

b. Tingkat signifikasi yang dipilih

( )

α 5 %. c. Menentukan statistik uji

Statistik uji yang digunakan adalah

t-rasio

T

i i⎟

⎠ ⎞ ⎜

⎝ ⎛ ₊ =

∑

−

= 1

1 ˆ 2 1

ˆ

l l

ρ ρ

d. Diasumsikan

{ }

r_t runtun stasioner Gaussian yang memenuhi ρj =0untuk l

>

j , t-rasio secara asimtotik berdistribusi normal standar. e. Menentukan wilayah kritis

0

H ditolak jika |t-rasio|>Z0,052

|t-rasio|>1,96 f. Perhitungan

t-rasio

(

₁

)

T

2

ˆ 2 1

ˆ ρ ρ + =

(

1 2 0.1875

)

10 20139 . 0

− +

− =

t-rasio=−0,80556 g. Kesimpulan

Dari perhitungan diperoleh |t-rasio| = 0,80556>1,96. Jadi, H₀ditolak. De-ngan demikian dapat dikatakan bahwa ρ₂ ≠0.

C. RUNTUN WHITE NOISE

Definisi 3.3

Sebuah runtun waktu rt disebut white noise, jika

{ }

rt merupakan variabel random

yang saling bebas dan berdistribusi identik, dengan 1. E

( )

rt =µ,

2.

( )

=σ2 <∞

t

r

Var

Sebuah runtun r_t yang merupakan white noise dinotasikan dengan

{ }

(

2

)

,

~WN µ σ

rt . Dari definisi tersebut, proses white noise

{ }

rt merupakan proses

stasioner. Secara khusus, sebuah runtun waktu rt yang berdistribusi normal

dengan E

( )

r_t =0 dan

( )

₌σ2

t

r

Var disebut Gaussian white noise.

Akan ditunjukkan bahwa dalam sebuah runtun white noise, semua ACF bernilai nol.

Bukti:

(

rt rt−l

)

Cov , merupakan autokovarian lag-l dari rt.

Karena runtun r_{t white noise, maka runtun} r_{t saling bebas} Dengan menggunakan Sifat 2.4.1.3 dapat diperoleh

(

rt,rt−l

)

=0

Cov untuk semua l (3.3.1)

Menurut Persamaan 3.2.1,

(

)

( )

t t t

r Var

r r

Cov _l

l

−

= ,

ρ

Dengan mensubstitusikan Persamaan (3.3.1) pada persamaan tersebut, maka diperoleh

( )

0

0 ₌

=

t

r Var

l

ρ

Dalam prakteknya, jika semua ACF untuk l>0dari sampel mendekati nol, maka runtun tersebut merupakan runtun white noise.

D. RUNTUN WAKTU LINEAR

Sebuah runtun waktu r_t dapat ditulis sebagai berikut

∑

∞

= −

+ =

0

i

i t i

t a

r µ ψ

dengan µrata-rata dari rt;ψikonstanta, ψ0 =1;{ }at merupakan runtun white

Jika r_t stasioner rata-rata, variansi, dan autokovariansinya diperoleh dengan menggunakan sifat{ }at yang saling bebas dan nilai harapan dari galat bernilai nol.

(i) Nilai harapan dari rt _adalah

( )

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + =

∑

∞

=0 −

i

i t i

t E a

r

E µ ψ

( )

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + =

∑

∞

=0 −

i

i t ia

E

E µ ψ

(

)

∑

∞ = − + = 0 i i t ia Eψ µ

( )

∑

∞ = − + = 0 i i t iE a

ψ µ

∑

∞ = + = 0 0 . i i ψ µ µ =

(ii) Variansi dari rt _adalah

( )

[

( )

]

2

t t t E r E r

r

Var = −

( )

2 , ₀ 1 0 0 0 2 2 ₌ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ + =

∑

∑∑

∞ < = ∞ = − − ∞ = − ψ ψ ψ ψ j i i j j t i t j i i i t i

t E a a a

r Var

Dengan menggunakan Sifat 2.4.1.1 diperoleh

( )

2 , ₀ 1

0 0 0 2 2 ₌ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

∑∑

∞ < = ∞ = − − ∞ = − ψ ψ ψ ψ j i i j j t i t j i i i t i

t E a E a a

r Var

( )

2

(

)

, 0 1 0 0

2 0

2 _{+ =}

= ∞ _{− −} <= ∞ = − ∞ =

∑∑

∑

ψ ψ ψ t i t j ψ

j i i j j i i t i

i E a E a a

Karena { }at saling bebas dan E

( )

at =0 , maka diperoleh

( )

, 0 1

2 0 2 ₌ =

∑

∞ = ψ σ ψ a i i t r Var 1 , 0 0 2 2 ₌ =

∑

∞ = ψ ψ σ i i a

Agar runtun linear stasioner maka perlu diasumsikan bahwa , 0 1 0 = ∞ <

∑

∞ = ψ ψ i i

untuk menjamin

( )

, 0 1

0 2

2 _{<∞ =}

=

∑

∞ = ψ ψ σ i i a t r Var .

Sehingga dapat dikatakan bahwa untuk runtun linear yang stasioner, semakin besar i, pengaruh galat at−ipada rtakan menghilang .

(iii) Autokovarian lag-ldari rtadalah

(

l

)

l =Covrt,rt−

γ

( )

(

)

(

( )

)

[

− −l− −l

]

(

)(

)

[

µ µ

]

γl =E rt − rt−l −

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ −} =

∑

∑

∞ = − − ∞ = − µ ψ µ µ ψ µ 0 0 j j t j i i t

ia a

E _l 1 , 0 0 0 = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

∑

∞ = −− ∞ = − ψ ψ ψ j j t j i i t

ia a

E _l 1 , 2 ₀ 0 2 0 0 = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ + =

∑∑

∑

∞ = + −− ∞ < = ∞ = − −− ψ ψ ψ ψ ψ j j t j j j i i j j t i t j

i a a a

E _{l l l}

Dengan menggunakan Sifat 2.4.1.1 dapat diperoleh

1 , 2 ₀ 0 2 0 0 = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ =

∑∑

∑

∞ = + − − ∞ < = ∞ = − − − ψ ψ ψ ψ ψ γ j j t j j j i i j j t i t j

i a a E a

E _{l l l}

l

(

)

(

)

, 1

2 0 2 0 0 0 = + = − − ∞ = + − − − ∞ <= ∞ =

∑

∑∑

ψ ψ ψ ψ t j ψ

j j j j t i t j i i j j

i E a a l l E a l

Karena { }at saling bebas dan E

( )

at =0 , maka diperoleh

1 , 0 2 0 = =

∑

∞ = + ψ σ ψ ψ γ _a j j j l l 1 , 0 0 2 ₌ =

∑

∞ = + ψ ψ ψ σ γ j j j a l l

Jika l=0, maka Var

( )

rt i j

i i a j

j

a = = =

=

∑

∑

∞ = ∞ = , 0 2 2 0 2 2

0 σ ψ σ ψ

γ , sehingga fungsi

autokorelasi dari proses linear adalah

0 , 0

≥ = l l

l _γ

0 , 0 2 2 0 2 ≥ =

∑

∑

∞ = ∞

= +l _l

l i i a i i i a ψ σ ψ ψ σ

ρ dan ψ0 =1

0 , 1 1 2 0 ≥ + =

∑

∑

∞ = ∞

= +l _l

i i i i i ψ ψ ψ

E. MODEL AUTOREGRESIF (AR)

Salah satu model runtun linear adalah model Autoregresif. Model ini seperti model Regresi dengan data masa lalu sebagai variabel bebasnya.

Definisi 3.5

Model Autoregresif berorde p [AR (p)] dapat didefinisikan sebagai berikut

t p t p t t

t r r r a

r =φ0+φ1 −1+φ2 −2 +L+φ − + (3.5.1)

dimana p bilangan bulat non-negatif dan

{ }

at diasumsikan sebuah runtun white

noise dengan rata-rata nol dan variansi 2

a

σ .

1. Sifat-sifat model AR (1)

Model AR (1) didefinisikan sebagai berikut

t t

t r a

r =φ0 +φ1 −1 + (3.5.2)

{ }

at diasumsikan sebuah runtun white noise dengan rata-rata nol dan variansi

2

a

Sifat 3.5.1.1

Diasumsikan bahwa runtun waktu rt pada model AR (1) stasioner .Maka nilai

harapan dari r_t bersyarat rt−_{1 adalah}

(

rt |rt−₁

)

= ₀ + ₁rt−₁

E φ φ

Bukti :

(

rt rt

)

E

(

rt at

)

E | −1 = φ0 +φ1 −1 +

( ) (

E rt

) ( )

E at

E + +

= φ0 φ1 −1

( )

0 + 1

( )

−1

=E φ φ E r_t

1 1

0+ −

=φ φr_t

Sifat 3.5.1.2

Diasumsikan bahwa runtun waktu rt pada model AR (1) stasioner. Maka nilai

harapan dari rt _adalah

( ) ( )

1

0

1 φ

φ − =

t

r E

Bukti:

Diketahui E

( )

rt =µ

( )

rt = E

[

E

(

rt |rt−1

)

]

E

( ) (

rt =E 0 + 1rt−1

)

E φ φ

( ) (

0 + 1 −1

)

=Eφ Eφr_t

( )

1 1

0 + −

Karena runtun stasioner, E

( )

rt =E

( )

rt−1 =µ, maka

µ φ φ µ= ₀ + ₁

0 1µ φ

φ

µ− =

(

1 φ1

)

φ0

µ − =

(

1

)

0 1 φ φ µ − =

Sehingga dapat diperoleh

( )

(

)

1 0 1 φ φ µ − = = t r E

Dari hasil tersebut dapat diimplikasikan bahwa (1) rata-rata rtada jika φ1 ≠1, dan

(2) rata-rata r_t bernilai nol jika dan hanya jika φ0 =0dan φ1 ≠1. Dengan

demikian, untuk sebuah proses stasioner AR (1), konstanta φ₀berelasi dengan rata-rata dari rt dan jika φ0 =0 dan φ1 ≠1 maka E

( )

rt =0.

Sifat 3.5.1.3

Diasumsikan bahwa runtun waktu rt pada model AR (1) stasioner. Maka variansi

dari rt _bersyarat rt−1 adalah

(

)

( )

2

1

| t t a

t r Var a

r

Var ₋ = =σ

Bukti:

(

)

[

(

)

]

2

1 1

1 | |

| t₋ = t t₋ − t t₋

t r E r r E r r

r Var

[

]

2

1 1 0 1

1

0 + − + − − −

=Eφ φ r_t a_t φ φ r_t

[ ]

2

t

(

)

2 1

| t a

t r

r

Var ₋ =σ

Sifat 3.5.1.4

Diasumsikan bahwa runtun waktu rt pada model AR (1) stasioner. Maka variansi

dari rt _adalah

( ) (

1 1

)

2

1 φ ρ σ − = a t

r Var

Bukti:

Substitusikan φ₀ =

(

1−φ₁

)µ

ke dalam persamaan (3.5.2)

(

)

t t

t r a

r = 1−φ1 µ+φ1 −1 +

=µ−φ1µ+φ1rt−1 +at

t t

t r a

r −µ=−φ₁µ+φ_{1 −1}+

(

− +rt

)

+at

=φ1 µ −1

(

rt −

)

+at

=φ_{1 −1} µ (3.5.3)

Kedua ruas pada persamaan 3.5.3 dikalikan dengan r_t −µ

(

rt −µ

)(

rt −µ

)

=φ1

(

rt−1−µ

)(

rt −µ

)

+at

(

rt −µ

)

(3.5.4)

Nilai harapan dari persamaan 3.5.4 adalah

(

)(

)

[

rt −µ rt −µ

]

=E

[

φ

(

rt− −µ

)(

rt −µ

)

+at

(

rt −µ

)

]

E _{1 1}

(

rt rt

)

=E

[

φ

(

rt− −µ

)(

rt −µ

)

]

+E

[

at

(

rt −µ

)

]

Cov , _{1 1} (3.5.5)

Persamaan 3.5.3 yaitu

(

t

)

t

t r a

r −µ=φ_{1 −1}−µ +

Kedua ruas dikalikan dengan a_t sehingga menjadi

(

)

(

)

2

1

1 t t

t t

t r a r a

a −µ = φ ₋ −µ +

Nilai harapannya adalah

(

)

[

]

[

(

)

2

]

1

1 t t

t t

t r Ea r a

a

E −µ = φ ₋ −µ +

(

)

[

]

[

(

)

]

( )

2

1

1 t t t

t

t r E a r Ea

a

E −µ =φ ₋ −µ + (3.5.6)

Mencari E

[

at

(

rt−1 −µ

)

]

Berdasarkan definisi model autoregresi, diperoleh

∑

∞ = − − − = 1 1 i i t i t a

r µ ψ , sehingga

(

)

[

]

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = −

∑

∞ = − − 1 1 i i t i t t

t r E a a

a

E µ ψ

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ =

∑

∞

=1 −

i

i t t iaa

E ψ

Dengan menggunakan sifat nilai harapan, maka diperoleh

(

)

[

]

∑

∞

[

]

= − − − = 1 1 i i t t i t

t r E aa

a

E µ ψ

Karena runtunat saling bebas dan E

[ ]

at =0maka diperoleh

(

)

[

at rt−1 −µ

]

=0 E

Dengan menggunakan hasil tersebut, maka Persamaan 3.5.6 menjadi

(

)

[

]

2

10 a

t t r

a

<