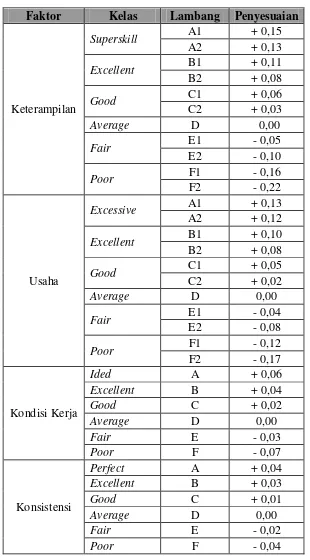
LAMPIRAN 1 Tabel Rating Factor Westinghouse Faktor Kelas Lambang Penyesuaian

(1)

(2)

LAMPIRAN 1

Tabel Rating FactorWestinghouse

Faktor Kelas Lambang Penyesuaian

(3)

LAMPIRAN 2

Tabel Allowance

Faktor Contoh pekerjaan Kelonggaran ( % )

A. Tenaga yang dikeluarkan

1. Dapat diabaikan 2. Sangat ringan 3. Ringan 4. Sedang 5. Berat 6. Sangat berat 7. Luar biasa berat

Bekerja dimeja, duduk Bekerja dimeja, berdiri Menyekop, ringan Mencangkul

Mengayun palu yang berat Memanggul beban

Memanggul karung berat

Ekivalen beban 2. Berdiri diatas

dua kaki 3. Berdiri diatas

satu kaki 4. Berbaring

5. Membungkuk

Bekerja duduk, ringan

Badan tegak, ditumpu dua kaki

Satu kaki mengerjakan alat kontrol

Pada bagian sisi, belakang atau depan badan

Badan dibungkukkan bertumpu pada kedua kaki

0,00-1,0 1,0-2,5

2,5-4,0

4,0-10

C. Gerakan kerja 1. Normal 2. Agak terbatas 3. Sulit

4. Pada anggota-anggota badan terbatas

5. Seluruh anggota badan terbatas

Ayunan bebas dari palu Ayunan terbatas dari palu

Membawa beban berat dengan satu tangan

Bekerja dengan tangan diatas kepala

Bekerja dilorong pertambangan yang sempit

3. Pandangan terus menerus dengan fokus berubah-ubah

4. Pandangan terus menerus dengan fokus tetap

Membawa alat ukur

Pekerjaan-pekerjaan yang teliti

Memeriksa cacat-cacat pada kain

Pemeriksaan sangat teliti

(4)

Faktor Contoh pekerjaan Kelonggaran ( % )

E. Keadaan temperatur tempat kerja**) 6. Sangat tinggi

Temperatur ( OC )

Kelembaban normal

Diatas 10 F. Keadaan atmosfer***)

1. Baik 2. Cukup 3. Kurang Baik 4. Buruk

Ruang yang berventilasi baik,udara segar

Ventilasi kurang baik, ada bau-bauan (tidak berbahaya) Adanya debu-debu beracun, atau tidak beracun tetapi banyak

Adanya bau-bauan berbahaya yang mengharuskan menggunakan alat-alat pernafasan

G. Keadaan lingkungan yang baik

1. Bersih, sehat, cerah dengan kebisingan rendah 2. Siklus kerja berulang-ulang antara 5-10 detik 3. Siklus kerja berulang-ulang antara 0-5 detik 4. Sangat bising

5. Jika factor-faktor yang berpengaruh dapat menurunkan kwalitas 6. Terasa adanya getaran lantai

7. Keadaan yang luar biasa (bunyi, kebersihan, dll)

0

*) Kontras antara warna hendaknya diperhatikan **) Tergantung juga pada keadaan ventilasi

***) Dipengaruhi juga oleh ketinggian tempat kerja dari permukaan laut dan keadaan iklim

(5)

LAMPIRAN 3

Uji Keseragaman Data Pipa AW AXX

1. Uji Keseragaman Data Pipa AW AXX 3/4 Inchi

1.1.Proses Ekstruksi, pencetakan, pendinginan, dan pemotongan a. Menghitung nilai rata-rata

299

b. Menghitung nilai standar deviasi

179

c. Menghitung batas kontrol (BKA dan BKB)

Dengan tingkat keyakinan 95% dan ketelitian 5% maka nilai Z = 2.

BKA = X + Zσ BKB = X - Zσ

= 370,299 + 2(3,179) = 370,299 - 2(3,179)

= 376,657 = 363,941

(6)

1.2. Proses Pembentukan kepala pipa a. Menghitung nilai rata-rata

186

792

= 92,186 + 2(3,792) = 92,186 - 2(3,792)

= 99,770 = 84,602

(7)

2. Uji Keseragaman Data Pipa AW AXX 3 Inchi 2.1. Proses Pencampuran

a. Menghitung nilai rata-rata

388

570

= 25,388 + 2(0,570) = 25,388 - 2(0,570)

= 26,528 = 24,248

(8)

2.2. Proses Ekstruksi, pencetakan, pendinginan, dan pemotongan a. Menghitung nilai rata-rata

895

265

= 200,895 + 2(2,265) = 200,895 - 2(2,265)

= 205,425 = 196,365

(9)

2.3. Proses Pembentukan kepala pipa a. Menghitung nilai rata-rata

857

436

= 55,857 + 2(3,436) = 55,857 - 2(3,436)

= 62,729 = 48,985

(10)

3. Uji Keseragaman Data Pipa AW AXX 4 Inchi 3.1. Proses Pencampuran

a. Menghitung nilai rata-rata

986

685

= 24,986 + 2(0,685) = 24,986 - 2(0,685)

= 26,356 = 23,616

(11)

3.2. Proses Ekstruksi, pencetakan, pendinginan, dan pemotongan a. Menghitung nilai rata-rata

265

566

= 143,265 + 2(3,566) = 143,265 - 2(3,566)

= 150,397 = 136,133

(12)

3.3. Proses pembentukan kepala pipa a. Menghitung nilai rata-rata

678

513

= 46,678 + 2(0,513) = 46,678 - 2(0,513)

= 47,704 = 45,652

(13)

LAMPIRAN 4

Uji Kecukupan Data Pipa AW AXX

1. Uji Kecukupan Data Pipa AW AXX 3/4 Inchi

a. Proses ekstruksi, pencetakan, pendinginan, dan pemotongan N Waktu Siklus (X) X2

Total 3702,99 1371304,47

1 pendinginan, dan pemotongan dikatakan cukup.

b. Proses pembentukan kepala pipa

(14)

3

Karena N‟ < N (2,44<10) maka data waktu proses pembentukan kepala pipa dikatakan cukup.

2. Uji Kecukupan Data Pipa AW AXX 3 Inchi a. Proses pencampuran

N Waktu Siklus (X) X2

Karena N‟ < N (0,73<10) maka data waktu proses pencampuran dikatakan cukup.

b. Proses ekstruksi, pencetakan, pendinginan, dan pemotongan N Waktu Siklus

(15)

c. Proses pembentukan kepala pipa

N Waktu Siklus

Karena N‟ < N (5,45<10) maka data waktu proses pembentukan kepala pipa dikatakan cukup.

3. Uji Kecukupan Data Pipa AW AXX 4 Inchi a. Proses pencampuran

(16)

2

Karena N‟ < N (1,08<10) maka data waktu proses pencampuran dikatakan cukup.

b. Proses ekstruksi, pencetakan, pendinginan, dan pemotongan N Waktu Siklus

Total 1432,65 205363,06

(17)

1

(18)

LAMPIRAN 5

Perhitungan Waktu Normal dan Waktu Baku Pipa AW AXX

1. Pipa AW AXX 3/4 Inchi

a. Proses ekstruksi, pencetakan, pendinginan, dan pemotongan WN = Waktu siklus × (1 + rating factor)

b. Proses pembentukan kepala pipa

WN = Waktu siklus × (1 + rating factor)

a. Proses pencampuran

(19)

=

a. Proses pencampuran

b. Proses ekstruksi, pencetakan, pendinginan, dan pemotongan WN = Waktu siklus × (1 + rating factor)

(20)

LAMPIRAN 6

Penyelesaian dengan Metode Dua Fase

Metode ini menyelesaikan kasus (Linear Programming) LP dalam dua fase : Fase I berusaha untuk mencari solusi layak awal, dan jika ditemukan, maka fase II dijalankan untuk menyelesaikan masalah aslinya.

Langkah-langkah metode dua fase :

Fase I : Mencari solusi layak dasar awal bagi program asli, dengan cara mengusahakan agar variabel artifisial terbuang. Pada tahap ini lebih dahulu dibuat fungsi objektif khusus untuk variabel artifisial.

Fase II : Pada fase ini, solusi layak dasar awal yang diperoleh pada fase pertama dilanjutkan untuk dioptimalkan.

Sebagai contoh penyelesaian akan dilakukan perhitungan model lower linear programming Januari 2011

Fungsi tujuan :

Pembentukan fungsi tujuan khusus untuk variabel artifisial yaitu S11, S12, S13

(21)

X2 - S9 + S12 = 2466

X3 - S10 + S13 = 1954

X1,X2,X3, S1, S2, ..., S13 ≥ 0

Karena S11, S12, dan S13 berfungsi sebagai variabel basis pada solusi awal,

maka koefisiennya pada fungsi tujuan harus sama dengan 0. Untuk mencapai itu, gantikan nilai S11 dari fungsi kendala 8 (kendala yang memuat S11), nilai

S12 dari fungsi kendala 9 (kendala yang memuat S12), dan S13 dari fungsi

kendala 10 (kendala yang memuat S13).

Dari kendala 8 diperoleh : S11 = 7779 - X1 + S8

Sehingga fungsi tujuan menjadi : max z = -S11 - S12 - S13

max z = -(7779 - X1 + S8) – (2466 - X2 + S9) – (1954 - X3 + S10)

max z = -7779 + X1 - S8– 2466 + X2 - S9– 1954 + X3 - S10

max z = X1 + X2 + X3 - S8 - S9 - S10– 12199

z - X1 - X2 - X3 + S8 + S9 + S10 = -12199

2. Pemeriksaan optimalitas

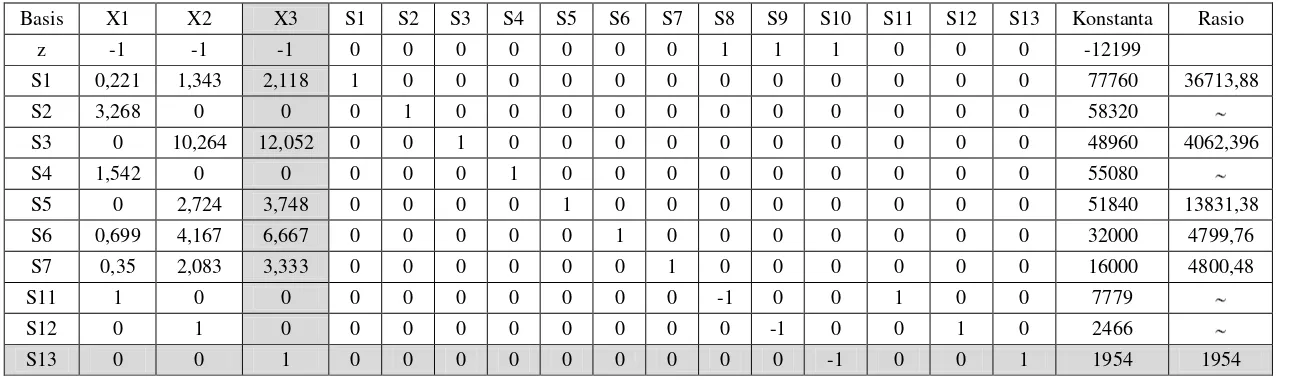
Solusi dikatakan layak jika z bernilai positif atau nol. Variabel non basis yang dipilih untuk menjadi variabel basis disebut entering variabel. Entering variabel yang dipilih adalah variabel z yang memiliki Crow paling negatif. Dan variabel basis yang akan keluar menjadi variabel non basis disebut leaving variabel. Leaving variabel dipilih dengan menggunakan rasio minimum yaitu perbandingan konstanta sisi kanan dengan elemen variabel. Pada tabel simpleks awal, X3 memiliki z paling negatif yaitu -1 sehingga X3

disebut entering variabel. Rasio minimum yaitu: Baris 1 = 77760 / 2,118 = 36713,88 variabel basis S13 yang disebut leaving variabel. Kemudian mencari sistem

(22)

(23)

Fase I

Tabel Simpleks Awal

Basis X1 X2 X3 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 S11 S12 S13 Konstanta Rasio z -1 -1 -1 0 0 0 0 0 0 0 1 1 1 0 0 0 -12199

S1 0,221 1,343 2,118 1 0 0 0 0 0 0 0 0 0 0 0 0 77760 36713,88 S2 3,268 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 58320

S3 0 10,264 12,052 0 0 1 0 0 0 0 0 0 0 0 0 0 48960 4062,396 S4 1,542 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 55080

S5 0 2,724 3,748 0 0 0 0 1 0 0 0 0 0 0 0 0 51840 13831,38 S6 0,699 4,167 6,667 0 0 0 0 0 1 0 0 0 0 0 0 0 32000 4799,76 S7 0,35 2,083 3,333 0 0 0 0 0 0 1 0 0 0 0 0 0 16000 4800,48 S11 1 0 0 0 0 0 0 0 0 0 -1 0 0 1 0 0 7779

S12 0 1 0 0 0 0 0 0 0 0 0 -1 0 0 1 0 2466

(24)

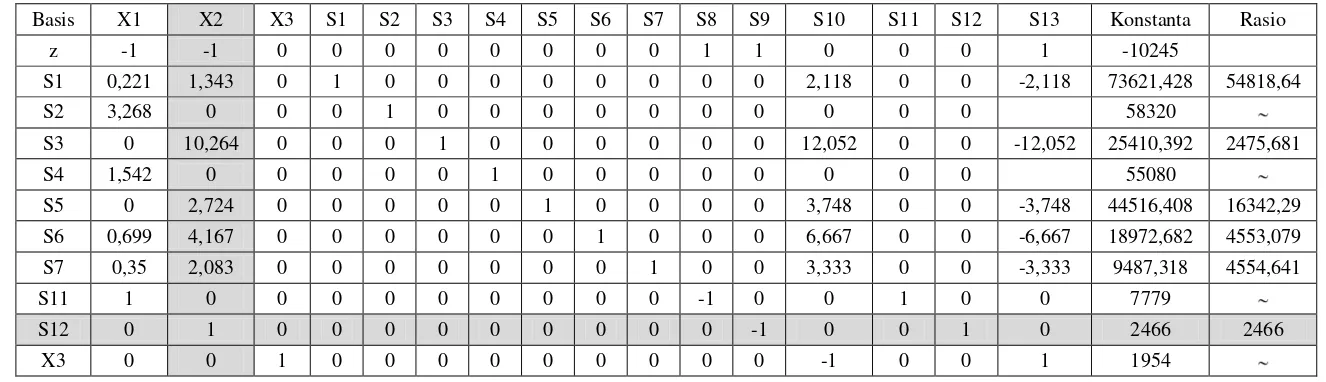
Tabel Iterasi I

Basis X1 X2 X3 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 S11 S12 S13 Konstanta Rasio z -1 -1 0 0 0 0 0 0 0 0 1 1 0 0 0 1 -10245

S1 0,221 1,343 0 1 0 0 0 0 0 0 0 0 2,118 0 0 -2,118 73621,428 54818,64 S2 3,268 0 0 0 1 0 0 0 0 0 0 0 0 0 0 58320

S3 0 10,264 0 0 0 1 0 0 0 0 0 0 12,052 0 0 -12,052 25410,392 2475,681 S4 1,542 0 0 0 0 0 1 0 0 0 0 0 0 0 0 55080

S5 0 2,724 0 0 0 0 0 1 0 0 0 0 3,748 0 0 -3,748 44516,408 16342,29 S6 0,699 4,167 0 0 0 0 0 0 1 0 0 0 6,667 0 0 -6,667 18972,682 4553,079 S7 0,35 2,083 0 0 0 0 0 0 0 1 0 0 3,333 0 0 -3,333 9487,318 4554,641 S11 1 0 0 0 0 0 0 0 0 0 -1 0 0 1 0 0 7779

(25)

Tabel Iterasi II

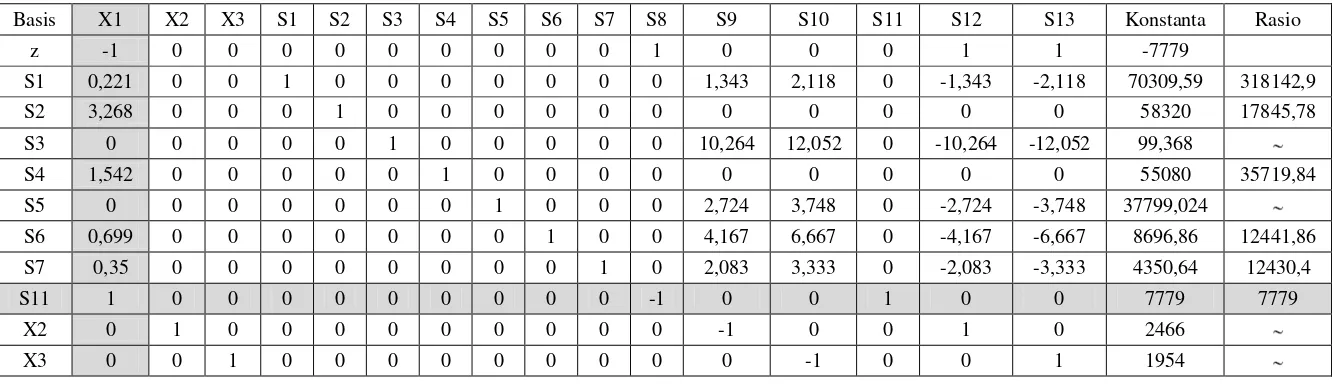
Basis X1 X2 X3 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 S11 S12 S13 Konstanta Rasio z -1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 -7779

S1 0,221 0 0 1 0 0 0 0 0 0 0 1,343 2,118 0 -1,343 -2,118 70309,59 318142,9 S2 3,268 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 58320 17845,78 S3 0 0 0 0 0 1 0 0 0 0 0 10,264 12,052 0 -10,264 -12,052 99,368

S4 1,542 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 55080 35719,84 S5 0 0 0 0 0 0 0 1 0 0 0 2,724 3,748 0 -2,724 -3,748 37799,024

S6 0,699 0 0 0 0 0 0 0 1 0 0 4,167 6,667 0 -4,167 -6,667 8696,86 12441,86 S7 0,35 0 0 0 0 0 0 0 0 1 0 2,083 3,333 0 -2,083 -3,333 4350,64 12430,4 S11 1 0 0 0 0 0 0 0 0 0 -1 0 0 1 0 0 7779 7779

(26)

Tabel Iterasi III

melanjutkan ke fase II.

Pada Fase II, fungsi tujuan yang mengandung variabel artifisial sudah tidak diikutsertakan lagi. Fungsi tujuan kembali ke bentuk awal

Max z = 2900X1 + 15800X2 + 21600X3

Dari tabel optimal tahap 1 diperoleh :

X1 = 7779 + S8 X2 = 2466 + S9 X3 = 1954 + S10

Sehingga Max z = 2900X1 + 15800X2 + 21600X3

Max z = 2900(7779 + S8) + 15800(2466 + S9) + 21600(1954 + S10)

Max z = 22559100 + 2900S8 + 38962800 + 15800S9 + 42206400 + 21600S10 Max z = 2900S8 + 15800S9 + 21600S10 + 103728300

(27)

Fase II

Tabel Simpleks Awal

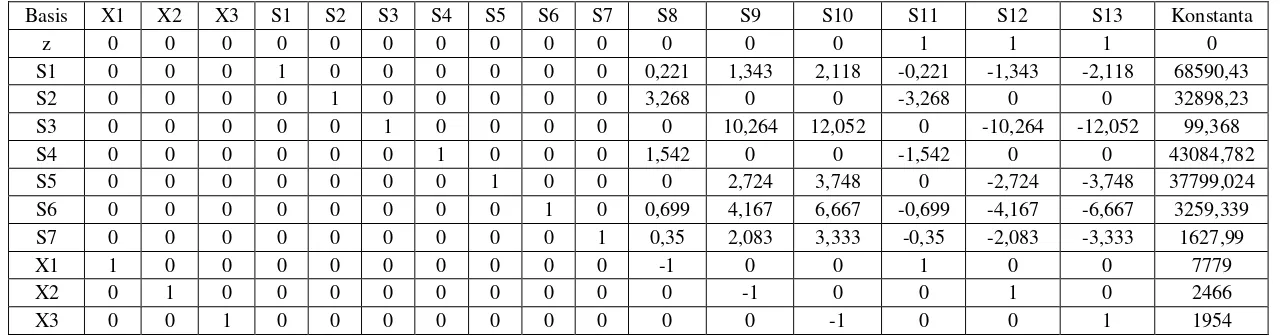
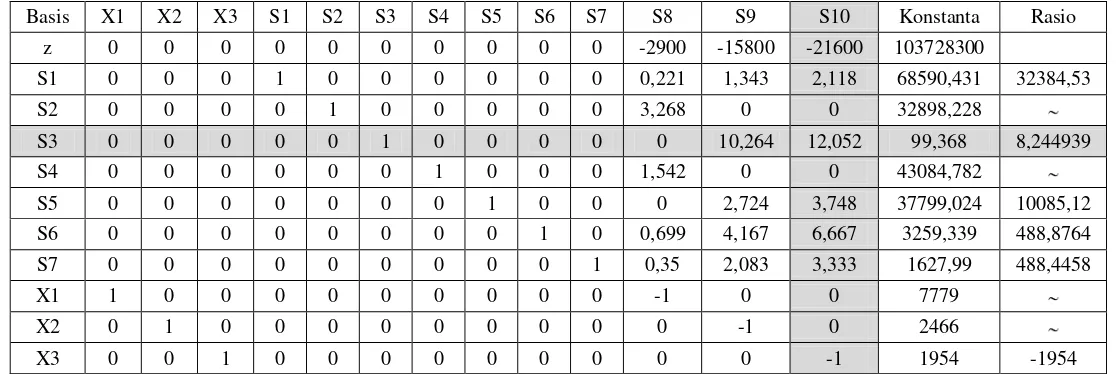
Basis X1 X2 X3 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 Konstanta Rasio z 0 0 0 0 0 0 0 0 0 0 -2900 -15800 -21600 103728300

S1 0 0 0 1 0 0 0 0 0 0 0,221 1,343 2,118 68590,431 32384,53 S2 0 0 0 0 1 0 0 0 0 0 3,268 0 0 32898,228

S3 0 0 0 0 0 1 0 0 0 0 0 10,264 12,052 99,368 8,244939 S4 0 0 0 0 0 0 1 0 0 0 1,542 0 0 43084,782

S5 0 0 0 0 0 0 0 1 0 0 0 2,724 3,748 37799,024 10085,12 S6 0 0 0 0 0 0 0 0 1 0 0,699 4,167 6,667 3259,339 488,8764 S7 0 0 0 0 0 0 0 0 0 1 0,35 2,083 3,333 1627,99 488,4458 X1 1 0 0 0 0 0 0 0 0 0 -1 0 0 7779

X2 0 1 0 0 0 0 0 0 0 0 0 -1 0 2466

(28)

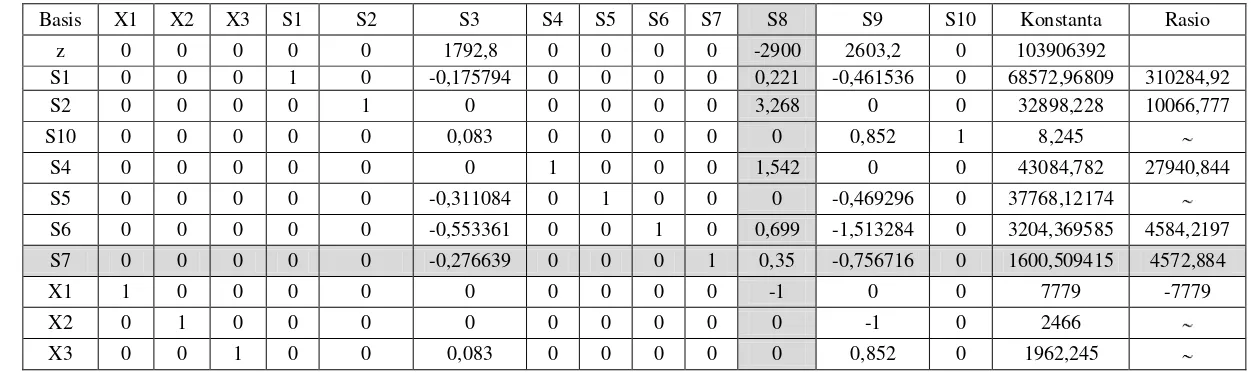
Tabel Iterasi I

Basis X1 X2 X3 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 Konstanta Rasio z 0 0 0 0 0 1792,8 0 0 0 0 -2900 2603,2 0 103906392

S1 0 0 0 1 0 -0,175794 0 0 0 0 0,221 -0,461536 0 68572,96809 310284,92 S2 0 0 0 0 1 0 0 0 0 0 3,268 0 0 32898,228 10066,777 S10 0 0 0 0 0 0,083 0 0 0 0 0 0,852 1 8,245

S4 0 0 0 0 0 0 1 0 0 0 1,542 0 0 43084,782 27940,844 S5 0 0 0 0 0 -0,311084 0 1 0 0 0 -0,469296 0 37768,12174

S6 0 0 0 0 0 -0,553361 0 0 1 0 0,699 -1,513284 0 3204,369585 4584,2197 S7 0 0 0 0 0 -0,276639 0 0 0 1 0,35 -0,756716 0 1600,509415 4572,884 X1 1 0 0 0 0 0 0 0 0 0 -1 0 0 7779 -7779 X2 0 1 0 0 0 0 0 0 0 0 0 -1 0 2466

(29)

Tabel Iterasi II

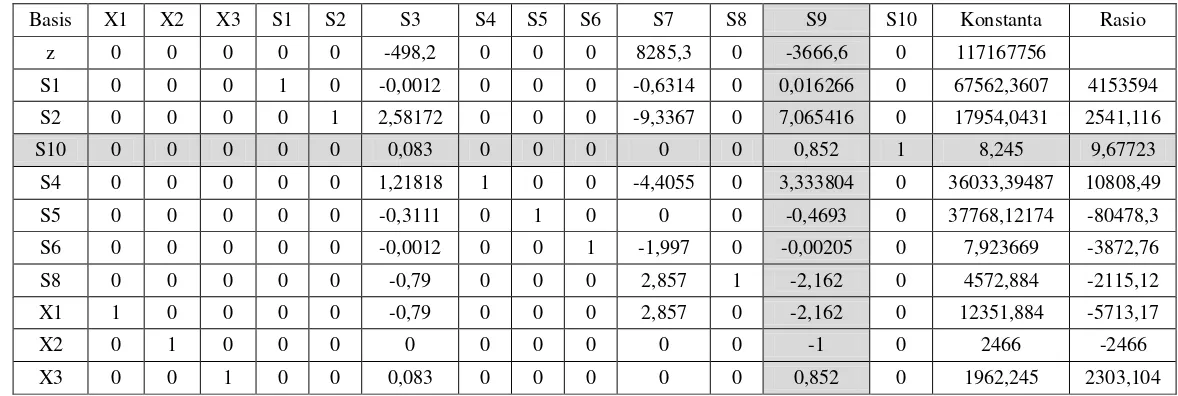
Basis X1 X2 X3 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 Konstanta Rasio z 0 0 0 0 0 -498,2 0 0 0 8285,3 0 -3666,6 0 117167756

S1 0 0 0 1 0 -0,0012 0 0 0 -0,6314 0 0,016266 0 67562,3607 4153594 S2 0 0 0 0 1 2,58172 0 0 0 -9,3367 0 7,065416 0 17954,0431 2541,116 S10 0 0 0 0 0 0,083 0 0 0 0 0 0,852 1 8,245 9,67723

(30)

Tabel Iterasi III

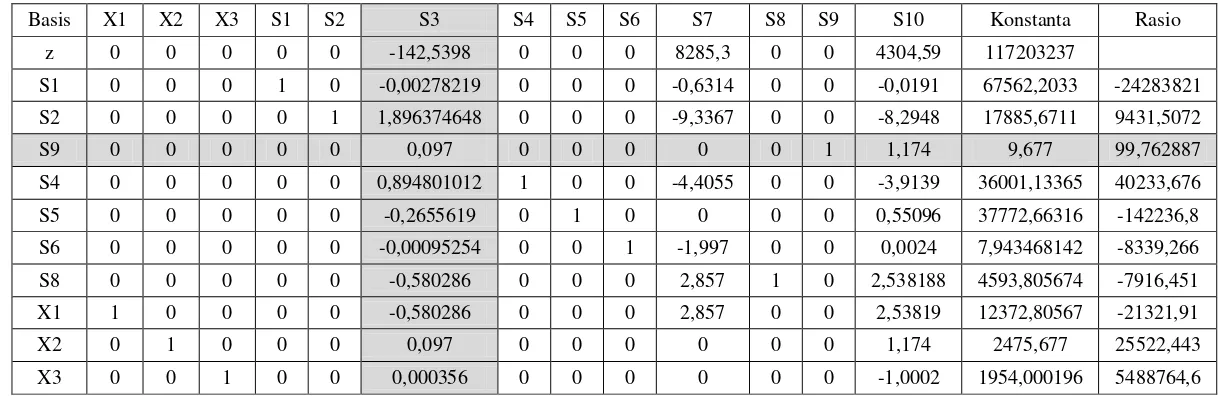
Basis X1 X2 X3 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 Konstanta Rasio z 0 0 0 0 0 -142,5398 0 0 0 8285,3 0 0 4304,59 117203237

(31)

Tabel Iterasi IV

Basis X1 X2 X3 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 Konstanta z 0 0 0 0 0 0,0002 0 0 0 8285,3 0 1469,44 6029,75 117217458 S1 0 0 0 1 0 0 0 0 0 -0,6314 0 0,02866 0,01455 67562,481 S2 0 0 0 0 1 0 0 0 0 -9,3367 0 -19,55 -31,247 17696,483 S3 0 0 0 0 0 1 0 0 0 0 0 10,309 12,103 99,763 S4 0 0 0 0 0 0 1 0 0 -4,4055 0 -9,2245 -14,744 35911,866 S5 0 0 0 0 0 0 0 1 0 0 0 2,73766 3,76503 37799,156 S6 0 0 0 0 0 0 0 0 1 -1,997 0 0,01031 0,01451 8,043 S8 0 0 0 0 0 0 0 0 0 2,857 1 5,98221 9,561438 4651,697 X1 1 0 0 0 0 0 0 0 0 2,857 0 5,98231 9,56156 12430,698 X2 0 1 0 0 0 0 0 0 0 0 0 -1 9E-06 2465,999 X3 0 0 1 0 0 0 0 0 0 0 0 -0,0037 -1,0046 1953,965

Tabel iterasi IV menunjukkan solusi sudah optimal dengan nilai : X1 = 12430,698 12431

(32)

LAMPIRAN 7

Penyelesaian Model Lower Linear Programming

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)