STRATEGI KOMBINASI UNTUK MENYELESAIKAN QUADRATIC ASSIGNMENT PROBLEM DISERTASI. Oleh
Teks penuh
Gambar
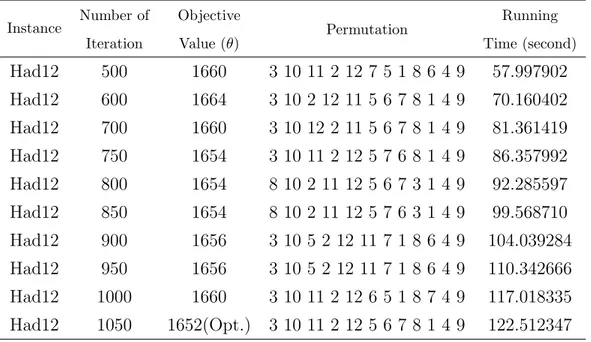
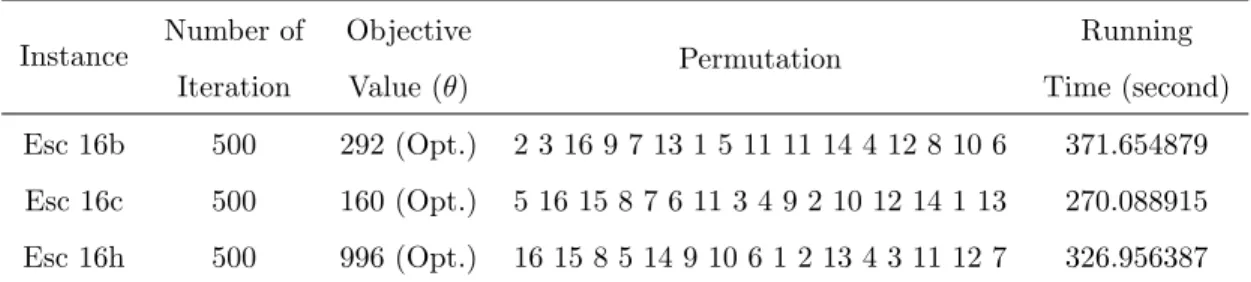
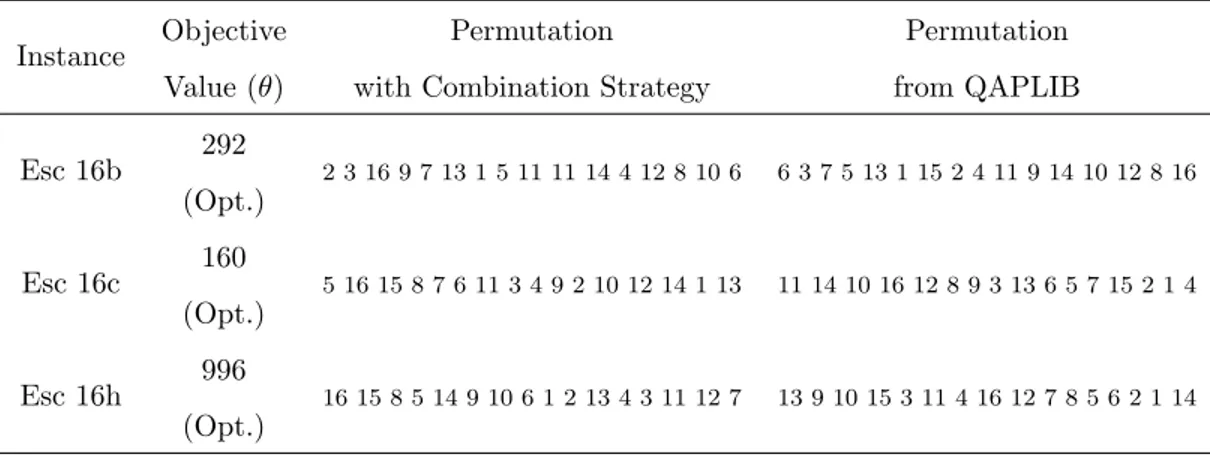
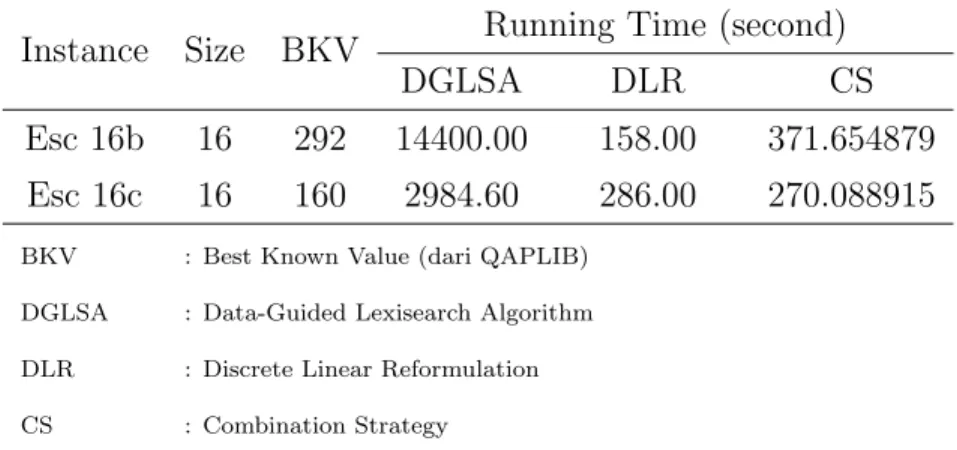
Dokumen terkait
Puji dan syukur kepada Tuhan Yang Maha Pengasih, yang telah memberikan berkat dan kasih-Nya sehingga penulis dapat menyelesaikan Tugas Akhir ini yang merupakan syarat utama yang
Sesuai Pasal 2 ayat (2) Undang-Undang Nomor 28 Tahun 2009 kepada Pemerintah Daerah Kabupaten dan Kota diberikan kewenangan untuk mengatur dan memungut 11 Jenis
Efektivitas program bimbingan dan konseling pribadi- sosial untuk meningkatkan kemampuan menjalin relasi pertemanan siswa Sekolah Menengah Pertama.. Skripsi, Psikologi
[r]
Tetapi sayangnya kebayakan dari game tersebut pada umumnya hanya berupa permainan yang tidak mempunyai nilai pendidikan, sehingga pemain game hanya tertarik pada gamenya saja dan
Akan dirancang suatu aplikasi Data Mining menggunakan metode Regresi Linier Berganda untuk memprediksi Prestasi siswa Berdasarkan setatus sosial dan kedisiplinan pada Smk
Puskesmas sebagai salah satu tempat pelayan kesehatan, telah melakukan upaya penanggulangan penyakit TB Paru melalui berbagai program kesehatan, berupa
Selain karena kesamaan komposisi tersebut, dipilihnya MU 301 sebagai bahan penelitian adalah karena diharapkan beton yang dihasilkan memiliki mutu yang tinggi karena pasir