Makalah: PEMBEKALAN OSN-2010 SMP N 1 Kebumen, Mata Pelajaran: Matematika

(1)

GEOMETRI BIDANG

Disampaikan dalam

PEMBEKALAN OSN-2010 SMP N I KEBBUMEN Mata Pelajaran: Matematika

Oleh: Murdanu, M.Pd. Jurusan Pendidikan Matematika FMIPA Universitas Negeri Yogyakarta

(2)

A. Teorema Pythagoras dan Teorema atau Topik lain yang Terkait dengan Teorema Pythagoras

1. Teorema Pythagoras

Dalam segitiga siku-siku, kuadrat panjang sisi miring samadengan jumlah kuadrat panjang kedua sisi siku-sikunya.

Jika dalam sebuah segitiga siku-siku, a dan b masing-masing menyatakan panjang kedua sisi siku-sikunya, dan c menyatakan panjang sisi miringnya, maka berlaku :

c2 = a2 + b2

Gambar 1

2. Kebalikan teorema Pythagoras.

Jika dalam suatu segitiga, kuadrat panjang salah satu sisinya samadengan jumlah kuadrat panjang kedua sisinya yang lain, maka segitiga tersebut merupakan segitiga siku-siku.

3. Tripel Pythagoras

Perangkat (a, b, c) dari tiga bilangan asli disebut tripel Pythagoras, jika kuadrat dari bilangan yang terbesar samadengan jumlah kuadrat dua bilangan yang lain.

Jika pada tripel Pythagoras (a, b, c), ketiga elemennya berupa bilangan asli yang faktor persekutuan terbesarnya adalah 1, maka (a, b, c) disebut tripel Pythagoras primitif. (3, 4, 5), (5, 12, 13) adalah contoh dua tripel Pythagoras primitif, sedang (15, 20, 25), (10, 24, 26) masing-masing bukan tripel Pythagoras primitif.

4. Teorema Proyeksi Segitiga Miring

Dari teorema Pythagoras dapat diturunkan teorema proyeksi pada segitiga miring, yaitu segitiga yang bukan segitiga siku-siku.

a. Teorema Proyeksi untuk Sisi di depan Sudut Lancip

1. Dalam suatu segitiga, kuadrat panjang sisi yang berhadapan dengan sudut lancip samadengan jumlah kuadrat panjang kedua sisi yang lain, dikurangi dengan dua kali hasilkali panjang salah satu sisi dengan panjang proyeksi sisi lain ke sisi tersebut.

Diketahui: Perhatikan Gambar 2. ,

90 A m , AB

CD o p panjang

proyeksi AC pada AB.

Berlaku:

a

2

= b

2

+ c

2

–

2cp.

a c

b

C

‘ b t a

‘ p c – p

A D B

(3)

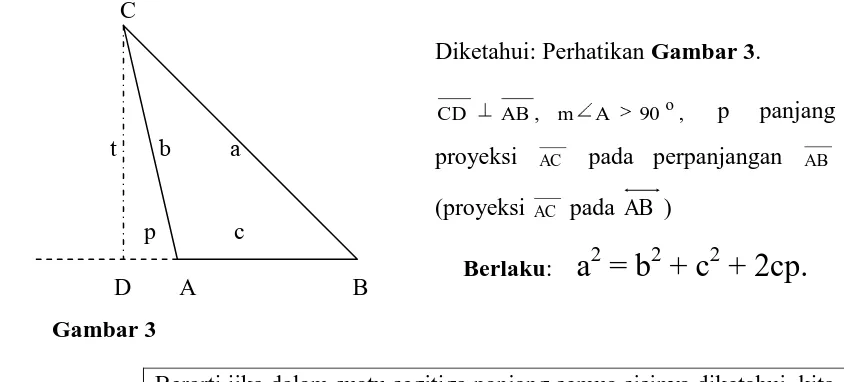
b. Teorema Proyeksi untuk Sisi di depan Sudut Tumpul

Dalam suatu segitiga, kuadrat panjang sisi yang berhadapan dengan sudut tumpul samadengan jumlah kuadrat panjang kedua sisi yang lain, ditambah dengan dua kali hasilkali panjang salah satu sisi dengan panjang proyeksi sisi lain ke sisi tersebut.

Diketahui: Perhatikan Gambar 3.

, 90 A m , AB

CD o p panjang

proyeksi AC pada perpanjangan AB

(proyeksi AC pada AB )

[image:3.595.104.526.168.359.2]

Berlaku:

a

2

= b

2

+ c

2

+ 2cp.

Gambar 3

Berarti jika dalam suatu segitiga panjang semua sisinya diketahui, kita dapat menghitung panjang proyeksi sebuah sisi pada sisi yang lain.

Latihan 1.

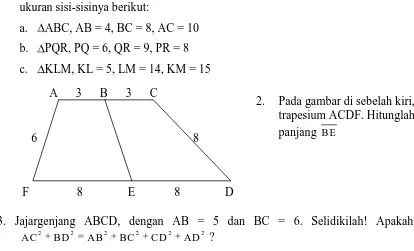
1. Selidikilah segitiga yang dideskripsikan ukuran sisi-sisinya berikut, merupakan segitiga lancip, siku-siku, ataukah tumpul:

a. ABC, AB = 4, BC = 8, AC = 10 b. PQR, PQ = 6, QR = 9, PR = 8 c. KLM, KL = 5, LM = 14, KM = 15

2. Pada ABC, AB = 13, BC = 20, AC = 21. Hitunglah panjang proyeksi sisi B C

ke sisi AB dan ke sisi A C !

5. Teorema Stewart

Jika dalam ABC, x menyatakan panjang ruasgaris yang menghubungkan titik sudut C dengan titik P yang terletak pada sisi AB, sehingga AP = c1 dan BP = c2, maka berlaku:

2 2 2

1 2 1 2

x c

a c

b c

c c c

C

‘ t b a

p c

(4)

Diketahui: perhatikan Gambar 4. P pada AB sehingga AP = c1 dan BP = c2, CD AB,

dan CP = x.

Berlaku:

x

2

c = a

2

c

1

+ b

2

c

2

–

c

1

c

2

c

Gambar 4

Dengan teorema Stewart tersebut memungkinkan kita untuk menentukan panjang ruasgaris yang menghubungkan salah satu titik sudut dari sebuah segitiga dengan sembarang titik pada sisi di depannya, jika letak titik tersebut dan panjang ketiga sisi segitiga tersebut diketahui.

Latihan 2.

A C D B

14 7 13 20 1. Berapakah panjang B C sesuai

informasi gambar di sebelah kanan?

A

B

C 8 D 6 7

12

2. Berapakah panjang A D sesuai informasi gambar di sebelah kanan? C

‘ b t x a

A D P B

‘ c1 c2

(5)

6. Teorema tentang Panjang Garis-tinggi pada sebuah Segitiga yang Diketahui Panjang Ketiga Sisinya.

Jika dalam ABC yang panjang sisi-sisinya a, b, dan c, panjang garis-tinggi ke sisi-sisi, BC, AC, dan AB, berturut-turut ta, tb, dan tc, serta s menyatakan setengah keliling

segitiga tersebut, maka berlaku:

Gambar 5

Latihan 3.

1. Hitunglah panjang ketiga garis tinggi pada setiap segitiga yang dideskripsikan ukuran sisi-sisinya berikut:

2. Hitunglah luas masing-masing segitiga pada nomor 1 tadi !

3. Hitunglah luas segitiga yang sisi-sisinya berukuran 17, 22, dan 39.

) c s )( b s )( a s ( s t ) c s )( b s )( a s ( s t ) c s )( b s )( a s ( s t c 2 c b 2 b a 2 a C

‘ a

D

‘ b p B

‘

t

a

(6)

7. Teorema tentang Panjang Garis-berat pada Sebuah Segitiga yang Diketahui Panjang Ketiga Sisinya (Teorema Apollonius)

Jika dalam ABC yang panjang ketiga sisinya masing-masing a, b, dan c, dan panjang garis-berat yang melalui titik-titik sudut A, B, dan C berturut-turut adalah ma,

mb, dan mc, maka:

[image:6.595.108.522.460.711.2]

2 4 1 2 2 2 1 2 c 2 4 1 2 2 2 1 2 b 2 4 1 2 2 2 1 2 a c ) b a ( m b ) c a ( m a ) c b ( m Gambar 6 Latihan 4.

1. Hitunglah panjang ketiga garis berat pada setiap segitiga yang dideskripsikan ukuran sisi-sisinya berikut:

3. Jajargenjang ABCD, dengan AB = 5 dan BC = 6. Selidikilah! Apakah

2 2 2 2 2 2

AC BD AB BC C D AD ?

A 3 B 3 C

6 8

F 8 E 8 D

2. Pada gambar di sebelah kiri, trapesium ACDF. Hitunglah panjang B E

A

‘ c b

‘ ma

B C ₂1a_D _a

2 1

Diketahui: Perhatikan Gambar 6. D

titik tengah BC , AD = ma.

Berlaku : 2 4 1 2 2 2 1 2

a

(

b

c

)

a

(7)

8. Teorema tentang Panjang Garis-bagi-dalam pada Sebuah Segitiga yang Diketahui Panjang Ketiga Sisinya.

Jika dalam ABC yang panjang sisi-sisinya masing-masing a, b, dan c, diketahui garis-bagi-dalam ACB memotong sisi AB atas bagian-bagian yang panjangnya c1 dan

c2, serta panjang garis-bagi-dalam tersebut dinyatakan dengan dc, maka berlaku:

2 1 2

c

ab

c

d

Diketahui: Perhatikan Gambar 7.

ACD BCD atau C1 C2

AD = c1 dan DB = c2.

Berlaku: 1 2

2

c ab c c

d

9. Teorema tentang Panjang Garis-bagi-luar pada Sebuah Segitiga yang Diketahui Panjang Ketiga Sisinya

Jika dalam ABC yang panjang sisi-sisinya masing-masing a, b, dan c, diketahui garis-bagi-luar ACB memotong sinargaris BA (memuat sisi AB ) pada titik D dengan D–A–B (A di antara D dan B) sedemikian, sehingga AB = c, AD = c1, dan BD = c2, serta

garis-bagi-luar tersebut adalah CD yang dilambangkan dengan dc, maka berlaku:

ab c

c d2_c ₁ ₂

Diketahui: Perhatikan Gambar 8.

ECD ACD atau C1 C2

AD = c1 dan BD = c2.

Berlaku:

d

c

1

c

2

ab

2 c

C 1 2

‘ b a

‘ dc

A B

‘ c1 D c2

Gambar 7

E

C 21

‘ dc b a

‘ c1 c

D A B

[image:7.595.106.488.161.348.2]

‘ c2

(8)

Latihan 5.

1. Pada PQR diketahui PQ = 10, PR = 14, dan QR = 6. Garis-bagi dalam sudut P memotong Q R di titik S dan garis-bagi-luar sudut P memotong Q R di titik T. Hitunglah panjang masing-masing: Q S, R S, Q T , P S, d an P T !

2. KLM siku-siku di titik K, KL = 6, KM = 8. Pada segitiga tersebut dibuat garis bagi K N. Hitunglah panjang masing-masing: L N , M N , d an K N !

3. Diketahui ABC siku-siku di titik A, m B = 30o, BC = 6. Garis bagi C memotong AB di titik D. Hitunglah panjang masing-masing: A D , B D , C D !

B. Teorema-teorema pada Lingkaran

A

O

g 1. Garissinggung lingkaran tegaklurus

terhadap jari-jari lingkaran ke titik-singgung.

O A

g

P B

C

D

E

2. Sebuah talibusur pada suatu lingkaran tegak lurus terhadap suatu jari-jari pada lingkaran yang memotong talibusur tersebut. Jari-jari tersebut juga merupakan sumbu bagi talibusur tersebut.

(9)

3. Sudut antara dua lingkaran yang berpotongan adalah sudut yang dibentuk oleh perpotongan garis-garis singgung dua lingkaran tersebut di titik-potong kedua lingkaran yang berpotongan

4. Garis-singgung persekutuan dua lingkaran adalah sebuah garis yang menyinggung dua lingkaran.

O O

P

O

P

A A

A P

Q

R Pg

Ph

(10)

Latihan 6.

1. Diketahui (M, 5), (N, 3), MN = 10.

(a) Berapakah panjang ruas-garis-singgung -dalam kedua lingkaran tersebut?; (b) Berapakah panjang ruas-garis-singgung -dalam kedua lingkaran tersebut? 2. Hitunglah masing-masing panjang A S, B S, d an O S dari gambar di bawah !

O P

A

B

S

5 2

9 O

O P

P A

A B

(11)

5. Sentral dua lingkaran yang tidak sepusat membagi dua samapanjang talibusur persekutuan dua lingkaran tersebut.

6. Besar sudut keliling dalam suatu lingkaran samadengan setengah dari besar busur di depan sudut keliling tersebut.

M P N A

B

M N

AB

P

AP BP

atau

AP = BP

O P

A

B

(12)

Latihan 6.

C. Teorema-teorema penerapan teorema sudut keliling:

A

B O

C

1 2

m

B A C

m B C

A B O

C

1 2

(13)

A

B

C

M D

AB

CD

A

B S

m

ASB

2

mAB

mCD

1

C O

D

C M B S A

mAC mBD

DSB

m ₂1

C

A B D M

AB

diameter lingkaran

(a)

CD

2

= AD × BD

(14)

C

AS × BS = CS × DS

A

S M

B

D

B

A

M P

C D

AP × BP = CP × DP

P

B

PA

2

= PB × PC

C

M

A

A B

O

N M

(15)

C

M P N

D

A B C

D

E M F

H G

K (a)

CEG

L . 4

EG . CE . GC MC

(b)

ADK 2

1

ADK

K L MH

(16)

Soal – soal Latihan

1. Dalam sebuah segitiga siku-siku, diketahui bahwa panjang kedua sisi siku-sikunya masing-masing 6 cm dan 8 cm. Hitunglah: panjang garis-tinggi ke sisi miringnya! 2. Dalam ABC, diketahui AB = 12 cm, m ABC = 60 , dan BC = 8 cm. Hitunglah:

keliling ABC tersebut!

3. Dalam PQR, diketahui PR = 10 cm, m PQR = 45 , dan QR = 15 cm. Hitunglah: panjang sisi ketiga dari PQR tersebut!

4. Dalam ABC, diketahui AB = 8 cm, BC = 6 cm, dan AC = 7 cm. Hitunglah: panjang ketiga garis-beratnya !

5. Dalam PQR, diketahui PQ = 14 cm, QR = 13 cm, dan RP = 15 cm. Hitunglah panjang dari:

a. Proyeksi PR pada QR ; b. garis-tinggi dari titik sudut Q.

6. Dari sebuah ABC, diketahui AB = 6 cm, BC = 8 cm, dan AC = 7 cm, titik P terletak pada BC sedemikian, sehingga P–C–B dan CP ₂1BC _{. Hitunglah panjang}

AP !

7. Diketahui PQR dengan PQ = 10 cm, QR = 6 cm, dan RP = 8 cm. Pada segitiga tersebut dipilih baris-berat PR dan garis-bagi RT . Hitunglah panjang ST !

8. Dalam setiap jajargenjang berlaku: jumlah kuadrat panjang kedua diagonalnya samadengan jumlah kuadrat panjang semua sisinya. Buktikan pernyataan tersebut! 9. Diketahui trapezium ABCD, dengan AB CD , AB = 20 cm, BC = 13 cm, CD = 6

cm, dan AD = 15 cm.

a. Lukislah dengan cermat, trapezium ABCD tersebut! b. Hitunglah panjang diagonal AC !

c. Hitunglah luas daerah trapezium ABCD tersebut !

10. Di halaman depan sebuah sekolah tumbuh pohon cemara A dan di halaman belakang sekolah tersebut tumbuh pohon mangga B (dilukiskan pada gambar sebelah kiri). Kedua pohon tersebut terhalang oleh bangunan sekolah. Jelaskan: bagaimana cara menentukan jarak kedua pohon tersebut, karena tidak mungkin dilakukan pengukuran secara langsung!

11. Diketahui B dengan diameterAC , talibusur-talibusur DE,AE,DC dengan DC

AE

F . Jika EF = 4, EA = 16, dan DE = 6, berapakah BC ? A

(17)

12. Diketahui A dengan jari-jari AB dan AD , garissinggung-garissinggung BC dan CD . Jika AB AD dan BC CD , buktikan ABCD suatu persegi.

13. Diketahui P dengan diameterAC , D dan B pada P berlainan pihak terhadap AC . (a) Jika m CAB = 30, berapakah mAB ?; (b) Jika mAB = 90, buktikan

ACB samakaki!; (c) Jika AC BC , buktikan AD AB.

14. Pada O terdapat titik-titik A, B, C, dan D secara berurutan sedemikian, sehingga mAB = 60, mBC = 90, dan mCD = 75. Susun talibusur-talibusur:

AD dan , CD , BC ,

AB . Segiempat yang terjadi, yaitu ABCD dinamakan segiempat-talibusur. Jika kedua diagonal pada segiempat tersebut dilibatkan, jelaskan ukuran sudut-sudut yang terjadi!

15. Dalam intM terdapat talibusur-talibusur yang ujung-ujungnya A, B, C, dan D sedemikian, sehingga AB CD S dan AB = CD. Buktikanlah: (a) AC BD ; (b)

DS

AS ; (c) CS BS .

16. Diketahui N, P extN, A N, B N, dan C N, PA = NA. Terdapat PN

dengan P–A–N dan A–N–B. Terdapat PC NC . Buktikan: (a) PAC samakaki; (b) PBC samakaki. Hitunglah: (c) L PAC; dan (d) L PBC.

17. Diketahui P merupakan lingkaran-luar ABC, BD , ABD CBD, D P, dan

DE diameter P. Buktikan: (a) AD CD ; (b) BE merupakan garis-bagi-luar ABC.

18. Diketahui Q merupakan lingkaran-luar ABC dengan m BAC = 50, m ABC = 60, titik A merupakan titik-singgung garis g terhadap Q, titik B merupakan titik-singgung garis h terhadap Q, titik C merupakan titik-singgung garis k terhadap

Q sedemikian, sehingga g h = P, g k = Q, dan h k = R. Hitunglah ukuran sudut-sudut dalam PQR.

19. Pada O, A O, B O, C O, OA = 4, OA OB , g O = C, g OA = E, g OA , OE = AE, M AB OC . (a) Hitunglah ukuran sudut-sudut yang terjadi dengan M sebagai titik-sudutnya!; (b) Berapakah AC ?; (c) Hitunglah L AOBC

!

20. Diketahui O Q = A, B = O Q, A B, C O dengan A–O–C, dan D Q dengan A–Q–D. Buktikanlah: (a) AB CD ; (b) B–C–D; (c)

OQ 2

CD ; (d) OQ CD .

21. Diketahui O Q = A, B = O Q, A B, garis g menyinggung O di titik A, dan garis h menyinggung Q di titik A. Buktikan: (g,h) QAO.

(18)

24. Dua buah sisi dari sebuah segitiga berukuran 17 dan 39. Ukuran garis-berat ke sisi yang ketiga sepanjang 22. Berapakah luas segitiga tersebut?

25. Carilah ukuran bagian-bagian sumbu-sumbu yang terdapat di interior sebuah segitiga yang berdimensi (10 12 14) !

DAFTAR PUSTAKA

De Baan dan J.C.Boss. 1956. Ilmu Ukur. Jilid IIA. Jakarta: J.B. Wolters.

Keedy, Jameson, Smith, Mould. 1967. Exploring Geometry. New York: Holt, Rinehart and Winston, Inc.

Travers, Dalton, Layton. 1987. GEOMETRY. River Forest, Illionis: Laidlaw Brothers, A Division of Doubleday & Company, Inc.

A

M P N

B