Practical modern statistics

Can modern statistical mechanics unravel some practical problems encountered in

model biomatter aggregations emerging in internal- & external-friction conditions?

A. Gadomski∗

and N. Kruszewska Institute of Mathematics and Physics, University of Technology and Life Sciences, Kaliskiego 7, Bydgoszcz PL–85796, Poland

I. Santamaria-Holek

Facultad de Ciencias, Universidad Nacional Autonoma de Mexico, Circuito exterior de Ciudad Universitaria, 04510 DF, Mexico

J.J. Uher

ZSMiO, Konopnickiej 6, Bielsko Bia la 43-300, Poland

Z. Pawlak

Faculty of Chemical Technology and Engineering,

University of Technology and Life Sciences, Kaliskiego 7, Bydgoszcz PL–85796, Poland Utah State Department of Health, Salt Lake City, UT 84113, USA

A. Oloyede

Queensland University of Technology, School of Engineering Systems, GPO Box 2434 Brisbane, Q 4001, Australia

E. Pechkova, C. Nicolini

Nanoworld Institute and Eminent Chair of Biophysics, Genoa University, Corso Europa 30, 16132, Genoa, Italy, Fondazione EL.B.A., Piazza SS. Apostoli, 66, 00187, Rome, Italy

(Dated: July 13, 2007) Abstract

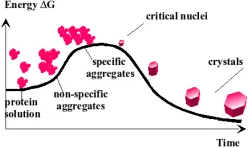
(Dis)ordered aggregations, in particular a crystal formation in biopolymer systems, appear recently complex tasks to be undertaken by many specialists of research and technology, among which sta-tistical physicists play their role, mainly in solving and/or elucidating the thermodynamic-kinetic and dynamic aspects of the aggregations. Biomatter aggregations are ubiquitous in both natural as well as laboratory systems, to mention but micelles emerging in aqueous solutions, biopolymer spherulites or non-Kossel (single) crystals.

Although their thermodynamic behavior has mostly been studied very close to equilibrium, there has appeared recently quite a new trend of benefiting readily from some out-of-equilibrium studies on the amphiphilic systems listed above. It turns out natural to see an accompanying role of kinetic effects, ranging over many time and space scales, somehow completing the way in which systems make an attempt towards attaining, slowly or vigorously, or sometimes ”normally”, their possibly closest-to-equilibrium states, measured along a naturally selected reaction coordinate.

The aggregations in question emerge naturally under a viscous (or, more generally, viscoelastic), which is to say - internal-friction context. They appear because of typically asymmetric distribu-tion(s) of structural viz hydrophobic forces throughout the amphiphilic system, thus they emerge mainly thanks to hydrophobicity. Such aggregations show up some interesting viscoelastic prop-erties, coming from a proper quantification of their diffusion-type non-Markovian characteristics. The memory-involving properties mentioned are attributed to a broad survey of microrheological effects, accompanying the aggregations of interest. They are seen at the levels of micelles as well as of non-Kossel crystal formations. They manifest, however, under no external perturbation (load), and the only interesting constraint one can announce is related to the degrees of freedom of the system, pointing directly to its also structural, i.e excluded-volume effect. It is very important from a practical viewpoint if one is capable of speeding up the process of interest, for example, a lysozyme crystal formation. The origin of all charged particles involving formations of interest is deeply rooted in the first law of thermodynamics for open Gibbs’ systems, here of amphiphilic nature, complemented by the entropy-production equation and suitable (linear) flux-force relations with Onsager’s coefficients playing their pivotal role.

they can absorb and distribute some quite heavy energy inflow to a complex interlayer, named the synovial fluid; (ii) they can facilitate the friction effect, contributing also hypothetically to a low-wear counter-effect, this time by a certain efficient roll-over sub-effect involved in the biolubrication of two solid surfaces of the articular cartilage. The system of special interest, termed the articular cartilage, being present in certain parts of our body, such as knees or hips, appears to be a highly dissipative system, characteristic of an anomalous chemical reaction the dynamic behavior of which ranges from regular to chaotic, also manifesting a certain sensitivity to a geometrical confinement, being additionally prone to certain random-walk (load-assisted) microscopic rheological conditions of versatile types. (At thermodynamic equilibrium, in turn, it exhibits an acid-base dynamic balance, to be observed in the multilayer protective structure of the membranes involved.)

The solutions to versatile biomatter-aggregation tasks formulated in the internal-friction empha-sized context, and in quite untypical, confinement-involving, dispersive conditions, look amenable to a statistical-mechanics approach, mainly based on the Smoluchowski equation with time-dependent Onsager’s coefficients, and with a Kramers’ barrier of controllable/adjustable characteristics. The aggregations emerging within the friction-lubrication context of external-friction nature, being in-volved when studying the dissipative dynamics of the model articular cartilage, leading presumably to formations of multilayers and (reverse) micelles, trapped within an interlayer between both solid surfaces, are also manageable to the modeling in terms of a thoroughly designed autonomous dynam-ical system, being able to reflect a plethora of its dynamdynam-ical (e.g., periodic) behaviors, manifesting during the load-duration periods. Both main ways of modeling emphasize a practical role played by statistical-mechanics in solving two types of particular non-ergodic problems of interdisciplinary (bioengineering and medicine; materials and surface science) character.

PACS numbers: 05.10.Gg, 05.10.Ln, 05.40.-a, 81.10.-h, 83.50.-v, 87.15.Nn

Keywords: aggregation, crystal growth, micelles, viscosity, friction, mesoscopic system, fluctuation-dissipation, biolubrication

Main abbreviations used throughout the Chapter

IFS - internal-friction system EFS - external-friction system

StatMech - statistical-mechanics and/or statistical-mechanical

ES - Einstein-Smoluchowski; eES - extended Einstein-Smoluchowski

CA - Coulomb-Amontons law

LB&S - Langmuir-Blodgett&Schaefer

AC - real articular cartilage; mAC - model articular cartilage

SPC-A - spherical protein crystal/aggregate

aD3DS - anomalous dissipative 3D dynamical system aRW - anomalous random walk

FP&S - Fokker-Planck & Smoluchowski FL - friction-lubrication

N-G - nucleation-growth

MNET - mesoscopic nonequilibrium thermodynamics AK - Avrami-Kolmogorov

RMs - reverse micelles

I. INTRODUCTION

Biomatter aggregations, such as the ones of am-phiphilic types, composed of proteins and/or lipids in a water-based polyelectrolyte, have become recently a

sub-∗_{Electronic address: agad@utp.edu.pl}

ject of intensive studies and interesting practical applica-tions [1, 2].

As for the biomatter aggregations based on proteins in aqueous solutions one could mention formations of pro-tein (non-Kossel) crystals and aggregates [3–5].

As for the biomatter aggregations based mainly on phospholipids one could invoke formations of mono-layers, bimono-layers, reverse micelles as well as liposomes [6, 7]. Both main types of aggregations listed above may emerge in solutions, also those of physiological na-ture, showing up their basic properties in many differ-ent friction-lubrication (FL) contexts. Depending upon whether the context is explicitly influenced by an exter-nal force, −−→Fext, causing some aggregation events in the system to occur/change, one can divide them into two groups:(i) internal-friction systems (IFS) when −−→Fext ≈ −

→

0 ; (ii) external-friction systems (EFS) when clearly −−→

Fext 6= −→0 . The IFS can typically belong to microrhe-ological systems [8], whereas EFS may generally develop full rheological behavior [9], with shear effects and non-Newtonian characteristics as their main landmarks [10]. Both IFS and EFS are of permanent interest coming from statistical-mechanical (StatMech) description.

the Einstein-Smoluchowski (ES) fluctuation-dissipation formula, namely:

Dsηs=β−1_{, (1)}

where β = _kB1_T, kB - Boltzmann’s constant, T - abso-lute system’s temperature. Certain plausible extensions of the ES formula, abbreviated throughout the whole Chapter by eES, typically lead to a time-dependent (non-Markovian) behavior that should always be assigned to a particular system of interest [11].

In recent years, the EFS dynamics, in turn, have not received considerable attention as far as the Coulomb-Amontons (CA) law,

µs= Ff r

Fext, (2)

is concerned (with all quantities in the CA having their usual meaning,e.g., µs is the static-friction coeffi-cient). A real challenge appears, however, when friction-adhesion effects at a nanoscale molecule-size level, char-acteristic of pN forces, come into play. Then, the CA context does not work effectively, and one must resort to more microscopic description of anyFLprocess of inter-est [12]. It is very important to realize that biomatter aggregations appear as decisive factors controlling both IFS and EFS dynamics [13]. However, due to its gener-ality, such a statement, cannot be proved satisfactorily in any other way than by examples. Therefore, in this study, we have carefully selected two adequate IFS- and EFS-involving examples that will emphasize the govern-ing role of aggregation events, both at their dynamic and quasi-static levels, in order to see how they could control a specific process of interest.

Thus, as the proposed example of the IFS we would like to offer a protein (poly)crystalline aggregation from solution. First, we will introduce a (dis)ordered protein-aggregate formation in a space without confinement [14]. Next, we will try to reconsider the same process in terms of a superimposed confinement, being typically of Langmuir-Blodget & Schaefer (LB&S) type [15]. Such confinement readily promotes incorporation of small or-dered aggregates into a crystal’s microstructure [16]. This incorporation causes the speed of a protein crystal to increase, which is an experimentally evidenced fact [17], also confirmed by means of a computer simulation [18]. Here, we also present an analytical rationale that absorp-tion of aggregates instead of monomers may increase the crystal/aggregate growing pace.

As for the proposed EFS example, we have made an attempt to embark on modeling a really complex but extremely important system - this is the so-called ar-ticular cartilage (AC), the dynamics of which, whether vigorous or slow, would influence the system’s behavior substantially [19]. In the case of the AC it appears inter-esting to see even a slight departure from the acid-base quasi-equilibrium of the system’s behavior, cf. [20]. A description of such a, typically small, nonequilibrium de-parture leads to conjecture the dynamics of the system

as a tribopolymerization process [21]. Here, we wish to reconsider the general tribopolymerization system [22] in terms of a specific (first order) tribomicellization process [23], in which a formation of lipid multilayers and (re-verse) micelles [24] is believed to control the kinetics of the AC friction-lubrication system, in which the lubrica-tion is thought of to proceed much easier by emergence of micelles and aggregates of various types. Their pivotal role can be extensively discussed throughout the second part of this study.

The Chapter is organized as follows. In the next part, we are dealing with a model IFS which is taken for sim-plicity as a spherical protein crystal/aggregate (SPC-A). Then, we are looking into main dynamic/kinetic features of a model AC, abbreviated for the purpose of the present study by mAC. Finally, we summarize our findings by concluding about the usefulness of StatMech approaches applied, and discuss some perspective of the proposal of-fered.

II. FIRST EXAMPLE:THE INTERNAL-FRICTION SYSTEM (IFS) EXPLAINED IN TERMS OF SPHERICAL PROTEIN CRYSTAL/AGGREGATE (SPC-A)

A. MNET-type theory of unconfined SPC-A

Brief overview

Proteins are main constituents of the living cells. They frequently aggregate under a variety of physiological as well as laboratory-designed conditions. Formation of or-dered protein aggregates, such as non-Kossel crystals, spherulites, fibrils , and lamellar crystals, yielding gel phases, etc., becomes nowadays a formidable practical task of modern science and technology [5, 25].

In case of protein crystals it also becomes a nar-row bottleneck of recent crystallographic research and structural-biology investigations towards resolving the chemical structure of an individual protein of interest be-cause both disciplines mentioned need high-quality crys-talline material in order to carry out its systematic ex-perimental (SAXS, AFM, etc.) investigations [15].

Amongst practitioners of protein crystal growth from solution, constantly trying to improve the quality of the crystals, there exists a belief that at least at low supersat-uration the Burton-Cabrera-Frank (BCF) model of crys-tal growth by screw dislocation would suffice to describe the formation, especially when it is completed by ap-propriate identification of the driving force(s), and when having the set of main thermodynamic-kinetic and chem-ical parameters under sufficient control [3].

be expected in colloidal suspensions [27], and in both protein- as well as colloid-containing solutions such a mechanism is proposed to be responsible for phase or-dering, although it, unfortunately, may finally induce de-fects into non-Kossel crystal’s structure. Such a behavior is commonly called viscoelastic phase separation, and has recently been established as an experimentally justified fact, both in synthetic as well as natural polymeric sys-tems [25–28].

Having right now permitted a historical excursion, let us ascertain that a few methods are employed to produce crystals. To make inorganic,e.g. semiconductor crystals, we are privileged to choose the Czochralski [29] method, and of course its modifications [30], or some methods characteristic of the growth from undercooled melt or su-persaturated solution. By the way, note that enormous technological progress toward contemporary High Tech

has been gained due to an almost accidental discovery of pulling out the single crystals from undercooled metallic melt, produced with extreme invention about 1916 in a German AEG lab (Berlin) by a crystallographer, chemist and materials scientist Jan Czochralski, born in western part of Poland (Kcynia near Pozna´n or Bydgoszcz), by means of a synergistic stepwise recovery of the regular atomic layers, constituting the needle-like single crystals by applying a synchronized external clocking device, the frequency of which was determined experimentally for several common-use metals, quite of interest from elec-trical community of those as well as recent times [31]. Let us underscore strongly that the method by Czochralski looks confidential, and very similar to the truly coming-from-nature crystal formation discovered by Burton and coworkers (BCF).

As usual, life becomes more complicated and there is, to authors’ best knowledge, no robust protocol developed that can be applied to any protein crystal nucleation-growth (N-G) phase transformations of practical interest - it is always carefully corroborated for each individual protein to be crystallized. The reason is due to tremen-dous complexity of the multi-parametric process we have to deal with, thus, its description from the first principles looks hopeless, and any use of approximate analytical and numerical methods renders it possible for at most certain specific systems of interest,e.g. that of lysozyme [4].

Thus, how can one remedy the problem that looks un-solved from the microscopic point of view? As one can learn from the below presented rationale the mesoscopic description might really be of help here [32].

In fact, in the fifties and sixties of the past century J.W. Cahn made for metallurgical purposes an interest-ing attempt for formulatinterest-ing the theory of crystal growth and interface motion in crystalline materials, also point-ing to its mesoscopic character deeply rooted in irre-versible thermodynamics. He mentioned certain prop-erties of a crystal advancing toward its external phase, such as continuous-growth property, whereby every ele-ment of the surface is capable of advancing normal to it-self, whether the surface is diffuse or sharp, and whether

there exist or not, the singularities of the surface ten-sion of the crystal. Trying then to judge whether the continuous growth is possible to occur he introduced a criterion of interaction of the crystallizing front with its nearby surroundings called lattice resistance - it will be seen in our model as some viscosity-dependent property characteristic of the interfacial region of the spherical ob-ject of radiusR that we will allow to grow in a bath of Brownian-type particles (proteins) dispersed in the near-crystal-surface aqueous solution.

The mesoscopic model that is offered here is qualita-tively in accord with Cahn’s conception of continuous-type crystal growth [32]: It is also rooted in nonequilib-rium thermodynamics at a mesoscopic level, commonly abbreviated by MNET [33]. Its dynamics is well de-scribed by the Smoluchowski-type equation in a configu-rational space, with the Kramers’ barrier being involved in the presented approach; moreover, a hydrodynamic mode, revealed in the context of global vs. local dy-namic properties of the complex system, appears to play a unifying role towards showing up some common (hy-dro)dynamic features of the formation [13, 14].

Certain polycrystalline round-shaped nonequilibrium microstructures, in turn, commonly termed spherulites, become nowadays a real challenge both scientifically and technologically [34]. In this study, we are go-ing to convince the reader that the simple concept of Avrami-Kolmogorov (AK) phase change, dealt with at a MNET based level, is fully able to elucidate in which kinetic and thermodynamic conditions may the spheri-cal (three-dimensional case) or circular (two-dimensional case) polycrystalline objects arise in an entropic milieu, being mostly by virtue of the examples studied an aque-ous protein solution.

The spherulites typically emerge during N-G phase transformation in nonequilibrium conditions. The ther-modynamic and kinetic conditions one may have in mind are supposed to be of competitive nature. Irrespective of the system in which the spherulites arise, whether bi-ological (natural) or not, the competition concerns the observation on how the main order-disorder effects man-ifest in the course of the spherulitic formation, see Fig. 1.

It has very recently been recognized that a reflection of an interplay between the ordering effect on crystalliza-tion, and the disordering effect on interfacial instabilities due to some formation of ”secondary” N-G front at the interface, leads to switching-on a possibly second crys-tallization mode subject to the emergence of fibrils that introduce polycrystalline misorientation-involving asym-metry to the system, thus spoiling the otherwise symmet-ric mode of the growth under consideration. It is then envisioned that such a principle already described above must be quite general, and to a large extent indepen-dent of the system details, namely, whether it consists of small-molecule or large-molecule building blocks or not [35].

FIG. 1: A schematic drawing of the protein spherulite: left, simplified general view of its microstructure with the amor-phous core in the center; right, the expanded part of the inter-nal fibrillar microstructure of the spherulite, with the amor-phous (blank) phase in between, for transparency shown in a rectangular frame.

our fairly coarse-grained description of the spherulitic for-mation in a complex fluctuating medium of entropic char-acter [14]. Based again on the first law of thermodynam-ics, and applying the well-known Gibbs’ equation for the rate of positive entropy production in the system, we are able, under a minimal set of necessary thermodynamic and boundary-conditions concerning assumptions, to un-ambiguously derive a kinetic equation of Fokker-Planck-Smoluchowski (FP&S) type being capable of revealing the evolution of a polynuclear system in the space of the size of the nuclei,χ, called further theχ–space.

A careful analysis of the basic properties of such a stochastic system, with specially emphasized phe-nomenological construction of its diffusion function D(χ, t), wheretis the time, virtually based upon the AK type rationale, gives us univocally the main kinetic signa-ture of the spherulite formation, namely, that it is a wave-like process, asymptotically arriving at a constant-speed limit for the overall formation. In what follows we are going to delineate the main landmarks of our argumen-tation on the formation of the protein-type spherulites by the switching-on competitive mode, including forma-tion of the spherulitic skeleton comprised of the rod-like segments, cf. Fig. 1, the emergence of which is merely described in terms of a fractional, typically one-half AK exponent,νr≈1₂.

Anomalous transport of finite-sized particles in a vis-coelastic medium is described in terms of a generalized FP&S type equation containing memory effects. This equation is derived from the principles of nonequilib-rium StatMech and nonequilibnonequilib-rium thermodynamics at the mesoscale, and is shown to account for the finite-size of the Brownian particles. At large times, the description leads to a non-Markovian diffusion equation for the mass density field suitable to describe anomalous subdiffusion and superdiffusion inside the intracellular environment. This description is carried out in terms of the evolution of the mean square displacement and compared with exper-iments. Good agreement between theoretical description and experimental data is found.

1. The complex interfacial motion involving hybrid model of crystal growth and (poly)crystalline aggregation

In what follows, the mesoscopics practically means a deterministic kinetic description of the formation with an account of the fluctuations of a properly chosen stochas-tic variable, included. The primary advantage of using MNET for the ordered protein-spheroid formation is that we do not arrive at a Langevin-type description, which is a stochastic version of the Newtonian dynamics, thus, being restricted to force-and-potential application. We rather end up with a more flexible tool which appears to be the Smoluchowski-type equation [36] for the probabil-ity densprobabil-ityρ(R, t) of forming a spheroid of radius R at timet[28, 33, 37].

In the deterministic part, we start with a mass-conservation law in a form of the standard integro-differential equation, where the integration goes over the volume of a nucleus, V, closed by its surface area, S, over which also the second matter-flux involving integral is taken. The differentiation, in turn, goes over time and is applied to the volume integral expressing a net mass change of the system. The nucleus, assumed for simplic-ity in our model as being homogeneous (of constant den-sityC) is fed by an external particle-concentration field, c(r, t), composed of Brownian-type particles viz proteins, and possibly their clusters, dispersed in the solution. All sources of chemical reaction, virtually contributing to al-teringCand/orc(r, t) are being neglected, this way, after applying the divergence (Gauss) theorem, giving rise to state explicitly [38, 39]

∂

∂tc(r, t) +div[J(r, t)] = 0, (3)

where r denotes the position of a protein [40, 41], and

Jrepresents the matter flux, i.e. ultimately arriving at a local version of the above mentioned mass conserva-tion law. After accepting the argumentaconserva-tion given in the literature [39, 41], let us confine ourselves to choose a ballistic-type case in which for a protein-type system the matter flux is of mass-convective nature [39]

J(r, t) =c(r, t)v(r, t), (4)

where v(r, t) represents the velocity vector field, acting mostly in the interfacial region that can be limited to the Stern-type macroion-depleted double layer enclosing the growing object, see Fig. 2 [39, 42].

FIG. 2: Cartoon of the Stern-type double layer surround-ing the SPC-A. The lysozyme-type proteins, performsurround-ing their random walks (two trials are depicted), would exceed by their mean-free paths (contributed to by a λB) the width of the

layer,λDL, which makes mostly time-correlational

contribu-tion to the formacontribu-tion dynamics, cf. text for addicontribu-tional expla-nation.

FIG. 3: Protein crystallization by LB&S thin film nanotem-plate: LB&S nanotemplate, used to modify classical hanging drop method [43], trigger the specific aggregates’ formation in the protein drop solution and thereby helps to overcome the nucleation free energy barrier, see Fig. 13.

K1(R) = 2/R- the mean curvature) but now applied for

low-dimensional viz non-macromolecular crystals emerg-ing from a supersaturated solution. The above yields the kinetic equation as follows

d

dtR=σR

e_{×vmi, (5)}

where the dimensionless supersaturation σRe ₌ ce(R)/(C−ce(R)), andvmican be considered as a param-eter, herein an average constant velocity of the macroion near the spheroid surface. This is by no means the case of high-dimensional or protein crystal growth, cf. Fig. 3: Here a modification of the GT boundary condition has to be expected [39]. This and the stochasticity ofv(r, t) (thus, considered in a scalar form) will be discussed be-low.

2. (Non)equilibrium boundary condition

Modification of the GT equilibrium boundary condi-tion for the protein crystal formacondi-tion results in either

some modified GT condition of equilibrium type (origi-nating from more refined consideration about the molec-ular nature of the surface tension, and the additional

e.g. curvature terms it may contain) or gives rise to readily nonequilibrium effects at the boundary, especially the ones coming from elastic interactions [39] between the boundary proteins and its nearby electrolyte sur-roundings (also, within the boundary when some addi-tional strain between the vacancies may arise), or when spherulites composed of fibrils tend to emerge, even with a tendency of lateral growth violating here somehow the continuous-growth mode invoked by Cahn which suits also our type of reasoning [41].

Thus, the overall (non)equilibrium boundary condition can be proposed as follows [39, 42]

cne(R) = co[1 + ΓD×K1(R) +δT2×K2(R) +

+Σ3i=1αix(i)(R)−βk×dRdt], (6)

where δT Tolman length, K2(r) = 1/R2 Gaussian

cur-vature, αi the elastic coefficients and x(i)_{(R) = (R}i ₋ Ri

o)/Rio (Ro is the initially taken object’s radius), with the latter representing three main crystal-surface nucle-ation mechanisms [39]. βk stands for the kinetic coef-ficient, and dR/dt points to the readily nonequilibrium character of the boundary condition [42], expected to oc-cur for spherulites, especially those of lysozyme type. Be-cause of stating Eq. (6) in such a general form one is then able to write down a more general kinetic equation [39]

d

dtR=σR

ne_{×vmi, (7)}

where

σRne= cne(R)

C−cne(R) (8)

under a necessary restriction that all (non)equilibrium mechanisms prescribed at the boundary, cf. Eq. (6), do not need to operate at the same time together. They can rather be switched on/off whenever physically legitimate [40, 41, 44, 45].

3. Protein-involving nearby velocity field

In the deterministic description one may notice the Frenkel-type velocity of the macroion incorporated in the resulting equation, see vmi in Eq. (7). In order to achieve a more realistic description of the process one is motivated to offer a correlational proposal forv(r, t). Although it can separate into its spatial (r) and tem-poral (t) parts, in the very vicinity of the crystal, i.e.

cannot be ruled out. They arise because the viscosity in the diffusive part of the Stern double layer decreases in time when the crystal grows. Since the crystal be-comes bigger the double layer expands too, and because the external-concentration conditions are assumed un-changed, a protein-influenced viscosity change near the crystal surface results in some viscosity decrease in time. This can be described as a depletion-zone effect around the growing object. It is due to some diffusivity, D(t), effective increase in time which comes from the time cor-relations in v(r, t) to be inferred from the Green-Kubo formula, i.e. when the fluctuation-dissipation theorem can be applied [33]. Thus, after postponement of the spatial correlations, the correlational proposal may be a stationary Gaussian but correlated, though with a zero average velocity part

< v(t)>= 0,

K(|t−s|) =< v(t)v(s)> f or t6=s, (9)

where the time correlations K(s′

), with the characteris-tic correlation timeτcor), given by means of an average < ... >, are related toD(t) by

D(t) = t

Z

0

K(s′ )ds′

f or s′

≥0. (10)

It is found out that the most interesting correlational proposal to be offered here appears to be the following [46]

D(t)≃ τcor 1−γ ×

t

τcor

1−γ

f or t≫to, (11)

where γ ∈ (0,1) is a characteristic fractional exponent, and to is taken as an initial time. It can be anticipated that [42], ifγ→0 is obeyed, the rounded protein-crystal formation points to an overall ballistic, hydrodynami-cally stable growing asymptotic mode, since D(t) ∝ t eventually applies. It greatly contributes to the total hydrodynamic stability of the formation, especially in a sufficiently mature growing stage (see, Fig. 4), since for t >> to the late-time solutions of the stochastic

d

dtR=σR

ne_{×v(t), (12)}

cf. relations (7) and (9), R≡R(t), are given by R∼t, pointing to on-average-constant speed of the formation dR/dt → const., which is true because σRne typically suppresses to a constant value, being an inverse of the supersaturation, whent >> to, andv(t)→vmi=const. on average as well.

There is another signature of the ballistic character of the process, herein at the mesoscopic level. At a ”macro-scopic level” of description one may see the relation given by Eq. (4) as some signature of a ballistic character of the process, whereas its microscopic counterpart corre-sponds to Eq. (11) correlation strength withγ→0. The

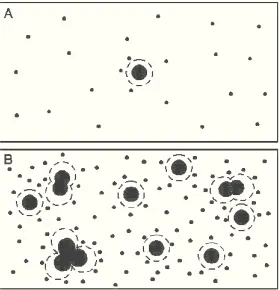
FIG. 4: Two consecutive snapshots of the FP&S type pictures in two different stages (A - early stage, B - late stage), show-ing how small randomly walkshow-ing clusters, or large monomers, are merged into some bigger ones. In the stage, B, under inhomogeneous solution’s regime, there is a possibility of cre-ating a ripe viz thermodynamically stable nucleus from which the crystal formation may likely start to develop. (Note, that the situation depicted by the stage A could possibly be seen as a formation of a (dis)ordered cluster under diluted solu-tion’s condition - for it the possibility of creating such nucleus markedly diminishes in the course of time). By the envelopes seen around each charged object the double layers, expected to emerge as depletion zones in electrorheological solutions, are marked [39, 42]. A liquid-liquid phase separation, en-abling to form precrystalline aggregates, is also more likely to occur in the stage B, cf. [48].

real challenge that can happen here is, however, that Eq. (12) is fully equivalent to a Smoluchowski-type equa-tion [36] in R–configurational space that can be solved with suitable viz reflecting boundary conditions charac-teristic of a two-state dynamic process with a surmount-able Kramers-type energetic barrier [47]. This barrier, given by Φ, can be determined exactly, and both its height and shape can be controlled by the fluctuations [45] of the radius of the SPC-A given by the diffusion function involved in the Smoluchowski-type dynamics, D(R, t) =D[R(t)], defined still undert >> to as

D[R(t)] = ∞

R

0

R2_{ρ(R, t)dR}

2t , (13)

whereby the above relation is the Einstein-type relation in the one-dimensional phase space (R).

4. Smoluchowski SPC-A scenario inR–space

Thus, the global mass conservation law for the protein-spheroid object grown in the entropic milieu (e.g., lysozyme non-Kossel crystals or spherulites in a water solution [39]) eventually yields the Smoluchowski-type equation for the probability densityρ(R, t), also named the probability distribution function (PDF)

∂

∂tρ(R, t) = ∂ ∂R

D[R(t)]∂ρ(R, t)

∂R +

+βD[R(t)]∂Φ(R) ∂R ρ(R, t)

, (14)

where Φ(R) ≡ Φ[R(t)] becomes the free energy of the thermodynamic process, ultimately contributing to the determination of the Kramers’ barrier, and β = 1/kBT with T the temperature. It is completely equivalent to Eq. (12) with Eq. (9) and Eq. (10). Now, we may speak

of an ensemble-average << R(t) >>= ∞

R

0

Rρ(R, t)dR

which is a well-defined quantity. This is also the case

of << R2_{(t) >>=} ∞

R

0

R2_{ρ(R, t)dR which stands for the}

mean-squared displacement of the Φ–drifted superdiffu-sive process in theR–space [36]. Thus, the reduced vari-ance,κ(t), given by

κ(t) = << R

2_(t)>>

<< R(t)>>2 −1, (15)

as a measure of the fluctuations in the R–space, can be determined too. Moreover, one is able to derive Φ(R) in a Boltzmann-like form [39] as

Φ(R) =−1 βln[(σR

ne₎−1_{], (16)}

with (σRne₎−1 _{determinable from Eq. (8), this quantity}

is suit to be the system’s nonequilibrium supersatura-tion. D[R(t)] is also determinable from the MNET-type proposal just offered, and reads ultimately

D[R(t)] =D(t)/[σRne]−2, (17)

whereD(t) is generally given by Eq. (10) (a general time-correlational proposal), or by Eq. (11) with the limit of γ → 0, i.e. when the specific ballistic-type pro-posal pointing to the fully hydrodynamic stable mode of the overall SPC-A process taking place within the Stern-type double layer is envisaged. Note that by comparing Eq. (17) with the Einstein-type definition of D[R(t)] :=<< R2_{(t) >> /2t ( Eq. (13)), one has to}

have for Φ(R)6= 0, and ∆Φ(R)<0 (thereby indicating a natural thermodynamic course of the process), that is a superdiffusion in our R–space. The case of Φ = 0 will particularly correspond to the standard (Einstein) diffusion. When Φ(R) 6= 0 again but ∆Φ(R) > 0 ap-pears to hold because of some unusual,e.g., auxetic-type boundary elastic effects [39, 49], one may detect some thermodynamic-kinetic anomalies either at the crystal

surface, or within the interface [41], apparently in a cer-tain conjunction with the protein-velocity correlational field, coupled to the curvatures-involving crystal’s bor-der.

5. Towards a morphological phase diagram

From the above, cf. Eq. (16), it is seen that the Kramers’ barrier [47] determinant, Φ(R), becomes a com-plicated function of the main parameters of the process, such as the ones involved in Eqs. (6)–(8), and the time t. Since we have built our time dynamics upon the interfacial-region concept [41] introduced above, we might be wondering which is a morphological phase dia-gram of the process. While stating the diadia-gram we may adopt a typical rationale offered by surface-science liter-ature, and simply look forD[R(t)]/D(t) as a function of βΦ. From Eq. (16) and Eq. (17) one obtains

D[R(t)] D(t) =e

2βΦ_{, (18)}

what straight (forwardly) leads to

Φ≡Φ[R(t)] = 1 2β ×ln

hD[R(t)]

D(t)

i

. (19)

This is now to say that Φ is unambiguously determined by the global Smoluchowski-type dynamics in the phase space as well as by the local temporal dynamics assigned to the protein velocity field in the interfacial region [39]. The morphological phase diagram can then be built upon systematically exploring Eq. (16) in close connection with Eq. (18), that means, to haveσRne _{from Eq. (8)} read-ily involved. It would enable someone to discriminate between different types of the (non)equilibrium struc-tures obtained, ranging from equilibrium protein mi-celles in the solution, via ”weakly” nonequilibrium non-Kossel SPC-A structures, to finally arrive at the highly nonequilibrium protein spherulitic (cylindrolitic) fibrils-containing structures.

6. Ballistic, hydrodynamically stable mode and beyond it

When approaching the ballistic mode completely, we have to introduce the long-time (super)diffusive scaling in a conventional way, namely

D[R(t)]∼tν, (20)

where ν ≥ 0 holds for t >> to. ν = 0 corresponds to the standard diffusion, and can serve as a reference case, wherein Φ = 0, and the detailed balance is as-sured this way in the R–space. Otherwise, because of Φ 6= 0 it is violated and the process is out of equilib-rium. The most intriguing case appears when ν = 1,

global and local modes coincide, and the reduced vari-ance, κ(t), given by Eq. (15) reduces, for t >> to, to a constant but again only if Eq. (11) under γ →0 holds. Under such conditions the global (R–space involving) and local (interfacial,v(t)–engaging) dynamic modes operate at a fully synergistic level, greatly contributing to the overall hydrodynamics-stability mode, presumably over all relevant dynamic scales, especially within meso- and to some extent micro-scales being mutually involved. It seems very promising from a theoretical viewpoint but above all looks very important when seeing things from its practical, let us say, technological counterpart.

To sum up, we have formulated a complex-interface-involving model of time (t) and temperature (T) depen-dent SPC-A formations. We have shown that it is capable of operating under fully ballistic conditions that might univocally point to the total hydrodynamic stability of the process manifested over certain meso-to-microscale ranges. At the microscale it implies that the mean free path of the macroion exceeds the width of the partially disordered double layer, while at the mesoscale the ballis-tic character mentioned above may contribute even more readily, merely via the constant-value-approaching grow-ing mode,dR/dt→const., as well as by means of the ES dynamics in the R–space. Since the main assumptions of the model have been verified on some experimental data on lysozyme [14, 39, 42], it seems that it looks also worth noting from a practical viewpoint, especially when recalling the crystal-formation protocol invoked above.

7. MNET applied to the spherulitic formation

As appropriately mentioned by someone: ”Biology is wet and dynamic”, therefore, any biological process should be examined for a description in terms of wetness and dynamics. In our case, the term ’wet’ should rather be assigned to the below invoked MNET description be-cause it is specially suited to any entropic liquid-involving milieu, such as the one characteristic of water-containing phase, thus being wet by definition (see, Fig. 5). The phase changes, such as liquid-liquid phase separations or solute-solvent segregations, and the likes, are typically recognized as (very) dynamic processes in which the slow-est dynamic (stochastic) mode is going to determine the pace of the change. Thus, there should be no doubt - the phase change under study is a very dynamic process, see below.

As was already mentioned, MNET provides a suitable framework based on which one can study the behavior of systems defined at the mesoscale. The formulation of any MNET-type theory heavily rests upon the fact that a reduction of the observational time and length scales of a system usually entails an increase in the number of degrees of freedom which have not yet equilibrated - they therefore exert a certain influence on the total dynamics of the system. Those degrees of freedom,χ–s (the num-ber of which can generally be reduced by the

adiabatic-+

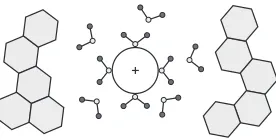
FIG. 5: A macroion viz model protein, or a fairly idealized spheroidal (lysozyme) protein cluster immersed in water, pre-sented here for simplicity as a big circle with a plus sign in the middle. It is typically surrounded by two kinds of sheath (ir-rotational and intermediate viz partly (ir-rotational, marked by angular arms with big dots). The ends of each water molecule in the sheaths are equipped with: oneO2−_{ion and twoH}1+ ions, marked by light and dark big dots, respectively. As an outer region, next to the macroion (or, charged cluster) and the sheaths, a bulk water phase can be seen, here as a hexagonal sub-matrix. The solute-solvent type interactions described by a Flory-Huggins-type mixing parameter, typi-cally can propagate from inner to outer water sheaths, being the strongest upon an electrostatic contact of the first partly rotational water sheath and the macroion (or, charged clus-ter) surfaces.

elimination procedure, thereby emphasizing the role of the slowest dynamic mode), withχ- herein the volumes of the growing nuclei, may represent the stochastic reac-tion coordinate of the system, properly defining the state of the system under N-G phase change in the χ–space. The characterization of the state of the system essentially relies on the knowledge of ρ ≡ ρ(χ, t), the probability density of finding the system at the stateχ∈(χ, χ+dχ) at timet.One can then formulate the Gibbs entropy pos-tulate in the form [33]

S−Seq =−kB

Z

ρ(χ, t) lnρ(χ, t)

ρeq(χ)dχ . (21)

HereSeq is the entropy of the system when the degrees of freedomχ are at local equilibrium. If they are out of equilibrium, the contribution to the entropy arises from deviations of the probability densityρ(χ, t) from its equi-librium valueρeq(χ) given by a Gibbs-Boltzmann type formula

ρeq(χ)∼exp

−∆W(χ) kBT

, (22)

where ∆W(χ) is the minimum reversible work required to establish that state,kB is Boltzmann’s constant, and T is the temperature of the bath.

Variations of the minimum work for an open thermo-dynamic system are typically given by [33]

∆W = ∆E−T∆S+p∆V −µ∆M +σ∆A+. . . , (23)

In order to obtain the dynamics of the mesoscopic de-grees of freedom [37] one first takes variations in Eq. (21)

δS=−kB

Z

δρ(χ, t) lnρ(χ, t)

ρeq(χ)dχ, (24)

focusing only on the nonequilibrated degrees of freedom. The probability density evolves in theχ−space along with the continuity equation

∂ρ(χ, t)

∂t +

∂J(χ, t)

∂χ = 0, (25)

whereJ(χ, t) is an unknown probability current [50]. In order to obtain its value, one proceeds to derive the ex-pression of the entropy production dS/dt which results from the continuity equation (25) and the Gibbs’ equa-tion (24). After a partial integraequa-tion, one then provides [33]

is the entropy production which is expressed in terms of currents and conjugated thermodynamic forces defined in theχ–space.

We will now assume a linear (meaning: small depar-ture from the equilibrium) dependence between fluxes and forces and establish a linear relationship between them [33]

whereL≡L[ρ(χ, t)] is an Onsager’s coefficient, which in general depends on the state variableρ(χ, t), in particular on the reaction coordinateχ [33]. To derive this expres-sion, locality inχ−space has to be assured, for which only fluxes and forces with the same tensorial characteristics become mutually coupled [37].

Then, the resulting kinetic equation follows by insert-ing Eq. (28) to the continuity equation (25)

∂ρ(χ, t)

where we have defined the diffusion coefficient as D(χ, t) ≡ kBL(ρ(χ,t))

ρ(χ,t) . This equation, which because of

Eq. (22) applied together with Eq. (23) can also be written as

is the FP&S type equation [36] accounting readily for the evolution of the probability densityρin ourχ-space. This implies that the spherulitic formation of interest is given the FP&S dynamics [33, 37], where the dynamics are realized as (drifted) diffusion in the phase space of the (mesoscopic) reaction coordinate,χ, which is the volume of a single spherulite: A ’real’ volume in the space of dE = 3 and an area indE= 2, wheredE - the Euclidean dimension of the space.

8. Avrami-Kolmogorov (AK) phase-change model and its two-phase modes

AK phase-change description continues to remain the most popular method for obtaining crystallization kinet-ics information [51, 52]. The conceptual foundation of this description is based on the famous combinatorial (raindrop) problem leading to Poisson statistics. For spherulites it can be reformulated by quantitatively de-termining the probability of a point being passed over by exactlyM evolving spherulites,ρsph(M), being in the original combinatorial description termed as the number of the wave-fronts.ρsph(M) takes on the standard Pois-sonian form

ρsph(M) =e −M_MM

F(M) , (31)

whereM stands for the average number of the evolving spherulites passing through a point; F(M) denotes the factorial ofM. The probability of any point not being passed over by a spherulite is given by value ofρsph(M = 0), eventually resulting in

ρsph(M = 0) =e−M_{, (32)}

since F(M = 0) = 1.

As a consequence of the above,ρsph(M = 0) also rep-resents the points being still amorphous, i.e. not been passed over by the spherulites, and thus, it is equal to amorphous fractional completion, θ, which, in turn, re-sults in having 1−θas the crystalline fractional comple-tion. Comparing then 1−θ with ρsph(M = 0) yields at once

θ= 1−e−M, (33)

which provides the formula for the crystallized fraction. The problem finally reduces to determineM as a func-tion of geometric assumpfunc-tions on the nuclei forms as well as the time t after which the children spherulitic phase is born from the parent phase of apparently amorphous overall character. It then leads to the general solution

θ≡θ(t) = 1−e−ωtν

, (34)

ν. ω is recognized to be dependent on the shape of the growing crystalline entities as well as on the amount and type of nucleation. ν depends upon the nucleation type and growth geometry but not upon the amount of nucle-ation [52]. For example, in (bio)polymers the so-called transcrystallization is a process in the course of which nucleation does not prevail to be a rate-determining fac-tor.

One of most solid observations on the spherulitic for-mation, as often as possible reported in the literature, is that the formation occurs asymptotically in a constant-tempo kinetic-thermodynamic regime [39–42, 44, 53–55]. This is due to the fact that the droplets-involving amor-phization kinetics, usually pronounced in a vigorous man-ner, is successfully balanced in a dynamic way during the phase change by a counter-effect which appears to be the fibrillization. It then leads in a common way to the typi-cally undesired formation of the the polycrystals termed spherulites, see Fig. 1 [51].

The effect is fully manifested in the late-time zone, and because the fibrillization leads ultimately to a surface-clustering sub-effect caused by the pieces (rodes) of the crystalline skeleton, it somehow acts in its final stage as the surface tension in case of equilibrium systems,i.e. as if the system was, at the moment, in equilibrium with its outer (thermostat) phase. Yet, the system unavoid-ably departs from this local quasi-equilibrium if there is still an ample place, left for the pieces to enter the as-yet unoccupied space within the growing object. If there is actually no ample place left, the overall evolution ter-minates, showing up a characteristic cessation-to-growth stage, frequently reported by experimenters [56].

9. Amorphization vs Polycrystallization: Switching off/on the asymmetric growing mode

Let us consider a situation in which the phase change takes place in a system of constant total volume,Vsph= const.[52–54]. The growth rate of the spherulitic forma-tion can be unambiguously determined by the MNET for-malism outlined above, with the volumeχplaying its piv-otal role. Proceeding as indicated previously one yields the growth rate [42]

J(χ, t) =−L(χ) T ρ

kBT∂ρ(χ, t)

∂χ +ρ(χ, t) ∂Φ ∂χ

. (35)

Interpreting Φ ≡ Φ(χ) as an entropic (Gibbs’) poten-tial (the free energy) suitable for the spherulitic forma-tion, with Φ(χ) ∼ ln(χ) asymptotically, and assuming naturally that the volume-dependent Onsager’s coeffi-cientL(χ) [33] follows a power law of the typeχδ_{, where} δ= (dE−1)/dE, withdE- the Euclidean dimension of the system, one provides the expression of the Smoluchowski-type [36] probability current

J(χ, t) =−D(χ, t)∂ρ(χ, t)

∂χ −

D(χ, t) kBT

∂Φ

∂χρ(χ, t), (36)

whereD(χ, t) is a spherulitic diffusion coefficient, asymp-totically obeying [53, 54]

D(χ, t) =D0χδtµ. (37)

Note that Φ(χ) may again fully participate in constitut-ing the so-called Kramers’ barrier, characteristic of the two-state amorphization-spherulitization picture that we would like to convey.

In Eq. (37) one sees that D(χ, t) is postulated to be factorized into two parts: aχ–dependent part, with the geometrical exponent δ being involved (it pinpoints to the spherulite-surface prevailing behavior, e.g. the one in which surface tension may thoroughly be in-volved), as well as some time-dependent part, in which the spherulite-formation exponent µ depends upon the Kolmogorov-type amorphization measuredE+ 1 [56] and upon the rod-like spherulitic-skeleton involving behavior, represented by the exponentνr, usually obeyingνr≈ 1

2

[53, 54].

The latter comes from the fact that the time-dependent part of D(χ, t) from Eq. (37) originates from a small ω approximation (the approximation applied to AK-parameter from Eq. (34)) [53], which typically holds for highly viscous systems as ours, and which arrives at an algebraic asymptotic behavior ofθ(t)

θ(t)∼tν, (38)

whereinν≃νr≈ 1₂ finally applies [53, 54]. This power-law type∼tνr _{contribution is assumed to enter then the}

diffusion functionD(χ, t) leading ultimately to a certain time-rescaling of the observables arising from the whole FP&S context[36].

Thus, the overall exponentµcan be defined, similarly as in a previous study [53, 54, 56], i.e. by means of a simple competition-type formula, as follows

µ≡µ(dE, νr) =ν(dE)−νr, (39)

where ν(dE) = dE+ 1 (a dE–dependent part) and νr generally obeys νr ∈ [1

2; 1] with a strong preference to

νr≈1₂,i.e. when the nucleation of rods is a-thermal but its rate manifests diffusively (kinetically), that means, not in an entirely thermodynamic way.

For the amorphization kinetic-thermodynamic formal-ism that does not lead at all to the typical spherulitic for-mation since it over-estimates its average tempodR/dt, withR the average spherulite radius [247] which has to conform asymptotically to constancy ofdR/dt, one has to conjecture the rods-involving contribution [57, 58] to be rejected,i.e. νr= 0. Thus, there is no above mentioned competition involved, and finally the overall exponent coincides with the Kolmogorov amorphization measure,

µ(dE, νr= 0) =ν(dE) =dE+ 1, (40)

TABLE I: Types of possible (poly)crystalline formations in model protein systems, and their characteristic integer vs non-integer Kolmogorov-type measures coming from application of the MNET-type formalism withdE= 2,3, cf. text.

Type of formation Geometric-exponent value System amorphization:

dR/dt6=const. µ(dE, νr= 0) =dE+ 1

Spherulitic formation:

dR/dt≈const. µ(dE, νr6= 0)≈dE+1₂

function of time - a hydrodynamically unstable mode [59]. This way, the asymmetric rods-involving crystalline mode is switched off, and we finally end up with a fluc-tuating randomly close-packed system (ν(dE) =dE+ 1 is also a generic measure of random close-packing, very characteristic of amorphous systems) containing the ran-domly placed and oriented crystalline drops [56–58].

When one is able to conjecture [51, 57, 58] that the rods-involving contribution is ultimately not being re-jected, i.e. νr 6= 0, one switches on the competition (asymmetry) mode, and finally arrives at

µ(dE, νr6= 0) =ν(dE)−νr≈dE+ 1−1

2 ≡dE+ 1 2, (41)

which leaves µ(dE, νr 6= 0) to be a non-integer competition-type exponent, pointing readily to a sym-metry breaking within the system. If it is involved for both spherulitic formations on either athermal or thermal nucleation seeds, it always properly yields the constant average tempo dR/dt of the overall formation [51, 53, 54, 60, 61] (a stable hydrodynamic mode, i.e.

when being stabilized by the counter-effect considered), which is also featured as a kinetic-thermodynamic signa-ture of the spherulitic growth by the presented rationale. The present study can be summarized concisely in a tab-ular form, cf. Table I.

To summarize in part, it can be ascertained that by switching on the asymmetric rod-like crystalline-skeleton based mode we are able to make somehow a specific, likely crystalline misorientation related de-amorphization of the system, finally arriving, due to the competition mode mentioned, at a constant-speed characteristic be-havior of the protein spherulites (SPC-A), readily emerg-ing from the offered MNET-type description. Such a de-scription can also be viewed as an interesting practical study on a passage between nano- (the fibrils as parts of the spherulites) and micro-structures (the spherulites for themselves) emerging in a complex viscoelastic sys-tem [62], contributing this way to modern concepts [51] of emerging science called often nanobiology.

10. MNET approach to viscoelasticity in unconfined systems

Outlook - As discussed previously, thermal fluctua-tions are central in the formation and behavior of soft

materials. In consequence, entropic forces are determi-nants of the microstructure formation and thus a main aspect of the (dis)order, slow dynamics and kinetics that will be the common ingredients in the systems of our interest.

Since these thermal fluctuations belong to the realm of mesosocopic world, the dynamics of the systems must be described by appropriate techniques. Generally speak-ing, one has two options for carry out this description:

a) through Langevin equations and b) through FP&S type equations.

On the one hand, due to the viscoelastic nature of the heat bath in which the particles perform their Brownian motion, the use of Langevin equations requires the speci-fication of the appropriate noise correlation [50, 63, 64] as well as the external forces. This is not clear in the general non-linear case due to the non-Markovian nature of the dynamics. As a consequence, it becomes difficult to per-form the corresponding analysis in both analytical and numerical way. On the other hand, kinetic equations of the FP&S type, may incorporate memory effects through the dependence on time of the transport coefficients, or by introducing memory functions [8, 11, 65, 66]. In prin-ciple, this second formulation of the problem seems to be more suitable to be generalized to the case when entropic or energetic barriers are present, in fact typically occur-ring in the systems under consideration, and when spatial restrictions and confinement are important. Here we will use the MNET formalism to derive these FP&S type ki-netic equations for the PDF depending on the variables of interest [8, 14, 33, 42, 67]. The advantage of using it will become clear later.

Our first approach to the problem, still presented in Part II A, will be analytical, a corresponding numerical analysis in a nonlinear case will be performed in Secs. II A 11, II B 3 and II C 2. Moreover, we will first study the dynamics of passively diffusing particles in unfined spaces. The generalization to the case when finement and finite size effects are important will be con-sidered later, in Part II B. It is worth stressing now that in experiments and computer simulations confinement is frequently unavoidable. This fact does not invalidates the results of this section because they can be considered valid at short or intermediate times.

Experiments and computer simulations have been per-formed to characterize the (single-point) viscoelastic properties and structure of, for instance, polymer gels or actin networks [68–70]. Other processes can be present in these system, they can involve dynamical processes as-sociated with conformation and growth of ’biomolecules’ [42, 71, 72]. Despite this complexity, the medium can be assumed as a viscoelastic matrix with a frequency depen-dent ’effective’ viscosityηef f(ω), [73]. Similar conditions can also be found in, for instance, the growth process of crystals or biomolecules in whose conformation mem-ory, elastic and finite-size effects play an important role [39, 42].

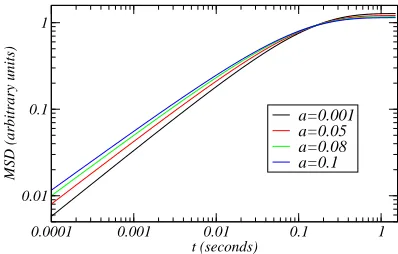
prop-erties is the power-law behavior of the complex shear modulus [68], the creep compliance and the diffusion co-efficient [69]. The viscoelasticity of these systems can be studied by means of microrheological techniques, such as the diffusing wave spectroscopy or video based methods which may characterize them in terms of the mean square displacement (MSD) of test particles that undergo sub-diffusion [74, 75]. The MSD of the particle manifests a power-law dependence on time in which, in the case of small particles, the exponent can depend on the aspect ratio between the particle radius and the characteristic length of the polymer network [11] for certain values of these quantities. In the case when the linear dimension of the particle (i.e., its radius a) and its mass are much larger than the polymers surrounding it, an apparently universal 3₄ exponent is found [74].

Mesoscopic nonequilibrium approach to vis-coelasticity - Consider the motion of a testing spher-ical Brownian particle (macroion, spherule) of radius a through a complex fluid composed by other Brownian particles (macroions, spherules) or by polymer molecules. The presence of these particles introduce spatial non-homogeneities and act on the test particles through elec-trostatic and elastic forces [8, 11].

As we have mentioned previously, at diffusion times the relevant microscopic variable determining the state of the test particle is the position vector r. Hence, the dynamics can be described by means of the PDFρ(r, t); cf. Eq. (14). Since the PDF is normalized, it will obey the continuity equation

∂ ∂tρ=−

∂

∂r·(ρVr), (42)

where the explicit form of the probability diffusion cur-rent ρVr can be found by assuming local equilibrium and using the rules of MNET [33, 76]. To obtain ρVr, this thermo-kinetic formalism uses an irreversibility crite-rion based upon the generalized Gibbs entropy postulate [33, 77]

s(t) =−kB

Z

ρ(r, t) ln ρ

ρledr+sle, (43)

cf. Eq. (21), wheres(t) is the nonequilibrium entropy,sle the entropy at local equilibrium. In Eq. (43), the refer-ence state is characterized through the local equilibrium PDF of Gibbs-Boltzmann form

ρle(r) =eβ[µle−∆φT]_{, (44)}

where µle is the chemical potential at local equilibrium, ∆φT(r) =φe+φB the total interaction potential related with external forcesφe(r) and with interactions between the particle and the bathφB(r), [28]. These interactions can be considered separately from those due to external agents, because of the two well known ”opposite” roles the bath plays in the dynamics of the particle: Supplying thermal energy and introducing dissipation. Note that,

since energy dissipation is due to surface forces, in general it depends on the size of the particle.

Specifically, the potential ∆φT(r) may in general in-volve energetic as well as entropic barriers [67] and, as a consequence, it could be responsible for Krames’ type dynamics of the system and thus useful to describe ag-gregation process, see Ref. [14] and references therein. In fact, this local equilibrium PDF can be written in a more general and suitable form by expressing it in terms of the minimum work necessary to change the state of the system [67], see Eq. (22), exactly in the form of Eq. (23) where ∆φT(r) ≡ ∆W. This expression also includes, among others, the presence of activated volumes ∆V (p the pressure) and surface effects through the surface ten-sionσ.

Now, using Eqs. (42)-(44) and (23), it is possible to derive a generalized FP&S type equation in the position space forρ(r, t) [8, 11, 14, 33]. To this end, one may first calculate the entropy production of the system by taking the time derivative of Eq. (43), after using (42), and integrating by parts assuming that the fluxes vanish at the boundaries. Once the entropy production is obtained, linear laws can be assumed for the relation between forces and fluxes

Vr=−ζ(t)∇φT −D(t)∇ρ(r, t), (45)

whereζ(t) is the time dependent Onsager coefficient en-tering through the linear law assumption [11, 14, 33]. Sinceζ(t) plays the role of an effective mobility, we have introduced, by a fluctuation-dissipation formula, the time dependent diffusion coefficient D(t) = β−1_{ζ(t), which}

constitutes a generalization of the ES formula, the eES formula. The substitution of Eq. (45) into (42) yields

∂

∂tρ=ζ(t)∇ ·[ρ∇φT] +β

−1_ζ(t)∇2_{ρ, (46)}

which is the desired generalized FP&S type equation. The time dependence of the transport coefficients intro-duces memory effects in the description [28, 65], whereas the first term at the right-hand side of the equation ac-counts for external and bath interactions with the par-ticle, and thus is suitable to be used in both unconfined and confined motion, and in IFS and EFS conditions.

For test particles moving under IFS in an unconfined space (the physically more simple case), and with lin-ear dimensions sufficiently large when compared with the length characterizing the heat bath, for instance the char-acteristic length of the polymer network in polymer so-lutions, the host complex fluid can be assumed as a con-tinuum. In this case, at the mesoscopic level of descrip-tion, the interactions between the test particle and the other components of the bath can be assimilated into the time dependence of the diffusion or effective friction coef-ficients. Notice however that, from a microscopic point of view, such interactions are responsible for the anomalous subdiffusion performed by the particle.

∆φT(r) = 0. As a consequence, the evolution equation for the test Brownian particle becomes

∂

∂tρ(r, t) =β

−1_ζ(t)∇2_{ρ(r, t). (47)}

The mesoscopic effective properties of the viscoelastic medium are often determined by analyzing the time de-pendence of the mean square displacement (MSD)hr2_i(t)

or, equivalently through the creep complianceχcc(t) or the complex shear modulus G′′

msd(ω), with ω the fre-quency [8, 11, 64, 68, 69]. The subindex msdstands for the fact that this quantity is obtained by using the gen-eralized ES relation [64, 78],i.e., by measuring the MSD of the test particle by means, for instance, of diffusing-wave spectrometry techniques or video-based methods [68, 69, 74, 75]. As an example, it is convenient to men-tion that in a certain range of frequencies, it has been shown in experiments that the complex shear modulus follows the scaling behavior G′′

msd ∼ ωα with α < 1 [64, 74, 75]. Bear in mind that this power-law behav-ior is the cornerstone of microrheological viscosities.

These experimental results can be explained in the context of hydrodynamics for which it has been proven that the mobility has the general form ˆζ(ω) = ζ0τD1 +aλ−1(ω)

−1

, [76, 79, 80], Here we have intro-duced τD as the characteristic diffusion time in order to keep the correct dimensions. Here, ζ0 is the inverse

Stokes friction coefficient and λ is the so called viscous penetration lengthλ−1₌p

iω/νK, whereνKis the kine-matic viscosity of the host fluid [80]. When the host fluid is viscoelastic, the kinematic viscosity becomes frequency dependent νK(ω) and then one may assume the form (48). For frequencies lying in the range 1/τD< ω≪β0, i.e., times satisfying τD > t≥β−1

0 , the mobility

coeffi-cient can be written as

ˆ

ζ(ω)≃ζ0τ_D−1(τDω) −(1−δ

2 )_{. (48)}

The exponent δ characterizes the subdiffusion. At this level of description, its value can be justified in terms of the characteristic dimension of diffusing particle [8, 71] or by simple comparison with the experiment. In a more detailed description, it can be justified that its value is determined by both, the elastic forces of the viscoelastic medium and the hydrodynamic interactions [11].

Here, it is essential to point out that the inverse Laplace transform of Eq. (48) yields a memory function ˜

ζ(t), this shall not be confused with the time dependent mobility coefficientζ(t) [65, 81]. Both quantities are re-lated through the relation

which represents a time average of the memory function. It is interesting to notice that this interpretation also arises when considering the non-Markovian FP&S equa-tion in the complete ordering prescripequa-tion (COP), that

is, in which memory effects are introduced through mem-ory functions [65, 82]. The actual description involving time-dependent coefficients [technically called partial or-dering prescription (POP)], can be related with the COP by taking into account that, in the case of slowly vary-ing fields, the integral becomes a temporal average of the memory function. The relation between both prescrip-tions is treated in detail in Refs. [65] and [63].

In view of these considerations, we have to accept that the inverse Laplace transform of Eq. (48) gives the mem-ory function

which in turn can be integrated over time in order to obtain the effective time dependent mobility

ζ(t)≃ 2ζ0τ

This expression is useful since it can be compared with experimental results in order to obtain the value of the exponent δ for each viscoelastic medium. This can be done by examining the time dependence of the MSD, de-fined byhr2_{i(t) =}R

r2_{ρ(r, t)dr. The evolution equation}

forhr2i(t) can by calculated from Eq. (47) and by using the definition above [11]. One obtains

dhr2_i(t)

dt =D(t) =β

−1_{ζ(t), (52)}

where, at first, we have equality in which we have used the definition of the current diffusion coefficient [65]. From this equation one obtains that the MSD is

hr2_{i(t) =} 4ζ0β−1

Eq. (53) can be compared with experimental and the-oretical results [8, 64, 68]. A typical behavior observed ishr2_i

exp≃t 3

4, from which one infers thatδ= 3

2.

More-over, Eq. (53) leads to good agreement with the large frequency experimental behaviorG′′

msd ∼ω 3

4, reported, for instance, in Ref. [74]. The comparison can be estab-lished by using the well known relationsζ(ω)∝η_{ef f}−1(ω) andG′′

msd(ω)≃ωηef f.

Here, it is important to stress that, when the trans-ported particles are smaller and lighter than the parti-cles forming the effective medium, the expression for the exponent δ depends on the ratio between the radius of the particle to the characteristic length of, for example, the polymer network [11, 75]. This case will be stud-ied in section corresponding to viscoelasticity in confined systems below.

0.1 1 10 ω(Hz)

0.1 1

G’’(

ω)

(arbitrary units)

τD=0.1

τ_D=0.2

τ_D=0.5

τD=1.0

FIG. 6: Dependence of the complex shear modulusG′′ _{as a} function of the frequencyωfor different values of the charac-teristic relaxation time (see text). This behavior is typical for the cytoskeleton of eukariotic cells, among other systems.

value and we have assumed ζ0 as a characteristic time,

see Ref. [8]. The value of the reference complex shear modulus wasG′′

0 = 0.1. Among others, this behavior of

the complex shear modulus as a function of the frequency is typical for the cytoskeleton of eukariotyc cells, see, for instance, Ref. [83].

Before analyzing the transport process from the point of view of numerical simulations, it is convenient to stress that our description can be complemented with that al-ready presented in Secs. II A 1-II A 9. Other generaliza-tions are still possible when there in a velocity gradient driving the whole system out from equilibrium. Such a case will be studied in Sec. III E.

11. Diffusing probe-particle spectroscopy applied to reveal nonlinear viscoelastic properties of biomatter - a computer

experiment

Diffusion-type phenomena such as the Random Walk (RW) of a probe particle can be successfully simulated using Monte Carlo (MC) methods. In order to test a RW along a crystal terrace made of H (hydrophobic) and P (polar) sites on a square lattice, a special prepa-ration of a h= 20 columnar deposit (h-height) has first been undertaken [84]. Next, the HP properties of the h= 20 deposit have been mapped onto a plane, this way constituting a planar terrace of the crystal. Each point of the terrace eitherH orP property has been assigned by applying a majority rule to each site labeled by i: a site(i) =H if number of H at site/column i is greater than a number of P at the same site/column. If this numbers are equal, a random sampling decided for the proper assignment toi. Afterwards, the terrace’s surface has been restructured in order to get a percolation track, built up ofP sites (a certain necessary replenishment of P sites, becomes effective), since the surface is always exposed towards water.

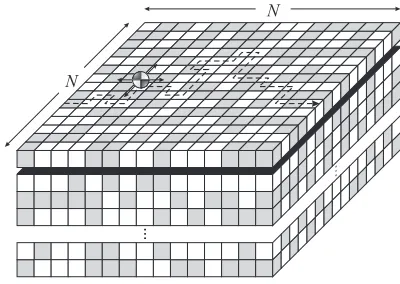
A RW of neutral testing walker has been carried out along so preparedN ×N terrace, with maximum N = 1024, see Fig. 7. First, the one-half diffusion exponent,

FIG. 7: Crystal’s terrace used in computer experiment with diffusing probe particle; gray: H-hydrophobic site, white: P -hydrophilic site

FIG. 8: Super- (left) versus sub-diffusion (right) RW charac-teristics derived from a computer simulation in which a testing hydrophilic-hydrophobic particle explores by a RW, equipped with the hydrophobic type interaction, a crystal’s terrace which is a 2D matrix composed of amphiphilic residues.

either with elastic/reflecting - case A (confined space) or with periodic - case B (unconfined space) boundary conditions (b.cs.), or both of them, has been approached and reflected properly by a scaling law of

N ∼tνd_{, (54)}

where t-time, and νd-RW exponent, in log−log scale. The reflecting b.cs. indicate an existence of external force which confines the particles’ motion. The periodic b.cs, in turn, remove this confinement and make that only in-ternal forces are included into the system. Then, a small (few lattice constants) lasting drift has been superim-posed on the RW, favoring a bit longer glides over sub-chains ofP sites, whereas glides overH sites were always forbidden.