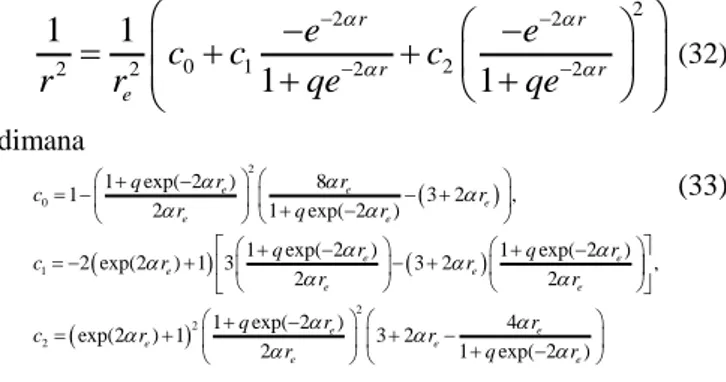Kata kunci: Persamaan Dirac, Potensial Rosen Morse Hiperbolik terdeformasi q, Metode Iterasi Asimtotik, Pendekatan Pekeris, Spin Simetri.

(1)

Solusi Analitik Persamaan Dirac Untuk Potensial Rosen Morse Hiperbolik Tedeformasi-q Pada Kasus Spin Simetri Bagian Radial Menggunakan Metode Iterasi Asimtotik

S. Pramono, Suparmi, Cari

Prodi Ilmu Fisika, Pascasarjana, Universitas Sebelas Maret Jl. Ir. Sutami 36A Kentingan, Surakarta 57126

Suburpramono.26@gmail.com

Intisari – Persamaan Dirac untuk potensial Rosen Morse Hiperbolik terdeformasi q pada kasus spin simetri bagian radial diselesaikan dengan menggunakan Metode Iterasi Asimtotik atau Asymptotic Iteration Method (AIM). Untuk pendekatan sentrifugal digunakan dengan pendekatan Pekeris. Penyelesaian persamaan Dirac dengan menggunakan metode Iterasi Asimtotik dilakukan dengan mereduksi persamaan differensial orde kedua menjadi persamaan differensial tipe Hipergeometri dengan cara substitusi variabel sehingga diperoleh persamaan energi relativistik. Energi relativistik sistem dihitung menggunakan software matlab 2013. Penelitian ini dibatasi untuk kasus spin simetri bagian radial.

Kata kunci: Persamaan Dirac, Potensial Rosen Morse Hiperbolik terdeformasi q, Metode Iterasi Asimtotik, Pendekatan Pekeris, Spin Simetri.

Abstract –.The radial part of Dirac equation for q deformed hyperbolik Rosen Morse Potential with spin simetry case is solved by using asymtotical iteration method (AIM). We use Pekeris Approximation for centrifugal term. Solution of Dirac equation with Asymtoticc Iteration Method is done by reducing the second orde differential equation into the form of Hypergeometry type equation by subtituting variable and then be obtained relativistic energy equation. The relativistic energy system is calculated by using matlab R2013a. This Research is limited to radial part of Dirac equation in the spin simmetry case.

Key words: Dirac Equation, q deformed Hyperbolic Rosen Morse, Asymtotic Iteration Method, Pekeris Approximation, Spin Simmetry

I. PENDAHULUAN

Persamaan Dirac merupakan persamaan gelombang relativistik yang dirusmuskan oleh fisikawan berkebangsaan inggris, P.A.M. Dirac pada tahun 1928. Persamaan ini memiliki fungsi yang sama seperti persamaan gelombang yang dirumuskan oleh Erwin Schrodinger, yaitu untuk menemukan solusi fungsi gelombang sistem kuantum yang dapat mendeskripsikan eksistensi suatu partikel pada skala mikroskopik pada kondisi tertentu. Karena persamaan Dirac adalah persamaan gelombang yang sudah mengikutsertakan keadaan relativistik dari partikel dimana v~c, sehingga hasil yang diperoleh dari penyelesaian persamaan Dirac merupakan fungsi gelombang sistem kuantum relativistik dan spektrum energi relativistik[1]. Persamaan Dirac mendeskripsikan tentang perilaku gerak partikel yang memiliki spin 1

2 untuk potensial shape invariance sentral maupun non sentral[2].

Penyelesaian persamaan Dirac secara langsung dari sistem partikel yang dipengaruhi oleh potensial yang energi potensialnya adalah fungsi posisi adalah dengan cara mereduksi persamaan Dirac menjadi persamaan differensial orde kedua sehingga didapatkan persamaan energi dan fungsi gelombang[3].

Pada beberapa tahun akhir ini banyak peneliti yang telah melakukan penelitian terkait persamaan Dirac dengan beberapa potensial dan metode. Beberapa potensial yang telah digunakan dalam penelitian tersebut adalah Hulthen[4,5], Non-sentral Rosen Morse Trigonometri[5], Eckart [6,7] Maning Rosen Trigonometri[7], Pöschl-Teller hiperbolik terdeformasi-q dan non-sentral Scarf trigonometri[8], Coulomb plus NAD[9], dan lain-lain. Metode yang telah digunakan oleh mereka adalah

supersymmetry quantum mechanics[10], polinomial Romanovski[5] Nikivorov-Uvarov[9], iterasi asimtotik [4,6,7,8,10,11]. Pada paper ini digunakan metode iterasi asimtotik untuk menentukan energi relativistik dan fungsi gelombang persamaan dirac bagian radial pada kasus spin simetri yang dipengaruhi oleh potensial Rosen Morse Hiperbolik terdeformasi-q. Dalam paper ini dibatasi pada kondisi potensial vektor sama dengan potensial skalar, langkah awal yang telah digunakan adalah dengan mereduksi persamaan Dirac menjadi persamaan differensial tipe hipergeometri.

II. METODE PENELITIAN Metode Iterasi Asimtotik

Metode iterasi asimtotik merupakan suatu metode alternatif yang akurat dan efisien untuk menentukan nilai energi eigen dan fungsi eigen suatu potensial jenis hiperbolik yang dapat diselesaikan secara analitik. Metode iterasi asimtotik juga memeberikan solusi untukmasalah yang dapat diselesaikan secara eksak[12].

Metode iterasi asimtotik digunakan untuk menyelesaikan persamaan differensial linier orde kedua homogen yaitu

0 0

( )

n n n

y



x





x y



x



s x y x

(1) Dimana dan tanda prime menunjukkan turunan terhadap x. Parameter lain yaitu n diartikan sebagai bilangan kuantum radial. Variabel dan adalah variabel yang cukup mudah untuk diturunkan. Untuk memperoleh suatu solusi umum dari persamaan (1), kita harus mendifferensialkan persamaan (1) tersebut terhadap x, sehingga kita peroleh

0

( )

x

0 



0

( )

x

(2)

1 1

( )

n n n

y



x





x y



x



s x y x

(2) dimana 2 1

( )

x

0

( )

x

s x

0

( )

0

( )

x



_





_



(3) 1

( )

0

( )

0

( )

0

( )

s x



s



x



s x



x

(4) Dengan 0( )x 0   dan s x₀( ) merupakan fungsi dari

C



(koefisien perssamaan differensial) Metode iterasi asimtotik dan dapat diaplikasikan secara langsung pada beberapa permasalahan jika sebuah fungsi gelombang diketahui terlebih dahulu dan memenuhi kondisi batas nol (0) dan tak hingga (∞)[13].

Persamaan (2) dapat diiterasikan dengan mudah sampai (k+1) dan (k+2), k = 1, 2, 3, ... sehingga diperoleh

1 1 1

( )

k n k n k n

y



x





_

x y



x



s

_

x y x

(5) 2

( )

k n k n k n

y



x





x y



x



s x y x

(6) Dimana 1 1 0 1

( )

k

x

k

x

s

k

x

k

x



_



_



_

_

_



_ (7) 1 0 1

( )

k k k

s x



s

_



x



s x



_

x

(8) Yang mana disebut recurrence relation. Dari rasio (k + 1) dan (k + 2), kita dapatkan

(k 2) (k 1) (k 1) 1 1 1 (z) (z) ( ) ( ) (z) ( ) ln ( ) ( ) (z) (z) ( ) ( ) (z) k k n k n n n k k n k s y z f z y z d y z dz y z s y z f z            _             _ _       (9)

Untuk nilai k yang cukup besar, maka 1 1

(z)

( )

(z)

k k k k

s

z









_



(10)

Yang mana adalah aspek metode iterasi asimtotik, kemudian kita subtitusikan

(k 1) 1

(z)

ln

( )

(z)

k n k

d

y

z

dz



 



 





(11) (k 1) 1

(z)

ln

( )

(z)

k n k

d

y

z



dz



 



 







(12)









(k 1) 1 1 1 1 0 (z) ( ) exp (z) (z) exp ( ) (z) k n k k y z C dz C z dz







        _ _   _ _ 



(13)









1 0 ( ) ( ) ( ) exp ( ) (z) n y z 



z f z C





z 



dz (14)











1



1 1 2 1 0 2 2 2 1

( )

exp

( ) d

exp

(z ) 2 ( )

z n z z

y z

z

C

z

dz dz

















_



_







(15) 1 1 ( ) (z) (z) (z) (z) 0 1, 2, 3, ... k z k sk k sk k







      (16)

Dimana n merepresentasikan bilangan quantum radial [5]. Persamaan (2) merupakan persamaan differensial orde kedua homogen linier yang mana dapat diselesaikan dengan

membandingkan terlebih dahulu dengan persamaan differensial orde kedua berikut[13]:

1 2 2 1 ( ) 2 ( ) ( ) 1 1 N N N N az t wz y z y z y z bz z bz         _  _       (17) Dimana

(

n)

2

3 ( )

,

( )

2

n

t

N



 

 







(18) dan

(2

1)

2 (

2)

t

b

a

N

b







(29)

Fungsi gelombang dari persamaan (2), dapat ditentukan mengikuti persamaan [13]: 2 2 2 1 ( ) ( 1)n (N 2) ( )n ( , ; ; N ) n n y z   C   F nn bz  (20) III.HASIL DAN PEMBAHASAN

Persamaan Dirac untuk sebuah partikel tunggal dengan massa M yang diengaruhi oleh potensial vektor V(r) dan potensial skalar S(r) dapat diberikan sebagai (dalam satuan ℏ = 𝑐 = 1)









.

p

M

S r

( )

r

E V r

( )

r

























(21)

Dimana

p

dan E adalah operator momentuum dan energi relativistik toal dari sistem, secara berturut-turut. Operator momentum sudut total

J

ˆ

dan operator matriksspin-orbit





ˆ _{ˆ. 1}ˆ

J L komut dengan Hamiltonian Dirac hanya untuk potensial yg simetris secara spherical.



dan



adalah matriks Dirac 4



4 yaitu

0 0 , , dan 0 0 i i I p i I            _ _ _ _      (22) Dimana I adalah matriks identitas 2



2 dan



_{i x y z}_ _{, ,} adalah matrik Pauli 2



2: 0 1 0 1 0 , , 1 0 0 0 1 x y z i i



_ _



_ _



_ _        (23)

Spinor Dirac dapat dituliskan menyesuaikan dengan kondisi upper (besar)

f

_n_ dan lower (kecil)

g

_n_sebagai

( )

( , )

1 ( )

( )

( , )

n jm n n n n jm

F

r Y

f

r

g

_{r iG}

r Y

    

 



 











_

_

 

_



_





_

_

(24)

Dimana

Y

jm

( , )

 

dan

Y

jm

( , )

 

adalah harmonik

bolaspin dan pseudospin. N adalah bilangan kuantum radial dan m adalah proyeksi momentum anguler pada sumbu z. Bilangan kuantum anguler orbital dan mengacu pada bilangan kuantum spin dan pseudospin. Untuk pemberian bilangan kuantum spin orbital



  

1, 2,...

, momentum anguler total 1

2

j







, momentum anguler orbital dan momentum anguler pseudo-orbital 1 1

2 2     , dan 1 1 2 2 

   berturut-turut. Dengan mensubtitusikan persamaan (24) ke dalam persamaan (21) maka kita dapat memperoleh secara langsung dua pasangan persamaan

(3)

differensial biasa untuk bagian radial dari fungsi iegen Dirac sebagai berikut:





( ) ( ) ( ) n n n d F r M E V r S r G dr r      _  __ _ _ _ _       (25) dan





( ) ( ) ( ) n n n d G r M E V r S r F dr r      _  __ _ _ _ _       (26)

Dengan megeliminasi

G

_n_dalam persamaan (20) dan

F

_n_

dalam (21), kita peroleh persamaan differensial orde kedua untuk komponen lower dan upper dari persamaan gelombang Dirac sebagai berikut [5]:

2 2 2 ( 1) ( ( ))( ( )) ( ) 0 ( ) ( ) n n n n d M E r M E r dr r G r d d dr dr r M E r         _  _ _ _{ } _ _{ }      _              (27) dan 2 2 2 ( 1) ( ( ))( ( )) ( ) 0 ( ) ( ) n n n n d M E r M E r dr r F r d d dr dr r M E r         _  _ _ _{ } _ _{ }      _              (28) Dimana ( )r V r( )S r( )dan ( )r V r( )S r( )[5]. Analisis Persamaan Dirac untuk Potensial Rosen Morse Hiperbolik Terdeformasi q pada Kasus Spin Simetri Bagian Radial.

Persamaan Dirac untuk kasus spin simetri ditandai dengan 0

d dr

  dan



( )

r



C

_s= konstan, karena selisish antara potensial vektor V(r) dan potensial skalar S(r) adalah konstan, dan penjumlahan keduanya sama dengan potensial yang mempengaruhi sistem, yang dalam studi ini adalah potensial Rosen Morse Hiperbolik terdeformasi-q. Dengan memperhatikan batasan pada kasus ini, maka persamaan (28) dapat dituliskan kembali ke dalam bentuk

2 2 2 ( 1) ( n s)( n ( )) n ( ) 0 d M E C M E r F r dr r       _  _ _ _ _ _{ }  _     (29) dan, bila



( )

r

adalah potensial Rosen Morse Hiperbolik terdeformasi q, yang didefinisikan sebagai

0 1 2

( )

tanh

cosh

_q q

V

V r

V

r







 



_





_





(30)

Dimana



adalah screening parameter, yang menentukan rentang potensial Rosen Morse [6]. Sehingga persamaan (29) dapat dituliskan kembali sebagai

2 2 2 0 1 2 ( 1) ( )( ) ( ) 0 ( ( )) tanh cosh n s n n n q q d M E C M E dr r F r V M E r V r r          _  _ _ _ _      _            _ _      (31)

Persamaan (31) tidak dapat diselesaikan secara langsung, dalam kasus ini kita menggunakan pendekatan untuk kasus sentrifugal dengan menggunakan pendekatan Pekeris sebagaimana yang diusulkan oleh Sameer [14]. Namun, dalam studi ini pendekatan Pekeris yang digunakan adalah dengan menuliskan kembali dalam bentuk fungsi eksponensial terseformasi-q. Untuk lebih jelasnya dapat

dilihat pada gambar 1 terkait kurva centrifugal term untuk masing-masing nilai parameter deformasi tampak tidak adanya pergeseran. Pendekatan untuk centrifugal term ini adalah sebagai berikut:

2 2 2 0 1 2 2 2 2 2

1

r r r r e

e

c

r

qe

       



_

_

_

_











_{ }

_





_



_







(32) dimana         2 0 1 2 2 2 1 exp( 2 ) 8 1 3 2 , 2 1 exp( 2 ) 1 exp( 2 ) 1 exp( 2 ) 2 exp(2 ) 1 3 3 2 , 2 2 1 exp( 2 ) 4 exp(2 ) 1 3 2 2 1 exp( 2 ) e e e e e e e e e e e e e e e e e q r r c r r q r q r q r c r r r r q r r c r r r q r   _                         _ _                                      _ _             (33)

Dengan mengubah bentuk centrifugal term ke dalam fungsi hiperbolik pada persamaan (32) dan (33), kemudian disubtitusikan ke persamaan (31) maka diperoleh bentuk persamaan









2 2 2 2 2 ( ) 2 tanhq 1 ( ) ( ) d U r r U r E U r dr          (34) Dengan



















2 1 2 0 2 1 2 2 1 2 2 2 0 2 2 2 2 2 1 4 s s s c c E c M E C M E q q c c V M E C q q c V M E C                  _ _   _    _            _  _                    (35)

Dengan substitusi variabel

tanh

q



r



1 

2 z

pada persamaan (31) dengan

   

z

, didapatkan

 





_{ }

2 2 (1 ) (1 2 ) 1 2 2 0 4 4(1 ) U z U z z z z z z E E U z q z z                     _  _        (36)

Persamaan (33) meimiliki dua buah titik regular singular di z = 0 dan z = 1 yang mana solusi umum untuk fungsi U adalah

( )

(1

)

( )

r n

U z



z





z



f

z

(37)

Gambar 1. Kurva Centrifugal Term

0 2E+29 4E+29 6E+29 8E+29 1E+30

0 1E-14 2E-14 3E-14

r -2 (f m -2) r (fm) 1/r^2 1/r^2 q=0,2 1/r^2 q=0,4 1/r^2 q=0,6 1/r^2 q=0,8 1/r^2 q=1

(4)

Setelah melalui beberapa trik matematis, didapatkan persamaan differensial tipe Hipergeometri kemudian dapat diubah ke dalam persamaan diffferensial orde kedua



 









_{  }

_

(1 ) ( ) 2 1 2 2 2 ( ) 1 1 ( ) 0 n n n z z f z z f z f z q





 

   

                    (38)























2

1 ( )

( )

(1

)

1

1 ( )

(1

)

n n n

z

f

z

f

z

q

f z

z







 

   









_













  













(39)

Persamaan (39) dapat diselesaikan dengan menggunakan metode iterasi asimtotik, dimana

2

4 



2 



E



(40)

dan 2

4 

 

2 



E



(41)

Dengan membandingkan persamaan (39) dengan persamaan (1), maka didapatkan



₀

( )

z

dan

s z

₀

( )

, kemudian dapat dihitung nilai



_k

( )

z

dan

s z

_k

( )

dengan menggunakan persamaan (7) dan (8).



 



)

1 (

1

2

2 )

(

0

z



















(42)







 





)

1 (

1 )

(

1 0

z

S

q







  









(43)



 





 



1 2 2 2

2

1

2

1 ( )

(1

)

(1

)

2

1

2

1 (1

)

A

z















 





_



_{ }



_



_



_











 

_



_







(44)



 



1( ) 2 2 (1 ) 2 1 2 1 (1 ) (1 ) A A S z z z A A z z z z





     _            _   _     (45)

Dengan mensubtitusikan persamaan (42-45) ke persamaan (16), diperoleh



















0 1 1 0 0 1 2 2 2 1 2 3 3 2 2

0

1

0

1

2

0

2

3 s

s





   





 





 



 





 



  

 



 



 

(46)

Dan seterusnya dengan

 

2 2



0





2 2 2 1 4 s n e V M E C c r q q             (47) Dari persamaan (46) dapat digeneralisasi manjadi



 

2



( 1) ( 1)

n nr nr





 

   

 

   (48)

Atau dalam bentuk lain

2 2 2 1 4

1

2

n

r















_



  



_





(49)

Dengan

n

_r adalah bilangan kuantum radial, dengan mensubtitusikan persamaan (40) dan (41) ke persamaan (49) maka diperoleh energi eigen yaitu

   2 2 1 2 4 2 1 4 1 2 0 1 2 1 2 2 2 R s R n r n r c M E C M E n n c c c q q         _ _        _    _  _{  }     _ _       _   _   (50) Dimana

 



2

1 0,1, 2,...

c e r

r

n









(51) r

n

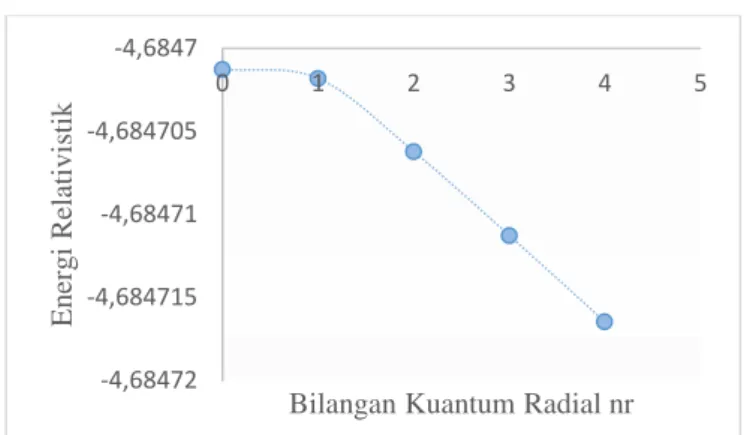
adalah bilangan kuantum radial.

Deformasi quantum yang diusulkan oleh Arai berhubungan dengan translasi spasial. Deformasi kuantum memiliki aplikasi yang luas[8], meliputi penerapan untuk inti atom, teori statistika kuantum, teori string dan teori medan conformal. Dari tabel 1 Juga tampak bahwa semakin tinggi nilai parameter deformasi sistem kuantum, maka energinya akan semakin kecil. Dalam studi ini nilai bilangan kuantum orbital l dibuat tetap yaitu l = 2, dengan tujuan untuk mengkaji spektrum energi partikel ketika dipengaruhi potensial Rosen-Morse. Potensial ini berguna dalam pengkajian energi vibrasional molekular poliatomik. Suatu contoh penerapannya adalah keadaan vibrasional NH3 [14].

Tabel 1. Energi Relativistik untuk Potensial Rosen Morse Hiperbolik Terdeformasi-q



= 0,005

V

₀ = 5,

V

₁= 3, M = 5,

C

_s = 0 l nr E q=0,5 E q=1 E q=1,5 2 0 -4,921736674 -4,684701257 -4,43495 2 1 -4,9217397 -4,6847018 -4,43495 2 2 -4,921744472 -4,684706203 -4,434954 2 3 -4,921749442 -4,684711258 -4,434959 2 4 -4,921754466 -4,684716463 -4,434964

Gambar 2. Kurva spektrum energi relativistik pada kasus spin simetri untuk q=0,5

-4,92176 -4,921755 -4,92175 -4,921745 -4,92174 -4,921735 0 1 2 3 4 5 E n er g i R elativ is tik

(5)

Gambar 3. Kurva spektrum energi relativistik pada kasus spin simetri untuk q=1

Gambar 4. Kurva spektrum energi relativistik pada kasus spin simetri untuk q=1,5

Untuk fungsi

( )

r n

f

z

pada persamaan (37) dapat diselesaikan menggunakan persamaan (20) sehingga

( )

r n

f

z

dapat dituliskan kembali ke dalam bentuk:

      

z

C

 

F

n

z



f

_n n n _n _r _r r r r r





1 '

1

2 



1

2 1



,

2 



2 



1 ,

2 



1 ,

(52) Yang mana nilai

1

2 







(53) Dan

1

2

2 











(54)

Persamaan fungsi gelombang U (z) untuk nilai n_r adalah sebagai berikut:

 





2 1





( ) (1 ) 1 ' 1 2 1 , 2 2 1, 2 1, r r r n n r r n U z z z C F n n z  







          (55)

Sehingga fungsi gelombang bagian upper untuk keadaan dasar n_r 0   _                 2 tanh 1 2 tanh 1 ' ) (r C r r U q q (56) Dan untuk n_r 1    

1 tanh 1 tanh 2 1 1 tanh ( ) ' 2 2 2 1 2 q r q r q r U r C                        _         (57) IV.KESIMPULAN

Persamaan Dirac untuk potensial Rosen-Morse hiperbolik terdeformasi-q pada kasus spin simetri bagian radial dapat diselesaikan dengan menggunakan metode iterasi asimtotik. Spektrum energi relativistik sistem dihitung menggunakan software matlab 2013. Dari Kurva tampak bahwa semakin besar nilai n maka energi sistem semakin besar.

UCAPAN TERIMA KASIH

Penelitian ini didukung oleh Hibah Penelitian Utama (PUT UNS) 2015 dari DIKTI dengan Nomor kontrak No. 698/UN27.11/PN/2015.

PUSTAKA

[1] Atkis, P.W., Quanta: A Handbook of Concepts, Oxford: Oxford Universiy Press, 1974.

[2] Greiner, W., Relativistic Quantum Mechanics Third Edition. Springer-Verlag Berlin Heidelberg, New York. 2000.

[3] Suparmi, Mekanika Kuantum II, Jurusan Fisika Fakultas MIPA, Universitas Sebelas Maret Surakarta, 2011. [4] Soylu, A., Bayrak, O.,Boztosun, I., An approximate

solution of Dirac-Hulthen problem with pseudospin and spin symmetry for any



state, Journal of Mathematical Physics, 082302, 2007, pp. 48.

[5] Suparmi, A., Cari, C., Anggraini, L.M., Bound state solution of Dirac equation for Hulthen plus trigonometric Rosen Morse non-central potential using Romanovski polynomial, AIP Conference Proceedings 1615, 111, 2014; doi: 10.1063/1.4895871

[6] Soylu, A. Bayrak, O. Boztosun, I.,Κ state solutions of the Dirac equation for the Eckart potential with pseudospin and spin symmetry. Journal of Physics A: Mathematical and Theoritical 41 doi : 10.1088/1751-8113/41/6/065308, 2008, 065308, pp. 8.

[7] Resita, Suparmi, Cari, Solution of Dirac equation for Eckart potential and trigonometric Manning-Rosen potential using asymptotic iteration method, Chinese Physics B, Vol 24, No. 11, 2015, DOI:10.1088/1674-1056/24/11/110301.

[8] Kurniawan, A., Suparmi, A., Cari, C., Approximate analytical solution of the Dirac equation with q-deformed hyperbolic Pöschl-Teller potential and trigonometric Scarf II non-central potential, Chinese Physics B Vol. 24, No. 3, 2015, DOI: 10.1088/1674-1056/24/3/030302.

[9] Bakkeshizadeh, S., Vahidi, S., Solution of the Dirac equation for the Coulomb potential plus NAD potential by using the Nikiforov-Uvarov Method, Advance Studies Theoretical Physics, Vol. 6, 2012, no. 15, pp. 733-742.

[10] Guo J Y, Zhou F, Guo F L and Zhou J H 2007 Mod. Phys. A 22 4825

[11] Kocak, G., Bayrak, O., Boztosun, I., Supersymmetric solution of Schrodinger equation by using the asymptotic iteration method, Annalen der Physik, (Berlin) 524, No. 6-7, 2012/DOI:10.1002/andp. 201200028, pp. 353-359. -4,68472 -4,684715 -4,68471 -4,684705 -4,6847 0 1 2 3 4 5 E n er g i R elativ is tik

Bilangan Kuantum Radial nr

-4,434966 -4,434964 -4,434962 -4,43496 -4,434958 -4,434956 -4,434954 -4,434952 -4,43495 -4,434948 0 1 2 3 4 5 E n er g i R elativ is tik

(6)

[12] Das, T., Exact Solutions of the Klein-Gordon Equation for q-Deformed Manning-Rosen Potential via Asymptotic Iteration Method. arXiv:1409.1457v1 [quant-ph], 2014, Hlm. 1-11.

[13] Debnath, S., Biswass, B., Analytical Solution of the Klein-Gordon Equation for Rosen Morse Potential via Asymptotic Iteration Method, Electronical Journal of Theoretical Physics, EJTP 9, No. 26, 2012, pp. 191-198.

[14] Sameer, M. Ikhdair, Approximate solution of the Dirac equation for the Rosen Morse potential including the spin-orbit centrifugal term. arXive:0912.0619v1 [quantum-ph] 3 Dec. 2009. pp. 1-23.