Matching the Quasi Parton Distribution in a Momentum Subtraction Scheme
Iain W. Stewart and Yong Zhao
Center for Theoretical Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
The quasi parton distribution is a spatial correlation of quarks or gluons along thez direction in a moving nucleon which enables direct lattice calculations of parton distribution functions. It can be defined with a nonperturbative renormalization in a regularization independent momentum subtraction scheme (RI/MOM), which can then be perturbatively related to the collinear parton distribution in the MS scheme. Here we carry out a direct matching from the RI/MOM scheme for the quasi-PDF to the MS PDF, determining the non-singlet quark matching coefficient at next-to-leading order in perturbation theory. We find that the RI/MOM matching coefficient is insensitive to the ultraviolet region of convolution integral, exhibits improved perturbative convergence when converting between the quasi-PDF and PDF, and is consistent with a quasi-PDF that vanishes in the unphysical region as the proton momentum Pz → ∞, unlike other schemes. This direct
approach therefore has the potential to improve the accuracy for converting quasi-distribution lattice calculations to collinear distributions.
I. INTRODUCTION
One of the great successes of QCD are factorization theorems, such as those that enable us to make predic-tions for deep inelastic scattering (DIS) and Drell-Yan processes at hadron colliders [1]. These theorems im-ply that the scattering cross section can be factorized as convolution of the partonic cross section and a universal parton distribution function (PDF). The former can be calculated analytically in perturbative QCD, thus allow-ing for a high precision extraction of the latter from cross section data. PDFs are the most basic and important ob-jects for us to obtain information about hadron structure in modern physics. Since PDFs are intrinsic properties of the hadron that include low energy degrees of free-dom, they can only be calculated with nonperturbative methods such as lattice QCD. Although their low-order moments have been directly calculated with lattice meth-ods [2–4], our most precise knowledge about them comes from global fits to experimental data [5–8] (see [9] for the LHAPDF comparisons).
In parton physics, PDFs are defined as the nucleon matrix elements of light-cone correlation operators. For example, in dimensional regularization with d= 4−2ǫ, the bare unpolarized quark distribution function is
qi(x, ǫ)≡
Z dξ− 4π e
−ixP+ξ−
P
ψ¯i(ξ−)γ+W(ξ−,0)ψi(0)
P
, (1)
wherexis the momentum fraction,iis a flavor index, the nucleon momentumPµ= (P0,0,0, Pz),ξ±= (t±z)/√2 are the light-cone coordinates, and the Wilson lineW is given by the path-ordered exponential
W(ξ−,0) =Pexp
−ig
Z ξ−
0
dη−A+(η−)
. (2)
The renormalized PDFs qj(y, µ) are defined in the MS
scheme as
qi(x, ǫ) =
X
j
Z 1
0
dy y Z
MS
ij
x y, ǫ, µ
qj(y, µ), (3)
ZMS is a function of x/y, the flavor indices i, j include
the gluon, and µ is the renormalization scale. The MS definition of the PDF has an interpretation as a parton number density in the light-cone gaugeA+ = 0, and is
the most widely used definition for the PDF in factoriza-tion theorems. The dependence of the PDF correlator on the light-cone makes it essentially impossible to directly calculate them using lattice QCD in Euclidean space with imaginary time.
In Ref. [10], Ji proposed that instead of calculat-ing light-cone correlations, one can start from a spatial correlation—called a quasi-PDF—which can be calcu-lated in lattice QCD. The bare quasi-PDF is defined in momentum space (x) and coordinate space (z) as
˜
q(x, Pz, ǫ)≡
Z ∞
−∞ dz 2π e
ixPz
zq˜B
i (z, Pz, ǫ), (4)
˜
qi(z, Pz, ǫ)≡ 1 2
P
ψ(z)γ¯ zWz(z,0)ψ(0)
P
,
where the spacelike Wilson line is
Wz(z,0) =Pexp
−ig
Z z
0
dz′Az(z′)
. (5)
Unlike the PDF in Eq. (1) that is invariant under a boost along the z direction, the quasi-PDF changes dynami-cally under such a boost, which is encoded by its non-trivial dependence on the nucleon momentumPz. The quasi-PDF in coordinate space ˜qj(z, Pz,µ) is multiplica-˜ tively renormalized in dimensional regularization we can write
˜
qi(z, Pz, ǫ) = ˜ZiX(z, Pz, ǫ,µ) ˜˜ qXi (z, Pz,µ)˜ . (6)
Here the position space renormalization factors ˜
ZX
i (z, ǫ,µ) are defined in a particular scheme˜ X,
such as MS, a momentum-subtraction scheme etc., and ˜
µ is a renormalization scale for the quasi-PDF (whose definition also depends on the scheme X). Fourier transforming to momentum space as in Eq. (4), the renormalization for the quasi-PDF involves a convolution in the momentum fraction,
˜
qi(x, Pz, ǫ) =Pz
Z +∞
−∞ dx′Z˜X
i (x−x′, Pz, ǫ,µ) ˜˜ qXi (x′, Pz,µ)˜ . (7)
The structure of the renormalization of the quasi-PDF in Eqs. (6) and (7) is similar to that of the quark beam-function [11, 12], which is a proton distribution with sep-arations along both the plus and minus light-cone di-rections. Ref. [12] gives an all orders proof of the po-sition space multiplicative renormalization of the beam function, and this proof also implied that Zij ∝ δij, so there is never parton mixing in this case. In dimen-sional regularization it has been explicitly demonstrated that the quasi-PDF is multiplicatively renormalized to two loops [13]. Recently a proof of the multiplicative renormalization has been given both non-perturbatively in Ref. [14] and diagrammatically in Ref. [15]. The mul-tiplicative renormalization property present in Eq. (6) essentially follows from the known renormalization struc-ture of QCD and of Wilson lines. Ref. [15] has also demonstrated that there is no flavor mixing in the renor-malization of the quasi-PDF.
For a nucleon moving with finite but large momen-tumPz ≫Λ
QCD, the quasi-PDF can be matched onto
the PDF through a momentum space factorization for-mula [10, 16]:1
˜
qXi (x, Pz,µ) =˜
Z +1
−1
dy
|y| C
X ij
x y,
˜ µ Pz,
µ
|y|Pz
qj(y, µ)
+O
M2
P2
z ,Λ
2 QCD
P2
z
, (8)
where Cij is the matching coefficient, and the
O(M2/P2
z,Λ2QCD/Pz2) terms are higher-twist corrections suppressed by the nucleon momentum (M is the nucleon mass). Here qj(y, µ) for negative y corresponds to the anti-quark contribution. Note that the matching coeffi-cient depends on the quasi-PDF scheme choice X, and that forqj(y, µ) we always assume the MS scheme. Both sides of Eq. (8) are formallyµindependent, but both do depend on the scale ˜µ for the renormalized quasi-PDF, and this dependence need not be small. The indicated power corrections are related to higher-twist contribu-tions in the quasi-PDF. Note that it is important to dis-tinguish between the renormalization of the PDF and
1 In this formula we writeµ/|y|P
z for the third argument of the matching coefficient. This has recently been proven to be the correct result in Ref. [17].
quasi-PDF given by the Zijs and ˜Zijs, and the match-ing coefficients given by the Cijs. The renormalization constants occur in a relation between bare and renor-malized matrix elements for the same operators. On the other hand the matching coefficients occur in a relation between renormalized matrix elements of different opera-tors. The ˜qandqhave the same infrared (IR) divergences (which are collinear divergences in Minkowski space), and at perturbative scalesµand ˜µtheCijs can be calculated order by order inαs.
Based on Ji’s proposal, the procedure of calculating PDF from lattice QCD can be summarized as:
1. Lattice simulation of the quasi-PDF;
2. Renormalization of the quasi-PDF in a particular scheme on the lattice;
3. Subtraction of higher-twist corrections;
4. Matching quasi-PDF in the particular scheme to PDF in the MS scheme.
Efforts have been made to use this proposal to calculate the iso-vector quark distributionsfu−d, including unpo-larized, pounpo-larized, and transversity distributions, as well as pion distribution amplitude, from lattice QCD [18– 25]. For this channel the mixing is not important and so the indicies i and j are dropped. The one-loop matching coefficients were first calculated in a trans-verse momentum cutoff scheme in Ref. [26], which we denote as CΛT(x,Λ
T/Pz, µ/pz). The result was con-firmed in Refs. [19, 27]. The nucleon-mass corrections ofO(M2/P2
z) have already been included in the lattice calculations [18–22, 24, 25], and theO(Λ2
QCD/Pz2) correc-tion was numerically fitted in Ref. [20]. (A direct lattice calculation of theO(Λ2
QCD/Pz2) correction is still desired from the theoretical point of view). In the analyses of Refs [18–21] the renormalization of the lattice matrix el-ement of quasi-PDF, i.e., Step 2, was absent. With in-creasing nucleon momentumPz, lattice renormalization will be the most important factor that limits the precision of the calculation of PDFs. Recently, renormalization of the quasi-PDF has been considered Refs [14, 22–25, 28– 32].
in progress to calculate the lattice quasi-PDFs in the RI/MOM scheme has been reported in [23–25, 32], and appears to be the most promising route for future higher precision quasi-PDF determinations.2
In this paper we focus on Step 4 when the lattice quasi-PDF is defined in the RI/MOM scheme. In particular we carry out a perturbative calculation of the matching co-efficient that enables this lattice quasi-PDF to be directly matched onto the MS PDF. We denote this matching co-efficient by COM and it will depend on the scale of the
off-shell subtraction µR. The renormalized matrix ele-ments in the RI/MOM scheme are independent of the UV regularization, so we carry out this matching per-turbatively with dimensional regularization. Our result for the matching coefficientCOMalso exhibits
insensitiv-ity to a UV cutoff in the integral in Eq. (8),|y| < ycut,
unlike the earlier result for CΛT. As a biproduct of our
calculations, we also determineCMS, which is the
match-ing coefficient to go between the MS quasi-PDF and MS PDF. We find that CMS behaves in a similar fashion to
CΛT.
An alternate to the approach we take here would be to convert the lattice quasi-PDF defined with nonperturba-tive renormalization in the RI/MOM scheme back to the MS scheme perturbatively [31]. This would then allow the CMS matching result to be used. Our approach is
more direct, with only a single step involving a pertur-bative calculation. Nevertheless it would be interesting to compare both approaches.
In Sec. II we elaborate on the procedure of implement-ing the RI/MOM scheme for the quasi-PDF. Then in Sec. III we calculate the RI/MOM scheme quasi-PDF and the one-loop matching coefficient between this quasi-PDF and the quasi-PDF in the MS scheme. We do this first in Feynman gauge and then in a general covariant gauge. We also give the analogous matching coefficient needed for the MS quasi-PDF, and quote the known result for the transverse cutoff quasi-PDF for comparison. In Sec. IV we analyze these results and give a numerical comparison between the quasi-PDF obtained with the matching coef-ficients and the PDF. We conclude in Sec. V. A few more detailed discussions are left to appendices, including our implementation of vector current conservation (App. A), a demonstration that the matching result is independent of the choice of infrared regulator (App. B), exploring an alternate RI/MOM scheme (App. C), and deriving a renormalization group equation for the RI/MOM scheme quasi-PDF (App. D).
2 Indeed, the result for the matching coefficient computed in this
paper has already been used in the lattice calculation in Ref. [24].
II. RENORMALIZATION OF QUASI PDF IN THE RI/MOM SCHEME
In the RI/MOM scheme we will define the renormaliza-tion constant ˜ZOM(z, pz
R,Λ, µR) in Eq. (6) by imposing a condition on the quasi-PDF evaluated with massless quark states|psiof momentumpand spinswithp26= 0.
We study the iso-vector (non-singlet) case, so that we do not have to consider operator mixing. Here the RI/MOM renormalization condition is
˜
ZOM(z, pzR,Λ, µR)−1 X
s
hps|ψ(z)γ¯ zW(z,0)ψ(0)|psi p2=−µ2R
pz
=pz
R
=X
s
hps|ψ(z)γ¯ zW(z,0)ψ(0)|psi
tree
= 4pze−izpz ζ
pz
=pz
R
, (9)
where in generalpµ= (p0,0,0, pz),
ζ= 1 4pz
X
s ¯
usγzus (10)
contains the non-singlet spinor factor and the sum over spinss, andµRis the renormalization scale. In Eq. (9) Λ denotes the UV cutoff and this definition applies for both lattice QCD calculations where Λ = a−1 is the inverse
lattice spacing, and for continuum dimensional regular-ization calculations where Λ = ǫ. In addition to fixing p2=−µ2
R, the choice of the momentumpz is also a free parameter that is part of what specifies the scheme, and which, for example, does not have to be equal to the proton momentumPz. For this reason we have denoted this dependence in ˜ZOM by pz
R. This slightly general-izes Eqs. (7) and (8) since now there are two arguments pz
R, and the momentum of the statePz appearing in the quasi-PDF matrix element. The factorization formula for matching in Eq. (8) with the quasi-PDF in the RI/MOM scheme therefore becomes
˜
qiOM(x, Pz, pzR, µR) (11) =
Z +1
−1
dy
|y| C
OM
ij
x
y, µR pz
R , µ
|y|Pz
qj(y, µ).
On the lattice the renormalization is imposed with a Euclidean momentum,p2=−p2
E, and we setp2E=µ2Rin the condition in Eq. (9). For an on-shell vector current matrix element the unique Dirac structure would beγz, but since the external state is off-shell, the Feynman di-agrams will lead to additional structures such aspz
/ p/p2.
To deal with this, we evaluate the external states with Dirac spinors ¯u(p, s) andu(p, s) and replace
X
s ¯
u(p, s)Υ(z)u(p, s)→Tr
/ pΥ(z)
ζ , (12)
An alternate to using Eq. (12) would be to reduce the Dirac structure of Υ to a minimal basis of{γz, /p}terms, and then only utilize the coefficient of the term propor-tional toγz to define the RI/MOM quasi-PDF,
X
s ¯
u(p, s)Υ(z)u(p, s)→Υ(z)
γz ζ . (13)
We will explore this alternate definition of the RI/MOM scheme in Appendix C, using the notation ˜
qOMγz
(x, Pz, pz
R, µR) andCOMγ
z
.
A key advantage of using the RI/MOM scheme is that although the renormalization factor ˜ZOM and bare ma-trix element depend on the choice of regulator, the renor-malized quasi-PDF does not,
˜
qOM(z, Pz, pz
R, µR) (14)
= ˜ZOM(z, pzR,Λ, µR)−1hP|ψ(z)γ¯ zW(z,0)ψ(0)|Pi, where the state|Pimay be a proton for the proton quasi-PDF, or a quark for the quark quasi-quasi-PDF, etc. Here the Λ dependence formally cancels out between ˜ZOMand the
matrix element on the RHS, and the final result for the renormalized quasi-PDF is independent of the choice of UV regulator. For this reason ˜qOM(z, Pz, pz
R, µR) is re-ferred to as regulator independent. In practice there may be power suppressed cutoff dependence in the renormal-ized quasi-PDF due to approximations used for its calcu-lation. For example, on the lattice there are discretiza-tion effects ofO(apz, ap
p2
E, aµR) which are small in the region ΛQCD ≪ pz,
p
p2
E, µR ≪ 1/a, and only formally vanish in the continuum limit. These effects can be re-duced toO(a2) with improved action methods [34].
In the lattice implementation it should be emphasized that the renormalization constant in Eq. (9) is com-puted in Euclidean space, but still properly renormal-izes the Minkowski space matrix elements. The quasi-PDF proton matrix element in Eq. (14) is computed as a Minkowskian matrix element, and hence has the same infrared behavior as the standard PDF, a point that is crucial for the matching in Eq. (8). Thus the difference between collinear singularities in Minkowski space and the Euclidean space [35] does not affect the quasi-PDF paradigm. This issue has been addressed in detail in Refs [36, 37].
As has been shown in Ref. [26], the quasi-PDF has a linear ultraviolet (UV) divergence. The linear diver-gence arises from the self energy of the finite length space-like Wilson lineW(z,0) in the quasi-PDF, which can be renormalized as [38–40]
WB(z,0) =Zzeδm|z|WR(z,0), (15)
where “B” and “R” stand for bare and renormalized. The exponential factor eδm|z| introduces counterterms that cancel the linear divergencesδm∼Λ, whereas the rest of the renormalization factorZzdepends on the end points of the Wilson line, including the coordinates 0 andz, and includes only logarithmic divergences. We can generalize
this renormalization relation to gauge-invariant nonlocal quark bilinear operators, as was proven in [14, 15], so that the quasi-PDF renormalization can be split into two parts
˜
Z(z, pzR,Λ,µ) =˜ eδm|z|Z˜ψ(z, pzR,µ)˜ , (16)
where δm contains all linear divergences ∝ Λ, while ˜
Zψ(z, pzR,µ) depends on the end points and includes all˜ logarithmic divergences. Bothδm and ˜Zψ can in prin-ciple depend on the UV cutoff Λ, renormalization pa-rameter ˜µ, and momentum of the state used to spec-ify the renormalization schemepz
R. In order to specify a well defined renormalization scheme with the split in Eq. (16), a distinct definition must be given forδm and
˜
Zψ. It would be useful if we can redefine the quasi-PDF to make it free of linear divergence, such as the treat-ment for transverse motreat-mentum distriutions [41, 42], or the gradient flow method [43], but a practical solution on the lattice has not yet been proposed or carried out. With a lattice regulatorδmwill include a linear divergent term
∝1/a, and properly canceling these linear divergences is important numerically. One strategy is to determineδm non-perturbatively from the renormalization of Wilson loop that corresponds to the static quark-antiquark po-tential [22, 28, 32, 44], which has been explicitly verified to cancel the linear divergence in the quasi-PDF at one loop [28].
In the RI/MOM scheme it is not necessary to sepa-rately define δm and ˜Zψ, and we can simply use ˜ZOM which includes all divergences. Both linear and logarith-mic UV cutoff dependence cancel out in Eq. (14), and this cancellation relies only on the multiplicative renormaliz-ability in Eq. (6). This appears to be the simplest ap-proach when carrying out a fully nonperturbative renor-malization on the lattice. (If ˜Zψ(z) is calculated in lattice perturbation theory, then it is likely beneficial to sepa-rately define and calculateδmnon-perturbatively.) This also suffices for our purposes for defining the renormal-ized quasi-PDF, since it is only needed as input for our calculation that matches directly onto the MS PDF by determining the coefficient COM to be used in Eq. (8).
We exploit the independence of the RI/MOM scheme to the choice of UV regulator to carry out this matching calculation using dimensional regularization.
III. MATCHING BETWEEN QUASI-PDF AND PDF
In this section we calculate the one-loop matching co-efficient that converts the renormalized quasi-PDF in the RI/MOM scheme to renormalized PDF in the MS scheme. To do the matching, we compare the two ma-trix elements in an off-shell quark state with momentum pµ= (p0,0,0, pz), andp2<0. In dimensional
gauge invariant, its off-shell matrix element is generally not. As a result, the renormalization constant defined in the momentum subtraction scheme will be gauge depen-dent too. We will start by carrying out this calculation in the Feynman gauge. The result in a general covariant gauge will then be given in Sec. III A, which includes the Landau-gauge result that is the most relevant for lattice simulations.
Although in this section we carry out the matching us-ing the off-shellness as an IR regulator, the result for the matching coefficient is independent of the choice of IR regulator. Therefore if we carry out the calculation with an on-shell IR regulator like dimensional regularization
we will obtain the same matching coefficient between the RI/MOM quasi-PDF and MS PDF. To demonstrate this explicitly in App. B we repeat the one-loop calculation carried out in this section using dimensional regulariza-tion as the IR regulator.
To define the off-shell quark matrix element we will use the definition in Eq. (12) (the results obtained for the alternate definition in Eq. (13) are given in App. C). For the quasi-PDF, we use the momentum space Feynman rules for the coordinate space ˜q(z, pz, ǫ) [28]. At tree level we obtain
˜
q(0)tree(z, pz) = 4pzζ e−izp
z
. (17)
The one-loop Feynman diagrams are shown in Fig. 1.
The displayed diagrams are given by
˜
where in addition we have a contribution from the standard one-loop quark wavefunction renormalization denoted ˜
q(1)w.fn.(z, pz, ǫ).
Here CF = 4/3 and Ta is the SU(3) color matrix in the fundamental representation. The second term in the bracket in the last line of Eq. (18), which is proportional z, does not contribute to the loop integral as it is odd under the exchange ofpz−kz→ −(pz−kz).
The quark self-energy correction is ˜qw(1).fn.(z, pz, ǫ) = δZψ q˜(0)tree(z, pz) with the tree level matrix element in
Eq. (17) andδZψdefined in the on-shell scheme to avoid the need for including residue factors when calculating S-matrix elements for the matching. For an off-shell mo-mentum regulator this is
δZψ=−
However, if we follow the definition in Eq. (12) and in-tegrate over the loop momentum with z = 0, then con-tributions from Eq. (18) do not exactly cancel the quark self-energy correction in Eq. (19), so the one-loop cor-rection to the conserved local vector current is not zero. This occurs due to the off-shell regulatorp2 6= 0, which
allows mixing with additional operators due to the off-shellness of the external state. When using Eq. (12), we can ensure that loop corrections to the vector current cancel, by instead defining δZψ in the on-shell scheme
using the Ward-Takahashi identity:
iΓµ[p, p] =
Here Γµ[p, p] and S(p) are the dressed vertex function and quark propagator, and Σ(p) is the quark self energy. For more details see App. A. Since we work with off-shell quarks for an IR regulator, we will use the latter approach. However, we note that since theδZψ contri-bution is the same for the PDF and quasi-PDF that we will in the end obtain the same result for the matching whether we use Eq. (19) or Eq. (20).
For the matching calculation it is convenient to use the identity
and carry out thez′ integral to express each Feynman di-agram as an inverse Fourier transform with respect to the variablex. For the quasi-PDF the range ofxis uncon-strained and we obtain contributions over the full range
p
k
k
p
z
˜
q
(1)vertex(
z
)
p
p
z
p
k
p
z
˜
q
sail(1)(
z
)
p
k
p
z
˜
q
(1)tadpole(
z
)
FIG. 1. One-loop Feynman diagrams for the quasi-PDF. The standard quark self energy wavefunction renormalization is also included, and denoted ˜qw(1).fn.(z).
For example, carrying out thez′ integral gives
˜
q(1)vertex(z, pz, ǫ) + ˜q(1)
w.fn.(z, pz, ǫ) =ζ pz
Z ∞
−∞
dx e−ixpz
zTr
/ p
Z ddk
(2π)d(−igT aγµ)i
/ kγ
zi / k(−igT
aγν) −igµν (p−k)2
×hδ(kz−xpz)−δ(pz−xpz)i, (22)
where the difference of δ-functions makes it clear that this contribution vanishes in the local limit z = 0. The analogous results for ˜q(1)sail(z, pz, ǫ) and ˜q(1)
tadpole(z, pz, ǫ) each also contain the same [δ(kz−xpz)−δ(pz−xpz)] factor.
For all contributions we therefore can write
pzZdkzZ ∞
−∞
dx e−ixpz
zhδ(kz−xpz)−δ(pz−xpz)i=pzZ ∞
−∞
dxhe−ixpz
z−e−ipz
ziZdkzδ(kz−xpz), (23)
and use theδ(kz−xpz) to perform the loop integral overkz. When evaluating the loop integrals in Eq. (18), we find that for finite xthey are all UV finite and regular as ǫ→0. Only the vertex plus wavefunction contribution is UV divergent asx→ ±∞, but for the RI/MOM scheme these divergences are removed by the counterterm contribution, and hence we can still carry out the calculation with ǫ = 0. We denote the bare contributions in this limit by ˜
q(z, pz,0, p2) where thep2 has been added to indicate the IR regulator. In carrying out the required integrals the
following results are useful
Z 1
0
dy 1
[(x−y)2+y(1−y)ρ]1/2 =
1
√
1−ρln
1
−x−ρ/2 +√1−ρ|1−x| −x+ρ/2 +√1−ρ|x|
, (24)
Z 1
0
dy (1−y)
[(x−y)2+y(1−y)ρ]3/2 =
2 ρ|x|
(ρ−2|x||1−x| −2x(1−x) ρ−4x(1−x) .
We find that the sum of one-loop contributions, ˜q(1) = ˜q(1)
vertex+ ˜q
(1)
w.fn.+ ˜q
(1)
sail+ ˜q
(1)
tadpole, for the bare quasi-PDF in
Feynman gauge is
˜
q(1)(z, pz,0, p2) =αsCF 2π (4p
zζ)Z ∞ −∞
dx e−ixpzz−e−ipzz
×
1
√
1−ρ
1 +x2
1−x − ρ 2(1−x)
ln2x−1 +
√
1−ρ 2x−1−√1−ρ−
ρ
4x(x−1) +ρ+ 1 x >1 1
√
1−ρ
1 +x2
1−x − ρ 2(1−x)
ln1 +
√
1−ρ 1−√1−ρ−
2x
1−x 0< x <1 1
√
1−ρ
1 +x2
1−x − ρ 2(1−x)
ln2x−1−
√
1−ρ 2x−1 +√1−ρ+
ρ
4x(x−1) +ρ−1 x <0
, (25)
where
ρ≡(−p
2−iε)
p2
z
, (26)
Eq. (25) is∝1/xand hence log-divergent (behavior that is cured by the RI/MOM subtraction). On the other hand, the x integral is convergent at x = 1. Here the exp(−ipzz) term gives a “real” contribution with support in−∞< x <∞, while the exp(−ipzz) gives a “virtual” contribution proportional toδ(1−x), and together they provide a well defined result at x = 1. The one-loop correction to the local vector current is exactly zero as the above integral vanishes atz= 0.
By imposing the condition in Eq. (9), we obtain the counterterm
To simplify the presentation of various formulae below we define the dimensionless ratio
rR≡ µR2
pz2
R
. (28)
In Euclidean space, p2
E = p24+pzR2 ≥ p2z, so the renor-malization scale µR one can reach on the lattice by
set-tingp2
E =µ2R always satisfiesµ2R ≥pzR2. Therefore, we can consider ˜qCT(1) after analytically continuing to the re-gionrR>1, which is easy to accomplish using theiε in Eq. (26).
Together these results give the renormalized one-loop quasi-PDF in the RI/MOM scheme
˜
qOM(1)(z, pz, pzR, µR) = ˜q(1)(z, pz,0, p2≪pz2) + ˜q(1)CT(z, pzR, µR). (29) As indicated, to setup the matching of the quasi-PDF to the PDF, we must keep our physical IR regulatorp2
small, i.e. ρ ≪ 1. Thus we identify the logarithmic IR divergences by Taylor expanding ˜q(1) in ρ. At
one-loop order there will only be a lnρterm, corresponding to the leading logarithmic IR singularity which will also appear in the PDF. Also, our notation in Eq. (29) makes clear that the momentum pz of the state for which we are considering the quasi-PDF in general need not be equal to the momentumpz
Rthat we use for the RI/MOM counterterm.
The renormalized quasi-PDF in the RI/MOM scheme is therefore
˜ dard MS scheme. Note that the collinear divergence lnρ only appears in the physical region of the PDF 0< x <1. For x→ ±∞ the integrand for the renormalized quasi-PDF in Eq. (30) now behaves as∝1/x2 and hence the
integral converges.
For the momentum space one-loop quasi-PDF ˜
q(1)OM(x, pz, µ
R) the difference of exponentials in Eq. (30) cause the functions ofxto act like plus-functions in each of the regions. To see this note that for any position space test functiong(zpz) that
Z dz
where g(x) is the momentum space test function. We therefore define the following plus functions with sub-tractions atx= 1
˜
Next we consider the PDF calculated with the same off-shellness regulator, once again using the same identity in Eq. (12) to uniquely define our treatment of the spinors when working off-shell. With this definition the renormalized one-loop matrix element of PDF in the MS scheme is given by
q(1)(x, µ) = αsCF
Considering the factorization formula in Eq. (11), the matching coefficientCOMbetween the renormalized quasi-PDF
in the RI/MOM scheme and standard PDF in the MS scheme is then determined by the difference between the momentum space quasi-PDF and PDF results
COM
which gives the one-loop matching coefficient
COM
where rR is given in Eq. (28). This is the result for the matching between quasi-PDF in the RI/MOM scheme and PDF in the MS scheme for the non-singlet case in Feynman gauge. As expected, COM is independent of the IR
regulator−p2since the logarithmic IR singularities cancel between the quasi-PDF and PDF. An alternate derivation
of Eq. (36) with a different choice for the IR regulator is given in App. B
The result in the RI/MOM scheme in Eq. (36) also exhibits convergent behavior asξ→ ±∞. In section III B below we compare this behavior with the results obtained with the quasi-PDF in the MS and transverse cutoff schemes.
A. Landau and General Covariant Gauge
In lattice QCD, the RI/MOM scheme is most easily implemented in the Landau gauge, so in this section we extend our calculation to give the matching result for a general covariant gauge where the gluon propagator is
iDτµν(k) =−
Hereτ = 0 corresponds to the Landau gauge. We write the quasi-PDF in a general covariant gauge as theτ= 1 Feynman gauge result plus a correction
˜ qOM
∆˜qτOM(x, ρ, rR) = (1−τ)
For the PDF with an off-shell momentum regulator, there is also an additional contribution,
q(1)τ (x, µ) = (1−τ)
As a result, the matching coefficient for a general covariant gauge is given by the Feynman gauge result from Eq. (36) plus an additional term
CτOM
When utilizing the matching equation with the RI/MOM scheme in a chosen gauge, we note that the RI/MOM quasi-PDF ˜qOM
τ is gauge dependent, as is the matching coefficient CτOM, and in both cases this is induced by the presence of the gauge dependent RI/MOM UV counterterm. Therefore this gauge dependence is the same and yields a gauge invariant result for the MS PDF order by order inαs. When the quasi-PDF is renormalized non-perturbatively and the matching is carried out perturbatively, then the cancellation will be incomplete, and it would be reasonable for example to look at the residual gauge dependence as a means of assessing an uncertainty from higher orders in perturbation theory. However we will see in Sec. IV that at one-loop the gauge dependent terms are much smaller than the residual scale dependence, and hence this is unlikely to be a significant source of uncertainty. For our numerical analysis in Sec. IV we will consider both the Feynman gauge result from Eq. (36), denoted COM, and the Landau
gauge result obtained from Eq. (41) withτ= 0, and denotedCOM
τ=0.
B. Comparison to Other Schemes
The one-loop matching coefficient between the quasi-PDF and quasi-PDF was originally calculated in Ref. [26] in
an on-shell scheme with the UV divergence regulated by a finite transverse momentum cutoff ΛT, using Feynman gauge. Using our notation for the plus functions the re-sult for this scheme is
CΛT
subtracted in the quasi-PDF in this scheme, so there is no renormalization scaleµR associated with it.
In the recent works [23, 31], the quasi-PDF is renormal-ized in the RI/MOM scheme and matched to the quasi-PDF in the MS scheme. Eventually, the quasi-quasi-PDF in
the MS scheme needs to be matched to PDF in the MS scheme. In this case, the matching coefficient is very similar to that in Ref. [26] except for the vanishing of the linear divergence, and a different polynomial ξ depen-dence in the 0< ξ <1 region. Subtracting our results in Eqs. (B3) and (B5) we find
CMSξ, µ pz
=δ(1−ξ) +αsCF 2π
1 +ξ2
1−ξ ln ξ ξ−1 + 1
⊕
ξ >1
1 +ξ2
1−ξ ln 4(pz)2
µ2 +
1 +ξ2
1−ξ lnξ(1−ξ) + (2−ξ)− 2ξ 1−ξ
+
0< ξ <1
1 +ξ2
1−ξ ln ξ−1
ξ −1
⊖
ξ <0
. (43)
This result forCMSis gauge invariant, which follows
be-cause on-shell definitions of the quasi-PDF and PDF in the MS scheme are gauge invariant (or alternatively be-cause any gauge dependence associated with off-shell reg-ulation of the infrared physics will be identical for the quasi-PDF and PDF).
IV. NUMERICAL ANALYSIS
In this section we numerically analyze the quasi-PDF by studying how the matching coefficient in Eq. (8) changes the PDF. To calculate the convolution between the momentum space matching coefficientCOM(x/y) and
a PDFf(y) we note that for−1< y <1 and fixedxthe variablex/y goes over the range −∞< x/y <−|x| and
|x|< x/y <∞, and we can simply implement the inte-gration using the plus functions in Eq. (32). Suppressing theµ/pzandµ
R/pzRarguments, and absorbing the limits θ(1− |y|) in the functionf(y) this gives
Z
dy COMx y
f(y)
|y| (44)
=
Z
dy′CrOM(y′)
x y′2
f(x/y′)
|x/y′| −x f(x)
|x|
=
Z ∞
−∞ dy
1
|y|C
OM
r
x
y
f(y)− 1 |x|C
OM
r
y
x
f(x)
.
Here the subscriptr onCOM
r denotes the pure function, which are the argument of the plus functions. For the first equality in Eq. (44) we changed variable toy′=x/y and then applied the plus functions. For the last equality in Eq. (44) we changed variable back toy =x/y′ in the first term, and toy′=y/xin the second term.
As an example we use for our analysis the unpolarized iso-vector parton distribution,
fu−d(x, µ) =fu(x, µ)−fd(x, µ)−fu¯(−x, µ) +fd¯(−x, µ),
(45)
where we includefu¯(−x, µ) =−fu¯(x, µ) andfd¯(−x, µ) =
−fd¯(x, µ), the anti-parton distributions. We use the
next-to-leading-order iso-vector PDFfu−dfrom “MSTW 2008” [7] with the corresponding running couplingαs(µ). For the numerical calculation we impose a UV cutoff on they-integral so that|y|< ycut= 10nfor anyxand some
n >1. Results in the RI/MOM scheme are independent of this cutoff, whereas we will show below that the trans-verse cutoff and MS schemes exhibit sensitivity toycut.
We also test soft cutoffs|y|>10−m and|y−x|>10−m withm >3, but find that the results in all schemes are independent of thism.
As default values for our figures we take Pz = 2√2 GeV, use the Feynman gauge RI/MOM matching resultCOM from Eq. (36) and the MS renormalization
scale µ = 4 GeV. To specify the RI/MOM scheme pa-rameters we take the renormalization scaleµR = 4 GeV and momentumpz
R =Pz. We consider variations about each of these default choices.
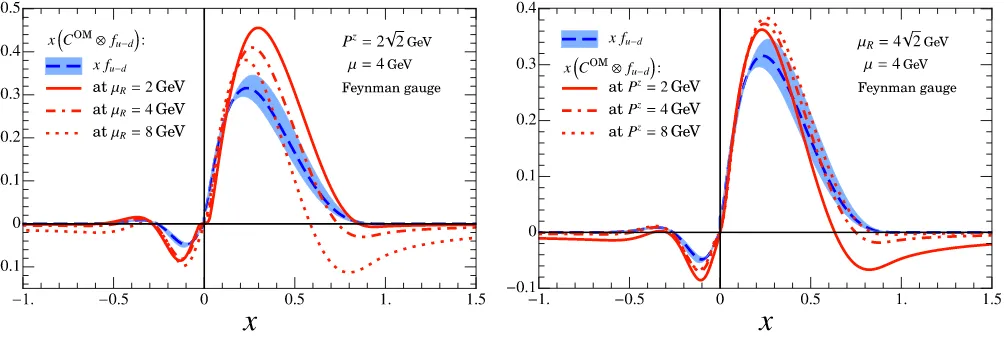
First consider Fig. 2 which shows a comparison of the RI/MOM quasi-PDF ˜qOM(x, Pz, pz
R, µR) = (COM⊗ fu−d) (red solid line) and the MS PDFfu−d(x, µ) (blue dashed line). In this figure and in others below we mul-tiply by x in order to more easily observe the small x region. The left panel shows the direct comparison, and the right panel makes the comparison subtracting xfu−d(x, µ). We see that the quasi-PDF and PDF are close to one another, which is appealing for the conver-gence of perturbation theory. In Fig. 2 we also vary the factorization scaleµby a factor of two, from µ= 2 GeV to µ = 8 GeV, showing the result by the blue and or-ange bands about the PDF and quasi-PDF respectively. For the quasi-PDF from Eq. (36) the dependence on µ cancels out betweenCandq, order by order in perturba-tion theory, whereas the PDF has a dependence onµat leading-logarithmic order, and this decrease in theµ de-pendence is observed as expected. As shown in Fig. 2, the COM⊗f
u−d has small non-zero values outside the region
FIG. 2. Comparison between the PDFxfu−dand the quasi-PDF result obtained fromx(C
OM⊗f
u−d) in Feynman gauge. The orange and blue bands indicate the results from varying the factorization scaleµby a factor of two. Left: x(COM⊗f
u−d) and xfu−d. Right: differences betweenx(C
OM⊗f
u−d),xfu−d, andxfu−d(x,4 GeV).
FIG. 3. Comparison between the PDFxfu−d and the quasi-PDF obtained fromx(C
OM⊗f
u−d) in the Landau gauge. The orange, blue, and green bands indicate the results from varying the factorization scaleµby a factor of two.
we subtract the central curvexfu−d(x, µ= 4 GeV) from bothxfu−d(x, µ) andx(COM⊗fu−d), and plot their dif-ferences in the right panel of Fig. 2.
Next we examine the gauge dependence of the quasi-PDF in the RI/MOM scheme. The result for Landau gauge (τ = 0) is shown in the left panel of Fig. 3, which is plotted in the same way as Fig. 2, and appears very similar. To examine the change to the quasi-PDF we therefore plot the difference between the Landau gauge and Feynman gauge result in the right panel of Fig. 3. We see that the theτ-dependent contribution in the match-ing coefficient are very small, on average bematch-ing only a 1% correction. Thus switching gauge only results in a small change to the matching coefficient.
Our next step is to fix the factorization scale atµ= 4 GeV and vary the renormalization scaleµR in the quasi-PDF. From Eq. (33) we see that the definition of the
RI/MOM quasi-PDF depends on the scale parameter µR, so different µRs correspond to different quasi-PDfs. For µR = 4,8,16 GeV, we plot in the left panel of Fig. 4 a comparison betweenx(COM⊗f
u−d)(x, µR) and xfu−d(x, µ) with µ = 4 GeV (blue dashed line). The blue band shows how the PDF changes when we take µ= 2 or 8 GeV. We see that the RI/MOM quasi-PDF is quite sensitive to the choice of µR, exhibiting larger variations than that of varying the renormalization scale µin the PDF. We also observe that the quasi-PDF moves away from the PDF whenµR> µ. The quasi-PDF in the RI/MOM scheme also satisfies a multiplicative renormal-ization group equation, derived in App. D, which can be analyzed with a perturbative anomalous dimension for µR≫ΛQCD.
In the right panel of Fig. 4 we hold µR = 4
√
FIG. 4. Left panel: Comparison between the PDFxfu−dand the quasi-PDF fromx(C
OM⊗f
u−d) determined at differentµRs. Right panel: ThePz dependence of the quasi-PDFx(COM⊗f
u−d), compared to the PDFxfu−dwhich is independent ofP
z.
In both panels the blue band indicates theµrenormalization scale dependence of the PDF from variation by a factor of two.
and x <−1) that the RI/MOM quasi-PDF approaches the PDF in the anticipated power-law fashion asPz gets large. On the other hand, in the central region−1< x < 1 the matching coefficient becomes a finite function in the Pz → ∞ limit, and hence there is always perturbative conversion needed between the quasi-PDF and PDF.
Finally we consider the comparison between our RI/MOM results and the matching results in the trans-verse cut-off and MS schemes. At Pz = 2√2 GeV, µ = µR = 4 GeV, and ΛT = 4 GeV, we calculate
CΛT ⊗f
u−d and CMS ⊗fu−d with ycut = 101,102,104
and plot the results with comparison to fu−d in Fig. 5. Unlike theCOM⊗f
u−d, bothCΛT⊗fu−dandCMS⊗fu−d suffer from UV divergences in the integration overy, and they differ significantly fromfu−d. This means that when one inverts the factorization formula in Eq. (8) to de-termine the PDF from the quasi-PDF, that there must be a large cancellation of UV divergences between the quasi-PDF from lattice QCD and the matching coeffi-cient in the convolution integral. Since the UV region of a matching factor C(x/y) is neary = 0, it is necessary to test the sensitivity of the convolution integral to the smallest momentum fraction of the quasi-PDF for the lat-tice calculations in Ref. [18–21, 23]. Using the RI/MOM scheme avoids this complication. Another advantage of the RI/MOM scheme is that in the unphysical regions
|x|>1 theαscorrections to the matching coefficient fall as 1/(Pz)2 asPz→ ∞, so the quasi-PDF will vanish in this region. This is not the case for the quasi-PDF in the transverse cutoff and MS schemes, where the quasi-PDF asymptotes to a non-trivial function for |x| > 1 when Pz→ ∞.
The reason why COM ⊗ f
u−d has better UV con-vergence than the other two schemes is that only the RI/MOM scheme introduces a counterterm to the quasi-PDF which will cancel out the UV divergences that arises when one integrates overy. The matching result in the
RI/MOM scheme therefore yields only a bounded small effect which one can be more confident about treating perturbatively. Thus, to reduce the uncertainties, our re-sults imply that it is reasonable to favor RI/MOM over the other two schemes.
V. CONCLUSION
re-FIG. 5. Results for the quasi-PDF in other schemes compared to the PDF fu−d. The left panel showsx(C
ΛT ⊗f
u−d) with three different values forycut. The right panel showsx(CMS⊗fu−d) also with three different values forycut.
sults in the transverse cutoff or MS schemes. To increase the accuracy of our results in the future, one can study theO(a) improvement for the lattice simulation of quasi-PDF and calculate the matching coefficient to higher or-ders in perturbation theory. As the capabilities for doing simulations with larger nucleon momentum on the lat-tice continue to improve, we believe that our results will provide an important ingredient for future lattice calcu-lations of PDF with the desired accuracy.
It should be noted that on the lattice there are not only discretization errors, but also mixings between the quasi-PDF and other operators due to the broken sym-metries. We should include all the possible operators that mix with the gauge-invariant quark bilinear and determine their renormalization constants nonperturba-tively [23, 24, 31, 32]. We must also be aware of the fact that one can only calculate the spatial correlation for the quasi-PDF at a finite number of discrete z’s on the lattice. As a result, its Fourier transform into mo-mentum space will exhibit an oscillatory behavior due to the truncation at|zmax| [23, 24, 32]. Nevertheless, if we
derive the parametric behavior of the spatial correlation at large |z|, we can use a proper set of basis functions to fit the data points and obtain a smooth curve. Then we can Fourier transform this smooth curve to obtain the quasi-PDF, which is free of the truncation error and should capture the correct behavior in the small x re-gion that can only be probed at large|z|. The choice of the basis functions could be based on results from global fits to the PDF with matching correction in Eq. (8). Two other approaches to reduce the truncation error were also proposed in the recent paper [25].
ACKNOWLEDGEMENT
The authors are thankful for discussions with J. W. Chen, W. Detmold, M. Constantinou, L. Jin,
Y. B. Yang, K. F. Liu, J. H. Zhang, M. Engelhardt, P. Shanahan and D. Horkel. This material was supported by the U.S. Department of Energy, Office of Science, Of-fice of Nuclear Physics, from de-sc0011090 and within the framework of the TMD Topical Collaboration. I.S. was also supported in part by the Simons Foundation through the Investigator grant 327942.
Appendix A: Vector Current Conservation
In dimensional regularization and the Feynman gauge, the one-loop correction to the local vector current in an off-shell quark state|piis
δΓz= αsCF 4π
1
ǫ + ln µ2
−p2+ 1
γz−2p z
/ p p2
+δZψγz .
(A1)
The quark self-energy graph gives
Σ(p) =−αs4πCF
1
ǫ+ ln µ2
−p2 + 1
/
p=δZψ/p , (A2)
whereδZψ is defined by the correction to the residue of the pole in the propagator. Thus for the on-shell renor-malization of the wavefunction in Eq. (19), we find that the γz terms exactly cancel in δΓz, but the
/
p term in Eq. (A1) remains. The correction to the vector current
¯
ψγzψ is zero, but there is mixing to the scalar operator ¯
ψ/pψ.
If we define the off-shell matrix element using Eq. (12), then
δΓ′z= αsCF 4π
1 ǫ + ln
µ2
−p2+ 1
−2
where the/pterm has made a nonzero contribution. Nev-ertheless, if we redefineδZψ according to Eq. (20),
δZψ′ =−
then the one-loop corrections to the vector current ex-actly cancel. Actually, this cancellation takes place even before loop integration as it is guaranteed by the Ward-Takahashi identity.
Appendix B: Matching On-shell
The operator mixing, non-vanishing one-loop correc-tion, and gauge-dependence are all due to the off-shellness of the external state. In this appendix we show that the same result is obtained for the matching coef-ficient C when we use dimensional regularization as the IR regulator.
If we work on-shell, using dimensional regularization for both UV and IR divergences, then we can use the equation of motion to eliminate the /p term and there
will be no difference in the two definitions of δZψ in Eqs. (19,20). With a massless quark the vertex renor-malization for the local vector current is
δΓz=αsCF
where 1/ǫUVand 1/ǫIRdenote the UV and IR divergences
respectively. The two definitions in Eqs. (19,20) give the sameδZψ, and one-loop correction to the vector current is strictly guaranteed to be zero. However, the off-shell momentum subtraction scheme cannot be implemented on-shell. Nevertheless, the matching calculation requires comparing renormalized matrix elements for the quasi-PDF and quasi-PDF, so we can carry out the matching on-shell with the 1/ǫIRIR regulator, where the renormalized
quasi-PDF is defined using the UV counterterm from the off-shell momentum subtraction scheme.
For on-shell massless quarks, the unrenormalized quasi-PDF calculated in this fashion is
˜
By adding the counter-term defined in Eq. (27), we have the renormalized quasi-PDF
˜
In pure dimensional regularization the bare PDF at one-loop is proportional to (1/ǫUV−1/ǫIR), so on-shell with
dimensional regularization regulating the IR divergence the renormalized PDF in the MS scheme is
qǫ(1)(x, µ) =
Computing the matching coefficient
then gives exactly the same result forCOM as in Eq. (36). This gives an explicit example showing that the matching
result is independent of the common IR regulator we choose to use for the PDF and quasi-PDF in the calculation.
Appendix C: An Alternate RI/MOM Scheme
Now let us turn to the alternate scheme for defining the RI/MOM quasi-PDF given in Eq. (13). With this choice the unrenormalized one-loop matrix element in a general covariant gauge is given by our earlier result in Eq. (38) plus an additional term
˜
In the RI/MOM scheme, the renormalized matrix element withρ→0 is
∆˜qγ(1)zτ x, rR
To carry out the matching we must implement the same infrared regulator (ie. treatment of spinors in the off-shell regulator) for the PDF calculation. To do this we decompose the light-cone PDF into {γz, /p} terms, and only keep theγz terms. Since γz = (γ+−γ−)/2, and ¯u(p)γ−u(p)→0 in a linear fashion asp2 →0, the γz coefficient turns out to be equivalent to the coefficient ofγ+ with a basis of{γ+, /p}. Extracting the coefficient ofγ+ in this basis, the
PDF matrix element calculation is modified as3
qγ(1)+τ(x, µ) =q
Using these results the matching coefficient becomes
COMγz
3 We note that our calculation of the PDF with an off-shell
regula-tor also agrees with the calculation of this quantity in Ref. [12]. To achieve this we decompose the PDF in a{γ+, γ−}basis and
then define the PDF as theγ+coefficient, while also accounting
FIG. 6. Comparison between the PDFxfu−dand the quasi-PDF obtained fromx(C
OMγz⊗f
u−d) in the Feynman gauge. The yellow, blue and green bands indicate the uncertainties in the factorization scaleµ. Left: x(COMγz
⊗fu−d) andxfu−d. Right: x(COMγz−COM)⊗f
u−d.
with
∆COMγz
ξ,µR pz
R
= αsCF 4π
×
"
2rR (rR−1)
3 2
2ξ2−r
R (1−ξ) arctan
√
rR−1 2ξ−1 +
2rR rR−1
rR+ 2ξ(ξ−1)(2ξ+ 1) (ξ−1)[rR+ 4ξ(ξ−1)] −
2(1−τ)r2
R
rR+ 4x(x−1)
2
#
⊕
ξ >1
2rR (rR−1)
3 2
2ξ2−r
R (1−ξ) arctan
√
rR−1 + 2 rR−1
rR(1−2ξ) + 2ξ(1−ξ)
1−ξ + 2(1−τ)
+
0< ξ <1
"
− 2rR
(rR−1)
3 2
2ξ2−r
R (1−ξ) arctan
√
rR−1 2ξ−1 −
2rR rR−1
rR+ 2ξ(ξ−1)(2ξ+ 1) (ξ−1)[rR+ 4ξ(ξ−1)]
+ 2(1−τ)r
2
R
rR+ 4x(x−1)
2
#
⊖ ξ <0
.
(C6)
Again this result is independent of the choice of IR regulator used for the matching calculation. If we repeat this calculation using the on-shell scheme discussed in App. B then it is easy to see that ∆COMγz
(ξ, µR/pzR) = ˜
q(1)γ
z
CT (ξ, pzR, µR)−q˜CT(1)(ξ, pzR, µR), which is the difference of the counterterms that specify the two RI/MOM schemes. Using Eq. (C2) this immediately yields Eq. (C6).
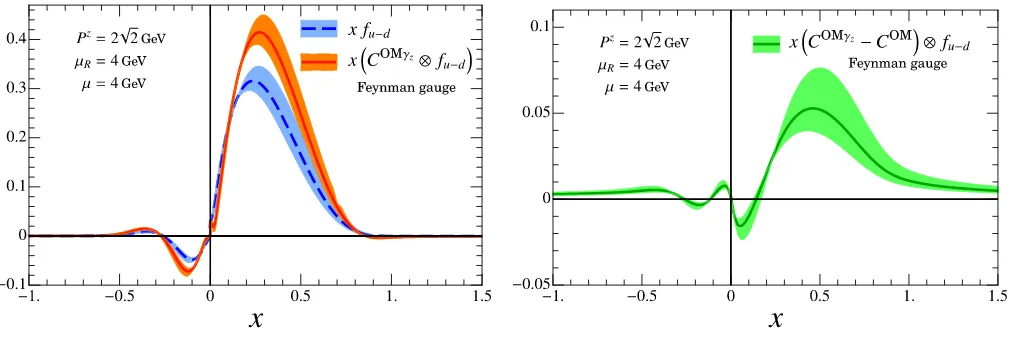
Using the same settings as in Fig. 2, we plot in the left panel of Fig. 6 the result for the quasi-PDF computed with the matching in this γz scheme, x(COMγz
⊗fu−d), and compare it with the MS PDF. In the right panel of Fig. 6 we plot the difference between the two treatments of the spinors,x(COMγz
−COM)⊗f
u−d. The modification to the matching from this alternate RI/MOM scheme is seen to be an effect of comparable size to the difference between the quasi-PDF and PDF shown in Fig. 2 (right panel), and hence it is important to carefully specify the treatment of spinors when defining an RI/MOM scheme. The results for the two schemes given here suffice to determine the result in any other possible scheme defined by a different treatment of the spinors at one-loop order.
Appendix D: Renormalization Group Equation for the RI/MOM Quasi-PDF
The µR dependence of the quasi-PDF takes a rather nontrivial form in the RI/MOM scheme, as shown in Eq. (30). It is useful to examine this dependence in the form of a renormalization group equation (RGE). Due to the multiplicative renormalization in Eq. (6), the RGE
of the quasi-PDF in position space has the form
d˜q(z, Pz, pz R, µR) dlnµR
= ˜γ(z, pzR, µR) ˜q(z, Pz, pzR, µR), (D1)
where the anomalous dimension ˜γcan be computed from the renormalization constant through
˜
γ(z, pzR, µR) =− d dlnµR
Based on the result in Eq. (30), at one-loop
˜
γ(1)(z, pzR, µR) =µR d dµR
˜
qCT(1)(z, pzR, µR) (4pzζ e−ipz
Rz) , (D3)
so
˜
γ(1)(z, pzR, µR) = αsCF
2π
Z ∞
−∞
dxei(1−x)pzRz−1
(D4)
×
2x
−1 x−1
rR rR−1
2(1 +x2)−r
R rR+ 4x(x−1)
+ 8rRx(x−1) [rR+ 4x(x−1)]2
− rR
(rR−1)3/2
2x2+r
R x−1 arctan
√
rR−1 2x−1
x >1
−r 1
R−1
2(1 +x2)−r
R
1−x +
rR (rR−1)3/2
2x2+r
R 1−x arctan
√
rR−1
0< x <1
−2xx −1 −1
rR rR−1
2(1 +x2)−r
R rR+ 4x(x−1) −
8rRx(x−1) [rR+ 4x(x−1)]2
+ rR
(rR−1)3/2
2x2+r
R x−1 arctan
√
rR−1 2x−1
x <0
where hererR= (µR/pzR)2. Though hard to evaluate analytically, the above integral is finite and complex.
In the limit ofµR≫pzR, we have
˜
γ(1)(z, pzR, µR) =αsCF 4
Z dx
(1−x)
ei(1−x)pzRz−1
µR
pz R
,
(D5)
so the anomalous dimension does exhibit linear behav-ior in µR. This shows that the RI/MOM scheme tracks the linear divergence from the Wilson line self-energy, and when solving Eq. (D1) generates an exponential of µR/pzR. (Equation (D5) appears to diverge for |x| ≫ µR/pzR, but this is just an artifact of expandingµR≫pzR
with fixedx, and the true integrand in Eq. (D4) goes to zero as 1/x2 forx→ ±∞.)
We can also consider the limit ΛQCD≪µR≪Pz. In this limit the contributions fromx >1 andx <0 vanish linearly, and analytically continuing to the regionrR<1, the result from the 0< x <1 region is
˜
γ(1)(z, Pz, µR) =αsCF
Z 1
0
dx π
ei(1−x)pzRz−1
1 +x2
1−x , (D6)
which is just the Fourier transform of the standard DGLAP momentum space anomalous dimension.
[1] J. C. Collins, D. E. Soper, and G. Sterman, Adv. Ser. Direct. High Energy Phys.5, 1 (1988), hep-ph/0409313. [2] W. Detmold, W. Melnitchouk, and A. W. Thomas, Eur. Phys. J.direct3, 13 (2001), arXiv:hep-lat/0108002 [hep-lat].
[3] W. Detmold, W. Melnitchouk, and A. W. Thomas, Phys. Rev. D66, 054501 (2002), arXiv:hep-lat/0206001 [hep-lat].
[4] D. Dolgovet al.(LHPC, TXL), Phys. Rev.D66, 034506 (2002), arXiv:hep-lat/0201021 [hep-lat].
[5] R. D. Ball et al. (NNPDF), JHEP 04, 040 (2015), arXiv:1410.8849 [hep-ph].
[6] S. Dulat, T.-J. Hou, J. Gao, M. Guzzi, J. Hus-ton, P. Nadolsky, J. Pumplin, C. Schmidt, D. Stump, and C. P. Yuan, Phys. Rev. D93, 033006 (2016),
arXiv:1506.07443 [hep-ph].
[7] A. D. Martin, W. J. Stirling, R. S. Thorne, and G. Watt, Eur. Phys. J.C63, 189 (2009), arXiv:0901.0002 [hep-ph]. [8] S. Alekhin, J. Bl¨umlein, S. Moch, and R. Placakyte,
(2017), arXiv:1701.05838 [hep-ph].
[9] A. Buckley, J. Ferrando, S. Lloyd, K. Nordstr¨om, B. Page, M. R¨ufenacht, M. Sch¨onherr, and G. Watt, Eur. Phys. J.C75, 132 (2015), arXiv:1412.7420 [hep-ph]. [10] X. Ji, Phys. Rev. Lett. 110, 262002 (2013),
arXiv:1305.1539 [hep-ph].
[11] I. W. Stewart, F. J. Tackmann, and W. J. Waalewijn, Phys.Rev. D81, 094035 (2010), arXiv:0910.0467 [hep-ph].
[13] X. Ji and J.-H. Zhang, Phys. Rev.D92, 034006 (2015), arXiv:1505.07699 [hep-ph].
[14] X. Ji, J.-H. Zhang, and Y. Zhao, (2017), arXiv:1706.08962 [hep-ph].
[15] T. Ishikawa, Y.-Q. Ma, J.-W. Qiu, and S. Yoshida, (2017), arXiv:1707.03107 [hep-ph].
[16] X. Ji, Sci. China Phys. Mech. Astron. 57, 1407 (2014), arXiv:1404.6680 [hep-ph].
[17] J. Luchang, et.al., in preparation (2017).
[18] H.-W. Lin, J.-W. Chen, S. D. Cohen, and X. Ji, Phys. Rev. D91, 054510 (2015), arXiv:1402.1462 [hep-ph]. [19] C. Alexandrou, K. Cichy, V. Drach, E.
Garcia-Ramos, K. Hadjiyiannakou, K. Jansen, F. Stef-fens, and C. Wiese, Phys. Rev. D92, 014502 (2015), arXiv:1504.07455 [hep-lat].
[20] J.-W. Chen, S. D. Cohen, X. Ji, H.-W. Lin, and J.-H. Zhang, Nucl. Phys.B911, 246 (2016), arXiv:1603.06664 [hep-ph].
[21] C. Alexandrou, K. Cichy, M. Constantinou, K. Had-jiyiannakou, K. Jansen, F. Steffens, and C. Wiese, (2016), arXiv:1610.03689 [hep-lat].
[22] J.-H. Zhang, J.-W. Chen, X. Ji, L. Jin, and H.-W. Lin, Phys. Rev.D95, 094514 (2017), arXiv:1702.00008 [hep-lat].
[23] C. Alexandrou, K. Cichy, M. Constantinou, K. Had-jiyiannakou, K. Jansen, H. Panagopoulos, and F. Stef-fens, (2017), arXiv:1706.00265 [hep-lat].
[24] J.-W. Chen, T. Ishikawa, L. Jin, H.-W. Lin, Y.-B. Yang, J.-H. Zhang, and Y. Zhao, (2017), arXiv:1706.01295 [hep-lat].
[25] H.-W. Lin, J.-W. Chen, T. Ishikawa, and J.-H. Zhang, (2017), arXiv:1708.05301 [hep-lat].
[26] X. Xiong, X. Ji, J.-H. Zhang, and Y. Zhao, Phys. Rev. D90, 014051 (2014), arXiv:1310.7471 [hep-ph].
[27] Y.-Q. Ma and J.-W. Qiu, (2014), arXiv:1404.6860 [hep-ph].
[28] T. Ishikawa, Y.-Q. Ma, J.-W. Qiu, and S. Yoshida, (2016), arXiv:1609.02018 [hep-lat].
[29] J.-W. Chen, X. Ji, and J.-H. Zhang, (2016), arXiv:1609.08102 [hep-ph].
[30] X. Xiong, T. Luu, and U.-G. Meißner, (2017), arXiv:1705.00246 [hep-ph].
[31] M. Constantinou and H. Panagopoulos, (2017), arXiv:1705.11193 [hep-lat].
[32] J. Green, K. Jansen, and F. Steffens, (2017), arXiv:1707.07152 [hep-lat].
[33] S. Capitani, Phys. Rept. 382, 113 (2003), arXiv:hep-lat/0211036 [hep-lat].
[34] G. Martinelli, C. Pittori, C. T. Sachrajda, M. Testa, and A. Vladikas, Nucl. Phys. B445, 81 (1995), arXiv:hep-lat/9411010 [hep-lat].
[35] C. E. Carlson and M. Freid, (2017), arXiv:1702.05775 [hep-ph].
[36] R. A. Brice˜no, M. T. Hansen, and C. J. Monahan, (2017), arXiv:1703.06072 [hep-lat].
[37] X. Ji, J.-H. Zhang, and Y. Zhao, (2017), arXiv:1706.07416 [hep-ph].
[38] V. S. Dotsenko and S. N. Vergeles, Nucl. Phys.B169, 527 (1980).
[39] N. S. Craigie and H. Dorn, Nucl. Phys.B185, 204 (1981). [40] H. Dorn, Fortsch. Phys.34, 11 (1986).
[41] J. Collins,Foundations of perturbative QCD (Cambridge University Press, 2013).
[42] X. Ji, P. Sun, X. Xiong, and F. Yuan, Phys. Rev.D91, 074009 (2015), arXiv:1405.7640 [hep-ph].
[43] C. Monahan and K. Orginos, (2016), arXiv:1612.01584 [hep-lat].