i
PERBANDINGAN METODE KEMUNGKINAN MAKSIMUM DAN METODE MOMEN DALAM PENDUGAAN PARAMETER DISTRIBUSI
PARETO DENGAN DUA PARAMETER Skripsi
Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Disusun oleh : I Made Yudha Pratama
NIM : 163114005
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
COMPARISON OF MAXIMUM LIKELIHOOD METHOD AND MOMENT METHOD FOR ESTIMATING THE TWO PARAMETER
PARETO DISTRIBUTION
Thesis
Presented as Partial Fulfillment of the Requirements to Obtain Sarjana Mathematics Degree in Mathematics
By :
I Made Yudha Pratama Student Number : 163114005
MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY 2020
v
HALAMAN PERSEMBAHAN
Karya tulis ini saya persembahkan untuk : Ida Sang Hyang Widhi Wasa
Kedua orang tua, yaitu Papa saya I Nyoman Sarjana
Ibu saya I Gusti Ayu Ariani
Kakak saya yang tercinta Putu Oksi Adrian Pratama
viii ABSTRAK
Distribusi Pareto adalah salah satu distribusi peluang kontinu. Distribusi Pareto tergolong dalam distribusi keluarga Eksponensial seperti distribusi peluang kontinu lainnya, yaitu distribusi binomial, distribusi Normal, distribusi geometrik, distribusi eksponensial, dan distribusi Poisson. Hal yang paling penting dalam mengkaji suatu distribusi adalah pendugaan parameter. Metode yang digunakan dalam pendugaan dua parameter distribusi Pareto adalah Metode Kemungkinan Maksimum dan Metode Momen. Metode Kemungkinan Maksimum adalah metode penduga yang memaksimumkan fungsi Likelihood 𝐿(𝜃|𝑋). Metode momen adalah metode penduga yang didasarkan pada momen pada suatu sampel yang dapat dijadikan sebagai penduga yang sesuai dengan momen pada suatu populasi. Pemilihan metode terbaik diantara keduanya didasarkan pada perbandingan Rata-Rata Kuadrat Galat (Mean Square Error). Metode yang lebih baik adalah metode yang memiliki Rata-Rata Kuadrat Galat minimum. Perbandingan kedua metode diterapkan pada data jumlah pendapatan perorangan pada tahun 1969 di daerah texas.
Kata kunci: distribusi Pareto, pendugaan parameter, Metode Kemungkinan
ix ABSTRACT
Pareto distribution is one of the continuous probability density function. Pareto distribution is a member of the Exponential family distribution like other continuous probability density function, namely the binomial distribution, Normal distribution, geometric distribution, exponential distribution, and Poisson distribution. The most important part in analyzing a distribution is parameter estimation. The method used in estimation of the two Pareto distribution parameters is Maximum Likelihood Method and Moment Method. Maximum Likelihood Method is an estimation method that maximizes the likelihood function 𝐿(𝜃|𝑋). Moment Method is an estimation method based on the sample moment become the estimator of the population related moment. Choosing the best method of the two method is done by comparising the Mean Square Error. The better method has the minimum Mean Square Error. The comparison of the two methods is applied to the total personal income for year 1969 in Texas.
Keyword: Pareto distribution, parameter estimation, Maximum Likelihood
x
KATA PENGANTAR
Puji syukur penulis panjatkan ke hadapan Tuhan Yang Maha Esa, karena berkat rahmat dan bimbingan-Nya penulis dapat menyelesaikan tugas akhir ini. Tugas akhir yang berjudul “Perbandingan Metode Kemungkinan Maksimum dan Metode Momen dalam Pendugaan Parameter Distribusi Pareto dengan Dua Parameter” dibuat sebagai salah satu persyaratan dalam memperoleh gelar Sarjana Matematika dalam program studi Matematika pada Fakultas Sains dan Teknologi Universitas Sanata Dharma.
Dalam penyusunan skripsi ini, penulis banyak mendapatkan bantuan dan dukungan moral dari berbagai pihak. Melalui kesempatan ini penuli menyampaikan ucapan terima kasih kepada :
1. Bapak Ir. Ig. Aris Dwiatmoko, M. Sc selaku dosen pembimbing yang dengan penuh kesabaran telah memberikan bimbingan, nasihat, dan arahan kepada penulis.
2. Bapak/ Ibu dosen program studi Matematika Universitas Sanata Dharma yang telah memberikan ilmu serta nasihat selama masa kuliah.
3. Kedua orang tua dan kakak dari penulis yang selalu memberikan dukungan dan semangat kepada penulis.
4. Teman seperjuangan Devita, Elisabeth, Lydia, Rika, dan Resti yang menemani penulis dalam bimbingan maupun proses pengerjaan tugas akhir.
5. Teman-teman program studi Matematika angkatan 2016 yang saling mendukung, membantu, dan memberikan semangat selama masa kuliah. 6. Semua pihak yang tidak bisa penulis sebutkan satu persatu yang telah memberikan dukungan baik secara langsung maupun tidak langsung dan membantu penulis dalam menyelesaikan tugas akhir ini.
xi
Penulis menyadari bahwa tugas akhir ini masih jauh dari kesempurnaan, maka saran dan kritik yang konstruktif dari semua pihak sangat diharapkan demi penyempurnaan selanjutnya. Semoga tugas akhir ini dapat bermanfaat bagi semua pihak, khususnya bagi penulis dan para pembaca pada umumnya.
Yogyakarta, 14 Januari 2020 Penulis
xii DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... v
HALAMAN PERNYATAAN KEASLIAN KARYA ... vi
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... vii
HALAMAN ABSTRAK ... viii
HALAMAN ABSTRACT ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
DAFTAR TABEL ... xiv
DAFTAR GAMBAR ... xv BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 2 C. Batasan Masalah ... 2 D. Tujuan Penulisan ... 3 E. Manfaat Penulisan ... 3 F. Metode Penulisan ... 3 G. Sistematika Penulisan ... 4
BAB II LANDASAN TEORI ... 6
A. Teori Peluang ... 6
B. Distribusi Peluang ... 7
xiii
D. Distribusi Fungsi dari Fungsi Variabel Acak ... 24
E. Statistik Terurut (Order Statistics) ... 27
F. Teorema Limit Pusat ... 29
G. Estimasi Parameter Fungsi Distribusi... 31
H. Bias dan Rata-Rata Galat Kuadrat dari Penduga Titik ... 34
BAB III DISTRIBUSI PARETO ... 36
A. Sejarah Distribusi Pareto ... 36
B. Model Distribusi Pareto ... 36
C. Estimasi Parameter Distribusi Pareto ... 42
D. Distribusi Pareto Sebagai Anggota Keluarga Distribusi Eksponensial 47 E. Parameter Tunggal pada Distribusi Pareto ... 48
F. Estimasi Parameter Tunggal pada Distribusi Pareto ... 48
G. Uji Kolmogorov-Smirnov ... 52
H. Uji Distribusi Pareto Menggunakan Uji Kolmogorov-Smirnov... 58
I. Kriteria Statistis pada Penduga Fungsi Distribusi Kumulatif Pareto ... 66
BAB IV PENERAPAN DISTRIBUSI PARETO ... 68
A. Data dan Sumbernya ... 68
B. Estimasi Model Distribusi Pareto ... 69
C. Uji Kecocokan Penduga Parameter Distribusi Pareto ... 71
D. Perbandingan Metode Kemungkinan Maksimum dan Metode Momen ... 73 BAB V PENUTUP ... 74 A. Kesimpulan ... 74 B. Saran ... 75 DAFTAR PUSTAKA ... 76 LAMPIRAN ... 77
xiv
DAFTAR TABEL
Tabel 3.1 Simulasi Data Kerugian dan Normalisasinya ... 49 Tabel 3.2 Data Kerugian Akibat Bencana Angin Topan Tahun 1977 ... 50 Tabel 3.3 Data Tekanan Darah Sistolik ... 54
xv
DAFTAR GAMBAR
Gambar 3.1 Plot fungsi distribusi kumulatif Pareto 𝐹(𝑥) dengan 𝑘 = 1 dan variasi nilai 𝑎, yaitu 𝑎 = 1 dengan grafik warna merah, 𝑎 = 2 dengan grafik warna biru dan 𝑎 = 3 dengan grafik warna hijau ... 37 Gambar 3.2 Plot fungsi distribusi kumulatif Pareto 𝐹(𝑥) dengan 𝑎 = 1 dan variasi nilai 𝑎, yaitu 𝑘 = 1 dengan grafik warna merah, 𝑘 = 2 dengan grafik warna biru dan 𝑘 = 3 dengan grafik warna hijau ... 37 Gambar 3.3 Plot fungsi peluang pareto 𝑓(𝑥) dengan 𝑘 = 1 dan variasi nilai 𝑎, yaitu 𝑎 = 1 dengan grafik warna merah, 𝑎 = 2 dengan grafik warna biru dan 𝑎 = 3 dengan grafik warna hijau ... 39 Gambar 3.4 Plot fungsi peluang pareto 𝑓(𝑥) dengan 𝑎 = 1 dan variasi nilai 𝑘, yaitu 𝑘 = 1 dengan grafik warna merah, 𝑘 = 2 dengan grafik warna biru dan 𝑘 = 3 dengan grafik warna hijau ... 39 Gambar 3.5 Grafik fungsi distribusi Normal dan fungsi empiris... 56 Gambar 3.6 Grafik fungsi distribusi Pareto berdasarkan penduga parameter dari Metode Kemungkinan Maksimum dan fungsi empiris ... 61 Gambar 3.7 Grafik fungsi distribusi Pareto berdasarkan penduga parameter dari Metode Momen dan fungsi empiris ... 64 Gambar 4.1 Histogram dari data jumlah pendapatan perorangan di Texas pada tahun 1969 ... 68 Gambar 4.2 Grafik fungsi peluang distribusi Pareto dengan 𝑘̂ = 20,2 dan 𝑎̂ = 0,826060967 ... 69 Gambar 4.3 Grafik fungsi peluang distribusi Pareto dengan 𝑘̂ = 20,06851803 dan 𝑎̂ = 1,105275084 ... 71
1 BAB I PENDAHULUAN
A. Latar Belakang Masalah
Pendugaan adalah pokok bahasan dalam statistika yang berhubungan dengan pendugaan nilai-nilai parameter berdasarkan data empiris yang berasal dari sampel acak. Tujuan dari statistika adalah menggunakan informasi yang terkandung dalam sampel untuk membuat kesimpulan tentang populasi dari mana sampel tersebut diambil. Parameter adalah suatu konstanta yang mencirikan (merupakan karakteristik) populasi. Pendugaan parameter dilakukan untuk mengaproksimasi parameter yang tidak diketahui dari suatu populasi berdasarkan sampel.
Dalam mengkaji suatu distribusi, hal yang paling penting adalah masalah menduga parameternya. Dalam teori peluang, distribusi Pareto adalah distribusi peluang kontinu dengan dua parameter, yaitu 𝑎 dan 𝑘 yang bernilai positif. Distribusi Pareto pertama kali diperkenalkan oleh Vilfredo Pareto yang merupakan ahli ekonomi, insinyur, ahli sosiologi, pengamat politik, sekaligus seorang filsuf kebangsaan Italia. Dalam bidang sosiologi Pareto dikenal karena teorinya tentang interaksi elit dalam masyarakat. Sementara pada bidang ekonomi, Pareto menekankan analisis ekonomi melalui pendekatan matematis. Pengamatan Pareto pada kedua bidang tersebut menghasilkan banyak teori atau prinsip yang tidak hanya digunakan di bidang ekonomi, namun juga digunakan di bidang keteknikan atau aplikasi lainnya. Vilfredo Pareto menyampaikan gagasannya tentang distribusi Pareto melalui buku Ekonomi yang dipublikasikan di Rome pada tahun 1897. Hingga saat ini distribusi Pareto banyak digunakan dalam bidang sosial-ekonomi seperti kependudukan, pendapatan, perpajakan, asuransi, dll.
Dalam menduga parameter distribusi Pareto dengan dua parameter, Penulis menggunakan Metode Kemungkinan Maksimum (Maximum Likelihood Method) dan Metode Momen (Moment Method). Metode Kemungkinan Maksimum adalah metode penduga yang memaksimumkan fungsi Likelihood 𝐿(𝜃|𝑋). Sedangkan
metode momen adalah metode penduga yang didasarkan pada momen pada suatu sampel yang dapat dijadikan sebagai penduga yang sesuai dengan momen pada suatu populasi.
Sesuai dengan uraian di atas, penulis ingin mempelajari lebih jauh tentang distribusi Pareto, sifat-sifatnya, dan membandingkan pendugaan parameter distribusi Pareto dengan dua parameter menggunakan Metode Kemungkinan Maksimum dan Metode Momen.
Dalam skripsi ini, penulis menggunakan Rata-Rata Kuadrat Galat (Mean
Square Error) untuk menentukan metode terbaik dalam menduga parameter
distribusi Pareto dengan dua parameter. Rata-Rata Kuadrat Galat adalah ukuran keakuratan dari penduga. Metode yang terbaik dalam menduga parameter distribusi Pareto adalah metode yang memiliki Rata-Rata Kuadrat Galat minimum.
B. Rumusan Masalah
Adapun rumusan masalah dalam tulisan ini adalah:
1. Bagaimana definisi dan sifat-sifat statistis distribusi Pareto?
2. Bagaimana mengestimasi parameter distribusi Pareto dengan dua parameter menggunakan Metode Kemungkinan Maksimum?
3. Bagaimana mengestimasi parameter distribusi Pareto dengan dua parameter menggunakan Metode Momen?
4. Bagaimana membandingkan metode terbaik dalam mengestimasi parameter distribusi Pareto dengan dua parameter?
C. Batasan Masalah
Adapun beberapa hal yang dibatasi penulis dalam tulisan ini adalah:
1. Dalam mengestimasi parameter distribusi Pareto, penulis hanya membahas pendugaan parameter distribusi Pareto dengan dua parameter menggunakan Metode Kemungkinan Maksimum dan Metode Momen.
2. Penulis hanya membahas generalisasi dari distribusi yang disebut juga dengan Pareto tipe I. Penulis tidak membahas distribusi Pareto tipe II,III, dan IV.
3. Penulis tidak membahas pendugaan interval dari distribusi Pareto dengan dua parameter.
4. Penulis menerapkan distribusi Pareto terhadap pendapatan.
D. Tujuan Penulisan
Tujuan penulisan tugas akhir ini adalah:
1. Mengetahui sifat-sifat statistis dari distribusi Pareto dan penerapan distribusi Pareto pada pemodelan distribusi pendapatan.
2. Mengestimasi parameter distribusi Pareto dengan Metode Kemungkinan Maksimum dan Metode Momen.
3. Membandingkan kedua metode tersebut untuk menentukan metode terbaik dalam mengestimasi parameter distribusi Pareto.
E. Manfaat Penulisan
Manfaat dari penulisan tugas akhir ini adalah dapat mempelajari sifat-sifat distribusi Pareto dan metode pendugaan distribusi Pareto dengan dua parameter serta menentukan metode terbaik dalam menduga parameter distribusi Pareto dengan dua parameter.
F. Metode Penulisan
Metode yang digunakan penulis dalam penyusunan tugas akhir adalah metode studi pustaka, yaitu dengan membaca dan mempelajari buku-buku atau jurnal-jurnal yang berkaitan dengan distribusi Pareto dan cara menduga parameter distribusi Pareto.
G. Sistematika Penulisan
Penulisan skripsi ini disusun dengan sistematika penulisan sebagai berikut:
BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan
BAB II LANDASAN TEORI A. Teori Peluang
B. Distribusi Peluang
C. Keluarga Distribusi Eksponensial
D. Distribusi Fungsi dari Fungsi Variabel Acak E. Statistik Terurut (Order Statistics)
F. Teorema Limit Pusat
G. Estimasi Parameter Fungsi Distribusi
H. Bias dan Rata-Rata Galat Kuadrat dari Penduga Titik
BAB III DISTRIBUSI PARETO A. Sejarah Distribusi Pareto B. Model Distribusi Pareto
C. Estimasi Parameter Distribusi Pareto
D. Distribusi Pareto Sebagai Anggota Keluarga Distribusi Eksponensial E. Parameter Tunggal pada Distribusi Pareto
G. Uji Kolmogorov-Smirnov
H. Uji Distribusi Pareto Menggunakan Uji Kolmogorov-Smirnov I. Kriteria Statistis pada Penduga Fungsi Distribusi Kumulatif Pareto
BAB IV PENERAPAN DISTRIBUSI PARETO A. Data dan Sumbernya
B. Estimasi Model Distribusi Pareto
C. Uji Kecocokan Penduga Parameter Distribusi Pareto
D. Perbandingan Metode Kemungkinan Maksimum dan Metode Momen
BAB V PENUTUP A. Kesimpulan B. Saran
DAFTAR PUSTAKA LAMPIRAN
6 BAB II
LANDASAN TEORI
A. Teori Peluang Definisi 2.1
Misalkan 𝑆 adalah ruang sampel yang terkait dengan suatu percobaan. Untuk setiap kejadian 𝐴 dalam 𝑆, dilambangkan dengan 𝑃(𝐴) disebut peluang dari 𝐴 yang memenuhi aksioma-aksioma sebagai berikut :
Aksioma 1 : 𝑃(𝐴) ≥ 0. Aksioma 2 : 𝑃(𝑆) = 1.
Aksioma 3 : Jika 𝐴1, 𝐴2, 𝐴3, … membentuk urutan berpasangan kejadian saling asing dalam 𝑆, maka 𝑃(𝐴1∪ 𝐴2∪ 𝐴3∪ … ) = ∑∞𝑖=1𝑃(𝐴𝑖) .
Definisi 2.2
Peluang bersyarat dari kejadian 𝐴 jika diketahui kejadian 𝐵 terjadi adalah : 𝑃(𝐴|𝐵) =𝑃(𝐴 ∩ 𝐵)
𝑃(𝐵)
dengan 𝑃(𝐵) > 0. Lambang 𝑃(𝐴|𝐵) dibaca “peluang bersyarat dari 𝐴 jika diketahui kejadian 𝐵 .
Definisi 2.3
Dua kejadian yaitu 𝐴 dan 𝐵 bersifat saling bebas jika memenuhi sifat sebagai berikut :
𝑃(𝐴|𝐵) = 𝑃(𝐴), 𝑃(𝐵|𝐴) = 𝑃(𝐵), 𝑃(𝐴 ∩ 𝐵) = 𝑃(𝐴)𝑃(𝐵).
Teorema 2.1
Peluang dari gabungan dua kejadian 𝐴 dan 𝐵 adalah 𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵)
Bukti :
Ingat bahwa 𝐴 ∪ 𝐵 = 𝐴 ∪ (𝐴 ̅ ∩ 𝐵) dimana 𝐴 dan (𝐴 ̅ ∩ 𝐵) saling asing. Selanjutnya, 𝐵 = (𝐴 ̅ ∩ 𝐵) ∪ (𝐴 ∩ 𝐵) dimana (𝐴 ̅ ∩ 𝐵) dan (𝐴 ∩ 𝐵) juga saling asing. Dengan aksioma ke-3 didapat :
𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐴 ̅ ∩ 𝐵) dan
𝑃(𝐵) = 𝑃(𝐴 ̅ ∩ 𝐵) + 𝑃(𝐴 ∩ 𝐵) 𝑃(𝐴 ̅ ∩ 𝐵) = 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵)
Kemudian substitusi 𝑃(𝐴 ̅ ∩ 𝐵) ke dalam persamaan 𝑃(𝐴 ∪ 𝐵), sehingga didapat
𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵) Jadi, terbukti bahwa 𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵) .
Teorema 2.2
Jika 𝐴 adalah suatu kejadian dan 𝐴̅ adalah komplemen kejadian 𝐴, maka 𝑃(𝐴) = 1 − 𝑃(𝐴̅).
Bukti :
Diketahui bahwa himpunan semesta 𝑆 = 𝐴 ∪ 𝐴̅. Karena 𝐴 dan 𝐴̅ saling asing, maka 𝑃(𝑆) = 𝑃(𝐴) + 𝑃(𝐴̅). Jadi berdasarkan definisi 2.1 didapat 1 = 𝑃(𝐴) + 𝑃(𝐴̅) atau 𝑃(𝐴) = 1 − 𝑃(𝐴̅).
B. Distribusi Peluang 1. Distribusi Peluang Diskrit
Definisi 2.4
Variabel acak adalah fungsi bernilai real yang domainnya merupakan suatu ruang sampel .
Definisi 2.5
Variabel acak 𝑋 bersifat diskrit jika himpunan nilai-nilainya berhingga atau tak berhingga terbilang .
Definisi 2.6
Peluang untuk 𝑋 yang bernilai 𝑥, yaitu 𝑃(𝑋 = 𝑥) didefinisikan sebagai jumlah peluang dari semua titik sampel dalam 𝑆 yang memberikan nilai 𝑥. Lambang 𝑃(𝑋 = 𝑥) juga dapat ditulis sebagai 𝑝(𝑥) .
Definisi 2.7
Setiap distribusi peluang diskrit memenuhi sifat sebagai berikut : a. 0 ≤ 𝑝(𝑥) ≤ 1 untuk semua 𝑥
b. ∑𝑥𝑝(𝑥) = 1
Definisi 2.8
Distribusi kumulatif 𝐹(𝑥) dari suatu variabel acak diskrit 𝑋 dengan distribusi peluang 𝑓(𝑥) dinyatakan oleh :
𝐹(𝑥) = 𝑝(𝑋 ≤ 𝑥) = ∑ 𝑓(𝑡) ,
𝑡≤𝑥 − ∞ < 𝑥 < ∞ .
Contoh-contoh distribusi peluang diskrit adalah distribusi Binomial, distribusi Geometrik, distribusi Binomial Negatif, distribusi Hipergeometrik, dan distribusi Poisson. Selanjutnya akan dibahas mengenai distribusi Binomial dan distribusi Poisson.
Definisi 2.9
Eksperimen Binomial memiliki sifat sebagai berikut : a. Eksperimen terdiri dari 𝑛 ulangan yang identik.
b. Setiap ulangan menghasilkan satu dari dua hasil, yaitu sukses (S) atau gagal (F).
c. Peluang sukses untuk sebuah ulangan adalah 𝑝 dan tetap sama untuk setiap ulangan lainnya. Peluang gagal pada ulangan tersebut adalah 𝑞 = (1 − 𝑝).
d. Setiap ulangan bersifat saling bebas.
e. Variabel acak 𝑋 adalah banyaknya sukses yang terjadi selama 𝑛 ulangan.
Definisi 2.10
Variabel acak 𝑋 dikatakan berdistribusi binomial dengan 𝑛 ulangan dan peluang sukses 𝑝 jika dan hanya jika fungsi peluangnya
𝑝(𝑥) = (𝑛
𝑥) 𝑝𝑥𝑞𝑛−𝑥, 𝑥 = 0,1,2, … , 𝑛 𝑑𝑎𝑛 0 ≤ 𝑝 ≤ 1.
Contoh 2.1
Sebuah percobaan dari suatu perusahaan obat menunjukan bahwa 30% orang yang terkena suatu penyakit dapat disembuhkan dari obat yang dibuat oleh perusahaan tersebut. Perusahaan obat ini akan mengembangkan suatu metode pengobatan yang baru. Dipilih 10 orang yang terkena penyakit untuk menjalani metode pengobatan baru tersebut dengan hasil 9 orang sembuh dari penyakit. Tentukan peluang bahwa terdapat minimal 9 dari 10 orang yang mengambil metode pengobatan tersebut akan sembuh !
Jawab :
Dimisalkan 𝑋 adalah banyaknya orang yang sembuh. maka peluang satu orang yang terkena penyakit akan sembuh dari obat yang dibuat perusahaan adalah 𝑝 = 0,3. Dengan jumlah percobaan yaitu 𝑛 = 10, peluang bahwa tepat 9 orang sembuh adalah
𝑃(𝑋 = 9) = 𝑃(9) = (10
9) 0,390,7 = 0,000138. Selanjutnya dihitung peluang bahwa tepat 10 orang sembuh, yaitu
𝑃(𝑋 = 10) = 𝑃(10) = (10
10) 0,3100,70 = 0,000006.
Jadi peluang bahwa terdapat minimal 9 dari 10 orang sembuh dari pengobatan adalah
𝑃(𝑋 ≥ 9) = 𝑃(9) + 𝑃(10) = 0,000138 + 0,000006 = 0,00144. Definisi 2.11
Variabel acak 𝑋 dikatakan berdistribusi Poisson jika dan hanya jika fungsi peluangnya
𝑝(𝑥) =𝜆 𝑥
𝑥!𝑒−𝜆, 𝑥 = 0,1,2, … 𝑑𝑎𝑛 𝜆 > 0
Contoh 2.2
Diketahui sistem acak dari patroli polisi sudah direncanakan sedemikan hingga petugas patroli berkemungkinan mengunjungi lokasi yang ditentukan sebanyak 𝑋 = 0,1,2,3, … kali dalam periode setengah jam dengan setiap lokasi dikunjungi dengan rata-rata sekali untuk setiap periode. Asumsikan bahwa 𝑋 diaproksimasikan berdistribusi Poisson. Tentukan peluang petugas patrol tersebut tidak mengunjungi lokasi yang ditentukan dalam periode setengah jam. Berapa peluang bahwa lokasi tersebut dikunjungi dua kali ?
Jawab :
Untuk contoh diatas, waktu periodenya adalah setengah jam dan rata-rata jumlah kunjungan untuk setiap interval setengah jam adalah 𝜆 = 1. Dengan asumsi bahwa 𝑋 diaproksimasikan berdistribusi Poisson, didapat
𝑝(𝑥) =1 𝑥 𝑥! 𝑒−1 =
𝑒−1
𝑥! , 𝑥 = 0,1,2, …
Kejadian bahwa lokasi yang ditentukan tidak dikunjungi dalam periode setengah jam dapat dikorrespondensikan dengan (𝑋 = 0), sehingga
𝑃(𝑋 = 0) = 𝑃(0) =𝑒 −1
0! = 𝑒−1= 0,368. Peluang lokasi tersebut dikunjungi dua kali adalah
𝑝(2) =𝑒 −1
2! = 0,184. 2. Distribusi Peluang Kontinu
Definisi 2.12
Diketahui 𝑋 adalah suatu Variabel acak. Fungsi distribusi dari 𝑋 dinotasikan dengan 𝐹(𝑥), dengan 𝐹(𝑥) = 𝑃(𝑋 ≤ 𝑥) untuk −∞ < 𝑥 < ∞ .
Definisi 2.13
Variabel acak 𝑋 dengan fungsi distribusi 𝐹(𝑥) dikatakan kontinu jika 𝐹(𝑥) kontinu untuk −∞ < 𝑥 < ∞ .
Definisi 2.14
Jika diketahui 𝐹(𝑥) adalah fungsi distribusi dengan variabel acak kontinu 𝑋, maka fungsi peluang dari 𝑥 dapat didefinisikan sebagai :
𝑓(𝑥) =𝑑𝐹(𝑥)
𝑑𝑥 = 𝐹′(𝑥)
Dari Definisi 2.13 dan 2.14, 𝐹(𝑥) dapat didefinisikan sebagai : 𝐹(𝑥) = ∫ 𝑓(𝑡) 𝑑𝑡𝑥
−∞ Definisi 2.15
Fungsi 𝑓(𝑥) adalah fungsi peluang dengan peubah acak kontinu 𝑋, jika memenuhi:
a. 𝑓(𝑥) ≥ 0, ∀𝑥 ∈ ℝ. b. ∫ 𝑓(𝑥) 𝑑𝑥 = 1−∞∞ .
Teorema 2.3
Jika variabel acak kontinu 𝑋 memiliki fungsi peluang 𝑓(𝑥) dan 𝑎 < 𝑏, maka peluang bahwa 𝑋 berada pada interval [𝑎, 𝑏] adalah
𝑃(𝑎 ≤ 𝑋 ≤ 𝑏) = ∫ 𝑓(𝑥) 𝑑𝑥.𝑏 𝑎
Bukti :
Jika 𝑋 adalah variabel acak kontinu dan 𝑎 dan 𝑏 adalah suatu konstanta dengan 𝑎 < 𝑏, maka 𝑃(𝑋 = 𝑎) = 0 dan 𝑃(𝑋 = 𝑏) = 0, sehingga didapat
𝑃(𝑎 < 𝑋 < 𝑏) = 𝑃(𝑎 ≤ 𝑋 < 𝑏) = 𝑃(𝑎 < 𝑋 ≤ 𝑏)
= 𝑃(𝑎 ≤ 𝑋 ≤ 𝑏) = ∫ 𝑓(𝑥) 𝑑𝑥. 𝑏
𝑎
Jadi, terbukti bahwa 𝑃(𝑎 ≤ 𝑋 ≤ 𝑏) = ∫ 𝑓(𝑥) 𝑑𝑥.𝑎𝑏
Definisi 2.16
Parameter dalam fungsi peluang adalah suatu konstanta yang menentukan bentuk spesifik dari fungsi peluang.
Contoh-contoh distribusi peluang kontinu adalah distribusi Normal, distribusi Gamma, distribusi Eksponensial, distribusi Uniform, dan distribusi Beta. Selanjutnya akan dibahas mengenai distribusi Uniform, distribusi Normal, dan distribusi Eksponensial.
Definisi 2.17
Jika 𝜃1 < 𝜃2, maka variabel acak 𝑋 dikatakan berdistribusi uniform secara kontinu pada interval (𝜃1, 𝜃2) jika dan hanya jika fungsi peluang dari 𝑋 adalah 𝑓(𝑥) = { 1 𝜃2 − 𝜃1, 𝜃1 ≤ 𝑥 ≤ 𝜃2 0, 𝑠𝑒𝑙𝑎𝑖𝑛𝑛𝑦𝑎 Contoh 2.3
Siklus waktu pada truk pengangkut beton yang mengunjungi lokasi pembangunan jalan raya berdistribusi uniform dengan interval 50 sampai 70 menit. Berapa peluang bahwa truk akan tiba dalam 5 menit terakhir dari siklus waktu yang ada.
Jawab :
Waktu kedatangan truk ke lokasi pembangunan jalan berdistribusi uniform dengan interval (50,70). Jika 𝑋 dinotasikan sebagai waktu kedatangan, maka peluang truk akan tiba dalam 5 menit terakhir dari interval di atas adalah : 𝑃(65 ≤ 𝑋 ≤ 70) = ∫ 1 70 − 50 70 65 𝑑𝑦 = 70 − 65 20 = 5 20= 1 4 .
Jadi peluang kedatangan truk ke lokasi pembangunan jalan dalam waktu 65 sampai 70 menit (5 menit terakhir dari siklus waktu) adalah 14 .
Definisi 2.18
Variabel acak 𝑋 dikatakan berdistribusi Normal jika dan hanya jika untuk 𝜎 > 0 dan −∞ < 𝜇 < ∞, fungsi peluang dari 𝑋 adalah
𝑓(𝑥) = 1 𝜎√2𝜋𝑒
− (𝑥−𝜇)2𝜎22 , −∞ < 𝑥 < ∞.
Definisi 2.19
Variabel acak 𝑋 dikatakan berdistribusi Eksponensial dengan parameter 𝛽 > 0 jika dan hanya jika fungsi peluang dari 𝑋 adalah
𝑓(𝑥) = { 1 𝛽 𝑒 −𝛽𝑥 , 0 ≤ 𝑥 < ∞ 0, 𝑠𝑒𝑙𝑎𝑖𝑛𝑛𝑦𝑎
Jika dimisalkan parameter 𝛽 =1𝜆 , maka bentuk lain dari fungsi peluang 𝑋 yang berdistribusi Eksponensial adalah :
𝑓(𝑥) = {𝜆𝑒
−𝜆𝑥 , 0 ≤ 𝑥 < ∞ 0, 𝑠𝑒𝑙𝑎𝑖𝑛𝑛𝑦𝑎 Teorema 2.4
Fungsi distribusi kumulatif Eksponensial dengan variabel acak 𝑋 dan parameter 𝛽 =1𝜆 adalah :
𝐹(𝑥) = {1 − 𝑒
−𝜆𝑥 , 0 ≤ 𝑥 < ∞ 0, 𝑠𝑒𝑙𝑎𝑖𝑛𝑛𝑦𝑎 Bukti :
Untuk 𝑥 ≥ 0, berlaku fungsi peluang Eksponensial, yaitu : 𝑓(𝑥) = 𝜆𝑒−𝜆𝑥
Dicari fungsi distribusi kumulatif Eksponensial 𝐹(𝑥) untuk 𝑥 ≥ 0 dengan perhitungan sebagai berikut :
𝐹(𝑥) = ∫ 𝑓(𝑡) 𝑑𝑡 𝑥 −∞ = ∫ 𝜆𝑒𝑥 −𝜆𝑡 𝑑𝑡 0 = 𝜆 ∫ 𝑒𝑥 −𝜆𝑡 𝑑𝑡 0
Misalkan −𝜆𝑡 = 𝑢, maka didapat 𝑑𝑢 𝑑𝑡 = −𝜆 𝑑𝑡 = −1 𝜆 𝑑𝑢 Jadi, 𝜆 ∫ 𝑒−𝜆𝑡 𝑑𝑡 = 𝜆 (−1 𝜆) ∫ 𝑒𝑢 𝑑𝑢 = −[𝑒𝑢] = −𝑒𝜆𝑡 Sehingga, 𝜆 ∫ 𝑒𝑥 −𝜆𝑡 𝑑𝑡 0 = [−𝑒𝜆𝑡] 0 𝑥 = [−𝑒𝜆𝑥− (−1)] 𝐹(𝑥) = 1 − 𝑒−𝜆𝑥, 𝑥 ≥ 0
Jadi fungsi distribusi kumulatif Eksponensial untuk 𝑥 ≥ 0 adalah 𝐹(𝑥) = 1 − 𝑒−𝜆𝑥.
3. Nilai harapan Definisi 2.20
Misalkan 𝑋 adalah variabel acak. Nilai harapan dari 𝑋 dilambangkan dengan 𝐸(𝑋) yang didefinisikan sebagai berikut :
𝐸(𝑋) = {
∑ 𝑥 𝑝(𝑥) 𝑥
, jika X adalah variabel acak diskrit ∫ 𝑥 𝑓(𝑥) 𝑑𝑥,
∞
−∞
jika X adalah variabel acak kontinu Teorema 2.5
Jika 𝑋 adalah variabel acak dan 𝑔(𝑋) adalah fungsi yang bernilai real dari 𝑋, maka nilai harapan dari 𝑔(𝑋) adalah sebagai berikut :
𝐸[𝑔(𝑋)] = {
∑ 𝑔(𝑥)𝑝(𝑥) 𝑥
, jika X adalah variabel acak diskrit ∫ 𝑔(𝑥) 𝑓(𝑥) 𝑑𝑥,∞
−∞
jika X adalah variabel acak kontinu
Bukti :
Akan dibuktikan bahwa 𝐸[𝑔(𝑋)] = ∑ 𝑔(𝑥)𝑝(𝑥)𝑥 pada kasus dengan nilai variabel acak diskrit 𝑋 berhingga yaitu 𝑥1, 𝑥2, … , 𝑥𝑛. Karena fungsi 𝑔(𝑥) mungkin bukan fungsi satu-satu, diasumsikan bahwa 𝑔(𝑋) mengambil nilai 𝑔1, 𝑔2, … , 𝑔𝑚 (dimana 𝑚 ≤ 𝑛). Hal ini berarti 𝑔(𝑋) adalah variabel acak sedemikian hingga untuk 𝑖 = 1,2, … , 𝑚,
𝑃[𝑔(𝑋) = 𝑔𝑖] = ∑ 𝑝(𝑥𝑗 ∀𝑥𝑗
) = 𝑝∗(𝑔 𝑖)
Sehingga berdasarkan definisi 2.20
𝐸[𝑔(𝑋)] = ∑ 𝑔𝑖𝑝∗(𝑔 𝑖) 𝑚
= ∑ 𝑔𝑖 𝑛 𝑖=1 {∑ 𝑝(𝑥𝑗) ∀𝑥𝑗 } = ∑ ∑ 𝑔𝑖 ∀𝑥𝑗 𝑚 𝑖=1 𝑝(𝑥𝑗) = ∑ 𝑔(𝑥𝑗)𝑝(𝑥𝑗) 𝑛 𝑗=1 .
Jadi, terbukti bahwa 𝐸[𝑔(𝑋)] = ∑ 𝑔(𝑥)𝑝(𝑥)𝑥 .
Untuk kasus 𝐸[𝑔(𝑋)] = ∫ 𝑔(𝑥) 𝑓(𝑥) 𝑑𝑥−∞∞ dapat dibuktikan secara analog. Teorema 2.6
Jika 𝑋 adalah variabel acak dan 𝑐 adalah suatu konstanta, maka 𝐸(𝑐) = 𝑐 . Bukti :
Kasus 1 : untuk 𝑋 variabel acak diskrit 𝐸(𝑐) = ∑ 𝑐𝑝(𝑥) =
𝑥
𝑐 ∑ 𝑝(𝑥) = 𝑐(1) = 𝑐 𝑥
Kasus 2 : untuk 𝑋 variabel acak kontinu
𝐸(𝑐) = ∫ 𝑐𝑓(𝑥) 𝑑𝑥 = 𝑐 ∫ 𝑓(𝑥) 𝑑𝑥 ∞ −∞ ∞ −∞ = 𝑐(1) = 𝑐 Jadi , terbukti bahwa 𝐸(𝑐) = 𝑐
Teorema 2.7
Jika diketahui 𝑋 adalah variabel acak dan 𝑐 adalah suatu konstanta, maka berlaku 𝐸[𝑐𝑋] = 𝑐𝐸[𝑋] .
Bukti :
𝐸[𝑐𝑋] = ∑ 𝑐𝑥𝑝(𝑥) = 𝑐 ∑ 𝑥𝑝(𝑥) = 𝑐𝐸[𝑋]. 𝑥
𝑥
Kasus 2 : untuk 𝑋 variabel acak kontinu 𝐸[𝑐𝑋] = ∫ 𝑐𝑥𝑓(𝑥)𝑑𝑥∞
−∞
= 𝑐 ∫ 𝑥𝑓(𝑥) 𝑑𝑥 = 𝑐𝐸[𝑋].∞ −∞
Jadi, terbukti bahwa 𝐸[𝑐𝑋] = 𝑐𝐸[𝑋].
Teorema 2.8
Jika diketahui 𝑋 adalah variabel acak diskrit dengan fungsi peluang 𝑝(𝑥) dan 𝑔1(𝑋), 𝑔2(𝑋), … , 𝑔𝑘(𝑋) adalah 𝑘 fungsi dari 𝑋, maka berlaku :
𝐸[(𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)] = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)] + ⋯ + 𝐸[𝑔𝑘(𝑋)] Bukti : 𝐸[(𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)] = ∑[𝑔1(𝑥) + 𝑔2(𝑥) + ⋯ + 𝑔𝑘(𝑥)]𝑝(𝑥) 𝑥 = ∑[𝑔1(𝑋)𝑝(𝑥) + 𝑔2(𝑥)𝑝(𝑥) + ⋯ + 𝑔𝑘(𝑥)𝑝(𝑥)] 𝑥 = ∑ 𝑔1(𝑥)𝑝(𝑥) 𝑥 + ∑ 𝑔2(𝑥)𝑝(𝑥) 𝑥 + ⋯ + ∑ 𝑔𝑘(𝑥)𝑝(𝑥 𝑥 ) = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)] + ⋯ + 𝐸[𝑔𝑘(𝑋)]
Jadi terbukti bahwa untuk 𝑋 adalah variabel acak diskrit dengan fungsi peluang 𝑝(𝑥) dan 𝑔1(𝑋), 𝑔2(𝑋), … , 𝑔𝑘(𝑋) adalah 𝑘 fungsi dari 𝑋 berlaku 𝐸[(𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)] = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)] + ⋯ + 𝐸[𝑔𝑘(𝑋)]
Teorema 2.9
Jika 𝑋 adalah variabel acak kontinu dengan fungsi densitas 𝑓(𝑥) dan 𝑔1(𝑋), 𝑔2(𝑋), … , 𝑔𝑘(𝑋) adalah 𝑘 fungsi dari 𝑋, maka
𝐸[(𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)] = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)] + ⋯ + 𝐸[𝑔𝑘(𝑋)] Bukti : 𝐸[(𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)] = ∫ [𝑔∞ 1(𝑥) + 𝑔2(𝑥) + ⋯ + 𝑔𝑘(𝑥)]𝑓(𝑥)𝑑𝑥 −∞ = ∫ [𝑔∞ 1(𝑥)𝑓(𝑥) + 𝑔2(𝑥)𝑓(𝑥) + ⋯ + 𝑔𝑘(𝑥)𝑓(𝑥)]𝑑𝑥 −∞ = ∫ 𝑔1(𝑥)𝑓(𝑥)𝑑𝑥 ∞ −∞ + ∫ 𝑔2(𝑥)𝑓(𝑥)𝑑𝑥 ∞ −∞ + ⋯ + ∫ 𝑔𝑘(𝑥)𝑓(𝑥)𝑑𝑥 ∞ −∞ = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)] + ⋯ + 𝐸[𝑔𝑘(𝑋)]
Jadi terbukti bahwa untuk 𝑋 adalah variabel acak kontinu dengan fungsi densitas 𝑓(𝑥) dan 𝑔1(𝑋), 𝑔2(𝑋), … , 𝑔𝑘(𝑋) adalah 𝑘 fungsi dari 𝑋 berlaku 𝐸[(𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)] = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)] + ⋯ + 𝐸[𝑔𝑘(𝑋)]
4. Variansi Definisi 2.21
Jika 𝑋 adalah variabel acak dengan rata-rata (𝑋) = 𝜇 , maka variansi dari variabel acak 𝑋 adalah nilai harapan dari (𝑋 − 𝜇)2 atau dapat ditulis :
𝑉(𝑋) = 𝐸[(𝑋 − 𝜇)2].
Nilai standar deviasi dari 𝑋 adalah akar kuadrat positif dari 𝑉(𝑋) atau dapat ditulis
Teorema 2.10
Jika 𝑋 adalah variabel acak dengan fungsi peluang 𝑝(𝑥) dan rata-rata 𝐸(𝑋) = 𝜇, maka 𝑉(𝑋) = 𝜎2 = 𝐸[(𝑋 − 𝜇)2] = 𝐸(𝑋2) − 𝜇2. Bukti : 𝑉(𝑋) = 𝜎2 = 𝐸[(𝑋 − 𝜇)2] = 𝐸[𝑋2− 2𝜇𝑋 + 𝜇2] = 𝐸[𝑋2] − 𝐸[2𝜇𝑋] + 𝐸[𝜇2] = 𝐸[𝑋2] − 2𝜇𝐸[𝑋] + 𝐸[𝜇2] = 𝐸[𝑋2] − 2𝜇2+ 𝜇2 = 𝐸[𝑋2] − 𝜇2.
Jadi, terbukti bahwa 𝑉(𝑋) = 𝜎2 = 𝐸[(𝑋 − 𝜇)2] = 𝐸(𝑋2) − 𝜇2
5. Momen dan Fungsi Pembangkit Momen Definisi 2.22
Momen ke-𝑘 dari variabel acak 𝑋 di sekitar titik asal adalah 𝐸(𝑋𝑘) = 𝜇′ 𝑘.
Definisi 2.23
Fungsi pembangkit momen 𝑚(𝑡) untuk variabel acak 𝑋 adalah 𝑚(𝑡) = 𝐸(𝑒𝑡𝑋). Fungsi pembangkit momen untuk 𝑋 dikatakan ada jika ada sebuah konstanta positif 𝑎 sedemikian hingga 𝑚(𝑡) berhingga untuk |𝑡| < 𝑎.
Teorema 2.11
Jika 𝑚(𝑡) ada, maka untuk sebarang bilangan positif 𝑘, 𝑑𝑘𝑚(𝑡) 𝑑𝑡𝑘 ] 𝑡=0 = 𝑚(𝑘)(0) = 𝜇′ 𝑘. Bukti : 𝑑𝑘𝑚(𝑡)
𝑑𝑡𝑘 atau 𝑚(𝑘)(𝑡) adalah turunan ke-𝑘 dari 𝑚(𝑡) terhadap 𝑡. Karena
𝑚(𝑡) = 𝐸(𝑒𝑡𝑋) = 1 + 𝑡𝜇′ 1+ 𝑡2 2!𝜇′2+ 𝑡3 3!𝜇′3 + ⋯, sehingga
𝑚(1)(𝑡) = 𝜇′1+ 2𝑡 2!𝜇′2+ 3𝑡2 3! 𝜇′3 + ⋯ 𝑚(2)(𝑡) = 𝜇′ 2+ 2𝑡 2!𝜇′3+ ⋯ Secara umum, 𝑚(𝑘)(𝑡) = 𝜇′ 𝑘+ 2𝑡 2!𝜇′𝑘+1+ 3𝑡2 3! 𝜇′𝑘+2+ ⋯
Ketika 𝑡 = 0, didapat 𝑚(1)(𝑡) = 𝜇′1 dan 𝑚(2)(𝑡) = 𝜇′2, sehingga secara umum
𝑚(𝑘)(𝑡) = 𝜇′ 𝑘 Jadi, terbukti bahwa
𝑑𝑘𝑚(𝑡) 𝑑𝑡𝑘 ]
𝑡=0
= 𝑚(𝑘)(0) = 𝜇′𝑘. Contoh 2.4
Tentukan fungsi pembangkit momen dari distribusi Binomial. Jawab : 𝑚(𝑡) = 𝐸(𝑒𝑡𝑋) = ∑ 𝑒𝑡𝑥𝑝(𝑥) 𝑛 𝑥=0 = ∑ 𝑒𝑡𝑥(𝑛 𝑥) 𝑛 𝑥=0 𝑝𝑥𝑞𝑛−𝑥 = ∑(𝑝𝑒𝑡)𝑥𝑞𝑛−𝑥(𝑛 𝑥) 𝑛 𝑥=0 = (𝑛 0) 𝑞𝑛+ ( 𝑛 1) 𝑝𝑒𝑡𝑞𝑛−1+ ( 𝑛 2) (𝑝𝑒𝑡)2𝑞𝑛−2+ ⋯ + ( 𝑛 𝑛) (𝑝𝑒𝑡)𝑛 = (𝑝𝑒𝑡+ 𝑞)𝑛 Ingat bahwa (𝑞 + 𝑝)𝑛 = (𝑛 0) 𝑞𝑛 + ( 𝑛 1) 𝑝𝑞𝑛−1+ ( 𝑛 2) 𝑝2𝑞𝑛−2+ ⋯ + ( 𝑛 𝑛) 𝑝𝑛 Jadi fungsi pembangkit momen dari distribusi Binomial adalah 𝑚(𝑡) = (𝑝𝑒𝑡+ 𝑞)𝑛 .
Contoh 2.5
Tentukan fungsi pembangkit momen dari distribusi Normal. Jawab : 𝑚(𝑡) = 𝐸(𝑒𝑡𝑋) = ∫ 1 𝜎√2𝜋𝑒 𝑡𝑥𝑒− (𝑥−𝜇) 2 2𝜎2 𝑑𝑥 ∞ −∞
Misalkan 𝑢 = 𝑥 − 𝜇 , maka 𝑥 = 𝑢 + 𝜇 dan 𝑑𝑢 = 𝑑𝑥. Sehingga diperoleh 𝑚(𝑡) = ∫ 1 𝜎√2𝜋 𝑒 𝑡𝑢+𝜇𝑡𝑒−𝑢 2 2𝜎2 𝑑𝑢 ∞ −∞ = 𝑒𝜇𝑡 ∫ 1 𝜎√2𝜋 𝑒 𝑡𝑢−2𝜎𝑢22 𝑑𝑢 ∞ −∞ = 𝑒𝜇𝑡 ∫ 1 𝜎√2𝜋 𝑒 2𝜎2𝑡𝑢−𝑢2 2𝜎2 𝑑𝑢 ∞ −∞ = 𝑒𝜇𝑡 ∫ 1 𝜎√2𝜋 𝑒 𝑢2−2𝜎2𝑡𝑢 −2𝜎2 𝑑𝑢 . ∞ −∞ Karena (𝑢 − 𝑡𝜎2)2 = 𝑢2− 2𝜎2𝑡𝑢 + 𝑡2𝜎4, maka = 𝑒𝜇𝑡 ∫ 1 𝜎√2𝜋 𝑒 (𝑢−𝑡𝜎2)2−𝑡2𝜎4 −2𝜎2 𝑑𝑢 ∞ −∞ = 𝑒𝜇𝑡𝑒𝑡 2𝜎4 2𝜎2 ∫ 1 𝜎√2𝜋 𝑒 (𝑢−𝑡𝜎2)2 −2𝜎2 𝑑𝑢 ∞ −∞ = 𝑒𝜇𝑡+𝑡 2𝜎2 2 ∫ 1 𝜎√2𝜋 𝑒 (𝑥−𝜇−𝑡𝜎2)2 −2𝜎2 𝑑𝑥 ∞ −∞ Karena ∫ 𝜎√2𝜋1 𝑒(𝑥−𝜇−𝑡𝜎2) 2 −2𝜎2 𝑑𝑥 ∞ −∞ = 1 , maka 𝑚(𝑡) = 𝑒𝜇𝑡+𝑡 2𝜎2 2 .
C. Keluarga Distribusi Eksponensial Definisi 2.24
Keluarga distribusi dalam ruang Euclidean dikatakan tergolong dalam keluarga Eksponensial jika fungsi peluangnya berbentuk :
𝑝Ѳ(𝑥) = 𝐶(𝜃) 𝑒𝑥𝑝 [∑ 𝑄𝑖(𝜃)𝑡𝑖(𝑥) 𝑘
𝑖=1
] ℎ(𝑥), dengan 𝜃 adalah parameter dan fungsi 𝑄 dan 𝑡𝑖 bernilai real.
Contoh 2.6
Diketahui 𝑥 = (𝑥1, 𝑥2, … , 𝑥𝑛) adalah sampel acak dari distribusi Normal 𝑁(𝜇, 𝜎2). Buktikan bahwa distribusi Normal tergolong dalam keluarga eksponensial !
Jawab :
Jadi untuk 𝜃 = (𝜇, 𝜎2) didapat : 𝑝Ѳ(𝑥) = 1 (2𝜋)𝑛𝜎𝑛 exp [− 1 2𝜎2∑(𝑥𝑖 − 𝜇)2 𝑛 𝑖=1 ] = 1 (2𝜋)𝑛𝜎𝑛exp [− 1 2𝜎2(∑ 𝑥𝑖2 − 2𝜇 𝑛 𝑖=1 ∑ 𝑥𝑖− 𝑛𝜇2 𝑛 𝑖=1 )] =𝑒𝑥𝑝 ( 𝑛𝜇2 2𝜎2) (2𝜋)12𝑛𝜎𝑛 exp [−∑ 𝑥𝑖 2 𝑛 𝑖=1 2𝜎2 + 𝜇 𝜎2∑ 𝑥𝑖 𝑛 𝑖=1 ] = 𝐶(Ѳ) exp{𝑄1(𝜃)𝑡1(𝑥) + 𝑄2(𝜃)𝑡2(𝑥)}, dimana 𝐶(Ѳ) = (2𝜋)−12𝑛𝜎−𝑛𝑒𝑥𝑝 [𝑛𝜇 2 2𝜎2] 𝑄1(𝜃) = − 1 2𝜎2 𝑡1(𝑥) = ∑ 𝑥𝑖2 𝑛 𝑖=1 𝑄2(𝜃) = 𝜇 𝜎2
𝑡2(𝑥) = ∑ 𝑥𝑖 𝑛
𝑖=1
Jadi berdasarkan definisi 2.24, distribusi Normal tergolong dalam keluarga eksponensial (Silvey, 1975).
Distribusi peluang yang termasuk dalam keluarga ekponensial adalah distribusi binomial, distribusi Normal, distribusi geometrik, distribusi eksponensial, dan distribusi Poisson (Silvey, 1975).
D. Distribusi Fungsi dari Fungsi Variabel Acak
Materi sebelumnya membahas tentang distribusi peluang, baik yang bersifat diskret maupun yang bersifat kontinu. Distribusi tesebut banyak digunakan dalam berbagai bidang, termasuk keandalan (reliabilitas), pengendali mutu, dan teknik penarikan sampel. Selanjutnya, akan dibahas topik yang lebih umum, yaitu distribusi fungsi dari fungsi variabel acak. Dalam metode statistik standar, hasil pengujian hipotesis statistik, pendugaan (estimasi), atau bahkan grafik statistik tidak melibatkan variabel acak tunggal melainkan suatu fungsi dari satu atau lebih variabel acak. Akibatnya, inferensi dalam statistik memerlukan distribusi fungsi yang ada. Sehingga penentuan distribusi fungsi sangat penting dalam berbagai bidang statistik yang ada (Walpole et al, 2012).
Berikut akan dibahas metode beserta langkah-langkahnya untuk menentukan distribusi fungsi untuk fungsi variabel acak, yaitu metode distribusi fungsi dan metode tranformasi.
1. Metode Distribusi Fungsi
Diketahui fungsi 𝑈 dengan variabel acak 𝑋1, 𝑋2, … , 𝑋𝑛. a. Tentukan daerah 𝑈 = 𝑢 pada ruang (𝑥1, 𝑥2, … , 𝑥𝑛). b. Tentukan daerah 𝑈 ≤ 𝑢.
c. Tentukan 𝐹𝑈(𝑢) = 𝑃(𝑈 ≤ 𝑢) dengan mengintegrasikan 𝑓(𝑥1, 𝑥2, … , 𝑥𝑛) pada daerah 𝑈 ≤ 𝑢.
d. Tentukan fungsi peluang 𝑓𝑈(𝑢) dengan mencari turunan dari 𝐹𝑈(𝑢), yaitu
𝑓𝑈(𝑢) =
𝑑𝐹𝑈(𝑢) 𝑑𝑢
Contoh 2.7
Proses memurnikan gula menghasilkan 1 ton gula murni setiap hari. Diketahui 𝑋 adalah variabel acak yang dinotasikan sebagai jumlah produksi gula sebenarnya dengan faktor mesin yang rusak atau bekerja kurang optimal. Fungsi peluang dari 𝑋 adalah sebagai berikut
𝑓(𝑥) = {
2𝑥, 0 ≤ 𝑥 ≤ 1 0, 𝑠𝑒𝑙𝑎𝑖𝑛𝑛𝑦𝑎
Perusahaan dibayar dengan rata-rata $300 per ton untuk gula murni tersebut dan harus membayar biaya perbaikan mesin sebesar $100 per hari. Dengan demikian, keuntungan hariannya adalah 𝑈 = 3𝑋 − 1 dalam ratusan dolar. Tentukan fungsi peluang dari 𝑈
Jawab :
Dengan metode distribusi fungsi, dicari 𝐹𝑈(𝑢), yaitu 𝐹𝑈(𝑢) = 𝑃(𝑈 ≤ 𝑢) = 𝑃(3𝑋 − 1 ≤ 𝑢) = 𝑃 (𝑋 ≤
𝑢 + 1 3 ) Jika 𝑢 < −1, maka (𝑢 + 1) 3⁄ < 0, sehingga
𝐹𝑈(𝑢) = 𝑃 (𝑋 ≤ 𝑢 + 1
3 ) = 0. Jika 𝑢 > 2, maka (𝑢 + 1) 3⁄ > 1, sehingga
𝐹𝑈(𝑢) = 𝑃 (𝑋 ≤𝑢 + 1 3 ) = 1.
Jika −1 ≤ 𝑢 < 2, maka peluang 𝑃(𝑋 ≤ (𝑢 + 1) 3⁄ ) dapat ditulis sebagai integral dari 𝑓(𝑥), sehingga
𝐹𝑈(𝑢) = 𝑃 (𝑋 ≤𝑢 + 13 ) = ∫(𝑢+1) 3𝑓(𝑥) 𝑑𝑥 ⁄ −∞ = ∫(𝑢+1) 32𝑥 𝑑𝑥 ⁄ 0
= (𝑢 + 1 3 )
2 . Jadi didapat 𝐹𝑈(𝑢) sebagai berikut
𝐹𝑈(𝑢) = { 0, 𝑢 ≤ −1, (𝑢 + 1 3 ) 2 , −1 ≤ 𝑢 ≤ 2 1, 𝑢 > 2, ,
dan fungsi peluang dari 𝑈 adalah
𝑓𝑈(𝑢) = 𝑑𝐹𝑈(𝑢) 𝑑𝑢 = { 2 9(𝑢 + 1), −1 ≤ 𝑢 < 2, 0, 𝑠𝑒𝑙𝑎𝑖𝑛𝑛𝑦𝑎 . 2. Metode Tranformasi
Diketahui 𝑈 = ℎ(𝑋) dimana ℎ(𝑥) adalah fungsi naik atau turun dari 𝑥 untuk semua nilai 𝑥 sesedemikian hingga 𝑓𝑋(𝑥) > 0.
a. Tentukan fungsi invers 𝑥 = ℎ−1(𝑢). b. Evaluasikan persamaan 𝑑ℎ−1 𝑑𝑢 = 𝑑[[ℎ−1(𝑢)] 𝑑𝑢 . c. Tentukan 𝑓𝑈(𝑢), yaitu 𝑓𝑈(𝑢) = 𝑓𝑋[ℎ−1(𝑢)] |𝑑ℎ−1 𝑑𝑢 | Contoh 2.8
Dari contoh 2.7, tentukan fungsi peluang dari 𝑈 dengan metode tranformasi. Jawab :
Fungsi keuntungan dari soal contoh 2.7 adalah ℎ(𝑥) = 3𝑥 − 1 yang merupakan fungsi naik dalam 𝑥. Jika 𝑢 = 3𝑥 − 1, maka
𝑥 = ℎ−1(𝑢) = 𝑢 + 1 3
dan 𝑑ℎ−1 𝑑𝑢 = 𝑑[[ℎ−1(𝑢)] 𝑑𝑢 = 1 3 Jadi, didapat 𝑓𝑈(𝑢) sebagai berikut
𝑓𝑈(𝑢) = 𝑓𝑋[ℎ−1(𝑢)] | 𝑑ℎ−1 𝑑𝑢 | = { 2[ℎ−1(𝑢)] |𝑑ℎ−1 𝑑𝑢 | = 2 ( 𝑢 + 1 3 ) | 1 3| , 0 ≤ 𝑢 + 1 3 ≤ 1, 0, 𝑠𝑒𝑙𝑎𝑖𝑛𝑛𝑦𝑎 atau ekuivalen dengan,
𝑓𝑈(𝑢) = { 2
9(𝑢 + 1), −1 ≤ 𝑢 < 2, 0, 𝑠𝑒𝑙𝑎𝑖𝑛𝑛𝑦𝑎 . E. Statistik Terurut (Order Statistics)
Banyak fungsi variabel acak yang menarik untuk dipraktikan tergantung pada besar relatifnya variabel yang diamati. Contoh penerapannya adalah pengamatan waktu tercepat dalam balap mobil atau tikus dengan berat paling besar diantara banyak tikus yang diberi makan pada waktu diet. Jadi dalam pengamatan tersebut, variabel acak yang diamati sering diurutkan sesuai dengan besar variabelnya. Variabel terurut yang dihasilkan disebut dengan statistik terurut (order statistics).
Secara formal diketahui 𝑋1, 𝑋2, … , 𝑋𝑛 adalah variabel acak kontinu yang saling bebas dengan fungsi distribusi 𝐹(𝑥) dan fungsi peluang 𝑓(𝑥). Dinotasikan variabel acak order 𝑋𝑖 dengan 𝑋(1), 𝑋(2), … , 𝑋(𝑛) dimana
𝑋(1) ≤ 𝑋(2) ≤ ⋯ ≤ 𝑋(𝑛).
Jadi, minimum dari variabel acak 𝑋𝑖 dinotasikan sebagai berikut, 𝑋(1)= 𝑚𝑖𝑛(𝑋1, 𝑋2, … , 𝑋𝑛)
dan maksimum dari variabel acak 𝑋𝑖 adalah
𝑋(𝑛) = 𝑚𝑎𝑥(𝑋1, 𝑋2, … , 𝑋𝑛)
Fungsi peluang densitas untuk 𝑋(1) dan 𝑋(𝑛) dapat ditentukan dengan metode distribusi fungsi. Pertama dicari fungsi peluang dari 𝑋(𝑛). Karena 𝑋(𝑛) adalah maksimum dari 𝑋1, 𝑋2, … , 𝑋𝑛, maka kejadian 𝑋(𝑛) ≤ 𝑥 berlaku jika dan hanya jika kejadian 𝑋𝑖 ≤ 𝑥 berlaku untuk setiap 𝑖 = 1,2, … , 𝑛. Jadi,
𝑃(𝑋(𝑛)≤ 𝑥 ) = 𝑃(𝑋1 ≤ 𝑥 , 𝑋2 ≤ 𝑥 , … , 𝑋𝑛 ≤ 𝑥 )
Karena 𝑋𝑖 saling bebas dan 𝑃(𝑋𝑖 ≤ 𝑥 ) = 𝐹(𝑥) untuk 𝑖 = 1,2, … , 𝑛, maka fungsi distribusi dari 𝑋(𝑛) adalah sebagai berikut :
𝐹𝑋(𝑛)(𝑥) = 𝑃(𝑋(𝑛) ≤ 𝑥 ) = 𝑃(𝑋1≤ 𝑥)𝑃(𝑋2 ≤ 𝑥) … 𝑃(𝑋𝑛 ≤ 𝑥)
= [𝐹(𝑥)]𝑛.
Dinotasikan 𝑔(𝑛)(𝑥) adalah fungsi peluang dari 𝑋(𝑛), sehingga dengan mengambil turunan dari kedua sisi, didapat
𝑔(𝑛)(𝑥) = 𝑛[𝐹(𝑥)]𝑛−1𝑓(𝑥).
Fungsi peluang untuk 𝑋(1) dapat ditentukan dengan cara yang serupa. Distribusi fungsi dari 𝑋(1) adalah
𝐹𝑋(1)(𝑥) = 𝑃(𝑋(1) ≤ 𝑥 ) = 1 − 𝑃(𝑋(1)> 𝑥).
Karena 𝑋(1) adalah minimum dari 𝑋1, 𝑋2, … , 𝑋𝑛, maka kejadian (𝑋(1) > 𝑥) berlaku jika dan hanya jika kejadian (𝑋𝑖 > 𝑥) berlaku untuk 𝑖 = 1,2, … , 𝑛. Karena 𝑋𝑖 saling bebas dan 𝑃(𝑋𝑖 > 𝑥 ) = 1 − 𝐹(𝑥) untuk 𝑖 = 1,2, … , 𝑛, maka berlaku :
𝐹𝑋(1)(𝑥) = 𝑃(𝑋(1) ≤ 𝑥 ) = 1 − 𝑃(𝑋(1) > 𝑥) = 1 − 𝑃(𝑋1 > 𝑥 , 𝑋2 > 𝑥 , … , 𝑋𝑛 > 𝑥)
= 1 − [𝑃(𝑋1 > 𝑥)𝑃(𝑋2 > 𝑥) … 𝑃(𝑋𝑛 > 𝑥)] = 1 − [1 − 𝐹(𝑥)]𝑛.
Jadi, jika 𝑔(1)(𝑥) dinotasikan sebagai fungsi peluang dari 𝑋(1), dengan menurunkan kedua sisi dari persamaan terakhir diatas, didapat,
𝑔(1)(𝑥) = 𝑛[1 − 𝐹(𝑥)]𝑛−1𝑓(𝑥). F. Teorema Limit Pusat
Teorema 2.12
Misalkan 𝑋 dan 𝑋1, 𝑋2, … , 𝑋𝑛 adalah variabel acak dengan fungsi pembangkit momen 𝑚(𝑡) dan 𝑚1(𝑡), 𝑚2(𝑡), 𝑚3(𝑡), … Jika
lim
𝑛→∞𝑚𝑛(𝑡) = 𝑚(𝑡), ∀𝑡 ∈ ℝ
Maka fungsi distribusi dari 𝑋𝑛 konvergen ke fungsi distribusi 𝑋 saat 𝑛 → ∞.
Bukti :
Bukti terdapat pada buku Williams, David. (1991). Probability With
Martingales. New York: Cambridge University Press. Halaman 185.
Teorema 2.13
Diketahui 𝑋1, 𝑋2, … , 𝑋𝑛 bersifat saling bebas dan variabel acak berdistribusi identik dengan 𝐸(𝑋𝑖) = 𝜇 dan 𝑉(𝑋𝑖) = 𝜎2 < ∞. Didefinisikan
𝑈𝑛 =∑ 𝑋𝑖− 𝑛𝜇 𝑛 𝑖=1 𝜎√𝑛 = 𝑋̅ − 𝜇 𝜎/√𝑛 dimana 𝑋̅ =1 𝑛∑ 𝑋𝑖 𝑛 𝑖=1
Kemudian, fungsi distribusi dari 𝑈𝑛 konvergen menuju fungsi distribusi Normal standar dengan 𝑛 → ∞. Dengan kata lain
lim 𝑛→∞𝑃(𝑈𝑛 ≤ 𝑢) = ∫ 1 √2𝜋 𝑢 −∞ 𝑒−𝑡 2 2 untuk setiap nilai 𝑢.
Bukti : Misalkan 𝑈𝑛 = √𝑛 (𝑋̅ − 𝜇𝜎 ) = 1 √𝑛( ∑ 𝑋𝑖 𝑛 − 𝑛𝜇 𝑛 𝑖=1 𝜎 ) = 1 √𝑛(∑ 𝑍𝑖 𝑛 𝑖=1 ) dengan
𝑍
𝑖=
𝑋𝑖−𝜇 𝜎Karena variabel acak 𝑋𝑖 saling bebas dan berdistribusi identik, maka 𝑍𝑖, 𝑖 = 1,2, … , 𝑛 juga berdistribusi identik dengan 𝐸(𝑍𝑖) = 0 dan 𝑉(𝑍𝑖) = 1. Karena fungsi pembangkit momen dari jumlahan variabel acak adalah perkalian dari masing-masing fungsi pembangkit momennya, maka
𝑚∑ 𝑧𝑖(𝑡) = 𝑚𝑧1(𝑡) × 𝑚𝑧2(𝑡) × … × 𝑚𝑧𝑛(𝑡)
= [𝑚𝑧1(𝑡)]
𝑛 .
Selanjutnya akan dicari fungsi pembangkit momen untuk 𝑈𝑛 , 𝑚𝑈𝑛(𝑡) = 𝐸 (𝑒𝑡√𝑛1 ∑ 𝑍𝑖) = 𝐸 (𝑒√𝑛𝑡 ∑ 𝑍𝑖) = 𝑚𝑍𝑖( 𝑡 √𝑛) = [𝑚𝑍1( 𝑡 √𝑛)] 𝑛 Deret Taylor dari 𝑚𝑍1(𝑡) adalah
𝑚𝑍1(𝑡) = 𝑚𝑍1(0) + 𝑚′
𝑍1(0)𝑡 + 𝑚𝑍1(𝜉)
𝑡2
2 , 0 < 𝜉 < 𝑡.
Karena 𝑚𝑍1(0) = 𝐸(𝑒0𝑍1) = 𝐸(1) = 1 dan 𝑚′𝑍1(0) = 𝐸(𝑍1) = 0, maka
𝑚𝑍1(𝑡) = 1 +𝑚"𝑧1(𝜉)
Sehingga 𝑚𝑈𝑛(𝑡) = [ 1 +𝑚"𝑧1(𝜉𝑛) 2 ( 𝑡 √𝑛) 2 2 ] 𝑛 = [1 +𝑚"𝑧1(𝜉𝑛) 𝑡 2 2 𝑛 ] 𝑛 , 0 < 𝜉𝑛 < 𝑡 √𝑛 . Ketika 𝑛 → ∞ , maka 𝜉𝑛 → 0 , sehingga
𝑚"𝑧1(𝜉𝑛) 𝑡2 2 → 𝑚"𝑧1(0) 𝑡2 2 Karena 𝐸(𝑍12) = 𝑉(𝑍 1) = 1, maka 𝑚"𝑧1(0)𝑡2 2 = 𝑡2 2 𝐸(𝑍12) = 𝑡2 2 (𝑉(𝑍1− [𝐸(𝑍1)]2) = 𝑡2 2 . Jika lim 𝑛→∞𝑏𝑛 = 𝑏 , maka lim𝑛→∞(1 + 𝑏𝑛 𝑛) 𝑛 = 𝑒𝑏. Sehingga lim 𝑛→∞𝑚𝑈𝑛 = lim𝑛→∞[1 + 𝑚"𝑧1(𝜉𝑛) 𝑡 2 2 𝑛 ] 𝑛 = 𝑒𝑡 2 2.
𝑒𝑡22 merupakan fungsi pembangkit momen bagi distribusi Normal Standar.
Menurut Teorema 2.12 Dapat disimpulkan bahwa 𝑈𝑛 memiliki fungsi peluang yang konvergen ke fungsi peluang Normal Standar.
G. Estimasi Parameter Fungsi Distribusi Definisi 2.25
Sebuah penduga (estimator) adalah aturan yang biasanya dalam bentuk rumus untuk menghitung nilai dari suatu dugaan berdasarkan pengukuran-pengukuran yang terkandung dalam sampel.
Contoh 2.9
Rata-rata sampel yang diperoleh dari 𝑋1, 𝑋2, … , 𝑋𝑛 dinyatakan dalam rumus 𝑋̅ =1
𝑛∑ 𝑋𝑖 𝑛
𝑖=1
Rata-rata 𝑋̅ adalah salah satu penduga titik dari rata-rata populasi 𝜇.
Definisi 2.26 Metode Kemungkinan Maksimum
Misalkan fungsi kemungkinan bergantung pada 𝑘 buah parameter 𝜃1, 𝜃2, … , 𝜃𝑘. Metode kemungkinan maksimum bertujuan memilih penduga nilai-nilai dari parameter sedemikian hingga memaksimalkan fungsi kemungkinan berupa
𝐿(𝑥1, 𝑥2, … , 𝑥𝑛|𝜃1, 𝜃2, … , 𝜃𝑘).
Contoh 2.10
Sebuah eksperimen Binomial terdiri dari 𝑛 percobaan dengan hasil 𝑥1, 𝑥2, … , 𝑥𝑛 dengan 𝑥𝑖 = 1 jika percobaan ke-𝑖 sukses dan 𝑥𝑖 = 0 jika percobaan ke-𝑖 gagal. Tentukan penduga kemungkinan maksimum bagi 𝑝 yang dinotasikan sebagai peluang suatu keberhasilan.
Jawab :
Fungsi kemungkinan dari sampel adalah peluang dari 𝑥1, 𝑥2, … , 𝑥𝑛 , sehingga
𝐿(𝑝) = 𝐿(𝑥1, 𝑥2, … , 𝑥𝑛|𝑝) = 𝑝𝑥(1 − 𝑝)𝑛−𝑥 dengan 𝑥 = ∑𝑛𝑖=1𝑥𝑖.
Jika 𝑥 = 0, maka 𝐿(𝑝) = (1 − 𝑝)𝑛 dan 𝐿(𝑝) akan maksimum jika 𝑝 = 0. dan 𝐿(𝑝) akan maksimum jika 𝑝 = 1. Untuk mempermudah perhitungan, dilakukan tranformasi ln pada kedua sisi persamaan, sehingga diperoleh :
𝑙𝑛[𝐿(𝑝)] = 𝑙𝑛[𝑝𝑥(1 − 𝑝)𝑥] = 𝑥 ln 𝑝 + (𝑛 − 𝑥) ln(1 − 𝑝)
Jika 𝑥 = 1,2, … , 𝑛 − 1, maka turunan dari ln[𝐿(𝑝)] terhadap 𝑝 dapat ditulis sebagai berikut : 𝑑 𝑙𝑛[𝐿(𝑝)] 𝑑𝑝 = 𝑥 ( 1 𝑝) + (𝑛 − 𝑥) −1 1 − 𝑝 .
Untuk 𝑥 = 1,2, … , 𝑛 − 1 , nilai 𝑝 yang memaksimalkan ln[𝐿(𝑝)] adalah penyelesaian dari persamaan berikut :
𝑥 𝑝̂− 𝑛 − 𝑥 1 − 𝑝̂= 0 𝑥 − 𝑛𝑝̂ 𝑝̂(1 − 𝑝̂)= 0
Penyelesaian dari persamaan diatas adalah 𝑥 − 𝑛𝑝̂ = 0, sehingga didapat 𝑝̂ =𝑥𝑛 yang merupakan penduga bagi 𝑝.
Definisi 2.27 Metode Momen
Diketahui bahwa momen dengan urutan 𝑘 pada variabel acak dapat ditulis berupa :
𝜇′𝑘= 𝐸(𝑋𝑘).
Koresponden dari sampel momen urutan 𝑘 adalah rata-rata dengan bentuk sebagai berikut :
𝑚𝑘′ = 1 𝑛∑ 𝑋𝑖𝑘
𝑛
𝑖=1
Kemudian metode momen dilakukan dengan memilih estimasi pada nilai parameter dimana estimasi tersebut merupakan solusi dari persamaan 𝜇′𝑘 = 𝑚𝑘′ untuk 𝑘 = 1,2, … , 𝑡, dimana 𝑡 adalah banyaknya parameter yang akan diestimasi.
Contoh 2.11
Sampel acak dari 𝑛 pengamatan, 𝑋1, 𝑋2, … , 𝑋𝑛 dipilih dari populasi dimana 𝑋𝑖 untuk 𝑖 = 1,2, … , 𝑛 memiliki fungsi peluang uniform pada interval (0, 𝜃) dimana 𝜃 tidak diketahui. Gunakan metode momen untuk mengestimasi parameter 𝜃.
Jawab :
Nilai dari 𝜇′1 untuk variabel acak uniform adalah 𝜇′1 = 𝜇 =
𝜃 2 . Koresponden dari sampel momen pertama adalah
𝑚′1 = 1 𝑛∑ 𝑋𝑖
𝑛
𝑖=1
= 𝑋̅
Kemudian dibuat persamaan antara koresponden populasi dan sampel momen, sehingga didapat
𝜇′1 =𝜃 2= 𝑋̅
Dengan metode momen untuk mengestimasi parameter 𝜃 didapat 𝜃̂ = 2𝑋̅. H. Bias dan Rata-Rata Galat Kuadrat dari Penduga Titik
Definisi 2.28
Misalkan 𝜃̂ adalah penduga titik dari parameter 𝜃, maka 𝜃̂ adalah penduga tak bias jika 𝐸(𝜃̂) = 𝜃.
Definisi 2.29
Bias dari penduga titik 𝜃̂ didefinisikan sebagai 𝐵(𝜃̂) = 𝐸(𝜃̂) − 𝜃.
Definisi 2.30
𝑀𝑆𝐸(𝜃̂) = 𝐸 [(𝜃̂ − 𝜃)2] .
Rata-Rata Kuadrat Galat dari sebuah penduga 𝜃̂ adalah fungsi dari variansi dan biasnya. Teorema 2.14 𝑀𝑆𝐸(𝜃̂) = 𝑉(𝜃̂) + [𝐵(𝜃̂)]2 Bukti : 𝑀𝑆𝐸(𝜃̂) = 𝐸 [(𝜃̂ − 𝜃)2] = 𝐸 [(𝜃̂ − 𝐸(𝜃̂) + 𝐸(𝜃̂) − 𝜃)2] = 𝐸 [(𝜃̂ − 𝐸(𝜃̂))2+ 2 (𝜃̂ − 𝐸(𝜃̂)) (𝐸(𝜃̂) − 𝜃) + (𝐸(𝜃̂) − 𝜃)2] = 𝐸 [(𝜃̂ − 𝐸(𝜃̂))2] + 𝐸 [2 (𝜃̂ − 𝐸(𝜃̂)) (𝐸(𝜃̂) − 𝜃)] + 𝐸 [(𝐸(𝜃̂) − 𝜃)2]
Karena 𝐵(𝜃̂) = 𝐸(𝜃̂) − 𝜃 yang merupakan nilai konstanta, maka dapat ditulis: 𝐸 [(𝜃̂ − 𝐸(𝜃̂))2] + 𝐸 [2 (𝜃̂ − 𝐸(𝜃̂)) (𝐸(𝜃̂) − 𝜃)] + 𝐸 [(𝐸(𝜃̂) − 𝜃)2] = 𝐸 [(𝜃̂ − 𝐸(𝜃̂))2] + 2(𝐸(𝜃̂) − 𝜃)𝐸[𝜃̂ − 𝐸(𝜃̂)] + (𝐸(𝜃̂) − 𝜃)2 = 𝐸 [(𝜃̂ − 𝐸(𝜃̂))2] + 2(𝐸(𝜃̂) − 𝜃) (𝐸(𝜃̂) − 𝐸(𝜃̂)) + (𝐵(𝜃̂))2 = 𝐸 [(𝜃̂ − 𝐸(𝜃̂))2] + (𝐵(𝜃̂))2 = 𝑉(𝜃̂) + [𝐵(𝜃̂)]2 Terbukti bahwa 𝑀𝑆𝐸(𝜃̂) = 𝑉(𝜃̂) + [𝐵(𝜃̂)]2
36 BAB III
DISTRIBUSI PARETO
A. Sejarah Distribusi Pareto
Titik awal dalam diskusi tentang distribusi Pareto dan distribusi yang mirip dengan Pareto adalah buku Ekonomi yang ditulis oleh Vilfredo Pareto yang diterbitkan di Roma pada tahun 1897. Dari buku tersebut, Pareto melakukan suatu observasi tentang jumlah penduduk dalam populasi penduduk yang memiliki pendapatan lebih dari suatu nilai tertentu dan membentuk suatu aproksimasi yang disebut dengan distribusi Pareto klasik. Observasi yang dilakukan Pareto menunjukkan suatu fakta bahwa distribusi pendapatan bersifat memiliki ekor panjang (heavy tail). Distribusi Pareto dan beberapa distribusi lain yang erat hubungannya dengan Pareto sangat fleksibel dengan suatu keluarga dari distribusi ekor panjang (heavy-tailed
distribution) yang dapat digunakan sebagai model distribusi pendapatan
serta berbagai macam distribusi sosial dan ekonomi lainnya. Pengembangan dan penyempurnaan dari model Pareto akan berpengaruh dalam meneliti sifat ketidakmerataan pada pendapatan dalam populasi penduduk. (Barry, 2015).
B. Model Distribusi Pareto Definisi 3.1
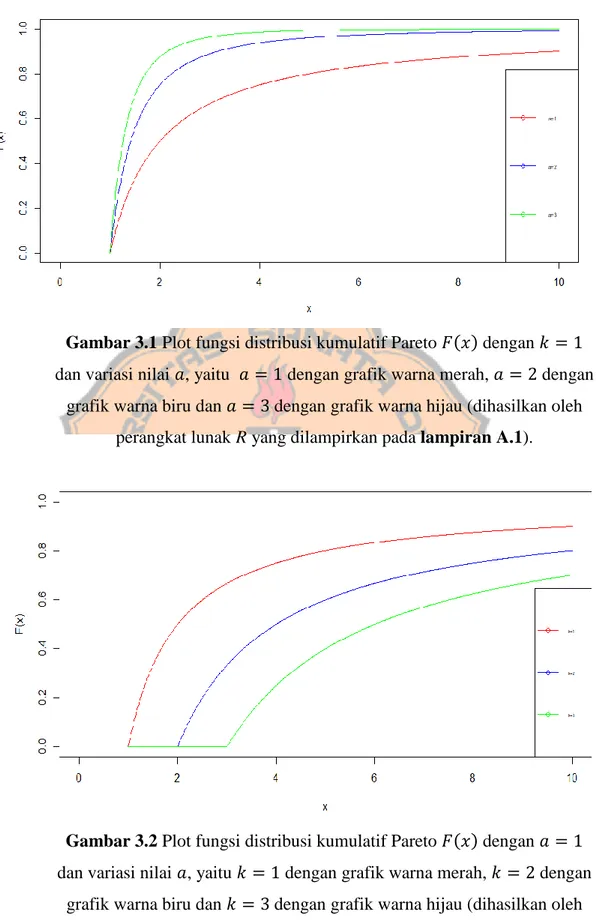
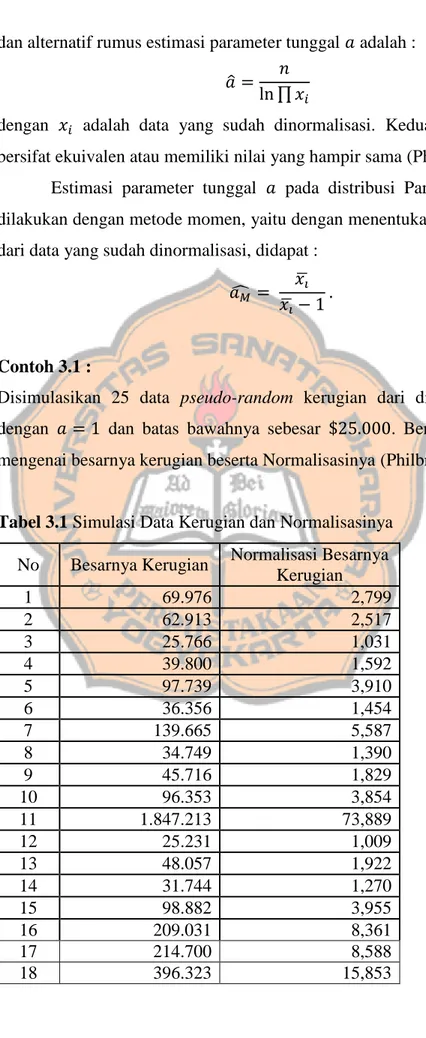
Fungsi distribusi kumulatif Pareto dari variabel acak 𝑋 dapat didefinisikan sebagai berikut : 𝐹(𝑥) = { 1 − ( 𝑘 𝑥) 𝑎 , 𝑥 > 𝑘 0, 𝑠𝑒𝑙𝑎𝑖𝑛𝑛𝑦𝑎.
Gambar 3.1 Plot fungsi distribusi kumulatif Pareto 𝐹(𝑥) dengan 𝑘 = 1 dan variasi nilai 𝑎, yaitu 𝑎 = 1 dengan grafik warna merah, 𝑎 = 2 dengan
grafik warna biru dan 𝑎 = 3 dengan grafik warna hijau (dihasilkan oleh perangkat lunak R yang dilampirkan pada lampiran A.1).
Gambar 3.2 Plot fungsi distribusi kumulatif Pareto 𝐹(𝑥) dengan 𝑎 = 1 dan variasi nilai 𝑎, yaitu 𝑘 = 1 dengan grafik warna merah, 𝑘 = 2 dengan
grafik warna biru dan 𝑘 = 3 dengan grafik warna hijau (dihasilkan oleh perangkat lunak R yang dilampirkan pada lampiran A.2).
Teorema 3.1
Suatu variabel acak berdistribusi Pareto dengan parameter 𝑎, 𝑘 > 0 jika fungsi peluangnya 𝑓(𝑥) = { 𝑎𝑘𝑎 𝑥𝑎+1 , 𝑥 > 𝑘 0, 𝑠𝑒𝑙𝑎𝑖𝑛𝑛𝑦𝑎 Bukti : 𝑓(𝑥) = 𝑑(𝐹(𝑥)) 𝑑𝑥 = 𝐹′(𝑥) = −(−𝑎)𝑥−𝑎−1 𝑘𝑎 = 𝑎𝑥−(𝑎+1) 𝑘𝑎 = 𝑎𝑘𝑎 𝑥𝑎+1
fungsi 𝑓(𝑥) di atas adalah fungsi peluang karena memenuhi sifat sebagai berikut :
1. Fungsi 𝑓(𝑥) ≥ 0 untuk semua x, −∞ < 𝑥 < ∞. 2. ∫ 𝑓(𝑥) 𝑑𝑥 = 1−∞∞ ∫ 𝑓(𝑥) 𝑑𝑥 ∞ −∞ = ∫ 𝑎𝑘𝑎 𝑥𝑎+1 𝑑𝑥 ∞ 𝑘 = 𝑎𝑘𝑎 ∫ 𝑥∞ −𝑎−1 𝑑𝑥 𝑘 = 𝑎𝑘𝑎lim 𝑙→∞∫ 𝑥 −𝑎−1 𝑑𝑥 𝑙 𝑘 = 𝑎𝑘𝑎lim 𝑙→∞[ 𝑥−𝑎 −𝑎]𝑘 𝑙 = 𝑎𝑘𝑎 −𝑎 [lim𝑙→∞(𝑙 −𝑎− 𝑘−𝑎)] = −𝑘𝑎 [−𝑘−𝑎] = −𝑘𝑎(− 1 𝑘𝑎 ) = 1
Gambar 3.3 Plot fungsi peluang pareto 𝑓(𝑥) dengan 𝑘 = 1 dan variasi nilai 𝑎, yaitu 𝑎 = 1 dengan grafik warna merah, 𝑎 = 2 dengan grafik
warna biru dan 𝑎 = 3 dengan grafik warna hijau (dihasilkan oleh perangkat lunak R yang dilampirkan pada lampiran A.3).
Gambar 3.4 Plot fungsi peluang pareto 𝑓(𝑥) dengan 𝑎 = 1 dan variasi nilai 𝑘, yaitu 𝑘 = 1 dengan grafik warna merah, 𝑘 = 2 dengan grafik
warna biru dan 𝑘 = 3 dengan grafik warna hijau (dihasilkan oleh perangkat lunak R yang dilampirkan pada lampiran A.4).
Teorema 3.2
Nilai rata-rata 𝐸[𝑋] dari distribusi Pareto ada jika 𝑎 > 1 dan 𝐸[𝑋] = 𝑎 𝑎 − 1 𝑘 Bukti : 𝐸[𝑋] = ∫ 𝑥 𝑓(𝑥) 𝑑𝑥∞ −∞ = ∫ 𝑥 𝑎𝑘𝑎 𝑥𝑎+1 𝑑𝑥 ∞ 𝑘 = 𝑎𝑘𝑎∫ 𝑥∞ −𝑎 𝑑𝑥 𝑘 = 𝑎𝑘𝑎lim 𝑙→∞∫ 𝑥 −𝑎 𝑑𝑥 𝑙 𝑘 = 𝑎𝑘𝑎lim 𝑙→∞[ 𝑥−𝑎+1 −𝑎 + 1]𝑘 𝑙 = 𝑎𝑘𝑎 −𝑎 + 1 [lim𝑙→∞(𝑙 −𝑎+1− 𝑘−𝑎+1)] = 𝑎𝑘𝑎 −𝑎 + 1 [−𝑘−𝑎+1] = 𝑎𝑘𝑎𝑘−𝑎+1 𝑎 − 1 = 𝑎𝑘 𝑎 − 1 , 𝑎 > 1 Teorema 3.3
Nilai Variansi dari distribusi Pareto ada jika 𝑎 > 2, yaitu :
𝑣𝑎𝑟(𝑋) = 𝑎
(𝑎 − 1)2(𝑎 − 2)𝑘2 Bukti :
𝐸[𝑋2] = ∫ 𝑥∞ 2𝑓(𝑥) 𝑑𝑥 −∞ = ∫ 𝑥2 𝑎𝑘𝑎 𝑥𝑎+1 ∞ 𝑘 𝑑𝑥 = 𝑎𝑘𝑎∫ 𝑥∞ −𝑎+1 𝑑𝑥 𝑘 = 𝑎𝑘𝑎lim 𝑙→∞∫ 𝑥 −𝑎+1 𝑑𝑥 𝑙 𝑘 = 𝑎𝑘𝑎lim 𝑙→∞[ 𝑥−𝑎+2 −𝑎 + 2]𝑘 𝑙 = 𝑎𝑘 𝑎 −𝑎 + 2 [lim𝑙→∞(𝑙 −𝑎+2− 𝑘−𝑎+2)] = 𝑎𝑘𝑎 −𝑎 + 2 [−𝑘−𝑎+2] = 𝑎𝑘𝑎𝑘−𝑎+2 𝑎 − 2 = 𝑎𝑘2 𝑎 − 2
Selanjutnya dicari 𝑉𝑎𝑟(𝑋) dengan perhitungan sebagai berikut : 𝑉𝑎𝑟(𝑋) = 𝐸[𝑋2] − 𝐸[𝑋]2 = 𝑎𝑘𝑎𝑘−𝑎+2 𝑎 − 2 − ( 𝑎𝑘 𝑎 − 1 ) 2 = 𝑎𝑘2(𝑎 − 1)2− 𝑎2𝑘2(𝑎 − 2) (𝑎 − 1)2(𝑎 − 2) = 𝑎𝑘2((𝑎 − 1)2 − 𝑎(𝑎 − 2)) (𝑎 − 1)2(𝑎 − 2) = 𝑎𝑘 2((𝑎2− 2𝑎 + 1) − (𝑎2− 2𝑎)) (𝑎 − 1)2(𝑎 − 2) = 𝑎𝑘2 (𝑎 − 1)2(𝑎 − 2) , 𝑎 > 2
Teorema 3.4 (Derivatif dari Distribusi Eksponensial menuju Distribusi Pareto)
Jika 𝑌 berdistribusi eksponensial dengan intensitas 𝑎, maka 𝑥 = 𝑢𝑒𝑦 berdistribusi Pareto.
Bukti :
Dengan metode perubahan variabel, didapat : 𝑃(𝑋 < 𝑥) = 𝑃(𝑋 < 𝑢𝑒𝑦) = 𝑃 (𝑋 𝑈 < 𝑒𝑦) = 𝑃 (𝑒𝑦 < 𝑥 𝑢) = 𝑃 (ln 𝑒𝑦 < 𝑙𝑛 𝑥 𝑢) = 𝑃 (𝑦 < ln𝑥 𝑢)
Berdasarkan Teorema 2.4, fungsi distribusi kumulatif dari distribusi Eksponensial adalah 1 − 𝑒−𝑦𝑎. Melalui substitusi pada fungsi peluang diatas, didapat : 𝐹(𝑦) = 1 − 𝑒−𝑦𝑎 = 1 − 𝑒−𝑎 ln𝑥𝑢 = 1 − 𝑒−(ln𝑥𝑢) 𝑎 = 1 − (𝑥 𝑢) 𝑎
yang merupakan distribusi Pareto dengan parameter (𝑥, 𝑎). C. Estimasi Parameter Distribusi Pareto
1. Metode Kemungkinan Maksimum
Fungsi kemungkinan maksimum 𝐿 untuk distribusi Pareto adalah sebagai berikut :
𝐿(𝑘, 𝑎|𝑥) = ∏ 𝑎𝑘𝑎 𝑥𝑖𝑎+1 𝑛 𝑖=1 = 𝑎𝑛𝑘𝑛𝑎 ∑ 𝑥 𝑖−(𝑎+1) 𝑛 𝑖=1 ; 0 < 𝑘 ≤ min{𝑥𝑖} , 𝑎 > 0 Pendugaan dengan metode kemungkinan maksimum untuk 𝑘 dan 𝑎 dilakukan dalam bentuk nilai dari 𝑘 dan 𝑎 agar menghasilkan 𝐿 sebesar mungkin dari data yang dimiliki. Memaksimumkan 𝐿 dapat dilakukan dengan menetapan nilai 𝑘 sedemikian hingga 𝑘 tidak lebih besar daripada nilai terkecil dari 𝑥 pada suatu data, sehingga dapat ditulis :
𝑘̂ = min{𝑥𝑖}
Untuk memaksimumkan 𝐿 dilakukan tranformasi dengan ln 𝐿 karena fungsi logaritma adalah fungsi bijektif dengan nilai 𝑎 yang memaksimumkan 𝐿 sekaligus memaksimumkan ln 𝐿, sehingga dapat ditulis : 𝑙𝑛 𝐿(𝑘, 𝑎|𝑥) = ∑ ln 𝑛 𝑖=1 (𝑎𝑘𝑎 𝑥𝑖𝑎+1 ) = 𝑛 𝑙𝑛(𝑎) + 𝑎𝑛 ln(k) − (𝑎 + 1) ∑ ln(𝑥𝑖) 𝑛 𝑖=1
Kemudian turunan terhadap 𝑎 dari 𝐿𝑛 𝐿 dibuat sama dengan 0 untuk memaksimumkan L, sehingga didapat :
𝑑 𝑙𝑛 𝐿(𝑘, 𝑎|𝑥) 𝑑𝑎 = 𝑛 𝑎̂+ 𝑛 ln(𝑘) − ∑ ln(𝑥𝑖) = 0 𝑛 𝑖=1 𝑛 𝑎̂ = ∑ ln(𝑥𝑖) 𝑛 𝑖=1 − 𝑛 ln(𝑘) 1 𝑎̂= ∑𝑛 ln(𝑥𝑖) 𝑖=1 − 𝑛 ln(𝑘) 𝑛 𝑎̂ = ∑ 𝑛 ln(𝑥𝑖) 𝑛 𝑖=1 − 𝑛 ln(𝑘)
2. Metode Momen
Jika diketahui 𝑋 berdistribusi Pareto (𝑘, 𝑎), maka didapat nilai rata-rata berupa 𝐸(𝑋). Proses menentukan estimasi dari 𝑎 dengan metode momen adalah sebagai berikut :
Nilai dari 𝜇′1 untuk variabel acak berdistribusi Pareto adalah 𝜇′1 = 𝐸(𝑋) = 𝑎𝑘
𝑎 − 1 . Koresponden dari sampel momen pertama adalah
𝑚′1 = 1 𝑛∑ 𝑋𝑖 𝑛 𝑖=1 = 𝑋̅.
Kemudian dibuat persamaan dengan 𝜇′1 = 𝑚′1, sehingga didapat 𝐸(𝑋) = 1 𝑛∑ 𝑥𝑖 𝑛 𝑖=1 𝑥̅ = 𝑎𝑘 𝑎 − 1 𝑎𝑘 = 𝑥̅𝑎 − 𝑥̅ 𝑥̅ = 𝑥̅𝑎 − 𝑎𝑘 𝑥̅ = 𝑎(𝑥̅ − 𝑘) sehingga didapat penduga momen dari 𝑎, yaitu
𝑎̂ = 𝑀 𝑥̅ 𝑥̅ − 𝑘 yang bergantung pada 𝑘.
Namun karena nilai 𝑘 tidak diketahui, maka penduga 𝑎̂ diatas tidak 𝑀 bisa dijadikan penduga bagi 𝑎. Petersen (2000) mulai memodifikasi metode momen, yaitu jika rata-rata sampel sama dengan nilai harapan dari distribusi Pareto dan jika 𝑥1 adalah sampel minimum yang ditetapkan bernilai sama dengan nilai harapan dari nilai minimum dari sampel berukuran 𝑛 yang berdistribusi Pareto (𝑘, 𝑎), maka didapat dua persamaan, yaitu :
𝑥̅ = 𝑎𝑘 𝑎 − 1
dan
𝑥1 = 𝑛𝑎𝑘 𝑛𝑎 − 1
Persamaan kedua didapat dengan metode statistik terurut (order
statistics), yaitu :
Dicari fungsi peluang dari sampel minimum 𝑥1 yang berdistribusi Pareto. Jika fungsi peluang dari 𝑥1 dinotasikan sebagai 𝑔(1)(𝑥), maka dengan metode statistik terurut (order statistics) didapat :
𝑔(1)(𝑥) = 𝑛[1 − 𝐹(𝑥)]𝑛−1𝑓(𝑥)
dengan 𝐹(𝑥) adalah fungsi distribusi kumulatif Pareto dan 𝑓(𝑥) adalah fungsi peluang dari distribusi Pareto. Jadi didapat :
𝑔(1)(𝑥) = 𝑛 [1 − (1 − ( 𝑘 𝑥) 𝑎 )] 𝑛−1 𝑎𝑘𝑎 𝑥𝑎+1 =𝑛𝑎𝑘𝑎 𝑥𝑎+1 [( 𝑘 𝑥) 𝑎 ] 𝑛−1 = 𝑛𝑎𝑘𝑎𝑥−(𝑎+1)𝑘𝑎(𝑛−1)𝑥−𝑎(𝑛−1) = 𝑛𝑎𝑘𝑎+𝑎𝑛−𝑎𝑥−𝑎−1−𝑎𝑛+𝑎 = 𝑛𝑎𝑘𝑎𝑛𝑥−𝑎𝑛−1.
Kemudian dari fungsi peluang 𝑔(1)(𝑥) yang didapat, dicari nilai harapan dari nilai minimum dari sampel berukuran 𝑛 yang berdistribusi Pareto dengan 𝐸[𝑋(1)] = 𝑥1 dengan perhitungan sebagai berikut :
𝑥1 = ∫ 𝑥 𝑔(1)(𝑥) 𝑑𝑥 ∞ −∞ = ∫ 𝑥 (𝑛𝑎𝑘∞ 𝑎𝑛𝑥−𝑎𝑛−1) 𝑑𝑥 𝑘 = 𝑛𝑎𝑘𝑎𝑛∫ 𝑥∞ −𝑎𝑛 𝑑𝑥 𝑘 = 𝑛𝑎𝑘𝑎𝑛[ 𝑥−𝑎𝑛+1 −𝑎𝑛 + 1 ] 𝑥 = ∞ 𝑥 = 𝑘
= 𝑛𝑎𝑘𝑎𝑛[0 − 𝑘−𝑎𝑛+1 −𝑎𝑛 + 1] = 𝑛𝑎𝑘𝑎𝑛𝑘−𝑎𝑛+1 𝑎𝑛 − 1 = 𝑛𝑎𝑘 𝑛𝑎 − 1 . Jadi didapat 𝑥1 = 𝑛𝑎𝑘 𝑛𝑎 − 1
Gunakan kedua persamaan untuk menghasilkan penduga dari 𝑎 dan 𝑘 dengan penyelesaian sebagai berikut :
𝑥̅ = 𝑎𝑘 𝑎 − 1 𝑘 =(𝑎 − 1)𝑥̅
𝑎
Substitusi persamaan 𝑘 diatas ke dalam persamaan 𝑥1, yaitu : 𝑥1 = 𝑛𝑎𝑘 𝑛𝑎 − 1 𝑥1 = 𝑛𝑎 ((𝑎 − 1)𝑥̅𝑎 ) 𝑛𝑎 − 1 𝑥1 = 𝑛𝑥̅(𝑎 − 1) 𝑛𝑎 − 1 𝑛𝑎𝑥1− 𝑥1 = 𝑛𝑎𝑥̅ − 𝑛𝑥̅ 𝑛𝑎𝑥̅ − 𝑛𝑎𝑥1 = 𝑛𝑥̅ − 𝑥1 𝑎(𝑛𝑥̅ − 𝑛𝑥1) = 𝑛𝑥̅ − 𝑥1 sehingga didapat penduga momen dari 𝑎, yaitu :
𝑎̂ = 𝑀 𝑛𝑥̅ − 𝑥1 𝑛(𝑥̅ − 𝑥1)
Karena 𝑎 dapat diestimasi berdasarkan nilai harapan dari distribusi Pareto dan sampel minimum 𝑥1, maka penduga dari 𝑘 juga dapat ditentukan, yaitu dari persamaan 𝑥1 didapat :
𝑘̂ =𝑀 (𝑛𝑎̂ − 1)𝑥𝑀 1 𝑛𝑎̂𝑀 .