PENCARIAN JALUR TERPENDEK ANTAR KOTA DI JAWA TENGAH DAN
D.I. YOGYAKARTA DENGAN ALGORITMA DIJKSTRA VIA SMS GATEWAY
Sunaryo (1), Drs. Jong Jek Siang, M.Sc (2), Antonius Rachmat C., S.Kom., M.Cs (3)
Abstrak :
Pencarian jalur terpendek (shortest path finding) dalam perjalanan antar kota merupakan masalah sehari-hari yang biasa ditemui disaat akan mencari jalur perjalanan terdekat ke tempat tujuan. Permasalahan yang terjadi adalah bagaimana menentukan jarak tempuh terdekat ketika berkunjung ke suatu kota melalui kota-kota terdekat yang sebaiknya dilalui.
Dalam skripsi ini dibuat sistem untuk mencari jalur terpendek antar kota yang diakses via SMS. Kota yang dapat dicari adalah kota-kota di Jawa Tengah dan D.I Yogyakarta. Pengukuran jarak antar kota didasarkan pengukuran dari Google Map. Algoritma Dijkstra melakukan pengecekan dengan membandingkan bobot dari kota asal ke semua kota tujuan yang ada, sehingga menghasilkan jarak terpendek. lalu informasi jalur terpendek tersebut dikirimkan ke pengguna melalui SMS (Send Message Service) setelah pengguna mengirim pesan permintaan jalur terpendek.
Hasil penelitian menyimpulkan bahwa algoritma Dijkstra dapat diterapkan pada sistem berbasis SMS gateway. Algoritma Dijkstra dapat mencari jalur terpendek dengan kecepatan perhitungan rata-rata 0.5 detik. Lamanya proses dari pesan masuk ke komputer hingga pesan informasi jalur terpendek terkirim ke user rata-rata 15 detik per request.
Kata Kunci: Algoritma Dijkstra, SMS Gateway, Jalur Terpendek
1. Pendahuluan
Bagi orang yang baru pertama kali mengenal propinsi Jawa Tengah (JATENG) dan DI.Yogyakarta (DIY) sangatlah penting untuk mendapatkan informasi mengenai kota mana saja yang harus dilewati agar dapat sampai ke kota tujuan.
Untuk menentukan kota mana saja yang harus dilalui, biasanya seseorang menggunakan peta yang dijual di toko buku, atau menggunakan aplikasi peta, ataupun bertanya kepada orang-orang yang dijumpai di jalan. Ketiga hal ini merupakan cara yang kurang efisien. Supaya lebih efisien dan lebih mudah dalam mendapatkan informasi jalur perjalanan terpendek, maka dibutuhkan suatu aplikasi informasi jalur perjalanan berbasis SMS gateway yang dapat diakses melalui telepon seluler yang memiliki fitur Send Message Service (SMS).
___________________________ (1)
Sunaryo, Mahasiswa Teknik Informatika, Fakultas Teknologi Informasi, Universitas Kristen Duta Wacana. Email : [email protected]
(2)Drs.Jong Jek Siang, M.Sc, Dosen Teknik Informatika, Fakultas Teknologi Informasi, Universitas Kristen Duta Wacana (3)
Antonius Rachmat C., S.Kom., M.Cs, Dosen Teknik Informatika, Fakultas Teknologi Informasi, Universitas Kristen Duta Wacana
Dalam membangun aplikasi komputer yang dapat menentukan jalur terpendek antar kota di JATENG dan DIY, dibutuhkan suatu algoritma pencarian jalur dan sistem berbasis SMS yang dapat mengirim pesan. Algoritma Dijkstra merupakan algoritma yang paling terkenal untuk mencari lintasan terpendek, dan Gammu adalah tool untuk membangun sistem berbasis SMS.
2. Tujuan Penulisan
Tujuan dari penulisan ini adalah mengimplementasikan algoritma Dijkstra untuk aplikasi perhitungan jarak terpendek berbasis komputer, dan mengimplementasikan SMS gateway kedalam sistem komputer agar dapat mengakses informasi yang berasal dari komputer dan dapat mengirimkan informasi tersebut ke pengguna melalui SMS.
3. Rumusan Masalah
Permasalahan dalam tulisan ini dapat dirumuskan sebagai berikut :
1. Bagaimana pesan masuk dapat diolah oleh algoritma Dijkstra dan menghasilkan jalur terpendek antar kota di propinsi Jawa Tengah dan D.I Yogyakarta.
2. Bagaimana mengimplementasikan SMS gateway kedalam program untuk menerima pesan masuk dan mengirimkan pesan keluar yang berisi informasi yang di-request.
4. Landasan Teori
4.1 Teori Algoritma Dijkstra
Menurut Siang (2004), algoritma Dijkstra menyelesaikan masalah pencarian jalur terpendek (sebuah lintasan yang mempunyai panjang minimum) dari verteks a ke verteks z dalam graf berbobot, bobot tersebut adalah bilangan positif jadi tidak dapat dilalui oleh node negatif.
Misalkan G adalah graf berarah berlabel dengan titik-titik V(G) = {v1,v2,…,vn} dan path
terpendek yang dicari adalah dari v1 ke vn. Algoritma Dijkstra dimulai dari titik v1. Dalam
iterasinya, algoritma akan mencari satu titik yang jumlah bobotnya dari titik 1 terkecil. Titik-titik yang terpilih dipisahkan, dan titik-titik tersebut tidak diperhatikan lagi dalam iterasi berikutnya. Langkah-langkah dalam menentukan lintasan terpendek pada algoritma Dijkstra yaitu:
1. Pada awalnya pilih node sumber sebagai node awal, diinisialisasikan dengan ‘1’. 2. Bentuk tabel yang terdiri dari node, status, bobot, dan predecessor. Lengkapi kolom
bobot yang diperoleh dari jarak node sumber ke semua node yang langsung terhubung dengan node sumber tersebut.
3. Jika node sumber ditemukan maka tetapkan sebagai node terpilih.
4. Tetapkan node terpilih dengan label permanen dan perbaharui node yang langsung terhubung.
5. Tentukan node sementara yang terhubung pada node yang sudah terpilih sebelumnya dan merupakan bobot terkecil dilihat dari tabel dan tentukan sebagai node terpilih berikutnya.
6. Apakah node yang terpilih merupakan node tujuan?. Jika ya, maka kumpulan node terpilih atau predecessor merupakan rangkaian yang menunjukkan lintasan terpendek.
PSEUDOCODE
Function Dijkstra (M: input graf dan bobot, a : integer) → tabel
{ Mencari lintasan terpendek dari simpul awal a ke semua smpul lainnya Masukan : dari graf berbobot G dan simpul awal a
Keluaran : panjang lintasan terpendek dari a ke simpul tujuan } Deklarasi D, S : array[1..n] of integer I, j, k min : integer Algoritma { Langkah 0 (inisialisais: ) for i ← 1 to n do S[i] ← 0 D[i] ← M[a, i] Endfor { Langkah 1: }
S[a] ← 1 { masukkan simpul awal ke dalam S } { Langkah 2, 3, ..., n-1 : }
for k ← 2 to n – 1 do
{ cari simpul j sedemikian sehingga S[j] = 0 Dan D[j] = Minimum{D[1], D[2], ..., D[n]} min ← D[1]
j ← l
for i ← 2 to n do
if (S[i] = 0) and (D[i] < min) then min ← D[i]
j ← i endif endfor
S[j] ← l { simpul j sudah terpilih ke dalam lintasan terpendek
}
{hitung D[i] yang baru dari a ke simpul i ∉ S }
for i ← l to n do if S[i] = 0 then
if D[i] > (D[j] + jarak[j,]) then D[i] ← D[j] + jarak[j,l] endif endif endfor endfor return D
4.2 SMS Gateway
SMS gateway sering diartikan sebagai suatu jembatan komunikasi yang
menghubungkan perangkat komunikasi (dalam hal ini modem) dengan perangkat komputer. Gambar dibawah ini menunjukkan ilustrasi aplikasi SMS gateway.
Gambar 1. Ilustrasi SMS Gateway
Dalam membangun SMS Gateway dibutuhkan:
a. Perangkat Komunikasi
Perangkat komunikasi SMS gateway merupakan perangkat yang dapat digunakan untuk mengirim atau menerima SMS. Perangkat tersebut dapat berupa: ponsel atau modem yang mendukung gammu sebagai tool SMS gateway.
b. Media Koneksi
Media koneksi digunakan untuk mengirimkan data dari perangkat komunikasi ke komputer atau sebaliknya. Media tersebut di antaranya adalah: kabel data, USB port, ataupun bluetooth.
c. Software
Adalah aplikasi yang menghubungkan perangkat komunikasi dengan perangkat komputer. Software yang akan digunakan untuk koneksi modem ke komputer dalam penelitian ini adalah Gammu (GNU All Mobile Management Utilities). Gammu merupakan software yang bersifat open source yang digunakan sebagai tool untuk mengembangkan aplikasi SMS Gateway.
Fungsi teknologi SMS gateway dibagi menjadi 2 bagian, yakni:
a. Input, komputer bisa menerima pesan dan mengolahnya. Caranya, komputer dihubungkan dengan modem yang sudah dilengkapi kartu seluler aktif (misalnya: Telkomsel, Indosat, atau XL), dan ketika ada pesan yang masuk maka, modem yang akan menerimanya, dan kemudian meneruskannya ke komputer melalui gammu, lalu gammu menyimpan pesan masuk di database mysql.
b. Output, komputer bisa mengirim pesan ke handphone atau deskphone yang memiliki fitur SMS. Caranya, komputer dihubungkan dengan modem, dan ketika komputer akan mengirim pesan ke pengguna handphone atau deskphone, maka komputer mengirim perintah inject SMS ke modem. Perintah inject dieksekusi oleh gammu dan diterjemahkan ke modem sebagai perintah untuk mengirim pesan.
Program (Excutable) Alat Komunikasi (HP/Modem) SMS Gateway (Modem/HP, Gammu, MysQL)
Gambar 2. Cara Kerja SMS Gateway
5. Hasil dan Pembahasan
5.1 Algoritma Dijkstra Dalam Pencarian Jalur Terpendek Via SMS Gateway
Algoritma Dijkstra menelusuri semua node dimulai dari node awal yaitu kota asal, kemudian menelusuri seluruh node yang lain dengan membandingkan semua jarak antar node dari node awal ke node tujuan, dan mendapatkan rute terpendek.
Untuk mengirim pesan kepada user yang berisikan informasi rute terpendek, digunakan perintah gammu yang disisipkan pada program. Perintah gammu tersebut dijalankan menggunakan komponen ShellAPI pada delphi.
PSEUDOCODE
Function KIRIM_SMS
NoHp = Ambil_NoHP(Number from Inbox)
Pesan = Ambil_Hasil_Dijkstra(Rute, Jarak)
Open = Command Prompt.Exe
Perintah =
Ada 2 jenis perintah yang dapat digunakan untuk mengirim pesan, yaitu:
1. gammu-smsd-inject -c c:\gammu\smsdrc TEXT +628995052526 -text "Hello World" Keterangan:
Perintah TEXT artinya hanya akan mengirim pesan tidak lebih dari 160 karakter. 2. gammu-smsd-inject -c c:\gammu\smsdrc EMS +628995052526 -text "Hello World"
Keterangan:
Perintah EMS artinya dapat mengirim pesan lebih dari 160 karakter.
5.2 Analisis Hasil
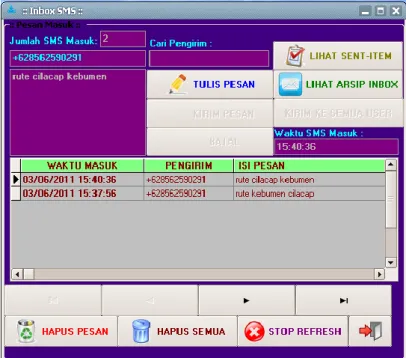
Berikut adalah visualisasi ketika SMS request jalur terpendek masuk ke komputer dan visualisasi SMS balasan dari komputer berdasarkan perhitungan Dijkstra.
Gambar 3. Capture SMS Masuk
Menu SMS Masuk bertujuan untuk melihat isi pesan masuk. Pada form ini dapat dilihat banyaknya SMS request yang masuk, dan dapat diketahui pesan apa yang diterima komputer. Setiap 1,5 detik program akan memeriksa SMS yang baru masuk ke tabel inbox di database MySQL. Pemeriksaan dilakukan secara otomatis menggunakan komponen Timer. SMS yang baru masuk menempati posisi record paling atas untuk memudahkan pemantauan proses.
Menu SMS Keluar bertujuan untuk melihat isi pesan yang dikirimkan komputer kepada
user. Pada form ini dapat dilihat hasil dari proses Dijkstra yang menghitung rute terpendek dari request user sebelumnya. Pada form ini akan terlihat apakah hasil proses algoritma Dijkstra
sesuai dengan request yang sebelumnya dikirim oleh user. SMS yang terakhir dikirim oleh komputer menempati posisi record paling atas untuk memudahkan pemantauan proses.
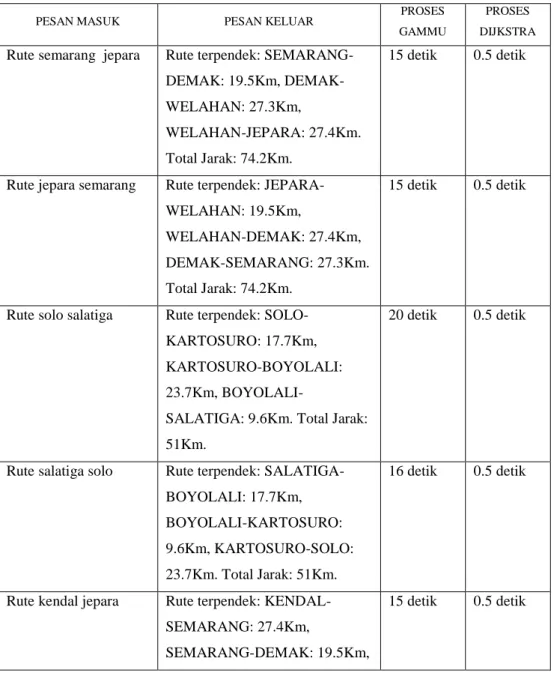
Tabel 1. Analisis Waktu Pada Proses Pengolahan Pesan
PESAN MASUK PESAN KELUAR PROSES
GAMMU
PROSES DIJKSTRA
Rute semarang jepara Rute terpendek: SEMARANG-DEMAK: 19.5Km, DEMAK-WELAHAN: 27.3Km,
WELAHAN-JEPARA: 27.4Km. Total Jarak: 74.2Km.
15 detik 0.5 detik
Rute jepara semarang Rute terpendek: JEPARA-WELAHAN: 19.5Km,
WELAHAN-DEMAK: 27.4Km, DEMAK-SEMARANG: 27.3Km. Total Jarak: 74.2Km.
15 detik 0.5 detik
Rute solo salatiga Rute terpendek: SOLO-KARTOSURO: 17.7Km, KARTOSURO-BOYOLALI: 23.7Km,
BOYOLALI-SALATIGA: 9.6Km. Total Jarak: 51Km.
20 detik 0.5 detik
Rute salatiga solo Rute terpendek: SALATIGA-BOYOLALI: 17.7Km, BOYOLALI-KARTOSURO: 9.6Km, KARTOSURO-SOLO: 23.7Km. Total Jarak: 51Km.
16 detik 0.5 detik
Rute kendal jepara Rute terpendek: KENDAL-SEMARANG: 27.4Km,
SEMARANG-DEMAK: 19.5Km,
DEMAK-WELAHAN: 27.3Km, WELAHAN-JEPARA: 31.3Km. Total Jarak: 105.5Km.
Rute jepara kendal Rute terpendek: JEPARA-WELAHAN: 19.5Km, WELAHAN-DEMAK: 27.4Km, DEMAK-SEMARANG: 31.3Km, SEMARANG-KENDAL: 27.3Km. Total Jarak: 105.5Km. 14 detik 0.5 detik
Rute kebumen kutoarjo Rute terpendek: KEBUMEN-PREMBUN: 12.4Km, PREMBUN-KUTOARJO: 17.4Km. Total Jarak: 29.8Km.
15 detik 0.5 detik
Rute kutoarjo kebumen Rute terpendek: KUTOARJO-PREMBUN: 17.4Km, PREMBUN-KEBUMEN: 12.4Km. Total Jarak: 29.8Km. 15 detik 0.5 detik Rute temanggung ungaran Rute terpendek: TEMANGGUNG-SUMOWONO: 21.6Km, SUMOWONO-UNGARAN: 27.1Km. Total Jarak: 48.7Km. 14 detik 0.5 detik Rute ungaran temanggung
Rute terpendek: UNGARAN-SUMOWONO: 27.1Km,
SUMOWONO-TEMANGGUNG: 21.6Km. Total Jarak: 48.7Km.
16 detik 0.5 detik
Lamanya waktu pengolahan pesan ditentukan oleh 3 proses, yaitu proses identifikasi pesan masuk yang belum diproses, proses pengubahan pesan menjadi perintah perhitungan jalur terpendek, dan proses pengiriman pesan keluar dari database ke modem.
Lamanya proses pesan terkirim ke komputer atau terkirim ke user bergantung pada kualitas jaringan provider penyedia layanan SMS.
Proses Dijkstra berjalan sangat cepat karena kemajuan teknologi pada processor yang mampu melakukan komputasi multi proses.
Tabel 2a. Jarak Antar Kota Yang Diuji
JOGJA KLATEN DELANGGU KARTOSURO SOLO SUKOHARJO
JOGJA - 28.5 - - - - KLATEN 28.5 - 15.6 - - 32.5 DELANGGU - 15.6 - 9.3 - 20.4 KARTOSURO - - 9.3 - 9.6 - SOLO - - - 9.6 - 14.1 SUKOHARJO - 32.5 20.4 - 14.1 -
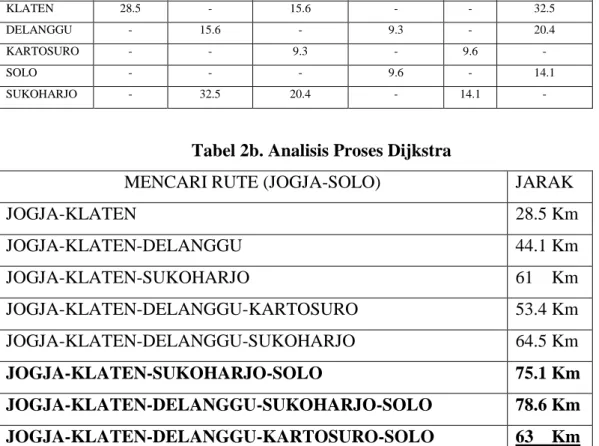
Tabel 2b. Analisis Proses Dijkstra
MENCARI RUTE (JOGJA-SOLO)
JARAK
JOGJA-KLATEN
28.5 Km
JOGJA-KLATEN-DELANGGU
44.1 Km
JOGJA-KLATEN-SUKOHARJO
61 Km
JOGJA-KLATEN-DELANGGU-KARTOSURO
53.4 Km
JOGJA-KLATEN-DELANGGU-SUKOHARJO
64.5 Km
JOGJA-KLATEN-SUKOHARJO-SOLO
75.1 Km
JOGJA-KLATEN-DELANGGU-SUKOHARJO-SOLO
78.6 Km
JOGJA-KLATEN-DELANGGU-KARTOSURO-SOLO
63 Km
Terbukti bahwa algoritma Dijkstra dapat memilih rute terpendek sekalipun ada
pilihan percabangan yang memiliki tujuan yang sama.
Tabel 3. Analisis Format Pesan Pada Pesan Masuk
PESAN MASUK PESAN KELUAR
ruTe jEPaRa KenDaL Rute terpendek: JEPARA-WELAHAN: 19.5Km, WELAHAN-DEMAK: 27.4Km, DEMAK-SEMARANG: 31.3Km,
SEMARANG-KENDAL: 27.3Km. Total Jarak: 105.5Km. Rute Jogja Yogya JOGJA dan YOGYA adalah kota yang sama. Format yg benar:
RUTE<spasi>KOTA_ASAL<spasi>KOTA_TUJUAN. Balas dengan ketik: BANTUAN, untuk daftar kota.
RUTE JOGJA tokyo KOTA_TUJUAN tidak ada. Hanya kota di JATENG dan DIY yg dikenali. Format yg benar:
RUTE<spasi>KOTA_ASAL<spasi>KOTA_TUJUAN. Balas dengan ketik: BANTUAN, untuk daftar kota.
Rute roma solo KOTA_ASAL tidak ada. Hanya kota di JATENG dan DIY yg dikenali. Format yg benar:
RUTE<spasi>KOTA_ASAL<spasi>KOTA_TUJUAN. Balas dengan ketik: BANTUAN, untuk daftar kota.
rUTe HaNoi JaKaRta KOTA_ASAL dan KOTA_TUJUAN tidak ada. Hanya kota di JATENG dan DIY yg dikenali. Format yg benar:
RUTE<spasi>KOTA_ASAL<spasi>KOTA_TUJUAN. Balas dengan ketik: BANTUAN, untuk daftar kota.
Format pesan masuk tidak casesensitive. Jumlah spasi antar kata juga tidak berpengaruh karena digunakan perintah split pada whitespace.
6. Kesimpulan
Dari hasil pengujian yang dilakukan pada sistem, maka didapatkan kesimpulan sebagai berikut:
1. Algoritma Dijkstra dapat diterapkan pada sistem berbasis SMS gateway karena agoritma Dijkstra menerima nilai-nilai verteks dan edge yang didapat dari SMS Masuk.
2. Algoritma Dijkstra dapat mencari jalur terpendek, dengan kecepatan perhitungan rata-rata 0.5 detik. Pesan yang masuk dapat diproses oleh algoritma Dijkstra jika pesan tersebut telah diolah terlebih dahulu oleh fungsi pengolah pesan. Lama proses dari pesan masuk melalui gammu hingga pesan terkirim oleh gammu rata-rata 15 detik per
request.
3. Program dapat menerima pesan ataupun dapat mengirimkan pesan jika service gammu berjalan dan pulsa pada kartu modem masih tersedia untuk mengirim pesan. Kegagalan proses pengiriman pesan dapat dilihat pada status pesan keluar.
7. Daftar Pustaka
Arbie. (2003). Manajemen Database dengan MYSQL. Yogyakarta: CV Andi Offset.
Bucknall, Julian. (2001). The Tomes of Delphi Algorithms and Data Structures. Texas: Wordware Publishing, Inc.
Bahri, Kusnassruyanto S. (2010). Teknik Pemrograman Delphi, Bandung: Informatika.
Cantu, Marco. (2003). Mastering Delphi 7, Alameda, CA: Sybex, inc.
Cihar, Michal. (2010). Gammu SMSD Daemon Manual Release 1.29.92,
http://wammu.eu/docs/pdf/smsd.pdf, tanggal akses 28 Pebruari 2011.
Dewi, Erawati. (2010). Pencarian Rute Terpendek Tempat Wisata Di Bali Dengan
Menggunakan Algoritma Dijkstra, Universitas Pendidikan Ganesha.
Johnsonbaugh, Richard. (1997). Discrete Mathematic-Fourth Edition, New Jersey: Prentice Hall, p.306.
Kadir, Abdul. (2003). Dasar Aplikasi Database MYSQL DELPHI, Yogyakarta: CV.Andi Offset.
Loekmono, Martinus Elianto. (2004). Implementasi Algoritma Dijkstra Untuk Menentukan
Rute Terpendek Menuju Daerah Wisata Di Pulau Jawa Berbasis Sistem Informasi Geografis,
Universitas Kristen Duta Wacana.
Lubis, Henny Syahriza. (2009). Perbandingan Algoritma Greedy dan Dijkstra Untuk
Menentukan Lintasan Terpendek, Universitas Sumatera Utara.
Muhadkly. (2007). SMS Gateway Menggunakan Gammu, IlmuKomputer.Com.
Novandi, Raden Aprias. (2007). Perbandingan Algoritma Dijkstra dan Algoritma
Floyd-Warshall Dalam Penentuan Lintasan Terpendek (Single Pair Shortest Path), Sekolah Teknik
Elektro dan Informatika, Institut Teknologi Bandung.
Rosihan, http://blog.rosihanari.net/setting-gammu-untuk-aplikasi-sms-gateway, tanggal akses 10 Nopember 2010.
Rosihan, http://blog.rosihanari.net/teknik-dasar-mengirim-sms-dengan-gammu, tanggal akses 10 Nopember 2010.
Siang, Jong Jek. (2004), Matematika Diskrit dan Aplikasinya pada Ilmu Komputer, Yogyakarta: CV Andi Offset.
Google Map. __________________, http://maps.google.co.id, tanggal akses 13 Nopember 2010.