Sanksi Pelanggaran Pasal 72 Undang-undang Nomor 19 Tahun 2002 Perubahan atas Undang-undang Nomor 7 Tahun 1987 Perubahan atas Undang-undang Nomor 6

Sanksi Pelanggaran Pasal 72

Undang-undang Nomor 19 Tahun 2002

Perubahan atas Undang-undang Nomor 7 Tahun 1987 Perubahan atas Undang-undang Nomor 6 Tahun 1982 Tentang Hak Cipta

1. Barang siapa dengan sengaja dan tanpa hak melakukan perbuatan sebagaimana dimaksud dalam Pasal 2 ayat (1) atau Pasal 49 ayat (1) dan ayat (2) dipidana dengan pidana penjara masing-masing paling singkat 1 (satu) bulan dan/atau denda paling sedikit Rp. 1.000.000,00 (satu juta rupiah), atau pidana penjara paling lama 7 (tujuh) tahun dan/atau denda paling banyak Rp. 5.000.000.000,00 (lima miliar rupiah).

2. Barang siapa dengan sengaja menyiarkan, memamerkan, mengedarkan atau menjual kepada umum suatu ciptaan atau barang hasil pelanggaran Hak Cipta atau Hak Terkait sebagaimana dimaksud dalam ayat (1), dipidana dengan pidana penjara paling lama 5 (lima) tahun dan/atau denda paling banyak Rp. 500.000.000,00 (lima ratus juta rupiah).

Sri Subanti

MATEMATIKA EKONOMI

Sri Subanti

Matematika Ekonomi. Cetakan ke-1 . Surakarta . UNS Press . 2015 viii + 132 Hal; 16 x 24.5 cm

MATEMATIKA EKONOMI.

Hak Cipta @ Sri Subanti. 2015

Penulis

Dr. Sri Subanti, M.Si.

Editor

Arif Rahman Hakim, S.E., M.SE. Dwi Setiawan

Ilustrasi Sampul UNS PRESS

Penerbit

Penerbitan dan Pencetakan UNS

Jl. Ir. Sutami 36 A Surakarta, Jawa Tengah, Indonesia 57126 Telp. 0271-646994 Psw. 341 Fax. 0271-7890628

Website : www.unspress.uns.ac.id Email : unspress@uns.ac.id Cetakan 1, Edisi I, Agustus 2015 Hak Cipta Dilindungi Undang-undang All Right Reserved

KATA PENGANTAR

Tidak ada kata yang paling baik dan indah kecuali mengucap syukur Alhamdulillahirabil-alamin kehadirat Allah SWT yang telah melimpahkan nikmat, rahmat dan karunia-Nya, akhirnya penulisan buku Matematika Ekonomi ini dapat terselesaikan.

Penulis menyadari bahwa penulisan buku Matematika Ekonomi ini tidak terlepas dari peran dan dukungan berbagai pihak di Prodi Statistika dan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret. Pada kesempatan ini penulis menyam-paikan ucapan terima kasih kepada:

1. Suami tercinta Drs. H.A. Jazuli atas kerelaan, kesabaran dan kesetiaannya hidup bersamaku, yang membimbing untuk menjadi lebih sabar, lebih baik, dan lebih bijak.

2. Kedua anakku Arif Rahman Hakim, SE., M.SE dan Inaki Maulida Hakim, ST, MT yang telah bersedia untuk mengorbankan banyak hal untuk mamah, dan memberikan kebahagiaan yang tiada taranya, serta kalian berdua juga membantu penyelesaian buku ini, terima kasih ya sayaang untuk kedua anak mamah.

3. Kedua menantuku dr. Riski Prihatningtias, SpM dan Anwar Efendy, ST yang telah memberi dukungan dan motivasi serta yang menyejuk-kan hati mamah dalam segala hal.

4. Para mahasiswa yang telah membantu pengetikan penulisan buku ini. Terima kasih kepada pihak lain yang terlibat langsung maupun tidak langsung yang juga membantu tetapi tidak disebutkan di sini atas bantuannya, sehingga buku ini dapat selesai. Akhirnya kepada semua pihak yang berhubungan dengan penulisan buku Matematika Ekonomi apabila selama ini ada banyak hal yang tidak berkenan, penulis mohon maaf. Kiranya buku Matematika Ekonomi ini masih banyak kekurangan, penulis menerima kritik dan saran demi kesempurnaan buku ini. Semoga Allah SWT selalu meridhloi kita untuk menjadi makhlukNya yang pandai bersyukur. Amin

Surakarta,Agustus 2015

Penulis Dr. Sri Subanti, M.Si

DAFTAR ISI

KATA PENGANTAR ... v

DAFTAR ISI ... vi

DAFTAR GAMBAR ... viii

BAB I. HIMPUNAN ... 1

A.Pengertian Himpunan ... 1

B. Macam-macam Himpunan ... 1

C. Relasi Antar Himpunan ... 2

D.Operasi Himpunan ... 3

E. Sifat-sifat Operasi Antar Himpunan ... 3

BAB II. FUNGSI LINIER DAN FUNGSI NON LINIER ... 5

A.Pengertian Fungsi ... 5

B. Penggolongan Fungsi ... 5

C. Fungsi Eksponensial dan Logaritma ... 7

D.Fungsi Linier ... 9

E. Fungsi Linier Dalam Ekonomi ... 10

F. Perpajakan ... 10

G.Fungsi Non Linier ... 14

H.Fungsi Kuadrat dalam Ekonomi ... 16

Contoh-Contoh Soal 16 BAB III. APLIKASI FUNGSI DALAM EKONOMI ... 29

A.Fungsi dan Curve Permintaan (Demand) ... 29

B. Fungsi Curve Penawaran (Supply) ... 30

C. Keseimbangan Pasar (Market Equilibrium) ... 31

D.Subsidi ... 33

BAB IV. DIFERENSIAL DAN INTEGRAL ... 37

A.Diferensial ... 37

B. Integral ... 47

BAB V. PENERAPAN GRAFIK DAN PERSAMAAN DALAM ILMU EKONOMI ... 51

A.Teori Permintaan ... 51

B. Teori Utiliti ... 54

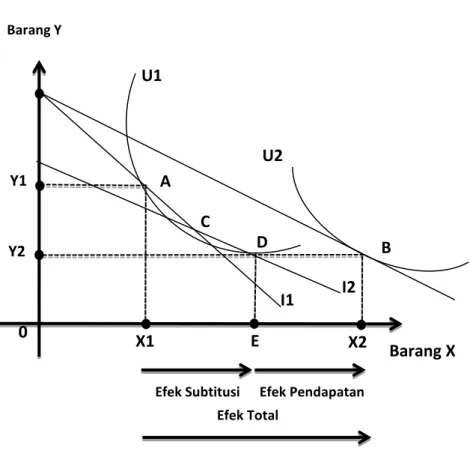
C. Efek Substitusi dan Efek Pendapatan ... 62

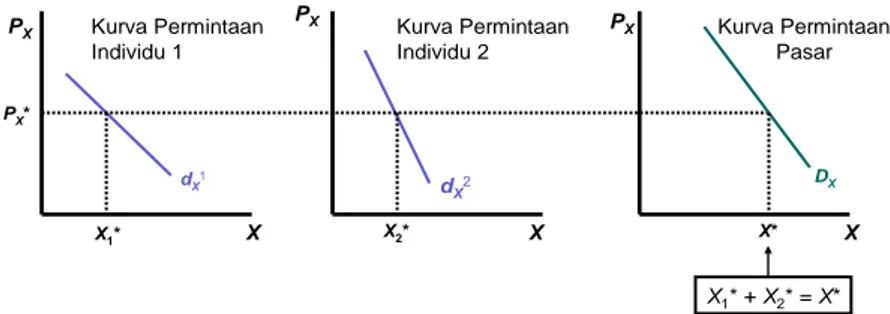
D.Permintaan Pasar dan Elastisitas Permintaan ... 67

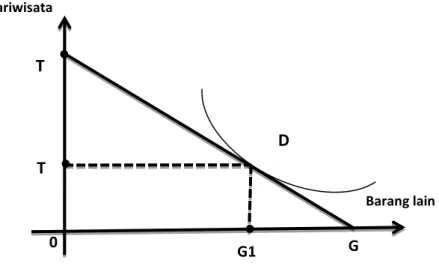
E. Permintaan Pariwisata ... 70

BAB VI. APLIKASI DIFERENSIAL DAN INTEGRAL DALAM EKONOMI ... 79

A.Konsep Elastisitas ... 79

B. Elastisitas Parsiil ... 84

C. Curve Biaya ... 85

D.Hasil Penerimaan Penjualan (Revenue) ... 92

E. Keseimbangan dari Suatu Perusahaan dalam Pasar Persaingan Murni ... 94

F. Laba Maksimal pada Monopoli... 96

BAB VII. ALJABAR DAN MATRIKS ... 107

A.Matriks dan Vektor ... 107

B. Model Linier dengan Pendekatan Matriks ... 114

DAFTAR GAMBAR

Gambar 5.1. Kurva Permintaan ... 53 Gambar 5.2. Efek Subsitusi dan Efek Pendapatan Untuk Barang

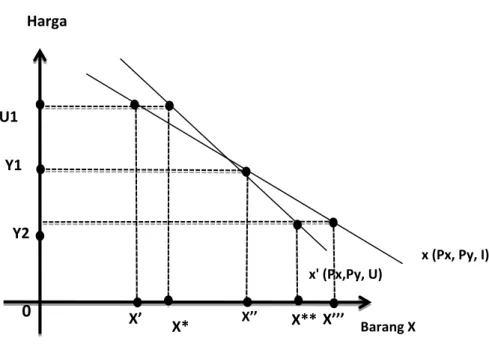
Normal ... 63 Gambar 5.3. Kurva Compensated Demand dan Uncompensated

Demand ... 65 Gambar 5.4. Kurva Permintaan Pasar ... 68 Gambar 5.5. Konsumsi Pariwisata dan Barang Lain ... 70 Gambar 5.6. Pengaruh Perubahan Pendapatan dalam Konsumsi

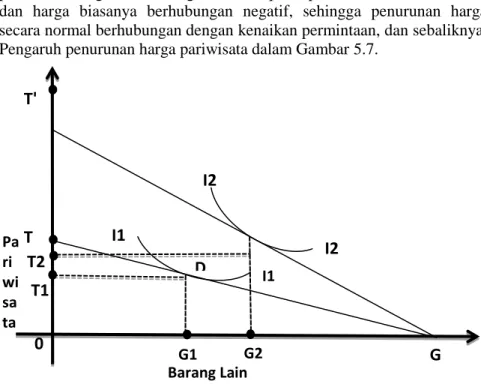
Pariwisata ... 74 Gambar 5.7. Pengaruh Perubahan Harga dalam Konsumsi

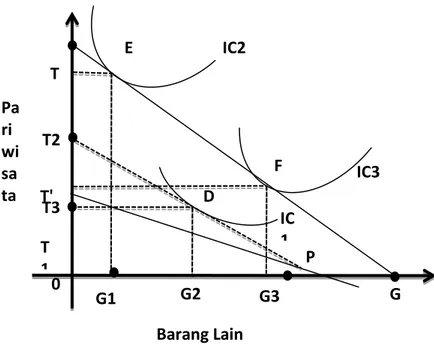
Pariwisata ... 75 Gambar 5.8. Efek Pendapatan dan Efek Substitusi pada

Matematika Ekonomi

BAB I

HIMPUNAN

A.

Pengertian Himpunan

Himpunan adalah sekumpulan objek-objek (benda-benda real atau abstrak) yang didefinisikan dengan jelas. Himpunan biasanya dinyatakan dalam huruf kapital; A,B,C,... atau ditandai oleh dua kurung kurawal,

{...}. Sedangkan anggota himpunan biasanya dinyatakan dalam huruf kecil ; a,b,c,....

Jika

x

anggota himpunan A, maka ditulis xA. Jikay bukan anggota himpunan B, maka ditulis yB.

Banyaknya anggota himpunan A, ditulis n(A).

B.

Macam-Macam Himpunan

Macam-macam Himpunan adalah sebagai berikut. 1. Himpunan kosong

Himpunan yang tidak mempunyai anggota dan ditulis dengan simbol



atau {}.

2. Himpunan semesta

Himpunan yang memuat semua anggota yang sedang dibicarakan, biasanya ditulis dengan simbol S.

Himpunan Bilangan

Himpunan Bilangan Asli: N{1,2,3,...}

Himpunan Bilangan Cacah: C{0,1,2,3,...} Himpunan Bilangan Bulat: Z{...,1,0,1,...}

Himpunan Bilangan Rasional:



{

:

p

,

q



Z

,

q



0

}

q

p

Q

Himpunan Bilangan Real :

R

3. Himpunan terhingga (finite) dan tak terhingga (infinite)

Himpunan terhingga (finite) adalah himpunan yang banyak anggota-nya terhingga, yaitu himpunan kosong atau himpunan yang mempuanggota-nyain

elemen. Contoh: } , , , {a b c d A {}  



B

Himpunan tak terhingga (infinite atau denumerable) adalah himpunan yang berkorespondensi satu-satu dengan bilangan asli, yaitu himpunan yang banyak anggotanya tak terhingga.

Contohnya seperti Himpunan bilangan genap, himpunan bilangan ganjil, himpunan bilangan bulat, himpunan bilangan rasional, dan sebagainya.

4. Himpunan Terhitung (countable) dan Tak Terhitung (uncountable) Himpunan Terhitung adalah himpunan terhingga atau denumerable. Contohnya: Misalnya, } 4 , 3 , 2 , 1 {  A ganjil bilangan himpunan B

5. Himpunan Tak Terhitung adalah himpunan yang tidak terhitung. Contohnya: Rhimpunan bilangan real

C.

Relasi Antar Himpunan

1. Himpunan equivalen

Dua himpunan yang memiliki banyak anggota yang sama. Jika A equivalen B,maka dinotasikan dengan A~B.

Matematika Ekonomi 2. Himpunan Bagian

Himpunan A dikatakan himpunan bagian dari himpunan B jika setiap anggota A termasuk anggota B, dinotasikan dengan AB. 3. Himpunan Kuasa

Himpunan yang anggotanya adalah himpunan-himpunan bagian dari suatu himpunan.

D.

Operasi Himpunan

1. Irisan } : {x x Adanx B B A    2. Gabungan } : {x x Aataux B B A    3. Penjumlahan )} ( , , : {x x Ax B x A B b A      4. Pengurangan } , : { \B x x A x B A B A     5. Komplemen

}

,

:

{

x

x

A

x

S

A

c







E.

Sifat-Sifat Operasi Antar Himpunan

1. Sifat komutatif A B B A  

A

B

B

A







2. Sifat asosiatif C B A C B A(  )(  ) C B A C B A(  )(  )

3. Sifat distributif ) ( ) ( ) (B C A B A C A      ) ( ) ( ) (B C A B A C A      4. Sifat Komplemen

,







c

A

A

,

S

A

A



c



,

)

(

A

c c



A





c

S

c c c

B

A

B

A



)





(

c c c

B

A

B

A



)





(

Matematika Ekonomi

BAB II

FUNGSI LINIER

DAN FUNGSI NON LINIER

A.

Pengertian Fungsi

Jika ada suatu hubungan sedemikian hingga bila x diberikan suatu nilai dan oleh hubungan itu dapat ditentukan suatu nilai y, maka dikatakan bahwa y adalah fungsi dari x biasanya ditulis y f(x).

x disebut variabel bebas (Independent variabel) dan y disebut dengan variabel tak bebas (dependent variabel). y variabel tak bebas sebab nilainya bergantung pada nilai x.

Himpunan yang dapat dijangkau oleh x dinamakan daerah asal (domain) dari fungsi dan himpunan bilangan yang dapat dijangkau disebut daerah hasil (range) atau daerah jangkauan dari fungsi. Dalam hal ini x dan y merupakan pasangan urut (x,y) dimana x sebagai unsur pertama dan y sebagai unsur kedua.

B.

Penggolongan Fungsi

Fungsi dapat digolongkan menjadi beberapa macam (tergantung dari sudut pandangnya):

1. Fungsi dilihat dari letak x dan y di dalam suatu persamaan. Dibagi menjadi:

a. Fungsi Explisit, bila letak x dan y tak seruas, contoh: yab. b. Fungsi Implisit, bila letak x dan y seruas, contoh:

xy



a

.

Pada umumnya setiap fungsi Explisit dapat dirubah menjadi fungsi implisit, tetapi tidak seluruhnya fungsi implisit dapat dirubah ke bentuk fungsi Explisit.

Contoh:

1

3 

 x

y ---> fungsi Impisit. Dapat ditulis y3x1 atau

0 1

3  

 x

y ---> fungsi Implisit, tetapi pandang fungsi

3 )

sin(xy  ---> fungsi implisit. Apakah dapat dirubah menjadi fungsi eksplisit?

2. Dilihat dari derajat pangkat x. Dibagi menjadi:

a. Fungsi linier/pangkat satu, bila x berpangkat satu. Bentuk umum: ymxn, m0.

b. Fungsi kuadrat, bila x berpangkat dua. Bentuk umum: yax2bxc, a0.

c. Fungsi pangkat tinggi, bila x berpangkat lebih dari tiga.

Bentuk umum: 0 1 1x .... a a x a y n n n n       0 1,..., , 0 a a a_n  _n (konstanta), n3.

3. Dilihat dari operasi fungsi

Fungsi digolongkan menjadi dua: a. Fungsi Aljabar

Fungsi aljabar digolongkan menjadi: 1) Fungsi Rasional

a) Fungsi rasional bulat

Bentuk umum: ya₀a₁x...a_nxn

n

a

a

a

0

,

1

,...,

(konstanta) n0 b) Fungsi Rasional Pecah

Bentuk umum: _n n n n x a x b b x a x a a y        ... ... 1 0 1 0 2) Fungsi Irrasional

Bentuk umum:

y



a

₀



a

₁

x



...



a

_m

x

m , m bilangan riil. b. Fungsi Transeden

Matematika Ekonomi 1) Fungsi Exponen: Bentuk umum:

y



b

x

,

2) Fungsi Logaritma: misal: ylogxloga,

3) Fungsi Trigonometri: misal: ysin2xcosx, 4) Fungsi Hyperbolik: misal: yarccosx,yarc tanx.

C.

Fungsi Eksponensial dan Logaritma

1. Fungsi Eksponensial

Eksponen (exponent) berarti indikator pangkat dimana suatu variabel harus dipangkatkan, dimana eksponennya berupa konstanta. Dalam bentuk sederhana, fungsi eksponensial dapat digambarkan dalam bentuk :

( ) t, ( 1)

y f t b b

Dimana y adalah variabel tidak bebas,

t

adalah variabel bebas, dan b menunjukkan basis (base) eksponen yang tetap.

Jika fungsi eksponensial menggunakan basis berupa bilangan irrasional e = 2,718. Fungsi eksponensial seperti ini disebut fungsi eksponensial natural. Contohnya antara lain: yet, ye3t, dan

rt

yAe .

2. Fungsi Logaritma

Bila ada angka 4 dan 16, kedua angka ini dapat dihubungkan oleh persamaan 42 16. Jika didefinisikan eksponen 2 sebagai logaritma dari 16 dengan bilangan poko 4, maka dapat ditulis :

4

log 162

Logaritma adalah pangkat dari bilangan pokok (4) yang harus dipangkatkan untuk menghasilkan suatu bilangan (16).

log

t b

y

  

b

t

y

log_by b  y

Proses pencarian logaritma log_b y disebut sebagai mengambil log y ke dalam bilangan pokok b. Proses sebaliknya, yaitu mencari y dari nilai logaritma logby yang diketahui, disebut sebagai mengambil antilog dari

Logaritma ada dua (2) jenis yaitu logaritma biasa dan logaritma natural. Logaritma dengan bilangan pokok 10 disebut logaritma biasa. Contohnya, log 1000₁₀ 3, log 100₁₀ 2, dan log 10 110  . Logaritma dengan

bilangan pokok e2, 718 disebut logaritma natural. Logaritma natural disimbolkan log_e atau ln (untuk log natural). Contohnya:

3 log

In e3 _ee3  In e2 log_ee2 2dan lne1log_ee11. Logaritma natural, hubungannya dapat ditulis sebagai berikut :

log

t

e

y

  

e

t

y

(atau t = ln y) a. Aturan-aturan Logaritma

1) Aturan 1 (log hasil kali)

ln(uv)lnuln , ( ,v u v0)

Contoh : ln(e e6 4)lne6lne4   6 4 10

7 7

ln(Ae )lnAlne lnA7

2) Aturan 2 (log pecahan)

ln( / )u v lnuln , ( ,v u v0)

Contoh : ln(e2/ )c lne2lnc 2 lnc

2 5 2 5

ln(e /e )lne lne    2 5 3

3) Aturan 3 (log pangkat)

lnua aln , (u u0)

Contoh : lne1515lne15

3

lnA 3lnA

4) Aturan 4 (konversi bilangan pokok log)

logbu(logbe)(logeu), (u0)

Contoh : (log₄e)(log 64)_e =3

5) Aturan 5 (pembalikan bilangan pokok log)

log_be1/(log_eb)

Matematika Ekonomi b. Fungsi Logaritma

Bila suatu variabel dinyatakan sebagai fungsi logaritma dari variabel lainnya, maka fungsi tersebut disebut sebagai fungsi logaritma. Dimana fungsi log merupakan fungsi invers dari fungsi eksponensial tertentu.

logb

t y dan tloge y( ln ) y

D.

Fungsi Linier

1. Bentuk-bentuknya:

Bentuk umum: ymxn,

m = gradien = koefisien arah,

n = penggal garis pada sumbu y bila nilai x = 0. Dari bentuk umum ini, fungsi linier di atas dapat dimodifikasi dari fungsi tersebut sebagai berikut.

a.

y



y

₁



m

(

x



x

₁

)

Adalah fungsi linier yang mempunyai koefisien arah m dan melalui satu titik

(

x

₁

,

y

₁

).

b.

1 2 1 2 1 1 x x y y x x y y     

Adalah fungsi linier antara yang melalui dua titik yaitu:

(

x

₁

,

y

₁

)

dan

(

x

₂

,

y

₂

).

2. Hubungan antara dua fungsi linier.

Pada umumnya hubungan antara dua fungsi linier dapat diklasifi-kasikan sebagai berikut.

Bentuk pers garis Syarat dua garis berpotongan Berpotongan Tegak lurus Sejajar

1 1 1

m

x

n

g





2 2 2

m

x

n

g





2 1

m

m



2 1

n

n



1

.

2 1

m



m

2 1

n

n



2 1

m

m



2 1

n

n



0 1 1 1AxByC  g 0 2 2 2 1AxB yC  g ₂ 2 2 1

B

A

B

A

_

2 2 1 1 B C B C _

1

.

2 2 2 1





B

A

B

A

2 2 1 1 B C B C _ 2 2 2 1

B

A

B

A

_

2 2 1 1 B C B C _

E.

Fungsi Linier Dalam Ekonomi

Pengertian mengenai fungsi linier penting dalam ekonomi, baik dalam ekonomi mikro maupun ekonomi makro, ekonomi moneter dan bagian-bagian dalam teori tersebut.

Contoh-contoh yang dapat dikategorikan di sini antara lain: 1. Dalam ekonomi mikro antara lain:

a. Fungsi permintaan: misal D Q202p, b. Fungsi penawaran: misal S Q102p,

c. Fungsi-fungsi marginal: misalkan: MR2520; MC5.p. 2. Dalam ekonomi makro dan moneter antara lain:

a. Fungsi konsumsi: misal C1000,75y, b. Fungsi Investasi: misal I 13502000i,

c. Fungsi permintaan untuk transaksi, misal

M

_t



0

,

25

y

.

2000

i

, d. Fungsi permintaan untuk spekulasi, misal

M

_s



1250



2000

i

, e. Fungsi IM, misal Y13503000i.

dan masih banyak lagi contoh-contoh penggunaannya.

Aplikasi teori mengenai hubungan antara dua garis dapat dijumpai dalam teori ekonomi. Sebagai contoh dalam kita membicarakan keseimbangan pasar, disini dibicarakan garis berpotongan.

Contoh:

a. keseimbangan pasar permintaan (D) = penawaran (S), b. keseimbangan pasar barang (di sektor rial), dimana I = S,

c. keseimbangan pasar uang Md = Ms (permintaan = penawaran uang).

F.

Perpajakan

Ini merupakan contoh penggunaan hubungan antara dua garis, baik berpotongan maupu sejajar. Dalam teori ekonomi, dikenal beberapa istilah pajak, namun dalam buku ini titik fokus pembicaraan hanya pada pajak per unit dan pajak yang proporsional terhadap harga.

Matematika Ekonomi Kedua jenis pajka tersebut akan mempengaruhi harga melalui penawaran. Sebagai ilustrasi, penjualan rokok, beras, tekstil, buku adalah beberapa contoh dimana pajak semacam ini. Penjual sebagai wajib pajak, dengan syarat-syarat tertentu si penjuai ini akan menggeserkan beban pajak kepada pihak lain dalam hal ini pembeli. Golongan pajak semacam ini disebut si wajib pajak tak langsung.

1. Pajak Per Unit

Andaikan penawaran SQabP,(a0 dan b0).

Pemerintah mengenakan pajak per unit = t, berarti harga barup* pm. P Q a bP bP a Q     

Q

b

b

a































1

Jadi, Q t b b a P                       1 * ) ( * t P b a Q bt bP a Q bt Q a bP           

Fungsi penawaran setelah pajak bila digambarkan:

P Q Q* 0 A abt ) / (a b  0 - t b a  ( / ) - 0 Q

P

Q*=a+b(p-t) Q=a+bp (0,-(a/b) +t ) (0, -(a/b))

0

2. Pajak Proporsional terhadap Harga Ada dua macam:

a. Pajak yang proporsional terhadap harga lama

Dalam aplikasi dikenal dengan pajak yang proporsional terhadap harga. Andaikan persamaan mengenakan pajak proporsional t% terhadap harga, penyelesaian:

bP a Q  Q b b a P                1 Setelah pajak: P t P

P**  * (Harga setelah pajak)

                        Q b a b a t l P P t i P** ( * ) ( *) ) *)( ( * * l t a Q bP    



l



t

*



P

*

*



(



a



Q

)



b

* * * * * P t l b a Q        



(Penawaran setelah pajak)

Bila digambarkan: P Q Q** 0 A A ) / (a b  0 - *) 1 )( / (a b t  - 0

Matematika Ekonomi

b. Pajak yang proporsional terhadap harga baru Andaikan penawaran : S QabP

Pemerintah mengenaan pajak proporsional sebesar t% terhadap harga yang baru.

                      Q b b a Q bP a Q 1 * * * ) ( ** * ) ( ) ( * * * ** * ** * bP t l a Q Q a bP t l P t l P tP P P            

3. Penerimaan pemerintah dari pajak dan beban pajak yang ditanggung oleh konsumen dan produsen.

Q

P Q**=a+ (b/(1+t*) P**) Q=a+bp (a,0) (0, -(a/b)) B Q P A Q2 D Q1 C P1 P2 P3 Q3 Q3

Besar pajak yang diterima oleh pemerintah



GFAB



P

₃

.

2 2

CQ

T

DEP





Beban pajak yang ditanggung konsumen



P

₂

BCP

₁ dan beban pajak yang ditanggung oleh produsen



P

₂

BCP

₂. Gambarnya sebagai berikut. P Q Q*** 0

A

A

) / (a b  0 - ) 1 )( / (a b t  - 0 Catatan:

- Pemberian

P

*

*

*

sebagai akibat pengaruh pajak hanya untuk membedakan klasifikasi tersebut tetapi pengertian secara fungsional tetap sebagai harga P.

- Untuk subsidi (S) cara sama dengan pajak yaitu tinggal mengganti t dengan minus s.

F.

Fungsi Non Linier

Persamaan derajat dua:

Bentuk umum, persamaan derajat dua dalam x dan y adalah : Q P Q***=a+ (b/(1+t*) P***) Q=a+bp (a,0) (0, -(a/b)) (0, -(a/b)(1+t)) 0

Matematika Ekonomi

,

0

2 2











F

Ey

Cy

Bxy

Ax

bila harga BCF0 maka diperoleh persamaan derajat dua daam x yang biasanya ditulis

. 0 2   c bx ax

Contoh-contoh persamaan derajat dua dalam x dan y antara lain: 1.

y



ax

2

;

x



ay

2

;

y



ax

2



bx



c

;

x



py

2



qy



r

(parabola). 2.

x

2



y

2



r

2

(Lingkaran).

3. ₂  ₂ 1 b y a x (Ellips). 4. ₂

1

2 2 2





b

y

a

x

(Hiperbola).

Dalam buku ini lebih ditekankan dalam fungsi kuadrat: 1. Bentuk umum:

a.

y



ax

2



bx



c

atau

Ay

2



By

2



Cx



D



0

b.

x



py

2



qy



r

atau

Px

2



Qy

2



Ry



S



0

2. Hubungan antara fungsi kuadrat (parabola) dengan fungsi linier.

+bx+c + bx+c Berpotongan

Q

Bersinggungan

P

Q

P

G.

Fungsi Kuadrat dalam Ekonomi

Pada umumnya apa yang dicantumkan pada penggunaan fungsi linier dalam ekonomi juga berlaku dalam kasus ini.

Misalnya

1. Fungsi Permintaan :

Q





P

2



2

P



10

2. Fungsi Total Revence :

TR



20

Q



Q

2 3. Fungsi Marginal Cost :

MC



20



4

Q



Q

2

Demikian juga penggunaan hubungan antara garis dengan parabola dapat dijumpai pada waktu membicarakan masalah keseimbangan. Namun demikian pula apabila kita telah mengenal derivatif, persoalan yang berhubungan dengan fungsi kuadrat atau fungsi non linier lainnya lebih mudah dipecahkan. Kasus mengenai fungsi non linier lebih banyak dijumpai dalam pembicaraan pada bab derivatif (aplikasi derivatif dalam ekonomi).

Contoh-Contoh Soal

1. Seorang bersedia membeli sejumlah barang “A” pada berbagai tingkat harga, seperti tabel di bawah ini:

Harga/Unit Jumlah barang A yang dibeli

15 50

30 40

45 30

Pertanyaan:

a. Bagaimana persamaan permintaan akan barang tersebut.

b. Berapa jumlah barang yang akan dibeli oleh orang kalau harga barang adalah Rp 42/unit.

c. Berapa harga barang tersebut harus dia bayar, kalau dia bersedia membeli 22 unit (dengan anggapan orang tersebut adalah pembeli tunggal).

Matematika Ekonomi

Jawab:

a. Misal harga = P Jumlah barang = Q Keadaan 1 : ---> P = 15 Q = 50 Keadaan 2 : ---> P = 30 Q = 40 Keadaan 3 : ---> P = 45 Q = 30

Diambil keadaan 1 dan 3, maka dengan menggunakan rumus:

1 2 1 1 2 1 P P P P Q Q Q Q      15 45 15 50 30 50      P Q ) 15 ( 20 ) 15 ( 30Q  P ) 15 ( 20 ) 15 ( 30Q  P 30 2 150 3Q  P 180 3 2P P 90 2 3 _   Q P

Persamaan permintaan barang A adalah :

90 2 3 _   Q P

Dimana P adalah harga sedangkan Q adalah jumlah barang. b. Kalau harga barang A adalah 42/unit maka P = 42 persamaan

permintaan adalah: 90 2 3 _   Q P Bila P = 42 maka 90 2 3 42 Q 48 2 3 _ Q 32  Q

Jadi bila harga = 42/unit, barang A yang akan dibeli adalah sebesar Q = 32 unit.

c. Bila orang yang bersangkutan hanya bersedia membeli 22 unit

(dengan anggapan ia adalah pembeli tunggal). Maka berarti Q = 22.

Persamaan permintaan adalah:

90 2 3 _   Q P

Jika Q = 22 maka persamaan permintaan menjadi:

90 ) 22 ( 2 3 _   Q P 57  P

Jadi jika jumlah barang yang dibeli hanya 22 unit maka harga keseimbangan adalah P = 57/unit.

2. Diketahui: fungsi permintaan D:Q252P Fungsi penawaran D:QP2

Pertanyaan:

a. Harga dan kuantitas keseimbangan.

b. Bila kemudian dikenakan pajak 0,5 per unit; tentukan harga dan kuantitas keseimbangan setelah pajak dan total pajak yang diterima pemerintah.

c. Gambarkan keadaan di atas.

Jawab:

a. Keseimbangan terjadi bila DS

2 2 25 PP P 3 27 9 3 29_  e P (harga keseimbangan) 2  P Q 7 2 9   e Q (kuantitas keseimbangan) b. Dikenakan pajak t ----> 0,5 5 , 0 2 ) ( 2       Q P t P Q_t P Qt 2,5

Matematika Ekonomi Keseimbangan baru : DS_t P P  2 2,5 25 P 3 5 , 27  P P  2 2,5 25

17

,

9

1



E

P

(harga keseimbangan pajak)

17 , 7 2 17 , 9 1    E

Q

(kuantitas keseimbangan setelah pajak)

585 , 3 17 , 7 5 , 0 .   tQ x

T_X (total pajak yang diterima pemerintah) c. Tabel P Q Q 0 25 -2 5 15 3 diterima yang jumlah Q_d  ditawarkan yang jumlah Qs 20 Qd/Qs 12,5 15 5 5 10 7,5 10 25 Q=25-2P 3 Q=P-2,5 Q=P-2 E

2

E1

3. Diketahui: Fungsi permintaan : P304Q Fungsi penawaran :P Q 2 3 6  P = harga; Q = kuantitas.

Pemerintah memungut pajak penjualan sebesar 15% dari tingkat harga.

Pertanyaan:

a. Harga dan kuantitas keseimbangan sebelum pajak b. Harga dan kuantitas keseimbangan sesudah pajak c. Berapakah penerimaan pemerintah dari pajak

Jawab:

a. Sebelum pajak Q P304 Q P 2 3 6  Q O 2 3 4 24  7 1 5  E Q Q O 2 3 4 24                  7 36 4 30 7 1 5 4 30 P 7 3 9  E P b. Sesudah pajak

Fungsi penawaran setelah pajak

) ( ). (l t f Q P            l Q 3 2 6 ) 15 , 0 ( Q Q 6,90 0,77 3 2 6 ) 15 , 1 (         

Matematika Ekonomi Syarat keseimbangan DS Q P304 Q P6,900,77 Q O22,104,7

84

,

4

77

,

4

10

,

23





E

Q

64 , 10 ) 48 , 4 ( 4 30   P c. Gambar sketsanya:

Besarnya pajak yang diterima pemerintah = ABCE

23 , 9 ) 84 , 4 ( 3 2 6 jadi , 84 , 4     DF Q_E 40 , 1 23 , 9 % 15 pajak tingkat    x DB

Luas ABDE = BD x AB = 4,84 x 1,40 = 6,776

Jadi besarnya pajak yang diterima pemerintah adalah 6,776. 4. Diketahui: bahwa pendapatan nasional yang dapat dibelanjakan

(national disposable incame) sebesar 80 milyar rupiah terjadi dissaving (tabungan yang negatif atau kekurangan tabungan) sebesar 5 milyar rupiah. Apabila tingkat dissposible naik sebesar 50 milyar rupiah maka tingkat tabungan nasional sebesar 12,5 milyar. Kalau dianggap bahwa kurve konsumsi dan kurve tabungan adalah linier.

E Q F (4,84) D C QS*(sesudah pajak) QS(sebelum pajak) B A -9

Pertanyaan:

a. Tentukan fungsi konsumsi dan tabungan. b. Gambarkan fungsi tersebut.

c. Berapakah besarnya konsumsi terendah.

d. Berapakah besarnya tingkat nasional disposable incame kalau tabungan = 0.

Jawab:

a. Misal fungsi tabungan :

S



a



bY

_d, dengan S = tabungan dan

d

Y

= pendapatan yang dapat dibelanjakan.

5

,

80







S

Y

_d 80 . 5ab  b a 80 5   ... (1) 25 , 0 50 5 , 12 5 , 12 50          Y S b S Y

Dimasukkan ke persamaan (1) menjadi :

25 20 ) 25 , 0 (( 80 5        a a a Fungsi tabungan :

S





25



0

,

25

Y

d Fungsi konsumsi :

C



Y



S



Y



(



25



0

,

25

Y

d

)

d

Y

C



25



0

,

75

b. Tabel d

Y

S

C 0 -25 25 100 5 100

Matematika Ekonomi

c. Besarnya konsumsi terendah = 25 milyar, yaitu konsumsi pada saat Y=0

d.

S



0



0





25



0

,

25

Y

d



Y

d



100

Pendapatan yang dapat dibelanjakan = 100 milyar.

5. Diketahui: fungsi tabungan S = 1/2Y – 100 dan investasi I = 200.

Pertanyaan:

a. Tentukan tingkat pendapatan keseimbangan jika S = I. b. Gambarkan fungsifungsi tersebut.

Jawab:

200 100 2 / 1 ,   I Y S

600 300 2 / 1 Y   100 Yd 75 25 50 50 75 100 25 C=25+0,75Yd S=-25+0,25Yd -25 C/S 600 500 _Y 400 100 200 300 200 100 I=200 S=-100+1/2Y -25 S/I

6. Diketahui: C400,80Y_d;I 72;T_X 0,10Y

Pertanyaan:

a. Berapa tingkat pendapatan nasional dalam keseimbangan

b. Jika naik menjadi 86, berapakah tingkat, pendapatan nasional dan konsumsi masyarakat.

Jawab:

72 28 , 0 40 2 , 0 40 72 , 0 40 ) 9 , 0 ( 80 , 0 40 ) 10 , 0 ( 80 , 0 40                 I Y Y Y C Y S Y C Y Y Y C a. S I 112 28 , 0 72 28 , 0 40     Y Y 400  Y b.

I

_baru



86

126 28 , 0 86 28 , 0 40     Y Y

450



baru

Y

7. Pendapatan full employment ditentukan sebesar 600, tingkat konsumsi masyarakat C100,2Y_d, Investasi = 60 pengeluaran pemerintah = 35 dan penerimaan pemerintah dari pajak

d

X Y

T 50,2 .

Pertanyaan:

a. Berapa tingkat pendapatan nasional keseimbangan.

b. Berapa tingkat konsumsi, investasi dan pajak pada tingkat pendapatan tersebut.

c. Selidikilah pada tingkat pendapatan tersebut perekonomian mengalami inflationary atau deflationary gap.

Jawab:

)

(

90

,

0

10

90

,

0

10

Y

d

Y

T

X

C











) 90 , 0 5 ( 90 , 0 10 ) 1 , 0 5 ( 90 , 0 10 Y  Y     Y  ) 81 , 0 5 , 4 10  Y  (pada keseimbangan)

Matematika Ekonomi a. YCIG5,50,81Y6035 Y 81 , 0 5 , 100   95 , 528 19 , 0 Y  b. C5,50,81(5,25)5,5428,4495 9495 , 433  C ) 95 , 528 ( 10 , 0 5 , 60    TX I 895 , 52 5  985 , 57  X T

c. Y full employment = 600; Y keseimbangan = 528,95.

Y full employment > Y keseimbangan, jadi perekonomian mengalami deflationary gap.

8. Diketahui: suatu perusahaan mendapat laba sebesar Rp 500,00 dari penjualan sebanyak 700 unit tetapi harus mengeluarkan biaya tetap Rp 2.000,00; harga penjualan per unit adalah sebesar Rp 20,00.

Pertanyaan:

a. Carilah fungsi ongkos, fungsi pendapatan total dan penjualan pada keadaan BEP.

b. Manager berpendapat bahwa keuntungan dapat diperbesar apabila harganya dinaikkan Rp 5,00. Benarkah pendapat itu bila penjualan berkurang 150 unit? Berapa besarnya tambahan laba atau rugi tersebut?

Jawab:

a. Pada penjualan sebanyak 700 unit terdapat laba Rp 500,00 TE = P.Q = P.700

Harga/unit = 20,00  TR = 20.700 = 14.000. Profit ( laba) :



= TR - TC

500 = 14.000 - TC



TC = 13.500

Padahal diketahui, biaya tetap (FC) = Rp 2.000,00 TC = FC+VC 13.500 = 2.000 + VC



VC = 11.500 (pada G = 700).

Ongkos variable per unit:

43 , 16 700 500 . 11 _  Q VC

Fungsi total Cost TC = 2000 + 16,43 Q & TR = 20,0 BEP = TR = TC 20 Q = 2000 + 16,43 QQ 3,57 Q = 2000 Q = 560,22

b. P naik dari Rp 20,00 menjadi Rp 25,00 Q turun dari 700 unit menjadi 550 unit TR = P.Q (fungsi TR batu)

TR = 25.Q = 25 (550) = 13.750 TC = 2000 + 16,43(550) = 11.036,5

Laba:



= TR – TC = 2.713,5 (laba baru) Jadi terdapat kenaikan laba (



)

baru



= 2.713,50

lama



= 500

Kenaikan laba

(





)

= Rp 2.213,50

9. Diketahui: Fungsi permintaan barang X oleh perusahaan P = 5-3Q, biaya rata-rata untuk memproduksi barang tersebut besarnya = ( 5 / Q ) + 3 .

Pertanyaan:

a. Gambar kurve TR dan TC

b. Break Even Point (BEP) terjadi pada tingkat produksi dan harga berapa

Jawab:

Q P153 2 3 15 ). 3 15 ( .Q Q Q Q Q P TR     3 5 _  Q AC Q Q Q AC T 5 3_. 53      _  

Matematika Ekonomi

a. 2

3 15Q Q

TR 

-

Titik potong dengan sumbu Q, terjadi bila TR = 0

2 3 15 0 Q Q 0 ) 5 ( 3     Q Q 0 , 5 ₂ 1 Q  Q

Titik potong dengan sumbu TR, terjadi bila Q = 0 0 ) 0 ( 3 ) 0 ( 15  2  TR

-

Titik puncak A adalah:

     _{ } a D a b A 4 , 2       4 3 18 , 2 1 2 A Q TC53 Q TC 0 ) 3 / 2 ( 1  50 Gambar sketsanya: 6 5 Q 4 1 18 3 2 -2 BEP TC=5+3Q BEP TR/TC 3,53 2,5 -1 2/3 0,47

BEP terjadi bila TRTC 2 2

3

12

5

0

3

5

3

15

Q



Q





Q







Q



Q

6 17 , 9 12 6 60 144 12 12      Q

53

,

3

1



Q

Q

2



0

,

47

41

,

4

)

53

,

3

(

3

15

3

15



2



₁









Q

P

P

59

,

13

)

47

,

0

(

3

15

2







P

Matematika Ekonomi

BAB III

APLIKASI FUNGSI DALAM EKONOMI

A.

Fungsi dan

Curve

Permintaan (

Demand

)

Demand adalah berbagai jumlah barang yang diminta pada berbagai tingkat harga. Dalam hukum permintaan kita melihat bahwa besar kecilnya jumlah barang yang diminta sangat tergantung pada barang tersebut dengan catatan variabel yang lain tetap. Oleh karena itu dengan pendapatan yang tetap apabila harga barang tersebut naik maka jumlah barang yang diminta akan berkurang dan sebaliknya.

Secara ringkas dapat disimpulkan adanya pola hubungan dari jumlah barang yang diminta dengan variable barang tersebut.

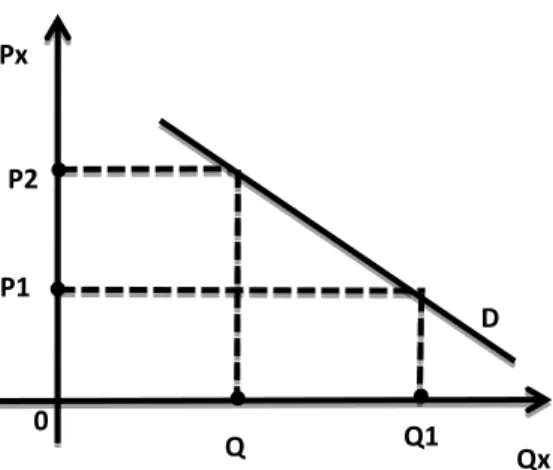
Dari gambar tersebut dapat dilihat bahwa bila harga turun dari P0 ke

P1 maka jumlah yang dimintanya akan bertambah dari x0 ke x1. Demikian

pula apabila harga naik dari P0 ke P1 maka jumlah yang diminta akan

berkurang dari x0 ke x1. X P X2 X1 P2 X0 P0 P1 0 D

Dari uraian di atas terlihat bahwa terdapat suatu pola hubungan antara variabel kuantitas barang yang diminta dengan variabel harga barang tersebut.

Hubungan antara kedua variabel tersebut dapat dinyatakan dalam suatau formula yang disebut fungsi permintaan. Dan dinyatakan x f(P) dimana x : variabel kuantitas dan P: variabe harga.

Di dalam fungssi permintaan, variabel yang menentukan (independent variabel) tidak harga barang saja, tetapi juga harga dan jumlah barang-barang substitusi. Hubungan variabel tersebut dinyatakan sebagai:

,...) , , (x2 x3 x4 f x

Dimana: x₁ : variabel kuantitas yang diminta x₂ : variabel harga barang

x₃: variabel kuantitas yang diminta akan barang substitusi x₄: harga barang substitusi

dan seterusnya.

Pola hubungan variabel yang diminta dengan variabel harga berbentuk garis lurus yaitu fungsi linear, dan dapat berbentuk garis tidak lurus yaitu fungsi non linear.

B.

Fungsi dan

Curve

Penawaran (

Supply

)

Supply adalah jumlah barang yang ditawarkan pada berbagai tingkat harga. Dalam hukum penawaran kita melihat bahwa besar kecilnya jumlah yang ditawarkan akan suatu barang tersebut, dengan catatan faktor-faktor yang lain tetap.

Jika harga dari suatu barang naik, maka jumlah yang ditawarkan akan barang tersebut bertambah karena produsen berusaha untuk menggunakan kesempatan memperbesar keuntungannya, sebaliknya jika harga barang itu turun maka jumlah yang ditawarkan akan berkurang karena produsen berusaha mengurangi kerugiannya. Gambar kurve penawaran suatu barang:

X P X2 X1 P2 X0 P0 P1 0 S

Matematika Ekonomi Dari gambar tersebut dapat dilihat bahwa bila harga suatu barang naik dari P0 ke P1 maka jumlah yang ditawarkan akan bertambah dari x0

ke x1. sebaliknya jika harga turun dari P0 ke P1 maka jumlah yang

ditawarkan akan berkurang.

Dari uraian di atas terlihat bahwa terdapat suatu pola hubungan dari variabel kuantitas atau jumlah barang yang ditawarkan dengan variabel harga barang tersebut.

Apabila pola hubungan tersebut dinyatakan dalam suatau formula maka formula tersebut dinyatakan sebagai fungsi penawaran. Dan dinyatakan x f(P)dimana x: variabel kuantitas dan P: variabe harga.

Di dalam fungsi penawaran yang menentukan tidak satu, tetapi dapat lebih dari satu maka hubungan variabel-variabel tersebut dinyatakan sebagai: ,...) , , ( 2 3 4 1 f x x x x 

Dimana: x₁

:

variable kuantitas

x2

:

variabel harga

x₃

:

biaya produksi

x4

:

kuantitas barang yang tersedia dari bahan bakunya

dan seterusnya.

Pola hubungan variabel kuantitas yang ditawarkan dengan variabel harga berbentuk garis lurus yaitu fungsi linear, dan dapat berbentuk garis tidak lurus yaitu fungsi non linear.

C.

Keseimbangan Pasar (

Market Equilibrium

)

Yang dimaksud dengan “pasar” adalah pertemuan antara pembeli (peminta) dan penjual (penawar) baik dalam pengertian langsung maupun tidak (secara komunikatif). Sedangkan “harga pasar” adalah harga yang terjadi pada titik keseimbanga pasar. Dan titik keseimbangan pasar adalah titik pertemuan permintaan dan penawaran. Sehingga titik keseimbangan pasar ditentukan oleh titik perpotongan antara curve permintaan dan

Curve penawaran.

Di dalam menentukan titik keseimbanagn pasar untuk suatu barang atau jasa, perlu diperhatikan syarat-syarat yang perlu dipenuhinya. Adapun syarat-syarat titik keseimbangan pasar adalah

1. Titik keseimbangan pasar hanya berlaku untuk nilai-nilai yang positif 2. Titik keseimbangan pasar hanya berlaku untuk titik yang memenuhi

ketentuan bagi Curve permintaan dan Curve penawaran.

Atas dasar dua persyaratan tersebut maka tidak mungkin terdapat dua titik keseimbangan pasar bagi Curve permintaan dan Curve

penawaran, walaupun mungkin terdapat dua titik potong dari fungsi permintaan dan penawaran.

Grafik

Apabila melihat gambar di atas, maka titik A adalah titik seimbangan pasar dan titik B bukan titik.

Contoh:

Curve permintaan barang tersebut dapat digambarkan dengan mencari titik potong fungsi dengan sumbu x dan p.

12 2 : x p D 3 2 : x p S Sehingga 3 2 12 2     p p 4p15 4 3 3  p 2 1 4  x

Titik keseimbangan pasar

Bukan titik keseimbangan pasar

X D B S A P

Matematika Ekonomi

Jadi, titik keseimbangan pasar pada E ) 4 3 3 , 2 1 4 ( .

D.

Subsidi

Subsidi merupakan bantuan yang diberikan pemerintah kepada produsen/suplier terhadap produk yang dihasilkan atau dipasarkannya sehingga harga yang berlaku di pasar adalah harga yang diinginkan pemerintah.

Besarnya subsidi yang diberikan biasanya tetap untuk setiap unit barang yang dihasilkan atau dipasarkan. Notasi besarnya subsidi untuk tiap unit barang yang dihasilkan atau dipasarkan dinyatakan dengan S.

Oleh karena adanya subsidi, maka tingkat harga yang berlaku di pasar lebih rendah. Hal ini disebabkan sebagian dari biaya-biaya untuk produksi dan memasarkan barang tersebut ditanggung pemerintah yaitu sebesar subsidi. Sehingga dengan adanya subsidi maka fungsi penawaran akan turun atau bergeser ke bawah, sedangkan fungsi permintaan tetap.

Dengan adanya subsidi sebesar

s

maka tingkat harga yang ditawar-kan oleh penjual (penawar) aditawar-kan turun sebesar

s

untuk setiap tingkat/ jumlah/kualitas yang ditawarkan. Bila dilihat pengaruh subsidi sebesar

s

ini, jika x adalah variabel kuantitas, p variabel harga maka fungsi penawaran akan bergeser ke bawah sebesar

s

untuk setiap kuantitas yang ditawarkan. Dalam bentuk fungsi penawaran sebelum subsidi adalah

) (x f

p maka fungsi penawaran sesudah subsidi adalah p f(x)s.

(12,0)

X

9 3 E 6 (0,6) D: x = -2p + 12 S: x = 2p - 3 P

Dalam bentuk umum yang lain dari fungsi penawaran x f(p) maka fungsi penawaran sesudah subsidi dapat dirubah dari p1 f(x)s menjadi f(x) p₁s. Dengan mensubstitusikan ke dalam bentuk fungsi

) (p f

x , maka didapat fungsi penawaran sesudah subsidi menjadi ) ( : _{1 1} 1 x f p s s   . Contoh:

Diketahui fungsi permintaan suatu barang adalah p x 2 1 10

 dan fungsi penawaran p42x dimana x = variabel kuantitas dan p = variabel harga. Bila terhadap barang tersebut diberikan subsidi sebesar

2



s , maka :

1. Tentukan titik keseimbangan pasar sebelum subsidi 2. Tentukan keseimbangan pasar sesudah subsidi

3. Gambarkan grafik fungsi atau Curve permintaan dan penawaran sebelum dan sesudah subsidi.

Penyelesaian:

1. Titik keseimbangan pasar sebelum subsidi:

x p D 2 1 10 :   x p S : 42 Sehingga x 2 4 2 1 10   E1 (X1,P1) X P S E (X0,P0) S1 X0 P1 X1 P0 D

Matematika Ekonomi 6 2 1 2 x 8 , 8 4 , 2 2 5 6    p x

Jadi titik keseimbangan pasar sebelum subsidi E (2,4; 8,8). 2. Titik keseimbangan pasar setelah subsidi:

x p D 2 1 10 :   x x s x p S : 42  42 222 Sehingga x 2 2 2 1 10   4 , 8 2 , 3 2 5 8 8 2 1 2     p x x

Jadi titik keseimbangan pasar sebelum subsidi E (3,2; 8,4). 3. Curve E X 1 0 D S1 S E1 P 2 0

E.

Monopoli dan Pengaruh Pajak

Tujuan utama dalam monopoli adalah memperoleh laba yang maksimal. Hal-hal yang berkaitan di dalam laba adalah harga dan kuantitas yang dikehendaki. Tiga faktor dalam monopoli:

1. T.R (Total Revenue) : P.Q 2. Biaya (TC)

3. Laba maksimal (NR) dimana : NR = TR – TC Syarat terjadinya laba yang maksimal:

MC MR dQ dTC dQ dTR dQ dTC dQ dTR dQ dTC dQ dTR NR dQ TC TR d NR TC TR NR NR NR             0 ' ) ( ' 0 '' 0 '

Dengan adanya pajak sebesar t/unit yang dikenakan terhadap barang yang diproduksi oleh seorang pengusaha monopoli maka akan menimbulkan seolah-olah biaya rata-rata per-unit meningkat sebesar p, berarti biaya secara keseluruhan meningkat sebesar tQ.

Misal: pajak : t/unit, maka andaikan:

10



AC (biaya rata-rata sebelum pajak)

t

AC

1



10



(biaya rata-rata sesudah pajak)

Q

AC

TC

₁



.

Q

t

AC

TC

₁



(



).

tQ

ACQ

TC

₁





Sehingga dirumuskan: AC₁ACt tQ ACQ TC₁ 

atau

TC₁TCtQ

Matematika Ekonomi

BAB IV

DIFERENSIAL DAN INTEGRAL

A.

Diferensial

1. Pengertian Diferensial

Definisi

Persamaan diferensial adalah suatu persamaan yang memuat variabel bebas, variabel tak bebas dan derivatif-derivatif dari variabel tak bebas terhadap variabel bebas. Menurut banyaknya variabel bebas persamaan diferensial dibedakan menjadi 2 yaitu:

a. Persamaan diferensial biasa (jika terdapat 1 variabel bebas), b. Persamaan diferensial parsial (jika terdapat lebih dari 1 variabel

bebas).

Untuk lebih jelasnya dapat dilihat pada Contoh 1. Contoh 1.

a. xy0 dx

dy

_,

_dengan dx

dy _{derivatif dari variabel tak bebas y}

terhadap variabel bebas

x

.

b. ₂ 0 2    y dy dz dx z d x , dengan ₂ 2 dx z d _dan dy

dz_{derivatif dari variabel tak}

bebaszterhadap variabel bebas

x

dan y. 2. Pengertian Diferensiabel

Suatu persamaan/fungsi dikatakan diferensiabel yaitu apabila fungsi/ persamaan tersebut dapat dicari/ditemukan turunannya. Suatu fungsi dapat dikatakan memiliki suatu turunan/diferensial apabila nilai limit

) ) ( ) ( (lim a x a f x f a x _   ada.

3. Aturan Diferensiasi dan Penggunaannya dalam Statika Komparatif Analisis statis komparatif, yaitu mencari tingkat perubahan, dapat diidentifikasi dengan permasalahan mencari derivatif dari beberapa fungsi y = f(x), asalkan hanya perubahan kecil dalam x. Jadi konsep derivatif menjelaskan tingkat perubahan dari suatu fungsi yang terdiri dari variabel dependen dan variabel independen. Tingkat perubahan tersebut menangkap sejumlah perubahan (atau perubahan dalam jumlah yang sangat kecil) dari variabel dependen sebagai dampak dari perubahan variabel independen. Istilah derivatif dapat dinyatakan dengan :

0 lim x dy y dx  x    Δ

Dalam hal ini, dy

dx merupakan suatu pernyataan gabungan yang dibaca dengan ”derivatif y berkaitan x”. Derivatif ini sama dengan limit

dari rasio y x 

 saat Δx mendekati nol. Selain itu, derivatif mengukur tingkat kemiringan kurva linear. Derivatif dapat dinyatakan dengan bentuk-bentuk lain, seperti :

a. dx dy b. f x'( ) untuk fungsi y f x( ) c. y x'( ) untuk fungsi y y x( )

Atau derivatif juga dapat dinyatakan dengan d y

dx atau ( ) d f x dx . Sebagai contoh :

Derivatif yψ( )x dapat dinyatakan sebagai : a. dy dx b.ψ' c.ψ_x d. d y dx e. d ( )x dxψ

Matematika Ekonomi 4. Aturan Diferensiasi untuk Fungsi dengan Satu Variabel

Proses penentuan derivatif dari suatu fungsi juga dikenal dengan istilah diferensiasi. Suatu fungsi terdiri dari satu variabel bebas (single independent variable) : y = k (fungsi konstan), y = xn, dan y = cxn (fungsi pangkat). Misalkan suatu fungsi y = f(x), derivatif mencari berapa besar perubahan y ketika terjadi perubahan x apabila perubahan x, yaitu Δx,

mendekati nol. Untuk menerapkan derivatif dalam konteks ekonomi, terlebih dahulu perlu dipahami beberapa aturan diferensiasi.

a. Aturan Fungsi Konstan

Derivatif fungsi konstan y = k, atau f(x) = k, adalah sama dengan nol, yakni nol untuk semua nilai x.

' 0, ( ) 0 dy dk f x dx  dx   atau ( ) 0 d d d y f x k dx  dx  dx  Bentuk d y dx

mempunyai dua bagian. Pertama, bentuk d dx merupakan simbol operator, yang memerintahkan untuk melakukan operasi diferensiasi. Kedua, fungsi yang akan dioperasikan (yang akan dideferensiasikan), y = f(x) = k. Contoh : 1) Apabila y = f(x) = 5 maka dy 0 dx 2) Apabila y = f(x) = -13 maka dy 0 dx  b. Aturan Fungsi Linear

Derivatif fungsi linear y = a+bx, maka derivatifnya adalah b

yang merupakan koefisien dari x. Misalkan :

bx a y  maka dy b dx  Contoh : 1) Apabila y = 5 + 6x maka 6 dx dy

2) Apabila y = -13 + 10x maka



10

dx

dy

3) Apabila y = -7 + (10/3)x maka 3 10  dx dy

Yang perlu dicatat adalah derivatif dy

dx mengukur tingkat

perubahan dari fungsi atau kemiringannya. Untuk fungsi y = a + bx, kemiringan fungsi linear adalah b. Nilai b adalah koefisien dari variabel bebas dan b adalah konstanta.

c. Aturan Fungsi Pangkat

Derivatif fungsi pangkat y = f(x) = axn, adalah naxn-1. Derivatif dari fungsi tersebut adalah :

1) Perkalian antara eksponen (n) dengan konstanta (a).

2) Selanjutnya, hasil perhitungan sebelumnya dikalikan dengan

x dengan dipangkatkan n-1.

Secara simbolis, hal ini dituliskan sebagai.

1 n n d ax nax dx  

atau

' 1 ( ) n f x nax  Contoh : 1) Derivatif y = x3 adalah _x3 _3x2 dx d dx dy_{ } 2) Derivatif y = -13 + 10x4 adalah _{x 13 10x}4 _40x3 dx d dx dy _{   } 3) Derivatif y = 1/x3 adalah 3 4 3 1_  _   x x dx d x dx d dx dy

Latihan

1) Carilah derivatif dari : y = 7x5, dan w = 3u-1. 2) Carilah f’(1) dan f”(2) dari fungsi berikut :

Matematika Ekonomi 5. Aturan Diferensiasi yang Melibatkan Dua atau Lebih Fungsi dari

Variabel yang Sama

a. Aturan Penjumlahan – Pengurangan

Derivatif penjumlahan (pengurangan) dari dua fungsi adalah penjumlahan (pengurangan) dari derivatif dua fungsi. Misalkan ada dua fungsi, f(x) dan g(x), maka derivatifnya adalah :





' ' ( ) ( ) ( ) ( ) ( ) ( ) d d d f x g x f x g x f x g x dx  dx dx   Contoh :

1) Derivatif dari penjumlahan f(x) = 5x3 dan g(x) = 9x3, adalah :

3 3 3 3 2 2 2

5 9 5 9 15 27 42

dy d d d

x x x x x x x

dxdx  dx dx   

2) Derivatif dari f(x) = 5x3 dikurangi g(x) = 9x3, adalah :

3 3 3 3 2 2 2

5 9 5 9 15 27 12

dy d d d

x x x x x x x

dxdx  dx dx    

b. Aturan Hasil – Kali

Derivatif dari hasil – kali dua fungsi (yang dideferensiasikan) adalah sama dengan fungsi yang pertama dikalikan derivatif fungsi kedua ditambah fungsi kedua dikalikan derivatif fungsi pertama.



( ) ( )



( ) ( ) ( ) ( ) d d d f x g x f x g x g x f x dx  dx  dx ' ' ( ) ( ) ( ) ( ) f x g x g x f x   Atau





' ' ( ) ( ) ( ) ( ) ( ) ( ) d f x g x f x g x f x g x dx   Contoh :

1) Carilah derivatif dari y = (2x + 3)(3x2).

Misalkan f(x) = 2x + 3 dan g(x) = 3x2. Selanjutnya f’(x) 2 dan g’(x) = 6x, maka derivatifnya adalah :





 

2



 

 

2

 

2

2 3 3 2 3 6 3 2 18 18

d

x x x x x x x

2) Carilah derivatif dari y = (2x – 5)(3x4).

Misalkan f(x) = 2x – 5 dan g(x) = 3x4. Selanjutnya f’(x) 2 dan g’(x) = 12x3

, maka derivatifnya adalah :





 

4







3

  

4

 

4 3 4 2 5 3 2 5 12 3 2 24 60 6 d x x x x x x x x dx        4 3 30x 60x  

c. Aturan Hasil – Bagi

Derivatif dari hasil – bagi dua fungsi (yang dideferensiasikan) adalah sama dengan derivatif fungsi yang berada pada pembilang dikalikan fungsi yang berada pada penyebut dikurangi fungsi yang berada pada pembilang dikalikan derivatif fungsi yang berada pada penyebut, kemudian dibagi dengan fungsi yang berada pada penyebut yang telah dikuadratkan.

' ' 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) d f x f x g x f x g x dx g x g x   Contoh : a. 2 2 ) 1 ( 5 ) 1 ( ) 1 )( 3 2 ( ) 1 ( 2 1 3 2                x x x x x x dx d b.









2 2 2 2 2 _{2 2} 5 5( 1) 5 (2 ) 5(1 ) 1 _{1 1} d x x x x x dx x _{x x}     _{  }  _     

6. Aturan Diferensiasi yang Melibatkan Fungsi-fungsi dari Variabel yang Berbeda

Untuk bentuk fungsi dari fungsi y = f(u) dimana u = g(x), maka derivatifnya adalah derivatif fungsi pertama yang berkaitan dengan u

dikalikan dengan derivatif fungsi kedua berkaitan dengan x. Aturan ini sering kali dikenal dengan ”aturan berantai” atau chain rule, sering disebut juga ”aturan fungsi komposit”. Bentuk Chain Rule adalah :

. dy dy du dx du dx Contoh :

a. Carilah derivatif dari z = 3y2, dimana y = 2x + 5.

. 6 (2) 12 12(2 5) 24 60

dz dz dy

y y x x

Matematika Ekonomi b. Carilah derivatif dari z = y – 3, dimana y = x3.

 

2 2

1 3 3

dz

x x

dx 

c. Carilah derivatif dari y = u4, dimana u = 2x2 + 3.





3 3 3 2 . 4 .4 16 16 2 3 dy dy du u x xu x x dxdu dx     Contoh: Jika f(x)= x3 + 7x, Carilah f’(c) Penyelesaian h c f h c f c f h ) ( ) ( lim ) ( ' 0     h c c h c h c c f h ) 7 ( )] ( 7 ) [( lim ) ( ' 3 3 0        h h h ch h c c f h ) 7 3 3 ( lim ) ( ' 3 2 2 0      7 3 ) 7 3 3 lim ) ( ' 2 2 2 0        c ch h c c f h

7. Diferensial Quotient / Diferensial Fungsi Aljabar

Secara umum diferensial quotient fungsi y = f(x) dilambangkan dengan: x x f x x f x y x _         ) ( ) ( lim 0 Bentuk x y 

 _{inilah yang disebut dengan hasilbagi perbedaan atau}

diferensial quotient, mencerminkan tingkat perubahan rata-rata variabel terikat y terhadap variabel bebas x.

Contoh: Carilah turunan dari fungsi f₍x₎₃x2x _! Turunan dari fungsi di atas, yaitu:

x x y₃ 2 ) ( ) ( 3_{x x} 2 _{x x} y y     x x x x x x y y 3( 22  ( )2) 