PENDEKATAN NUMERIK KONTROL SISTEM PILOT
OTOMATIS UNTUK GERAK LONGITUDINAL
PESAWAT DENGAN METODE PARKER-SOCHACKI
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Fisika
oleh
NIKEN SAWITRI NIM: 073214001
PROGRAM STUDI FISIKA JURUSAN FISIKA
FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS SANATA DHARMA
ii
NUMERICAL APPROACH FOR AUTOMATIC CONTROL
OF THE LONGITUDINAL MOTION OF FLIGHT SYSTEM
USING PARKER-SOCHACKI METHODS
SCRIPTION
Presented as Partial Fulfillment for the Requirement to Obtain the Sarjana Science
in Physics Department
by
NIKEN SAWITRI NIM : 073214001
PHYSICS STUDY PROGRAM PHYSICS DEPARTMENT
FACULTY OF SCIENCE DAN TECHNOLOGY SANATA DHARMA UNIVERSITY
v
tiada burung yang terbang terlalu tinggi saat dia
terbang dengan sayapnya sendiri
usaha yang tanpa menyerah jauh
lebih berharga dibanding hasil
yang gemilang
Saya persembahkan karya ini kepada
Orang tua dan Kakak tercinta
viii
ABSTRAK
PENDEKATAN NUMERIK KONTROL SISTEM PILOT OTOMATIS UNTUK GERAK LONGITUDINAL PESAWAT DENGAN METODE
PARKER-SOCHACKI
ix
ABSTRACT
NUMERICAL APPROACH FOR AUTOMATIC CONTROL OF THE LONGITUDINAL MOTION OF FLIGHT SYSTEM USING
PARKER-SOCHACKI METHODS
xii
DAFTAR ISI
Halaman
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN MOTTO ... v
HALAMAN PERSEMBAHAN ... v
HALAMAN PERNYATAAN KEASLIAN KARYA ... vi
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ... vii
ABSTRAK ... viii
ABSTRACT ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
DAFTAR GAMBAR ... xv
xiii
1.1. Latar Belakang Masalah ... 1
1.2. Rumusan Masalah ... 3
1.3. Batasan Masalah ... 3
1.4. Tujuan Penelitian ... 4
1.5. Manfaat Penelitian ... 4
1.6. Sistematika Penulisan ... 5
BAB II DASAR TEORI ... 6
2.1. Sistem Kontrol ... 6
2.2. Pendekatan Numerik dengan Metode Parker- Sochacki ... 9
2.3. Pendekatan Numerik dengan Metode Runge-Kutta Orde Empat ... 10
2.4. Persamaan Gerak Longitudinal Pesawat ... 12
BAB III METODE PENELITIAN ... 17
3.1. Desain Sistem Kontrol Pilot Otomatis ... 17
3.2. Penyelesaian Analitik Sistem Kontrol Pilot Otomatis Sebagai Pembanding ... 20
3.3. Penerapan Metode Parker-Sochacki ... 21
xiv
3.5. Algoritma ... 26
BAB IV HASIL DAN PEMBAHASAN ... 29
4.1. Komputasi Penyelesaian Analitik Sistem Kontrol Pilot Otomatis untuk Penerbangan ... 30
4.2. Pendekatan Numerik Sistem dengan Gangguan dan Tanpa Kontrol ... 34
4.3. Pendekatan Numerik Sistem Terkontrol dengan Gangguan Bervariasi dengan Metode Parker-Sochacki 36 4.4. Pendekatan Numerik dengan Metode Runge-Kutta Sebagai Pembanding ... 44
BAB V KESIMPULAN ... 51
5.1. Kesimpulan ... 51
5.2. Saran ... 52
DAFTAR PUSTAKA ... 53
xv
DAFTAR GAMBAR
Halaman
Gambar 2.1 : Grafik pendekatan Runge-Kutta ... 12
Gambar 2.2 : Gambar arah gerak pesawat ... 15
Gambar 3.1 : Algoritma penyelesaian analitik sistem kontrol pilot
otomatis untuk penerbangan ... 26
Gambar 3.2 : Algoritma pendekatan numerik penyelesaian sistem
kontrol pilot otomatis untuk penerbangan dengan metode
Parker-Sochacki ... 27
Gambar 3.3 : Algoritma pendekatan numerik penyelesaian sistem
kontrol pilot otomatis untuk penerbangan dengan metode
Runge-Kutta ... 28
Gambar 4.1 : Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dengan
penyelesaian analitik ... 31 Gambar 4.2 : Perbandingan penyelesaian analitik, pendekatan numerik
Parker-Sochacki, dan pendekatan numerik Runge-Kuta .... 32 Gambar 4.3 : Perubahan sudut kemiringan pesawat (∆𝜃𝜃) tanpa
xvi
Gambar 4.4 : Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator
(∆𝛿𝛿𝑒𝑒) tanpa gangguan angin, dengan kontrol ... 37 Gambar 4.5 : Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator
(∆𝛿𝛿𝑒𝑒) untuk 𝑢𝑢𝑔𝑔R
𝑞𝑞𝑔𝑔 = 0 derajat/s ... 38 = 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan
Gambar 4.6 : Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator (∆𝛿𝛿𝑒𝑒) untuk 𝑢𝑢𝑔𝑔R
Gambar 4.8 : Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator (∆𝛿𝛿𝑒𝑒) untuk 𝑢𝑢𝑔𝑔R
𝑞𝑞𝑔𝑔 = 1 × 10−3 derajat/s... 42 = 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan
Gambar 4.9 : Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator (∆𝛿𝛿𝑒𝑒) untuk 𝑢𝑢𝑔𝑔R
𝑞𝑞𝑔𝑔 = 1 × 10−2 derajat/s ... 43 = 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan
Gambar 4.10 : Perubahan sudut kemiringan pesawat (∆𝜃𝜃) untuk ℎ = 0,1 s 45 Gambar 4.11 : Perubahan sudut kemiringan pesawat (∆𝜃𝜃) untuk
xvii
ℎ = 0,001 s ... 47 Gambar 4.13 : Perbandingan simulasi menggunakan pendekatan numerik
Runge-Kutta untuk interval waktu 0,1 detik, 0,01 detik, dan 0,001 detik dengan pendekatan numerik
1
BAB I
PENDAHULUAN
1.1. Latar Belakang Masalah
Pada saat pesawat terbang dibuat dan diterbangkan pertama kali, pesawat
tersebut hanya mampu bekerja dalam waktu yang relatif singkat. Seiring dengan
perkembangan teknologi, kemampuan kerja pesawat terbang mulai ditingkatkan
melalui berbagai penelitian. Kemampuan kerja yang meningkat tersebut
memungkinkan pesawat untuk terbang lebih jauh dan lebih lama. Penerbangan yang
lebih lama membutuhkan konsentrasi tinggi dan terus menerus dari pilot yang
menerbangkannya. Hal tersebut dapat menimbulkan kelelahan yang mengakibatkan
menurunnya konsentrasi pilot sehingga dapat terjadi kecelakaan pesawat terbang.
Untuk mengatasi hal tersebut, mulai dikembangkan sistem untuk
mengendalikan laju pesawat terbang tanpa pengawasan manusia. Sistem ini sering
disebut sistem pilot otomatis. Sistem pilot otomatis berfungsi mengatur gerak kontrol
pesawat untuk menggerakkan pesawat sesuai dengan yang diharapkan. Ada beberapa
jenis gerak pesawat, salah satunya adalah gerak longitudinal, yaitu gerak pesawat
naik dan turun yang disebabkan perubahan sudut antara pesawat dengan garis
horisontal. Gerak pesawat ini diatur menggunakan bagian pesawat yang disebut
elevator [Nelson, 1998]. Oleh karena itu, untuk mengendalikan gerak longitudinal
Terdapat beberapa metode yang dapat digunakan untuk mendesain kontrol
sistem pilot otomatis. Salah satunya adalah dengan metode state space (ruang
keadaan). Metode ini pada dasarnya digunakan untuk mendeskripsikan karakteristik
suatu sistem dalam bentuk persamaan diferensial [Groesen dan Molenaar, 2007].
Dengan mengetahui karakteristik suatu sistem, dapat dicari kontrol yang tepat untuk
mengendalikan sistem agar stabil.
Persamaan-persamaan diferensial yang merupakan karakter sistem yang
telah dikontrol tersebut dapat disimulasikan menggunakan pendekatan numerik.
Simulasi ini berguna untuk memprediksi respon sistem terhadap kontrol yang
diberikan sebelum kontrol yang sebenarnya dibuat. Hal ini membantu menekan biaya
eksperimen dengan mencegah kesalahan yang mungkin dibuat dalam mendesain
kontrol sistem tersebut.
Salah satu pendekatan numerik yang dapat dilakukan adalah dengan metode
iterasi Picard.
Untuk menanggulangi kelemahan dari metode iterasi Picard, G. Edgar
Parker dan James S. Sochacki melakukan modifikasi untuk menyatakan iterasi Picard
dalam bentuk yang lebih sederhana. Modifikasi ini kemudian disebut metode
Parker-Sochacki [Steward dan Bair, 2009]. Berkat metode Parker-Parker-Sochacki, pendekatan
Kelebihan dari metode iterasi ini adalah akurasi nilai keluaran yang
lebih tinggi untuk pendekatan dengan orde yang lebih tinggi. Namun, karena
menggunakan integrasi untuk menyatakan pendekatan pada setiap orde, untuk orde
numerik suatu persamaan diferensial lebih mudah dilakukan dengan hasil yang lebih
akurat dibandingkan dengan solusi menggunakan metode numerik lainnya.
Pendekatan numerik dengan metode Parker-Sochacki ideal digunakan untuk
melakukan simulasi kontrol dan respon sistem pilot otomatis untuk penerbangan yang
dirumuskan dengan metode ruang keadaan. Selain itu, metode pendekatan numerik
ini mampu memprediksi keadaan sistem dengan lebih akurat sehingga kontrol sistem
dapat disesuaikan dengan keadaan sistem secara lebih cepat dan akurat. Dengan
demikian, diharapkan dapat dirumuskan desain kontrol sistem pilot otomatis untuk
penerbangan yang lebih baik dengan bantuan metode ini.
1.2. Rumusan Masalah
Berdasarkan latar belakang yang telah disampaikan, yang menjadi
permasalahan adalah perumusan desain kontrol sistem pilot otomatis gerak
longitudinal pesawat menggunakan kombinasi antara metode ruang keadaan dan
metode pendekatan numerik Parker-Sochacki.
1.3. Batasan Masalah
Permasalahan yang diteliti pada penelitian ini dibatasi pada masalah yang
menyangkut:
1. Penggunaan metode ruang keadaan untuk merumuskan karakter sistem dan
kontrol optimal pilot otomatis untuk mengendalikan gerak longitudinal
2. Penggunaan penyelesaian analitik untuk merumuskan respon pesawat yang
tidak terkena gangguan terhadap kontrol dan dibandingkan dengan
penyelesaian menggunakan pendekatan numerik dengan metode
Parker-Sochacki dan metode Runge-Kutta untuk kasus yang sama.
3. Penggunaan kombinasi metode ruang keadaan dan pendekatan numerik
dengan metode Parker-Sochacki untuk merumuskan desain kontrol dan
respon sistem pilot otomatis pesawat yang mendapatkan gangguan.
4. Penggunaan kombinasi metode ruang keadaan dan pendekatan numerik
dengan metode Runge-Kutta untuk merumuskan desain kontrol untuk
pesawat yang dikenai gangguan dan dibandingkan dengan pendekatan
numerik menggunakan metode Parker-Sochacki untuk kasus yang sama.
1.4. Tujuan Penelitian
Tujuan dari penelitian ini adalah untuk merumuskan desain kontrol sistem
pilot otomatis untuk mengendalikan gerak longitudinal pesawat menggunakan
kombinasi metode ruang keadaan dan pendekatan numerik dengan metode
Parker-Sochacki.
1.5. Manfaat Penelitian
Manfaat dari penelitian ini adalah:
1. Mendapatkan desain optimal kontrol sistem pilot otomatis untuk
2. Menambah pustaka di bidang fisika komputasi mengenai pendekatan
numerik dengan metode Parker-Sochacki untuk melakukan desain kontrol
sistem pilot otomatis untuk mengendalikan gerak longitudinal pesawat.
1.6. Sistematika Penulisan
BAB I Pendahuluan
Pada bab I akan diuraikan latar belakang masalah, rumusan masalah,
batasan masalah, tujuan penelitian, manfaat penelitian, dan sistematika
penulisan.
BAB II Dasar Teori
Bab II berisi penguraian tentang sistem kontrol dengan metode ruang
keadaan, pendekatan numerik dengan metode Parker-Sochacki,
pendekatan numerik dengan metode Runge-Kutta orde 4, dan
persamaan gerak longitudinal pesawat terbang.
BAB III Metode Penelitian
Bab III menguraikan langkah-langkah yang dilakukan saat penelitian.
BAB IV Hasil dan Pembahasan
Pada bab IV akan diuraikan hasil penelitian dan pembahasan
penelitian.
BAB V Penutup
6
BAB II
DASAR TEORI
2.1. Sistem Kontrol
Sistem merupakan kumpulan berbagai elemen yang saling berinteraksi
sedemikian rupa sehingga perubahan keadaan sebuah elemen akan mempengaruhi
keadaan elemen yang lain. Interaksi antar elemen tersebut dapat dikendalikan
sedemikian rupa sehingga dihasilkan keadaan elemen yang sesuai dengan keluaran
yang diharapkan. Sistem yang telah dikendalikan disebut sistem terkontrol [Meyers,
1992].
Perumusan proses kontrol sebuah sistem dimulai dengan menganalisis
karakter sistem tersebut. Untuk mempermudah proses analisis, suatu sistem dapat
dinyatakan dalam bentuk persamaan-persamaan diferensial. Salah satu metode yang
dapat digunakan untuk menyatakan persamaan karakter sistem adalah metode ruang
keadaan (state space). Metode ruang keadaan pada dasarnya merupakan perumusan
persamaan-persamaan diferensial orde satu yang mendeskripsikan karakteristik
sistem yang dianalisis [Nelson, 1998].
Metode ruang keadaan dinyatakan dalam bentuk persamaan [Ogata, 1985]
𝑥𝑥⃗̇=𝑨𝑨𝑥𝑥⃗+𝑩𝑩𝜇𝜇⃗ (2.1)
Dengan 𝑨𝑨 adalah matriks keadaan sistem, 𝑩𝑩 adalah matriks masukan, 𝑪𝑪 adalah
matriks keluaran, 𝑥𝑥⃗ adalah variabel keadaan, 𝜇𝜇⃗ adalah masukan yang diberikan, dan 𝑦𝑦⃗
adalah keluaran yang dihasilkan.
Dengan memperhitungkan pengaruh gangguan pada sistem, persamaan
ruang keadaan suatu sistem juga dapat dituliskan sebagai berikut [Nelson, 1998]
𝑥𝑥⃗̇=𝑨𝑨𝑥𝑥⃗+𝑩𝑩𝜇𝜇⃗+𝑫𝑫𝜀𝜀⃗ (2.3)
𝑦𝑦⃗=𝑪𝑪𝑥𝑥⃗ (2.4)
Dengan 𝑫𝑫 adalah matriks gangguan sistem dan 𝜀𝜀⃗ adalah variabel gangguan.
Pengendalian pada sistem dalam bentuk ruang keadaan dengan
menggunakan karakter sistem melalui huku m kontrol dinyatakan dalam persamaan
[Nelson, 1998]
𝜇𝜇⃗=−𝑘𝑘𝑇𝑇𝑥𝑥⃗+𝜇𝜇′ (2.5)
dengan 𝑘𝑘𝑇𝑇 adalah transpose feedback dan 𝜇𝜇′ adalah masukan yang diberikan tanpa
adanya feedback (masukan awal).
Persamaan (2.1) yang dikombinasikan dengan persamaan (2.5) akan
mengubah persamaan ruang keadaan sistem terkontrol menjadi [Nelson, 1998]
𝑥𝑥⃗̇= (𝑨𝑨 − 𝑩𝑩𝑘𝑘𝑇𝑇)𝑥𝑥⃗+𝑩𝑩𝜇𝜇′ (2.6)
Desain kontrol suatu sistem dapat dilakukan dengan cara menyamakan
diharapkan. Persamaan karakteristik sistem diperoleh melalui persamaan [Nelson,
1998]
|𝜆𝜆𝜆𝜆 −(𝑨𝑨 − 𝑩𝑩𝑘𝑘𝑇𝑇)| = 0 (2.7)
Sedangkan, karakteristik sistem yang diharapkan ditunjukkan melalui persamaan
[Nelson, 1998]
�𝜆𝜆2+ 2𝜉𝜉
𝑠𝑠𝑝𝑝𝜔𝜔𝑛𝑛𝑠𝑠𝑝𝑝𝜆𝜆+𝜔𝜔𝑛𝑛2𝑠𝑠𝑝𝑝� �𝜆𝜆2+ 2𝜉𝜉𝑝𝑝𝜔𝜔𝑛𝑛𝑝𝑝𝜆𝜆+𝜔𝜔𝑛𝑛2𝑝𝑝�= 0 (2.8)
Dengan 𝜉𝜉𝑠𝑠𝑝𝑝 adalah damping ratio untuk pergerakan dalam waktu singkat (short
phugoid motion), 𝜔𝜔𝑛𝑛𝑠𝑠𝑝𝑝 adalah frekuensi natural tak teredam untuk pergerakan dalam
waktu singkat, 𝜉𝜉𝑝𝑝 adalah damping ratio untuk pergerakan dalam waktu yang lama
(long phugoid motion) 𝜔𝜔𝑛𝑛𝑝𝑝 adalah frekuensi natural tak teredam untuk pergerakan
dalam waktu yang lama. Kontrol optimal diperoleh dengan memasukkan persamaan
karakteristik sistem yang diharapkan ke dalam persamaan karakteristik sistem yang
dimiliki sehingga dapat diperoleh nilai k yang optimal untuk setiap keadaan.
Persamaan (2.1) dapat diselesaikan dengan menggunakan metode analitik
dengan persamaan sebagai berikut
𝚽𝚽(𝑡𝑡) =ℒ−1[(𝑠𝑠𝐈𝐈 − 𝑨𝑨)−1] (2.9)
Dengan 𝚽𝚽(𝑡𝑡) adalah transisi matriks keadaan dan 𝑥𝑥⃗(0) adalah keadaan awal (pada
saat t = 0). Persamaan (2.9) dan (2.10) adalah penyelesaian persamaan keadaan
dengan matriks transisi dengan metode transformasi Laplace [Nelson, 1998].
2.2. Pendekatan Numerik dengan Metode Parker-Sochacki
Metode ruang keadaan digunakan untuk menyatakan kontrol sistem dalam
persamaan diferensial. Persamaan diferensial ini dapat dijabarkan melalui pendekatan
secara numerik menggunakan metode Picard. Metode ini pada dasarnya digunakan
untuk mencari solusi persamaan diferensial sederhana berbentuk
� 𝑦𝑦
′(𝑡𝑡) =𝑓𝑓(𝑡𝑡,𝑦𝑦)
𝑦𝑦(𝑡𝑡0) =𝑦𝑦0
(2.11)
dari hubungan berulang yang memenuhi [Parker dan Sochacki, 1996]
𝑦𝑦(𝑡𝑡) =𝑦𝑦0+∫ 𝑓𝑓�𝑠𝑠𝑡𝑡𝑡𝑡 ,𝑦𝑦(𝑠𝑠)�𝑑𝑑𝑠𝑠
0 (2.12)
dengan asumsi 𝑓𝑓 dan 𝜕𝜕𝑓𝑓 𝜕𝜕𝑦𝑦⁄ kontinyu di daerah sekitar (𝑡𝑡0,𝑦𝑦0). Secara khusus,
hubungan berulang tersebut dapat dinyatakan dalam bentuk [Parker dan Sochacki,
1996]
Untuk orde n yang semakin tinggi, metode tersebut semakin sulit dilakukan.
Picard pada persamaan diferensial sederhana dengan 𝑡𝑡0 = 0. Persamaan diferensial
sederhana tersebut dikonversi menjadi persamaan polinomial menggunakan substitusi
dan sistem penjumlahan [Parker dan Sochacki, 1996].
Pada metode ini, variabel sistem dengan orde yang lebih tinggi diselesaikan
menggunakan kondisi awal yang adalah variabel sistem orde sebelumnya. Bentuk
umum dari modifikasi iterasi Picard oleh Parker-Sochacki yaitu [Steward dan Bair,
2009]:
𝑦𝑦(𝑡𝑡+𝛥𝛥𝑡𝑡) =𝑦𝑦(𝑡𝑡) +∑𝑛𝑛𝑝𝑝=1𝑦𝑦𝑝𝑝(𝛥𝛥𝑡𝑡)𝑝𝑝 (2.14)
dengan 𝑦𝑦(𝑡𝑡) adalah nilai 𝑦𝑦 pada iterasi sampai ke 𝑡𝑡, 𝑦𝑦𝑝𝑝 adalah komponen y.
Metode Parker-Sochacki menawarkan penyelesaian yang lebih sederhana
dibandingkan dengan metode Picard, dengan tingkat ketelitian yang sama. Hanya
diperlukan satu persamaan untuk mendapatkan pendekatan numerik untuk setiap nilai
pada 𝑡𝑡.
2.3. Pendekatan Numerik dengan Metode Runge-Kutta Orde Empat
Selain menggunakan metode Parker-Sochacki, pendekatan numerik untuk
menjabarkan persamaan diferensial suatu sistem dapat dilakukan dengan metode
Runge-Kutta. Metode Runge-Kutta yang paling sering digunakan adalah metode
Runge-Kutta orde empat. Pada metode ini, persamaan diferensial dengan ketentuan
seperti pada persamaan (2.11), didekati dengan menggunakan persamaan [Chapra,
𝑦𝑦𝑖𝑖+1 =𝑦𝑦𝑖𝑖 +𝜙𝜙ℎ (2.15)
Dengan 𝜙𝜙 adalah fungsi penambahan, ℎ adalah interval waktu yang dipilih, 𝑘𝑘1adalah
slope pertama, 𝑘𝑘2 adalah slope kedua, 𝑘𝑘3 adalah slope ketiga, 𝑘𝑘4 adalah slope
keempat.
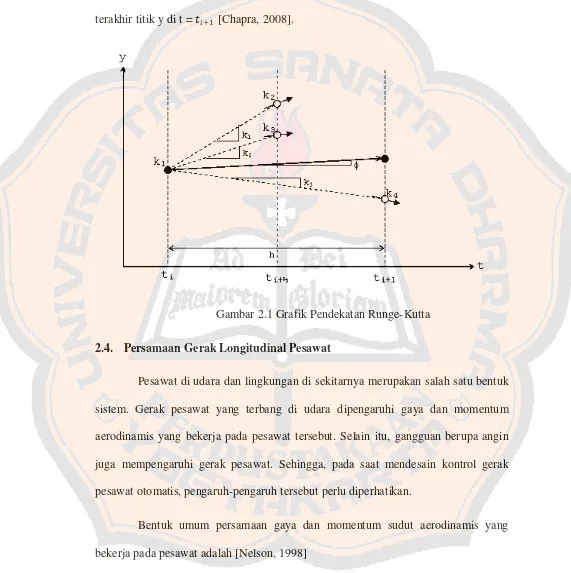
Grafik metode Runge-Kutta digambarkan pada grafik 2.1. 𝑘𝑘1 adalah kemiringan grafik pada awal interval waktu (pada saat t = 𝑡𝑡𝑖𝑖). Kemiringan grafik 𝑘𝑘1
ini kemudian digunakan untuk menentukan pendekatan pertama titik y dengan
kemiringan grafik 𝑘𝑘2 dan berada di t = 𝑡𝑡𝑖𝑖+1 2
. Kemiringan grafik 𝑘𝑘2 kemudian
digunakan untuk menentukan pendekatan titik y dengan kemiringan grafik 𝑘𝑘3 yang juga berada di titik t = 𝑡𝑡𝑖𝑖+1
2
. Kemiringan grafik 𝑘𝑘3 digunakan untuk menentukan
pendekatan ketiga titik y dengan kemiringan grafik 𝑘𝑘4 yang berada di t = 𝑡𝑡𝑖𝑖+1.
(2.16) untuk menghasilkan kemiringan rata-rata 𝜙𝜙 dalam menentukan pendekatan
terakhir titik y di t = 𝑡𝑡𝑖𝑖+1 [Chapra, 2008].
Gambar 2.1 Grafik Pendekatan Runge-Kutta
2.4. Persamaan Gerak Longitudinal Pesawat
Pesawat di udara dan lingkungan di sekitarnya merupakan salah satu bentuk
sistem. Gerak pesawat yang terbang di udara dipengaruhi gaya dan momentum
aerodinamis yang bekerja pada pesawat tersebut. Selain itu, gangguan berupa angin
juga mempengaruhi gerak pesawat. Sehingga, pada saat mendesain kontrol gerak
pesawat otomatis, pengaruh-pengaruh tersebut perlu diperhatikan.
Bentuk umum persamaan gaya dan momentum sudut aerodinamis yang
𝐹𝐹𝑥𝑥 − 𝑚𝑚𝑔𝑔 𝑠𝑠𝑖𝑖𝑛𝑛 𝜃𝜃= 𝑚𝑚(𝑢𝑢̇+𝑞𝑞𝑤𝑤 − 𝑟𝑟𝑟𝑟) (2.21)
𝐹𝐹𝑦𝑦 +𝑚𝑚𝑔𝑔cos𝜃𝜃sin𝜃𝜃= 𝑚𝑚(𝑟𝑟̇+𝑟𝑟𝑢𝑢 − 𝑝𝑝𝑤𝑤) (2.22)
𝐹𝐹𝑧𝑧 +𝑚𝑚𝑔𝑔cos𝜃𝜃cos𝜙𝜙 =𝑚𝑚(𝑤𝑤̇+𝑝𝑝𝑟𝑟 − 𝑞𝑞𝑢𝑢) (2.23)
𝐿𝐿𝑥𝑥 =𝜆𝜆𝑥𝑥𝑝𝑝̇ − 𝜆𝜆𝑥𝑥𝑧𝑧𝑟𝑟̇+𝑞𝑞𝑟𝑟�𝜆𝜆𝑧𝑧 − 𝜆𝜆𝑦𝑦� − 𝜆𝜆𝑥𝑥𝑧𝑧𝑝𝑝𝑞𝑞 (2.24)
𝐿𝐿𝑦𝑦 = 𝜆𝜆𝑦𝑦𝑞𝑞̇+𝑟𝑟𝑞𝑞(𝜆𝜆𝑥𝑥− 𝜆𝜆𝑧𝑧) +𝜆𝜆𝑥𝑥𝑧𝑧(𝑝𝑝2− 𝑟𝑟2) (2.25)
𝐿𝐿𝑧𝑧 = −𝜆𝜆𝑥𝑥𝑧𝑧𝑝𝑝̇+𝜆𝜆𝑧𝑧𝑟𝑟̇+𝑝𝑝𝑞𝑞�𝜆𝜆𝑦𝑦 − 𝜆𝜆𝑥𝑥�+𝜆𝜆𝑥𝑥𝑧𝑧𝑞𝑞𝑟𝑟 (2.26)
dengan 𝐹𝐹𝑥𝑥 , 𝐿𝐿𝑥𝑥 , 𝑢𝑢, 𝑝𝑝, dan 𝜆𝜆𝑥𝑥 adalah komponen gaya aerodinamis, komponen
momentum sudut aerodinamis, komponen kecepatan linier pesawat, komponen
kecepatan sudut pesawat, dan komponen momen inersia pesawat searah sumbu x, 𝐹𝐹𝑦𝑦,
𝐿𝐿𝑦𝑦, 𝑟𝑟, 𝑞𝑞, dan 𝜆𝜆𝑦𝑦 adalah komponen gaya aerodinamis, komponen momentum sudut
aerodinamis, komponen kecepatan linier pesawat, komponen kecepatan sudut
pesawat, dan komponen momen inersia pesawat searah sumbu y, 𝐹𝐹𝑧𝑧, 𝐿𝐿𝑧𝑧, 𝑤𝑤, 𝑟𝑟, dan 𝜆𝜆𝑧𝑧
adalah komponen gaya aerodinamis, komponen momentum sudut aerodinamis,
komponen kecepatan linier pesawat, komponen kecepatan sudut pesawat, dan
komponen momen inersia pesawat searah sumbu z, 𝑚𝑚 adalah massa pesawat, 𝜃𝜃
adalah sudut kenaikan pesawat, dan 𝜆𝜆𝑥𝑥𝑧𝑧 adalah produk komponen momen inersia
Didefinisikan
∆𝛿𝛿𝑎𝑎 adalah perubahan sudut aileron.
Pada pesawat yang bergerak dengan tenang (tidak melakukan gerakan yang
ekstrim), gerak pesawat tersebut dapat diasumsikan terbagi menjadi dua grup
persamaan yaitu, persamaan gerak longitudinal (gerak yang disebabkan perubahan
sudut 𝜃𝜃) dan persamaan gerak lateral (gerak yang disebabkan perubahan sudut 𝜙𝜙).
komponen momentum sudut searah sumbu z (𝐿𝐿𝑧𝑧), dan persamaan komponen gaya searah sumbu y (𝐹𝐹𝑦𝑦) [Nelson, 1998].
Gambar 2.2 Gambar arah gerak pesawat
Persamaan gerak longitudinal dan lateral pesawat yang bergerak tenang
dapat dianalisis secara terpisah. Untuk persamaan gerak longitudinal, pada proses
analisis variabel 𝑟𝑟, 𝑝𝑝, 𝑟𝑟, dan turunannya dianggap nol. Dengan adanya pengaruh angin pada atmosfer, melalui proses linearisasi, persamaan gerak longitudinal
pesawat menjadi [Nelson, 1998]
�𝑑𝑑𝑡𝑡𝑑𝑑 − 𝑋𝑋𝑢𝑢� ∆𝑢𝑢+𝑋𝑋𝑢𝑢𝑢𝑢𝑔𝑔+�𝑤𝑤𝑔𝑔− ∆𝑤𝑤�𝑋𝑋𝑤𝑤 +𝑔𝑔∆𝜃𝜃 =𝑋𝑋𝛿𝛿∆𝛿𝛿𝑒𝑒 (2.33)
�𝑑𝑑𝑡𝑡𝑑𝑑 − 𝑍𝑍𝑤𝑤� ∆𝑤𝑤+𝑍𝑍𝑤𝑤𝑤𝑤𝑔𝑔+�𝑢𝑢𝑔𝑔 − ∆𝑢𝑢�𝑍𝑍𝑢𝑢 − 𝑢𝑢0∆𝑞𝑞=𝑍𝑍𝛿𝛿∆𝛿𝛿𝑒𝑒 (2.34)
�𝑑𝑑𝑡𝑡𝑑𝑑 − 𝑀𝑀𝑞𝑞� ∆𝑞𝑞+𝑀𝑀𝑞𝑞𝑞𝑞𝑔𝑔+�𝑢𝑢𝑔𝑔 − ∆𝑢𝑢�𝑀𝑀𝑢𝑢 +�𝑤𝑤𝑔𝑔 − ∆𝑤𝑤�𝑀𝑀𝑤𝑤 = 𝑀𝑀𝛿𝛿∆𝛿𝛿𝑒𝑒 (2.35)
Dengan 𝑢𝑢𝑔𝑔 adalah gangguan searah u, 𝑤𝑤𝑔𝑔 adalah gangguan searah w, 𝑞𝑞𝑔𝑔 adalah
gangguan searah q, dan didefinisikan
17
BAB III
METODE PENELITIAN
3.1. Desain Sistem Kontrol Pilot Otomatis
Analisis sistem yang terdiri atas pesawat dan lingkungan di sekitarnya yang
mempengaruhi gerak pesawat tersebut dilakukan dengan menggunakan metode ruang
keadaan. Berdasarkan persamaan umum dari metode ruang keadaan pada persamaan
(2.3), persamaan gerak longitudinal pesawat (persamaan (2.33) sampai (2.36))
dituliskan sebagai berikut
⎣
Persamaan (3.1) tersebut kemudian ditata ulang menjadi
Secara umum, persamaan (3.2) dapat ditulis
𝑥𝑥̇=𝑨𝑨′(𝑥𝑥 − 𝜀𝜀) +𝑩𝑩𝜇𝜇 (3.3)
Dari persamaan ini diperoleh matriks keadaan sistem yang baru (𝑨𝑨′) yang
berubah-ubah sesuai dengan nilai 𝑞𝑞′.
Dipilih 𝜉𝜉𝑠𝑠𝑝𝑝 = 0,6, 𝜉𝜉𝑝𝑝 = 0,05, 𝜔𝜔𝑠𝑠𝑝𝑝 = 3,0 derajat/s, dan 𝜔𝜔𝑝𝑝 = 0,1 derajat/s. Nilai yang diberikan ini mempengaruhi kontrol dan gerak pesawat sebagai respon
terhadap kontrol. Damping ratio dan frekuensi natural tak teredam untuk pergerakan
dalam waktu singkat mempengaruhi pola gerak pesawat saat mulai mendapat
gangguan (awal dilakukan simulasi). Sedangkan, damping ratio dan frekuensi natural
tak teredam untuk pergerakan dalam waktu yang lama mempengaruhi pola gerak
pesawat selama simulasi dilakukan. Diperoleh persamaan karakteristik yang
dikehendaki, yaitu
𝜆𝜆4+ 3,61𝜆𝜆3+ 9,05𝜆𝜆2+ 0,126𝜆𝜆+ 0,09 = 0 (3.4)
Pada penelitian, diambil nilai 𝑋𝑋𝑢𝑢, 𝑋𝑋𝑤𝑤, 𝑍𝑍𝑢𝑢, 𝑍𝑍𝑤𝑤, 𝑀𝑀𝑢𝑢, 𝑀𝑀𝑤𝑤, 𝑀𝑀𝑞𝑞, 𝑢𝑢0,
𝑋𝑋𝛿𝛿𝑒𝑒,𝑍𝑍𝛿𝛿𝑒𝑒, 𝑀𝑀𝛿𝛿𝑒𝑒, dan 𝑔𝑔 dari data penanganan pesawat Boeing 747 [Heffley dan Jewell,
1972]. Matriks keadaan sistem dan matriks masukan menjadi
𝑩𝑩=�
Persamaan karakteristik sistem dicari menggunakan persamaan (2.7). Nilai
𝑨𝑨′ dan 𝑩𝑩 dimasukkan ke dalam persamaan tersebut sehingga diperoleh konstanta
persamaan karakteristik sistem untuk setiap orde 𝜆𝜆 sebagai berikut
𝜆𝜆3 ∶(0,959 𝑘𝑘
Dengan menyamakan konstanta persamaan (3.4) dengan persamaan (3.5)
sampai (3.8), diperoleh nilai 𝑘𝑘1, 𝑘𝑘2, 𝑘𝑘3, dan 𝑘𝑘4 sebagai kontrol yang sesuai untuk
sistem tersebut. Sehingga, sesuai dengan persamaan (2.5), tanpa adanya masukan
∆𝛿𝛿𝑒𝑒(𝑡𝑡) =− �𝑘𝑘1�∆𝑢𝑢(𝑡𝑡)− 𝑢𝑢𝑔𝑔�+𝑘𝑘2�∆𝑤𝑤(𝑡𝑡)− 𝑤𝑤𝑔𝑔�+𝑘𝑘3�∆𝑞𝑞(𝑡𝑡)− 𝑞𝑞𝑔𝑔�+
𝑘𝑘4∆𝜃𝜃(𝑡𝑡)� (3.9)
3.2. Penyelesaian Analitik Sistem Kontrol Pilot Otomatis Sebagai Pembanding
Berdasarkan persamaan (2.6), persamaan (3.3) dapat ditulis sebagai berikut
𝑥𝑥̇=𝑨𝑨′′(𝑥𝑥 − 𝜀𝜀) (3.10)
𝑨𝑨′′ =𝑨𝑨′ − 𝑩𝑩𝑘𝑘𝑇𝑇 (3.11)
Dengan menggunakan persamaan (2.9), diperoleh
𝚽𝚽(𝑡𝑡) =ℒ−1[(𝑠𝑠𝐈𝐈 − 𝑨𝑨′′)−1] (3.12)
Namun, nilai 𝑨𝑨′ yang terus berubah karena adanya varibel 𝑞𝑞′ yang terus berubah
menyebabkan 𝚽𝚽(𝑡𝑡) juga terus berubah. Artinya, penyelesaian analitik untuk setiap
nilai 𝑡𝑡 berbeda. Hal ini sangat sulit dilakukan. Karena itu, sebagai pembanding,
dilakukan penyelesaian analitik sistem kontrol pilot otomatis tanpa gangguan (𝜀𝜀 =
Jika matriks 𝑨𝑨 dan 𝑩𝑩 dimasukkan ke dalam persamaan (3.11) dan dengan nilai awal
∆𝑢𝑢(0) = 0, ∆𝑤𝑤(0) = 0, ∆𝑞𝑞(0) = 0, ∆𝜃𝜃(0) = 5, berdasarkan persamaan (2.10) dan
(3.12) diperoleh penyelesaian
∆𝜃𝜃(𝑡𝑡) = 5�(−0,00208712−0,0102818𝑖𝑖)𝑒𝑒(−1,80014−2,40155𝑖𝑖)𝑡𝑡 −
(0,00208712−0,0102818𝑖𝑖)𝑒𝑒(−1,80014 +2,40155𝑖𝑖)𝑡𝑡+ (0,502087 +
0,234752𝑖𝑖)𝑒𝑒(−0,00499923−0,0998723𝑖𝑖)𝑡𝑡+
(0,502087−0,234752𝑖𝑖)𝑒𝑒(−0,00499923 +0,0998723𝑖𝑖)𝑡𝑡� (3.13)
3.3. Penerapan Metode Parker-Sochacki
Untuk mengawali metode Parker-Sochacki, diperlukan pendefinisian
beberapa variabel, seperti
∆𝑢𝑢(𝑡𝑡) =∆𝑢𝑢1+∆𝑢𝑢2𝑡𝑡+∆𝑢𝑢3𝑡𝑡2+∆𝑢𝑢
4𝑡𝑡3+⋯+∆𝑢𝑢𝑛𝑛+1𝑡𝑡𝑛𝑛 (3.14)
∆𝑤𝑤(𝑡𝑡) =∆𝑤𝑤1+∆𝑤𝑤2𝑡𝑡+∆𝑤𝑤3𝑡𝑡2+∆𝑤𝑤4𝑡𝑡3+⋯+∆𝑤𝑤𝑛𝑛+1𝑡𝑡𝑛𝑛 (3.15)
∆𝑞𝑞(𝑡𝑡) =∆𝑞𝑞1+∆𝑞𝑞2𝑡𝑡+∆𝑞𝑞3𝑡𝑡2+∆𝑞𝑞
4𝑡𝑡3+⋯+∆𝑞𝑞𝑛𝑛+1𝑡𝑡𝑛𝑛 (3.16)
∆𝜃𝜃(𝑡𝑡) =∆𝜃𝜃1+∆𝜃𝜃2𝑡𝑡+∆𝜃𝜃3𝑡𝑡2+∆𝜃𝜃4𝑡𝑡3+⋯+∆𝜃𝜃𝑛𝑛+1𝑡𝑡𝑛𝑛 (3.17)
sehingga
∆𝑢𝑢̇(𝑡𝑡) =∆𝑢𝑢2+ 2 ∆𝑢𝑢3𝑡𝑡+ 3 ∆𝑢𝑢4𝑡𝑡2+ 4 ∆𝑢𝑢
5𝑡𝑡3+⋯+ (𝑛𝑛+ 1)∆𝑢𝑢𝑛𝑛+2𝑡𝑡𝑛𝑛
(3.18)
∆𝑤𝑤̇(𝑡𝑡) =∆𝑤𝑤2+ 2 ∆𝑤𝑤3𝑡𝑡+ 3 ∆𝑤𝑤4𝑡𝑡2+ 4 ∆𝑤𝑤5𝑡𝑡3+⋯+ (𝑛𝑛+ 1)∆𝑤𝑤𝑛𝑛+2𝑡𝑡𝑛𝑛
∆𝑞𝑞̇(𝑡𝑡) =∆𝑞𝑞2+ 2 ∆𝑞𝑞3𝑡𝑡+ 3 ∆𝑞𝑞4𝑡𝑡2+ 4 ∆𝑞𝑞5𝑡𝑡3+⋯+ (𝑛𝑛+ 1)∆𝑞𝑞𝑛𝑛+2𝑡𝑡𝑛𝑛
(3.20)
∆𝜃𝜃̇(𝑡𝑡) =∆𝜃𝜃2+ 2 ∆𝜃𝜃3𝑡𝑡+ 3 ∆𝜃𝜃4𝑡𝑡2+ 4 ∆𝜃𝜃5𝑡𝑡3+⋯+ (𝑛𝑛+ 1)∆𝜃𝜃𝑛𝑛+2𝑡𝑡𝑛𝑛
(3.21)
Berdasarkan persamaan ruang keadaan sistem pilot otomatis,
∆𝑢𝑢̇(𝑡𝑡) =𝑋𝑋𝑢𝑢�∆𝑢𝑢(𝑡𝑡)− 𝑢𝑢𝑔𝑔�+𝑋𝑋𝑤𝑤�∆𝑤𝑤(𝑡𝑡)− 𝑤𝑤𝑔𝑔� − 𝑔𝑔∆𝜃𝜃(𝑡𝑡) +𝑋𝑋𝛿𝛿𝑒𝑒∆𝛿𝛿𝑒𝑒(𝑡𝑡)
(3.22)
∆𝑤𝑤̇(𝑡𝑡) =𝑍𝑍𝑢𝑢�∆𝑢𝑢(𝑡𝑡)− 𝑢𝑢𝑔𝑔�+𝑍𝑍𝑤𝑤�∆𝑤𝑤(𝑡𝑡)− 𝑤𝑤𝑔𝑔�+𝑢𝑢0𝑞𝑞′�∆𝑞𝑞(𝑡𝑡)− 𝑞𝑞𝑔𝑔�+
𝑍𝑍𝛿𝛿𝑒𝑒∆𝛿𝛿𝑒𝑒(𝑡𝑡) (3.23)
∆𝑞𝑞̇(𝑡𝑡) =𝑀𝑀𝑢𝑢�∆𝑢𝑢(𝑡𝑡)− 𝑢𝑢𝑔𝑔�+𝑀𝑀𝑤𝑤�∆𝑤𝑤(𝑡𝑡)− 𝑤𝑤𝑔𝑔�+𝑀𝑀𝑞𝑞�∆𝑞𝑞(𝑡𝑡)− 𝑞𝑞𝑔𝑔�+
𝑀𝑀𝛿𝛿𝑒𝑒∆𝛿𝛿𝑒𝑒(𝑡𝑡) (3.24)
∆𝜃𝜃̇(𝑡𝑡) =𝑞𝑞′�∆𝑞𝑞(𝑡𝑡)− 𝑞𝑞𝑔𝑔� (3.25)
Melalui proses substitusi persamaan (3.14) sampai (3.21) ke dalam
persamaan (3.22) sampai (3.25), diperoleh
∆𝑢𝑢2 =𝑋𝑋𝑢𝑢�∆𝑢𝑢1− 𝑢𝑢𝑔𝑔�+𝑋𝑋𝑤𝑤(∆𝑤𝑤1− 𝑤𝑤𝑔𝑔)− 𝑔𝑔∆𝜃𝜃1 +𝑋𝑋𝛿𝛿𝑒𝑒∆𝛿𝛿𝑒𝑒(𝑡𝑡) (3.26)
∆𝑤𝑤2 = 𝑍𝑍𝑢𝑢�∆𝑢𝑢1− 𝑢𝑢𝑔𝑔�+𝑍𝑍𝑤𝑤(∆𝑤𝑤1− 𝑤𝑤𝑔𝑔) +𝑢𝑢0𝑞𝑞′(∆𝑞𝑞1− 𝑞𝑞𝑔𝑔) +𝑍𝑍𝛿𝛿𝑒𝑒∆𝛿𝛿𝑒𝑒(𝑡𝑡)
∆𝑞𝑞2 =𝑀𝑀𝑢𝑢�∆𝑢𝑢1− 𝑢𝑢𝑔𝑔�+𝑀𝑀𝑤𝑤(∆𝑤𝑤1− 𝑤𝑤𝑔𝑔) +𝑀𝑀𝑞𝑞(∆𝑞𝑞1− 𝑞𝑞𝑔𝑔) +𝑀𝑀𝛿𝛿𝑒𝑒∆𝛿𝛿𝑒𝑒(𝑡𝑡)
(3.28)
∆𝜃𝜃2 =𝑞𝑞′(∆𝑞𝑞1− 𝑞𝑞𝑔𝑔) (3.29)
dan
∆𝑢𝑢𝑛𝑛+1 =
𝑋𝑋𝑢𝑢∆𝑢𝑢𝑛𝑛 +𝑋𝑋𝑤𝑤∆𝑤𝑤𝑛𝑛 − 𝑔𝑔∆𝜃𝜃𝑛𝑛 +𝑋𝑋𝛿𝛿𝑒𝑒∆𝛿𝛿𝑒𝑒(𝑡𝑡)
𝑛𝑛
(3.30)
∆𝑤𝑤𝑛𝑛+1 =
𝑍𝑍𝑢𝑢∆𝑢𝑢𝑛𝑛 +𝑍𝑍𝑤𝑤∆𝑤𝑤𝑛𝑛+𝑢𝑢0𝑞𝑞′∆𝑞𝑞𝑛𝑛 +𝑍𝑍𝛿𝛿𝑒𝑒∆𝛿𝛿𝑒𝑒(𝑡𝑡)
𝑛𝑛
(3.31)
∆𝑞𝑞𝑛𝑛+1 =
𝑀𝑀𝑢𝑢∆𝑢𝑢𝑛𝑛 +𝑀𝑀𝑤𝑤∆𝑤𝑤𝑛𝑛 +𝑀𝑀𝑞𝑞∆𝑞𝑞𝑛𝑛 +𝑀𝑀𝛿𝛿𝑒𝑒∆𝛿𝛿𝑒𝑒(𝑡𝑡)
𝑛𝑛
(3.32)
∆𝜃𝜃𝑛𝑛+1 =
𝑞𝑞′∆𝑞𝑞𝑛𝑛
𝑛𝑛
(3.33)
dengan n = 2, 3, 4, ... adalah orde persamaan (3.14) sampai (3.17).
Melalui persamaan (3.26) sampai (3.33), didapatkan nilai setiap variabel
pada persamaan (3.14) sampai (3.17). Dari persamaan-persamaan tersebut diperoleh
nilai ∆𝑢𝑢, ∆𝑤𝑤, ∆𝑞𝑞, dan ∆𝜃𝜃 pada saat 𝑡𝑡. Dengan demikian, komputasi dari pendekatan
numerik dengan metode Parker-Sochacki sistem pilot otomatis untuk penerbangan
3.4. Penerapan Metode Runge-Kutta Orde Empat sebagai Pembanding
Persamaan ruang keadaan sistem pilot otomatis pesawat seperti pada
persamaan (3.22) sampai (3.25) dijabarkan dengan pendekatan numerik dengan
metode Runge-Kutta orde empat. Sesuai dengan persamaan (2.15) sampai (2.20),
persamaan ruang keadaan sistem pilot otomatis pesawat dijabarkan sebagai berikut
𝑘𝑘𝜃𝜃2 =𝑞𝑞′ ��∆𝑞𝑞(𝑡𝑡)− 𝑞𝑞𝑔𝑔�+
1
2ℎ𝑘𝑘𝜃𝜃1� (3.50)
𝑘𝑘𝜃𝜃3 =𝑞𝑞′ ��∆𝑞𝑞(𝑡𝑡)− 𝑞𝑞𝑔𝑔�+
1
2ℎ𝑘𝑘𝜃𝜃2� (3.51)
𝑘𝑘𝜃𝜃4 =𝑞𝑞′ ��∆𝑞𝑞(𝑡𝑡)− 𝑞𝑞𝑔𝑔�+ℎ𝑘𝑘𝜃𝜃3� (3.52)
𝜃𝜃(𝑡𝑡+ℎ) =𝜃𝜃(𝑡𝑡) +1
6ℎ�𝑘𝑘𝜃𝜃1+ 2𝑘𝑘𝜃𝜃2 + 2𝑘𝑘𝜃𝜃3 +𝑘𝑘𝜃𝜃4� (3.53)
Dengan persamaan-persamaan yang diperoleh (persamaan (3.34) sampai
(3.53)), komputasi dari pendekatan numerik dengan metode Runge-Kutta sistem pilot
otomatis untuk penerbangan dapat dilakukan.
3.5. Algoritma
Flowchart untuk penyelesaian analitik sistem kontrol pilot otomatis
digambarkan pada gambar 3.1
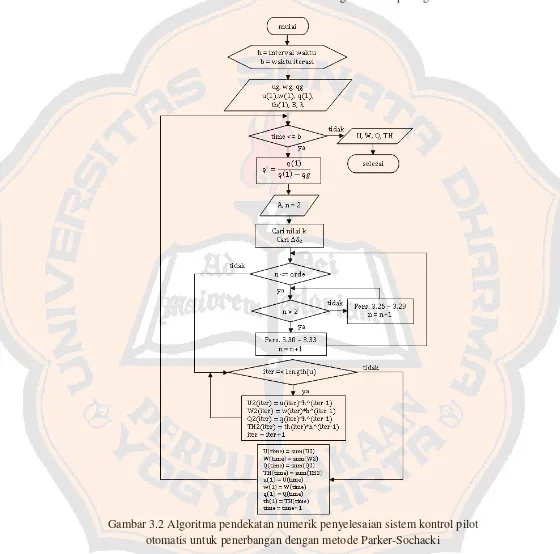
Flowchart untuk metode Parker-Sochacki digambarkan pada gambar 3.2
Flowchart untuk metode Runge-Kutta digambarkan pada gambar 3.3
Gambar 3.3 Algoritma pendekatan numerik penyelesaian sistem kontrol pilot otomatis untuk penerbangan dengan metode Runge-Kutta
Listing program untuk penyelesaian analitik, pendekatan numerik dengan
metode Parker-Sochacki, dan pendekatan numerik dengan metode Runge-Kutta
29
BAB IV
HASIL DAN PEMBAHASAN
Pendekatan numerik sistem kontrol pilot otomatis untuk penerbangan
dilakukan dengan menggunakan metode Parker-Sochacki, dengan masukan awal
∆𝑢𝑢1 =∆𝑤𝑤1 = 0 ft/s, ∆𝑞𝑞1 = �𝑞𝑞𝑔𝑔 + 0,1� derajat/s, dan ∆𝜃𝜃1= 5𝑜𝑜. Nilai ∆𝑢𝑢1, ∆𝑤𝑤1,
∆𝑞𝑞1, dan ∆𝜃𝜃1 menunjukkan nilai ∆𝑢𝑢(0), ∆𝑤𝑤(0), ∆𝑞𝑞(0) dan ∆𝜃𝜃(0). Nilai 0 pada ∆𝑢𝑢1
dan ∆𝑤𝑤1 menandakan tidak terjadi perubahan nilai 𝑢𝑢 dan 𝑤𝑤 pada awal simulasi yang
dilakukan. Sedangkan, nilai 5o
Dipilih nilai ∆𝑞𝑞1 =�𝑞𝑞𝑔𝑔 + 0,1� karena pada saat mendesain kontrol sistem
pesawat, 𝑞𝑞𝑔𝑔 tidak boleh sama dengan 𝑞𝑞1. Jika hal ini terjadi, maka nilai 𝑞𝑞′ akan
menjadi tidak terdefenisi sehingga desain tidak dapat dilakukan. Penambahan nilai
0,1 pada 𝑞𝑞1 tidak terlalu berpengaruh pada perhitungan nilai ∆𝑞𝑞 selanjutnya. Selain
itu, jika 𝑞𝑞1 diberi nilai 0, maka berapa pun nilai 𝑞𝑞𝑔𝑔 yang diberikan, nilai 𝑞𝑞′ pertama
akan sama dengan 0. Hal ini akan mengakibatkan matriks keadaan sistem menjadi
singular dan desain kontrol sistem tidak dapat dilakukan.
pada ∆𝜃𝜃1 menunjukkan nilai simpangan sudut awal
pesawat (𝜃𝜃).
Komputasi dilakukan dengan ketentuan
2. Gangguan angin diberi nilai yang bervariasi (0 sampai dengan 500 ft/s untuk 𝑢𝑢𝑔𝑔
dan 𝑤𝑤𝑔𝑔, serta 0 sampai dengan 1 × 10−2 derajat/s untuk 𝑞𝑞
𝑔𝑔) pada komputasi
yang dilakukan.
3. Komputasi dilakukan sampai detik ke 1000 dengan interval waktu 0,1 detik
dan orde persamaan 4 untuk setiap nilai yang ditampilkan.
Sebagai pembanding, dilakukan juga pendekatan numerik menggunakan
metode Runge-Kutta dengan masukan awal yang sama. Pada bagian ini dilakukan
komputasi dengan ketentuan
1. Gangguan angin (𝑢𝑢𝑔𝑔, 𝑤𝑤𝑔𝑔, dan𝑞𝑞𝑔𝑔) konstan sepanjang waktu dengan nilai untuk
𝑢𝑢𝑔𝑔R
2. Komputasi dilakukan sampai detik ke 1000 untuk interval waktu 0,1 detik dan
sampai detik ke 100 untuk interval waktu 0,01 detik dan 0,001 detik.
= 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan𝑞𝑞𝑔𝑔 = 1 × 10−3derajat/s.
4.1. Komputasi Penyelesaian Analitik Sistem Kontrol Pilot Otomatis untuk
Penerbangan
Dilakukan komputasi penyelesaian analitik sistem kontrol pilot otomatis
untuk penerbangan tanpa gangguan angin seperti yang dijabarkan pada subbab 3.2.
Gambar 4.1 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dengan penyelesaian analitik
Perubahan sudut kemiringan pesawat terhadap bidang horisontal dinyatakan
dengan ∆𝜃𝜃. Dari data yang diperoleh, nilai lonjakan maksimum pada awal
∆𝜃𝜃 menurut penyelesaian analitik adalah 5,4293o. Nilai di mana ∆𝜃𝜃 dianggap cukup
stabil (2% dari nilai maksimum ∆𝜃𝜃) adalah 0,108587o
Dilakukan juga perbandingan antara simulasi perubahan sudut pesawat
menggunakan penyelesaian analitik, pendekatan numerik Parker-Sochacki, dan . ∆𝜃𝜃 mencapai nilai stabil
pendekatan numerik Runge-Kutta. Diperoleh hasil seperti ditampilkan seperti pada
gambar 4.2.
Gambar 4.2 Perbandingan penyelesaian analitik, pendekatan numerik Parker-Sochacki, dan pendekatan numerik Runge-Kuta
Simulasi dilakukan dengan interval waktu 0,1 detik untuk penyelesaian
analitik, 0,1 detik dan orde persamaan 4 untuk pendekatan numerik Parker-Sochacki,
dan 0,0001 detik untuk pendekatan numerik Runge-Kutta. Simulasi hanya dilakukan
sampai detik ke 100 karena diperlukan waktu yang lama untuk melakukan simulasi
Persentase kesalahan pada pendekatan numerik dengan metode
Parker-Sochacki dan Runge-Kutta terhadap penyelesaian analitik simulasi desain kontrol
sistem pilot otomatis diperoleh melalui persamaan
𝑒𝑒=|𝑝𝑝𝑛𝑛𝑝𝑝−𝑝𝑝𝑎𝑎|
𝑎𝑎 × 100% (4.1)
Dengan 𝑒𝑒 adalah persentase kesalahan dari pendekatan numerik yang dilakukan
terhadap penyelesaian analitiknya, 𝑝𝑝𝑛𝑛 adalah besarnya hasil yang diperoleh melalui
pendekatan numerik, dan 𝑝𝑝𝑎𝑎 adalah besarnya hasil yang diperoleh melalui
penyelesaian analitik.
Berdasarkan data yang diperoleh, nilai lonjakan maksimal simulasi desain
kontrol sistem pilot otomatis yang dilakukan menggunakan penyelesaian analitik
adalah 5,4293o. Sedangkan, nilai lonjakan maksimal simulasi desain kontrol sistem
pilot otomatis yang dilakukan menggunakan pendekatan numerik dengan metode
Parker-Sochacki dan Runge-Kutta adalah 5,4432o dan 5,4370o
Pendekatan numerik dengan metode Parker-Sochacki dan Runge-Kutta
mampu melakukan simulasi kontrol dan respon pesawat terhadap kontrol dengan
cukup akurat. Dengan demikian, pendekatan numerik tersebut sesuai digunakan untuk . Sehingga, persentase
kesalahan pendekatan numerik yang dilakukan adalah 0,256% untuk pendekatan
numerik dengan metode Parker-Sochacki dengan interval waktu 0,1 detik dan 0,14%
untuk pendekatan numerik dengan metode Runge-Kutta dengan interval waktu
melakukan simulasi kontrol sistem pilot otomatis untuk penerbangan yang didesain
menggunakan persamaan ruang keadaan.
4.2. Pendekatan Numerik Sistem Dengan Gangguan Angin dan Tanpa Kontrol
Untuk mendesain kontrol sistem pesawat dengan gangguan angin, perlu
dilakukan penataan ulang matriks keadaan sistem pesawat dengan memasukkan
elemen gangguan angin ke dalam sistem tersebut. Gangguan angin pada pesawat ini
menyebabkan matriks keadaan sistem pesawat berubah-ubah sehingga penyelesaian
analitik untuk melakukan simulasi kontrol yang didesain menjadi sulit dilaksanakan.
Karena itu, pendekatan numerik dengan komputasi diperlukan untuk melakukan
simulasi tersebut.
Dilakukan penataan ulang matriks keadaan sistem dengan persamaan
dengan 𝑢𝑢𝑔𝑔 = 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan 𝑞𝑞𝑔𝑔 = 1 × 10−3derajat/s.
Untuk mengecek kebenaran penataan ulang matriks keadaan sistem seperti
pada persamaan (4.3), dilakukan perbandingan hasil simulasi perubahan sudut
pesawat sesuai dengan persamaan (4.2) dan (4.3). Diperoleh hasil seperti terlihat pada
gambar 4.3.
Gambar 4.3 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) tanpa kontrol berdasarkan
persamaan (4.2) dan (4.3)
Pada gambar 4.3, ditunjukkan kemiripan hasil yang diperoleh dari
matriks keadaan sistem dengan adanya nilai 𝑞𝑞′ seperti pada persamaan (4.3) dapat
dilakukan.
Grafik perubahan sudut kemiringan pesawat tanpa kontrol menunjukkan
bahwa tanpa adanya kontrol pada pesawat tersebut, sudut kemiringan pesawat
menjadi semakin tidak terkendali selama komputasi dilakukan. Hal ini ditunjukkan
dengan nilai ∆𝜃𝜃 yang semakin tinggi selama komputasi dilakukan. Sistem yang telah
ditata ulang tersebut kemudian dikontrol sedemikian rupa sehingga kestabilannya
terjaga.
4.3. Pendekatan Numerik Sistem Terkontrol dengan Gangguan Angin
Bervariasi dengan Metode Parker-Sochacki
Dilakukan komputasi pendekatan numerik menggunakan metode
Parker-Sochacki untuk melakukan simulasi respon sistem terhadap kontrol dengan gangguan
angin yang bervariasi.
Gambar 4.4 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator (∆𝛿𝛿𝑒𝑒) tanpa gangguan angin, dengan kontrol
Nilai ∆𝜃𝜃 maksimum dari data yang diperoleh yaitu 5,4432o. ∆𝜃𝜃 mencapai
nilai yang dianggap stabil pada detik ke 821,9. Nilai maksimum ∆𝛿𝛿𝑒𝑒 dari data yang
diperoleh yaitu 1,7757o. Waktu yang diperlukan untuk melakukan komputasi yaitu
1878,41 detik. Garis biru dan merah pada grafik ∆𝜃𝜃 menunjukkan nilai stabil yang
2. Untuk 𝑢𝑢𝑔𝑔R= 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan𝑞𝑞𝑔𝑔 = 0 derajat/s
Gambar 4.5 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator (∆𝛿𝛿𝑒𝑒) untuk 𝑢𝑢𝑔𝑔R
= 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan𝑞𝑞𝑔𝑔 = 0 derajat/s
Nilai ∆𝜃𝜃 maksimum dari data yang diperoleh yaitu 5,4470o. ∆𝜃𝜃 mencapai
nilai yang dianggap stabil pada detik ke 821,3. Nilai maksimum ∆𝛿𝛿𝑒𝑒 dari data yang
diperoleh yaitu 2,8936o. Waktu yang diperlukan untuk melakukan komputasi yaitu
3. Untuk 𝑢𝑢𝑔𝑔R= 500 ft/s, 𝑤𝑤𝑔𝑔 = 500 ft/s, dan𝑞𝑞𝑔𝑔 = 0 derajat/s
Gambar 4.6 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator (∆𝛿𝛿𝑒𝑒) untuk 𝑢𝑢𝑔𝑔R
= 500 ft/s, 𝑤𝑤𝑔𝑔 = 500 ft/s, dan𝑞𝑞𝑔𝑔 = 0 derajat/s
Nilai ∆𝜃𝜃 maksimum dari data yang diperoleh yaitu 7,7287o.∆𝜃𝜃 mencapai
nilai yang dianggap stabil pada detik ke 882,4. Nilai maksimum ∆𝛿𝛿𝑒𝑒 dari data yang
diperoleh yaitu 13,1532o. Waktu yang diperlukan untuk melakukan komputasi yaitu
Pada gambar 4.4 sampai 4.6 ditunjukkan bahwa perubahan nilai 𝑢𝑢𝑔𝑔 dan 𝑤𝑤𝑔𝑔
berpengaruh pada bagian awal perubahan sudut pesawat (∆𝜃𝜃). Untuk nilai 𝑢𝑢𝑔𝑔 dan 𝑤𝑤𝑔𝑔 yang semakin tinggi, lonjakan pada awal perubahan juga semakin tinggi. Lonjakan
ini berpengaruh pada kontrol yang segera bekerja mengendalikan pesawat tersebut.
Terlihat nilai maksimal ∆𝛿𝛿𝑒𝑒 pada masing-masing grafik semakin tinggi pada
gangguan yang semakin besar. Karena lonjakan perubahan sudut pesawat ini hanya
terjadi pada saat pesawat mulai mendapat gangguan angin (awal dilakukan simulasi),
lonjakan ∆𝛿𝛿𝑒𝑒 yang tinggi juga hanya terjadi itu. Setelah pesawat mulai terkendali,
nilai ∆𝛿𝛿𝑒𝑒 kembali menurun.
Nilai gangguan ini juga berpengaruh pada kerja kontrol untuk membuat ∆𝜃𝜃
mencapai nilai yang dianggap stabil. Hal ini terlihat pada waktu yang diperlukan
kontrol pada masing-masing grafik untuk membuat ∆𝜃𝜃 mencapai nilai stabil. Pada
gangguan yang semakin besar, waktu yang diperlukan untuk membuat ∆𝜃𝜃 mencapai
4. Untuk 𝑢𝑢𝑔𝑔R= 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan𝑞𝑞𝑔𝑔 = 1 × 10
−4 derajat/s
Gambar 4.7 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator (∆𝛿𝛿𝑒𝑒) untuk 𝑢𝑢𝑔𝑔R
= 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan𝑞𝑞𝑔𝑔 =1 × 10−4 derajat/s
Nilai ∆𝜃𝜃 maksimum dari data yang diperoleh yaitu 5,4553o. ∆𝜃𝜃 mencapai
nilai yang dianggap stabil pada detik ke 821,6. Nilai maksimum ∆𝛿𝛿𝑒𝑒 dari data yang
diperoleh yaitu 2,8931o. Waktu yang diperlukan untuk melakukan komputasi yaitu
5. Untuk 𝑢𝑢𝑔𝑔R= 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan𝑞𝑞𝑔𝑔 = 1 × 10−
3 derajat/s
Gambar 4.8 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator (∆𝛿𝛿𝑒𝑒) untuk 𝑢𝑢𝑔𝑔R
= 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan𝑞𝑞𝑔𝑔 = 1 × 10−3 derajat/s
Nilai ∆𝜃𝜃 maksimum dari data yang diperoleh yaitu 5,4470o. ∆𝜃𝜃 mencapai
nilai yang dianggap stabil pada detik ke 740,6. Nilai maksimum ∆𝛿𝛿𝑒𝑒 dari data yang
diperoleh yaitu 32,0741o. Waktu yang diperlukan untuk melakukan komputasi yaitu
Adanya nilai 𝑞𝑞𝑔𝑔 menyebabkan proses penstabilan nilai ∆𝜃𝜃 menjadi
terganggu. Pada grafik 4.8 ditunjukkan adanya lonjakan kecil pada grafik ∆𝜃𝜃. Hal ini
menyebabkan adanya lonjakan nilai ∆𝛿𝛿𝑒𝑒 (kontrol) yang berfungsi mempertahankan
kestabilan nilai ∆𝜃𝜃. Pada nilai 𝑞𝑞𝑔𝑔 yang kecil, kontrol masih mampu mempertahankan
kestabilan nilai ∆𝜃𝜃 seperti ditunjukkan pada gambar 4.8.
6. Untuk 𝑢𝑢𝑔𝑔R= 100 ft/s, 𝑤𝑤𝑔𝑔 = 100 ft/s, dan𝑞𝑞𝑔𝑔 = 1 × 10−
2 derajat/s
Gambar 4.9 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) dan elevator (∆𝛿𝛿𝑒𝑒) untuk 𝑢𝑢𝑔𝑔R
Nilai ∆𝜃𝜃 maksimum dari data yang diperoleh yaitu 5,4470o. Nilai maksimum
∆𝛿𝛿𝑒𝑒 dari data yang diperoleh yaitu 436,9073o
Gambar 4.9 menunjukkan proses penstabilan ∆𝜃𝜃 (perubahan sudut
kemiringan pesawat) yang kurang sempurna. Hal ini disebabkan karena nilai
gangguan 𝑞𝑞𝑔𝑔 yang konstan (1 × 10−2 derajat/s) sementara nilai ∆𝑞𝑞1 berubah-ubah sesuai dengan persamaan yang diberikan. Pada saat tertentu, terjadi lonjakan nilai 𝑞𝑞′
yang menyebabkan ikut melonjaknya nilai ∆𝜃𝜃. Hal ini berpengaruh pada kontrol yang
diberikan untuk menjaga kestabilan nilai ∆𝜃𝜃. Terlihat pada gambar 4.9, pada saat ∆𝜃𝜃
melonjak, kontrol ∆𝛿𝛿𝑒𝑒 (sudut kemiringan elevator) ikut melonjak secara ekstrim.
Lonjakan ini menandakan kontrol bekerja mengembalikan kestabilan ∆𝜃𝜃 setelah
terjadi lonjakan seperti terlihat pada gambar 4.9. Setelah terjadi lonjakan, nilai ∆𝜃𝜃
kembali bergerak menuju 0 (stabil). Namun, hal ini sulit dilakukan pada alat yang
sebenarnya karena lonjakan ∆𝛿𝛿𝑒𝑒 yang terlalu ekstrim. Hal ini menunjukkan bahwa
kontrol yang didesain mampu mengendalikan gerak longitudinal pesawat untuk
gangguan 𝑞𝑞𝑔𝑔 yang kecil.
. Karena dilakukan sampai detik ke
4000, waktu yang diperlukan untuk melakukan komputasi menjadi lebih lama, yaitu
7705,22 detik.
4.4. Pendekatan Numerik dengan Metode Runge-Kutta sebagai Pembanding
Dilakukan komputasi pendekatan numerik menggunakan metode
Runge-Kutta untuk melakukan simulasi respon sistem terhadap kontrol dengan interval
1. Untuk ℎ (interval waktu) = 0,1 detik
Gambar 4.10 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) untuk ℎ = 0,1 s
Untuk ℎ (interval waktu) 0,1 detik, komputasi tidak memberikan hasil yang
akurat. Hal ini ditunjukkan dengan nilai ∆𝜃𝜃 yang menuju tak berhingga seperti
terlihat pada gambar 4.10. Padahal, pada pendekatan numerik dengan metode
Parker-Sochacki untuk kasus yang sama (gambar 4.8), kontrol masih mampu mengendalikan
∆𝜃𝜃 untuk nilai 𝑞𝑞𝑔𝑔 = 1 × 10−3 derajat/s. Waktu yang diperlukan untuk melakukan
2. Untuk ℎ = 0,01 detik
Gambar 4.11 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) untuk ℎ = 0,01 s
Untuk interval waktu 0,01 detik, komputasi tidak dapat memberikan hasil
yang cukup akurat. Hal ini ditunjukkan pada nilai ∆𝜃𝜃 yang melonjak sangat rendah
seperti pada gambar 4.11. Waktu yang diperlukan untuk melakukan komputasi ini
yaitu 1909,73 detik. Komputasi yang menghasilkan gambar 4.11 ini hanya dilakukan
untuk simulasi selama 100 detik. Dibutuhkan waktu yang jauh lebih lama untuk
3. Untuk ℎ = 0,001 detik
Gambar 4.12 Perubahan sudut kemiringan pesawat (∆𝜃𝜃) untuk h = 0,001 s
Untuk interval waktu 0,001 detik, komputasi juga belum dapat memberikan
hasil yang cukup akurat. Hal ini ditunjukkan pada nilai ∆𝜃𝜃 yang melonjak sangat
tinggi seperti pada gambar 4.12, walaupun lonjakan sudat tidak setinggi lonjakan ∆𝜃𝜃
pada saat dilakukan simulasi untuk interval waktu 0,01 detik (gambar 4.11). Seperti
pada komputasi untuk interval waktu 0,01 detik, simulasi hanya dilakukan selama
100 detik karena dibutuhkan waktu komputasi yang sangat lama untuk memperoleh
data simulasi selama 1000 detik. Waktu yang diperlukan untuk melakukan komputasi
Dilakukan simulasi menggunakan pendekatan numerik dengan metode
Runge-Kutta selama 3,5 detik pertama dan dibandingkan dengan pendekatan numerik
Parker-Sochacki dalam waktu yang sama. Hasil simulasi dijabarkan pada tabel 4.1.
Tabel 4.1 Perbandingan tingkat keberhasilan pendekatan numerik untuk interval waktu 0,1 detik, 0,01 detik, dan 0,001 detik antara metode Runge-Kutta dan
Parker-Sochacki
No. Interval waktu (detik)
Metode Runge-Kutta Metode Parker-Sochacki
Pada data tabel ditunjukkan bahwa pada interval waktu 0,1 detik pendekatan
numerik dengan metode Runge-Kutta hanya mampu melakukan simulasi sampai
detik ke 0,3. Pada detik ke 0,4 nilai ∆𝜃𝜃 mulai melonjak sehingga menghasilkan
simulasi seperti terlihat pada gambar 4.10. Pada interval waktu 0,01 detik, pendekatan
numerik dengan metode Runge-Kutta mampu melakukan simulasi sampai detik ke
1,07. Pada detik ke 1,08 nilai ∆𝜃𝜃 mulai melonjak dan menghasilkan simulasi seperti
terlihat pada gambar 4.11. Pada interval waktu 0,001 detik, pendekatan numerik
dengan metode Runge-Kutta mampu melakukan simulasi sampai detik ke 3,232. Pada
pada gambar 4.12. Grafik hasil simulasi pendekatan numerik Runge-Kutta
ditunjukkan pada gambar 4.13.
Gambar 4.13 Perbandingan simulasi menggunakan pendekatan numerik Runge-Kutta untuk interval waktu 0,1 detik, 0,01 detik, dan 0,001 detik dengan pendekatan
numerik Parker-Sochacki untuk interval waktu 0,1 detik
Berdasarkan grafik di atas, dapat dilihat bahwa dengan metode Runge-Kutta,
pada interval waktu 0,001 detik hasil yang diperoleh lebih akurat dibandingkan hasil
yang diperoleh pada interval waktu yang lebih besar (0,01 detik dan 0,1 detik).
Namun, diperlukan waktu jauh lebih lama untuk memperoleh hasil yang lebih akurat.
Hal ini disebabkan banyaknya iterasi yang harus dilakukan untuk mendapatkan hasil
iterasi untuk mensimulasikan gerak pesawat selama 100 detik. Untuk interval waktu
yang lebih besar, jumlah iterasi yang diperlukan menjadi lebih sedikit sehingga
diperlukan waktu komputasi yang lebih singkat. Namun, hasil yang diperoleh
menjadi semakin tidak akurat.
Pendekatan numerik dengan metode Parker-Sochacki yang dilakukan pada
penelitian ini menggunakan interval waktu 0,1 detik untuk setiap pelaksanaan
komputasi. Hasil yang diperoleh jauh lebih akurat dibandingkan dengan metode
Runge-Kutta untuk interval waktu yang sama (0,1 detik). Karena itu, untuk
mendapatkan hasil yang cukup akurat bagi metode ini, iterasi yang diperlukan jauh
lebih sedikit. Akibatnya, waktu komputasi yang diperlukan juga lebih sedikit. Maka,
metode Parker-Sochacki lebih baik dibandingkan metode Runge-Kutta untuk
melakukan pendekatan numerik sistem pilot otomatis untuk penerbangan dengan
51
BAB V
PENUTUP
5.1. Kesimpulan
Telah dilakukan komputasi pendekatan numerik sistem pilot otomatis untuk
penerbangan menggunakan metode Parker-Sochacki. Dari penelitian ini dapat
disimpulkan bahwa
1. Metode ruang keadaan dapat digunakan untuk mendesain kontrol optimal gerak
longitudinal pesawat.
2. Gangguan angin searah elemen kecepatan sudut pesawat searah sumbu 𝑦𝑦 yang
terus menerus mengakibatkan penyelesaian analitik untuk simulasi kontrol dan
respon pesawat sulit dilakukan. Kombinasi metode Parker-Sochacki dan
metode ruang keadaan dapat digunakan untuk mendesain kontrol dan
melakukan simulasi respon pesawat dengan adanya gangguan tersebut.
3. Desain kontrol yang dihasilkan dari kombinasi metode ruang keadaan dan
pendekatan numerik Parker-Sochacki pada kasus pesawat yang terkena
gangguan angin mampu menanggulangi gangguan yang searah kecepatan sudut
pesawat dengan nilai kecil.
4. Metode Parker-Sochacki menghasilkan pendekatan yang lebih akurat
dibandingkan dengan metode Runge-Kutta pada interval waktu yang sama (0,1
5. Metode Runge-Kutta dengan interval waktu 0,001 detik mampu menghasilkan
pendekatan yang hampir sama akurat dengan metode Parker-Sochacki untuk
3,5 detik pertama. Namun, setelah 3,5 detik, kesalahan pendekatan dengan
metode Runge-Kutta semakin besar sehingga hasil yang diperoleh tidak lagi
akurat.
5.2. Saran
Pada penelitian ini, matriks keadaan sistem pesawat dianggap hanya berubah
pada elemen kecepatan pesawat. Pada sistem yang sebenarnya, saat terkena
gangguan, matriks keadaan sistem berubah secara keseluruhan. Untuk penelitian yang
selanjutnya, sebaiknya perubahan matriks keadaan sistem lebih diperhatikan agar
hasil yang diperoleh lebih baik.
Pada penelitian ini, nilai gangguan searah elemen kecepatan sudut pesawat
searah sumbu 𝑦𝑦 dibatasi pada nilai yang kecil. Diharapkan pada penelitian
selanjutnya dapat dimodifikasi kontrol pesawat yang dapat menanggulangi nilai
53
DAFTAR PUSTAKA
Chapra, S. C. 2008. Applied Numerical Methods with MATLAB, for Engineers and
Scientists. New York: McGraw-Hill.
van Groesen, E. dan Molenaar, J. 2007. Continuum Modelling in the Physical
Sciences. Philadelphia: Siam.
Heffley, R. K. dan Jewell, W. F. 1972. Aircraft Handling Qualities
Data.
2011.
Meyers, R. A. 1992. Encyclopedia of Physical Science and Technology Second
Edition. San Diego: Academic Press, Inc.
Nelson, R. C. 1998. Flight Stability and Automatic Control Second Edition.
Singapore: McGraw-Hill.
Ogata, K. 1985. Teknik Kontrol Automatik.Jakarta: Erlangga.
Parker, G. E. dan Sochacki, J. S. 1996. Implementing the Picard
Iteration.
Steward, R. D. dan Bair, W. 2009. Spiking Neural Network Simulation: Numerical
Integration With the Parker-Sochacki
Method.
54
Lampiran 1
Listing Program untuk Penyelesaian Analitik
tic
Listing Program untuk Pendekatan Numerik dengan Metode Parker-Sochacki
for time=1:b
s=q(1)/(q(1)-qg);
A=[-0.0209 0.122 0 -32.2;-0.202 -0.512 218.5725*s 0;0.000117
u(n)=(A(1,1)*u(n-1)+A(1,2)*w(n-1)+A(1,3)*q(n-subplot(2,1,1)
Listing Program untuk Pendekatan Numerik dengan Metode Runge-Kutta
tic
A=[-0.0209 0.122 0 -32.2;-0.202 -0.512 218.5725*s 0;0.000117
0.00177 -0.357 0;0 0 s 0];
(3.8687e-1)*s-82.6204*k2*s-(3.78e-1)*k4*s+(2.2559e-kq1=A1(3,1)*u2+A1(3,2)*w2+A1(3,3)*q2+A1(3,4)*th(time-1);
kq2=A1(3,1)*(u2+0.5*h*kq1)+A1(3,2)*(w2+0.5*h*kq1)+A1(3,3)*(q2+0.
5*h*kq1)+A1(3,4)*(th(time-1)+0.5*h*kq1);
kq3=A1(3,1)*(u2+0.5*h*kq2)+A1(3,2)*(w2+0.5*h*kq2)+A1(3,3)*(q2+0.
5*h*kq2)+A1(3,4)*(th(time-1)+0.5*h*kq2);
kq4=A1(3,1)*(u2+h*kq3)+A1(3,2)*(w2+h*kq3)+A1(3,3)*(q2+h*kq3)+A1(
3,4)*(th(time-1)+h*kq3);
q(time)=q(time-1)+1/6*h*(kq1+2*kq2+2*kq3+kq4);
kth1=A1(4,1)*u2+A1(4,2)*w2+A1(4,3)*q2+A1(4,4)*th(time-1);
kth2=A1(4,1)*(u2+0.5*h*kth1)+A1(4,2)*(w2+0.5*h*kth1)+A1(4,3)*(q2
+0.5*h*kth1)+A1(4,4)*(th(time-1)+0.5*h*kth1);
kth3=A1(4,1)*(u2+0.5*h*kth2)+A1(4,2)*(w2+0.5*h*kth2)+A1(4,3)*(q2
+0.5*h*kth2)+A1(4,4)*(th(time-1)+0.5*h*kth2);
kth4=A1(4,1)*(u2+h*kth3)+A1(4,2)*(w2+h*kth3)+A1(4,3)*(q2+h*kth3)
+A1(4,4)*(th(time-1)+h*kth3);
th(time)=th(time-1)+1/6*h*(kth1+2*kth2+2*kth3+kth4);
end
plot(h:h:(h*(b)),th)
ylabel('\fontsize{16}\it{\theta}^o')
xlabel('\fontsize{14}waktu (detik)')