www.elsevier.comrlocateratmos
Heterogeneous nucleation on rough surfaces:
implications to atmospheric aerosols
Mihalis Lazaridis
a, Øystein Hov
a, Kostas Eleftheriadis
a,b,)a ( )
Norwegian Institute for Air Research NILU , Postoboks 100, N-2007 Kjeller, Norway b
N.C.S.R. Demokritos, 15310 Ag. Paraskeui, Attiki, Greece
Received 23 August 1999; accepted 9 June 2000
Abstract
The effect of the surface roughness of solid atmospheric aerosol particles on their heteroge-neous nucleation capability has been examined using the concept ofAself-affineB rough surfaces. The surface roughness has a great influence on the contact angle between the particle surface and the nucleating liquid droplets. Roughness enhances wetting and the rate of heterogeneous nucleation from the vapor to the liquid phase. The paper furthermore discusses the considerable influence of the surface roughness on the physico-chemical characteristics of atmospheric insolu-ble aerosol particles.q2000 Elsevier Science B.V. All rights reserved.
Keywords: Surface roughness; Heterogeneous nucleation; Aerosol; Wetting
1. Introduction
Ž
Aerosol particles are important for weather and climate Charlson et al., 1992; Covert
.
et al., 1992 . Aerosols determine the formation of Type I Polar Stratospheric clouds
ŽPSCs , water condensation, ice, Cloud Condensation Nuclei CCN and contribute to. Ž . Ž
the radiation forcing of the atmosphere Charlson et al., 1992; Clarke, 1992; Luo et al.,
. Ž .
1994 . The activation processes of atmospheric aerosols CCN have considerable consequences on the optical properties of clouds and eventually on earth’s climate.
)Corresponding author. Norwegian Institute for Air Research NILU , Postoboks 100, 2007 Kjeller,Ž . Norway.
0169-8095r00r$ - see front matterq2000 Elsevier Science B.V. All rights reserved.
Ž .
Atmospheric aerosols consist of soluble and insoluble particles. In reality, atmo-spheric aerosols consist of complex surfaces with soluble and insoluble parts and details
Ž
of their aerosol dynamics history may further influence their surface energetics Knight,
.
1971; Lazaridis et al., 1991 . The activation process of soluble aerosols due to nitric acid
Ž .
vapor has been studied in a recent paper Kulmala et al., 1993 . Modification of the Kohler equilibrium curves of soluble particles due to the presence of insoluble material
¨
Ž .
in the aqueous solution drop has been also studied Seinfeld and Pandis, 1998 . However, the assumption of no interaction between the insoluble portion and the liquid part was used. In the present work we examine the effect of surface roughness on the heterogenous nucleation process of insoluble and solid particles where there is an interaction between the solid surface and the liquid solution of the nucleating embryo. One reason for the complex geometry of atmospheric particles is the coagulation process itself which leads to the appearance of complex surfaces with varying geometric orientations. The effect of aerosol shape and rigidity upon particle activation is very
Ž .
important and complicated Knight, 1971; Lin et al., 1993; Lazaridis et al., 1992 .
Ž .
Fletcher 1969 has treated the case of a distribution of conical pits in the surfaces of
Ž . Ž
aerosols, Huh and Mason 1977 considered surfaces with periodicity cross, hexagonal
. Ž .
and radial grooves , Lin et al. 1993 considered concentric rings of cones and Lazaridis
Ž .
et al. 1992 studied the effect of active sites on the process of heterogeneous nucleation, but it is obvious that all possible shapes are not excluded in determining the particle
Ž .
roughness. Knight 1971 referred to similar approaches as Aacademic exercisesB. However, the effect of surface roughness on the physical characteristics of atmospheric particles is an important issue which needs to be eventually resolved since in the majority of current modeling studies aerosols have been treated as smooth and spherical
Ž
and their surfaces energetically uniform Luo et al., 1994; Charlson et al., 1992;
.
Lazaridis et al., 1991 . For a detailed discussion on the activation processes of
Ž .
atmospheric aerosols we refer to Pruppacher and Klett 1997 .
Here we examine the effect of surface inhomogeneities on the nucleating effective-ness of atmospheric aerosol particles. The approach we follow is based on fluctuations
Ž
and noise correlation of the quenched disorder on self-affine rough surfaces Barabasi
.
and Stanley, 1994 . The paper follows the approaches adopted by the pioneering work of
Ž . Ž .
De Gennes 1985 on wetting phenomena and recent studies by Chow 1997, 1998 on the wetting of rough surfaces. Here the focus is on the nucleation of atmospheric vapors
Ž .
on pre-existing insoluble aerosol particles heterogeneous nucleation . In the current work, the effect of rough surfaces on wetting is analyzed using the theory of the
Ž
quenched disorder with the basis of stochastic differential and integral equations Chow,
. Ž
1997 . In Section 2.1, we consider the effect of weak fluctuations chemical
contamina-.
tion effects on the nucleation process. In Section 2.2, we consider the effect of
Ž .
2. Surface roughness
We examine first the effect of small surface inhomogeneities on the nucleation
Ž
process. The focus is on the formation of liquid embryos from atmospheric vapors such
.
as the sulfuric acid–water binary system onto a curved rough surface which corre-sponds to an atmospheric insoluble aerosol particle. Binary nucleation is important in the atmosphere, where usually various condensible vapors exist at low supersaturations. The classical theory of heterogeneous nucleation will be used for the description of vapor association on pre-existing surfaces and for calculating the effect of contact angle changes on the nucleation probability of atmospheric insoluble particles. The interaction between the liquid embryo and the solid substrate has been described in the classical
Ž Ž . .
model with the help of Young’s equation cosus gvsygls rglv where u is the
Ž
contact angle between the substrate and the liquid embryo Fletcher, 1969; Lazaridis et
.
al., 1991 andg refers to the surface tension. The sub-terms l, s, v refer to liquid, solid and vapor, respectively. As we can see, the classical theory describes the interactions between the embryo and the substrate by the use of the macroscopic quantity of contact angle.
Furthermore, we proceed with studying the effect of surface roughness on the mechanism of heterogeneous nucleation. Actually, we examine the effect of the surface roughness on the contact angle. Since the nucleation flux is very sensitive to changes in the value of the contact angle, small changes in the contact angle can result in large differences in the nucleation rate.
Ž
Rough surfaces of aerosols can be viewed as a Aself-affine fractalB Barabasi and
.
Stanley, 1994; Chow, 1997 . Self-affine fractals are defined as the fractal objects that are
Ž .
invariant under anisotropic transformations Barabasi and Stanley, 1994 , a description which is generally valid for many surfaces. The same approach will be adopted in the current paper.
2.1. Weak fluctuations–chemical contamination
Here we consider the effect of small inhomogeneities on the surface of aerosol particles for the value of the contact angle. The situation corresponds to the case of weak fluctuations that may result from small chemical contamination on the surface of a smooth aerosol surface. The case corresponds to an ideal situation but it is an interesting
Ž .
example to consider first. We follow here the approach of De Gennes 1985 where the chemical contamination can be described in terms of the local interfacial energies gsv,
gsl. The new local contact angle can be written as:
² :
glvcosusHq gsvygsl
Ž .
1² :
where the unperturbed angle u0 can be expressed as glvcosu0s gsvygsl and H corresponds to the fluctuating value of the term glvcosu. After performing a Taylor expansion atusu0 for small H, we get:
glvcosusglvcosu0qglv
Ž
uyu0. Ž
ysinu0.
Ž .
2Ž . Ž .
Since the above equation holds for small values of H, we can conclude that the
Ž .
changes in the contact angle are minimal much lower than a degree and would not change significantly the process of heterogeneous nucleation. However, in the case that the surface contamination has a size similar to that of the nucleating embryo, the situation changes and we may expect considerable differences in the nucleation rate
Ž .
compared to the case of an energetically homogeneous surface Lazaridis et al., 1992 . In the next section, we examine the effect of rough surfaces on the heterogeneous nucleation mechanism.
2.2. Rough surfaces
The main objective in this section is to evaluate changes of the value of contact angle between a smooth and a rough solid surface of aerosol particles. The current approach does not assume that the nucleation is controlled by the equilibrium contact angle. We begin with the ideal situation of smooth surface, where the equilibrium contact angle is
Ž .
adopted but we introduce spatial x, y dependent interfacial energy densities to
Ž
determine a generalized contact angle for describing the local wetting phenomena see
.
also Chow, 1998; Barabasi and Stanley, 1994 . As we have already mentioned above, in the case of rough substrates, the Young equation has to be modified in order to include the changes in the interfacial energiesgsv,gsl and contact angle in the description of the
Ž .
wetting behavior of the aerosol particle Barabasi and Stanley, 1994 :
gsvygslsglvcos u
Ž
x , y.
sglvcos uŽ
x , y.
0yfŽ
x , y.
Ž .
3Ž .
where x, y are the spatial coordinates on the surface of the aerosol particle andf x, y
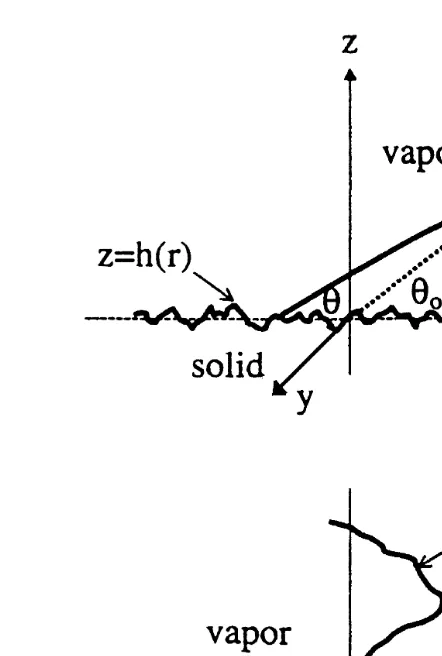
is the change of the contact angle because of roughness. The geometry of the system under investigation is shown in Fig. 1. As shown in Fig. 1, the contact line is expressed
Ž .
in the form xsl y and the contact free energy is the sum of the vapor-substrate and
liquid-substrate interactions.
The rough surface of the particle can be described as a self-affine fractal and the change of the height correlation can be obtained with the solution of the following
Ž .
stochastic Langevin-like differential equation Chow, 1997, 1998 :
d
Ž
Dh.
Dhs y qh
Ž .
rŽ .
4d r 2j
Ž
whereDhshyh0 h describes the unperturbed height of the nucleating liquid cluster0
.
on the surface of the aerosol particle , r is the position vector of the reference surface
Žvertical distance equal to zero ,. j is the function which describes the fluctuations
Ž .
parallel to the surface andh r is the noise term that is the source of fluctuations of Dh
ŽBarabasi and Stanley, 1994 . The first term on the right side of Eq. 4 is the average. Ž .
local slope. During the growth process, all sites on the particle surface are uncorrelated. However, there is a typical distance over which the heights of neighbor sites are
Ž .
correlated, and this correlated length is denoted by j. The noise term h r is an
Ž² : .
Ž .
Fig. 1. Definitions of contact angle and contact line adopted from Chow, 1998 .
² Ž . Ž .: Ž .
second moment is given by: h r1 h r2 sconstant=d r1sr , which implies that2
the noise has no correlations in space.
Ž .
The solution of Eq. 4 provides the change of the contact angle as function of the
Ž .
unperturbed contact angleu x, y , the function0 s that is the standard deviation of the
Ž .
fluctuations normal to the surface and the correlation length j Chow, 1998 :
cos u
Ž
x , y.
0yfŽ
x , y.
Casu0,1q .
Ž .
5cosu
Ž
x , y.
0 2jŽ .
The above derivation is based on the assumption that the noise term h r has a long-range slope correlation. The non-dimensional term C , which can be viewed as aa
correction factor, includes the effect of the correlated noise due fluctuations that interact between them. The function C can be written with the help of Gamma functions asa
wŽ Ž Ž ...ŽŽ Ž .. Ž Ž ...x1r2 Ž
Ž
is the roughness exponent that describes the fractal properties of the surface Chow,
.
1998 . The correlated noise is due to the microstructure of rough surfaces in agreement with experimental data. In the case where there is no correlated noise the right-hand side
Ž . Ž .
of Eq. 5 can be written as 1q su0r2j .
3. Classical theory of heterogeneous nucleation
In the present paper, we are using the classical theory of heterogeneous nucleation to evaluate the effect of surface roughness on the activation of atmospheric insoluble aerosol particles. As we have already argued, surface roughness reduces the value of the contact angle and consequently, will increase the nucleation capability of the aerosol particles. The classical theory of heterogeneous nucleation is based on a macroscopic description of an embryo in contact with a substrate using the concept of the contact angle u. Under the capillarity approximation, the free energy of formation of a liquid embryo from a single vapor on a substrate can be expressed as:
DGs ynkT ln SqSlvglvq
Ž
glsygvs.
SlsŽ .
6where n is the number of molecules in the droplet, S is the saturation ratio,gi j and Si j are the surface tension and surface area of the interface between phases i and j.
The interaction between the liquid embryo and the solid substrate has been described in the classical model with the help of the Young’s equation. The critical droplet composition is given by the composition at the saddle point. It is defined by the extremal
Ž . Ž .
conditions Gibbs–Thomson equations Lazaridis and Drossinos, 1997 .
Ž .
The critical value for the Gibbs free energy is obtained as Lazaridis et al., 1992 : 2
denotes the radius of the pre-existing aerosol particle, m is the cosine of the contact
) .
angle and r is the radius of the critical nucleating cluster .
In the classical nucleation theory, we can derive a steady-state expression for the
Ž
heterogeneous nucleation rate that can be written as Lazaridis and Drossinos, 1997;
.
wherelirefer to the eigenvalues that result from a rotation of a matrix, that includes the impingement rates of the two components, from the coordinate system that has as coordinates the number of molecules in the cluster and energy to a new one in such a
Ž
way that the mathematical manipulations of the equations are easier see also Barrett,
. < <
1994; Langer, 1969; Lazaridis and Drossinos, 1997 . Furthermore, the term k is the
Ž ) ).
absolute value of a growth rate, S12 n , n1 2 is the surface area of the nucleating droplet
Žincluding n) molecules of the specie i ,. s is the mean-square energy fluctuations, b
i ´
critical cluster. The energy fluctuations contribution arises from the fact that a condens-ing or evaporatcondens-ing monomer not only alters the composition of the formcondens-ing droplet, but it also adds or removes the latent heat of condensation.
The dependence of the nucleation rate on the contact angle arises from the terms R ,a a
Ž ) ). )
S12 n , n1 2 and F . For a detailed description of the kinetics and energetics of the
Ž . Ž .
heterogeneous nucleation, we refer to Fletcher 1969 and Lazaridis et al. 1991 . However, there are many aspects missing from the simple version of the theory such
Ž
as the concepts of surface diffusion and line tension Joanny and De Gennes, 1986;
.
Talanquer and Oxtoby, 1996; Lazaridis, 1993, 1994; Lazaridis and Ford, 1993 . An important aspect of the interaction between the liquid nucleating embryo and the substrate is the consideration of the long-range forces that exist between the liquid and solid. An approach which has been used is the introduction of the line energy that arises from the line discontinuity between two or more surface phases. In the present paper, we are mainly concerned with the effect of surface roughness on the heterogeneous nucleation rate and we will not be concerned with the effects of surface diffusion and line tension. Surface diffusion and negative values for the line tension may result in even higher values for the heterogeneous nucleation process as shown in a number of
Ž .
previous studies De Gennes, 1985; Lazaridis, 1993 .
In the following, the correction factor we derived for the contact angle due to existence of a rough surface will be evaluated. The sensitivity of the nucleation flux on the value of the contact angle will also be evaluated for the H SO –H O binary system.2 4 2
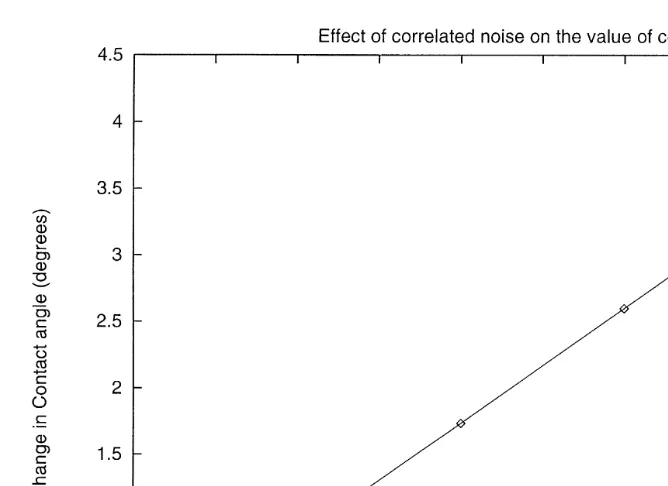
In Fig. 2, we show the effect of the ratio xssCarj on the contact angle. Increased values of the ratio x result in a further decrease of the unperturbed value of the contact angle in an almost linear way. Therefore, surface roughness enhances wetting and leads to higher nucleation rates for the solid fraction of the atmospheric aerosols. The initial contact angle used in the calculations was 308.
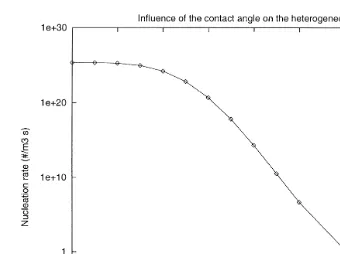
Fig. 3 shows the nucleation dependence on the contact angle for the H SO –H O2 4 2
binary system. The nucleation rate is very sensitive to small changes in the value of the contact angle and its value decreases as the contact angle increases. Of course, this strong dependence is a consequence of the parametrization of the interactions between the solid surface and the liquid droplet through the contact angle. Since surface roughness can decrease the value of the contact angle by several degrees, it is expected that it will also modify the nucleating properties of the aerosol surfaces and enhance the nucleation flux. In the calculations, the radius of the particle is chosen to be 1mm, the temperature equal to 262.15 K, the water activity equal to 0.178 and the sulfuric acid activity equal to 2.86=10y2. The above values correspond to atmospheric conditions at altitude of 4 km.
The effect of surface roughness on the binary heterogeneous nucleation of the sulfuric acid–water system at atmospheric conditions was further examined with respect to the probability of nucleation occurrence on the surface of the aerosol particles.
In the simulations, we have chosen a contact angle of 708to correspond to the case of smooth surface and contact angles of 688 and 668 to describe the situation of rough surface where the contact angle is reduced by 28and 48. This corresponds to values for the function x of 2 and 4.5, respectively, as can be seen from Fig. 2. The value of 708
Ž .
Fig. 2. Effect of the factor x ssCarj on the value of the contact angle. The y-axis shows the decrease of
Ž .
the contact angle in degrees due to the effect of surface roughness.
Ž .
sulfuric acid and solid sulfur Hamill et al., 1982 . However, there is a considerable variability of the contact angle between various surfaces due to chemical composition of the liquid embryo and the particle surface. For example, the contact angle of water on
Ž .
over 100 low energy organic surfaces ranges between 608and 1208 Hamill et al., 1982 . In the calculations, the radius of the particle is also chosen to be 1mm.
In Fig. 4, we show the effect of the ambient temperature on the heterogeneous nucleation probability of atmospheric aerosols. The background aerosol concentration was chosen equal to 300 cmy3 and the background concentrations of water, sulfuric acid and temperature similar to the conditions at altitude of zero kilometers. Change of 158in the ambient temperature can lead to considerable changes in the activation process of atmospheric aerosols. Again, the shape of aerosol particles has a crucial impact on their activation potential. The results of Fig. 4 highlight the importance of processes such as isobaric and adiabatic cooling as effective mechanisms of aerosol activation and cloud formation.
Fig. 3. Dependence of the nucleation rate on the contact angle.
4. Conclusions
From the calculations above we can conclude the importance of the surface roughness on the activation process of insoluble particles in the atmosphere which may have also important consequences on the CCN activation process. The strong dependence of the nucleating characteristics of solid surfaces on their roughness is an important aspect that has to be taken into account in modeling studies of aerosol activation processes in the atmosphere. There has been a considerable increase in the last years in emissions of solid aerosol particles such as diesel soot, fly ash and combustion generated ultrafine particles which will contribute significantly to the aerosol background concentration
ŽEPA, 1996 . The activation of these particles in the atmosphere is an important area of.
future research. Surface characteristics of aerosols have to be studied carefully, experi-mentally and theoretically to determine the effect of surface roughness on their potential
Ž
on the heterogeneous nucleation process. However, small inhomogeneities that lead to a
.
change in the contact angle of much less than a degree on the aerosol surface is expected to have minor effects on the physico-chemical characteristics of atmospheric particles as shown in Section 2.1.
Another conclusion from the present calculations is that aerosols are more readily enriched with sulfuric acid in the atmosphere compared to the results of classical nucleation theory with smooth surfaces, affecting therefore their surface chemical composition. The chemical composition of aerosols in the atmosphere has an important
Ž
effect on climate change and ozone destruction in the stratosphere Charlson et al.,
.
1992 . The present work indicates that the composition of pre-existing aerosol particles in the upper troposphere and stratosphere may be altered due to heterogeneous nucle-ation of sulfuric acid molecules. Similar effects may occur due to nuclenucle-ation of other gaseous species with low vapor pressures such as organic species.
Acknowledgements
The authors acknowledge the partial financial support from the European
Commis-Ž
sion Fift Framework Programme, Environment and Sustainable Development, Project
.
SUB-AERO, contract EVK2-CT-1999-00052 .
References
Barabasi, A.L., Stanley, H.E., 1994. Fractal Concepts in Surface Growth. Cambridge Univ. Press, Cambridge, MA.
Barrett, J.C., 1994. Equilibrium and steady-state distributions of vapour clusters in nucleation theory. J. Phys. A: Math. Gen. 27, 5053–5068.
Charlson, R.J., Schwartz, S.E., Hales, J.M., Cess, J.A., Coakley, J.E., Hansen, J.E., Hofmann, D.J., 1992. Climate forcing by antropogenic aerosols. Science 255, 423–430.
Covert, D.S., Kapustin, V.N., Quinn, P.K., Bates, T.S., 1992. New particle formation in the marine boundary layer. J. Geophys. Res. 97, 20581–20587.
De Gennes, P.G., 1985. Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863. Fletcher, N.H., 1969. Active sites and ice nucleation. J. Atmos. Sci. 26, 1266.
EPA, U.S. Environmental Protection Agency, 1996. Air Quality Criteria for Particulate Matter. EPAr600rP-95r001aF.
Hamill, P., Turco, R.P., Kiang, C.S., Toon, O.B., Whitten, R.C., 1982. An analysis of various nucleation mechanisms for sulfate particles in the stratosphere. J. Aerosol Sci. 13, 561–585.
Ž .
Huh, C., Mason, S.G., 1977. Effects of surface roughness on wetting theoretical . J. Colloid Interface Sci. 60, 11–38.
Joanny, J.F., De Gennes, P.G., 1986. Role of long-range forces in heterogeneous nucleation. J. Colloid Interface Sci. 111, 94–101.
Ž .
Knight, C.A., 1971. Aerosols and atmospheric chemistry. In: Hidy, G.M. Ed. , Proceedings of the American Chemical Society, Los Angeles, California 155. Academic Press.
Kulmala, M., Laaksonen, A., Korhonen, P., Vesala, T., Ahonen, T., Barrett, J.C., 1993. The effect of atmospheric nitric acid on cloud condensation nucleus activation. J. Geophys. Res. 98, 22949–22958. Langer, J.S., 1969. Statistical theory of the decay of metastable states. Ann. Phys. 54, 258–275.
Lazaridis, M., Ford, I.J., 1993. A statistical mechanical approach to heterogeneous nucleation. J. Chem. Phys. 99, 5426–5429.
Lazaridis, M., 1993. The effects of surface diffusion and line tension on the mechanism of heterogeneous nucleation. J. Colloid Interface Sci. 155, 386–391.
Lazaridis, M., 1994. A statistical mechanical model of heterogeneous nucleation including the effects of line tension and surface diffusion. J. Colloid Interface Sci. 162, 431–436.
Lazaridis, M., Kulmala, M., Laaksonen, A., 1991. Binary heterogeneous nucleation of a water–sulphuric acid system: the effect of hydrate interaction. J. Aerosol Sci. 22, 823–830.
Lazaridis, M., Kulmala, M., Gorbunov, B., 1992. Heterogeneous nucleation at a non uniform surface. J. Aerosol Sci. 23, 457–466.
Lazaridis, M., Drossinos, Y., 1997. Energy fluctuations in steady state binary nucleation. J. Phys. A: Math. Gen. 30, 3847–3865.
Lazaridis, M., 1998. Steady-state homogeneous nucleation of the sulfuric acid–water system. Chem. Phys. Lett. 296, 477–482.
Lin, F.Y.H., Li, D., Neumann, A.W., 1993. J. Colloid Interface Sci. 159, 86–95.
Luo, B.P., Peter, T., Crutzen, P.J., 1994. Freezing of sulfuric aerosol droplets in the stratosphere: I. Formation of SAT. Geophys. Res. Lett. 21, 1447–1450.
Pruppacher, H.R., Klett, J.D., 1997. Microphysics of Clouds and Precipitation. Kluwer Academic Publishing, Dordrecht, The Netherlands.
Seinfeld, J.H., Pandis, S., 1998. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. John Wiley & Sons, New York.