BAB 2
TINJAUAN PUSTAKA
2.1 Konsep Dasar Statistika
Statistika merupakan cara – cara tertentu yang digunakan dalam mengumpulkan, menyusun atau mengatur, menyajikan, menganalisa, dan memberi informasi serta interpretasi terhadap sekumpulan data. Sehingga kumpulan bahan keterangan yang dikumpulkan dapat memberi pengertian dan makna tertentu. Seperti pengambilan kesimpulan membuat estimasi dan juga prediksi yang akan datang.
Ruang lingkup statistika meliputi statistika deduktif atau deskriptif dan statistika induktif atau inferensial. Statistika induktif terdiri dari menghimpun, menyusun, mengolah, menyajikan dan menganalisa data angka. Sedangkan statistika deduktif adalah meliputi teori probability, distribusi teoritis, distribusi sampling, penaksiran, pengujian hipotesa, korelasi, komparasi, dan regresi. Sumber data statistik dapat dikumpulkan langsung oleh peneliti dari pihak yang bersangkutan, disebut dengan data primer. Dan data juga dapat juga diperoleh dari pihak lain atau data yang sudah ada disebut data sekunder.
2.2 Analisis Jalur
Analisis jalur yang dikenal dengan path analysis dikembangkan pertama pada tahun 1920-an oleh seorang ahli genetika yaitu Sewall Wright (Joreskog dan Sorbom, 1996; Johnson dan Wichern, 1992). Teknik analisis jalur sebenarnya merupakan perkembangan korelasi yang diuraikan menjadi beberapa interpretasi akibat yang ditimbulkannya. Lebih lanjut, analisis jalur mempunyai kedekatan dengan regresi berganda. Dengan kata lain, regresi berganda merupakan bentuk khusus dari analisis jalur. Teknik ini juga dikenal sebagai model sebab akibat (causing modeling). Penanaman ini didasarkan pada alas an bahwa analisis jalur memungkinkan pengguna dapat menguji proposisi teoritis mengenai hubungan sebab akibat tanpa memanipulasi variabel-variabel (Sarwono, 2007).
Analisis jalur adalah suatu teknik untuk menganalisa hubungan sebab akibat yang terjadi pada regresi berganda jika variabel bebasnya mempengaruh variabel tergantung tidak hanya secara langsung, tetapi juga secara tidak langsung (Robert D. Rutherford 1993).
2.3 Pengertian Analisis Jalur
Telaah statistika menyatakan bahwa untuk tujuan peramalan atau pendugaan nilai Y atas dasar nilai-nilai X1, X2, ….., Xi, pola hubungan yang sesuai adalah pola hubungan yang mengikuti model regresi, sedangkan untuk menganalisis pola hubungan kausal antar variabel dengan tujuan untuk
mengetahui pengaruh langsung dan tidak langsung, secara serempak atau mandiri beberapa variabel penyebab terhadap sebuah variabel akibat, maka pola yang tepat adalah model analisis jalur. Analisis jalur (path analysis) dikembangkan oleh Sewall Wright (1934). Path analysis digunakan apabila secara teori kita yakin berhadapan dengan masalah yang berhubungan sebab akibat. Tujuannya adalah menerangkan akibat langsung dan tidak langsung seperangkat variabel, sebagai variabel penyebab, terhadap variabel lainnya yang merupakan variabel akibat.
Terdapat beberapa defenisi mengenai analisis jalur, diantaranya adalah sebagai berikut:
1. Analisis jalur adalah suatu teknik untuk menganalisis hubungan sebab akibat yang terjadi pada regresi berganda jika variabel bebasnya mempengaruhi variabel tergantung tidak hanya secara langsung, tetapi juga secara tidak langsung (Robert D. Rutherford 1993).
2. Analisis jalur merupakan pengembangan langsung bentuk regresi berganda dengan tujuan untuk memberikan estimasi tingkat kepentingan (magnitude) dan signifikansi (significance) hubungan sebab akibat hipotetikal dalam seperangkat variabel (Paul Webley, 1997).
3. Model perluasan regresi yang digunakan untuk menguji keselarasan matriks korelasi dengan dua atau lebih model hubungan sebab akibat yang dibandingkan oleh peneliti. Modelnya digambarkan dalam bentuk gambar lingkaran dan panah dimana anak panah tunggal menunjukkan sebagai penyebab. Regresi dikenakan pada masing-masing variabel dalam suatu model
sebagai variabel tergantung (pemberi respon) sedang yang lain sebagai penyebab. Pembobotan regresi diprediksikan dalam suatu model yang dibandingkan dengan matriks korelasi yang diobservasi untuk semua variabel dan juga dilakukan perhitungan uji keselarasan statistik (David Garson, 2003).
Dari defenisi-defenisi diatas, dapat disimpulkan bahwa sebenarnya analisis jalur merupakan kepanjangan dari analisis regresi berganda. Jadi, model path analysis digunakan untuk menganalisis pola hubungan antar variabel dengan tujuan untuk mengetahui pengaruh langsung maupun tidak langsung seperangkat variabel bebas (eksogen) terhadap variabel terikat (endogen). Oleh sebab itu, rumusan masalah penelitian dalam kerangka path analysis berkisar pada:
a. Apakah variabel eksogen (X1, X2, ….., Xk) berpengaruh terhadap variabel endogen Y
b. Berapa besar pengaruh kausal langsung, kausal tidak langsung, kausal total maupun simultan seperangkat variabel eksogen (X1, X2, ….., Xk) terhadap variabel endogen
2.4 Kegunaan Analisis Jalur
Kegunaan model path analysis adalah untuk:
a. Penjelasan terhadap fenomena yang dipelajari atau permasalahan yang diteliti.
b. Prediksi nilai variabel terikat (Y) berdasarkan nilai variabel bebas (X), dan prediksi dengan path analysis ini bersifat kualitatif.
c. Faktor determinan yaitu penentuan variabel bebas (X) mana yang berpengaruh dominan terhadap variabel terikat (Y), juga dapat digunakan untuk menelusuri mekanisme (jalur-jalur) pengaruh variabel bebas (X) terhadap variabel terikat (Y).
d. Pengujian model, menggunakan teori trimming, baik untuk uji reliabilitas konsep yang sudah ada ataupun uji pengembangan konsep baru.
2.5 Asumsi-asumsi Analisis Jalur
Sebelum melakukan analisis, hendaknya diperhatikan beberapa asumsi sebagai berikut:
1. Pada model analisis jalur, hubungan antar variabel adalah bersifat linier, adaptif dan bersifat normal.
2. Hanya system aliran kausal kesatu arah artinya tidak ada arah kausalitas yang berbalik.
3. Variabel terikat (endogen) minimal dalam skala ukur interval dan rasio. 4. Menggunakan sampel probability sampling yaitu teknik pengambilan
sampel untuk memberikan peluang yang sama pada setiap anggota populasi untuk dipilih menjadi anggota sampel.
5. Observed variables diukur tanpa kesalahan instrument pengukuran valid dan reliable artinya variabel yang diteliti dapat diobservasi secara langsung.
6. Model yang dianalisis dispesifikasikan dengan benar berdasarkan teori-teori dan konsep-konsep yang relevan artinya model teori-teori yang dikaji atau
diuji dibangun berdasarkan teoritis tertentu yang mampu menjelaskan hubungan kausalitas antar variabel yang diteliti.
2.6 Model Analisis Jalur
Beberapa istilah dan defenisi dalam path analysis:
1. Dalam path Analysis, kita hanya menggunakan sebuah lambung variabel, yaitu X. Untuk membedakan X yang satu dengan X yang lainnya, kita menggunakan subscript (indeks). Contoh : X1, X2, X3, ….., Xk.
2. Kita membedakan dua jenis variabel, yaitu variabel yang menjadi pengaruh (exogenous variable), dan variabel yang dipengaruhi (endogenous variable).
3. Lambang hubungan langsung dari eksogen ke endogen adalah panah bermata satu, yang bersifat recursive atau arah hubungan yang tidak berbalik/satu arah.
4. Diagram jalur merupakan diagram atau gambar yang mensyaratkan hubungan terstruktur antar variabel (Harun Al Rasyid, 2005).
Ada beberapa model jalur mulai dari yang paling sederhana sampai dengan yang lebih rumit, diantaranya diterangkan di bawah ini:
a. Analisa Jalur Model Trimming
Model Trimming adalah model yang digunakan untuk memperbaiki suatu model struktur analisis jalur dengan cara mengeluarkan dari model variabel eksogen yang koefisien jalur diuji secara keseluruhan apabila ternyata ada variabel yang tidak signifikan. Walaupun ada satu, dua, atau lebih variabel yang tidak
signifikan, perlu memperbaiki model struktur analisis jalur yang telah dihipotesiskan.
b. Analisis Jalur Model Dekomposisi
Model dekomposisi adalah model yang menekankan pada pengaruh yang bersifat kausalitas antar variabel, baik pengaruh langsung ataupun tidak langsung dalam kerangka path analysis, sedangkan hubungan yang sifatnya nonkausalitas atau hubungan korelasional yang terjadi antar variabel eksogen tidak termasuk dalam perhitungan ini. Perhitungan menggunakan analisis jalur dengan menggunakan model dekomposisi pengaruh kausal antar variabel dapat dibedakan menjadi tiga: 1. Direct causal effects (Pengaruh Kausal Langsung) adalah pengaruh satu variabel eksogen terhadap variabel endogen yang terjadi tanpa melalui variabel endogen lain.
2. Indirect causal effects (Pengaruh Kausal Tidak Langsung) adalah pengaruh satu variabel eksogen terhadap variabel endogen yang terjadi melalui variabel endogen lain terdapat dalam satu model kausalitas yang sedang dianalisis.
3. Total causal effects (Pengaruh Kausal Total) adalah jumlah dari pengaruh kausal langsung dan pengaruh kausal tidak langsung.
c. Model Regresi Berganda
Model ini merupakan pengembangan regresi berganda dengan menggunakan dua variabel eksogenous, yaitu X1 dan X2 dengan satu variabel endogenous Y.
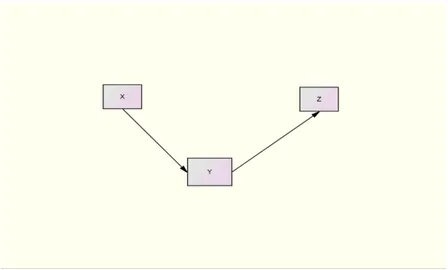
d. Model Mediasi
Model mediasi atau perantara dimana variabel Y memodifikasi pengaruh variabel X terhadap variabel Z. Model digambarkan sebagai berikut:
Gambar 2.1 Model Mediasi
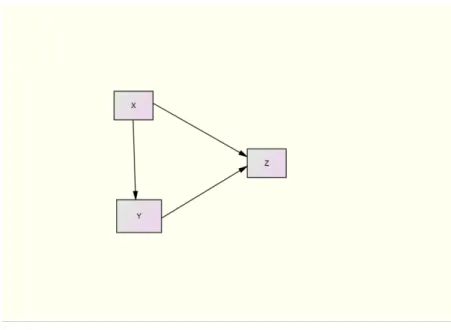
e. Model Kombinasi Regresi Berganda Dan Mediasi
Model ini merupakan kombinasi antara model regresi berganda dan mediasi, yaitu variabel X berpengaruh terhadap variabel Z secara langsung dan tidak langsung mempengaruhi variabel Z melalui variabel Y . Model digambarkan sebagai berikut:
Gambar 2.2 Model kombinasi regresi berganda dan mediasi
f. Model Kompleks
Model ini merupakan model yang lebih kompleks, yaitu variabel X1 secara langsung mempengaruhi Y2 dan melalui variabel X2 secara tidak langsung mempengaruhi Y2, sementara variabel Y2 juga dipengaruhi oleh variabel Y1. Model digambarkan sebagai berikut:
g. Model Rekursif dan Model Non Rekursif
Dari sisi pandang arah sebab dan akibat, ada dua tipe model jalur, yaitu jalur rekursif dan non rekursif. Model rekursif ialah jika semua anak panah menuju satu arah.
Pada bagian berikut untuk mempermudah kita dalam memahami analisis jalur, maka kita bisa menggunakan model-model jalur berikut:
1. Model Persamaan Satu Jalur
Model persamaan satu jalur merupakan hubungan sebenarnya sama dengan regresi berganda, yaitu variabel bebas terdiri lebih dari satu variabel dan variabel tergantungnya hanya satu.
2. Model Persamaan Dua Jalur
Model ini terdiri dari tiga variabel bebas dan mempunyai dua variabel tergantung.
3. Model Persamaan Tiga jalur
Model ini terdiri dari tiga variabel bebas, salah satu variabel bebas menjadi variabel perantara dan mempunyai dua variabel tergantung.
2.7 Diagram Jalur dan Persamaan Struktural
Pada saat akan melakukan analisis jalur, disarankan untuk terlebih dahulu menggambarkan secara diagramatik struktur hubungan kausal antara variabel penyebab dengan variabel akibat. Diagram ini disebut diagram jalur (Path
Diagram), dan bentuknya ditentukan oleh proposisi teoritik yang berasal dari kerangka pikir tertentu.
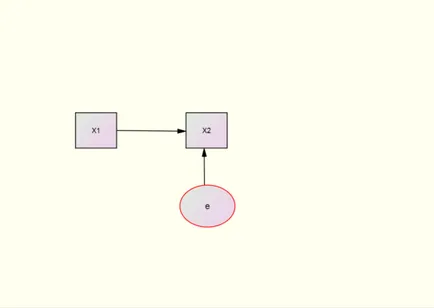
Gambar 2.4 Diagram Jalur Yang Menyatakan Hubungan Kausal Dari X1 Sebagai Penyebab Ke X2 Sebagai Akibat
Keterangan:
X1 adalah variabel eksogenus (exogenous variable), untuk itu selanjutnya variabel penyebab akan kita sebut sebagai variabel eksogenus. X2 adalah variabel endogenus (endogenous variable), sebagai akibat, dan ε adalah variabel residu (residual variable), yang merupakan gabungan dari: (1) Variabel lain, di luar X1, yang mungkin mempengaruhi X2 dan telah teridentifikasi oleh teori, tetapi tidak dimasukkan dalam model. (2) Variabel lain, di luar X1, yang mungkin mempengaruhi X2 tetapi belum teridentifikasi oleh teori. (3) Kekeliruan pengukuran (error of measurement), dan (4) Komponen yang sifatnya tidak menentu (random component).
Langkah kerja yang dilakukan untuk menghitung koefisien jalur adalah:
1. Gambarkan dengan jelas diagram jalur yang mencerminkan proposisi hipotetik yang diajukan, lengkap dengan persamaan strukturalnya. Di sini kita harus bisa menterjemahkan hipotesis penelitian yang kita ajukan ke dalam diagram jalur, sehingga bisa tampak jelas variabel apa saja yang merupakan variabel eksogenus dan apa yang menjadi variabel endogenusnya.
2. Menghitung matriks korelasi antar variabel formula untuk menghitung koefisien korelasi yang dicari adalah menggunakan Product Moment Coeffisient dari Karl Pearson. Alasan penggunaan teknik koefisien korelasi dari Karl Pearson adalah karena variabel-variabel yang hendak dicari korelasinya memiliki skala pengukuran interval.
3. Identifikasikan sub-struktur dan persamaan yang akan dihitung koefisien jalurnya. Misalkan saja dalam sub-struktur yang telah kita identifikasi terdapat k buah variabel eksogenus, dan sebuah (selalu hanya sebuah) variabel endogenus Xu yang dinyatakan oleh persamaan:
𝑥𝑢 = 𝜌𝑥𝑢𝑥1𝑥1+ 𝜌𝑥𝑢𝑥2𝑥2+ … + 𝜌𝑥𝑢𝑥𝑘𝑥𝑘
Kemudian hitung matriks korelasi antar variabel eksogenus yang menyusun substruktur tersebut.
4. Menghitung matriks invers korelasi eksogenus
2.8 Besarnya Pengaruh Variabel Eksogen Terhadap Variabel Endogen
Pengaruh yang diterima oleh sebuah variabel endogenus dari dua atau lebih variabel eksogenus, dapat secara sendiri-sendiri maupun secara bersama-sama. Pengaruh secara sendiri-sendiri (parsial), bisa berupa pengaruh langsung, bisa juga berupa pengaruh tidak langsung, yaitu melalui variabel eksogen yang lainnya. Menghitung besarnya pengaruh langsung, pengaruh tidak langsung serta pengaruh total variabel eksogenus terhadap variabel endogenus secara parsial, dapat dilakukan dengan rumus:
1. Besarnya pengaruh langsung variabel eksogenus terhadap variabel endogenus
= 𝝆
𝒙𝒖𝒙𝒊𝒙 𝝆
𝒙𝒖𝒙𝒊2. Besarnya pengaruh tidak langsung variabel eksogenus terhadap variabel endogenus
= 𝝆
𝒙𝒖𝒙𝒊𝒙 𝒓
𝒙𝟏𝒙𝟐𝒙 𝝆
𝒙𝒖𝒙𝒊3. Besarnya pengaruh total variabel eksogenus terhadap variabel endogenus adalah penjumlahan besarnya pe ngaruh langsung dengan besarnya pengaruh tidak langsung
= �𝝆
𝒙𝒖𝒙𝒊𝒙 𝝆
𝒙𝒖𝒙𝒊� + �𝝆
𝒙𝒖𝒙𝒊𝒙 𝒓
𝒙𝟏𝒙𝟐𝒙 𝝆
𝒙𝒖𝒙𝒊�
Selanjutnya pengaruh bersama-sama (simultan) variabel eksogenus terhadap variabel endogenus dapat dihitung dengan menggunakan rumus:
𝑹
𝟐𝒙
𝒖(𝒙𝟏,𝒙𝟐,…,𝒙𝒌)= �𝝆
𝒙𝒖𝒙𝟏𝝆
𝒙𝒖𝒙𝟐… 𝝆
𝒙𝒖𝒙𝒌� �
𝒓
𝒙𝒖𝒙𝟏𝒓
𝒙𝒖𝒙𝟐…
𝒓
𝒙𝒖𝒙𝒌�
Dimana: 𝑅2𝑥𝑢(𝑥1,𝑥2,…,𝑥𝑘) adalah koefisien determinasi total X1, X2, … Xk terhadap Xu atau
besarnya pengaruh variabel eksogenus secara bersama-sama (gabungan) terhadap variabel endogenus.
𝜌𝑥𝑢𝑥1 𝜌𝑥𝑢𝑥2… 𝜌𝑥𝑢𝑥𝑘adalah koefisien jalur.
𝑟𝑥𝑢𝑥1 𝑟𝑥𝑢𝑥2… 𝑟𝑥𝑢𝑥𝑘 adalah koefisien variabel eksogenus X1, X2, ... Xk dengan
variabel endogenus Xu.
2.9 Pengujian Koefisien Jalur
Menguji kebermaknaan (test of significance) setiap koefisien jalur yang telah dihitung, baik secara sendiri-sendiri maupun secara bersama-sama, serta menguji perbedaan besarnya pengaruh masing-masing variabel eksogenus terhadap variabel endogenus, dapat dilakukan dengan langkah kerja berikut: 1. Nyatakan hipotesis statistik (hipotesis operasional) yang akan diuji.
Ho : 𝜌𝑥𝑢𝑥𝑖 = 0, artinya tidak terdapat pengaruh variabel eksogenus (Xu) terhadap variabel endogenus (Xi).
H1 : 𝜌𝑥𝑢𝑥𝑖 ≠ 0, artinya terdapat pengaruh variabel eksogenus (Xu) terhadap variabel endogenus (Xi).
Dimana u dan i = 1, 2, …, k
2. Gunakan statistik uji yang tepat, yaitu: Untuk menguji setiap koefisien jalur:
𝒕 =
𝝆
𝒙𝒖𝒙𝒊�� 𝟏 − 𝑹
𝟐𝒙
𝒖(𝒙𝟏,𝒙𝟐,…,𝒙𝒌)�𝒄
𝒊𝒊𝒏 − 𝒌 − 𝟏
dimana:
i = 1, 2, …, k
k = Banyaknya variabel eksogenus dalam sub-struktur yang sedang diuji
t = Mengikuti tabel distribusi t, dengan derajat bebas = n – k – 1
Kriteria pengujian:
Ditolak Ho jika nilai hitung t lebih besar dari nilai tabel thit > ttabel (n-k-1)
• Untuk menguji koefisien jalur secara keseluruhan atau bersama-sama:
𝑭 =
(𝒏 − 𝒌 − 𝟏) (𝑹
𝟐𝒙
𝒖(𝒙𝟏,𝒙𝟐,…,𝒙𝒌))
𝒌� 𝟏 − 𝑹
𝟐𝒙
𝒖(𝒙𝟏,𝒙𝟐,…,𝒙𝒌)
�
dimana:i = 1, 2, …, k
k = Banyaknya variabel eksogenus dalam sub-struktur yang sedang diuji
t = Mengikuti tabel distribusi F snedecor, dengan derajat bebas (degrees of freedom) k dan n – k – 1
Kriteria pengujian :
Ditolak Ho jika nilai hitung F lebih besar dari nilai tabel Fhit > Ftabel(k, n-k-1)
• Untuk menguji perbedaan besarnya pengaruh masing-masing variabel eksogenus terhadap variabel endogenus.
𝒕 =
𝝆
𝒙𝒖𝒙𝒊− 𝝆
𝒙𝒖𝒙𝒋�� 𝟏 − 𝑹
𝟐𝒙
𝒖(𝒙𝟏,𝒙𝟐,…,𝒙𝒌)�(𝒄
𝒊𝒊+ 𝒄
𝒋𝒋− 𝒄
𝒊𝒋𝒏 − 𝒌 − 𝟏
Kriteria pengujian:
Ditolak Ho jika nilai hitung t lebih besar dari nilai tabel thit > ttabel(n-k-1) 3. Ambil kesimpulan, apakah perlu trimming atau tidak.
Apabila terjadi trimming, maka perhitungan harus diulang dengan menghilangkan jalur yang menurut pengujian tidak bermakna (no signifikan).