Manajemen dan Rekayasa Struktur C-25
BENDING OF FUNCTIONALLY GRADED THICK PLATES RESTING
ON WINKLER–PASTERNAK ELASTIC FOUNDATIONS
BENYOUCEF Samir (1), BACHIR BOUIADJRA Rabbab(2),ZIDI Mohamed(1), BOURADA Mohamed(1), TOUNSI Abdelouahed(1),ADDA BEDIA El Abbas
(1) Laboratoire des Matériaux et Hydrologie, Université de Sidi Bel Abbes, BP 89 Cité Ben M’hidi 22000 Sidi Bel Abbes, Algérie.
(1)
(2) Université de Sciences et Technologie d’Oran (USTO), Algérie.
Abstract— The static response of simply supported functionally graded plates (FGP)
subjected to a transverse uniform load (UL) or sinusoidally distributed load (SL) and resting on an elastic foundation is examined by a new hyperbolic displacement model in this paper. Present theory exactly satisfies stress boundary conditions on the top and the bottom of the plate. No transversal shear correction factors are needed because a correct representation of the transversal shearing strain is given. Materials properties of the plate are assumed to be graded in the thickness direction according to a simple power-law distribution in terms of the volume fractions of the constituents. In the analysis, the foundation is modeled as two parameter Pasternak type foundation and Winkler type if the second foundation parameter is zero. The equilibrium equations of a functionally graded plate are given based on the present hyperbolic shear deformation plate theory. Effects of stiffness of the foundation and gradient index on mechanical responses of the plates are discussed. It is established that elastic foundations affects significantly the mechanical behavior of functionally graded thick plates. Numerical results presented in the paper can serve as benchmarks for future analyses of functionally graded thick plates on elastic foundations.
Keywords— FG plates; Winkler–Pasternak elastic foundation; Shear deformation
1. INTRODUCTION
In conventional laminated composite structures, homogeneous elastic laminae are bonded together to obtain enhanced mechanical and thermal properties. The main inconvenience of such an assembly is to create stress concentrations along the interfaces, more specifically when high temperatures are involved. This can lead to delaminations, matrix cracks, and other damage mechanisms which result from the abrupt change of the
Manajemen dan Rekayasa Struktur C-26 fractions of the constituents. That leads to a
continuity of the material properties of FGM: this is the main difference between such a material and an usual composite material. The FGM is suitable for various applications, such as thermal coatings of barrier for ceramic engines, gas turbines, nuclear fusions, optical thin layers, biomaterial electronics, etc.
accurate solution of catamaran passenger vessel operated in the river.
Several studies have been performed to analyze the behaviour of functionally graded plates and shells. Reddy [2] has analyzed the static behaviour of functionally graded rectangular plates based on his third-order shear deformation plate theory. Cheng and Batra [3] have related the deflections of a simply supported functionally graded polygonal plate given by the first-order shear deformation theory and a third-order shear deformation theory to that of an equivalent homogeneous Kirchhoff plate. Cheng and Batra [4] have also presented results for the buckling and steady state vibrations of a simply supported functionally graded polygonal plate based on Reddy’s plate theory. Loy et al. [5] have studied the vibration of functionally graded cylindrical shells using Love’s shell theory. By using the sinusoidal shear deformation theory (SSDT), Zenkour [6] presented Navier’s analytical solution of FG plates. However, bending analyses of FGMs are quite limited, especially of those on elastic foundations. To describe the interactions of the plate and foundation as more appropriate as possible, scientists have proposed various kinds of foundation models, as documented well in Ref. [7]. The simplest model for the elastic foundation is the Winkler model, which regards the foundation as a series of separated springs without coupling effects between each other, resulting in the disadvantage of discontinuous deflection on the interacted
surface of the plate. Zhemochkin and Sinitsyn [8] introduced an elastic combined foundation which is a classical foundation covered by a layer of a Winkler foundation. Filonenko-Borodich [9] developed a model that improved upon the Winkler model by connecting the top ends of the springs with an elastic membrane stretched to a constant tension. Hetényi [10, 11] created an interaction among the springs in the foundation by imbedding an additional plate with flexural rigidity in the Winkler foundation. Vlasov [12] proposed also a more refined model, mainly the two-parameter model. Gorbunov-Posadov [13] presented also the problems of flexure of plates and beams lying on a linearly deformable foundation. Pasternak [14] improved upon the Winkler model by connecting the ends of the springs to a plate, or "shear layer," consisting of incompressible, vertical elements, which can deform only by lateral shear. From then on, the Pasternak model was widely used to describe the mechanical behavior of structure– foundation interactions [15–20].
Cheng and Kitipornchai [21] proposed a membrane analogy to derive an exact explicit eigenvalues for compression buckling, hydrothermal buckling, and vibration of FGM plates on a Winkler–Pasternak foundation based on the first-order shear deformation theory. The same membrane analogy was later applied to the analyses of FGM plates and shells based on a third-order plate theory [22, 23].
Manajemen dan Rekayasa Struktur C-27 of deflections and stresses, and satisfy the zero
tangential traction boundary conditions on the surfaces of the plate. However, the present theory and HPT do not require the use of shear correction factors. In conclusion, the present theory gives accurate results, especially transverse shear stresses, than other theories including HPT.
The FGM plate is made of an isotropic material with material properties varying in the thickness direction only. The governing partial differential equations are reduced to a set of coupled ordinary differential equations in the thickness direction, which are then solved by using the Navier solutions for simply supported rectangular plates. Numerical results are presented for an aluminum/alumina functionally graded plate. To make the study reasonably, effects of the foundation stiffness and gradient index of the Young’s modulus on the mechanical behavior of FGM plates are investigated.
2. THEORETICAL FORMULATIONS Consider a rectangular FG plate having the thickness h, length a, and width b, as
depicted in Fig. 1. It is assumed to be rested on a Winkler–Pasternak type elastic foundation with the Winkler stiffness of k0 and shear stiffness of k1. The FGM plate is subjected to a transverse load q(x,y). The material properties of the plate are assumed to vary continuously through the thickness of the plate. Also, it is assumed that the Poisson’s ratio ν is constant. Based on the power law distribution, the relationship between the Young’s modulus E and zfor ceramic and metal FGM plate is assumed as [6]:
p index which takes values greater than or equal to zero. Subscripts M and C refer to the metal and ceramic constituents which denote the material property of the bottom and top surface of the plate, respectively.
2.1. Constitutive equations
For elastic and isotropic FGMs, the constitutive relations can be written as:
components, respectively. Using the material properties defined in Eqs. (1), stiffness coefficients, Qij, can be expressed as
,
Based on the thick plate theory, the assumed displacement field can be defined in unified form as follows:
Manajemen dan Rekayasa Struktur C-28 function determining the distribution of the transverse shear strains and stresses along the thickness. (),x and (),y are partial derivative with respect to x and y, respectively. In this study a new hyperbolic shear deformation plate theory is obtained by setting
(
)
This function helps to satisfy zero transverse shear stresses at top and bottom surfaces of the plate. The parabolic distributions of transverse shear stresses through the plate thickness are taken into account for the analysis, by means of the hyperbolic function of the assumed displacement field.
By substituting the displacement relations (5) into the strain-displacement equations of the elasticity, the normal and shear strain components are obtained as:
x
The stress and moment resultants of the FGM plate can be obtained by integrating Eq. (3) over the thickness, and are written as:
stress resultants and stress couples, P are additional stress couples associated with the transverse shear effects, Q is transverse shear
Manajemen dan Rekayasa Struktur C-29
stress resultant. Note that the superscript t denotes the transpose of the given vector. The stiffness coefficients Aij and Bij,… etc., are defined as
Since the bottom surface of the plate is assumed subjected to Winkler–Pasternak elastic foundation (see Fig. 1), the reaction– deflection relation at the bottom surface of the model is expressed by
.
foundation. If the foundation is modeled as the linear Winkler foundation, the coefficient k1
in Eq. (12) is zero.
The governing equations of equilibrium can be derived by using the principle of virtual displacements in the same way as described by Akavci [24].
2.2. EXACT SOLUTIONS FOR FGM PLATes
Rectangular plates are generally classified in accordance with the type support used. We are here concerned with the exact solutions for simply supported FGM plate. The following boundary conditions are imposed at the side edges.
To solve this problem, Navier presented the external force in the form of a double trigonometric series:
∑∑
∞are modes numbers. The coefficients qmn for the case of uniformly distributed load are defined as follows:
where q0 represents the intensity of the load at the plate center. For the case of sinusoidally distributed load,
Following the Navier solution procedure, the static bending solution can be obtained as
[ ]
K{ } { }
∆ = Fparameters to be determined.
Manajemen dan Rekayasa Struktur C-30 3. NUMERICAL RESULTS
In this study, bending analysis of FG plates on elastic foundation by a new hyperbolic shear
deformation theory is suggested for
investigation. For simplicity, Poisson’s ratio of plate is assumed to be constant in this study for that the effect of Poisson’s ratio on the deformation is much less than that of Young’s modulus [25]. The Poisson’s ratio is fixed atν =0.3. Comparisons are made with available solutions in literature. In order to verify the accuracy of the present analysis, some numerical examples are solved. The material properties used in the present study are:
Metal (Aluminium, Al): 9
10
Ceramic (Alumina, Al2O3 9
10
In all examples, the foundation parameters are presented in the non-dimensional form of
and K1 =k1a2/D, where
rigidity of the plate.
As a first example; the deflections and the dimensionless stresses of the square FG plate (a/h=10) for different values of the power law p are compared with those of sinusoidal shear deformation plate theory (SSDPT) of Zenkour [6] in Table 1.
The various non-dimensional parameters used are
It may be observed from Table 1 that results of the present theory are compared with those obtained using sinusoidal shear deformation plate theory (SSDPT). As the plate becomes more and more metallic, the difference increases for deflection w and in-plane longitudinal stress σx while it decreases for
in-plane normal stressσy. It is important to
observe that the stresses for a fully ceramic plate are the same as that for a fully metal plate. This is because the plate for these two cases is fully homogeneous and the stresses do not depend on the modulus of elasticity.
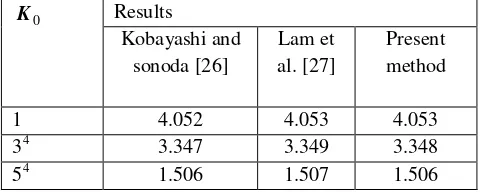
In order to validate the present method in the case of plates resting on elastic foundation, the results for the dimensionless deflections of isotropic thick plate are compared with the previously published results. Table 2 presents the deflections of a uniformly loaded homogeneous square simply supported plate on Winkler foundation. The results are compared with those exact values for Mindlin plates obtained by Kobayashi and Sonoda [26] who used the Levy-series method and by Lam et al. [27] using Green’s functions. It can be seen that the results are in close agreement. Table 3 presents the central deflections of a uniformly loaded homogeneous square simply supported plate on Winkler–Pasternak foundations. The results are compared with those obtained by Lam et al. [27] using Green’s functions. It can be seen that the results are in close agreement.
Figs. 2–7 depict the through-the-thickness distributions of the shear stressesτxz; the
in-plane longitudinal and normal stressesσx, and
the longitudinal tangential stress τxy in the
Manajemen dan Rekayasa Struktur C-31 stress (τxz) increases gradually with
decreasing K0 or K1. It is indicated that large moduli of elastic foundation can enhance bending rigidity of the plate. The through-the-thickness distributions of the shear stress τxz
are not parabolic as in the plate made of pure material. It is to be noted that the maximum value occurs at z≅0.2, not at the plate center as in the homogeneous case.
As exhibited in Figs. 4 and 5, the in-plane longitudinal and normal stress, σx, is
compressive throughout the plate up to
153 . 0
=
z and then they become tensile. The
maximum compressive stresses occur at a point on the bottom surface and the maximum tensile stresses occur, of course, at a point on the top surface of the FGM plate. In addition, it can be seen from these figures that the elastic foundation has a significant effect on the maximum values of the in-plane longitudinal and normal stress, σx. It is
observed that normal stress (σx) increases
gradually with decreasing K0 or K1.
Contrary to the in-plane longitudinal and normal stress, the tensile and compressive values of the longitudinal tangential stress, τxy
(Figs. 6 and 7), is maximum at a point on the bottom and top surfaces of the FGM plate, respectively. It is clear that the minimum value of zero for all in- plane stresses σx and τxy
occurs atz=0.153.
Finally, the exact maximum deflections of simply supported FGM square plate are compared in Figs. 8 and 9 for various ratios of moduli,Em /Ec. This means that the deflections are computed for plates with different ceramic–metal mixtures. It is clear that the deflections decrease smoothly as the ratio of metal-to-ceramic moduli increases. Further, the deflections decrease gradually as either K0 or K1 increases.
4. CONCLUSION
In the present study, closed form solutions for bending analysis of functionally graded plates resting on a Winkler–Pasternak elastic foundation are developed on the assumption that transverse shear displacements vary as a hyperbolic function through the thickness of plate. The stress and displacement response of the plates have been analyzed under sinusoidal loading. The gradation of properties through the thickness is assumed to be of the power law type and comparisons have been made with homogeneous isotropic plates. Non-dimensional stresses and displacements are computed for plates with ceramic–metal mixture. It is seen that the basic response of the plates that correspond to properties intermediate to that of the metal and ceramic, is necessarily lie in between that of ceramic and metal. This behaviour is found to be true irrespective of boundary conditions. Thus, the gradients in material properties play an important role in determining the response of the FGM plates. It can be seen from the results that deflections and the stresses decrease gradually as either K0 or K1 increases. Numerical results given in the present paper render a benchmark for the analyses of FGM thick plates on elastic foundations in the future
REFERENCES
1. Koizumi M. (1997), “FGM Activities in Japan”, Composites, 28, 1–4.
2. Reddy J.N. (2000), “Analysis of functionally graded plates”, Int. J.
Num. Meth. Eng., 47, 663–684.
Manajemen dan Rekayasa Struktur C-32 4. Cheng Z.Q., Batra R.C. (2000), “Exact
correspondence between eigenvalues of membranes and functionally graded simply supported polygonal plates”, J.
Sound Vib., 229, 879–895.
5. Loy C.T., Lam K.Y., Reddy J.N. (1999), “Vibration of functionally graded cylindrical shells”, Int. J. Mech.
Sic., 41, 309–324.
6. Zenkour AM. (2006), “Generalized shear deformation theory for bending analysis of functionally graded materials”, Appl. Math. Modell., 30, 67–84.
7. Kerr AD. (1964), “Elastic and
viscoelastic foundation models”, ASME J. Appl. Mech., 31(3), 491–498.
8. Zhemochkin B.N., Sinitsyn A.P.
(1947), “Practical methods of calculation of foundation beams and slabs on elastic foundation” (in Russian), Stroiizdat, Moscow.
9. Filonenko-Borodich MM. (1940), "Some approximate theories of die elastic foundation" (in Russian), Uchenyie Zapiski Moslcovskogo Gosudarstvennoyo Universiteta Mekhanica., 46, 3-18.
10. Hetényi M. (1946), “Beams on Elastic Foundations”. The University of Michigan Press, Ann Arbor, Michigan. 11. Hetényi, M. (1950), "A general
solution for the bending of beams on an elastic foundation of arbitrary continuity." Journal of Applied Physics, 21, 55-58.
12. Vlasov, V.Z. (1949). “Structural Mechanics of Thin Walled Three-Dimensional Systems.” Stroizdat.
13. Gorbunov-Posadov, M.I. (1949).
“Beams and plates on elastic foundation” Gosstroiizdat [in Russian].
14. Pasternak PL. (1954), “On a new method of analysis of an elastic foundation by means of two foundation constants. Cosudarstrennoe Izdatelstvo
Literaturi po Stroitelstvu i
Arkhitekture, Moscow, USSR, 1–56 [in
Russian].
15. Shen HS. (1995), “Postbuckling analysis of composite laminated plates on two-parameter elastic foundations.
Int. J. Mech. Sci., 37(12), 1307–1316.
16. Omurtag MH, Ozutok A, Akoz AY. (1997), “Free vibration analysis of Kirchhoff plates resting on elastic foundation by mixed finite element formulation based on Gateaux differential”, Int. J. Num. Meth. Eng.,
40(2), 295–317.
17. Matsunaga H. (2000), “Vibration and stability of thick plates on elastic foundations”, ASCE. J. Eng. Mech.,
126(1), 27–34.
18. Filipich CP, Rosales MB. (2002), “A further study about the behavior of foundation piles and beams in a Winkler–Pasternak soil”, Int. J. Mech.
Sci., 44(1), 21–36.
19. Zhou D, Cheung YK, Lo SH, Au
FTK. (2004), “Three-dimensional vibration analysis of rectangular thick plates on Pasternak foundations”, Int.
J. Num. Meth. Eng., 59(10), 1313–
1334.
20. Huang Z.Y, Lu C.F, Chen W.Q.
(2008) “Benchmark solutions for functionally graded thick plates resting on Winkler–Pasternak elastic foundations”, Compos. Struct., 85, 95– 104.
Manajemen dan Rekayasa Struktur C-33
ASCE. J. Eng. Mech., 125(11), 1293–
1297.
22. Cheng ZQ, Batra BC. (2000), “Exact correspondence between eigenvalues of membranes and functionally graded simply supported polygonal plate”, J.
Sound. Vib., 229(4), 879–895.
23. Reddy JN, Cheng ZQ. (2002),
“Frequency correspondence between membranes and functionally graded spherical shallow shells of polygonal plan form”, Int J Mech Sci., 44(5), 967–985.
24. Akavci S. S. (2005), “Analysis of thick laminated composite plates on an elastic foundation with the use of various plate theories” Mechanics of Composite Materials, 44(5), 445 – 460. 25. Delale F, Erdogan F. (1983). The
crack problem for a nonhomogeneous plane, Journal of Applied Mechanics, 50, 609–614.
26. Kobayashi H, Sonoda K. (1989), “Rectangular Mindlin plates on elastic foundations”, Int. J. Mech. Sci., 31, 679–692.
27. Lam K.Y., Wang C.M., He X.Q.
(2000), “Canonical exact solutions for Levy-plates on two-parameter foundation using Green’s functions”,
Eng. Struct., 22, 364–378.
Figure1: FGM plate resting on elastic foundation
-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5
0,00 0,02 0,04 0,06 0,08 0,10 0,12
K0=0
K0=20
K0=40
K0=60
K0=80
K0=100
Figure2: Variation of transversal shear stress (τxz) through-the-thickness of a square FGM
plate for different values of K0. (a/h=10,
2
=
Manajemen dan Rekayasa Struktur C-34 -0,5
-0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5
0,00 0,05 0,10 0,15 0,20 0,25 0,30
K1=0
K1=2
K1=4
K1=6
K1=8
K1=10
Figure.3: Variation of transversal shear stress (τxz) through-the-thickness of a square FGM
plate for different values of K1. (a/h=10, 2
=
p and K0 =10).
-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5
-0,6 -0,4 -0,2 0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6
K0=0
K0=20
K0=40
K0=60
K0=80
K0=100
Figure4: Variation of in-plane longitudinal stress (σx) through-the-thickness of a square
FGM plate for different values of K0. (a/h=10, p=2 and K1 =10).
-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5
-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0
K1=0
K1=2
K1=4
K1=6
K1=8
K1=10
Figure5: Variation of in-plane longitudinal stress (σx) through-the-thickness of a square
FGM plate for different values of K1. (a/h=10, p=2 and K0 =10).
-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5
-1,0 -0,8 -0,6 -0,4 -0,2 0,0 0,2 0,4
K0=0
K0=20
K0=40
K0=60
K0=80
K0=100
Figure.6: Variation of longitudinal tangential stress (τxy) through-the-thickness of a square
Manajemen dan Rekayasa Struktur C-35 -0,5
-0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5
-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0
K1=0
K1=2
K1=4
K1=6
K1=8
K1=10
Figure7: Variation of longitudinal tangential stress (τxy) through-the-thickness of a square
FGM plate for different values of K1. (a/h=10, p=2 and K0 =10).
0,0 0,1 0,2 0,3 0,4 0,5 0,20
0,25 0,30 0,35 0,40 0,45
K0=0
K0=20
K0=40
K0=60
K0=80
K0=100
Figure.8: The effect of material anisotropy on the dimensionless maximum deflection (w) of a square FGM plate for different values ofK0. (a/h=10, p=2 and K1=10).
0,0 0,1 0,2 0,3 0,4 0,5
0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8
K1=0 K1=2 K1=4 K1=6 K1=8 K1=10
Manajemen dan Rekayasa Struktur C-36 Table. 1: Comparison of the dimensionless
deflections and stresses in square FG-plates subjected to sinusoidal distributed load.
Table2: Comparison of the deflection
( 4 3
10 / ) 5 . 0 , 5 . 0
( a a qa
Dw ) of a uniformly loaded
homogeneous square simply supported plate on Winkler foundation.
0
K Results
Kobayashi and sonoda [26]
Lam et al. [27]
Present method
1 4.052 4.053 4.053
34 3.347 3.349 3.348
54 1.506 1.507 1.506
Table. 3: Comparisons of central deflections
( 4 3
10 / ) 5 . 0 , 5 . 0
( a a qa
Dw ) of a uniformly
loadedhomogeneous square simply supported plate (a/h=100) on Winkler–Pasternak foundations.
0
K K1 Results
Lam et al. [27]
Present method
1
1 3.853 3.8550
34 0.763 0.7630
54 0.115 0.1153
3
1
4
3.210 3.2108
34 0.732 0.7317
54 0.115 0.1145
5
1
4
1.476 1.4765
34 0.570 0.5704