MODEL SKEDUL MIGRASI DAN APLIKASINYA DALAM PROYEKSI PENDUDUK MULTIREGIONAL MUSLIMAH

MUSLIMAH

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2008

Dengan ini saya menyatakan bahwa tesis Model Skedul Migrasi dan

Aplikasinya dalam Proyeksi Penduduk Multiregional adalah karya saya dengan

arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada

kepada perguruan tinggi manapun. Sumber data dan informasi yang berasal atau

dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah

disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir

tesis ini.

Bogor,

Juli

2008

Muslimah

ABSTRACT

MUSLIMAH.

Model of Migration Schedules and its Application in Multiregional Population Projection. Under supervision of HADI SUMARNO and ALI KUSNANTO.

Migration is one of demographic components beside fertility and mortality.

The objective of this thesis is to find a model of migration schedules and its

application to multiregional population projection. Rogers

et al

. (1978) proposed

one model of migration schedules which consists of 11 parameters. As the

comparison to that model, this paper proposed another model which uses

polynomial function. By considering Indonesia as two regions, Java-Bali and

outer Java-Bali, it could be found the model of migration schedules. This model is

implemented to multiregional population projection data based on SUPAS 2005.

The result shows that Indonesian annual population growth rate continue to

decrease and will reach -0.066 percent in stable condition.

Multiregional. Dibimbing oleh HADI SUMARNO dan ALI KUSNANTO.

Negara Indonesia dewasa ini dihadapkan pada beberapa masalah

kependudukan, antara lain jumlah penduduk yang besar, laju pertumbuhan

penduduk yang pesat serta penyebaran penduduk yang tidak merata. Pertumbuhan

dan penyebaran penduduk dipengaruhi oleh hubungan tiga komponen demografi

yaitu kelahiran, kematian dan migrasi.

Dalam proyeksi penduduk, migrasi merupakan komponen penting selain

faktor kelahiran dan kematian.Umumnya proyeksi penduduk hanya melibatkan

komponen kelahiran dan kematian saja, karena menganggap bahwa migrasi bersih

suatu negara mendekati nol. Namun demikian jika dilakukan proyeksi penduduk

antar wilayah maka komponen migrasi tidak dapat diabaikan. Oleh karena itu

masalah proyeksi penduduk secara multiregional yang melibatkan migrasi

menjadi faktor penting untuk pengembangan wilayah, sehingga tingkat

pembangunan dapat disejajarkan.

Kajian ini bertujuan untuk menentukan model skedul migrasi dan

mengaplikasikan model tersebut ke dalam proyeksi penduduk multiregional.

Rogers

et al

. (1978) telah mengusulkan suatu model skedul migrasi yang terdiri

atas 11 parameter berdasarkan penjumlahan empat komponen penting migrasi,

yaitu pra-angkatan kerja, angkatan kerja, pasca-angkatan kerja dan sebuah

konstanta. Namun pada perkembangan selanjutnya Rogers (1984) kemudian

menyederhanakan parameter model tersebut menjadi 9 parameter dan 7 parameter

berdasarkan bentuk pola migran pada usia pasca-angkatan kerja. Sebagai

pembanding, dalam kajian ini juga ditawarkan model lain berupa persamaan

polinom yang terdiri atas 8 parameter dan 16 parameter.

Dengan menggunakan data SUPAS 2005, analisis data dilakukan dengan

mengelompokkan wilayah Indonesia menjadi dua wilayah, yaitu Jawa Bali dan

Luar Jawa Bali. Kemudian dilakukan

fitting

kurva model terhadap data dengan

pendekatan metode kuadrat terkecil dibantu

software Mathematica 6.0

. Dari

kelima model tersebut dipilih satu model terbaik yang kemudian diaplikasikan ke

dalam proyeksi penduduk.

Dengan melibatkan komponen migrasi, kelahiran dan kematian, maka

proyeksi penduduk secara multiregional berdasarkan waktu dapat diperoleh

dengan menghitung individu yang bertahan hidup pada daerah dan kelompok

umur tertentu, ditambah dengan jumlah total bayi lahir yang bertahan hidup

sampai akhir selang waktu.

Pada populasi model proyeksi generalisasi matriks Leslie yang telah

mencapai sebaran umur stabil berlaku jumlah penduduk pada periode

t

+1 adalah

jumlah penduduk pada periode

t

dikali laju perubahannya yaitu

λ

. Selanjutnya

λ

dikenal sebagai akarciri dominan matriks pertumbuhan penduduk secara

multiregional. Jika

λ

> 1 maka terjadi kenaikan laju perubahan, jika

λ

< 1 maka

terjadi penurunan laju perubahan, dan jika

λ

=1 maka laju perubahan konstan.

Berdasarkan

fitting

data yang dilakukan ternyata model yang ditawarkan

Rogers (1984) tetap lebih baik daripada model polinom. Model skedul migrasi

keluar dari wilayah Jawa Bali lebih didominasi anak-anak, sedangkan model

skedul keluar dari wilayah Luar Jawa Bali lebih didominasi tenaga kerja.

Berdasarkan hasil perhitungan

life table

multiregional ditunjukkan bahwa

penduduk Jawa Bali mempunyai angka harapan hidup (

68,72 tahun, dimana

60,67 tahun waktunya dihabiskan untuk tetap tinggal di wilayah Jawa Bali dan

8,04 tahun waktunya dihabiskan di wilayah Luar Jawa Bali. Sedangkan penduduk

Luar Jawa Bali mempunyai angka harapan hidup (

66,51 tahun, dimana 51,15

tahun waktunya dihabiskan untuk tetap tinggal di wilayah Luar Jawa Bali dan

14,36 tahun waktunya dihabiskan di wilayah Jawa Bali.

Hasil penelusuran matriks Leslie diperoleh nilai

λ

= 0,996721 sebagai laju

perubahan. Hal ini menunjukkan bahwa laju pertumbuhan penduduk di Indonesia

akan mengalami tingkat penurunan dan pada saat sebaran umur mencapai kondisi

stabil maka laju pertumbuhan (

r

) akan mencapai -0,066 persen pertahun.

© Hak cipta milik Institut Pertanian Bogor, tahun 2008

Hak cipta dilindungi Undang-undang

1.

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa

mencantumkan atau menyebutkan sumber.

a.

Pengutipan hanya untuk kepentingan pendidikan, penelitian,

penulisan karya ilmiah, penyusunan laporan, penulisan kritik

atau tinjauan suatu masalah.

b.

Pengutipan tidak merugikan kepentingan yang wajar Institut

Pertanian Bogor.

2.

Dilarang mengumumkan dan memperbanyak sebagian atau seluruh

karya tulis dalam bentuk apapun tanpa izin Institut Pertanian

Bogor.

MODEL SKEDUL MIGRASI DAN APLIKASINYA

DALAM PROYEKSI PENDUDUK MULTIREGIONAL

MUSLIMAH

Tesis

sebagai salah satu syarat untuk memperoleh gelar

Magister Sains pada

Departemen Matematika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2008

rahmat, karunia dan hidayah-Nya sehingga penulis dapat menyelesaikan tesis yang berjudul Model Skedul Migrasi dan Aplikasinya dalam Proyeksi Penduduk Multiregional. Penelitian ini didanai oleh beasiswa BUD Pascasarjana Departemen Agama RI.

Ucapan terimakasih yang tulus dan ikhlas penulis sampaikan kepada Bapak Dr. Ir. Hadi Sumarno, MS dan Bapak Drs. Ali Kusnanto, M.Si atas kesediaan dan kesabarannya memberi bimbingan dalam penulisan tesis ini. Ucapan terimakasih disampaikan pula kepada Ibu Dr. Ir. Endar H. Nugrahani, MS sebagai dosen penguji dalam ujian tesis atas saran dan masukan yang diberikan. Di samping itu, terimakasih dan penghargaan penulis sampaikan kepada Biro Pusat Statistik yang telah memberikan ijin menggunakan data SUPAS 2005.

Ungkapan terimakasih yang tulus juga disampaikan kepada suamiku tercinta Mas Khamidinal, M.Si, ayah, ibu, kakak, serta seluruh keluarga, atas segala do’a, pengorbanan, motivasi dan kasih sayangnya. Terimakasih juga penulis ucapkan kepada segenap dosen dan karyawan Departemen Matematika, Kepala Madrasah dan rekan-rekan guru MTs Negeri Galur, serta rekan-rekan BUD Matematika.

Penulis berharap semoga tesis ini bermanfaat.

Bogor, Juli 2008

Penulis dilahirkan di Kulon Progo, Daerah Istimewa Yogyakarta pada tanggal 12 Nopember 1974 dari ayah Ali Muhammad dan ibu Rubiyem. Penulis merupakan putri bungsu dari empat bersaudara. Pendidikan sarjana ditempuh di Program Studi Pendidikan Matematika, FMIPA Universitas Negeri Yogyakarta lulus pada tahun 1998. Pada tahun 2006 penulis mendapat kesempatan untuk diterima di Program Studi Matematika Terapan pada Program Pascasarjana IPB. Beasiswa pendidikan Pascasarjana diperoleh dari Departemen Agama Republik Indonesia.

Sejak tahun 1999 penulis bekerja menjadi Pegawai Negeri Sipil di lingkungan Departemen Agama Republik Indonesia sebagai guru bidang studi Matematika di Madrasah Tsanawiyah Negeri Galur Kulon Progo Yogyakarta.

x

DAFTAR TABEL ……….. xi

DAFTAR GAMBAR……….. xii

DAFTAR LAMPIRAN………... xiv

I PENDAHULUAN 1.1 Latar Belakang Masalah ... 1

1.2 Tujuan Penelitian ... 3

1.3 Manfaat Penelitian ... 3

II LANDASAN TEORI 2.1 Beberapa Definisi dan Teorema ... 4

2.2 Pengertian Migrasi ... 6

2.3 Metode Kuadrat Terkecil Persamaan Polinom……… 8

2.4 Metode Kuadrat Terkecil Persamaan Nonlinear………. 10

2.5 Kecocokan Model Skedul Migrasi ... 11

2.6 Model Proyeksi penduduk Multiregional ………... 11

2.7 Life Table Uniregional... 12

2.8 Konsep Demografi Multiregional ... 13

2.8.1 Survivorship……… 14

2.8.2 Life Table Multiregional……….. 15

2.8.3 Kelahiran………. 17

2.9 Matriks Proyeksi Multiregional ... 18

III METODOLOGI PENELITIAN 3.1 Sumber Data ... 21

3.2 Konsep dan Definisi ……… 21

3.3 Metode Analisis Data ……….. 22

IV HASIL DAN PEMBAHASAN 4.1 Analisis Model ………. 23

4.2 Analisis Kurva Angkatan Kerja………... 28

4.3 Arus Migrasi Keluar dari Wilayah Jawa Bali……….... 29

4.4 Arus Migrasi Keluar dari Wilayah Luar Jawa Bali………... 32

4.5 Model Skedul Migrasi Keluar dari Wilayah Jawa Bali ………….... 34

4.6 Model Skedul Migrasi Keluar dari Wilayah Luar Jawa Bali………. 40

4.7 Proyeksi Penduduk Multiregional………... 46

4.7.1 Survivorship ……….. ……. 48

4.7.2 Kelahiran……….. 48

V KESIMPULAN DAN SARAN 5.1 Kesimpulan……….……… 52

5.2 Saran………... 53

DAFTAR PUSTAKA……….... 54

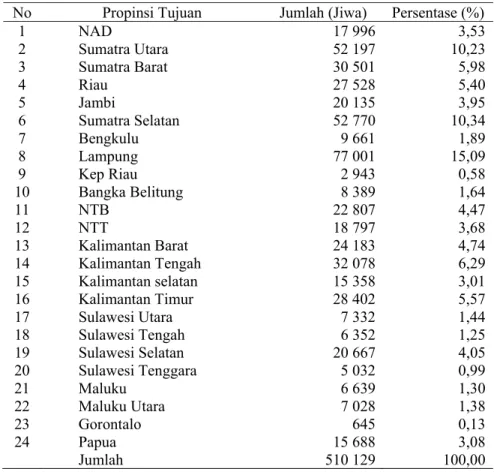
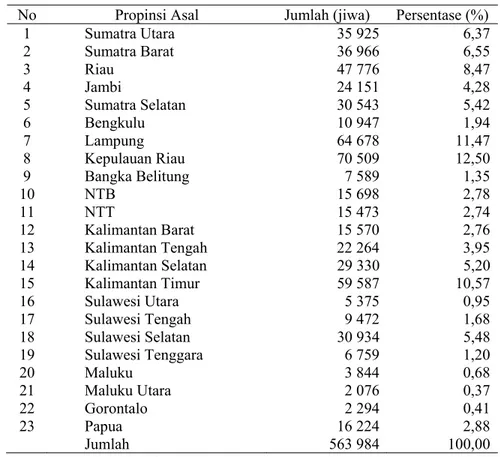
xi Halaman 1 Distribusi migran keluar dari wilayah Jawa Bali menurut propinsi

tujuan……….. 30

2 Distribusi migran keluar dari wilayah Jawa Bali menurut propinsi

asal……….. 31

3 Distribusi migran keluar dari wilayah Luar Jawa Bali menurut

propinsi tujuan……… 32

4 Distribusi migran keluar dari wilayah Luar Jawa Bali menurut

propinsi asal……… 33

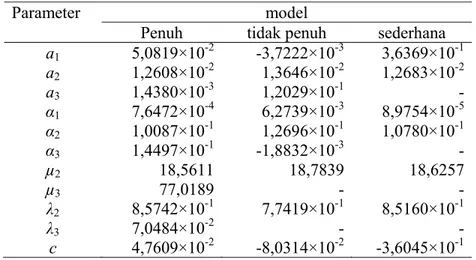
5 Hasil dugaan parameter migran keluar dari wilayah Jawa Bali…... 34 6 Perbandingan nilai proportional error pola migran keluar dari

Jawa Bali ………... 38 7 Hasil dugaan parameter migran keluar dari wilayah Luar Jawa Bali… 40 8 Perbandingan nilai proportional error pola migran keluar dari

Luar Jawa Bali ………. 44

9 Hasil perhitungan matriks A(x) dan P(x) wilayah Jawa Bali dan Luar

Jawa Bali……….. 47

10 Hasil perhitungan S(x) wilayah Jawa Bali dan Luar Jawa Bali……..… 48 11 Hasil perhitungan F(x) dan B(x) wilayah Jawa Bali dan Luar

Jawa Bali………. 49 12 Jumlah penduduk Jawa Bali dan Luar Jawa Bali tahun 2005………….. 50 13 Hasil perhitungan proyeksi penduduk Jawa Bali dan Luar

xii

1 Skedul migrasi model penuh……….. 23

2 Kurva migrasi pra-angkatan kerja……….. 24

3 Kurva migrasi angkatan kerja………. 24

4 Kurva migrasi pasca angkatan kerja……….. 25

5 Kurva konstanta……….. 25

6 Distribusi migran keluar dari wilayah Jawa Bali menurut propinsi tujuan……….. 31

7 Distribusi migran keluar dari wilayah Jawa Bali menurut propinsi asal……….. 31

8 Distribusi migran keluar dari wilayah Luar Jawa Bali menurut propinsi tujuan……….. 32

9 Distribusi migran keluar dari wilayah Luar Jawa Bali menurut propinsi asal……….. 33

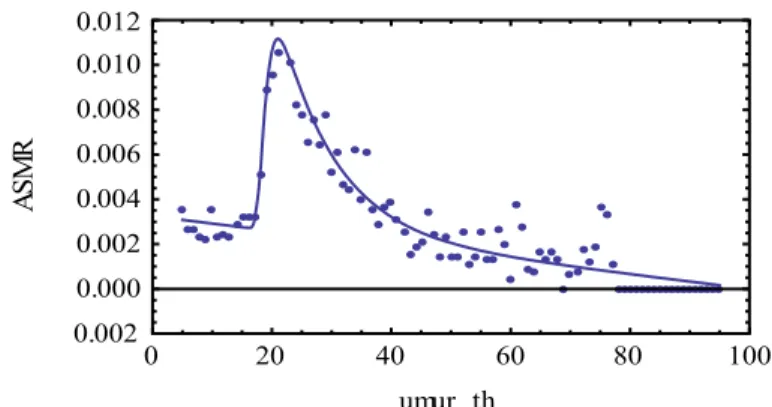
10 Plot scatter diagram migran keluar dari wilayah Jawa Bali…………. 34

11 Plot pendugaan parameter model penuh migran risen keluar dari Jawa Bali………. 35

12 Plot pendugaan parameter model tidak penuh migran risen keluar dari Jawa Bali………. 35

13 Plot pendugaan parameter model sederhana migran risen keluar dari Jawa Bali………. 36

14 Plot pendugaan parameter model polinom berderajat-7 migran risen keluar dari Jawa Bali……….. 37

15 Plot pendugaan parameter model polinom berderajat-15 migran risen keluar dari Jawa Bali……….. 38

16 Plot scatter diagram migran keluar dari wilayah Luar Jawa Bali … 40 17 Plot pendugaan parameter model penuh migran risen keluar dari Luar Jawa Bali……… 41

18 Plot pendugaan parameter model tidak penuh migran risen keluar dari Luar Jawa Bali………. 41

19 Plot pendugaan parameter model sederhana migran risen keluar dari Luar Jawa Bali……… 42

20 Plot pendugaan parameter model polinom berderajat-7 migran risen keluar dari Luar Jawa Bali……… 43

xiii 22 Perbandingan jumlah penduduk Indonesia tahun 2005 dan 2010 ….. 51

xiv

1 Tabel Migran Keluar dari Wilayah Jawa Bali menuju Luar Jawa Bali……. 57

2 Tabel Migran Keluar dari Wilayah Luar Jawa Bali menuju Jawa Bali …. 59 3 Data Jumlah Penduduk Jawa Bali dan Luar Jawa Bali Menurut Kelompok Umur (SUPAS, 2005)……….. 61

4 Data Penduduk Wanita Usia Reproduksi Menurut Kelompok Umur (SUPAS, 2005) ………. 62

5 Data Angka Harapan Hidup (e0) penduduk Indonesia menurut propinsi dan jenis kelamin (SUPAS 2005)……… 63

6 Data Angka Kelahiran Menurut Umur Wanita, Daerah, Periode, dan Propinsi (SUPAS, 2005)……….. 64

7 Perhitungan Life Table Uniregional ……… 65

8 Hasil perhitungan tingkat migrasi menurut kelompok umur ……… 68

9 Perhitungan Matriks Peluang Transisi P(x) ……… 69

10 Perhitungan Life Table Multiregional ……….……… 70

11 Perhitungan Matriks Survivorship S(x) ……….. 74

12 Perhitungan Matriks Kelahiran B(x) ……….. 75

13 Menentukan Formula Matriks Transisi P(x) ………. 77

14 Bukti Sistem Logit life table ………. 78

15 Tabel Nilai α dan β dalam menentukan l(x) dengan sistem Brass logit (United Nation, 1983) ………. 79

16 Contoh perhitungan l(x) menggunakan Brass Logit ………. 80

17 Uji Maksimum Kurva Angkatan Kerja……….. 81

18 Matriks Pertumbuhan G dan Hasil Proyeksi K(t+1) ………... 82

19 Program pendugaan parameter……….. 83

BAB I

PENDAHULUAN

1.1 Latar Belakang

Keadaan penduduk di Indonesia dewasa ini dihadapkan pada beberapa masalah kependudukan, diantaranya jumlah penduduk yang besar, laju pertumbuhan penduduk yang pesat dan penyebaran penduduk yang tidak merata. Tercatat dari BPS hasil SUPAS 2005 bahwa jumlah penduduk Indonesia adalah 218.086.288 jiwa, dengan laju pertumbuhan penduduk sebesar 1,3 persen pertahun. Suatu penduduk yang besar jumlahnya dan yang tumbuh dengan pesat dapat mengekang pembangunan ekonomi karena selalu perlu diadakan perluasan kesempatan kerja. Akibat-akibat lain dari pertumbuhan penduduk yang pesat juga terasa dalam keharusan penyediaan makanan, sarana kesehatan, pendidikan, perumahan, serta sarana kehidupan lainnya.

Di daerah tertentu kepadatan penduduk lebih besar dibandingkan daerah yang lain. Kepadatan penduduk dipengaruhi oleh beberapa faktor antara lain faktor sosial, ekonomi dan lain-lain. Daerah-daerah yang laju pertumbuhan ekonominya lebih tinggi cenderung memiliki kepadatan penduduk yang lebih tinggi. Selain beberapa faktor di atas, faktor lain yang mempengaruhi laju pertumbuhan penduduk adalah karena adanya hubungan tiga komponen demografi, yaitu tingkat kelahiran, kematian, dan adanya migrasi.

Pesatnya laju pertumbuhan penduduk di Indonesia mendorong minat para peneliti khususnya di bidang demografi untuk lebih memfokuskan pada teknis pengukuran fertilitas dan mortalitas sebagai komponen penting dalam proyeksi penduduk. Namun demikian pada perkembangan selanjutnya tidak hanya dua komponen tersebut yang perlu mendapat perhatian. Komponen ketiga yang juga penting adalah migrasi.

Dalam ilmu demografi dikenal dua macam kajian yaitu demografi multiregional dan demografi uniregional. Demografi multiregional atau demografi antar wilayah menganalisis secara simultan dinamika ruang atau wilayah dari sebuah sistem populasi yang saling bergantung yang dihubungkan oleh arus migrasi berarah (Rogers 1995). Perbedaan yang mendasar antara pendekatan

uniregional dan multiregional adalah bahwa analisis populasi dilakukan dengan mengasumsikan terjadinya interkoneksi antar wilayah. Sebagai ilustrasi misalnya ada dua wilayah populasi, dengan masing-masing wilayah dihubungkan oleh adanya arus migrasi dari wilayah yang satu ke wilayah yang lain. Dalam sistem ini misalkan arus keluar migrasi dari satu wilayah didefinisikan sebagai arus masuk migrasi untuk wilayah kedua. Analisis uniregional untuk perubahan populasi pada sistem dua wilayah ini difokuskan pada perubahan masuk dan keluar hanya pada masing-masing wilayah pada suatu waktu tertentu. Dalam perspektif multiregional, dipandang bahwa dua wilayah sebagai suatu sistem dari dua populasi yang saling berinteraksi, dengan sebuah pola arus keluar dan arus masuk sebagai sebuah sistem simultan yang saling berhubungan.

Analisis demografi multiregional dalam studi migrasi mempunyai salah satu keunggulan yaitu dalam pengukuran migrasi yang tidak lagi konvensional (Chotib 1998). Secara konvensional, analisis uniregional melakukan pengukuran migrasi yang selalu dilihat dari pembahasan migrasi masuk, migrasi keluar dan migrasi neto pada suatu wilayah. Sedangkan dalam analisis demografi multiregional, studi migrasi tidak lagi membahas ketiga macam migrasi tersebut. Pembahasan didasarkan kepada migrasi keluar dari suatu propinsi ke propinsi lain, yang pengukurannya selalu mengacu kepada jumlah penduduk asal. Misalkan wilayah Indonesia dibagi menjadi dua bagian, yaitu wilayah Jawa Bali (JB) dan wilayah Luar Jawa Bali (LJB). Dalam pengukuran migrasi multiregional yang berperan hanya migrasi keluar. Maka tingkat migrasi keluar untuk wilayah Jawa

Bali dirumuskan dengan

JB oJB oJB P x l x) ( ) ( =

π , dimana loJB (x) menyatakan

banyaknya orang yang keluar dari wilayah Jawa Bali dan PJB menyatakan

banyaknya populasi yang berada di wilayah Jawa Bali. Sedangkan tingkat migrasi

keluar dari wilayah Luar Jawa Bali dirumuskan dengan

LJB oLJB oLJB P x l x) ( ) ( = π ,

dimana loLJB(x) menyatakan banyaknya orang yang keluar dari wilayah Luar Jawa

Bali dan PLJB menyatakan banyaknya populasi yang berada di wilayah Luar Jawa

Jadi migrasi masuk ke wilayah JB sama dengan migrasi keluar dari wilayah LJB ke wilayah JB. Dengan demikian pembahasan migrasi penduduk di suatu wilayah sesungguhnya merupakan bagian integral yang tidak terpisahkan dari sistem migrasi secara nasional. Oleh sebab itu masalah proyeksi penduduk secara multiregional yang melibatkan migrasi menjadi faktor penting untuk pengembangan wilayah, sehingga tingkat pembangunan di Indonesia dapat disejajarkan.

1.2 Tujuan Penelitian

Tujuan dari penelitian ini adalah :

1. Menentukan pola migrasi dalam rangka membuat model menurut umur di dua wilayah Indonesia yaitu Jawa Bali (JB) dan Luar Jawa Bali (LJB).

2. Menyusun life table multiregional di dua wilayah yaitu Jawa Bali (JB) dan Luar Jawa Bali (LJB).

3. Menyusun model pertumbuhan penduduk multiregional dalam bentuk matriks yang mengungkapkan kelas-kelas populasi yang mempertimbangkan umur dan migrasi secara multiregional.

1.3 Manfaat Penelitian :

Dengan melihat tujuan yang ada maka penelitian ini diharapkan:

1. Dapat bermanfaat bagi keilmuan khususnya bidang kependudukan untuk menambah referensi guna penelitian lebih lanjut.

2. Penelitian ini diharapkan dapat bermanfaat bagi pemerhati masalah kependudukan maupun para perencana pembangunan dalam mengambil keputusan khususnya di bidang kependudukan.

BAB II

LANDASAN TEORI

2.1 Beberapa Definisi dan Teorema Definisi 1 Nilai Maksimum dan Minimum

Misalkan S daerah asal dari fungsi f, yang memuat titik c. Maka :

(i) f(c) adalah nilai maksimum f pada S jika f(c) ≥f(x) untuk semua x di S

(ii) f(c) adalah nilai minimum f pada S jika f(c) ≤f(x) untuk semua x di S

(iii) f(c) adalah nilai ekstrim f pada S jika f(c) adalah nilai maksimum atau nilai minimum.

(Purcell 1984)

Definisi 2 Bilangan Kritis

Bilangan kritis dari suatu fungsi f adalah suatu bilangan c di dalam daerah asal f

sedemikian sehingga f′(c) = 0 atau f′(c) tidak ada. Jika f mempunyai maksimum atau minimum lokal di c, maka c adalah bilangan kritis f.

(Purcell 1984)

Teorema 1 : Uji Turunan Kedua untuk Ekstrim Lokal

Misalkan ′ dan ′′ ada pada setiap titik dalam selang terbuka (a,b) yang memuat c, dan andaikan ′ = 0.

(i) Jika ′′(c) < 0, f(c) adalah nilai maksimum lokal f.

(ii) Jika ′′(c) > 0, f(c) adalah nilai maksimum lokal f

Bukti : (Lihat Purcell 1984)

Definisi 3 Fungsi Polinom

Fungsi P disebut polinom jika

P(x) = a0 + a1x + a2x2 + a3x3 + …+ an-1xn-1 + anxn

dengan n adalah bilangan bulat tak negatif dan bilangan a0, a1, a2, …, an adalah

konstanta yang disebut koefisien polinom. Daerah asal sembarang polinom adalah

( = (-∞,∞). Jika koefisien an≠ 0, maka derajat polinom adalah n.

(Stewart J 2001)

Definisi 4 Akarciri dan Vektorciri

Jika A adalah matriks berukuran nxn maka skalar λ dan vektor x≠ 0 yang memenuhi Ax = λx masing-masing disebut akarciri dan vektorciri matriks A.

Akarciri juga disebut sebagai nilai eigen (eigenvalue), nilai karakteristik (characteristic value), atau akar laten (latent root).

Untuk mendapatkan penyelesaian λ dari persamaan Ax = λx dengan x≠ 0 atau (A- λI)x = 0 sedemikian sehingga vektor penyelesaiannya tak trivial, haruslah dipenuhi det(A- λI) = 0.

Fungsi pA(λ) = det(A- λI) disebut polinom karakteristik matriks A, dan persamaan pA(λ) = det(A- λI) = 0 disebut persamaan karakteristik matriks A.

(Anton H 1989)

Teorema 2:

Jika A adalah matriks berukuran n×n maka berlaku : (i) det(A- λI) merupakan polinom pA(λ) berderajat n.

(ii) Akarciri matriks A merupakan penyelesaian dari pA(λ) = 0.

Bukti :

(i) Akan dibuktikan dengan induksi matematika. 

Jika A berukuran 2×2 maka det(A- λI) = (a11 – λ)(a22 – λ) – a12a21 merupakan

polinom λ yang berderajat 2.

Jika A berukuran k×k, andaikan benar bahwa det(A- λI) merupakan polinom λ

berderajat k.

Jika A berukuran (k+1)×(k+1) maka

det(A- λI) = ∑ (-1)i+j det(Mij) (1) untuk suatu i = 1, 2, …, k+1, dengan

aij = unsur pada baris ke-i dan kolom ke-j matriks (A- λI).

Mij = matriks (A- λI) yang telah dihapus baris ke-i dan kolom ke-j.

Dengan mengambil i sebagai baris ke-(k+1) matriks (A- λI), diperoleh : det(A- λI) = ∑ (-1)(k+1)+j det(M(k+1)j) (2)

Karena M(k+1)j merupakan anak matriks (A-λI) yang diperoleh dengan

menghilangkan baris ke-(k+1) dan kolom ke-j, maka matriks M(k+1)j

berukuran k×k. Dengan demikian det(M(k+1)j) merupakan polinom λ berderajat k, dan berderajat 1. Akibatnya persamaan (2) merupakan polinom

λ berderajat k+1.

(ii) Misalkan λ merupakan akarciri matriks A maka terdapat x yang tidak nol

sedemikian sehingga : 

↔Ax – λx = 0

↔ (A – λI)x = 0

Karena (A – λI)x = 0 akan mempunyai penyelesaian yang tak nol jika dan hanya jika det(A – λI) = 0, dan det(A – λI) = pA(λ), maka λ memenuhi persamaan pA(λ) = 0. Berarti λ merupakan penyelesaian bagi pA(λ) = 0.

(Anton H 1989)

Definisi 5 Akarciri dan Vektociri dominan

Jika A adalah matriks berukuran n×n dan λ1, λ2, …, λn adalah akarciri-akarciri

matriks A, λi dikatakan sebagai akarciri dominan matriks A jika berlaku |λ | > λ

untuk suatu i = 1, 2, 3, … dan untuk semua j ≠ i. Vektorciri yang bersesuaian dengan λi disebut sebagai vektorciri dominan mariks A.

(Anton H 1989)

2.2 Pengertian Migrasi

Migrasi adalah perpindahan penduduk dari suatu tempat ke tempat lain, baik melewati batas politis negara maupun batas administrasi/batas bagian dalam suatu negara dengan tujuan untuk menetap. Migrasi sering diartikan sebagai perpindahan yang relatif permanen dari suatu tempat ke tempat yang lain. Data migrasi dapat disusun berdasar pola migrasi keluar, migrasi masuk, menurut umur, dan jenis kelamin (BPS 1995).

Data migrasi yang tersedia berdasarkan hasil sensus penduduk hanya dapat membedakan tiga jenis migran, yaitu migran seumur hidup (a lifetime migrant), migran total dan migran risen (recent migrant). Migran seumur hidup adalah mereka yang pindah dari tempat lahir ke tempat tinggal sekarang tanpa melihat kapan pindahnya. Dalam konsep ini migrasi diperoleh dari keterangan tempat lahir dan tempat tinggal sekarang, jika kedua keterangan tersebut berbeda maka termasuk migran seumur hidup. Migran total adalah mereka yang pindah sehingga tempat tinggal sebelumnya berbeda dengan tempat tinggal sekarang. Migrasi ini diperoleh dari keterangan tempat tinggal sebelumnya dan tempat tinggal sekarang. Sedangkan migran risen adalah mereka yang pernah pindah dalam kurun waktu 5 tahun terakhir, keterangan ini diperoleh dari pertanyaan tempat tinggal 5 tahun yang lalu dan tempat tinggal sekarang. Jika keterangan tersebut berbeda maka termasuk migran risen (BPS 1995).

Menurut Rogers et al. (1978) pola pengamatan migrasi menurut umur secara matematis terdiri atas empat komponen penting yaitu :

1. Pra-angkatan kerja (pre-labor force), yang ditunjukkan dengan suatu persamaan eksponensial dengan angka penurunan sebesar α1 yaitu :

f1(x) = a1 exp(-α1x) ; ∀x∈(+ (3)

2. Angkatan kerja (labor force), yaitu suatu persamaan eksponensial ganda dengan satu titik puncak, dengan usia rata-rata µ2, serta memiliki angka

kenaikan λ2 dan penurunan α2 yaitu :

f2(x) = a2 exp{-α2(x - µ2) – exp[-λ2(x-µ2)]} ; ∀x∈(+ (4)

3. Pasca angkatan kerja (post-labor force), yaitu suatu persamaan eksponensial ganda, dengan usia rata-rata µ3, serta memiliki angka kenaikan λ3 dan

penurunan α3 yaitu :

f3(x) = a3 exp{-α3(x - µ3) – exp[-λ3(x-µ3)]} ; ∀x∈(+ (5)

4. Suatu konstanta c, yaitu suatu persamaan yang diperlukan untuk memperbaiki ketepatan matematis penaksiran skedul ini yaitu :

f4(x) = c   (6) 

   

Penjumlahan dari keempat persamaan diatas dirumuskan oleh persamaan model skedul migrasi sebagai berikut:

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ c x x a x x a x a x M + )]} -( ) -( {-exp + )]} -( ) - ( {-exp + ) (-exp = ) ( 3 3 3 3 3 2 2 2 2 2 1 1 μ λ μ α μ λ μ α α ∀x∈(+ (7)

Pola migrasi menurut kelompok umur di suatu wilayah belum tentu sama dengan model seperti yang dikemukakan di atas. Pola dapat berbeda sesuai dengan karakteristik individu penduduk atau wilayahnya. Pola yang dihasilkan oleh negara maju belum tentu sama dengan pola dari negara berkembang. Namun demikian Rogers (1984) telah menyederhanakan pola yang ada menjadi tiga keluarga model skedul migrasi berdasarkan bentuk pola migran pada umur pasca-angkatan kerja, yaitu:

1. Model penuh. Pada model ini mempunyai bentuk persamaan eksponensial ganda pada usia pasca-angkatan kerja yang diperlihatkan oleh persamaan (7).

2. Model tidak penuh. Dalam model ini tidak terdapat puncak pada umur pasca angkatan kerja. Sehingga persamaan matematisnya menjadi:

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ c x a x x a x a x M + ) ( exp + )]} -( ) - ( {-exp + ) (-exp = ) ( 3 3 2 2 2 2 2 1 1 α μ λ μ α α ∀x∈(+ (8)

3. Model sederhana. Dalam model ini tidak ada pola pada usia pasca-angkatan kerja. Sehingga persamaan matematisnya menjadi: 

⎪ ⎭ ⎪ ⎬ ⎫ c x x a x a x M + )]} -( ) - ( {-+ ) (-= ) ( 2 2 2 2 2 1 1 μ λ μ α α exp exp exp ∀x∈(+ (9)

Ledent dan Termote (1992) didalam Chotib (1998) telah memperlihatkan pola yang berbeda dari migran yang keluar dari DKI Jakarta dan dari luar DKI Jakarta berdasarkan data SP 1980 dan SP 1990.

Angka Migrasi menurut kelompok umur (Age Specific Migration Rate/ASMR) diperoleh dari proporsi penduduk yang berstatus migran (propinsi tempat tinggal sekarang berbeda dengan propinsi tempat tinggal lima tahun yang lalu) pada umur tertentu. Indeks yang menunjukkan ringkasan dari ASMR adalah GMR yang dirumuskan sebagai berikut:

GMR = ∑ , dimana i = umur migran.

2.3 Metode Kuadrat Terkecil Persamaan Polinom

Di dalam pengepasan kurva, misalkan diberikan n titik yang berupa pasangan bilangan (x1,f(x1), (x2, f(x2), …, (xn, f(xn) dan diminta untuk menentukan

sebuah fungsi P(x) sedemikian rupa sehingga P(xi)≈f(xi) , dengan i = 1, 2, 3,…,n.

Misalkan P(x) merupakan jenis fungsi polinomial yang dicocokkan (fitted) terhadap data f(xi). Sifat fitting tidak selalu P(xi) = f(xi) untuk semua i. Sehingga

nilai-nilai parameter yang diperoleh dari sebuah percobaan akan mengandung galat percobaan. Pada kasus yang sederhana pengepasan kurva dapat dilakukan cukup dengan mata telanjang. Namun jika titik itu terpencar, maka cara ini tidak dapat diandalkan sehingga lebih baik digunakan metode kuadrat terkecil.

Prinsip penentuan fungsi polinom P(x) berderajat m dengan metode kuadrat terkecil:

(i) P(x) merupakan polinomial berderajat m dengan bentuk umum:

P(x) = a0 + a1x + a2x2 + a3x3 + …+ amxm (10)

dengan a0, a1, a2, …, am merupakan nilai-nilai parameter.

(ii) Selisih antara P(x) dan f(x) untuk titik data tertentu adalah:

∆i = f(xi) – P(xi), (i=1, 2, 3, …, n) (11)

(iii) Sedangkan jumlah kuadrat selisih antara P(x) dan f(x) utuk semua titik data adalah:

S = ∑ ₁∆2 ∑ ₁ 2

= ∑ 2 ∑ ∑

= ∑ 2 ∑ ∑ ∑ ∑ ∑

(iv) Syarat yang harus dipenuhi agar S minimum adalah :

0,…, _{2∑ 2 ∑ ∑ = 0 (j = 0,1, …m)}

Sehingga akan membangkitkan suatu sistem persamaan sebagai berikut:

∑ ₀ ∑ ₁ ∑ ₁ (j = 0,1, …,m) (12) Berikut ini sistem persamaan untuk m+1 parameter yang belum diketahui:

a0n + a1∑ ∑ ∑

∑ ∑ ∑ ∑

+ + … +

∑ ∑ ∑ ∑

Dalam bentuk matriks dapat dinyatakan sebagai:

∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ = ∑ ∑ ∑ atau A =

Sehingga a0, a1, …, am dapat diperoleh sebagai solusi persamaan linear dari:

2.4 Metode Kuadrat Terkecil Persamaan Nonlinear

Misalkan diberikan n titik data berupa pasangan bilangan (x1,y1), (x2, y2), …,

(xn, yn) dan akan ditentukan sebuah fungsi nonlinear f (x,p1,p2,…,pm) sedemikin

rupa sehingga f(xi,p1,p2,…,pm)≈yi , dimana pi, i = 1, 2, …, m<n adalah parameter.

Diasumsikan utuk n titik data yang diberikan adalah :

y1 = f(x1,p1,p2,…,pm)

y2 = f(x2,p1,p2,…,pm)

yn = f(xn,p1,p2,…,pm)

Dapat dicari nilai-nilai parameter dari fungsi dengan meminimumkan

zi = yi - f(xi,p1,p2,…,pm), i = 1, 2, … n.

Turunan zi terhadap parameter-parameter adalah = ∑

Atau dalam bentuk matriks dapat dinyatakan sebagai

d = Ad , dimana

A = , d = , dan d =

Dengan pemberian nilai awal parameter-parameter: = ,

dan perhitungan dilakukan untuk nilai i = 1, 2, …, n, maka diperoleh:

∆ =

∆ ∆ ∆

Sistem ini akan bekerja secara iterasi dengan ∆ , dimana ∆ ∆

sehingga: ∆ , , , … ,

   Nilai-nilai parameter akan diperoleh dengan cara meminimumkan ∆ ,

2.5 Kecocokan Model Skedul Migrasi

Untuk menilai kecocokan model (goodness-of-fit) yang tersedia dalam model skedul bila hal tersebut diterapkan pada data yang diamati, kita menghitung

PE (Proportional Error), dengan menggunakan nilai dari persamaan berikut :

PE = ∑ _∑| | , M(x) = aktual , = dugaan (13) (Wei WWS 1990)

2.6  Model Proyeksi Penduduk Multiregional

Perhitungan jumlah dan komposisi penduduk dilakukan dengan memperhatikan komponen fertilitas, mortalitas dan migrasi secara terpisah. Ketiganya kemudian mempengaruhi jumlah dan komposisi penduduk di suatu wilayah. Dalam demografi multiregional, jumlah dan komposisi penduduk di suatu wilayah merupakan hasil dari interaksi antara ketiga komponen tersebut secara bersamaan, dimana primadona dari ketiga komponen tersebut sebenarnya adalah migrasi (Chotib 1998). Secara umum baik dalam perspektif uniregional maupun multiregional perhitungan sederhana tentang jumlah penduduk sebagai hasil interaksi dari tiga komponen di atas adalah sebagai berikut :

K(t+1) _{= (1+r) K}(t) _{, (14)}

dimana :

K(t+1) = Jumlah penduduk pada tahun (t+1)

r = angka pertumbuhan penduduk

K(t) _{= Jumlah penduduk pada awal tahun (t)}

Angka pertumbuhan penduduk (r) merupakan penjumlahan dari pertumbuhan penduduk alami (natural increase), yaitu perbedaan angka kelahiran dan kematian (b-d) dan angka migrasi netto (i-o). Dan secara umum dapat dirumuskan sebagai berikut :

r = b – d + i – o ,

dimana b, d, i dan o masing-masing adalah angka kelahiran, angka kematian, angka migrasi masuk dan angka migrasi keluar. Perbedaan antara uniregional dan multiregional terletak pada pengukuran parameter migrasi masuk (i). Dalam uniregional, pembagi migrasi masuk adalah penduduk wilayah yang didatangi, sedangkan pada multiregional pembaginya adalah penduduk wilayah asal migran.

2.7 Life Table Uniregional

Menurut Brown (1997) Life Table adalah suatu gambaran yang menunjukkan riwayat kematian dalam masyarakat pada waktu tertentu yang meliputi:

l(x) adalah jumlah orang yang bertahan hidup dari lahir hingga tepat umur ke-x.

d(x) adalah banyaknya kematian antara umur x hingga x+1, dimana

d(x) = l(x) – l(x+1) (15)

p(x) adalah peluang bertahan hidup dari umur x hingga umur x+1, dimana

p(x) = ) ( ) 1 ( x l x l + (16)

q(x) adalah peluang kematian seseorang yang hidup pada tepat umur x dan akan mati sebelum mencapai umur x+1, dimana

q(x) = ) ( ) ( x l x d ₌ ) ( ) 1 ( ) ( x l x l x l − + (17)

L(x) adalah banyaknya penduduk pertengahan tahun yang hidup antara umur x dan

x+1, dimana

L(x) = l(x) - ₂1_{d(x) =} 2

1_{(l(x) + l(x+1)) (18)}

T(x) adalah total waktu hidup yang akan dijalani oleh l(x) penduduk berumur x,

dimana

T(x) = L(x) + L(x+1) + L(x+2) + .... (19)

e0(x) adalah angka harapan hidup bagi penduduk umur x, dimana e0_{(x) =} ) ( ) ( x l x T ₍₂₀₎

m(x) adalah tingkat kematian bagi penduduk umur x, dimana m(x) = ) ( ) ( x L x d ₍₂₁₎

Dalam menentukan life table uniregional dapat dilakukan dengan menggunakan modifikasi Brass yang dikenal dengan sistem model logit life table

(Anonim 1983). Brass telah menemukan adanya hubungan linear antara l*(x) dan

l(x). Misalkan λ(l(x) menyatakan transformasi dari nilai l(x), maka dapat ditulis hubungan linear antara λ(l*(x)) dan λ(l(x) sebagai berikut:

dimana l*(x) dan l(x) menyatakan dua nilai life table yang berbeda level, α dan β

merupakan konstanta. Persamaan (22) akan berlaku untuk semua nilai x jika λ

didefinisikan sebagai :

λ(l(x)) = logit (1.0 – l(x)) = 0,5 ln ((1.0 – l(x))/l(x)) (23) Dari persamaan (22) dan persamaan (23) dapat diturunkan sebuah persamaan:

l*(x) = (1.0 + exp(2α + 2βλ(l(x))))-1 (24) (Bukti: Lihat Lampiran 14)

Persamaan (24) dapat digunakan untuk membuat life table uniregional secara sederhana dengan menggunakan nilai α dan β yang sesuai dengan level.

2.8 Konsep Demografi Multiregional

Selanjutnya akan dijelaskan beberapa konsep berkaitan dengan demografi multiregional yang meliputi survivorship, life table multiregional, dankelahiran. Berikut definisi dan notasi yang digunakan :

h_{pij (x) : peluang seseorang yang sekarang berumur x dan tinggal di wilayah-i,}

dan bertahan hidup hingga umur x+h dan tinggal di daerah-j

h_{qi (x) : peluang seseorang yang sekarang berumur x dan tinggal di wilayah-i,}

akan mati sebelum mencapai umur x+h.

h_{pii (x) : peluang seseorang yang sekarang berumur x dan tinggal di wilayah i,}

bertahan hidup hingga umur x+h dan tidak pindah ke wilayah lain.

h_{pii (x) = 1 -}

∑

=

m

j 1

h_{pij (x) -} h_{qi (x) i,j = 1, 2, ....,m} ixlj(y) : banyaknya penduduk yang bertahan hidup hingga umur y tahun dan

tinggal di wilayah j dari li(x) penduduk yang pada saat umur x tahun tinggal di wilayah i

ixLj(y) : total jumlah penduduk yang pada umur y ada di daerah j dan sebelumnya tinggal di daerah i pada umur x.

ixLj(y) = ₂h_{[ ixlj(y)]}

bji (x) : intensitas kelahiran bayi dalam selang waktu x sampai x+4 dan pada awal interval waktu yang tinggal di wilayah j dan pada akhir interval tinggal di wilayah i

sji (x) : proporsi penduduk dari semua umur x hingga x+4 yang tinggal di daerah j pada periode t dan bertahan hingga 5 tahun. Kemudian umur

x+5 hingga x+9 tinggal di wilayah i pada periode t+1.

S(x) :matriks sij (x) dengan elemen baris ke-i dan kolom ke-j.

K(t)

i (x) : total jumlah penduduk pada wilayah i pada periode t pada kelompok

umur x sampai x+4.

α

: usia reproduksi terendah

β : usia reproduksi tertinggi

2.8.1 Survivorship

Berikut ini adalah sistem penduduk dengan m-daerah, jumlah penduduk pada kelompok umur x sampai x+4 pada daerah i adalah :

K(t) i (x) =

∑

= m j t i jK x 1 ) ( _{( ) , i = 1, 2, ...., m (25)} dimana (t) i

jK (x) adalah individu lahir di daerah-j, yang ada di daerah-i pada

kelompok umur x sampai x+4 pada saat t.

Survivorship adalah proporsi penduduk yang bertahan hidup pada suatu periode sampai periode berikutnya, dinyatakan dengan:

sij (x) = ) ( ) 5 ( x L x L ij j i + (26) Pada populasi multiregional penduduk yang diharapkan bertahan hidup sampai interval waktu 5 tahun adalah:

Kj (x+5) =

∑

= m i i ij x K x s 1 ) ( ) ( , j = 1, 2, ..., m (27) dimana sij (x) adalah proporsi bahwa individu di daerah-i umur x sampai x +4 dan tinggal di daerah-j pada saat umur x+5 sampai umur x+9.

Dari hubungan persamaan (25) dan persamaan (27) dan fakta bahwa bayi yang lahir di daerah-i tidak dapat menjadi anggota populasi bayi yang lahir di daerah-j, atau sebaliknya maka:

) 1 (t+ i jK (x+5) =

∑

= m k t k j ki x K x s 1 ) ( _{( )} ) ( i,j = 1,2,3,...,m (28) atau dalam bentuk matriks :

) ( ) ( ) 5 ( () ) 1 ( _{x S x K x} Kt+ _{+ =} t ₍₂₉₎ dengan : ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ) ( ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 ) ( 1 ) ( 2 ) ( 2 2 ) ( 2 1 ) ( 1 ) ( 1 2 ) ( 1 1 ) ( x K x K x K x K x K x K x K x K x K x K t m m t m t m t m t t t m t t t

Dengan matriks survivorship dari sij (x):

S(x) = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 1 2 22 12 1 21 11 x s x s x s x s x s x s x s x s x s mm m m m m … … …

Sehingga dari persamaan (26) untuk sistem populasi dua wilayah elemen baris ke j, kolom ke i dapat diformulasikan:

sij(x)

=

i,j = 1,2 (30)

2.8.2 Life Table Multiregional

Perhitungan life table multiregional dimulai dengan pendugaan migrasi keluar menurut umur dan tingkat kematian. Setelah menyusun life table, kita dapat mencari matriks G yaitu matriks operator pertumbuhan multiregional untuk memprediksi jumlah penduduk pada satu interval waktu tertentu. Pada dasarnya semua fungsi life table berasal dari matriks peluang transisi P(x) yang didefinisikan untuk semua umur dan untuk mengkonstruksinya dilakukan dengan cara mentransformasikan tingkat migrasi dan tingkat kematian menurut umur A(x) atau proporsi survivorshipS(x) ke matriks transisi.

Ada dua prosedur dalam melakukan pendugaan A(x), P(x), S(x). Prosedur pertama difokuskan pada tingkat migrasi dan tingkat kematian menurut umur yang diamati, sedangkan prosedur kedua difokuskan pada proporsi survivorship. Menurut Rogers(1975) dalam Rogers(1995) kedua jenis penduga ini disebut dengan “metode Option I” dan “metode Option II”

a. Pendugaan menggunakan metode Option I

Pada metode ini pendugaan dimulai dengan mendefinisikan matriks migrasi dan kematian yaitu:

A(x) = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 1 2 22 12 1 21 11 x M x M x M x M x M x M x M x M x M mm m m m m dimana Mii(x) =

∑

≠ + i j ij id x M x M ( ) ( )

yang menyatakan bahwa Mid(x) adalah tingkat kematian tahunan menurut umur di daerah-i dan

∑

Mij(x) adalah jumlah tingkat migrasi menurut umur dari daerah-i

ke daerah-j, untuk semua j, j≠i.

Rogers dan Ledent(1976) dalam Rogers(1995) menunjukkan bahwa matriks peluang P(x) untuk interval 5 tahunan dihitung dari matriks A(x) menggunakan persamaan : P(x) =

[

]

1 2 5 _{( )}− + A x I

[

_I−25_A(_x)

]

_{, (32)} dimana : P(x) = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 1 2 22 12 1 21 11 x p x p x p x p x p x p x p x p x p mm m m m m

Dengan pij(x) adalah peluang individu hidup di daerah-i pada tepat umur x

kehidupan dan hidup 5 tahun setelahnya di daerah-j.

b. Pendugaan menggunakan metode Option II

Dalam metode ini akan digunakan jika data migrasi dan kematian tidak ada yaitu dengan menggunakan data survivorship. Ledent dan Rees (1986) dalam Rogers (1995) mengatakan bahwa metode ini dimulai dengan mendefinisikan hubungan antara matriks P(x) dan matriks proporsi survivorship

S(x) = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 1 2 22 12 1 21 11 x s x s x s x s x s x s x s x s x s mm m m m m … … …

Proporsi survivorship untuk interval waktu umur 5 tahunan dihitung dengan cara:

ij S~ (x-5) =

∑

= m k ik ij x K x K 1 ) ( ) ( (33)

Dimana Kij(x) menunjukkan jumlah migran yang dicatat dengan sensus dari daerah-i pada waktu t-5 di daerah-j pada waktu t dan

∑

Kik(x) adalah jumlah migran dari daerah-i pada waktu t-5 untuk semua k daerah pada waktu t, proporsi tersebut mengacu pada kelompok umur 5 tahun lebih muda dari umur yang dilaporkan ketika sensus diambil.

Matriks peluang transisi bersyarat P~(x)diperoleh dari matriks proporsi

survivorship bersyarat menurut umur, S~(x), menggunakan interpolasi linear pertama yang diberikan oleh Rees dan Wilson(1977) dalam Rogers(1995):

P(x) = _P~(_x)_P(_x) 1₂

[

_S~(_x 5) _S~(_x)

]

_P(_x) σ σ = − + ₍₃₄₎ ) ( ~ x S = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ) ( ~ ) ( ~ ) ( ~ ) ( ~ ) ( ~ ) ( ~ ( ) ~ ~ ) ( ~ 2 1 2 22 12 1 ) ( 21 11 x s x s x s x s x s x s x s s x s mm m m m m x ) ( ~ _x P = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ) ( ~ ) ( ~ ) ( ~ ) ( ~ ) ( ~ ) ( ~ ( ) ~ ) ( ~ ) ( ~ 2 1 2 22 12 1 21 11 x p x p x p x p x p x p x p x p x p mm m m m m

Dan P_σ(x)adalah matriks diagonal dari peluang bertahan hidup tidak bersyarat, bentuk matriksnya : ) (x P_σ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ) ( 0 0 0 ) ( 0 0 0 ) ( 2 1 x p x p x p mσ σ σ

Formula untuk menghitung setiap elemen diagonal dalam P_σ(x)menggambarkan definisi uniregional dari peluang bertahan hidup (Ledent & Rees 1986, diacu dalam Rogers 1995): ) (x P_iσ =

∑

= + − m k id ik id x M x p x M 1 2 5 2 5 ) ( ) ( ~ 1 ) ( 1 (35) dimana M_id(x)adalah tingkat kematian umur x sampai x+4 di daerah-i.

2.8.3 Kelahiran

Proyeksi penduduk multiregional tidak lengkap tanpa memperkirakan jumlah total kelahiran yang bertahan hidup selama satu selang waktu.

Tingkat kelahiran penduduk wanita pada usia x di daerah-i dinotasikan dengan Fi(x)= ) ( ) ( x x i i ρ β _{, dimana (x)} i

β

merupakan banyaknya kelahiran pada waktu umur x

di daerah-i dan

ρ

_i(x)merupakan banyaknya penduduk wanita pada waktu umur x

di daerah i.

Jumlah bayi yang lahir selama selang interval 5 tahun adalah:

= ∑ 5 5

Jumlah bayi yang bertahan hidup di daerah-j sampai akhir selang interval adalah:

0 5 0

Sehingga diperoleh jumlah bayi yang lahir dari wanita usia reproduksi α sampai β selama selang waktu 5 tahun adalah:

0 = ∑ 0 0 5 5

= ∑ 0 0 5

= ∑ elemen pada baris ke-i kolom ke-j matriks B(x) adalah:

bji(x) = ₂1 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + +

∑

= m k k k i k jk j j i j _{F x} l L x S x F l L 1 0 0 _{( 5)} ) 0 ( ) 0 ( ) ( ) ( ) 0 ( ) 0 ( (31) Dengan matriks kelahiran dari bji (x) :

B(x) = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 1 2 22 12 1 21 11 x b x b x b x b x b x b x b x b x b mm m m m m … … …

2.9 Matriks Proyeksi Multiregional

Dari matriks survivorship dan matriks kelahiran, dapat di susun matriks operator pertumbuhan penduduk secara multiregional (Rogers 1995) yaitu :

G = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − 0 ) 5 ( 0 0 0 0 0 0 ) 10 ( 0 0 0 0 ) 5 ( 0 0 0 0 ) 0 ( 0 0 ) 5 ( ) 5 ( 0 0 z S S S S B Bα β

Matriks G di atas yang kemudian disebut sebagai proses pertumbuhan dengan generalisasi matriks Leslie. Setelah membuat matriks operator G maka dapat dilakukan proyeksi penduduk dengan menggunakan model proyeksi :

K(t+1) = G K(t) (36)

Dari persamaan (36) kita dapat memperoleh persamaan-persamaan berikut: K(t+1) = GK(t)

K(t+2) = GK(t+1) = G2K(t)

…

K(t+n) _{= G}n_K(t) ₍₃₇₎

Dengan demikian apabila kita mengetahui vektor sebaran umur awal K(t)

dan matriks G, maka kita dapat menentukan vektor sebaran umur populasi di waktu yang akan datang.

Model proyeksi di atas kemudian disebut dengan model proyeksi generalisasi matriks Leslie yang melibatkan migrasi secara multiregional, dimana:

K(t)₌ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ) ( ) ( ) 5 ( ) 0 ( ) ( ) ( ) ( ) ( z K x K K K t t t t , K(t)_{(x) =} ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ) ( ) ( ) ( ) ) ( 2 ) ( 1 x K x K x K t m t t

Pada populasi yang telah mencapai sebaran umur stabil maka jumlah penduduk pada periode t+1 adalah jumlah penduduk pada periode t dikali laju perubahannya, sehingga terjadi persamaan :

K(t+1) _{= λ K}(t)_{, (38)}

dimana λ adalah laju perubahan. Apabila λ > 1 maka terjadi kenaikan, λ < 1 terjadi penurunan, dan untuk λ = 1 maka konstan.

Dari persamaan (38) di atas kita dapat memperoleh persamaan-persamaan berikut:

K(t+1) = λK(t)

K(t+2) = λK(t+1) = λ2K(t)

…

K(t+n) = λnK(t) (39) Dalam model proyeksi generalisasi matriks Leslie yang melibatkan komponen migrasi secara multiregional diketahui bahwa:

sehingga jika suatu populasi dengan model matriks Leslie yang telah mencapai sebaran umur stabil akan berlaku :

K(t+1) = G K(t) = λK(t) (40)

dimana λ adalah konstanta akarciri dominan dari matriks G. Dari persamaan (37) dan (39) dapat diformulasikan :

K(t+n) = GnK(t) = λnK(t) (41) Berdasarkan teorema 2 untuk mendapatkan penyelesaian λ pada persamaan (40) maka terdapat K(t) _{≠ 0 sedemikian rupa sehingga (G-λI) K}(t) _{= 0 akan}

mempunyai penyelesaian yang tak nol harus dipenuhi det(G- λI) = 0. Untuk mengetahui gambaran populasi setelah sebaran umur stabil tercapai, maka dapat dilakukan penelusuran terhadap akarciri matriks Leslie.

Pada populasi yang telah mencapai sebaran usia stabil maka akarciri matriks

G adalah bersifat positif, tunggal dan real (sebut sebagai λ1) dan berlaku λ1> ,

j = 2, 3, …, dan berdasarkan definisi 5 maka λ1 adalah akarciri dominan dari

matriks G. Di dalam Jatminingtias (1996) telah ditunjukkan bahwa akarciri positif matriks Leslie (λ1) hanya satu. Vektorciri (x1) yang berpadanan dengan λ1

memiliki unsur-unsur yang positif. Jika terdapat dua kelas umur atau lebih yang berurutan, maka akarciri dominan matriks Leslie adalah akarciri positifnya.

Di dalam Brown (1997) model laju pertumbuhan penduduk pada populasi stabil dapat nyatakan sebagai :

K(t+1) = erK(t) (42)

dimana r merupakan laju pertumbuhan penduduk. Sehingga dari persamaan (40) dan (42) laju pertumbuhan penduduk pada populasi mencapai kondisi stabil untuk interval umur 5 tahunan dapat ditentukan dengan:

BAB III

METODOLOGI PENELITIAN

3.1 Sumber Data

Sampai saat ini sumber utama data statistik migrasi di Indonesia hanya mengandalkan pada hasil sensus penduduk (SP) ataupun survei penduduk antar sensus (SUPAS) yang secara operasional dilakukan oleh Biro Pusat Statistik (BPS). SP dilakukan 10 tahun sekali. Sejak Indonesia merdeka sensus penduduk telah dilaksanakan lima kali yaitu 1961, 1971, 1980, 1990 dan 2000. Untuk mengetahui keadaan penduduk antar sensus yang cukup panjang tersebut, BPS melaksanakan SUPAS. Sampai saat ini SUPAS telah dilakukan empat kali, yaitu pada tahun 1976, 1985, 1995 dan 2005.

Dalam penelitian ini data yang digunakan adalah data yang diambil dari BPS hasil SUPAS terakhir tahun 2005. Data yang diambil meliputi data migrasi risen menurut umur, data kematian, data kelahiran dan data jumlah penduduk.

3.2 Konsep dan Definisi

Penduduk adalah semua orang yang berdomisili di wilayah geografis Indonesia selama 6 bulan atau lebih atau mereka yang berdomisili kurang dari 6 bulan tetapi bertujuan untuk menetap. Umur seseorang dapat diketahui apabila tanggal, bulan, dan tahun kelahiran diketahui. Di dalam proses pencacahan, pencacah akan menanyakan tanggal kelahiran setiap orang dan dinyatakan dalam kalender Masehi. Penghitungan umur seseorang harus selalu dibulatkan ke bawah atau menurut ulang tahun yang terakhir. Apabila tanggal, bulan maupun tahun kelahiran seseorang tidak diketahui, maka pencacah harus berusaha mendapatkan keterangan mengenai umur dengan beberapa cara misalnya dengan menghubungkan kejadian-kejadian penting baik yang bersifat nasional maupun daerah, misalnya Proklamasi kemerdekaan RI tahun1945 dan Pemilihan Umum Pertama tahun 1955.

Dengan cara penghitungan umur seperti di atas maka:

a. Penduduk berumur 0 tahun adalah penduduk yang berumur kurang dari satu tahun.

b. Penduduk berumur 1 tahun adalah penduduk yang berumur satu tahun lebih tetapi kurang dari dua tahun.

c. Penduduk umur 0-4 tahun adalah penduduk yang berumur kurang dari lima tahun

d. Penduduk umur 5-9 tahun adalah penduduk yang berumur lima tahun atau lebih, kurang dari 10 tahun dan seterusnya.

e. Penduduk berumur 85+ adalah penduduk yang berumur 85 tahun dan lebih.

3.3 Metode Analisis Data

Langkah-langkah yang dilakukan dalam menganalisis data yang telah diperoleh adalah sebagai berikut :

a. Mengelompokkan wilayah Indonesia menjadi dua wilayah yaitu Jawa Bali (JB) dan Luar Jawa Bali (LJB).

b. Pengolahan data dasar migrasi untuk dua wilayah tersebut.

c. Membuat pola model skedul migrasi untuk dua wilayah dengan cara melakukan pendugaan parameter model dibantu Software Mathematica 6.0 dengan pendekatan metode kuadrat terkecil:

i). Dengan mengikuti pola model Rogers.

ii). Membuat pola baru berupa model fungsi polinom. d. Membuat life table untuk dua wilayah tersebut.

e. Membuat life table multiregional yang melibatkan migrasi keluar menurut umur dan peluang kematian.

f. Mencari matriks operator G (matriks Leslie) untuk menduga jumlah penduduk pada satu interval waktu tertentu yang melibatkan survivorship dan kelahiran.

BAB IV

HASIL DAN PEMBAHASAN

4.1 Analisis Model Migrasi

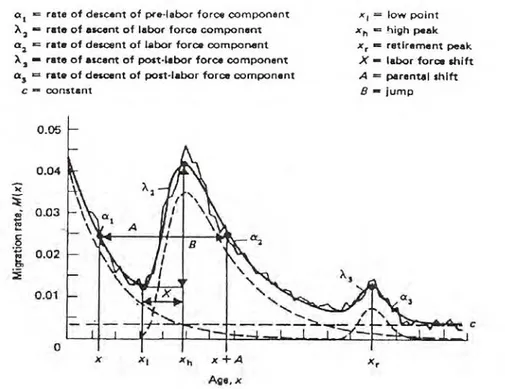
Secara umum persamaan model skedul migrasi model penuh yang dikemukakan oleh Rogers (1978) dapat digambarkan menjadi sebuah grafik yang diberikan pada gambar berikut ini:

Gambar 1 Skedul migrasi model penuh

Grafik di atas dengan menggunakan simulasi dapat dikaji sebagai berikut: 1. Kurva pra-angkatan kerja (pre-labor force), berupa persamaan eksponensial

dengan angka penurunan sebesar α1 yaitu :

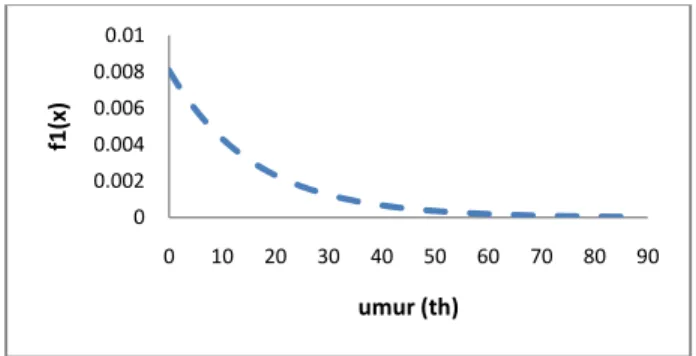
f1(x) = a1 exp(-α1x) ; ∀x≥ 0 ,

dengan nilai-nilai parameter a1 = 0,008 ; α1 = 0,062

Gambar 2 Kurva migrasi pra-angkatan kerja

Kurva di atas menggambarkan bahwa pola migrasi pra-angkatan kerja (usia 5-15 tahun) mengalami penurunan sejalan dengan meningkatnya umur. Pada usia tersebut mereka memiliki resiko yang sama. Artinya mereka masih tergantung pada orangtua. Jadi kemanapun orangtua mereka pergi akan selalu diikutsertakan. Sehingga pada tahap ini semakin bertambahnya umur maka tingkat ketergantungan mereka terhadap orangtua akan semakin kecil. Hal ini akan berakibat tingkat migrasi semakin rendah.

2. Kurva angkatan kerja (labor force), berupa persamaan eksponensial ganda dengan satu titik puncak, dengan usia rata-rata µ2, serta memiliki angka

kenaikan λ2 dan penurunan α2 yaitu :

f2(x) = a2 exp{-α2(x - µ2) – exp[-λ2(x-µ2)]} ; ∀x≥ 0,

dengan nilai-nilai parameter a2 = 0,029 ; α2 = 0,075 ; µ2 = 19,45 ; λ2 = 0,365

Gambar 3 Kurva migrasi angkatan kerja

Kurva di atas menggambarkan bahwa pola migrasi angkatan kerja (15-60 tahun) umumnya mereka memiliki resiko yang berbeda. Artinya mereka tidak tergantung pada orangtua, karena mereka umumnya akan belajar mandiri dan menentukan tujuan hidup. Sehingga mengakibatkan tingkat migrasi pada usia 15-25 tahun mengalami peningkatan, sedangkan pada usia 25-60 tahun

0 0.002 0.004 0.006 0.008 0.01 0 10 20 30 40 50 60 70 80 90 f1 (x ) umur (th) ‐0.005 0 0.005 0.01 0.015 0.02 0 10 20 30 40 50 60 70 80 90 100 f2(x ) umur (th)

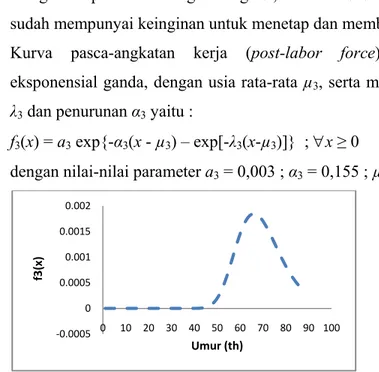
mengalami penurunan tingkat migrasi, hal ini disebabkan mereka umumnya sudah mempunyai keinginan untuk menetap dan membina rumah tangga. 3. Kurva pasca-angkatan kerja (post-labor force), berupa persamaan

eksponensial ganda, dengan usia rata-rata µ3, serta memiliki angka kenaikan

λ3 dan penurunan α3 yaitu :

f3(x) = a3 exp{-α3(x - µ3) – exp[-λ3(x-µ3)]} ; ∀x≥ 0

dengan nilai-nilai parameter a3 = 0,003 ; α3 = 0,155 ; µ3 = 75,35 ; λ3 = 0,073

Gambar 4 Kurva migrasi pasca angkatan kerja

Kurva di atas menggambarkan bahwa pola migrasi pasca-angkatan kerja (usia

≥ 60 tahun) tingkat migrasi yang terjadi sangat kecil bila dibandingkan dengan tahap pekerja. Sebagian dari mereka umumnya melakukan migrasi ke daerah asal karena keinginan mereka untuk menetap dan menghabiskan usia pensiun, dan sebagian lagi akan menetap di daerah yang baru.

4. Suatu konstanta c, yaitu suatu persamaan:

f4(x) = c ; ∀x≥ 0

dengan nilai-nilai parameter c = 0,0006

Gambar 5 Kurva konstanta

Kuva di atas menggambarkan suatu persamaan yang diperlukan untuk memperbaiki ketepatan matematis penaksiran skedul.

‐0.0005 0 0.0005 0.001 0.0015 0.002 0 10 20 30 40 50 60 70 80 90 100 f3 (x ) Umur (th) 0 0.0002 0.0004 0.0006 0.0008 0 10 20 30 40 50 60 70 80 90 100 f4 (x ) umur (th)

Gambar 1 menggambarkan skedul migrasi model “penuh” yang mempunyai 11 parameter: a1, α1, a2, µ2, α2, λ2, a3, α3, µ3, λ3 dan c. Dari sebelas parameter

tersebut mencerminkan hal-hal sebagai berikut:

1. Parameter yang menyatakan tingkat (level), yaitu: a1, a2, a3, dan c.

2. Parameter yang menyatakan pola (profil), yaitu: α1, α2, µ2, λ2, α3, µ3 dan λ3.

Perubahan dalam pola akan mengubah ketujuh parameter ini, tetapi belum tentu mengubah keempat parameter lainnya.

Beberapa hal yang menarik dari Gambar 1 adalah terdapatnya tiga titik istimewa dalam pola migrasi menurut kelompok umur, yaitu:

1. x1 yang merupakan titik terendah angka migrasi pada usia pra angkatan kerja.

Angka migrasi atau M(x) pada titik ini biasanya merupakan angka terendah. 2. xh sebagai titik puncak atau tertinggi, yatu titik yang menghasilkan M(x)

tertinggi pada usia angkatan kerja. Pada titik tersebut M(x) merupakan titik tertinggi jika dibandingkan dengan titik-titik lain di luar usia angkatan kerja. 3. xr yang merupakan titik tertinggi pada usia pasca-angkatan kerja. Titik ini

lebih rendah daripada xh.

Dari ketiga titik istimewa di atas (lihat dari Gambar 1), diperoleh tiga hal lain yaitu:

1. “Pergeseran angkatan kerja” (labor force shift) X = xh – x1, yaitu perbedaan

umur antara titik terendah dan titik tertinggi. Atau tahun yang dibutuhkan dari

x1 ke xh.

2. “Lompatan” (jump) B, yang merupakan perbedaan antara M(x) yang dihasilkan oleh x1 dan xh.

3. “Gesekan orang tua” (parental shift) A, yang mencerminkan hubungan erat antara migrasi anak-anak dan migrasi orang tua. Nilai ini diperoleh dengan menghitung selisih antara nilai x pada usia pra-angkatan kerja dan angkatan kerja untuk M(x) yang sama. Rata-rata selisih dua usia untuk suatu M(x) tersebut disebut dengan A (gesekan orang tua)

Karakteristik model skedul migrasi juga dapat dilihat dari kaitan antara kelompok umur pra-angkatan kerja dan angkatan kerja. Model skedul dikatakan memiliki puncak awal, jika µ2 kurang dari 19 tahun. Artinya rata-rata migran