PENERAPAN FUZZY AHP DAN TOPSIS UNTUK SELEKSI KANDIDAT PENERIMA BANTUAN RUMAH TIDAK LAYAK HUNI (RTLH) (STUDI KASUS : DESA BANTARWUNI)
Teks penuh
Gambar
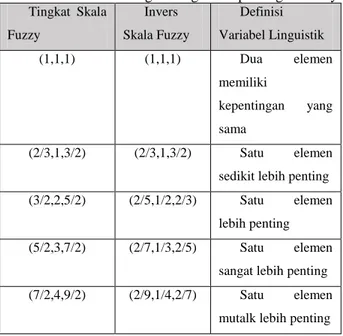
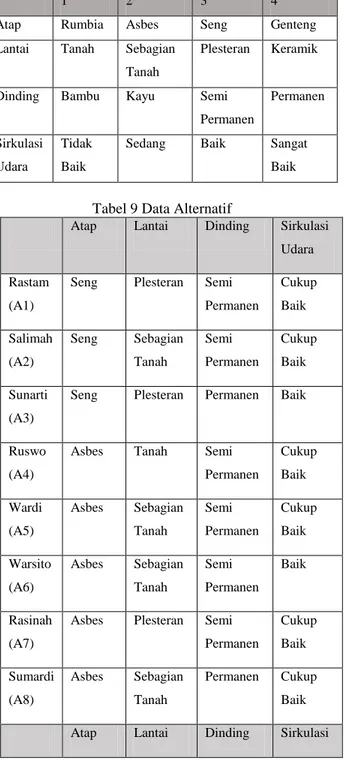
Dokumen terkait
Puji syukur kepada Tuhan Yesus Kristus atas kasih dan penyertaan-Nya, sehingga karya tulis yang berjudul “Pengaruh Lama Cuti Bersalin terhadap Kelangsungan
Hipotesis ketiga diduga faktor product, price, place, promotion, people, physical evidence dan process secara parsial berpengaruh keputusan mengajukan kredit usaha
Dari uraian makna laba di atas, terlihat bahwa laba dalam Ekonomi Islam terbagi menjadi dua yaitu laba material dan laba spiritual.Kerena laba dapat dimaknai dengan multi-dimensional
Pendedahan dan data rasmi daripada syarikat penerbitan komik yang dikongsi dalam kajian akan datang mampu menjadi sumber bagi melihat sejauh mana penerimaan komik
Menemukan daratan ini berawa-rawa dan penduduknya tidak begitu ramah (sepuluh dari awak kapalnya terbunuh pada beberapa ekspedisi di pesisir ini),
Fase ini merupakan fase yang sulit dan pen- ting, karena hubungan saling percaya sudah terbina dan berada pada tingkat optimal. Pe- rawat dan klien keduanya merasa
Salah satu isu yang perlu diperhatikan dalam kaitannya dengan penelitian ini adalah isu lingkungan yang ada di objek wisata Lovina, khususnya dalam konteks
Dan sebagai keturunan Jawa, para informan juga memiliki panggilan untuk saling menghormati satu sama lain, contohnya setiap Irene beradu argumen maupun mengkritik