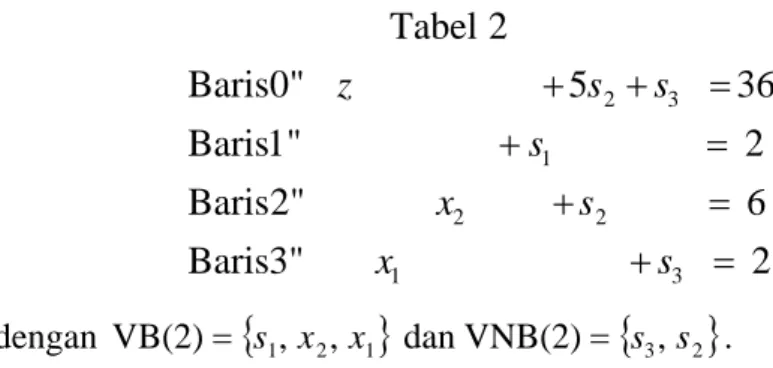1 BAB I
PENDAHULUAN A. Latar Belakang Persoalan
Indonesia merupakan salah satu negara yang mempunyai wilayah hutan yang cukup luas dan merupakan negara terpenting penghasil berbagai kayu bulat tropis, kayu gergajian, kayu lapis dan hasil kayu lainnya. Hasil produksi hutan Indonesia mempunyai keunggulan komparatif (comparative advantage) jika dibandingkan dengan negara-negara lain dan sebagian dari produksi hasil hutan diekspor ke negara lain. Selain itu produk kayu juga merupakan penghasil devisa utama dari sektor non migas.
Kayu merupakan salah satu hasil hutan yang dalam proses pembaharuannya membutuhkan waktu yang cukup lama, sehingga perlu pengelolaan yang baik, yaitu dengan memperhatikan sistem tebang pilih serta menindak para pembalak liar, agar pemenuhan kayu dalam proses pembangunan, baik bagi perumahan dan infrastruktur lain tidak terhambat.
Perusahaan kayu biasanya mengkonversikan kayu bulat menjadi kayu berbentuk balok, papan atau bentuk-bentuk yang sesuai dengan tujuan penggunaannya. Selanjutnya kayu-kayu yang telah berbentuk balok, maupun papan diolah kembali menjadi ukuran-ukuran tertentu sesuai dengan pesanan dari para pemilik usaha dagang (UD) kayu.
Dalam praktik, suatu pesanan dipenuhi dengan menyetel pisau pemotong sesuai dengan panjang yang diminta. Biasanya untuk memenuhi pesanan terdapat beberapa cara atau pola pemotongan standar. Adapun pola-pola ini digunakan
2
dengan tujuan mengoptimalkan penggunaan balok kayu yang tersedia dengan cara meminimumkan sisa pemotongan.
Jika suatu perusahaan kayu mendapatkan pesanan dalam jumlah banyak, misalnya sejumlah m pesanan dengan panjang kayu yang bervariasi, maka dilakukan pola-pola pemotongan yang beraneka ragam untuk memenuhi pesanan tersebut, banyaknya pola pemotongan misal n pola pemotongan. Persoalan yang dihadapi perusahaan kayu tersebut dapat disusun ke dalam persoalan program linear dan dapat dipecahkan atau dicari solusinya menggunakan teknik-teknik penyelesaian dalam program linear.
Program linear adalah suatu metode yang dapat digunakan dalam mencari solusi persoalan optimasi dengan merencanakan langkah-langkah yang perlu diambil dengan tujuan memperoleh hasil yang optimal, yaitu hasil yang mencapai tujuan terbaik diantara seluruh hasil yang mungkin. Banyak persoalan yang penyelesaiannya menggunakan program linear, diantaranya persoalan transportasi, persoalan penugasan, program dinamis serta program bilangan bulat.
Program linear bilangan bulat merupakan bentuk khusus dari program linear, dengan solusinya harus bernilai bilangan bulat dan sebagian lainnya boleh bernilai pecahan. Persoalan program linear bilangan bulat yang penyelesaian persoalannya hanya sebagian dari variabel solusinya yang harus bernilai bilangan bulat dinamakan persoalan program linear bilangan bulat campuran. Apabila seluruh variabel solusi dari penyelesaian suatu persoalan program linear harus bernilai bilangan bulat maka disebut persoalan bilangan bulat murni. Penyelesaian persoalan program linear bilangan bulat memerlukan suatu metode khusus.
3
Terdapat dua metode yang digunakan, yaitu metode cabang dan batas (branch and
bound) dan metode bidang potong (cutting plane).
Dalam mencari penyelesaian persoalan program linear, metode yang sering digunakan yaitu metode simpleks. Terdapat teknik lain untuk menyelesaikan persoalan program linear yaitu teknik pembangkit kolom (column
generation technique). Salah satu aplikasi dari teknik ini yaitu untuk
menyelesaikan persoalan pemotongan stok atau cutting stock problem (CSP). Langkah pertama dalam menyelesaikan persoalan optimasi pemotongan balok kayu yaitu menentukan pola pemotongan yang mungkin kemudian menentukan kombinasi-kombinasi pola pemotongan yang layak. Meskipun menentukan semua pola yang mungkin tidak begitu sulit, namun menentukan kombinasi yang layak merupakan pekerjaan yang berat. Disinilah model program linear memainkan peranan dan teknik pendekatan yang sistematis diperlukan.
Langkah selanjutnya yaitu persoalan dibentuk kedalam bentuk program linear baku, bentuk ini kemudian diselesaikan dengan teknik pembangkit kolom. Teknik pembangkit kolom digunakan untuk mengefisiensi metode simpleks direvisi. Sehingga langkah-langkah pengerjaannya banyak mengacu kepada metode simpleks direvisi, mulai dari perhitungan B 1 (matriks yang diperoleh dari koefisien variabel-variabel slack untuk baris ke-i, i 1,2,...,m dari tabel akhir simpleks), harga akhir (price out), penggunaan test rasio untuk menentukan variabel basis, sampai diperoleh penyelesaian optimal. Perbedaan mendasar antara teknik pembangkit kolom dan metode simpleks direvisi terletak pada perhitungan harga akhir (zj cj) variabel non basis yang akan masuk menjadi variabel basis.
4
Perhitungan harga akhir untuk tiap-tiap variabel non basis menjadi variabel basis dalam skala besar pemotongan balok kayu dengan menggunakan metode simpleks direvisi adalah suatu pekerjaan yang tidak efektif dan juga tidak efisien. Untuk mengatasi hal ini maka teknik pembangkit kolom dapat digunakan untuk mencari penyelesaiannya. Ide dasar dari teknik pembangkit kolom adalah untuk mengefisiensi suatu kolom dengan harga akhir yang efisien (positif dalam persoalan minimum).
Dalam optimasi pemotongan balok kayu, yang diinginkan adalah sisa pemotongan dan produksi suplus seminimum mungkin. Untuk mendapatkan hasil ini dilakukan dengan mengkombinasikan pola-pola pemotongan berdasarkan panjang pesanan yang diinginkan dengan menerapkan teknik pembangkit kolom. Pola-pola yang paling baik di antara pola-pola yang mungkin dapat diperoleh dengan menggunakan teknik pembangkit kolom.
Penyelesaian persoalan program linear dapat diselesaikan dengan cara menghitung secara manual maupun dengan menggunakan bantuan software aplikasi. Jika dalam persoalan program linear telah melibatkan banyak variabel dan kendala (pembatas), maka menyelesaikannya dengan cara manual tentunya akan memerlukan waktu yang lama. Maka disinilah peran software aplikasi untuk menyelesaikannya secara cepat.
Dalam penulisan ini contoh persoalan yang disajikan adalah persoalan pemotongan balok kayu dan dibahas juga bagaimana implementasi dari teknik pembangkit kolom untuk mendapatkan solusi yang optimal persoalan pemotongan
5
stok, lebih khusus lagi mengenai pemotongan balok kayu dengan pola pemotongan satu dimensi.
B. Pembatasan Persoalan
Persoalan dalam penulisan ini dibatasi hanya pada pemotongan balok kayu untuk pola pemotongan satu dimensi.
C. Rumusan Persoalan
Berdasarkan latar belakang persoalan, dapat dirumuskan persoalan sebagai berikut:
a. Bagaimana menentukan pola awal dan kombinasi pola paling layak pemotongan balok kayu dengan pola pemotongan satu dimensi ?
b. Bagaimana implementasi teknik pembangkit kolom dalam menyelesaikan persoalan pemotongan balok kayu ?
c. Bagaimana implementasi software aplikasi dalam mencari solusi optimal pemotongan balok kayu dengan lebih cepat ?
D. Tujuan Penulisan
Berdasarkan rumusan persoalan, maka tujuan dari penulisan ini adalah: a. Mendeskripsikan pola dan kombinasi yang layak dari persoalan
pemotongan balok kayu.
b. Mendeskripsikan penerapan teknik pembangkit kolom dalam menyelesaikan persoalan pemotongan balok kayu.
c. Mendeskripsikan penerapan software aplikasi dalam mencari solusi optimal pemotongan balok kayu secara cepat.
6
E. Manfaat Penulisan
Adapun manfaat dari penulisan ini yaitu diharapkan dapat memperluas penerapan matematika, khususnya bidang riset operasi pada industri dan perusahaan. Selain itu juga riset-riset atau penelitian-penelitian yang berkenaan dengan pengoptimalan penggunaan dan pemanfaatan sumber daya alam.
7
BAB II
LANDASAN TEORI
Di dalam membahas optimasi pemotongan balok kayu diperlukan beberapa pengetahuan tentang program linear, sistem persamaan, matriks, persoalan knapsack, metode simpleks, metode simpleks direvisi dan program linear bilangan bulat serta penyelesaiannya menggunakan metode cabang dan batas.
A. Program Linear 1. Definisi
Menurut Tjutju Tarliah dan Ahmad Dimyati (1992: 17), program linear diterjemahkan dari Linear Programming (LP) adalah suatu cara untuk menyelesaikan persoalan alokasi sumber-sumber terbatas (misal, tenaga kerja terampil, bahan mentah, lahan subur, mesin, modal) di antara beberapa aktivitas yang bersaing dengan cara seoptimal mungkin. Persoalan pengalokasian ini akan muncul manakala seorang harus memilih tingkat aktivitas-aktivitas tertentu yang bersaing dalam hal penggunaan sumber daya yang dibutuhkan untuk melaksanakan aktivitas-aktivitas tersebut. Beberapa persoalan pengalokasian antara lain persoalan pengalokasian fasilitas produksi, persoalan pengalokasian sumber daya nasional untuk keperluan domestik, penjadwalan produksi, solusi permainan (game), dan pemilihan pola pengiriman.
Program linear menurut Frederick S. Hiller and Gerald J. Lieberman (1980: 27), menggunakan suatu model matematis untuk menggambarkan suatu persoalan, aplikasi yang umum adalah mencakup alokasi sumber-sumber daya
8
yang berkaitan dengan memaksimumkan maupun meminimumkan. Kata program merupakan padanan kata perencanaan. Kata sifat linear berarti bahwa semua fungsi matematis dalam model ini harus merupakan fungsi-fungsi linear. Jadi membuat program linear adalah merencanakan kegiatan-kegiatan untuk memperoleh hasil yang optimal, yaitu suatu hasil untuk mencapai tujuan yang ditentukan dengan cara paling baik di antara semua alternatif yang mungkin.
Program linear banyak dipakai dalam persoalan ekonomi, industri, militer dan bidang sosial lainnya. Adapun persoalan yang sering dihadapi dalam berbagai bidang tersebut adalah alokasi optimal dari sumber daya tersebut. Manfaat program linear yaitu membuat model matematis dalam mencari solusi terbaik dari persoalan keterbatasan sumber daya untuk mencapai tujuan tertentu.
Dalam membangun model matematis dari formulasi persoalan program linear diperlukan karakteristik-karakteristik sebagai berikut:
a. Variabel keputusan
Variabel keputusan adalah variabel yang menguraikan secara lengkap keputusan-keputusan yang akan dibuat, yang merupakan formulasi dari apa yang dicari dalam persoalan tersebut.
Variabel keputusan ini dituliskan dengan xj, j 1,2,...,n. b. Fungsi tujuan
Fungsi tujuan merupakan fungsi dari variabel keputusan yang harus dicapai agar penyelesaian optimal dapat ditentukan dari semua nilai-nilai yang layak.
9
c. Fungsi kendala
Fungsi kendala merupakan formulasi dari kendala-kendala yang dihadapi dalam menentukan nilai variabel-variabel keputusan.
d. Pembatas tanda
Pembatas tanda adalah pembatas yang menjelaskan apakah variabel keputusan hanya bernilai nonnegatif atau boleh positif, nol, negatif (tidak terbatas dalam tanda).
Terdapat dua jenis keoptimalan untuk fungsi tujuan yaitu memaksimumkan dan meminimumkan. Untuk mencari solusi dari suatu persoalan program linear biasanya diselesaikan dengan memaksimumkan fungsi tujuan. Hal ini bukan berarti mengesampingkan persoalan meminimumkan. Karena berdasarkan sifat, persoalan meminimumkan dapat diubah menjadi memaksimumkan.
Sifat 2.1:
Meminimumkan f(x) (memaksimumkan f( x)),x S atau biasa ditulis dengan min f(x) (maks f(x)),x S.
Bukti:
Dimisalkan terdapat suatu program linear bilangan bulat dengan fungsi tujuan f dan himpunan kendala S. Ambil fungsi g, dengan g(x) f(x), x S. a. Jika x S y S sehingga f(x) (y) f(x) f(y) g(x) g(y),
maka tidak ada nilai minimum fungsi f dan tidak ada nilai maksimum fungsi g. Pada keadaan ini didefinisikan min f (x) dan maksimum (ming(x)) . b. Jika y S x S dan f(x) f(y)maka f( y) f(x) g(y) g(x)
10 jadi min f (x) = f ( y) = ( f(y))
= (g(y)) = (maks [g (x)]) = (maks [f(x)])
2. Bentuk baku atau bentuk umum dan bentuk kanonik program linear Program linear adalah suatu teknik matematis yang bertujuan untuk mendapatkan keputusan optimal dari sebuah fungsi dan dari sejumlah variabel tertentu. Variabel-variabel tersebut terkait pada sekelompok kendala (constraint) yang berbentuk persamaan atau pertidaksamaan.
Fungsi kendala dapat berbentuk pertidaksamaan lebih kecil atau sama dengan )
( , lebih besar atau sama dengan ( ) dan juga berbentuk sama dengan ( ). Bentuk umum atau bentuk baku program linear yaitu bentuk formulasi yang memiliki sifat-sifat sebagai berikut:
a. Semua kendala harus berbentuk persamaan (bertanda =) dengan ruas kanan yang nonnegatif.
b. Semua variabel harus merupakan variabel nonnegatif.
c. Fungsi tujuannya dapat berupa meminimumkan atau memaksimumkan. Bentuk program linear secara umum dapat dijelaskan sebagai berikut:
11
Memaksimumkan atau meminimumkan z(xj) c1x1 c2x2 ... cnxn,
terhadap kendala: . ,..., 2 , 1 , 0 , ) , , ( ... , ) , , ( ... , ) , , ( ... 2 2 1 1 2 2 2 22 1 21 1 1 2 12 1 11 n j x b x a x a x a b x a x a x a b x a x a x a j m n mn m m n n n n
(Akbar Sutawijaya: 1)
Koefisien-koefisien dalam z( xj),cj dinamakan koefisien ongkos, x j dinamakan peubah keputusan dan a ij dinamakan koefisien teknis. Jika perumusan program linear telah diaplikasikan dalam bentuk soal maka z disebut fungsi sasaran, kendala-kendala disebut kendala utama dan x j 0 disebut kendala nonnegatif.
Bentuk kanonik program linear diperoleh dengan cara:
a. Jika kendala ke-i suatu program linear adalah suatu persoalan maka ditambahkan variabel slack s untuk kendala ke-i dan ditambahkan i
kendala si 0,i 1,2,...,m.
b. Jika kendala ke-i dari suatu program linear adalah persoalan maka merubah ke bentuk kanonik program linear yaitu dikurangi dengan suatu variabel yang dinamakan variabel surplus (excess variable) t pada i
kendala ke-i dan ditambahkan kendala ti 0,i 1,2,...,m.
c. Jika kendala ke-i dari suatu program linear sudah berbentuk persamaan ( ) tetapi belum memuat variabel basis maka merubah ke bentuk kanonik dilakukan dengan menambahkan variabel semu misal qi 0,i 1,2,...,m.
12 Contoh 2.1 Memaksimumkan z(x1,x2,x3) 8x1 6x2 8x3
terhadap kendala: x 1 x2 2x3 12 (2.1) 4 6 2x 1 x2 x3 (2.2) x 1 2x2 x3 8 (2.3) x 1,x2,x3 0
Terhadap persoalan di atas, perlu diubah terlebih dahulu kendala-kendala yang ada menjadi bentuk kanonik dengan kendala bertanda sama dengan ( ) yang memuat variabel basis, yaitu
1. Kendala (2.1) ditambahkan variabel slack s 0, kendala menjadi 0 , 12 2 3 2 1 x x s s x (2.4)
sehingga pada kendala (2.14) variabel basis adalah s , dengan kata lain 3
2 1,x ,x
x menjadi variabel nonbasis yang nilainya adalah nol. Jadi kendala memberikan nilai s 12.
2. Kendala (2.2) ditambahkan variabel surplus pada ruas kanan yaitu t 0, kendala menjadi 0 , 4 6 2x 1 x2 x3 t t (2.5)
selanjutnya variabel t dipindah ke ruas kiri, menjadi 0
, 4 6
2x1 x2 x3 t t . (2.6)
Jika pada kendala (2.4) s dianggap variabel basisnya 0, sedangkan 3
2 1,x ,x
x menjadi variabel nonbasis yang nilainya adalah nol, maka pada kendala (2.6) nilainya menjadi t 4atau t 4.
13
Perlu diingat bahwa syarat awal persoalan program linear yaitu
m i
bi 0, 1,2,..., . Karena t 4 maka t tidak memenuhi syarat. Dengan kata lain t tidak bisa menjadi variabel basis, sehingga perlu ditambahkan suatu variabel yang dinamakan variabel semu (artificial variable). Misal variabel tersebut adalah q 1 dengan q1 0, sehingga pada (2.6) menjadi
0 , , 4 6 2x1 x2 x3 t q1 t q1 .
Jika x1 , x2,x3dan t adalah variabel nonbasis yang nilainya nol, maka q1 4. 3. Kendala (2.3) sudah berbentuk persamaan tetapi belum memuat variabel basis,
maka ditambahkan variabel semu misal q2 0. Sehingga kendala menjadi 0 , 8 2 2 3 2 2 1 x x q q x . Nilai q2 8.
Karena setiap kendala sudah berbentuk persamaan, maka rumusan program linear dalam bentuk kanonik adalah
Memaksimumkan z(x1,x2,x3,s,t,q1,q2) 8x1 6x2 8x3 0s 0t Mq1 M q2
terhadap kendala: . 0 , , , , , , 8 2 4 6 2 12 2 2 1 3 2 1 2 3 2 1 1 3 2 1 3 2 1 q q t s x x x q x x x q t x x x s x x x (2.7)
Koefisien fungsi sasaran pada (2.7) untuk variabel semu yaitu M. Koefisien fungsi sasaran untuk variabel semu bernilai negatif ( ) jika persoalan program linear adalah memaksimumkan dan bernilai positif ( ) jika persoalan program linear adalah meminimumkan. Dengan M
adalah bilangan positif yang besar.
14
B. Sistem Persamaan
Suatu persamaan dalam matematika merupakan sebuah ekspresi kesamaan (memuat tanda sama dengan " ") yang melibatkan konstanta, peubah atau variabel (variable) dan operasi-operasi hitung matematika. Di dalam persamaan, komponen-komponen yang dijumlahkan atau dikurangkan disebut suku. Ekspresi di sebelah kiri tanda " " disebut ruas kiri, sedangkan disebelah kanannya disebut ruas kanan.
Jika diberikan suatu persamaan yang berbentuk a1x1 a2y1 b, maka
persamaan ini dinamakan persamaan linear dalam variabel x dan y. Secara umum pesamaan linear dalam n variabel x1,x2,...,xn, dapat dinyatakan dalam
bentuk a1x1 a2x2 ... anxn b, dengan a1 ,a2,...,an dan b adalah konstanta real; x, y real. Contoh 2.3 berikut ini merupakan contoh persamaan linear. Contoh 2.2
(i) 2x 3y 7 (ii) x1 2x2 3x3 x4 6.
Solusi persamaan linear a1 x1 a2x2 ... anxn b adalah urutan dari n bilangan s1 ,s2,...,sn sehingga persamaan tersebut dipenuhi bila bilangan-bilangan
n
s s
s1, 2,..., disubstitusikan terhadap x1 s1,x2 s2,...,xn sn. Himpunan semua solusi persamaan dinamakan himpunan solusi.
Pada Contoh 2.2.(i), untuk mendapatkan solusinya maka ditetapkan sebarang nilai
x dan mencari solusi persamaan untuk y, atau sebaliknya memilih sebarang nilai y
15 maka diperoleh t y t x 3 2 3 7 , .
Sebuah himpunan berhingga dari persamaan-persamaan linear dalam vaiabel x1 , x2,...,xn disebut sistem persamaan linear (SPL) atau sistem linear. Sebuah urutan bilangan-bilangan s1 ,s2,...,sn disebut solusi dari SPL, jika untuk setiap s1 ,s2,...,sn memenuhi x1, x2,...,xn. Misal diberikan SPL, . 4 9 3 , 1 3 4 3 2 1 3 2 1 x x x x x x
SPL di atas mempunyai banyak solusi karena terdiri atas dua persamaan dengan tiga variabel. Salah satu solusi solusinya adalah x 1 1,x2 2,x3 1 karena nilai-nilai ini memenuhi kedua persamaan tersebut.
Tidak semua SPL mempunyai solusi, misal diberikan SPL,
6 2 2 4 y x y x
jika persamaan kedua dari SPL dikalikan dengan 2 1 maka SPL menjadi . 3 , 4 y x y x
Jelas bahwa SPL tidak mempunyai solusi, karena untuk (x,y) yang memenuhi persamaan pertama, nilai 2x 2y 2(x y) 2 4 8 6, yang tidak pernah memenuhi persamaan kedua.
Suatu sistem persamaan yang tidak mempunyai solusi disebut takkonsisten (inconsistent). Jika setidak-tidaknya terdapat satu solusi, maka sistem persamaan
16
disebut konsisten (consistent). Untuk melukiskan kemungkinan-kemungkinan yang dapat terjadi dalam mencari solusi sistem-sistem persamaan linear, berikut ini diberikan sistem umum dari dua persamaan linear dalam variabel x dan y:
) 0 , ( ) 0 , ( 2 2 2 2 2 1 1 1 1 1 b a c y b x a b a c y b x a
Grafik dari persamaan-persamaan di atas merupakan garis; misal kedua garis ini dinamakan l1dan l2. Titik (x ,y) terletak pada garis l 1 atau l 2 jika dan hanya jika
y
x dan memenuhi persamaan garis l1atau l2, maka solusi sistem persamaan akan bersesuaian dengan titik perpotongan dari garis l1atau l2.
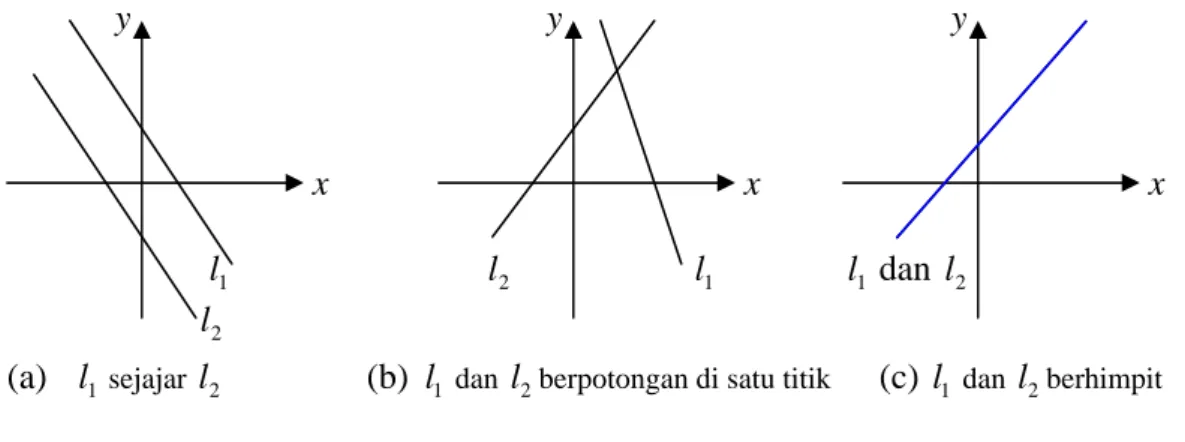
Terdapat tiga kemungkinan solusi system pesamaan yang diperoleh seperti diperlihatkan pada Gambar 2.1 berikut:
y y y x x x 1 l l 2 l 1 l 1 dan l 2 2 l
(a) l 1sejajar l 2 (b) l 1 dan l2berpotongan di satu titik (c) l 1 dan l2berhimpit Gambar 2.1 Tiga kemungkinan solusi SPL
Pada Gambar 2.1 (a) garis l 1 sejajar dengan garis l2, maka sistem persamaan tidak mempunyai solusi. Gambar 2.1 (b) garis l 1 berpotongan dengan garis l2, maka sistem persamaan tepa t mempunyai satu solusi. Gambar 2.1 (c) garis l 1 berhimpit dengan garis l2, maka sistem persamaan mempunyai takhingga solusi.
17
Sistem persamaan yang ditinjau di atas hanya dua persamaan dengan dua variabel, akan tetapi hasil yang sama akan berlaku untuk sebarang sistem; yaitu sistem persamaan tidak mempunyai solusi, tepat satu solusi dan tak hingga solusi. Suatu sistem terdiri dari m persamaan linear dan n variabel membentuk SPL sebagai berikut: m n nn m m n n n n b x a x a x a b x a x a x a b x a x a x a ... ... ... ... 2 2 1 1 2 2 2 22 1 21 1 1 2 12 1 11 (2.8)
Kuantitas-kuantitas a ij (untuk i 1,2,...,m; j 1,2,...,n) disebut koefisien. Nilai
koefisien-koefisien a ij dan ruas kanan b pada setiap persamaan diketahui. i
Kuantitas-kuantitas x disebut variabel, yang nilainya belum diketahui. i
C. Matriks
Sistem persamaan dapat ditulis dalam bentuk matriks. Matriks adalah jajaran bilangan berbantuk empat persegi panjang. Bilangan-bilangan dalam susunan tersebut dinamakan elemen matriks (Wono Setya Budhi, 1995: 16). Ukuran (order) dari sebuah matriks dikatakan sebesar m n jika matriks tersebut memiliki m baris dan n kolom. Matriks biasanya dinyatakan dengan huruf besar
, , B
A . Entri-entri dalam matriks dinyatakan dengan huruf kecil yang berkaitan dan diberi dua indeks. Jadi matriks m n yang umum dapat dituliskan sebagai
n m ij b mn m m n n a b b a b b b b b atau 2 1 2 22 21 1 12 11 B .
18
Misalkan n bilangan asli. Kumpulan terurut yang terdiri dari n bilangan ditulis sebagai (x1,x2,...,xn). Himpunan dari semua kumpulan terurut
) ..., , ,
(x 1 x2 xn disebut ruang Rn (Wono Setya Budhi, 1995: 164). Elemen dari
n
R disebut titik atau vektor. Vektor biasanya ditulis dengan huruf kecil dan notasi tebal atau diberi garis di atasnya. Komponen ke-i dari x (x1,x2,...,xn) disebut koordinat ke-i dari vektor atau titik x.
Sistem persamaan (2.8) jika ditulis dalam bentuk matriks: Ax b, dengan A adalah matriks m n:
mn m m n n a a a a a a a a a 2 1 2 22 21 1 12 11 A ,
x dan b adalah vektor dengan n-komponen:
n n b b b x x x 2 1 2 1 dan b x .
Matriks A disebut matriks koefisien, vektor kolom b disebut vektor konstanta. Gabungan Matriks A dan vektor kolom b disebut matriks diperbesar (augmented matriks), sebagai berikut:
m mn m m n n b a a a b a a a b a a a 2 1 2 2 22 21 1 1 12 11 b A .
19
Metode dasar untuk mencari solusi sistem persamaan adalah mengganti sistem yang diberikan dengan sistem baru yang mempunyai himpunan solusi yang sama dengan solusi yang lebih mudah. Sistem baru ini umumnya diperoleh dalam beberapa tahapan dengan menerapkan operasi pada matriks diperbesar yang dinamakan operasi baris elementer (OBE), yaitu:
1) Menukar dua baris, R ij (baris ke-i ditukar dengan baris ke-j) dari suatu
SPL.
2) Mengalikan sebuah baris dengan konstanta tidak nol k, kR (baris ke-i i
dikali dengan konstanta tidak nol k).
3) Menambah suatu baris dengan kelipatan baris yang lain, Ri kRj (baris ke-i ditambah k kali baris ke-j).
1. Jenis-jenis matriks
1) Matriks kuadrat atau matriks persegi adalah sebuah matriks yang berorder
n
m atau matriks yang berorder n n.
2) Matriks identitas adalah sebuah matriks kuadrat yang semua elemen diagonal bernilai satu dan semua elemen di luar diagonal bernilai nol; yaitu aij 1, untuk i j dan aij 0, untuk i j.
3) Vektor baris adalah sebuah matriks dengan satu baris dan n kolom. 4) Vektor kolom adalah sebuah matriks dengan m baris dan satu kolom. 5) Matriks AT disebut transpose dari A jika elemen a ij dalam A adalah sama
dengan elemen a ji dari
T
A untuk semua i dan j. Misal,
20 6 3 5 2 4 1 A maka
6
5
4
3
2
1
TA
.Secara umum, AT diperoleh dengan menukar baris dan kolom dari A. Akibatnya, jika A memiliki order m n, AT memiliki order n m.
6) Matriks B 0 disebut matriks nol jika setiap elemen dari B sama dengan nol.
7) Matriks diagonal adalah matriks kuadrat yang elemen-elemennya bernilai nol kecuali elemen-elemen pada diagonal utama.
8) Matriks eselon
Suatu matriks disebut matriks eselon jika memenuhi dua sifat sebagai berikut:
a. Setiap baris yang hanya terdiri dari elemen nol terletak di bawah. b. Elemen pivot pada suatu baris terletak di sebelah kanan dari elemen
pivot sebelumnya. 9) Matriks eselon tereduksi
Matriks eselon tereduksi adalah matriks eselon yang mempunyai sifat: a. Setiap elemen pivotnya bernilai satu.
b. Setiap elemen pivot merupakan satu-satunya elemen tidak nol pada kolom tersebut.
10)Dua buah matriks A
a
ij
dan Bb
ij
, dikatakan matriks yang sama jika dan hanya jika keduanya memiliki order yang sama dan setiap elemenij
21
2. Matriks elementer
Sebuah matriks n n dinamakan matriks elementer jika matriks tersebut dapat diperoleh dari matriks satuan (identitas) n n yakni I dengan melakukan n sebuah operasi baris elementer tunggal (Anton. H, 1987: 40).
Contoh 2.3 Diberikan matriks I : 3 1 0 0 0 1 0 0 0 1 3 I .
Misalkan dilakukan OBE dengan menambahkan lima kali baris ketiga dari I 3 pada baris pertama, maka diperoleh matriks elementer E:
1 0 0 0 1 0 5 0 1 E .
Misal diberikan matriks A:
0 4 4 1 6 3 1 2 3 2 0 1 A .
Pada matriks A dilakukan OBE yang sama dengan I (Contoh 2.3), diperoleh 3
0 4 4 1 6 3 1 2 3 22 20 6 ' A .
22
Hal ini sesuai dengan teorema berikut ini yang dinyatakan tanpa bukti (Anton. H, 1987: 41).
Teorema 2.1
Jika matriks elementer E dihasilkan dengan melakukan sebuah OBE pada I dan m jika A adalah matriks m n, maka hasil kali EA adalah matriks yang dihasilkan bila operasi baris yang sama dilakukan pada A.
Jika suatu SPL semua suku konstanta sama dengan nol, maka SPL tersebut dinamakan SPL homogen. Tiap-tiap SPL homogen adalah sistem yang konsisten, karena x 1 0,x2 0,...,xn 0 selalu merupakan solusi. Solusi tersebut dinamakan solusi trivial (trivial solution). Jika terdapat solusi lain, maka solusi tersebut dinamakan solusi tak trivial (nontrivial solution).
Metode yang sering digunakan untuk mencari solusi dari suatu SPL yaitu metode eliminasi Gauss dan metode eliminasi Gauss-Jordan. Kedua metode ini langkah-langkah pengerjaannya menggunakan serangkaian OBE.
3. Eliminasi Gauss
Metode eliminasi Gauss digunakan untuk menyelesaikan suatu SPL dengan mengubah SPL tersebut ke dalam matriks yang berbentuk matriks eselon. Matriks eselon dapat diselesaikan dengan substitusi mundur (back substitution). Sebarang matriks dapat diubah menjadi matriks eselon dengan melakukan serangkaian OBE. Penggunaan OBE pada suatu SPL tidak akan mengubah solusi SPL. Algoritma untuk mengubah sebarang matriks menjadi matriks eselon dengan
23
menggunakan OBE disebut eliminasi Gauss. Algoritma adalah urutan langkah-langkah logis penyelesaian masalah yang disusun secara sistematis.
Algoritma untuk eliminasi Gauss adalah:
1. Cari kolom paling kiri yang memuat unsur tidak nol.
2. Jika elemen pertama yang diperoleh dari langkah-langkah pertama sama dengan nol, tukar baris pertama dari matriks dengan baris yang unsur pada kolom tersebut tidak nol.
3. Setelah elemen pertama dari kolom yang diperoleh pada kolom pertama tidak sama dengan nol, dengan OBE dapat dibuat elemen di bawahnya sama dengan nol.
4. Kembali ke proses 1 sampai dengan 3. Contoh 2.4 Diberikan SPL 3 11 5 3 3 5 5 2 1 3 2 3 2 1 3 2 1 3 2 1 x x x x x x x x x (2.9)
Akan dicari solusi SPL (2.9) menggunakan eliminasi Gauss. Penyelesaian
SPL (2.9) ditulis dalam bentuk matriks diperbesar menjadi:
2 11 5 3 3 5 5 2 1 3 2 1 (2.10)
Pada (2.10) diubah menjadi matriks eselon dengan menggunakan eliminasi Gauss: 1) Kolom paling kiri sudah memuat unsur tidak nol.
24
2) Membuat nol elemen a dan 21 a dengan cara menambahkan baris ke-2 31 dengan ( 2) kali baris pertama dan baris ke-3 dengan ( 3) kali baris pertama, menghasilkan 1 2 1 0 5 1 1 0 1 3 2 1 (2.11)
3) Membuat nol elemen a pada (2.11) dengan cara menambahkan baris ke-32
3 dengan baris ke-2, menghasilkan
6 1 0 0 5 1 1 0 1 3 2 1 (2.12)
(2.12) merupakan matriks eselon dan dengan substitusi mundur diperoleh solusi SPL (2.9) yaitu x1 31,x2 11dan x3 6.
4. Eliminasi Gauss-Jordan
Metode eliminasi Gauss-Jordan pada dasarnya hampir sama dengan metode eliminasi Gauss. Pada eliminasi Gauss, dibentuk elemen-elemen matriks A dibawah diagonal utama menjadi nol (matriks eselon). Pada metode eliminasi Gauss-Jordan dibentuk menjadi nol elemen-elemen di bawah maupun di atas diagonal utama matriks A. Hasilnya adalah matriks eselon tereduksi yang berupa matriks diagonal yaitu matriks kuadrat yang elemen-elemennya bernilai nol kecuali elemen-elemen pada diagonal utama. Proses menjadikan suatu matriks A menjadi matriks eselon terduksi disebut eliminasi Gauss-Jordan.
Algoritma eliminasi Gauss-Jordan: 1. Ubah matriks menjadi matriks eselon.
25
2. Bagi baris yang mempunyai elemen pivot dengan besarnya elemen pivot (untuk memenuhi sifat matriks eselon tereduksi a ).
3. Dengan OBE, elemen di atas elemen pivot dibuat menjadi nol.
Dari Contoh 2.9, solusi SPL dicari dengan menggunakan metode eliminasi Gauss-Jordan. Langkah-langkahnya yaitu setelah langkah ke-3, langkah berikutnya adalah:
1) Membuat nol elemen a pada (2.12) dengan cara menambahkan baris ke-23
2 dengan baris ke-3, menghasilkan
6 1 0 0 11 0 1 0 1 3 2 1 (2.13)
2) Membuat nol elemen a pada (2.13) dengan cara menambahkan baris ke-13 1 dengan ( 3) kali baris ke-3, menghasilkan
6 1 0 0 11 0 1 0 19 0 2 1 (2.14)
3) Membuat nol elemen a 12 pada (2.14) dengan cara menambahkan baris ke-1 dengan ( 2) kali baris ke-2, menghasilkan
6 1 0 0 11 0 1 0 31 0 0 1
Pada langkah ke-3 diperoleh matriks eselon tereduksi, sehingga solusi dari SPL (2.9) dapat dibaca pada kolom terakhir, yaitu x (31, 11, 6)T.
26
Contoh 2.9 merupakan contoh mencari solusi suatu SPL menggunakan metode eliminasi Gauss dan eliminasi Gauss-Jordan. Jika kedua metode ini dibandingkan maka menggunakan eliminsai Gauss-Jordan akan lebih efektif, karena dapat langsung dilihat hasilnya dengan membaca kolom terakhir tanpa harus melakukan substitusi.
5. Operasi matriks
Operasi matriks berupa penambahan, pengurangan dan perkalian yang didefinisikan. Pembagian, walaupun tidak didefinisikan digantikan dengan konsep inversi.
1) Penambahan atau pengurangan matriks.
Dua matriks A
a
ij
dan Bb
ij
dapat ditambahkan atau dikurangkan jika keduanya memiliki order yang sama, misalnyam n. Jumlah D A B diperoleh dengan menambahkan elemen-elemen yang bersesuaian. Jadin
m
ij
b
ij
a
n
m
ij
d
. 2) Perkalian matriks Dua matriksij
a
A danij
b
B dapat dikalikan dalam urutan AB jika dan hanya jika jumlah kolom A adalah sama dengan jumlah baris B, yaitu, jika A memiliki order m r, maka B harus memiliki order r n, dengan m dan n order sebarang.
Misal D AB. Maka D memiliki urutan m n, dan elemen d ij diketahui: kj r k ik ij a b d 1
27 Contoh 2.5 maka , 0 8 6 9 7 5 dan 4 2 3 1 B A ) 0 4 ( ) 9 2 ( ) 8 4 ( ) 7 2 ( ) 6 4 ( ) 5 2 ( ) 0 3 ( ) 9 1 ( ) 8 3 ( ) 7 1 ( ) 6 3 ( ) 5 1 ( 0 8 6 9 7 5 4 2 3 1 D 18 46 34 9 31 23 .
Jika diperhatikan, secara umum AB BA sekalipun BA didefinisikan. 6. Invers matriks
Invers suatu matriks persegi A dilambangkan dengan A 1 adalah matriks yang memenuhi A 1A AA 1 I.
Invers ini ada jika A tidak singular. Jika diketahui matriks A n n
nn n n n n a a a a a a a a a 2 1 2 22 21 1 12 11 A , maka ) adj( ) det( 1 1 A A A
T C A)
adj( dan C adalah matriks kofaktor A, dengan
nn n n n n C C C C C C C C C 2 1 2 22 21 1 12 11 C
28
7. Hasil perkalian matriks
Sebagian besar perhitungan pada metode simpleks direvisi adalah mengenai penggantian B 1 dari satu tabel ke tabel berikutnya. Hasil dari invers ini akan digunakan untuk mempermudah perhitungan B 1 yang baru. Diasumsikan bahwa x akan masuk menjadi basis, uji rasio menunjukkan bahwa k x menjadi k
basis pada baris ke-r, dengan xk a1k a2k ark amk T.
Didefinisikan matriks E m m sebagai berikut:
1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ) 1 ( 2 1 rk mk rk k m rk rk k rk k a a a a a a a a a E
E adalah matriks identitas (Im m) dengan kolom ke-r nya diganti dengan vektor
kolom T rk mk rk k m rk rk k rk k a a a a a a a a a1 2 1 ( 1) .
Selanjutnya didefinisikan E sebagai matriks elementer E yang berkaitan dengan i iterasi simpleks ke-i. Hasil kali invers (invers product) secara umum dapat ditulis:Bk 1 Ek 1Ek 2 E1E0(Winston 2004).
29
D. Persoalan Knapsack
Persoalan knapsack didefinisikan sebagai persoalan yang menyangkut pemilihan objek dengan bobot dan keuntungan tertentu sedemikian sehingga tidak melebihi kapasitas yang telah ditentukan dan keuntungan yang ditargetkan dapat tercapai (Douglas R. Stinson, 1995: 191).
Persoalan knapsack atau persoalan ransel adalah persoalan program linear bilangan bulat yang hanya memiliki kendala tunggal (Tjutju Tarliah dan Ahmad Dimyati, 1992: 228). Nilai variabel-variabel kendala pada persoalan knapsack dapat berupa sebarang nilai. Akan tetapi ada juga persoalan knapsack yang seluruh variabelnya harus bernilai 0 atau 1, yang dapat diformulasikan:
Memaksimumkan z(xj) c1 x1 c2x2 ... cnxn terhadap kendala:
,
...,
,
2
,
1
;
)
...,
,
2
,
1
(
1
atau
0
...
2 2 1 1m
i
n
j
x
b
x
a
x
a
x
a
j n mn(2.15)
dengan c j adalah manfaat yang dapat diperoleh apabila barang ke-j dipilih, b
adalah jumlah sumber yang tersedia dan a adalah jumlah sumber yang digunakan i
oleh barang ke-i.
Meskipun secara teoritis persoalan knapsack sulit diselesaikan, namun metode pencabangan dan pembatasan (branch and bound method) cukup efisisen dan praktis untuk menyelesaikannya (Taha 1996; Winston 2004). Pada persoalan (2.15) jika diselesaikan dengan branch and bound, maka ada dua aspek pendekatan dari branch and bound yang disederhanakan. Pertama, karena setiap variabel harus berharga 0 atau 1, maka pencabangan pada x j akan menghasilkan
30
cabang xj 0 dan xj 1. Kedua, solusi persoalan program linear relaksasi; yaitu bentuk program linear yang diperoleh dengan mengabaikan kendala (pembatas) bilangan bulat (integer) serta subpersoalan yang lain dapat diselesaikan dengan melakukan pengecekan terhadap nilai
i j
a c
. Untuk melihat hal ini maka nilai
i j
a c
dapat diinterpretasikan sebagai manfaat yang diperoleh barang ke- j dari setiap unit sumber yang digunakan barang ke-i. Jadi, barang yang terbaik adalah barang yang memiliki nilai
i j
a c
terbesar dan barang yang terburuk adalah barang yang
memiliki nilai i j a c tekecil.
Untuk menyelesaikan setiap subpersoalan yang dihasilkan dari suatu persoalan ransel, dihitung seluruh rasio nilai
i j
a c
. Kemudian barang yang terbaik dimasukkan ke dalam ransel. Selanjutnya barang kedua terbaik dan seterusnya, hingga ransel terisi dengan sebanyak-banyaknya dari barang-barang ini.
E. Metode Simpleks
Metode simpleks merupakan prosedur umum untuk menyelesaikan persoalan-persoalan program linear. Prosedur ini dikembangkan oleh George Dantziq pada tahun 1947. Metode simpleks juga merupakan salah satu metode yang efisien yang digunakan untuk menyelesaikan persoalan program linear skala besar dengan komputer masa kini.
31
Metode simpleks merupakan suatu algoritma, karena dalam menyelesaikan persoalan dengan metode simpleks, prosesnya dilakukan secara iteratif. Setiap prosedur iteratif merupakan suatu algoritma. Suatu algoritma ialah suatu prosedur sistematis diulang-ulang (iterasi) sampai hasil yang diinginkan tercapai.
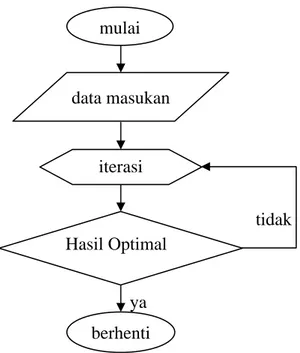
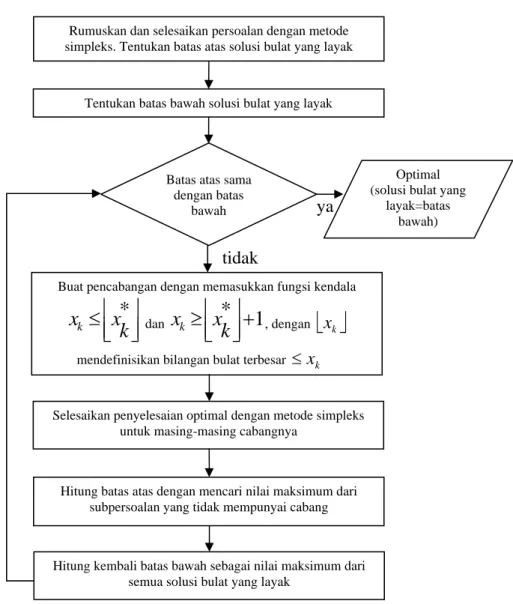
Selain iterasi, algoritma juga mencakup suatu prosedur untuk memulai dan suatu kriteria untuk menentukan kapan berhenti. Bagi kebanyakan algoritma riset operasi, termasuk metode simpleks, hasil yang diinginkan yang tercantum dalam aturan berhenti yaitu penyelesaian pada iterasi tertentu adalah optimal. Dalam hal ini, aturan berhenti sebenarnya merupakan suatu uji optimalitas, dijelaskan dalam diagram alir berikut.
tidak
ya
Gambar 2.2 Diagram alir metode simpleks
Metode simpleks juga merupakan struktur aljabar yang bersifat iteratif, dimulai dari suatu titik ekstrem pada daerah layak atau fisibel (feasible) menuju ke titik ekstrem yang optimum, sehingga diperoleh solusi layak titik ekstrem.
mulai
data masukan
berhenti iterasi
32
Solusi titik ekstrem atau titik sudut pada persoalan dua atau tiga variabel adalah solusi layak yang tidak terletak pada suatu segmen garis yang menghubungkan dua solusi layak lainnya. Untuk mendapatkan solusi layak titik ekstrem ini, kendala-kendala dibuat dalam bentuk grafik. Pasangan (x ,y) yang memenuhi semua kendala disebut solusi layak. Titik wakilnya dalam bidang koordinat disebut titik layak. Himpunan titik-titik layak disebut daerah layak.
Langkah-langkah penyelesaian persoalan program linear dengan metode simpleks adalah sebagai berikut:
1. Menambahkan variabel slack, surplus dan artifisial ke dalam kendala-kendala sehingga kendala-kendala berubah menjadi bentuk kanonik dan mempunyai variabel basis .
2. Persamaan pada ruas kanan fungsi sasaran dipindah ke ruas kiri sehingga fungsi sasaran mempunyai nilai awal nol dan algoritma simpleks berawal dari titik nol.
3. Menyusun tabel awal simpleks, lengkap dengan variabel basisnya.
4. Melakukan uji optimal pada tabel awal tersebut, dengan langkah-langkah sebagai berikut:
a. Untuk persoalan memaksimumkan dicari variabel basis baru, dengan memilih kolom pivot, yaitu kolom dengan zj cj negatif terbesar. Untuk persoalan meminimumkan dicari variabel basis baru dengan memilih kolom pivot, yaitu kolom dengan nilai zj cj positif terbesar.
33
b. Dicari nilai R , yaitu i b dibagi unsur-unsur pada kolom pivot yang bernilai i
positif ( , ikpositif ik i i a a b
R ). Selanjutnya dipilih R terkecil. i
c. Baris dengan R terkecil menjadi baris pivot dengan menunjukkan i
variabel basis lama yang akan diganti. Perpotongan antara baris pivot dan kolom pivot disebut sebagai elemen pivot.
d. Disusun tabel selanjutnya dengan variabel basis baru dan koefisien ongkos menyesuaikan dengan variabel basis baru tersebut.
e. Dilakukan Operasi Baris Elementer (OBE) dengan tujuan elemen pivot bernilai 1.
5. Tabel berikutnya sudah siap, dilakukan uji optimal pada tabel tersebut dengan langkah-langkah (a) sampai (e).
Tabel dikatakan optimal jika zj cj nonnegatif untuk setiap j .
34
Tabel 2.1 Metode Simpleks
j c c 1 c 2 c 3 c n i c x \i xj x 1 x 2 x 3 x n b i R i 1 c x 1 a 11 a 12 a 13 a1 n b 1 R 1 2 c x 2 a 21 a 22 a 23 a2 n b 2 R 2 3 c x 3 a 31 a 32 a 33 a3 n b 3 R 3
m c x m a m1 a m2 a m3 a mn b m R m j z z 1 z 2 z 3 z n Z
j j c z z1 c1 z2 c2 z3 c3
n n c z Z
keterangan: j
c : koefisien biaya untuk variabel x j
i
c : koefisien biaya untuk variabel xi, i
x : variabel yang menjadi basis dalam tabel yang ditinjau,
j
x : variabel-variabel lengkap,
i
b : suku tetap (tak negatif),
i R : rasio, ij a : koefisien teknis, j z : ij m i ia c 1
(hasil kali dari c i dengan aij),
Z : i m i ib c 1
(hasil kali dari c i dengan b ), i j
j c
35 Contoh 2.6 Memaksimumkan z(x1, x2, x3) 60x1 30x2 20x3 terhadap kendala: 0 , , 5 8 2 1 2 3 3 20 2 3 2 4 48 6 8 3 2 1 2 3 2 1 3 2 1 3 2 1 x x x x x x x x x x x x x (2.16) Penyelesaian
1) Tambahkan variabel slack si , i 1,2,3,4 pada kendala (2.16), menjadi Memaksimumkan z(x1,x2,x3,si) 5x1 4x2 6x3 0s1 0s2 0s3 0s4 terhadap kendala: 0 , , , , , , 5 0 0 0 8 0 0 0 2 1 2 3 3 20 0 0 0 2 3 2 4 48 0 0 0 6 8 4 3 2 1 3 2 1 4 3 2 1 2 4 3 2 1 3 2 1 4 3 2 1 3 2 1 4 3 2 1 3 2 1 s s s s x x x s s s s x s s s s x x x s s s s x x x s s s s x x x
36
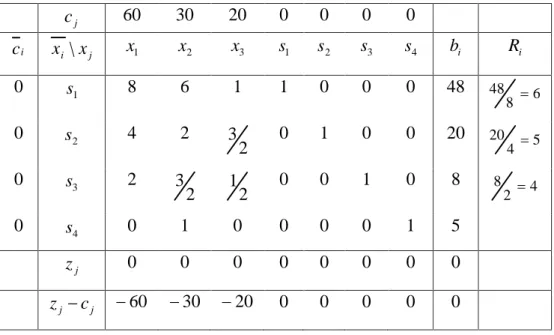
Tabel 2.2 Tabel Awal Simpleks
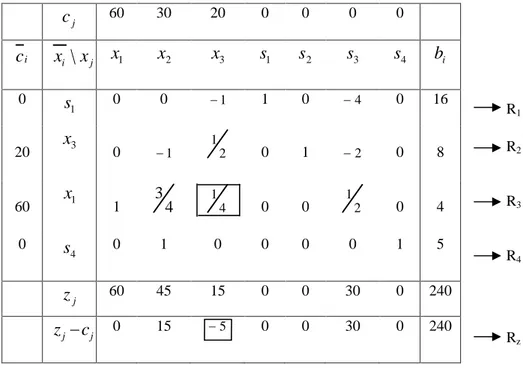
j c 60 30 20 0 0 0 0 i c x \ i xj x 1 x 2 x 3 s 1 s 2 s 3 s 4 b i R i 0 s 1 8 6 1 1 0 0 0 48 6 8 48 0 s 2 4 2 2 3 0 1 0 0 20 5 4 20 0 s 3 2 2 3 2 1 0 0 1 0 8 4 2 8 0 s 4 0 1 0 0 0 0 1 5 j z 0 0 0 0 0 0 0 0 j j c z 60 30 20 0 0 0 0 0
Langkah-langkah uji optimum tabel (Tabel 2.2):
(a) Memilih kolom zj cj terbesar (negatif) adalah 60 , jadi x 1 merupakan variabel masuk,
(b) Memilih rasio terkecil: 4 2 8 31 3 a b
, jadi s variabel keluar, 3
(c) Membagi baris ke-3 dengan a , 31 (d) Membuat Tabel Antara, yaitu:
37
Tabel 2.3 Tabel Simpleks Antara
j c 60 30 20 0 0 0 0 i c j x i x \ x 1 x 2 x 3 s 1 s 2 s 3 s 4 b i 0 1 s 8 6 1 1 0 0 0 48 R1 0 4 2 2 3 0 1 0 0 20 R2 0 3 s 1 4 3 4 1 0 0 2 1 0 4 R3 0 4 s 0 1 0 0 0 0 1 5 R4
j z 0 0 0 0 0 0 0 0 j j c z 60 30 20 0 0 0 0 0 Rz
(e) Melakukan Operasi Baris Elemeter (OBE), dengan menolkan elemen yang diberi tanda persegi panjang. (Diperoleh Tabel 2.4)
R1= R1 – 8R3
R2= R2 – 4R3
Rz= Rz + 60R3
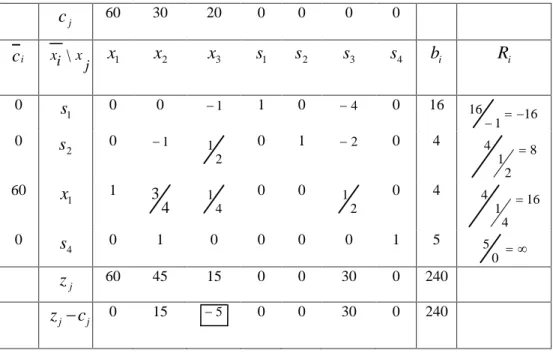
Tabel 2.4 Tabel Kedua Simpleks
j c 60 30 20 0 0 0 0 i c j x i x \ x 1 x 2 x 3 s 1 s 2 s 3 s 4 b i R i 0 1 s 0 0 1 1 0 4 0 16 16 1 16 0 2 s 0 1 2 1 0 1 2 0 4 8 2 1 4 60 1 x 1 4 3 4 1 0 0 2 1 0 4 16 4 1 4 0 4 s 0 1 0 0 0 0 1 5 0 5 j z 60 45 15 0 0 30 0 240 j j c z 0 15 5 0 0 30 0 240
38
3) Pada langkah ini sama dengan langkah 2 (a sampai e), dengan memperhatikan Tabel 2.4,
(a) zj cj terbesar (negatif) adalah 5 , jadi x merupakan variabel masuk, 3
(b) Memilih rasio terkecil: 8 4 1 4 32 2 a b
, jadi s2variabel keluar,
(c) Membagi baris ke-2 dengan a , 23 (d) Membuat Tabel Antara, yaitu:
Tabel 2.5 Tabel Simpleks Antara
j c 60 30 20 0 0 0 0 i c x \ i xj x 1 x 2 x 3 s 1 s 2 s 3 s 4 b i 0 1 s 0 0 1 1 0 4 0 16 R1'
20 x 3 0 1 2 1 0 1 2
0 8 R2
'
60 x 1 1 3 4 4 1 0 0 2 1 0 4 R3
'
0 4 s 0 1 0 0 0 0 1 5 R4'
j z 60 45 15 0 0 30 0 240 j j c z 0 15 5 0 0 30 0 240 Rz
'
(e) Melakukan Operasi Baris Elemeter (OBE), dengan menolkan elemen yang diberi tanda persegi panjang. (Diperoleh Tabel 2.6)
2 z z 2 3 3 2 1 1 R 5 R R R 3 1 R R R R R
'
'
'
39
Tabel 2.6 Tabel Ketiga Simpleks
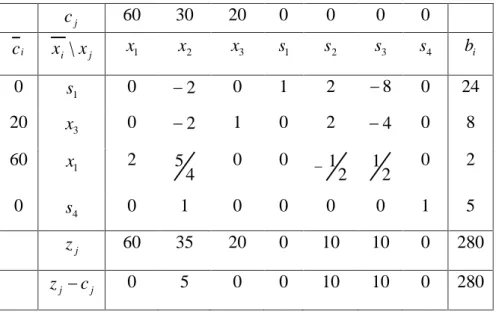
j c 60 30 20 0 0 0 0 i c x \ i xj x 1 x 2 x 3 s 1 s 2 s 3 s 4 b i 0 s 1 0 2 0 1 2 8 0 24 20 x 3 0 2 1 0 2 4 0 8 60 x 1 2 4 5 0 0 2 1 2 1 0 2 0 s 4 0 1 0 0 0 0 1 5 j z 60 35 20 0 10 10 0 280
j j c z 0 5 0 0 10 10 0 280
Karena z j cj 0 untuk setiap j, maka tabel sudah optimal dengan nilai fungsi sasaran z 280, solusi layak basisnya
) 5 , 0 , 0 , 24 , 8 , 0 , 2 ( ) , , , , , , (x1 x2 x3 s1 s2 s3 s4 .
F. Metode Simpleks Direvisi
Metode simpleks direvisi merupakan kelanjutan dari metode simpleks. Dalam menyelesaikan persoalan program linear, metode simpleks bukan merupakan suatu prosedur perhitungan yang paling efisien jika diaplikasikan perhitungannya menggunakan komputer. Kode-kode pada komputer tidak secara tepat mengikuti bentuk aljabar atau bentuk tabel dari metode simpleks. Kode-kode ini memakai suatu bentuk matriks yang sesuai dengan komputer. Hal inilah yang mendorong berkembangnya metode simpleks direvisi.
Gagasan utama dari metode simpleks direvisi adalah menggunakan inversi basis B-1 (data awal dari persoalan) untuk melakukan perhitungan yang diperlukan
40
untuk menentukan variabel masuk dan variabel keluar. Metode simpleks direvisi secara eksplisit memakai manipulasi matriks, maka persoalan harus dinyatakan dalam notasi matriks. Dengan menggunakan matriks, bentuk baku model program linear menjadi:
Memaksimumkan z cx,
terhadap kendala: Ax( , , )b dan x 0
(2.17) dengan: n c c c1, 2,...,
c merupakan vektor baris,
0 0 0 , , 2 1 2 1 0 b x m n b b b x x x
merupakan vektor-vektor kolom,
A merupakan matriks m n: mn m m n n a a a a a a a a a 2 1 2 22 21 1 12 11 A .
Untuk memperoleh persoalan program linear bentuk kanonik dalam bentuk matriks maka pada (2.17) ditambahkan variabel slack:
n s s s 2 1 s ,
41 Memaksimumkan z(x,s) cVBxVB cNBs
terhadap kendala: 0 s x b s x I A, dan , dengan VB
c koefisien-koefisien fungsi tujuan yang berkaitan dengan x B VB
x variabel basis NB
c koefisien-koefisien fungsi tujuan yang berkaitan dengan s
s
variabel slack I
matriks identitas m n. 1. Solusi layak basis
Pendekatan umum dari metode simpleks dan metode simpleks direvisi adalah memperoleh suatu ururtan solusi-solusi layak basis yang semakin baik sampai tercapai suatu solusi optimal. Salah satu ciri pokok dari metode simpleks direvisi mencakup dengan cara mana setiap solusi layak basis akan diselesaikan, yaitu setelah variabel-variabel basis dan nonbasis diketahui.
Jika diketahui b
s x I
A , , memiliki m persamaan dan n variabel
yang tidak diketahui, dengan x (x1,x2,...,xn)T dan s (s1,s2,...,sn)T adalah variabel slack; suatu solusi layak basis diperoleh dengan menetapkan n m sama dengan nol. Jika n variabel ini dieliminasi dengan membuatnya sama dengan nol maka masih ada suatu himpunan m persamaan dengan m variabel yang tidak diketahui. Himpunan persamaan ini dapat dinyatakan BxVB b,
42 dengan m 2 1 VB VB VB VB x x x x
merupakan vektor kolom variabel basis, diperoleh dengan menghilangkan variabel-variabel nonbasis dari
s x , mm m m m m B B B B B B B B B 2 1 2 22 21 1 12 11 B
merupakan matriks basis yang diperoleh dengan mengeliminasi kolom-kolom yang berkaitan dengan kofisien- kofisien variabel basis dari A,I .
Metode simpleks memperkenalkan hanya variabel-variabel basis sedemikian sehingga B adalah nonsingular, sehingga B 1 akan selalu ada. Oleh karena itu, untuk menyelesaikan BxVB b, kedua ruas harus dikalikan terlebih dahulu dengan B , sehingga diperoleh 1
b B Bx
B 1 VB 1 .
Karena B 1B I, maka solusi yang diharapkan untuk variabel-variabel basis adalah
b B xVB 1 .
43
Misal c VB adalah vektor yang unsur-unsurnya merupakan koefisien-koefisien fungsi tujuan (termasuk nol untuk variabel-variabel slack) yang berkaitan dengan
VB
x , maka nilai fungsi tujuan untuk solusi basisnya adalah
b B c x cVB VB VB 1 z .
Dalam metode simpleks direvisi, iterasi simpleks hanya berbeda dalam definisi basis B menunjukkan keuntungan dalam perhitungan:
1) Dalam persoalan program linear skala besar, penggunaan operasi Gauss-Jordan umumnya mengarah pada kesalahan pembulatan yang tidak dapat dikendalikan sehingga memberikan pengaruh yang merugikan terhadap hasil akhir. Dalam metode simpleks direvisi digunakan B-1 dan data awal dari persoalan. Dengan demikian akurasi perhitungan dapat dikendalikan dengan mengendalikan kesalahan pembulatan dalam perhitungan B-1 saja.
2) Dengan menggunakan manipulasi matriks menunjukkan bahwa tidak perlu menghitung semua entri dari tabel simpleks, untuk ukuran persoalan program linear tertentu kemungkinan memerlukan lebih sedikit perhitungan. 2. Langkah-langkah metode simpleks direvisi
Langkah-langkah dari metode simpleks direvisi pada intinya sama dengan metode simpleks. Dengan diketahui basis awal I, ditentukan koefisien tujuan yang berkaitan dengancVB.
Adapun langkah-langkah metode simpleks direvisi adalah:
1. Menetapkan bahwa kolom B 1 yang bersangkutan akan selalu dibaca B 1 I pada awalnya.
44
2. Menghitung c VBB 1 untuk tabel bersangkutan.
3. Menghitung harga akhir (price out) semua variabel nonbasis dalam tabel bersangkutan. Jika harga akhir tiap-tiap variabel nonbasis nonnegatif maka basis bersangkutan adalah optimal. Jika basis bersangkutan tidak optimal maka dimasukkan ke dalam basis yaitu variabel nonbasis yang mempunyai nilai koefisien negatif terbesar dalam baris 0. Misal variabel nonbasis yang masuk menjadi variabel basis didefinisikan dengan xk,k 1,2,...,n.
4. Untuk menentukan dalam baris mana x menjadi basis masuk, hitung kolom k
k
x dari tabel bersangkutan (B 1xk) dan hitung sisi kanan dari tabel bersangkutan (B 1b). Kemudian digunakan test rasio untuk menentukan dimana baris x k seharusnya masuk menjadi basis, sehingga diperoleh himpunan variabel basis untuk tabel baru (menggunakan OBE).
5. Gunakan kolom x dalam tabel bersangkutan untuk menentukan aturan atau k
langkah ini pada B 1 yang bersangkutan untuk memperoleh B 1 baru. Kembali ke langkah 1. Contoh 2.7 Memaksimumkan z(x1,x2) 3x1 5x2 terhadap kendala: bulat. bilangan dan 0 , 18 2 3 6 4 2 1 2 1 2 1 x x x x x x (2.18)
45
Penyelesaian
1. Persoalan (2.18) diubah ke bentuk program linear kanonik dengan menambahkan variabel slack menjadi:
Memaksimumkan z(x1, x2,s1,s2,s3) 3x1 5x2 0s1 0s2 0s3
terhadap kendala: bulat bilangan dan 0 , , , , 18 2 3 6 4 3 2 1 2 1 3 2 1 2 2 1 1 s s s x x s x x s x s x
atau ditulis dalam bentuk tabel, yaitu:
18 2 3 3 Baris 6 2 Baris 4 1 Baris 5 3 0 Baris 0 Tabel 3 2 1 2 2 1 1 2 1 s x x s x s x x x z dengan VB(0) s1,s2,s3 dan VNB(0) x1, x2 . Kolom B 0 1 terbaca awalnya yaitu B0 1 I
1 0 0 0 1 0 0 0 1 0 1 0 B I B .
2. Menentukan variabel nonbasis yang akan masuk menjadi variabel basis dengan menghitung koefisien dari tiap-tiap variabel nonbasis dalam baris 0, diperoleh 0 0 0 VB c , sehingga 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 VBB c
46
3. Dari langkah (2) diperoleh nilai dari tiap-tiap variabel nonbasis adalah:
5 5 2 1 0 0 0 0 3 3 3 0 1 0 0 0 2 2 1 0 VB 2 1 1 1 0 VB 1 c a c c a c B c B c
(c1,c2 0, maka basis belum optimal), dicari variabel nonbasis x yang k
mempunyai koefisien negatif terbesar dari baris 0 dalam Tabel 0 yang menjadi variabel basis masuk . Karena x 2 mempunyai koefisien negatif terbesar dalam baris 0, maka x 2 variabel basis masuk menggantikan variabel basis keluar s2. 4. Kolom untuk x 2 dalam tabel bersangkutan:
2 1 0 2 1 0 1 0 0 0 1 0 0 0 1 2 1 0 2 a a B
Sisi kanan tabel bersangkutan
18 6 4 18 6 4 1 0 0 0 1 0 0 0 1 1 0 b B
Selanjutnya digunakan test rasio untuk menentukan x 2 masuk ke dalam baris yang mana, yaitu:
9 2 18 , 3 Baris terkecil) rasio test ( 6 1 6 , 2 Baris efinisi tidak terd 0 4 , 1 Baris 2 2 2 x x x
Jadi x 2 masuk sebagai basis dalam baris 2.
47
a) Pada baris ke-1 tetap, karena nilai di atas baris ke-2 kolom 2 dari kiri sudah bernilai nol. (baris 1') b) Baris ke-2 tetap. (baris2') c) Menambahkan baris ke-3 dengan ( 2) kali baris ke-2 (baris '3 ) d) Menambahkan baris ke-0 dengan ( 5 ) kali baris ke-2. (baris '0)
Diperoleh tabel baru, misal dinamakan Tabel 1
6 3 3' Baris 6 2' Baris 4 ' 1 Baris 30 5 3 0' Baris 1 Tabel 3 1 2 2 1 1 2 1 s x s x s x s x z dengan VB(1) s1,x2,s3 dan VNB(1) x1,s2 .
6. Melakukan OBE pada B 0 1 dengan langkah seperti pada langkah (5) (a sampai c), diperoleh: 1 2 0 0 1 0 0 0 1 1 1 B 7. 0 5 0 1 2 0 0 1 0 0 0 1 0 5 0 1 1 VBB c
8. Dari langkah (7) diperoleh nilai dari tiap-tiap variabel nonbasis x1, s2:
5 0 0 1 0 0 5 0 0 0 1 0 3 3 3 0 1 0 5 0 1 0 VB 2 1 1 1 1 VB 1 B c B c s c a c
48
Tabel belum optimal, karena masih terdapat c j yang negatif, yaitu c1 0; x 1 mempunyai koefisien negatif terbesar dalam baris 0 dari Tabel 1, sehingga x 1
masuk sebagai basis dalam Tabel 1. 9. Kolom untuk x 1 pada Tabel 1 yaitu:
3 0 1 3 0 1 1 2 0 0 1 0 0 0 1 1 1 1 a B
Sisi kanan pada Tabel 1
6 6 4 18 6 4 1 2 0 0 1 0 0 0 1 1 1 b B Test rasio: terkecil) rasio (test 2 3 6 , 3 Baris efinisi tidak terd 0 6 , 2 Baris 4 1 4 , 1 Baris 1 1 1 x x x
Dari test rasio terlihat bahwa x 1 masuk sebagai basis dalam baris 3. 10.Dari langkah (9) dibentuk Tabel 2 dengan OBE:
a) Menambahkan baris ke-1 Tabel 1 dengan ) 3 1
( kali baris ke-3. (baris1") b) Baris ke-2 tetap, karena x 1 pada baris 2 sudah nol. (baris 2") c) Mengalikan baris ke-3 dengan
3
1 . (baris "3 ) d) Menambahkan baris ke-0 dengan baris ke-3. (baris "0 )
49
2
3"
Baris
6
2"
Baris
2
"
1
Baris
36
5
0"
Baris
2
Tabel
3 1 2 2 1 3 2s
x
s
x
s
s
s
z
dengan VB(2) s1, x2, x1 dan VNB(2) s3,s2 .11.Melakukan OBE pada B 11 seperti pada langkah (10) (a sampai c), sehingga diperoleh: 3 3 2 0 0 1 0 3 3 2 1 1 1 1 2 B 12. 0 3 1 3 3 2 0 0 1 0 3 3 2 1 3 5 0 1 1 1 2 VBB c
13.Dari langkah (12) diperoleh nilai variabel nonbasis s 3, s2 adalah
3 0 0 1 0 1 3 0 0 0 1 0 1 0 1 0 0 1 3 0 0 1 0 0 1 0 VB 2 1 0 VB 3 B c B c s s
Tabel 2 sudah optimal karena setiap koefisien variabel nonbasis dalam baris "
0 sudah tidak ada yang negatif. 14.Sisi kanan dari Tabel 2:
50 2 6 2 18 6 4 3 3 2 0 0 1 0 3 3 2 1 1 1 1 2 b B
Sehingga VB(2) s1,x2,x1 dan solusi layak basisnya adalah
0 , 2 6 2 3 2 1 2 1 s s x x s
Jadi diperoleh tabel optimal untuk nilai z yaitu:
36 18 6 4 1 3 0 1 2 VBB b c .
Jadi nilai fungsi sasaran yaitu z 36, solusi layak basisnya ) 0 , 0 , 2 , 6 , 2 ( ) , , , , (x1 x2 s1 s2 s3 .
G. Program Linear Bilangan Bulat
Program linear bilangan bulat merupakan bentuk khusus dari program linear, dengan satu atau lebih dari variabel-variabel dalam penyelesaiannya disyaratkan memiliki nilai-nilai bilangan bulat. Dalam program linear kebanyakan variabel yang dilibatkan berupa variabel-variabel bilangan bulat, variabel tersebut hanya diperkenankan untuk memiliki nilai-nilai bilangan bulat yang terletak di antara batas yang tetap.
Program linear bilangan bulat adalah program linear dengan beberapa atau
semua variabelnya adalah anggota himpunan
,... 2 , 1 , 0 ), ,..., , ( ,x x1 x2 xj xj b Ax x