BAB 2
LANDASAN TEORI
2.1 Sistem Persamaan Linier dan Matriks
2.1.1 Sistem Persamaan Linier
Salah satu masalah yang selalu dihadapi dalam mempelajari atau memecahkan problem dalam bidang matematika adalah menyelesaikan sistem persamaan linier. Bentuk umum persamaan linier adalah:
a1 x1 + a2 x2 + a3 x3 + . . . + an xn = b (2.1)
dimana b merupakan faktor yang menghubungkan peubah-peubah x1, x2, x3, . . ., xn dan
a1, a2, a3, . . ., an
1. Salah satu koefisien a
merupakan koefisien peubah dari persamaan (2.1). Kejadian yang mungkin terjadi dari persamaan (2.1) adalah sebagai berikut:
i ≠ 0 (i = 1, 2, 3, . . ., n) misalnya ai ≠ 0, sehingga persamaan dapat ditulis dengan: x1 = a1-1b – a1-1 a2 x2 – a1-1 a3 x3 – a1-1 a4 x4 – . . . – a1-1 an
xn. Dengan memberikan harga-harga sembarang untuk x2, x3, x4, . . ., xn, maka harga xi dapat diketahui yang merupakan penyelesaian dari persamaan itu. Kejadian khusus dari persamaan ini adalah: ax = b, a ≠ 0 dengan penyelesaian: x = a-1
2. Semua koefisien a
b
(unique solution). i
3. Semua koefisien a
= 0 (i = 1, 2, 3, . . ., n) sedangkan koefisien b ≠ 0. Dengan demikian persamaan (2.1) menjadi: 0 = b, b ≠ 0. Dalam hal ini persamaan tidak mempunyai penyelesaian (no solution).
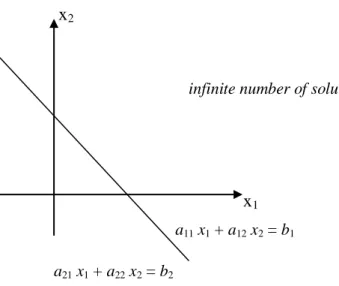
i = 0 (i = 1, 2, 3, . . ., n) dan b = 0. Dengan demikian persamaan mula-mula menjadi 0 = 0. Artinya n buah bilangan di dalam R merupakan penyelesaian dari sistem persamaan (infinite number of solution).
Contoh di bawah ini menunjukkan bahwa sistem persamaan linier dapat mempunyai unique solution, no solution, infinite number of solution. Pandang sistem persamaan linier dengan dua persamaan dengan dua peubah di bawah ini:
= + = + 2 2 22 1 21 1 2 12 1 11 b x a x a b x a x a (2.2) x2 x1
Gambar 2.1 Garis berpotongan pada sebuah titik persekutuan
x2
x
Gambar 2.2 Garis sejajar; tidak ada titik persekutuan 1 a21x1 + a22x2 = b2 a11x1 + a12x2 = b1 a21x1 + a22x2 = b2 a11x1 + a12x2 = b1 no solution unique solution
x2
x
Gambar 2.3 Garis berimpit; tidak dapat ditentukan banyaknya jumlah titik persekutuan
Sistem persamaan (2.2) diselesaikan dengan mengalikan persamaan pertama dengan a
1
22 dan persamaan kedua dengan a12
= + = + 2 12 2 22 12 1 21 12 1 22 2 22 12 1 22 11 b a x a a x a a b a x a a x a a , sehingga diperoleh: (2.3)
Bila persamaan pertama dikurang persamaan kedua, maka diperoleh:
− = − − = − 2 12 1 22 1 21 12 22 11 2 12 1 22 1 21 12 1 22 11 ) (a a a a x a b a b b a b a x a a x a a (2.4)
Jika a11a22 – a12a21≠ 0, maka harga x1
21 12 22 11 2 12 1 22 1 a a a a b a b a x − − =
dapat ditentukan yaitu:
(2.5)
Dengan diperolehnya nilai x1 dapat ditentukan nilai x2 dari persamaan (2.2) yang merupakan unique solution. Determinan persamaan (2.2) didefinisikan dengan:
a11a22 – a12 a21
1. Mempunyai unique solution jika dan hanya jika determinan ≠ 0.
(2.6)
Dari hasil ini dapat ditentukan solusi persamaan (2.2) sebagai berikut:
2. Tidak mempunyai penyelesaian atau mempunyai banyak penyelesaian jika dan hanya jika determinan = 0.
a21x1 + a22x2 = b2
a11x1 + a12x2 = b1
Suatu sistem persamaan linier (m x n) adalah kumpulan dari m buah sistem persamaan dengan n peubah yang disajikan secara serentak. Secara umum sistem persamaan linier tersebut berbentuk:
= + + + + = + + + + = + + + + = + + + + m n mn m m m n n n n n n b x a x a x a x a b x a x a x a x a b x a x a x a x a b x a x a x a x a 3 3 2 2 1 1 3 3 3 33 2 32 1 31 2 2 3 23 2 22 1 21 1 1 3 13 2 12 1 11 (2.7)
dimana: a11, a12, a13, . . ., aij, . . ., amn merupakan konstanta dari sistem persamaan, sedangkan x1, x2, x3, . . ., xn merupakan peubah dan b1, b2, b3, . . ., bm
= − − = + − = − + 16 3 5 5 2 2 3 5 3 2 3 2 1 3 2 1 3 2 1 x x x x x x x x x merupakan nilai masing-masing sistem persamaan dengan i = 1, 2, 3, . . ., m dan j = 1, 2, 3, . . ., n.
Contoh:
(2.7)
Jika semua konstanta bi = 0, (i = 1, 2, 3, . . ., m), maka sistem persamaan disebut sistem persamaan linier homogen. Andaikan xi = ki, (i = 1, 2, 3, . . ., n) memenuhi sistem persamaan (2.7), maka himpunan harga xi = ki, ditulis dengan x = (x1, x2, x3, . . ., xn = + + + + = + + + + = + + + + = + + + + 0 0 0 0 3 3 2 2 1 1 3 3 33 2 32 1 31 2 3 23 2 22 1 21 1 3 13 2 12 1 11 n mn m m m n n n n n n x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a
) disebut penyelesaian partikulir dari sistem persamaan itu. Himpunan dari semua penyelesaian disebut dengan penyelesaian umum.
Suatu sistem persamaan linier homogen dengan orde m x n, bentuk umumnya dapat ditulis sebagai berikut:
(2.8)
dimana: aij merupakan konstanta dengan 1 ≤ i ≤ m, 1 ≤ j ≤ n sedangkan xi sebagai peubah (1 ≤ i≤ n).
Contoh: = − − = + − = − + 0 3 5 0 2 2 3 0 3 2 3 2 1 3 2 1 3 2 1 x x x x x x x x x (2.8)
Bila sistem persamaan linier disajikan secara serentak dimana jumlah peubah sama dengan jumlah persamaan, maka bentuk umumnya adalah:
= + + + + = + + + + = + + + + = + + + + n n nn n n n n n n n n n b x a x a x a x a b x a x a x a x a b x a x a x a x a b x a x a x a x a 3 3 2 2 1 1 3 3 3 33 2 32 1 31 2 2 3 23 2 22 1 21 1 1 3 13 2 12 1 11 (2.9)
dimana: aij sebagai koefisien dan bi konstanta dari sistem persamaan linier dengan peubah xj
∑
= = = n j i j ijx b i n a 1 . ., . . , 3 , 2 , 1 ,, i = j = 1, 2, 3, . . ., n. Dalam bentuk lain sistem persamaan linier ini dapat disajikan sebagai berikut:
2.1.2 Matriks
Penggunaan operasi matriks memberikan proses yang teratur dan logis yang dapat diterima untuk penyelesaian komputer dalam sistem persamaan-persamaan simultan.
Pandang sistem persamaan linier dengan tiga persamaan, tiga peubah sebagai berikut: = − − = + − = − + 3 3 5 1 2 2 2 4 3 3 2 1 3 2 1 3 2 1 x x x x x x x x x (2.9)
Jika koefisien sistem persamaan linier tersebut ditulis dalam bentuk array empat persegi panjang (rectangular array), maka diperoleh:
− − − − 1 3 5 2 2 2 3 1 1
yang menggambarkan tentang informasi sebelah kiri ketiga persamaan tersebut. Suatu array empat persegi panjang yang diurutkan disebut matriks. Secara umum perhatikan matriks m buah persamaan linier dengan n peubah di bawah ini:
= + + + + = + + + + = + + + + = + + + + m n mn m m m n n n n n n b x a x a x a x a b x a x a x a x a b x a x a x a x a b x a x a x a x a 3 3 2 2 1 1 3 3 3 33 2 32 1 31 2 2 3 23 2 22 1 21 1 1 3 13 2 12 1 11 (2.7)
Sistem persamaan linier di atas dapat ditulis dalam bentuk array empat persegi panjang dan dinamakan matriks A yaitu:
= mn m m m n n n a a a a a a a a a a a a a a a a A 3 2 1 3 33 32 31 2 23 22 21 1 13 12 11
Susunan array yang berbentuk persegi panjang yang terdiri dari m baris dan n
kolom disebut matriks m x n atau matriks berorde m x n. Komponen ke-ij matriks A
dinotasikan dengan aij, yang merupakan baris ke-i dan kolom ke-j dari matriks A. Dalam bentuk lain, matriks A dapat ditulis A = (aij).
Bila A adalah matriks m x n dimana m = n, maka matriks A disebut matriks bujur sangkar (square matriks).
Definisi 1
Andaikan A = (aij) matriks berorde m x n. Transpose dari A ditulis At, adalah matriks berorde n x m yang diperoleh dengan mempertukarkan baris dan kolom dari A. Jelasnya dapat ditulis: At = (aij = mn m m m n n n a a a a a a a a a a a a a a a a A Jika 3 2 1 3 33 32 31 2 23 22 21 1 13 12 11
). Dalam bentuk lain:
= mn n n n m m m t a a a a a a a a a a a a a a a a A maka 3 2 1 3 33 23 13 2 32 22 12 1 31 21 11
Jelasnya, letak baris ke-i dari A adalah kolom ke-i pada At dan kolom ke-j dari A
adalah baris ke-j pada At.
Definisi 2
Matriks bujursangkar A beorde n x n disebut simetrik jika At = A. Suatu matriks bujursangkar disebut upper triangular bila semua komponen di bawah diagonal nol dalam bentuk lain ditulis: A = (aij) upper triangular jika aij = 0, i > j. Suatu matriks bujursangkar disebut lower triangular bila semua elemen di atas diagonal nol dalam bentuk lain ditulis: A = (aij) jika aij = 0, i < j. A = (aij) matriks diagonal jika aij = 0, i ≠
j. Definisi 3 Andaikan A = (aij) dan B = (bij + + + + + + + + + = + = + mn mn m m m m n n n n ij ij b a b a b a b a b a b a b a b a b a b a B A 2 2 1 1 2 2 22 22 21 21 1 1 12 12 11 11 ) (
) adalah matriks berorde m x n. Jumlah A dan B adalah matriks A + B dengan orde m x n yang dinyatakan dengan:
Definisi 4 Jika A = (aij = = mn m m n n ij a a a a a a a a a a A α α α α α α α α α α α 2 1 2 22 21 1 12 11 ) (
) matriks berorde m x n dan jika α adalah saklar, maka matriks αA berorde
m x n yang dinyatakan dengan:
Definisi 5
Andaikan A = (aij) matriks berorde m x n dengan elemen baris ke-i dinotasikan dengan
ai. Andaikan B = (bij) matriks berorde n x p dimana elemen kolom ke-j dinotasikan dengan bj. Maka product (perkalian) A dan B adalah matriks C = (cij) dengan orde m x
p dimana cij = ai bj. Elemen ke-ij dan AB adalah perkalian saklar baris ke-i dari A(ai) dan kolom ke-j dari B(bj
nj in j i j i ij a b a b a b C = 1 1 + 2 2 +...+
). Hal ini dinyatakan dengan:
Contoh:
Jika A = [aij] koefisien matriks berorde m x n dan x = (x1, x2, x3, . . ., xn
= n mn m m m n n n x x x x a a a a a a a a a a a a a a a a Ax 3 2 1 3 2 1 3 33 32 31 2 23 22 21 1 13 12 11 ) adalah matriks kolom berorde n x 1, sehingga product matriks Ax adalah matriks berorde m x 1 yaitu: + + + + + + + + = n mn m m n n n n n n x a x a x a x a x a x a x a x a x a x a x a x a Ax 2 2 1 1 3 2 32 1 31 2 2 22 1 21 1 2 12 1 11
Bila sistem persamaan di atas disamakan dengan b yang merupakan vektor kolom, maka Ax = b yang dinyatakan dengan:
= + + + + + + + + m n mn m m n n n n n n b b b b x a x a x a x a x a x a x a x a x a x a x a x a 3 2 1 2 2 1 1 3 2 32 1 31 2 2 22 1 21 1 2 12 1 11 Definisi 6
Identitas matriks bujursangkar berorde n x n adalah matriks berorde n x n dimana semua elemen diagonal adalah 1 (satu) dan elemen yang lain 0 (nol) dan dapat dinotasikan dengan: In = (bij ≠ = = j i jika j i jika bij 0 1 ) dimana ; i = j = 1, 2, 3, . . ., n (2.10) Teorema 1
Andaikan A matriks bujursangkar berukuran n x n, maka:
A In= In A = A
Catatan: Fungsi In pada matriks n x n sama dengan fungsi bilangan 1 (satu) dalam bilangan riel (sebab: 1 . a = a . 1 = a, ∀aε R).
Bukti:
Andaikan cij elemen ke-ij dari A In, maka dapat ditulis:
cij = ai1 bi1 + ai2 bi2 + . . . + aij bij + . . . + ain b dari persamaan (2.10) jumlah c
in
ij = aij, sehingga A In = A. Dengan cara yang sama dapat diperlihatkan A In
Misalkan A dan B matriks berukuran n x n. Andaikan bahwa: A B = B A = I. B disebut invers dari mariks A dinotasikan dengan A
A = A. Jelas terbukti.
Notasi: Untuk lebih singkatnya identitas ditulis I.
Definisi 7
-1
I. Jika matriks A mempunyai invers maka matriks A disebut invertible. Dari definisi di atas diperoleh bahwa (A-1)-1
Andaikan B dan C invers dari matriks A. Akan diperlihatkan B = C. Dari definisi diketahui bahwa AB = BA = I dan AC = CA = I. Maka B(AC) = BI = B dan B(AC) = IC = C. B(AC) = (BA)C sebab berlaku hukum assosiatif dalam perkalian matriks. Dengan demikian B = C, sehingga pernyataan diatas terbukti.
Teorema 3
Andaikan A dan B matriks berorde n x n yang invertible. Maka AB invertible dan (AB) = A bila A invertible.
Teorema 2
Bila matriks A invertible, maka inversnya unique (tunggal)
Bukti:
-1 = B-1 A-1.
Bukti:
Untuk membuktikannya, akan diarahkan ke definisi 7.
B-1A-1=(AB)-1jika dan hanya jika B-1A-1(AB)=(AB)(B-1A-1)= I. (B-1A-1)(AB)= B-1(A-1A)B = B-1IB = B-1
(AB)(B
B = I dan -1
A-1) = A(BB-1)A-1= AIA-1= AA-1= I
Pandang sistem persamaan (2.9) dengan n persamaan dan n peubah, dapat dinyatakan dengan: AX = b dan andaikan A invertible. Maka persamaan dapat ditulis dalam bentuk: A-1AX = A-1b (kedua ruas persamaan dikali dengan A-1)
IX = A-1b ; A-1A = I X = A-1
Sehingga dapat disimpulkan, bila A invertible, sistem pesamaan AX = b
mempunyai unique solution: X = A
b ; IX = X
-1
2.2 Metode Cramer
Sebelum diuraikan bagaimana metode cramer digunakan dalam meyelesaikan sistem persamaan linier non-homogen, maka akan diuraikan terlebih dahulu faktor-faktor yang mendukung metode cramer.
Teorema 4
Jika Ainvertible det A ≠ 0, maka det A-1
A det
1 =
Bukti:
Dari sifat-sifat aljabar diketahui bahwa:
1 =det I =det A A-1=det A det A-1 dimana hal ini ekivalen dengan: det A-1
A det
1 =
Sebelum digunakan determinan untuk menghitung invers, akan didefinisikan tentang adjoint matriks A = (aij). Misalkan B = (Aij
= nn n n n n n n A A A A A A A A A A A A A A A A B 3 2 1 3 33 32 31 2 23 22 21 1 13 12 11
) matriks kofaktor dari A sehingga:
Definisi 8
Andaikan A matriks berorde n x n dan B matriks kofaktor. Adjoint A ditulis adj A
adalah transpose matriks B berorde n x n yaitu:
= = nn n n n n n n t A A A A A A A A A A A A A A A A B A adj 3 2 1 3 33 23 13 2 32 22 12 1 31 21 11
Contoh: Misalkan: − = 7 5 3 1 1 0 3 4 2 A
Dari matriks di atas diperoleh: A11 = 12, A12 = 3, A13 = -3, A21 = -13, A22 = 5, A23 = 2, A31 = -7, A32 = 2, A33 − − − 2 2 7 2 5 13 3 3 12 = 2. maka: B = dan Adj A = Bt − − − 2 2 3 2 5 3 7 13 12 = Teorema 5
Andaikan A matriks berorde n x n. A invertible jika dan hanya jika det A≠ 0. Jika det A
≠ 0 maka: A-1 adjA A det 1 = Bukti: Karena A≠ 0, maka: (A) A adj A det 1 =
(
)
(det ) . det 1 ) ( det 1 I I A A A adj A A = =Sebab diketahui bahwa jika A B = I
maka B = A-1 1 det 1 = − A A adj A . Dengan demikian:
Pandang sistem persamaan linier non-homogen dengan n persamaan dan n
peubah dibawah ini:
= + + + + = + + + + = + + + + = + + + + n n nn n n n n n n n n n b x a x a x a x a b x a x a x a x a b x a x a x a x a b x a x a x a x a 3 3 2 2 1 1 3 3 3 33 2 32 1 31 2 2 3 23 2 22 1 21 1 1 3 13 2 12 1 11 (2.9)
Sistem persamaan linier di atas dapat ditulis dalam bentuk: Ax = b (2.11) dimana: = nn n n n n n n a a a a a a a a a a a a a a a a A 3 2 1 3 33 32 31 2 23 22 21 1 13 12 11 , = n x x x x x 3 2 1 , = n b b b b b 3 2 1
Jika det A ≠ 0 maka persamaan (2.11) mempunyai unique solution yang ditentukan oleh: x = A-1 = nn n n n n n n a a a b a a a b a a a b a a a b A 3 2 3 33 32 3 2 23 22 2 1 13 12 1 1 b.
Misalkan D = det A. Didefinisikan matriks baru yaitu:
, = nn n n n n n n a a b a a a b a a a b a a a b a A 3 1 3 33 3 31 2 23 2 21 1 13 1 11 2 , . . ., = n n n n n b a a a b a a a b a a a b a a a A 3 2 1 3 33 32 31 2 23 22 21 1 13 12 11
Ai adalah matriks yang diperoleh dengan menempatkan pada kolom ke-i dari A dengan matriks kolom b. Misalkan D1 = det A1, D2 = det A2, . . ., Dn = det An.
Teorema 6 (Cramer’s Rule)
Andaikan A matriks berorde n x n dan det A ≠ 0. Penyelesaian tunggal (unique solution) dari sistem persamaan Ax = b ditentukan oleh:
D D x D D x D D x D D x n n = = = = , , 3,..., 3 2 2 1 1 Bukti:
Penyelesaian dari Ax = b adalah x = A-1
(
)
= = − n nn n n n n n n b b b b A A A A A A A A A A A A A A A A D b A adj D b A 3 2 1 3 2 1 3 33 23 13 2 32 22 12 1 31 21 11 1 1 1 b dimana:Sehingga (adj A)b adalah merupakan n-vektor yaitu:
(
)
j j j n nj n nj j j j bA b A b A b A b b b b A A A A = + + + + 3 1 1 2 2 3 3 2 1 3 2 1 . Pandang matriks Aj = nn n n n n n n j a b a a a b a a a b a a a b a a a 2 1 3 3 32 31 2 2 22 21 1 1 12 11 :Bila ditentukan determinan dari Aj 1. D
pada kolom ke-j, diperoleh:
j = b1 (kofaktor dari b1) + b2 (kofaktor dari b2) + b3 (kofaktor dari b3) + . . . +
bn (kofaktor dari bn 2. Kofaktor dari b
).
j diperoleh dengan menghilangkan baris ke-i dan kolom ke-j dari Aj (sebab bi berada pada kolom ke-j di Aj). Tetapi kolom ke-j dari Aj adalah b, sehingga diperoleh minor ij, Mij
maka kofaktor dari b
dari A. i pada Aj = Aij D sehingga: j = b1 A1j + b2 A2j + b3 A3j + . . . +bn Anj. kolom ke-j
Komponen ke-i dari (adj A)b adalah Di = = = = − D D D D D D D D D D D D D b A x x x x x n n n / / / / 1 3 2 1 3 2 1 1 3 2 1 dan diperoleh:
2.3 Metode Eliminasi Gauss-Jordan
Pandang sistem persamaan linier non-homogen di bawah ini:
= + + + + = + + + + = + + + + = + + + + n n nn n n n n n n n n n b x a x a x a x a b x a x a x a x a b x a x a x a x a b x a x a x a x a 3 3 2 2 1 1 3 3 3 33 2 32 1 31 2 2 3 23 2 22 1 21 1 1 3 13 2 12 1 11 (2.9)
Persamaan di atas dapat dinyatakan dalam bentuk koefisien matriks sebagai berikut: = n n nn n n n n n n b b b b x x x x a a a a a a a a a a a a a a a a 3 2 1 3 2 1 3 2 1 3 33 32 31 2 23 22 21 1 13 12 11
Persamaan di atas dapat ditulis dalam bentuk matriks yang diperbesar (augmented matrix) yang bentuknya seperti di bawah ini:
n nn n n n n n n b a a a a b a a a a b a a a a b a a a a 3 2 1 3 3 33 32 31 2 2 23 22 21 1 1 13 12 11
Untuk menentukan nilai-nilai x1, x2, x3, . . ., xn
1. Gunakan a
, maka matriks yang diperbesar (augmented matrix) di atas harus diubah kedalam bentuk echelon dengan proses pengerjaan sebagai berikut:
11 sebagai pivot pertama untuk mengeliminasi elemen-elemen a21, a31,
a41, . . ., an1
Proses sebagai berikut:
menjadi 0 (nol).
a. M21 (-a21/a11): kalikan baris pertama dengan (-a21/a11
b. M
) dan hasilnya dijumlahkan dengan baris kedua.
31 (-a31/a11): kalikan baris pertama dengan (-a31/a11 c. M
) dan hasilnya dijumlahkan dengan baris ketiga.
41 (-a41/a11): kalikan baris pertama dengan (-a41/a11 d. M
) dan hasilnya dijumlahkan dengan baris keempat. Hal ini dilakukan hingga elemen ke-n.
n1 (-an1/a11): kalikan baris pertama dengan (-an1/a11
maka diperoleh matriks di bawah ini:
) dan hasilnya dijumlahkan dengan baris ke-n.
n nn n n n n n b a a a b a a a b a a a b a a a a 3 2 3 3 33 32 2 2 23 22 1 1 13 12 11 0 0 0
2. a22 digunakan sebagai elemen pivot untuk mengeliminasi elemen-elemen a12, a32,
a42, . . ., an2 a. M
menjadi 0 (nol), dengan operasi:
12 (-a12/a22): kalikan baris kedua dengan (-a12/a22) dan hasilnya dijumlahkan dengan baris pertama.
b. M32 (-a32/a22): kalikan baris kedua dengan (-a32/a22
c. M
) dan hasilnya dijumlahkan dengan baris ketiga.
42 (-a42/a22): kalikan baris kedua dengan (-a42/a22 d. M
) dan hasilnya dijumlahkan dengan baris keempat.
n2 (-an2/a22): kalikan baris kedua dengan (-an2/a22 maka diperoleh matriks di bawah ini :
) dan hasilnya dijumlahkan dengan baris ke-n.
n nn n n n n b a a b a a b a a a b a a a 3 3 3 33 2 2 23 22 1 1 13 11 0 0 0 0 0 0
3. a33 digunakan sebagai elemen pivot untuk mengeliminasi elemen-elemen a13, a23,
a43, . . ., an3 a. M
menjadi 0 (nol) dengan operasi;
13 (-a13/a33): kalikan baris ketiga dengan (-a13/a33 b. M
) dan hasilnya dijumlahkan dengan baris pertama.
23 (-a23/a33): kalikan baris ketiga dengan (-a23/a33 c. M
) dan hasilnya dijumlahkan dengan baris ketiga.
43 (-a43/a33): kalikan baris ketiga dengan (-a43/a33 d. M
) dan hasilnya dijumlahkan dengan baris keempat.
n3(-an3/a33): kalikan baris ketiga dengan (-an3/a33
maka diperoleh matriks di bawah ini:
) dan hasilnya dijumlahkan dengan baris ke-n.
n nn n n n b a b a a b a a b a a 0 0 0 0 0 0 0 0 0 3 3 33 2 2 22 1 1 11
Operasi di atas terus dilakukan hingga ann sebagai elemen pivot ke-n, untuk mengeliminasi a1n, a2n, a3n, . . ., a(n-1)n menjadi 0 (nol) dengan operasi:
a. M1n (-a1n/ann): kalikan baris ke-n dengan (-a1n/ann
b. M
) dan hasilnya dijumlahkan dengan baris pertama.
2n (-a2n/ann): kalikan baris ke-n dengan (-a2n/ann c. M
) dan hasilnya dijumlahkan dengan baris kedua.
3n (-a3n/ann): kalikan baris ke-n dengan (-a3n/ann d. M
) dan hasilnya dijumlahkan dengan baris ketiga.
(n-1)n (-a(n-1)n/ann): kalikan baris ke-n dengan (-a(n-1)n/ann
sehingga diperoleh bentuk matriks di bawah ini:
) dan hasilnya dijumlahkan dengan baris ke-(n – 1).
− − − − − − − − − ) 1 ( ) 1 ( ) 1 ( 3 ) 1 ( 3 ) 1 ( 33 ) 1 ( 2 ) 1 ( 22 ) 1 ( 1 ) 1 ( 11 0 0 0 0 0 0 0 0 0 0 0 n n n nn n n n n n n n n b a b a a b a b a
dari matriks di atas ini nilai-nilai x1, x2, x3, . . ., xn
) 1 ( 11 ) 1 ( 1 1 / − − = n n a b x dinyatakan dengan: , ) 1 ( 22 ) 1 ( 2 2 / − − = n n a b x , ) 1 ( 33 ) 1 ( 3 3 / − − = n n a b x , ) 1 ( 44 ) 1 ( 4 4 / − − = n n a b x , . . ., ) 1 ( ) 1 ( / − − = n nn n n n b a x . 2.4 Bahasa C
Bahasa C merupakan perkembangan dari bahasa BCPL yang dikembangkan oleh Martin Richards pada tahun 1967. Selanjutnya bahasa ini memberikan ide kepada Ken Thompson yang kemudian mengembangkan bahasa yang disebut bahasa B pada tahun 1970. Perkembangan selanjutnya dari bahasa B adalah bahasa C oleh Dennis Ricthie sekitar tahun 1970-an di Bell Telephone Laboratories Inc. (sekarang adalah AT&T Bell Laboratories). Bahasa C pertama kali digunakan di komput er Digital Equipment
Corporation PDP-11 yang menggunakan system operasi UNIX. Hingga saat ini penggunaan bahasa C telah merata di seluruh dunia. Selain itu, banyak bahasa pemrograman populer seperti PHP dan Java menggunakan sintaks dasar yang mirip bahasa C.
2.4.1 Struktur Program Bahasa C
Setiap bahasa komputer mempunyai struktur program yang berbeda. Jika struktur dari program tidak diketahui, maka akan sulit untuk memulai menulis suatu program dengan bahasa yang bersangkutan. Struktur dari program memberikan gambaran secara luas dari bentuk program.
Struktur dari program Bahasa C dapat dilihat dari kumpulan sebuah atau lebih fungsi-fungsi. Fungsi pertama yang harus ada dalam program Bahasa C sudah ditentukan namanya, yaitu bernama main(). Suatu fungsi dalam program Bahasa C dibuka dengan kurung kurawal ({) dan di tutup dengan kurung kurawal (}). Di antara kurung-kurung kurawal dapat dituliskan statemen-statemen program Bahasa C. Berikut ini adalah struktur program Bahasa C.
a. Struktur Program Bahasa C main() { statemen-statemen; } Fungsi_Fungsi_Lain() { statemen-statemen; } fungsi utama
fungsi-fungsi lain yang ditulis oleh pemrogram
b. Program Bahasa C yang Sederhana
/* Program Bahasa C Yang Sederhana */ #include<stdio.h>
main() {
float Celcius, Fahrenheit;
printf(“Masukkan Nilai Celcius ?”); scanf(“%f”,&Celcius);
/* Menghitung Konversi */ Fahrenheit = Celcius * 1.8 + 32;
printf(“%f celcius adalah %f fahrenheit\n”, Celcius, Fahrenheit); }
Jika program ini dijalankan akan didapatkan hasil: Masukkan Nilai Celcius ? 10
10.000000 celcius adalah 50.000000 fahrenheit
2.4.2 Fungsi Input/Output
a. printf()
statemen-statemen dalam program Bahasa C berbentuk kata kunci
komentar
nama fungsi
bagian suatu fungsi
pendeklarasian variabel
Fungsi : Mencetak output ke layar Include : #include<stdio.h>
Hasil : Menghasilkan jumlah byte dari output tersebut, bila gagal print
menghasilkan end of file
Contoh :
printf(“SUKSES SELALU”);
Tabel 2.1 Kode-Kode Format untuk Fungsi printf()
Kode Format Kegunaan
%c %s %d %i %f
Menampilkan sebuah karakter Menampilkan nilai string
Menampilkan nilai desimal integer Menampilkan nilai desimal integer Menampilkan nilai pecahan
b. scanf()
Fungsi : Membaca data dari stdin Include : #include<stdio.h>
Hasil : Data tersebut, bila salah atau menjumpai end of file maka hasilnya adalah NULL
Contoh :
printf(“Jari-Jari Lingkaran: “);
scanf(“%f”, & jari);
c. getch()
Fungsi : Membaca karakter dari keyboard, hasilnya tidak ditampilkan dilayar Include : #include<conio.h>
Hasil : Karakter yang diketikkan Contoh :
printf(“Ketikkan suatu huruf (A-Z)“);
getch(); d. getche()
Include : #include<conio.h>
Hasil : Karakter yang dibaca dari layar Contoh :
printf(“Tekan Sembarang Tombol“); x = getche();
e. putch()
Fungsi : Mencetak karakter di layar Include : #include<conio.h>
Hasil : Karakter yang dicetak, bila terjadi kesalahan fungsi ini memberi nilai
end of file
Contoh :
putch(karakter); f. puts()
Fungsi : Mencetak string ke stdout Include : #include<stdio.h>
Hasil : Bila berhasil akan memberikan nilai non-negatif, bila gagal akan menghasilkan end of file
Contoh :
char teks[ ] = “Selamat”;
puts(teks);
2.4.3 Jenis-Jenis Variabel dalam Bahasa C
Variabel-variabel dalam Bahasa C digolongkan menjadi dua bagian yaitu variabel numerik dan variabel teks.
1. Variabel numerik digolongkan atas: a. Bilangan Bulat atau Integer
Integer mampu menampung bilangan bulat yang berkisar antara -32.786 sampai dengan 32.786.
b. Floating Point
Dalam bentuk bilangan berpangkat, floating point dapat menampung data dari 10-38 sampai dengan 1038, sedang dalam bentuk desimal dapat menampung hingga enam desimal.
Contoh : nilai_max = 102.234567 hasil = 1.34566e – 20 c. Double Precision
Dalam bentuk bilangan berpangkat, double precision dapat mengolah angka berkisar 10-308 sampai dengan 10308
int gaji
, sedang dalam bentuk desimal dapat menampung 15 digit.
Contoh : teliti = 1234.5678901234 std_dev = 1.34567e – 100
2. Variabel teks dibedakan atas: a. Karakter (Tunggal)
Variabel ini digunakan untuk menampung sebuah karakter ataupun variabel yang dikonversikan dalam bentuk bilangan (ASCII code).
b. String
String merupakan rangkaian dari beberapa karakter yang diakhiri dengan karakter NULL (‘\0’). Untuk menggunakan variabel-variabel di atas dalam Bahasa C maka variabel haruslah diperkenalkan kepada Bahasa C yang dikenal dengan istilah deklarasi variabel.
Contoh:
Bila dideklarasikan variabel total sebagai integer, variabel nilai_akhir sebagai
floating point, variabel jumlah sebagai double precision, ini dinyatakan dengan:
int total;
float nilai_akhir;
double jumlah;
Tabel 2.2 Tipe Variabel
nama variabel type variabel
Tipe Variabel Simbol Deklarasi Format Specifier Integer Floating Point Double Precision Karakter int float double char % d % f % lf % c