KOMPUTASI JARAK MINIMUM
Mike Susmikanti*
ABSTRAK
KOMPUTASI JARAK MINIMUM. Perhitungan jarak minimum diperlukan pada beberapa aplikasi seperti aplikasi logika samar (fuzzy logic), pengolahan citra (image processing) untuk bidang kedokteran, jaringan saraf (neural network) dan pengolahan sumber bumi khususnya serta sistim informasi geografi umumnya. Metoda jarak minimum yang dikemukakan di sini didasarkan pada konsep vektor dan matrik sehingga dapat memudahkan perhitungan dan kesamaannnya dalam ruang dimensi-n untuk banyak data. Pertama-tama dalam hal ini dikemukakan jarak antara dua titik, jarak antara satu titik dengan titik-titik lain yang membentuk bidang dalam ruang Euclidean-n. Selanjutnya perhitungan jarak minimum di sini akan memberikan jarak terdekat bagi titik tersebut dengan suatu bidang serta posisi dari titik tersebut pada bidang. Konsep jarak minimum tersebut di atas dapat digunakan selanjutnya untuk persoalan analisis pengelompokan dalam penerapan logika samar menggunakan metoda Mahalanobis
Distance. Metoda ini menyarankan penggunaan titik-titik terdekat tetapi masih di dalam anggota
kelompok yang sama dengan memperhatikan matrik kovarian karena ada kemungkinan data berasal dari kelompok yang berbeda.
ABSTRACT
MINIMUM DISTANCE COMPUTATION. Minimum distance calculation is used for many applications such as neural network, fuzzy logic, image processing for medical science, geology source processing and geografy information system. The minimum distance we discuss here is based on the concept of some geometric interpretation of vectors and matrices, that may be helpful in computation and analogy in Euclidean n-space. The first we calculate the distance between two points, the distance between one point and other points in the same plane in Euclidean n-space which are defined as the minimum distances. Then the calculation of minimum distance will give the minimum distance of the point and a plane as well as a position of the point in the plane. The minimum distance concept above can be used in the cluster analysis problem in fuzzy logic application using the Mahalanobis distance method. This method suggests the nearest points but they are still in same subsets with respect to covarian matrix rule, since the data probability come from different subsets.
PENDAHULUAN
Perhitungan jarak minimum dirasakan banyak diperlukan dalam berbagai bidang di antaranya pada tehnik clustering atau pengelompokan yang digunakan pada
*
sistem jaringan saraf (neural network), logika samar (fuzzy logic) dan pengolahan citra
(image processing) untuk bidang kedokteran, pengolahan sumber bumi khususnya dan
sistim informasi geografi umumnya dan lain-lain. Adapun analisis pengelompokan yang sifatnya deterministik dapat digunakan metoda statistik, akan tetapi untuk tehnik pengelompokan yang bersifat stochastik dapat digunakan fuzzy logic sebagai suatu pendekatan fungsi.
Dalam analisis berikut ini akan digunakan beberapa interpretasi geometrik dari vektor-vektor yang mungkin dapat membantu dalam perhitungan jarak minimum (minimum distance) ini, dan selanjutnya dapat diperluas untuk ruang berdimensi n atau ruang-n. Salah satu keunggulan interpretasi geomerik dari vektor-vektor adalah situasi untuk ruang berdimensi dua atau berdimensi tiga secara analog dapat diperluas menjadi ruang-n. Interpretasi vektor secara geometrik dalam ruang-n dapat dipandang sebagai suatu titik dalam ruang koordinat-n dan dapat diartikan pula sebagai suatu segmen garis dari titik pusat ke titik tertentu yang direpresentasikan sebagai vektor.
Konsep jarak minimum tersebut di atas dapat digunakan selanjutnya untuk persoalan analisis pengelompokan dalam penerapan logika samar menggunakan metoda Mahalanobis Distance. Metoda ini menyarankan penggunaan titik-titik terdekat tetapi masih di dalam anggota kelompok yang sama dengan memperhatikan matrik kovarian karena ada kemungkinan data berasal dari kelompok yang berbeda.
METODA JARAK MINIMUM
Jarak antara dua titik (vektor ) a dan b dalam ruang Euclidean-n didefinisikan sebagai : d = [
∑
= n i 1 (ai – bi) 2 ] 1/2 atau dapat ditulis dalam bentuk vektord = [ ( a - b )T ( a - b) ] ½ di mana a = (a1, a2, …., an) dan b = (b1, b2, …., bn)
Kumpulan titik-titik yang melalui 2 titik a dan b dalam ruang Euclidean-n didefinisikan sebagai
L = { x : x =
λ
b + ( 1-λ
) a ;λ
∈ R }Segmen garis yang menghubungkan 2 titik a dan b dalam ruang Euclidean-n adalah kumpulan dari titik-titik l yang didefinisikan dengan :
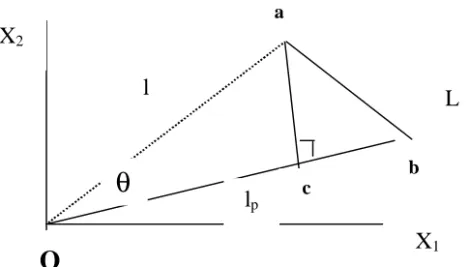
Jarak antara titik p dan suatu garis l yang melalui titik a dan b (gambar 1), di mana titik x pada garis l ialah :
Dx = [ ( p – x )T ( p – x ) ] ½.
Jarak terdekat dari suatu titik p ke garis l dalam ruang Euclidean-n (gambar 1) :
D= minimum [ ( p – x ) T ( p – x ) ] 1/2
x
∈
lGambar 1. Jarak terdekat dari titik p terhadap garis l yang dinyatakan dengan D Bidang yang melalui n titik-titik b1, b2, …., bn sedemikian sehingga matrik
B = [b1, b2, …., bn] mempunyai rank n, didefinisikan sebagai kumpulan titik-titik P
yaitu : P = { Y : Y =
∑
= n i 1λ
i bi ;∑
= n i 1λ
i = 1 ;λ
i ∈ R }Bidang dalam ruang Euclidean-n dengan dimensi k yang melalui titik a1, a2, …., ak, O (titik pusat), didefinisikan sebagai kumpulan titik-titik Pk
n : Pk n = { Y : Y =
∑
= k i 1λ
i ai ;λ
i ∈ R , i = 1, 2, ……., k}Dalam bentuk vektor, persamaan untuk Pkn, dapat ditulis Y = A
λ
;λ
∈ Rk ; A = [ a1, a2, …., ak ],p
D
Dxa
bl
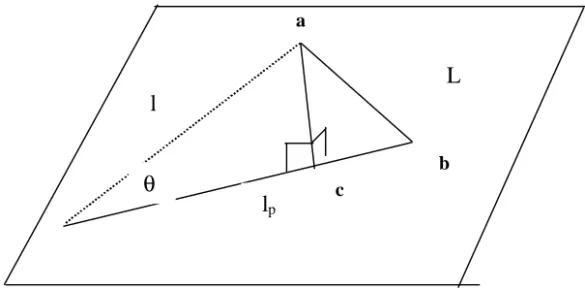
Proyeksi lp ( gambar 2) didefinisikan sebagai
lp = { y : y =
λ
c ; 0≤
λ
≤
1 } (1)O
Gambar 2. Proyeksi dari titik a terhadap garis L yang dinyatakan dengan lp. Sudut antara dua segmen garis a dan b dalam ruang Euclidean-n :
cos
θ
=b
b
a
a
b
a
T T T .Untuk menghitung lp, diperlukan terlebih dahulu menghitung titik c yaitu titik
dengan posisi yang akan menghasilkan jarak minimum, dari suatu titik tertentu terhadap titik-titik yang membentuk bidang.
Misal c pengganda skalar dari garis b yang dapat dinyatakan sebagai c =
λ
b.Misal d adalah segmen garis dari 0 ke c dan b* adalah unit vektor dengan arah dari O ke b , maka c = d b*.
Dapat diperoleh bahwa : c = (
b
b
b
a
T T ) b.Dengan cara yang sama, apabila l adalah segmen garis dari a1 ke a2 dalam ruang
euclidean-n dan L adalah garis dari b1 dan b2 dalam ruang euclidean-n (gambar 3,
maka proyeksi dari l pada L didefinisikan dengan segmen garis lp dari O ke c adalah : c = [
)
(
)
(
)
(
)
(
1 2 1 2 1 2 1 2b
b
b
b
b
b
a
a
T T−
−
−
−
] (b2 – b1).l
l
p aθ
bL
X
1X
2 cGambar 3. Proyeksi segmen garis l pada garis L yang dinyatakan dengan posisi titik c Misal Pk
n
adalah bidang yang melalui titik pusat dan titik b1, ……, bk dalam
ruang euclidean-n dan B = [ b1, ……, bk ]. Misalkan l adalah segmen garis dari titik
pusat ke titik a. Maka titik c merupakan titik proyeksi dari l pada Pk n
yang dapat ditentukan posisinya dengan perhitungan ;
C = B ( B T B )-1 B T a (2)
yang merupakan proyeksi dari titik a ke bidang Pk n
. Titik c merupakan titik akhir dari proyeksi l pada Pk
n
. Sehingga c adalah titik pada Pk n
yang mempunyai jarak minimum dari titik a.
Berarti bahwa jarak dari suatu titik a ke bidang Pkn yang dinyatakan dengan d,
dapat didefinisikan sebagai jarak minimum dari titik a ke titik c yang terletak pada bidang Pk
n
sebagai
d = [ ( a – B ( B T B )-1 B T a )T ( a – B ( B T B )-1 B T a ) ] 1/2 (3)
MAHALANOBIS DISTANCE
Dalam suatu sistim fuzzy, tehnik pengelompokan dapat memberikan pendekatan untuk data yang samar. Salah satu metoda yang dapat digunakan dalam tehnik pengelompokan yaitu Mahalanobis Distance.
Sistem fuzzy merupakan kumpulan yang memenuhi aturan dalam memetakan input menjadi output, yang apabila dinyatakan dalam bentuk fungsi merupakan
l
l
p aθ
bL
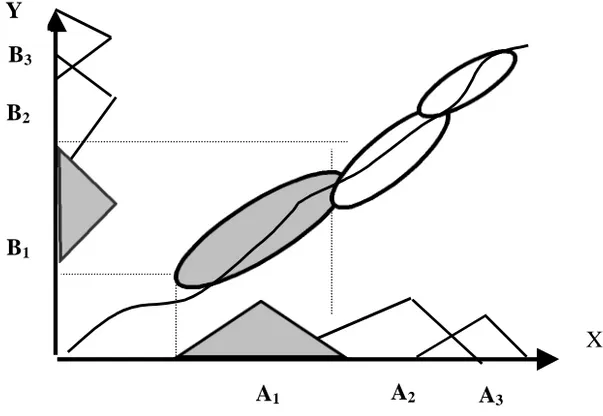
cfungsif : X à Y. Pola fuzzy dapat didefinisikan sebagai berikut : jika input x adalah pola A maka output y adalah pola B. Ruang Cartesian-product A x B memenuhi berlakunya aturan fuzzy untuk ruang Input-Output : X x Y (gambar 4). Aturan fuzzy dapat mempunyai bentuk elipsoida dalam ruang sistim input-output. Sistim fuzzy memberikan pendekatan fungsi yang diwakili oleh grafik. Penyebaran data membentuk bidang elipsoida yang kemungkinan tumpang tindih (gambar 4).
Gambar 4. Penyebaran data pada ruang Input-Output XXY
Sistim Mahalanobis memberikan suatu kumpulan untuk mengetahui apakah sampel data termasuk sebagai anggota kumpulan. Mahalanobis distance menghasilkan gabungan kumpulan data yang memenuhi aturan kovariasi-samar elipsoida. Dapat diperoleh proyeksi pada kumpulan fuzzy yang memenuhi, dengan memperhatikan struktur korelasi diantara input.
Bidang elipsoida menentukan keberadaan semua titik z yang memenuhi
)
(
)
(
2c
z
A
c
z
−
T−
=
α
Eigenvektor dan eigenvalue dari matrik A mendefinisikan bentuk elipsoida dalam ruang input dan output dimensi-q. q = n + p, n merupakan jumlah input dan p merupakan jumlah output. Matrik A dimisalkan matrik positif-definite.
α
adalahY
X
A
1A
2A
3B
1B
2B
3bilangan nyata yang positif, sedangkan c adalah pusat elipsoida. Dalam hal ini dimungkinkan adanya kehilangan struktur korelasi di antara komponen input.
Matrik kovariansi Kj dapat digunakan untuk mengukur penyebaran data. Matrik kebalikan Kj
-1
membantu mendefinisikan elipsoida E sebagai lokasi semua titik z yang memenuhi :
)
(
)
(
1 2 j j T jK
z
m
m
z
e
=
−
−−
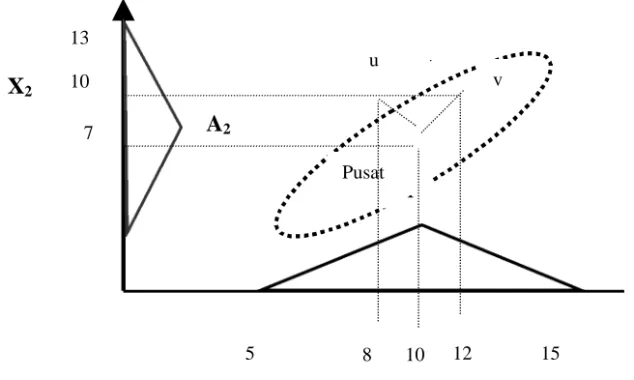
Dengan proyeksi elipsoida pada sumbu x1 dan x2, diperoleh dua vektor yaitu vektor u
dan v yang berjarak sama dari titik pusat (gambar 5).
Gambar 5. Proyeksi Elipsoida pada sumbu X1 & X2.
Bentuk elipsoida di atas disarankan dengan Mahalanobis distance sebagai dasar untuk kumpulan fungsi a(x) yang similar di mana penyebaran datanya kemungkinan saling tumpang tindih.
)
(
)
(
)
(
)
(
x
2x
m
ij TK
ij 1x
m
ijd
=
−
−−
n : vektor
m
ij mempunyai sub matrik kovarian i jK
d(x) : jarak input vektor x terhadap rata-rata pusat
m
ij berskala kovariansiA
1A
2X
2X
1 Pusat v u 12 8 5 10 12 7 13 10 15PEMBAHASAN
Suatu bidang dapat dibentuk dari suatu titik pusat dan dua titik, masing-masing titik b1(1,1,0) yang dinyatakan dalam bentuk vektor b1
T
= [1,1,0] dan titik b2 (1,0,1)
yang dinyatakan dalam vektor b2 T
= [1,0,1]. Kumpulan vektor-vektor b dapat dibentuk menjadi matriks B sebagai berikut
B =
1
0
0
1
1
1
Dapat ditentukan persamaan garis lp, sebagai proyeksi dari l pada bidang P2 3
dimana l adalah segmen garis dari titik pusat ke titik a(1,1,1) dengan menggunakan persamaan (1) tersebut di atas. Adapun titik a dapat dinyatakan dalam bentuk vektor aT = [1,1,1]. Dalam bentuk matrik titik a dapat dinyatakan sebagai berikut
a =
1
1
1
Persamaan garis lp dapat dihitung dengan sebelumnya menentukan terlebih dahulu
posisi titik yang merupakan proyeksi dari l pada bidang P2 3
. Misalkan posisi titik yang merupakan proyeksi dari l pada bidang P2
3
dinyatakan sebagai titik c. Maka posisi titik c dapat dihitung dengan menggunakan persamaan (2) sebagai berikut
BTB =
1
0
1
0
1
1
1
0
0
1
1
1
=
2
1
1
2
(BTB)-1 =
−
−
6667
.
0
3333
.
0
3333
.
0
6667
.
0
C =
1
0
0
1
1
1
−
−
6667
.
0
3333
.
0
3333
.
0
6667
.
0
1
0
1
0
1
1
1
1
1
=
6667
.
0
6667
.
0
3333
.
1
Persamaan untuk proyeksi lp adalah : Y =
λ
λ
λ
6667
.
0
6667
.
0
3333
.
1
0≤
λ
≤
1Jarak terdekat dari titik a terhadap bidang P23 yang didefinisikan sebagai d yaitu jarak
minimum dari titik a ke titik c dengan posisi (1,3333,0.6667,0.6667), dapat dihitung dengan menggunakan persamaan (3) tersebut di atas.
d = [{(1,1,1)–(1.3333,0.6667,0.6667)}T{ (1,1,1)–(1.3333,0.6667,0.6667)}]1/2 d = [(-0.3333,0.3333,0.3333) T(-0.3333,0.3333,0.3333)] 1/2
d = [0.3333] 1/2
Sehingga diperoleh jarak minimum dari titik a ke titik c, adalah : d = 0.58.
Misalkan suatu bidang dilalui oleh beberapa titik masing b1(1,0,1), b2(0,1,1)
dan b3(1,1,0). Agar syarat ruang vektor P terpenuhi yaitu mengandung vektor nol,
maka salah satu titik harus digeser menjadi titik pusat yaitu dimisalkan titik b1(1,0,1)
menjadi titik pusat O(0,0,0). Sehingga titik-titik lain yaitu b2 menjadi b1(-1,1,0) dan b3
menjadi b2(0,1,-1). Dapat ditentukan jarak minimum dari titik a(1,1,1) terhadap
bidang tersebut di atas, yang sebelumnya titik a digeser pula menjadi a(0,1,0). Dalam bentuk matrik titik a dapat dinyatakan sebagai berikut
a =
0
1
0
Maka posisi titik c dapat dihitung dengan menggunakan persamaan (2) sebagai berikut BTB =
−
−
1
1
0
0
1
1
−
−
1
0
1
1
0
1
=
2
1
1
2
(BTB)-1 =
−
−
6667
.
0
3333
.
0
3333
.
0
6667
.
0
C =
−
−
1
0
1
1
0
1
−
−
6667
.
0
3333
.
0
3333
.
0
6667
.
0
−
−
1
1
0
0
1
1
0
1
0
=
−
−
3333
.
0
6667
.
0
3333
.
0
Karena salah satu vektor b digeser sebelumnya, maka hasil posisi titik c harus dikembalikan ke bentuk semula yaitu sebelum digeser. Sehingga posisi titik c menjadi;
C = (-0.3333,0.6667,-0.3333) + (1,0,1) = (0.6667,0.6667,0.6667) Diperoleh jarak minimum dari titik a ke titik c(0.6667,0.6667.0.6667) adalah :
d = [{(1,1,1)-(0.6667,0.6667,0.6667)}T{ (1,1,1)-(0.6667,0.6667,0.6667)}]1/2 d = [(0.3333,0.3333,0.3333) T(0.3333,0.3333,0.3333)] 1/2
d = 0.58.
Untuk persoalan diatas apabila titik a diambil titik lain yaitu a(0,0,0), maka titik a sebelumnya digeser menjadi a(-1,0,-1), karena satu titik b yaitu titik b1 digeser
menjadi titik pusat. Dalam bentuk matrik titik a dapat dinyatakan sebagai berikut;
a =
−
−
1
0
1
Maka posisi titik c dapat dihitung dengan menggunakan persamaan (2) sebagai berikut; BTB =
−
−
1
1
0
0
1
1
−
−
1
0
1
1
0
1
=
2
1
1
2
(BTB)-1 =
−
−
6667
.
0
3333
.
0
3333
.
0
6667
.
0
C =
−
−
1
0
1
1
0
1
−
−
6667
.
0
3333
.
0
3333
.
0
6667
.
0
−
−
1
1
0
0
1
1
−
−
1
0
1
=
−
−
3333
.
0
6667
.
0
3333
.
0
Karena salah satu vektor b digeser sebelumnya, maka hasil posisi titik c harus dikembalikan ke bentuk semula yaitu sebelum digeser. Sehingga posisi titik c menjadi;
C = (-0.3333,0.6667,-0.3333) + (1,0,1) = (0.6667,0.6667,0.6667) Sehingga diperoleh jarak minimum dari titik a ke titik c, adalah :
d = [{(0,0,0)-(0.6667,0.6667,0.6667)}T{(0,0,0)-(0.6667,0.6667,0.6667)}]1/2 d = [{-0.6667,-0.6667,-0.6667}T{-0.6667,-0.6667,-0.6667}]1/2
d = [1.3334] 1/2 d = 1.15.
Pada permasalahan lain, misalnya ingin ditentukan proyeksi dari a1(1,0,-1) ke a2
(2,-1,1) pada bidang P2 3
yang dilalui titik O(0,0,0), x1’=[1,1,1] dan x2’=[1,-1,1].
Perhitungan diatas dapat digunakan secara umum yaitu dengan sebelumnya membentuk vektor a menjadi vektor a2 – a1 yang diperoleh nilainya adalah a(1,-1,2). Konsep ini sama dengan menggeser titik a1 menjadi titik asal atau titik pusat 0(0,0,0).
Dalam bentuk matrik titik a dapat dinyatakan sebagai berikut
a =
−
2
1
1
Maka posisi titik c dapat dihitung dengan menggunakan persamaan (2) sebagai berikut BTB =
−
1
1
1
1
1
1
−
1
1
1
1
1
1
=
3
1
1
3
(BTB)-1 =
−
−
375
.
0
125
.
0
125
.
0
375
.
0
C =
−
1
1
1
1
1
1
−
−
375
.
0
125
.
0
125
.
0
375
.
0
−
1
1
1
1
1
1
−
2
1
1
=
−
5
.
1
1
5
.
1
Dari perhitungan diatas, diperoleh bahwa proyeksi dari a1(1,0,-1) ke a2(2,-1,1) pada
bidang P2 3
yang dilalui titik O(0,0,0), x1’=[1,1,1] dan x2’=[1,-1,1] adalah titik c dengan
Dalam persoalan filter terhadap pengaruh noise untuk suatu alat, yang telah dihitung matrik kovarian dari input data diperoleh
K =
2
1
1
2
Mahalanobis distance dari titik x (1,1) terhadap titik pusat, dengan matrik kovarin di atas diperoleh :
))
0
,
0
(
)
1
,
1
((
5
4
4
5
))
0
,
0
(
)
1
,
1
((
)
(
1 2−
−
=
− Tx
d
d (x) = 0.47Mahalanobis distance untuk titik (-1,1) terhadap titik pusat, dengan matrik kovarian (penyebaran data) yang sama, diperoleh :
))
0
,
0
(
)
1
,
1
((
5
4
4
5
))
0
,
0
(
)
1
,
1
((
)
(
1 2−
−
−
−
=
− Tx
d
d ( x ) = 1.41Jika dilihat secara Ruang-Euclidian posisi titik (-1,1) dan titik (1,1), mempunyai jarak yang sama dengan titik pusat. Akan tetapi jarak mahalanobis untuk titik (1,1) lebih kecil dibandingkan jarak dari (-1,1). Hal ini disebabkan dengan perhitungan Mahalanobis distance diperhatikan pula faktor penyebaran datanya. Sehingga posisi titik (1,1) yang terpilih karena jika dilihat pula dari proyeksi bidang elipsoida, maka titik tersebut termasuk dalam bidang tersebut.
KESIMPULAN
1. Perhitungan jarak minimum dapat digunakan pada tehnik clustering (pengelompokan) dalam logika samar (fuzzy logic) khususnya, dan pengolahan citra (image processing) umumnya.
2. Perhitungan jarak di antara dua titik dapat diperluas menjadi perhitungan mencari jarak minimum dari satu titik ke beberapa titik yang membentuk bidang.
3. Apabila l adalah segmen garis dari a1 ke a2 dalam ruang euclidean-n dan L adalah garis dari b1 dan b2 dalam ruang euclidean-n. Dapat ditentukan proyeksi dari l
pada L yang memberikan posisi terdekat dari segmen garis l dan garis L
4. Apabila suatu bidang dilalui oleh beberapa titik dan titik-titik tersebut tidak melalui titik pusat maka agar syarat suatu ruang vektor terpenuhi yaitu harus mengandung vektor nol, maka salah satu titik harus digeser menjadi titik pusat, yang diikuti oleh titik-titik lain. Kemudian hasil posisi titik proyeksi harus dikembalikan ke bentuk semula demikian pula titik yang diproyeksikan.
5. Sistim Mahalanobis sangat baik untuk input data yang berkorelasi.
6. Mahalanobis Distance membantu analisis pengelompokan dalam konsep jarak minimum untuk data yang berkorelasi, dengan memperhitungkan matrik kovarian.
DAFTAR PUSTAKA
1. BANDEMER, HANS; GOTTWALD, SIEGFRIED, “Fuzzy Sets, Fuzzy Logic, Fuzzy Methods with Applications”, John Wiley & Sons Ltd., England (1995) 2. GRAYBILL, FRANGKLIN A., “Introduction to Matrices with Application in
Statistics”, Colorado State University, Wadsworth Publishing Company, Inc., Belmont, California (1969)
3. KOSKO, BART, “Fuzzy Engineering”, University of Southern California, Prentice-Hall, Inc., New Jersey, (1997)
4. ROMLI, UPT-LAGG, BPP TEKNOLOGI, “Clustering Analysis”, Lokakarya Komputasi dalam Sains dan Teknologi Nuklir VI, BATAN, Jakarta (1996)
DISKUSI
M. SYAMSA ARDISASMITA
Jika suatu titik-titik terkorelasi kuat, bagaimana pengaruhnya terhadap pengukuran jarak Mahalanobis?
MIKE SUSMIKANTI
Jarak Mahalanobis dapat digunakan tergantung pada data. Bilamana sampel data menyebar atau noise, kovariansi dari cluster akan besar. Hal ini akan memberikan elipsoida yang besar. Sebaliknya bila penyebaran data-data menyempit/rapat, kovariansi dari cluster akan kecil berarti elipsoidanya kecil. Penyebaran data dapat merubah ukuran dari bidang elipsoida. Berarti setiap matrik kovariansi membentuk elipsoida. Jadi, jika suatu titik-titik terkorelasi kuat maka jarak Mahalanobis akan kecil.
MUSTANGIMAH
Dikatakan bahwa jarak minimum banyak diaplikasikan dalam clustering. Dalam
clustering secara berhirarki atau non-hirarki jarak minimum ini dapat diterapkan untuk
memperoleh hasil yang terbaik?
MIKE SUSMIKANTI
Dapat diterapkan pada clustering non-hirarki. Jarak Mahalanobis merupakan pengembangan dari clustering non-hirarki K-mean.
DAFTAR RIWAYAT HIDUP
1. Nama : MIKE SUSMIKANTI
2. Tempat/Tanggal Lahir : Jakarta, 12 November 1956
3. Instansi : P2TIK - BATAN
4. Pekerjaan / Jabatan : Bidang Matematika dan Komputasi/ Pranata Komputer
5. Riwayat Pendidikan : (setelah SMA sampai sekarang)
• FMIPA-UI, Jurusan Matematiak Statistika (S1)
• STIE-IGI, Jurusan Manajemen (S2)
6. Pengalaman Kerja :
• Staf Pengolahan Data Biro Bina Program • Ka. Sub. Bidang Statistik, Bidang Analis Sistem • Staf Bidang Komputasi (Pranata Komputer) 7. Organisasi Professional :
![Gambar 1. Jarak terdekat dari titik p terhadap garis l yang dinyatakan dengan D Bidang yang melalui n titik-titik b 1 , b 2 , …., b n sedemikian sehingga matrik B = [b 1 , b 2 , …., b n ] mempunyai rank n, didefinisikan sebagai kumpulan titik-titik P ya](https://thumb-ap.123doks.com/thumbv2/123dok/4233004.2869945/3.918.156.653.219.615/gambar-jarak-terdekat-dinyatakan-bidang-mempunyai-didefinisikan-kumpulan.webp)