BEBERAPA FAKTOR YANG MEMENGARUHI KEBERHASILAN PENGGABUNGAN DUA PERUSAHAAN ARIF WICAKSONO UTOMO

BEBERAPA FAKTOR YANG MEMENGARUHI

KEBERHASILAN PENGGABUNGAN

DUA PERUSAHAAN

ARIF WICAKSONO UTOMO

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

BOGOR 2013

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*

Dengan ini saya menyatakan bahwa skripsi berjudul Beberapa Faktor yang Memengaruhi Keberhasilan Penggabungan Dua Perusahaan adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Desember 2013 Arif Wicaksono Utomo NIM G54061662

ABSTRAK

ARIF WICAKSONO UTOMO. Beberapa Faktor yang Memengaruhi Keberhasilan Penggabungan Dua Perusahaan. Dibimbing oleh I GUSTI PUTU PURNABA dan RETNO BUDIARTI.

Perusahaan akan membayar dividen kepada para pemegang saham sedemikian rupa sehingga besarnya akumulasi total pembayaran dividen yang dihitung berdasarkan nilai sekarang sesuai harapan pemegang saham. Dividen akan dibayarkan berdasarkan strategi barier, artinya jika surplus perusahaan telah melebihi optimal barrier keuntungan perusahaan, maka kelebihan dari barrier keuntungan tersebut semuanya akan dibayarkan sebagai dividen kepada para pemegang saham. Pembayaran dividen akan terhenti bila perusahaan mengalami kebangkrutan. Jumlah pendapatan bersih yang dihasilkan oleh gabungan dua perusahaan dimodelkan dengan gerak Brown bivariat dengan parameter drift µ dan ragam per satuan waktu. Fungsi surplus merupakan turunan model gerak Brown dan dari fungsi surplus didapatkan hasil tentang potensi untung dan rugi pada penggabungan dua perusahaan. Jika optimal barrier perusahaan gabungan lebih kecil dari hasil penjumlahan optimal barrier setiap perusahaan, untuk nilai koefisien korelasi  sama dengan satu, dan hasil kali dari nilai tingkat bunga  dengan koefisien ragam dari proses agregat pendapatan bersih setiap perusahaan pada tingkat suku bunga kurang dari 6,87%, maka merger akan mendapatkan keuntungan.

Kata kunci: gabungan, dividen optimal, strategi barrier, gerak Brown.

ABSTRACT

ARIF WICAKSONO UTOMO. Several Factors that Influence the Merger Process of Two Companies. Supervised by I GUSTI PUTU PURNABA and RETNO BUDIARTI.

A company will payout dividends to its shareholders in such a way it maximizes the expectation of discounted dividends. Dividends are paid according to strategy barrier. The strategy barrier is to pay dividends to shareholders whenever the surplus attains the optimal barriers. The dividend payments are stopped whenever the company becomes ruin. The aggregate net income stream of two companies are modeled by bivariate Brownian motion with µ as a drift parameter and as a variance parameter per unit time. Surplus function can be obtained by using the model of Brownian motion. It is used to obtain result about the potensial gain or loss upon merging two companies. If the combined company's optimal barrier is smaller than the sum of the optimal barrier of each companies, for the value of correlation coefficient  equals to one, and for each companies, multiplication of interest  and the square of the coefficient of variation of its aggregate net income process is less than 6,87%, so the merger of two companies would be benefit.

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

BEBERAPA FAKTOR YANG MEMENGARUHI

KEBERHASILAN PENGGABUNGAN DUA PERUSAHAAN

ARIF WICAKSONO UTOMO

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

BOGOR 2013

Judul Skripsi : Beberapa Faktor yang Memengaruhi Keberhasilan Penggabungan Dua Perusahaan

Nama : Arif Wicaksono Utomo

NIM : G54061662

Disetujui oleh

Dr Ir I Gusti Putu Purnaba, DEA Pembimbing I Ir Retno Budiarti, MS Pembimbing II Diketahui oleh Dr Toni Bakhtiar, MSc Ketua Departemen Tanggal Lulus:

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Topik yang dipilih dalam penelitian yang dilaksanakan sejak bulan Juli 2012 ini optimasi dividen, dengan judul Beberapa Faktor yang Memengaruhi Keberhasilan Penggabungan Dua Perusahaan.

Terima kasih penulis ucapkan kepada Bapak Dr. Ir. I Gusti Putu Purnaba, DEA. dan Ibu Ir. Retno Budiarti MS. selaku dosen pembimbing, serta seluruh dosen di Departemen Matematika IPB yang telah banyak memberikan pelajaran tentang berbagai ilmu Matematika kepada penulis. Tak lupa terima kasih juga untuk para staf tata usaha serta staf perpustakan Departemen Matematika IPB yang telah banyak membantu penulis dalam hal administrasi perkuliahan semasa penulis menjalani masa-masa kuliah. Terima kasih juga untuk teman-teman Math 43 untuk dukungan dan doa serta persahabatan yang telah terjalin selama ini. Ungkapan terima kasih juga disampaikan kepada ayah, ibu, adik serta seluruh keluarga atas segala doa, dukungan dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

Bogor, Desember 2013 Arif Wicaksono Utomo

DAFTAR ISI

DAFTAR GAMBAR x DAFTAR LAMPIRAN x PENDAHULUAN 1 Latar Belakang 1 Perumusan Masalah 1 Tujuan Penelitian 1 TINJAUAN PUSTAKA 2

HASIL DAN PEMBAHASAN 10

Formulasi Masalah 10

Optimal Barrier 13

Situasi Sebelum dan Setelah Penggabungan 14

Syarat Cukup untuk Penggabungan 16

Generalisasi 17

SIMPULAN DAN SARAN 18

Simpulan 18

Saran 18

DAFTAR PUSTAKA 19

LAMPIRAN 20

DAFTAR GAMBAR

1 Ilustrasi M(t), D(t), dan X(t) 11

2 Ilustrasi nilai harapan dari present value dividen perusahaan V(x;b)

sebagai fungsi dari modal awal x 13

3 Grafik turunan kedua g(y)terhadap y 14

DAFTAR LAMPIRAN

1 Pembuktian Teorema 2 21

2 Pembuktian Persamaan (2) 23

3 Pembuktian Persamaan (5), (7) dan (8) 25

4 Pembuktian Persamaan (11) 27

5 Pembuktian Persamaan (12) 28

6 Pembuktian Persamaan (14) 29

PENDAHULUAN

Latar Belakang

Pada zaman modern seperti sekarang ini, perusahaan melakukan berbagai cara untuk meningkatkan keuntungan serta mempelajari cara untuk mengantisipasi risiko-risiko yang menyebabkan kerugian hingga berpotensi menyebabkan kebangkrutan bagi perusahaan tersebut. Salah satu solusi untuk mengantisipasi hal di atas adalah dengan melakukan penggabungan antara dua perusahaan dan menentukan faktor-faktor apa saja sehingga penggabungan dua perusahaan dapat meningkatkan surplus atau keuntungan perusahaan tersebut.

Proses surplus adalah proses akumulasi kekayaan yang diperoleh dengan penjumlahan modal awal (initial capital) dengan total pendapatan yang masuk kemudian dikurangi dengan total dividen yang dibayarkan kepada pemegang saham. Bila suatu ketika besar modal dan total pendapatan perusahaan lebih kecil dari jumlah akumulasi dari dividen yang harus dibayar maka perusahaan mengalami kerugian yang berpotensi mengalami kebangkrutan. Kerugian ini disebabkan karena jumlah dividen yang dibayar melebihi batas kemampuan dari perusahaan tersebut sehingga diperlukan suatu strategi optimasi dividen untuk menentukan batasan banyaknya modal yang optimal sehingga dividen dapat mulai dibayar pada suatu batasan modal tersebut.

Tulisan ini merupakan rekonstruksi dari tulisan Gerber dan Shiu (2006) yang berjudul “ On The Merger of Two Companies”.

Perumusan Masalah

Asumsi awal, perusahaan akan membayar dividen kepada pemegang saham sedemikian rupa sehingga dapat memaksimalkan present value dari total angsuran pembayaran dividen sesuai harapan pemegang saham. Pembayaran dividen akan terhenti bila perusahaan mengalami kebangkrutan. Nilai sekarang (present value) dari perusahaan sendiri adalah nilai dari total pendapatan yang masuk kas perusahaan dikurangi dengan dividen yang dibayarkan sebagai kas keluar, yang nilainya sesuai dengan yang telah disepakati antara para pemegang saham dengan perusahaan sesuai dengan strategi optimasi dividen.

Tujuan Penelitian

Tujuan karya ilmiah ini adalah untuk mengetahui faktor-faktor yang memengaruhi keberhasilan penggabungan dua perusahaan.

2

TINJAUAN PUSTAKA

Untuk memahami masalah-masalah yang terjadi pada karya tulis ini diperlukan pengertian beberapa konsep berikut ini.

Ruang Contoh, Kejadian, dan Peluang

Definisi 1 (Percobaan Acak)

Suatu percobaan yang dapat diulang dalam kondisi yang sama, yang hasilnya tidak bisa diprediksi secara tepat, tetapi kita bisa mengetahui semua kemungkinan hasil yang muncul disebut percobaan acak.

(Hogg dan Craig 1995)

Definisi 2 (Ruang Contoh)

Ruang contoh adalah himpunan semua hasil yang mungkin dari suatu percobaan acak, dan dinotasikan dengan .

(Grimmett dan Stirzaker 1992)

Definisi 3 (Kejadian)

Kejadian adalah suatu himpunan bagian dari ruang contoh .

(Grimmett dan Stirzaker 1992)

Definisi 4 (Kejadian Lepas)

Kejadian A dan B disebut saling lepas jika irisan dari keduanya adalah himpunan kosong

(Grimmett dan Stirzaker 1992)

Definisi 5 (Medan- )

Medan- adalah suatu himpunan yang anggotanya terdiri atas himpunan bagian ruang contoh , yang memenuhi syarat berikut:

1.

2. Jika , maka

3. Jika , maka

(Hogg et al. 2005)

Definisi 6 (Ukuran Peluang)

Misalkan adalah ruang contoh suatu percobaan acak dan adalah medan-pada . Suatu fungsi P yang memetakan unsur-unsur ke himpunan bilangan nyata () atau  disebut ukuran peluang jika:

1. P tak negatif, yaitu untuk setiap ,

2. P bersifat aditif tak hingga, yaitu jika dengan maka

3. P bernorma satu, yaitu

Pasangan disebut ruang peluang atau ruang probabilitas.

3

Definisi 7 (Kejadian Saling Bebas)

Kejadian A dan B dikatakan saling bebas jika: = .

Secara umum, himpunan kejadian dikatakan saling bebas jika

untuk setiap himpunan bagian J dari I.

(Grimmett dan Stirzaker 1992)

Peubah Acak dan Fungsi Sebaran

Definisi 8 (Peubah Acak)

Misalkan Ω adalah ruang contoh dari suatu percobaan acak. Fungsi yang terdefinisi pada Ω yang memetakan setiap unsur  ke satu dan hanya satu bilangan real disebut peubah acak.

Ruang dari adalah himpunan bagian bilangan real

Peubah acak dinotasikan dengan huruf kapital, misalnya Sedangkan nilai peubah acak dinotasikan dengan huruf kecil seperti x, y, z.

(Hogg et al. 2005)

Definisi 9 (Peubah Acak Diskret)

Peubah acak dikatakan diskret jika semua himpunan nilai dari peubah acak tersebut merupakan himpunan tercacah.

(Hogg et al. 2005)

Definisi 10 (Fungsi Sebaran)

Misalkan adalah peubah acak dengan kejadian Misalkan kejadian maka peluang dari kejadian adalah

Fungsi F_X disebut fungsi sebaran dari peubah acak .

(Hogg et al. 2005)

Definisi 11 (Fungsi Massa Peluang)

Fungsi massa peluang dari peubah acak diskret adalah fungsi  yang diberikan oleh:

(Hogg et al. 2005)

Definisi 12 (Peubah Acak Poisson)

Suatu peubah acak dikatakan menyebar Poisson dengan parameter , jika memiliki fungsi massa peluang:



_

(Hogg et al. 2005)

Definisi 13 (Peubah Acak Kontinu)

Peubah acak dikatakan kontinu jika fungsi sebarannya dapat diekspresikan sebagai

4

untuk suatu fungsi  yang dapat diintegralkan. Selanjutnya fungsi disebut fungsi kepekatan peluang (probability density function)bagi .

(Hogg et al. 2005)

Definisi 14 (Peubah Acak Eksponensial)

Peubah acak kontinu disebut menyebar eksponensial dengan parameter  jika fungsi kepekatan peluangnya diberikan oleh

 

(Hogg et al. 2005)

Definisi 15 (Peubah Acak Gamma)

Peubah acak kontinu disebut menyebar Gamma dengan parameter jika fungsi kepekatan peluangnya diberikan oleh

  _

(Hogg et al. 2005)

Definisi 16 (Fungsi Sebaran dan Kepekatan Peluang Marjinal)

Misalkan and adalah peubah acak kontinu yang menyebar bersama dengan fungsi sebaran dan fungsi kepekatan peluang bersama . Fungsi sebaran marjinal dari peubah acak dan adalah masing-masing

Fungsi kepekatan peluang marjinal dari peubah acak X dan Y adalah masing-masing

(Ghahramani 2005)

Teorema 1 (Peubah Acak Bebas)

Misalkan adalah n peubah acak kontinu dengan fungsi kepekatan peluang bersama dan fungsi kepekatan peluang marjinal masing-masing Peubah-peubah acak dikatakan bebas secara bersama jika dan hanya jika

Bukti Teorema 1 dapat dilihat di Ghahramani, 2005.

Definisi 17 (Sebaran Bersyarat Peubah Acak Kontinu)

Misalkan dan adalah peubah acak kontinu dengan fungsi sebaran bersama

Fungsi sebaran bersyarat dari dengan syarat ditulis

5

untuk sembarang x dan fY(y)0.

(Ghahramani 2005)

Definisi 18 (Fungsi Kepekatan Peluang Bersyarat)

Misalkan dan merupakan dua peubah acak kontinu dengan fungsi kepekatan peluang bersama maka fungsi kepekatan peluang bersyarat X dengan syarat ditulis diberikan oleh

untuk sembarang x dan

(Ghahramani 2005)

Momen, Nilai Harapan, dan Ragam

Definisi 19 (Nilai Harapan Peubah Acak Kontinu)

Misalkan adalah peubah acak kontinu dengan fungsi kepekatan peluang Nilai harapan dari dinotasikan dengan adalah

jika integral di atas konvergen. Jika integral di atas divergen, maka nilai harapan dari tidak ada.

(Hogg et al. 2005)

Definisi 20 (Ragam Peubah Acak Kontinu)

Misalkan adalah peubah acak kontinu dengan fungsi kepekatan peluang dan nilai harapan . Ragam dari X dinotasikan dengan atau _X2 adalah 2_X E((X E(X))2)



     (x E(X))2 f_X(x)dx

jika integral di atas konvergen. Jika integral di atas tidak konvergen maka ragam dari tidak ada.

(Hogg et al. 2005)

Definisi 21 (Nilai Harapan Bersyarat)

Misalkan dan merupakan peubah acak kontinu dengan fungsi kepekatan peluang bersama dan fungsi kepekatan peluang bersyarat dari dengan syarat adalah Nilai harapan bersyarat dari dengan syarat diberikan oleh dengan

(Ghahramani 2005)

Proses Stokastik Definisi 22 (Proses Stokastik)

Proses stokastik adalah suatu himpunan dari peubah acak yang memetakan suatu ruang contoh  ke suatu ruang state (state space) S.

6

(Ross 1996)

Definisi 23 (Proses Pencacahan)

Proses stokastik disebut proses pencacahan (counting process) jika menyatakan banyaknya kejadian (events) yang telah terjadi sampai waktu t. Jadi proses pencacahan N(t)harus memenuhi:

(i)

(ii) Nilai adalah integer. (iii) Jika , maka

(iv) Untuk , maka sama dengan banyaknya kejadian yang terjadi pada selang

(Ross 1996) Kadangkala, proses pencacahan ditulis yang menyatakan banyaknya kejadian yang terjadi pada selang waktu ].

Suatu proses pencacahan disebut memiliki inkremen bebas jika banyaknya kejadian yang terjadi pada sembarang dua selang waktu yang tidak tumpang tindih (tidak overlap) adalah bebas. Sedangkan suatu proses pencacahan disebut memiliki inkremen stasioner jika sebaran dari banyaknya kejadian yang terjadi pada sembarang selang waktu, hanya tergantung dari panjang selang tersebut. Salah satu proses pencacahan yang penting adalah proses Poisson, yang juga merupakan salah satu contoh penting dari proses stokastik dengan waktu kontinu.

Definisi 24 (Proses Poisson)

Suatu proses pencacahan disebut proses Poisson dengan intensitas ,

 jika: (i)

(ii) Proses tersebut memiliki inkremen bebas dan stasioner.

(iii) Banyaknya kejadian pada sembarang waktu dengan panjang t, memiliki sebaran Poisson dengan rataan (mean)  . Jadi, untuk semua dan maka:

 

(Ross 1996)

Definisi 25 (Waktu Antar Kedatangan)

Barisan {Xn,n1,2,...} disebut barisan waktu antar kedatangan (sequence of interarrival times) dari suatu proses Poisson, dengan X_n menyatakan jarak antar waktu kejadian proses Poisson ke-(n-1) dengan kejadian proses Poisson ke-n.

7

Integral Parsial Definisi 26 (Integral Parsial)

Aturan yang berkaitan dengan aturan hasil kali untuk turunan disebut aturan pengintegralan parsial dengan formula Misalkan, jika dan , maka turunannya adalah dan . Dengan demikian, menurut aturan substitusi, rumus pengintegralan parsial menjadi

(Stewart 1998)

Hukum Total Peluang

Definisi 27 (Hukum Total Peluang)

Misalkan ruang contoh  dipartisi ke dalam buah kejadian yang saling lepas satu dengan yang lainnya. Kejadian-kejadian tersebut memiliki , dimana Misalkan terdapat suatu kejadian yang lain dengan , maka berlaku kejadian-kejadian terhadap sebagai berikut:

di mana diasumsikan saling lepas satu dengan yang lain, sehingga diperoleh sebagai berikut:

dengan peluang bersyarat dapat ditulis

Jadi didapat dengan penguraian secara rinci sebagai beirikut:

inilah yang disebut sebagai hukum total peluang.

(Hogg et al. 2005)

Waktu Kebangkrutan

Definisi 28 (Waktu Kebangkrutan)

Misalkan T menyatakan waktu kebangkrutan dan U(t) surplus perusahaan pada waktu t. Maka waktu kebangkrutan yang dinotasikan dengan T adalah waktu di mana nilai surplus perusahaan bernilai negatif U(t)<0.

(Dickson et al. 2004)

Gerak Brown (Brownian Motion)

Definisi 29 (Gerak Brown)

Proses stokastik waktu kontinu adalah Gerak Brown jika: 1) , di mana adalah fungsi kontinu dari

8

3) Untuk setiap , W_t berdistribusi normal dengan nilai harapan 0 dan ragam

(Klugman et al 1998)

Definisi 30 (Gerak Brown dengan Parameter Drift)

Proses stokastik waktu kontinu dinamakan gerak Brown adalah proses stokastik dengan nilai harapan dan ragam 2

, untuk suatu dan

0



 . Persamaannya sebagai berikut:

) ( )

(t t W t

X  

Dengan kata lain gerak Brown adalah proses stokastik dengan  _sebagai parameter drift dan 2 parameter ragam, dengan modal awal X(0) = x. Berdasarkan salah satu sifat gerak Brown menyatakan setiap inkremen menyebar normal dangan dan

Misal didefinisikan dan maka (a1) Dari persamaan (a1) dapat dilihat

(a2) (a3) (a4) , (a5) (Taylor dan Karlin 1998)

Teorema 2

Gerak Brown (Brownian motion) dengan parameter driftdan parameter ragam , untuk a < x < b dapat dituliskan.

, untuk a < x < b. (Taylor dan Karlin 1998) Bukti Teorema 2 disajikan pada Lampiran 1.

9

HASIL DAN PEMBAHASAN

Formulasi Masalah

Gerber et al. (2004) menyatakan bahwa sebuah perusahaan memiliki modal awal x > 0. Jika tidak ada dividen yang dibayarkan maka fungsi surplus yang diturunkan dari model gerak Brown dengan parameter drift  dan parameter ragam sehingga modelnya dapat ditulis sebagai berikut:

(1) Keterangan:

 adalah fungsi surplus yang merupakan model gerak Brown dengan parameter drift  dan ragam untuk nilai .

 x adalah modal awal, .

 adalah gerak Brown.

Perusahaan akan membayarkan dividen berdasarkan optimal barrier-nya dengan parameter optimal barrier . Artinya, pada saat surplus perusahaan mencapai atau melebihi b, maka kelebihan arus kas tersebut akan dibayarkan sebagai dividen.

Misalkan adalah nilai maksimum yang dapat dicapai oleh maka dapat ditulis:

Kemudian, misalkan dinotasikan sebagai dividen agregat yang dibayarkan antara waktu 0dan waktu t, maka

Diasumsikan bahwa pembayaran dividen tidak memiliki pengaruh terhadap keberlangsungan perusahaan, sehingga fungsi surplus pada waktu t dapat diubah menjadi X(t) – D(t)di mana X(t) adalah surplus perusahaan dan D(t) adalah dividen yang dibayar oleh perusahaan.

Misalkan juga D menyatakan present value dari akumulasi pembayaran dividen hingga terjadinya kebangkrutan dengan

di mana

10

menyatakan waktu ketika perusahaan bangkrut. Misalkan , menyatakan nilai harapan present value dari akumulasi pembayaran dividen hingga bangkrut, ditulis:

Gambar 1 Ilustrasi Grafik

Sebagai fungsi dari modal awal x, memenuhi persamaan diferensial homogen orde-2 sehingga dapat ditulis menjadi:

(2) Bukti Persamaan 2 disajikan pada Lampiran 2.

Nilai harapan present value dari akumulasi dividen perusahaan hingga perusahaan tersebut mengalami bangkrut dinotasikan dengan di mana x adalah modal awal dan b adalah ambang batas optimal dividen (optimal barrier).

Fungsi memiliki syarat

, (3) . (4) Persamaan (3) menjelaskan bahwa jika perusahaan mengalami kebangkrutan dan tidak ada dividen yang dibayar. Persamaan (4) menjelaskan bahwa terdapat dua situasi, pertama perusahaan memiliki modal awal sebesar , kedua perusahaan memiliki modal awal sebesar dan bernilai sangat kecil).

Berdasarkan Persamaan (3) dan (4) solusi pada persamaan diferensial homogen Persamaan (2) adalah

11

Misalkan dan berturut-turut adalah pembilang dan penyebut pada fungsi dan (6) dengan ₂ 2 2 2        r (7) dan 2 2 2 2        s (8) 0 

 adalah tingkat suku bunga.

Bukti Persamaan (5), (7), dan (8) disajikan pada Lampiran 3.

Misalkan, b* menyatakan nilai optimal b, artinya b* adalah nilai dari b (ambang batas besarnya modal awal (x) pada saat dividen dapat mulai dibayar) yang meminimumkan misalkan, buat turunan sama dengan nol,

Maka turunan sebagai berikut:

sehingga, (9) (10) Berdasarkan Persamaan (9) dan (5) diperoleh

. (11) Bukti Persamaan (11) disajikan pada Lampiran 4.

Berdasarkan Persamaan (11) dan (2) turunan kedua dari fungsi adalah fungsi kontinu pada saat nilai x sebesar , atau , maka

(12) Bukti Persamaan (12) disajikan pada Lampiran 5.

Bentuk dari fungsi , , dapat dengan mudah diperoleh dengan syarat untuk , dan untuk (lihat Gambar 2).

12

Optimal Barrier

Subbab ini akan menjelaskan mengenai b* yang merupakan optimal barrier atau batasan banyaknya modal yang optimal sehingga dividen bisa dibayarkan kepada pemegang saham. Misalkan merupakan koefisien ragam dari gerak Brown, dapat ditulis sebagai berikut:

(13) Selanjutnya, berdasarkan Persamaan (10), (7), dan (8) diperoleh :

dengan kata lain dapat ditulis sebagai berikut:

(14) di mana (15)

Bukti Persamaan (14) dan (15) disajikan pada Lampiran 6.

Untuk mempermudah melihat hubungan fungsi dengan dapat ditambahkan suatu fungsi bebas pada di mana , dapat ditulis ₍₁₆₎ sehingga (17) dan (18) Gambar 2 Ilustrasi nilai harapan dividen perusahaan

13

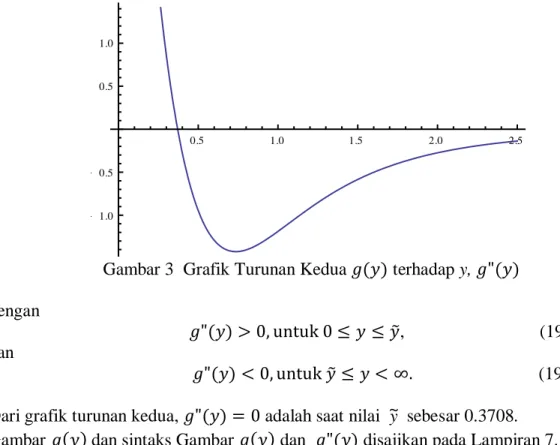
Fungsi dengan y ≥ 0, adalah fungsi naik, dengan dan . Dengan menggunakan suatu software matematika ditemukan nilai saat y~= 0.3708.

Gambar 3 Grafik Turunan Kedua terhadap y, dengan

, (19a) dan

(19b) Dari grafik turunan kedua, adalah saat nilai ~y sebesar 0.3708.

Gambar dan sintaks Gambar dan disajikan pada Lampiran 7.

Situasi Sebelum dan Setelah Penggabungan

Misalkan dua perusahaan, dengan variabel j = 1, 2, diasumsikan bahwa keuntungan perusahaan yang merupakan selisih dari pemasukan perusahaan dikurangi pengeluaran perusahaan dalam bentuk dividen adalah gerak Brown dengan parameter drift jdan ragam

2 j

 per satuan waktu. Optimal barrier untuk dividen perusahaan j adalah

b*_j _jf(_j), (20) dengan f(j)didefinisikan pada Persamaan (17) dan

j j j _    (21) Misalkan V_j(x;b)menunjukkan nilai harapan dari present value akumulasi dividen perusahaan j hingga mengalami kebangkrutan, x adalah modal awal perusahaan dan strategi barrier sesuai dengan parameter b yang digunakan. Selanjutnya, diasumsikan bahwa jumlah dari proses pendapatan bersih (sebelum pembayaran dividen) adalah gerak Brown bivariat dengan koefisien korelasi . Diasumsikan bahwa penggabungan tidak memengaruhi model dan parameternya. Karena itu, setelah penggabungan hasil dari penjumlahan proses surplus (sebelum pembayaran dividen) adalah gerak Brown, dengan:

0.5 1.0 1.5 2.0 2.5

1.0 0.5 0.5 1.0

14

(22) dan

(23) sehingga, optimal barrier dari dividen perusahaan setelah penggabungan adalah

(24) dengan

(25)

Misalkan V_m(x;b)menyatakan nilai harapan dari present value akumulasi dividen perusahaan yang digabung hingga mengalami kebangkrutan. Kemudian keuntungan hasil penggabungan dua perusahaan adalah

(26) di mana x_jadalah banyaknya modal awal dari perusahaan j, j = 1, 2 dan adalah banyaknya modal dari dua perusahaan yang bergabung. Setiap persamaan dari tiga persamaan yang ada pada Persamaan (26) dapat dihitung dengan menggunakan penjabaran dari Persamaan (5), (7), (8) dan (10). Keuntungan penggabungan adalah jika persamaan (26) bernilai positif. Kemudian dari persamaan (12) dan (25) dapat ditarik kesimpulan di mana Persamaan (26) dapat menggambarkan kondisi perusahaan yang digabung akan mengalami untung atau rugi sebagai berikut:

(27) dengan asumsi  yang sama berlaku untuk setiap perusahaan. Misalkan diasumsikan bahwa present value perusahaan j adalah , j = 1, 2 dan ) adalah jumlah banyaknya modal perusahaan yang telah bergabung. Terdapat dua kesimpulan yang diakibatkan Persamaan (26):

a. Jika (28) maka, (29) artinya, hasil penggabungan perusahaan dalam kondisi positif atau perusahaan untung.

b. Jika

15 maka, (31) artinya, present value penggabungan perusahaan dikurangi dengan jumlah present value dari dua perusahan jika tidak digabung bernilai negatif yang artinya penggabungan perusahaan dinilai merugikan untuk dua perusahaan tersebut.

Penjelasan lebih lanjut mengenai keuntungan hasil penggabungan adalah dengan melihat Gambar 2, dengan menyesuaikan menjadi dan menjadi . Keuntungan penggabungan dapat dilihat dari banyaknya jumlah modal pada masing-masing perusahaan.

Jika Persamaan (28) terpenuhi maka penggabungan menghasilkan keuntungan: . Jika Persamaan (30) terpenuhi maka penggabungan mengakibatkan kerugian:

.

Syarat Cukup untuk Penggabungan

Subbab ini memiliki tujuan mendapatkan syarat cukup untuk Persamaan (24). Jika=1, berdasarkan Persamaan (25) bahwa

Persamaan di atas dapat ditulis sebagai rata-rata tertimbang dari dan :

.

Jadi, jika maka juga memiliki nilai yang sama dengan dan , dan * 2 * 1 * b b

bm   . Jika , berdasarkan Persamaan (28)

(32)

Persamaan (32) sesuai dengan kondisi penggabungan menghasilkan keuntungan pada Persamaan (28) yang disebabkan dari Persamaan (24) dan (20), untuk membuktikan syarat cukup Persamaan (32), merupakan fungsi convex untuk nilai antara dan , atau f"()0 untuk nilai  antara dan . Sekarang dapat dilihat Persamaan (19a), g"(y)0 _untuk 0 y~y0,3708 hal tersebut diketahui dari Persamaan (17) bahwa

16

untuk j = 1 dan j = 2, kita dapat membuktikan Pertidaksamaan (30). Akibatnya, untuk kedua perusahaan (perusahaan 1 dan perusahaan 2) berlaku

Dari hasil di atas, dapat disimpulkan bahwa perusahaan akan untung bila hasil kali dari nilai tingkat suku bunga ( ) dengan ragam (2) kurang dari 6,87%.

Generalisasi

Cai et al. (2006) mengembangkan model pada Persamaan (12) dengan mengasumsikan bahwa tingkat bunga yang dikenakan pada seluruh akumulasi modal pada tingkat bunga konstan, yang pada karya ilmiah ini dinyatakan dengan , Kita misalkan menyatakan nilai harapan dari dividen yang didiskon hingga bangkrut, jika strategi barrier sesuai dengan parameter b yang digunakan, dan misalkan *b menyatakan optimal barrier. Untuk  0, Cai et al (2006) membuktikan bahwa

(33) merupakan pengembangan dari Persamaan (17). Selanjutnya, dan untuk 0 < x < b*, dan untuk . Oleh karena itu, Gambar 1 tetap berlaku jika kita mengganti pada sumbu x dengan . Misal dua saham perusahaan, yang diberi label 1 dan 2, kemudian V₁ dan 2

V adalah nilai harapan dari present value fungsi dividen, dan dan berturut-turut adalah optimal barrier. Untuk perusahaan yang akan digabung, misalkan merupakan nilai harapan dari present value fungsi dividen gabungan dua perusahaan dan adalah optimal barrier-nya. Dari Persamaan (22) dan (32) bahwa

yang merupakan Persamaan (27) yang diperumum (generalisasi).

Penggabungan menghasilkan keuntungan bila kondisi pada Persamaan (28) terpenuhi. Jika Persamaan (28) terpenuhi maka keuntungan yang didapatkan sebesar

Sebaliknya jika yang terpenuhi Persamaan (30) maka kerugian yang diakibatkan penggabungan perusahaan sebesar

17

SIMPULAN DAN SARAN

Simpulan

Berdasarkan pembahasan yang telah disajikan sebelumnya dapat disimpulkan bahwa terdapat beberapa faktor yang harus dipenuhi sehingga perusahaan akan menghasilkan keuntungan. Pada saat surplus perusahaan mencapai optimal barrier penggabungan dua perusahaan akan menguntungkan jika:

sehingga

.

Untuk nilai  =1, didapatkan suatu syarat cukup sehingga penggabungan dua perusahaan dapat menguntungkan, yaitu pada saat

Artinya perusahaan akan untung pada saat hasil kali dari tingkat suku bunga () dan ragam ) kurang dari 6,87% untuk kedua perusahaan yang bergabung.

Saran

Untuk permasalahan selanjutnya disarankan untuk menganalisis lebih lanjut mengenai waktu dapat dilakukannya penggabungan, atau lebih tepatnya, kapan waktu yang tepat untuk malakukan penggabungan dua perusahaan.

DAFTAR PUSTAKA

Cai J, Gerber HU, Yang H. 2006. Optimal dividends in an ornstein-uhlenbeck type model with credit and debit interest. North American Actuarial Journal Vol 10(2):94-108.

Dickson, David CM, Waters HR. 2004. Some optimal dividends problems. ASTIN Bulletin 34:49–74.

Gerber HU, Shiu ESW. 2004. Optimal dividends analysis with brownian motion. North American Actuarial Journal Vol. 8(1):1-20.

Gerber HU, Shiu ESW. 2006. On the merger of two companies. North American Actuarial Journal Vol. 10(3):1-8.

Ghahramani S. 2005. Fundamentals of Probability with Stochastic Processes. Ed ke-3. New Jersey (US): Pearson Prentice Hall.

18

Grimmet GR, Stirzaker DR. 1992. Probability and Random Process. Ed ke-3. Oxford (GB): Clarendon Press.

Hogg RV, Craig AT. 1995. Introduction to Mathematical Statistics. Ed ke-5. New Jersey (US): Prentice Hall, Inc.

Hogg RV, Craig AT, McKean JW. 2005. Introduction to Mathematical Statistics. Ed Ke-6. New Jersey (US): Prentice Hall, Englewood Cliffs.

Klugman SA, Panjer HH, Willmot GE. 1998. Loss Models – From Data to Decisions. NewYork (US):John Wiley & Sons.

Ross SM. 1996. Stochastic Processes. Ed ke-2. New York. John Wiley & Sons. Ross SM. 2000. Introduction to Probability Models. Ed ke-7. California (US):

Academic Press.

Stewart J. 1998. Terjemahan dari: Calculus. Ed. ke-4. Susila IN dan Gunawan H. Jakarta (ID): Penerjemah Erlangga.

Taylor HM, Karlin S. 1998. An Introduction to Stochastic Modeling. Ed ke-3. New York (US): Academic Press.

19

Lampiran 1 Pembuktian Teorema 2

Berdasarkan Taylor dan Karlin (1998) untuk membuktikan Teorema 2, terdapat dua asumsi yang harus dipenuhi, yaitu:

1. Diasumsikan u(x) merupakan fungsi yang dapat diturunkan dua kali. 2. Diasumsikan inkremen t, t pada interval (a,b), (t_b t_a), memiliki selisih

nilai yang sangat kecil sehingga dapat diabaikan. Kemudian berdasarkan hukum peluang total, maka:

u(x) = P{X(T) = b|X(0) = x} = [P{X(T) = b|X(0) = x, X(t) = x+X} |X(0) = x] = E[u(x+X)], di mana a < x < b.

Selanjutnya, menggunakan ekspansi deret Taylor maka persamaan u(x+X) dapat ditulis menjadi:

u(x+X)= 2 2 ) ( ) )( ( " 2 1 ) ( ' ) (x u x X u x X o X u       .

Kemudian berdasarkan definisi u(x) di atas maka:

u(x)=E[u(x+X)]=E[ "( )( )2 ( )2 2 1 ) ( ' ) (x u x X u x X o X u       ] = "( ) [( ) ] [ ( ) ] 2 1 ] [ ) ( ' ) (x u x E X u x E X 2 E o X 2 u       .

Kemudian berdasarkan (a2), (a3), a(5) pada Definisi 30, maka: u x u x u x t u"(x) 2tot 2 1 ) ( ' ) ( ) (   u x u x u x t u"(x) 2tot 2 1 ) ( ' ) ( ) (   u x t u"(x) 2tot 2 1 ) ( ' 0    u x  u"(x) o]t 2 1 ) ( ' [ 0  2 .

Misalkan t 0 maka persamaan di atas menjadi suatu persamaan diferensial "( ) 2 2 1 ) ( ' 0u x  u x  , untuk a < x < b. Solusi dari persamaan diferensial di atas adalah:

Misalkan dan , maka persamaan menjadi:  2A2A 2 1 0 A )A 2 1 ( 0 2  . Akar-akar dari persamaan di atas adalah

A= 0 dan 2 2 2₂ 2 1 2 1 0              A A A atau A₁ 0 dan 2 2 2     A

20 ) 2 ( ) 0 ( 2 ) (      x x De Ce x u 2 2 ) (  x De C x u    

di mana C dan D adalah konstanta. Menentukan nilai dari C dan D berdasarkan peluang u(a)=0 dan u(b)=1, artinya peluang u pasti terjadi saat x = b, dan tidak terjadi saat x = a sehingga:

( ) 0 ) 2 ( 2       a De C a u (L1) ( ) 1 ) 2 ( 2       b De C b u (L2) kemudian 0 ) ( ) 2 ( 2       a De C a u 1 ) ( ) 2 ( 2       b De C b u _ 1 2 2 2 2         a b De De [ 2 2 ] 1 2 2          b a e e D 2 2 2 2 1    b a e e D _{ }   . Subtitusi 2 2 2 2 1    b a e e D _{ }   ke Persamaan u(a): ( ) 0 0 . 2 2 2 2 2 2 2 2 2 ) 2 ( 2 2 ) 2 ( ) 2 (               a b a a b a a e e e C e e e C De C a u _{ }                 Didapatkan nilai 2 2 2 2 2 ) 2 (       a b a e e e C _{ }     dan 2 2 2 2 1    b a e e D _{ }   .

Maka solusi khusus untuk u(x) adalah:

2 2 2 2 2 2 2 2 2 2 2 ) 2 ( 1 ) (             x a b a b a e e e e e e x u             2 2 2 2 2 2 2 2 ) (         a b a x e e e e x u _{ }      .

21

Lampiran 2 Pembuktian Persamaan 2

) ( )

(t t W t

X  

Di mana adalah gerak Brown,  adalah parameter drift dan 2 adalah parameter ragam,dengan modal awal

Selanjutnya, V V(xX), dengan menggunakan ekspansi deret Taylor

X x

V( ) dapat ditulis menjadi:

2 2 ) ( ) )( ( " 2 1 ) ( ' ) ( ) (x X V x V x X V x X X V         kemudian V(x)E[V(xX)] "( ) [( )] [ ] 2 1 )] [( ) ( ' ) (x V x E X V x E X2 E t V         sehingga "( ; ) [( )] [ ] 2 1 )] [( ) ; ( ' ) ; ( ) ; (_{x b V x b V x b E X V x b E X}2 _{E t} V        . Berdasarkan Definisi (30) V xb V x b V x bdt V"(x;b)dt 2 ) ; ( ' ) ; ( ) ; ( 2      . Selanjutnya diketahui E[V(x;b)]edtV(x;b). (a5) Dengan menggunakan pendekatan deret Taylor

x n x e n n x _{  }



 1 ! 1 0 . Sehingga ) ; (x b V edt (1dt)V(x;b) V(x;b)dt[V(x;b)]_.

Kemudian dari (a5)

)] ; ( [ ) ; ( )] ; ( [V x b V x b dtV x b E   )] ; ( [ ) ; ( ) ; ( " 2 ) ; ( ' ) ; ( 2 b x V dt b x V dt b x V dt b x V b x V       "( ; ) 0 2 ) ; ( ' )] ; ( [ ) ; ( ) ; ( 2     V xb dtV xb V xb dt V x b dt b x V     "( ; ) 0 2 ) ; ( ' )] ; ( [ 2    dtV x b V x bdt  V x bdt .

22

Lampiran 3 Pembuktian Persamaan (5), (7) dan (8)

0 ) ; ( ) ; ( ' ) ; ( " 2 2    V x b V x b b x V   

Dengan menggunakan persamaan diferensial orde-2 persamaan di atas menjadi 0 2 2 2      A A .

Solusi dari persamaan di atas dapat dicari dengan menggunakan rumus ABC

.

Dari hasil di atas didapatkan dua akar untuk persamaan diferensial di atas

dan

maka solusi umum menjadi:

2 2 2 2 2 2 2 2 ) (               Wex Vex x V

W dan E adalah konstanta, berdasarkan Persamaan (3) dan (4) yang menyatakan dan , maka

V(0)We0(r)Ve0(s) 0V(0)WV 0 dan

V'(b)rWeb(r) sVeb(s) 1 kemudian, untuk V(0) kedua ruas dikalikan reb(r)

V(0)W V 0 b(r)

re

 dan untuk V'(b)kedua ruas dikalikan 1

V

'

(

b

)



rWe

b(r)



sVe

b(s)



1

1 Kemudian untuk mendapatkan V eliminasi b(r)

rWe dari dua persamaan diatas: V(0)rWeb(r) rVeb(r) 0 V'(b)rWeb(r) sVeb(s) 1 _ rVeb(r) sVeb(s) 1 V[reb(r) reb(s)]1 _b(r) 1 _b(s). se re V    

Kemudian untuk mendapatkan W, substitusi V ke Persamaan (0) _{( )} 1 _{( )} 0     _{b r b s} se re W V _b(r) 1 _b(s) se re W   

23 ( ) ₍1_{) ( ) b(r)}1 _b(s) xs s b r b xr se re e se re e x V        _{br bs} xs xr se re e e x V     ( )  atau _{rb sb} sx rx se re e e x V    ) ( dengan 2 2 2 2        r dan ₂ 2 2 2         s

Lampiran 4 Pembuktian Persamaan 11

* * *) ; ( _{rb sb} sx rx se re e e b x V    . Saat x = b*, maka: * * * * *) *; ( _{rb sb} sb rb se re e e b b V    Misal: u = erb*esb* u’ = rerb* sesb* v = rerb* sesb* v’ = r2erb*s2esb* 2 ' ' *) *; ( ' v uv v u b b V   = ) )( ( )] )( [( )] )( [( * * * * * 2 * 2 * * * * * * sb rb sb rb sb rb sb rb sb rb sb rb se re se re e s e r e e se re se re        = ) )( ( ) )( ( 1 _{* * * *} * 2 * 2 * * sb rb sb rb sb rb sb rb se re se re e s e r e e      berdasarkan Persamaan (10) r2erb*s2esb* 0 maka: ) )( ( ) 0 )( ( 1 *) *; ( ' _{* * * *} * * sb rb sb rb sb rb se re se re e e b b V      = 10 1 *) *; ( ' b b  V 0 *) *; ( " b b  V .

Lampiran 5 Pembuktian Persamaan 12

Akan dibuktikan bahwa :    *) *; (b b V Bukti: Berdasarkan Lampiran 3

24 V'(b*;b*)1 dan V"(b*;b*)0 serta ''( ; ) 0 2 ) ; ( ' ) ; ( 2    V x b V x b  V x b (2) Jika x = b = b* merupakan kondisi yang optimal, maka Persamaan Diferensial (2) dapat ditulis menjadi:

0 *) *; ( ' ' 2 *) *; ( ' *) *; ( 2    V b b V b b  V b b

Sehingga dengan cara subtitusi (2.6.1) dan (2.6) ke Persamaan (2)

0 ) 0 ( 2 ) 1 ( *) *; ( 2    V b b   0 *) *; (   V b b  V(b*;b*)    *) *; (b b V .

Lampiran 6 Pembuktian Persamaan 14

Akan dibuktikan bahwa

). ( * f  b 

Berdasarkan Persamaan (7), (8), dan (11)          r s s r b* 2 ln . Di mana 2 2 2 2        r dan ₂ 2 2 2        s sehingga                              2 2 2 2 2 2 2 2 2 2 2 2 2 2 ln 2 2 2 *                 b                2 2 2 2 2 2 2 2 2 ln 2 *          b . Misalkan

subtitusi ke persamaan di atas                2 2 2 2 2 2 2 2 2 2 2 2 2 ln 2 *              b       

25                 2 2 2 2 2 2 2 2 2 2 2 2 2 ln 2 *                b                 2 2 2 2 2 2 1 1 ( 2 1 1 ( ln 2 1 *         b                 2 2 2 2 2 1 1 ( 2 1 1 ( ln 2 1 *      b                 2 2 2 2 2 1 1 ( 2 1 1 ( ln 2 1 *      b . terbukti ) ( * f  b  dengan                2 2 2 2 2 1 1 ( 2 1 1 ( ln 2 1 ) (      f .

Lampiran 7 Sintaks software Mathematica 7 untuk Grafik 3

f[y_] := f''[y] f''[0]0; f''[]2; Plot[f''[y],{y,0,4}]

26 Grafik fungsi Grafik fungsi 1 2 3 4 5 6 7 0.5 1.0 1.5 2.0 0.5 1.0 1.5 2.0 2.5 1.0 0.5 0.5 1.0

27

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta pada tanggal 11 Desember 1987 sebagai anak pertama dari dua bersaudara, anak dari pasangan bapak Grambang Suwahyo dan ibu Sri Nurdayani.

Tahun 1999 penulis lulus dari MI (Madrasah Ibtidaiyah) pambangunan UIN Jakarta. Tahun 2002 penulis lulus dari MTs (Madrasah Tsanawiyah) UIN Jakarta. Tahun 2005 penulis lulus dari SMA Muhammadiyah 25 Setia Budi. Penulis melanjutkan kuliah di IPB pada tahun 2006 melalui jalur SPMB.

Selama mengikuti perkuliahan, penulis aktif dalam bebagai kegiatan kemahasiswaan antara lain GUMATIKA (Gugus Mahasiswa Matematika) sebagai staf kewirausahaan periode 2008-2009. Selain itu penulis terlibat dalam beberapa kegiatan, antara lain: Matematika Ria 2008 dalam rangkaian Pesta sains Nasional 2008, dan berbagai kegiatan yang diselenggarakan oleh GUMATIKA maupun BEM FMIPA IPB.