OPTIMASI TAKLINEAR. (berdasarkan data-data penelitian, disertai program MATLAB 6.5 ) Dr. H.A. Parhusip

(1)

(2)

G R A F I K A

Penerbit Tisara Grafika SALATIGA

2014

Dr. H.A. Parhusip

OPTIMASI TAKLINEAR

(berdasarkan data-data penelitian, disertai

(3)

Hak Cipta dilindungi oleh Undang-undang

Dilarang mengutip atau memperbanyak sebagian atau seluruh buku ini tanpa seijin penulis

Cetakan pertama : Maret 2014

ISBN : 978-602-9493-14-6

Hak Cipta : Pada Penulis

Editor : Dr. Widowati

Desain Sampul : Tisara Grafika Tata letak : Harrie Siswanto Percetakan : Tisara Grafika Penerbit : Tisara Grafika

Diterbitkan oleh:

JL. DIPONEGORO 98 D - SALATIGA 50714 - JAWA TENGAH Telp.: 0298-321798 | Fax : 0298-321798

Mobile: 081 228 598 985 | 0819 0488 340| 0298-6138702

Katalog Dalam Terbitan

519.72

PAR Parhusip, H. A.

o Optimasi taklinier (berdasarkan data-data penelitian, disertai program MATLAB 6.5) / H. A. Parhusip. -- Salatiga : Tisara Grafika, 2014.

x, 221 hlm. ; 25 cm.

ISBN

1.Linier programming. 2. Mathematical analysis. 4. MATLAB. I. Title.

(4)

(5)

(6)

PRAKATA

akultas Sains dan Matematika (FSM) Universitas Kristen Satya Wacana (UKSW) merupakan salah satu Fakultas Sains yang menekankan penelitiannya pada aplikasi sains dan matematika. Adapun aplikasi yang dimaksud terkait dengan lingkungan sekitar UKSW yaitu Salatiga, Jawa Tengah dan sekitarnya seperti berbagai kasus industri kecil dan perusahaan dari pemerintah maupun instansi swasta.

Kasus yang dihadapi seringkali memerlukan pemrograman untuk dapat menyelesaikan. Program yang digunakan umumnya adalah MATLAB, MAPLE, GEOGEBRA untuk matematika deterministic dan SPSS, Excell dan R untuk pengolahan data statistik. Program-program ini juga banyak dibutuhkan pada berbagai perusahaan. Oleh karena itu teknik menggunakan program-program tersebut perlu diketahui. Pada buku ini diperkenalkan penggunaan program MATLAB dalam menterjemahkan problem optimasi. Selain untuk kebutuhan pada dunia kerja, MATLAB juga banyak digunakan pada keperluan riset pada berbagai jenjang akademik (S1 hingga S3). Jadi program yang disediakan pada buku ini juga untuk memberikan wawasan bagi peneliti awal.

Kurangnya buku ber-ISBN yang sesuai dengan penelitian di FSM (bahkan belum ada) sangat memungkinkan agar segera buku ini dapat dibuat dan dapat dimanfaatkan secara umum terlebih lagi adanya dorongan yang terus menerus untuk mendisain penelitian yang berkualitas.

Buku ini diharapkan dapat menjembatani kebutuhan-kebutuhan tersebut di atas dan buku yang berbasis penelitian ini dapat terus diperbaharui sesuai dengan penelitian yang berkembang di FSM bahkan pada lingkungan yang lebih luas pada masa mendatang.

Salatiga, Maret 2014

Dr. Suryasatriya Trihandaru, MSc.nat, S.Si.

Dekan Fakultas Sains & Matematika Universitas Kristen Satya Wacana

(7)

(8)

KATA PENGANTAR

enggunaan komputer pada perkuliahan aras S1 sekarang khususnya matematika sangat diperlukan khususnya mata kuliah yang terkait dengan aplikasi matematika seperti metode numerik, pemodelan matematika, program linear, optimasi linear dan tak linear dan komputasi matematika. Demikian pula beberapa mata kuliah dasar seperti kalkulus dan aljabar linear juga sangat didukung oleh komputer.

Sehubungan dengan hal itu, buku-buku ajar yang mendukung untuk mahasiswa dapat menganalisa hasil keluaran dari program juga sangat jarang. Selain itu, buku-buku bidang terkait dalam bahasa Inggris mempunyai ilustrasi kasus yang muncul dari negara Eropa atau Amerika. Sedangkan mahasiswa seringkali menjumpai kasus justru dengan data dan kasus dari daerah lokal setempat. Kesenjangan dalam menganalisa dan contoh kongkrit yang kurang mendorong penulis untuk menyusun buku ini.

Buku ini ditujukan pada mahasiswa matematika S1 pada khususnya dan pengguna matematika pada umumnya yang bergelut dengan masalah optimasi. Untuk itulah buku ini disusun. Program yang terkait dengan algoritma yang ditulis juga disajikan dalam bahasa MATLAB secara bertahap sehingga pembaca dapat meng-copy program dengan mudah. Cara mengemukakan hasil analisa umumnya bermasalah bagi mahasiswa. Panduan cara menganalisa juga diberikan pada buku ini sehingga pengguna/mahasiswa dapat mengikuti cara mengemukakan pendapat.

Cara membaca buku ini

Pembaca perlu memahami optimasi pada kalkulus dan bahasa MATLAB. Teori-teori terkait pada kalkulus diulas kembali pada Bab 1, sehingga bagi pengguna matematika yang kurang memahami kalkulus dapat mengikuti. Untuk memenuhi kondisi kritis (stasioner) umumnya diperlukan menyelesaikan persamaan taklinear dan sistem persamaan taklinear. Hal ini dapat dibaca pada Bab 7.

Pembaca dapat belajar MATLAB mulai dari Bab 1 untuk memahami teori yang diberikan. Sepanjang Bab 2- Bab 7 diberikan program yang dapat

(9)

dipelajari dan modul cara menganalisa. Demikian pula soal-soal yang memuat hasil-hasil penelitian juga disajikan khususnya pada Bab 6 dan dilanjutkan pada Bab 7.

Tentunya masih banyak kekurangan penulis dalam menyusun buku ini. Saran dan pendapat yang mendukung perbaikan buku ini sangatlah diharapkan.

Salatiga, Maret 2014

(10)

DAFTAR ISI

PRAKATA v

KATA PENGANTAR vii

DAFTAR ISI ix

Bab 1

DASAR-DASAR OPTIMASI TAKLINEAR 1-48

1.1 Permasalahan Optimasi dengan Satu Variabel 1

1.2 Optimum Global dan Lokal 2

1.3 Fungsi Cembung (convex) dan fungsi cekung (concave) 3

1.4 Permasalahan Optimasi dengan Multivariabel 16

1.4.1 Maksimum Lokal dan Global 16

1.5 Metode-metode dasar untuk optimasi 18

1.5.1 Metode penyelesaian untuk masalah opti-misasi berkendala persamaan

18

1.5.2 Persyaratan Kuhn-Tucker 22

1.5.3 Metode Finalti (Penalty Method) 26

1.6 Beberapa definisi penting 28

1.6.1 Tak Bebas Linear dan Bebas Linear 28

1.6.2 Kombinasi Konveks 29

1.6.3 Himpunan Konveks 29

1.6.4 Penyelesaian Titik Ekstrim 30

1.7 Metode Numerik untuk Optimasi tanpa kendala 30

1.7.1 Metode Golden Search (GS) 31

1.8 Optimasi dari penelitian 34

Bab 2

PEMROGRAMAN KUADRATIK 49-62

2.1 Bentuk standar 49

2.2 Optimasi Pemrograman Kuadratik (Quadratik programming QP) 51

2.3 Menggambar fungsi tujuan dengan MATLAB 55

2.4 Latihan Soal 57

Bab 3

FUNGSI-FUNGSI OPTIMASI PADA MATLAB 63-78

3.1 Fungsi fmincon ( ) 63

3.2 Optimasi dengan kendala persamaan dan tidak persamaan 68

3.3 Optimasi Pemrograman Kuadratik 70

3.4 Fungsi fminimax () 72

3.5 Fungsi lsqlin dan lsqnonlin 72

(11)

Bab 4

PEMROGRAMAN STOKASTIK 79-98

4.1 Program Linear Stokastik 80

4.2 Pemrograman Stokastik Nonlinear 94

Bab 5

METODE MODERN DALAM OPTIMASI 99-138

5.1 Simulasi Anneling (SA) 99

5.2 Algoritma SA untuk optimasi Ciri-ciri alogoritma SA 5.3 Optimasi dengan koloni semut

Sifat perilaku semut

Lintasan kembali dan memperbaharui Peremon Penguapan jejak Peromon

100 103 109 110 111 111 Algoritma 5.4. Algoritma Genetik 112 117

5.4.1 Kelahiran Algoritma Genetik 117

5.4.2 Representasi variabel disain (variabel keputusan) 120 5.4.3 Representasi fungsi tujuan dan kendala

5.4.4 Reproduksi, Crossover dan mutasi Crossover

Crossover program (dan mutasi)

120 122 125 129 Bab 6

KEGIATAN PENELITIAN BERDASARKAN HASIL-HASIL OPTIMASI DARI PENELITIAN

139-182 Kegiatan Penelitian A 139 Kegiatan Penelitian B 146 Kegiatan Penelitian C 150 Kegiatan Penelitian D 154 Kegiatan Penelitian E 157

Kegiatan Penelitian G: Optimasi dengan kendala 165

Kegiatan Penelitian H 171

Kegiatan Penelitian I 175

Bab 7

SISTEM PERSAMAAN TAK LINIEAR 183-221

7.1 Persamaan Taklinear 183

7.2 Sistem Persamaan Taklinear 187

7.2.1 Metode Newton 188

7.2.2 Metode Broyden 194

(12)

Bab 1

DASAR-DASAR OPTIMASI TAKLINEAR

asalah optimasi pada dasarnya meminimalkan atau memaksimalkan fungsi tujuan. Karena memaksimalkan suatu fungsi tujuan sama artinya meminimalkan negatif dari fungsi tujuan, maka hampir pada keseluruhan pembahasan buku ini membahas tentang meminimalkan fungsi tujuan. Selain itu, adanya kendala seringkali membatasi hasil yang diperoleh. Akan tetapi untuk dapat mempelajari sifat-sifat umum dalam optimasi, kita membahas masalah optimasi tanpa kendala terlebih dahulu.

Secara matematis, kita harus mengetahui terlebih dahulu ada tidaknya peminimal sebelum mencari nilai minimal fungsi tujuan. Oleh karena itu berbagai cara mengenal ada tidaknya peminimal dibahas lebih lengkap.

1.1 Permasalahan Optimasi dengan Satu Variabel

Sebuah program tak linear satu variabel yang tak berkendala berbentuk:

minimumkan :

 

x f

z (1.1)

dimana f

 

x adalah sebuah fungsi (tak linear) dari variabel tunggal x , dan pencarian nilai optimumnya (maksimum atau minimum) ditinjau dalam selang tak berhingga



 , . Jika peninjauannya dibatasi pada selang 



berhingga [a,b], maka persoalannya menjadi:

minimumkan : z f

 

x (1.2)

dengan kendala : axb

yang merupakan sebuah program tak linear satu variabel yang berkendala.

(13)

1.2 Optimum Global dan Lokal

Sebuah fungsi obyektif f

 

x memiliki sebuah minimum lokal (atau relatif) di x* jika terdapat sebuah selang (yang kecil) yang berpusat di x*

sedemikian sehingga f

 

x  f

 

x* untuk semua x dalam selang ini dimana fungsi ini didefinisikan. Jika f

 

x  f

 

x* untuk semua x dalam selang ini dimana fungsi ini didefinisikan, maka fungsi minimum di x* (di samping adalah lokal) adalah suatu minimum global atau mutlak. Maksimum-maksimum lokal dan global didefinisikan dengan cara yang sama tetapi dengan tanda ketidaksamaan yang terbalik.

Contoh 1.1

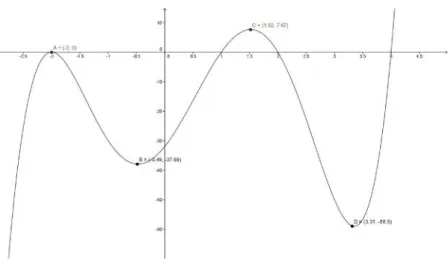
Fungsi yang digambarkan pada Gambar 1 hanya didefinisikan pada R Fungsi ini memiliki minimum relatif pada 2 titik B dan D dan maksimum relatif pada titik A dan C

Gambar 1.1 Fungsi f(x) =(x² - 4) (x - 4) (x - 1) (x + 2) dengan minimum dan maksimum lokal

Berikut ini teorema yang mendefinisikan minimum lokal dan maksimum lokal maupun global.

(14)

Teorema 1.1 : Jika f

 

x kontinu pada selang tertutup dan terbatas [a,b], maka f

 

x memiliki optimum global (baik maksimum maupun minimum) pada selang ini.

 

x memiliki optimum lokal di x* dan jika f

 

x dapat

didefinisikan pada sebuah selang kecil yang berpusat di x*, maka

 

* 0

' 

x

f . Inilah syarat mendapatkan titik *

x _.

 

x dapat didefinisikan dua kali pada sebuah selang

kecil yang berpusat di *

x , dan jika f '

 

x* 0 f ''

 

x* 0, maka f

 

x

memiliki sebuah minimum lokal di x*. Jika f'

 

x* 0dan f ''

 

x* 0, maka

 

x

f memiliki sebuah maksimum lokal di x*.

Dari kedua teorema yang pertama ini diperoleh bahwa jika f

 

x kontinu di [a,b] , maka optimum lokal dan global akan terjadi diantara titik-titik dimana

 

0

' 

x

f (yang pada umumnya disebut titik-titk stasioner atau titik kritis , atau antara titik-titik ujung xa dan x ). Selanjutnya teorema inib

dikembangkan pada optimasi fungsi multivariabel.

Salah satu cara mengenali ada tidaknya peminimum fungsi tujuan adalah dengan mengenali sifat fungsi tujuan yaitu apakah fungsi tujuan cembung (convex) atau cekung (concave) sebagaimana didefinisikan pada subbab berikut.

1.3 Fungsi Cembung (convex) dan fungsi cekung (concave)

fungsi 1 variabel

Sebuah fungsi f

 

x adalah cembung pada sebuah selang  (berhingga atau tak berhingga),jika untuk setiap dua titik x dan₁ x di dalam₂  dan untuk semua 0₁ 1berlaku

(15)

(1.3) Jika pernyataan (1.3) berlaku dengan tanda pertidaksamaan yang terbalik, maka f

 

x adalah cekung . Jadi, negatif dari sebuah fungsi cembung adalah cekung, dan sebaliknya.

Teorema 1.4: Jika f

 

x dapat terdiferensial dua kali pada suatu interval 

maka f

 

x adalah cembung pada

  f"

 

x 0  dalamx .

Fungsi cekung  f"

 

x 0 dalamx .

Teorema 1.5: Jika f

 

x cembung pada , maka setiap minimum lokal pada

 adalah suatu minimum global pada . Jika f

 

x cekung pada , maka setiap maksimum lokal pada  adalah suatu maksimum global pada .

Tidak ada jaminan bahwa metode numerik akan menemukan suatu maksimum global. Dapat terjadi bahwa metode ini hanya konvergen ke suatu maksimum lokal atau lebih buruk lagi, sama sekali tidak konvergen. Perkecualiannya adalah pada program-program yang memiliki fungsi obyektif yang cekung (concave function).

fungsi multivariabel

Kita perlu mengenal beberapa definisi penting berikut ini.

Vektor gradien f yang berkaitan dengan sebuah fungsi



x x x xn



f ₁, ₂, ₃,..., yang semua turunan pertamanya ada, didefinisikan sebagai

T n x f x f x f f _              , ,...., 2 1 (1.4.a)







x1 1 x2



f

  

x1 1

  

f x2 f      

(16)

Notasi * x f 

 menunjukkan nilai gradien di x* dalam berbagai arah. Untuk simpangan yang kecil dari x*dalam berbagai arah, maka arah yang memberikan pertambahan maksimum dalam f(x*) adalah arah vektor f _x*.

Contoh 1.2 Untuk





3 3 2 2 2 2 1 3 2 1,x ,x 3x x x x x f   , dengan x* 



1,2,3



T,maka :               2 3 2 2 3 3 2 2 1 2 1 3 2 3 6 x x x x x x x f sehingga

  

 

  

   

                          108 105 12 3 2 3 3 2 2 1 3 2 1 6 2 2 3 2 * x f 

Untuk menyelidiki sifat pengoptimum (pemaksimum atau pemi-nimum) maka kita menyelidiki tanda dari pada fungsi 1 variabel (menurut Teorema 1.3). Secara sama, kita perlu membangun kondisi untuk fungsi tujuan multivariabel. Hal ini ditunjukkan dengan tanda dari matriks Hessian fungsi tujuan f



x₁,x₂,...,x_n



pada titik kritis x*. Jika ada tanda positif atau negatif untuk suatu skalar, maka perlu ada notasi ’positif’ atau ’negatif’ yang diperumum untuk matriks.

.

Matriks Hessian yang berkaitan dengan sebuah fungsi



x x xn



f ₁, ₂,..., yang memiliki turunan-turunan kedua yang kontinu adalah:

            j i f x x f H 2



i,j 1,2,3,...,n



(17)

Berdasarkan komponennya, matriks Hessian ditulis dalam bentuk: 2 2 2 2 1 2 2 2 2 1 2 2 1 2 2 1 2 2 1 2 .. .... ... .... .... ... ... .... ... ... ... ... n n n n f x f x x f x x f x f x x f x x f x x f x f H                       (1.4.b) Notasi _* x f

H  menunjukkan nilai dari matriks Hessian di x*



.

Contoh 1.3 Untuk fungsi dari contoh 1.2, dan x* 



1,2,3



T_maka

               3 2 2 2 3 2 2 3 2 3 3 1 1 2 6 6 0 6 2 6 0 6 6 x x x x x x x x x x Hf sehingga _* x f H  = . 72 108 0 108 54 6 0 6 12              

Beberapa contoh masalah optimasi yang berkendala maupun tanpa kendala ditunjukkan sebagai berikut:

a). min f(x₁,x₂,x₃)2x₁3x₂ 3x₃ kendala x₁ x2 ₂ 3 3 3 1  x  x 0 , , 2 3 1 x x  x b). max f(x₁,x₂,x₃) 2x₁2 3x₂2 3x₁x₃ c). min f(x₁,x₂,x₃)2x₁3x₂x₃ kendala x₁  x₂ 4 3 3 1x  x 0 , , ₂ ₃ 1 x x  x

(18)

Selanjutnya notasi ‘positif’ dan ‘negatif’ untuk matriks yang digunakan untuk matriks Hessian didefinisikan sebagai berikut. Definisi berikut ini kurang aplikatif tetapi lebih bersifat umum.

Definisi 1.5 :

Sebuah matriks simetris A berukuran n (yang memiliki sifat A =n AT) adalah semi negatif tegas (definite negative) jika xTA x untuk setiap0 vektor x  yang berdimensi n. Jika x0 TA x_{< untuk setiap vektor x} 0 maka A di atas disebut negatif tegas (definite negative). Secara sama dapat didefinisikan untuk semi positif tegas (definite positive).

Matriks simetris yang akan dibahas adalah matriks Hessian Teorema berikut terkadang digunakan untuk menguji sifat matriks Hessian.

Teorema 1.6: Misalkan A 

 

a_ij sebuah matriks simetris nn dan

didefinisikan determinan-determinan A₁ a₁₁ A₂ 22 21 12 11 a a a a   A₃ 33 32 31 23 22 21 13 12 11 a a a a a a a a a   ... A_n 

 

1 n1det A (1.5)

Matriks A adalah negatif tegas (definite negative) jika dan hanya jika

A1,A2,...,An semuanya negatif. Dengan kata lain A adalah semi negatif

tegas (definite negative) jika dan hanya jika A₁ 0, A₂ 01, A3 0,…,

0  r

A (r < n) semuanya negatif dan A_k 0 yang tersisa semuanya nol. Teorema berikut ini sering digunakan untuk menguji sifat matriks Hessian pada masalah optimasi.

Teorema 1.6.b: Suatu matriks simetris semi negatif tegas (definite negative)

(semi definite negative) untuk semua xdalam D yaitu setiap nilai eigen matriks tersebut lebih kecil atau sama dengan 0.

(19)

Contoh 1.4

Untuk _*

x f

H  pada Contoh 1.3, A1= 12 > 0, maka Hfbukan negatif tegas

(definite negative) ataupun semi negatif tegas (semi definite negative) di x*

Kita kembali pada definisi konveks dan konkaf untuk fungsi tujuan multivariabel. Perhatikan bahwa variabel bebas diberi notasi vektor yang artinya x merupakan multivariabel di n

R . Sehingga notasi diferensial

menjadi notasi gradient (dengan operator ‘nabla’, atau ditulis  ). Sepanjang buku ini, maka yang dimaksud dengan vektor adalah merupakan daftar bilangan sebanyak n.

Definisi 1.6.c:

Sebuah fungsi f

 

x adalah semi cembung (semi convex) pada suatu daerah konveks D, jika untuk dua vektor sembarang x dan y dan untuk semua 0 1berlaku y x f y x f((1)) ()(1) (1.6.a) Sebuah fungsi adalah semi cekung (semi concave) pada D jika dan hanya tanda pada persamaan (1.6.a) sebaliknya pada D yaitu

y x f y x f((1)) ()(1)_. (1.6.b) Jika tanda sama tidak berlaku pada persamaan (1.6.a) maka f dikatakan sangat cembung (strictly convex) dan dikatakan sangat cekung (strictly concave) pada persamaan (1.6.b).

Daerah konveks D dapat berhingga atau tak berhingga.

Teorema 1.7.a : Jika f

 

x memiliki turunan parsial kedua pada D, maka

 

x

f  cekung pada D jika dan hanya jika matriks Hessian Hf semi negatif

tegas (definite negative) (semi definite negative) untuk semua x dalam D yaitu setiap nilai eigen matriks dari matriks Hessian Hf lebih kecil atau sama

(20)

Teorema 1.7.b : Jika f

 

x cekung pada D, maka setiap maksimum lokal pada D adalah suatu maksimum global pada D.

Jika fungsi f

 

x adalah cembung (convex) dan terdiferensial di n R ,

maka titik x*adalah peminimum global pada fungsi f

 

x  jika memenuhi kondisi stasioner yaitu

 

* 0

 xf . (1.7)

Bukti: jika f

 

x adalah cembung dan terdiferensial, maka dimiliki

 

*

  

* *



x x x f x f x f         x, x*. Tetapi jika fungsinya stasioner di titik x* berlaku

 

  



  

* *

  

* * * * * , 0 x x f x x x x f x x x f x f x f                       

sehingga dapat dikatakan bahwa x* adalah peminimum global.

Perhatikan cara menuliskan perkalian. Karena f

 

x* adalah vektor dan



x x*



juga vektor, sedangkan hasil perkalian haruslah skalar, maka perlu notasi dot product.

Definisi fungsi cembung dan cekung seringkali membingungkan mahasiswa. Untuk itu studi secara khusus tentang hal ini dapat didukung dengan yang ditunjukkan sebagai berikut ini.

Kegiatan 1.1

Tujuan: Studi konveks

Menyelidiki apakah f(x(1)y)f(x)(1)y dipenuhi, untuk 1

0 pada domain konveks yang didefinisikan. Kegiatan A:

Kita akan menguji studi konveks fungsi

3 2 2 5 ) , ( 1 2 2 2 2 1 2 1 2 1 x  x  x x x x  x  x f pada D = R .2

(21)

Fungsi ini dapat digambar dengan MAPLE untuk menambahkan visualisasi fungsi tersebut yang ditunjukkan pada perintah dan Gambar 1.2

> plot3d(5*x^2 + 2*x*y + y^2 – x + 2*y + 3, x=-5..5, y=-5..5);

Gambar 1.2. Grafik fungsi f(x₁,x₂)5x₁2 2x₁x₂ x₂2 x₁ 2x₂ 3

Pada kita tidak bisa menyelidiki pada semua bidang R2 dan untuk semua nilai  . Hal ini karena kita perlu mendiskritkan data. Kita akan menyelidiki tahap demi tahap.

Tahap 1.

Perhatikan notasi x(1)y jika dituliskan atas komponen-komponennya maka y x (1 )    = _      2 1 x x  + _       2 1 ) 1 ( y y  = _          2 2 1 1 ) 1 ( ) 1 ( y x y x     .

Kita akan menyebut _       2 1 u u u = _          2 2 1 1 ) 1 ( ) 1 ( y x y x     .

Sehingga untuk menyelidiki f(x₁,x₂)5x₁2 2x₁x₂ x₂2 x₁2x₂ 3

convex

atau strictly convex (Teorema 1.7.a-1.7.b) adalah mengerjakan/menyelidiki pertidak-samaan. ) ( ) 1 ( ) ( ) (u f x f y f       atau f(u)f(x)(1)f(y)

> plot3d(5*x^2 + 2*x*y + y^2 – x + 2*y + 3, x=-5..5, y=-5..5);

Gambar 1.2. Grafik fungsi f(x₁,x₂)5x₁2 2x₁x₂ x₂2 x₁ 2x₂ 3

Tahap 1.

convex

atau strictly convex (Teorema 1.7.a-1.7.b) adalah mengerjakan/menyelidiki pertidak-samaan. ) ( ) 1 ( ) ( ) (u f x f y f       atau f(u)f(x)(1)f(y)

> plot3d(5*x^2 + 2*x*y + y^2 – x + 2*y + 3, x=-5..5, y=-5..5);

Gambar 1.2. Grafik fungsi f(x₁,x₂)5x₁2 2x₁x₂ x₂2 x₁2x₂ 3

Tahap 1.

convex

atau strictly convex (Teorema 1.7.a-1.7.b) adalah mengerjakan/menyelidiki pertidak-samaan. ) ( ) 1 ( ) ( ) (u f x f y f       atau f(u)f(x)(1)f(y)

(22)

dipenuhi atau tidak.

Misal diambil D adalah garis x = 0 ,  =0.5 buat file dengan nama Studikonveks.m dengan isi sebagai berikut

%studi konveks lamda=0.5;

%memilih D adalah himpunan titik-titik pada garis x = 0 c=0; y=-5:1:5; n=length(y); x=c*ones(1,n); plot(x,y,'-') axis([-3 3 -3 3]) xy=[x' y'] vx(1)=xy(1,1) vx(2)=xy(1,2) vy(1)=xy(2,1) vy(2)=xy(2,2) u(1)=lamda*vx(1) + (1-lamda)*vy(1) u(2)=lamda*vx(2) + (1-lamda)*vy(2)

fu=5*u(1)^2 + 2*u(1)*u(2) + u(2)^2 - u(1) + 2*u(2) + 3

fx=5*vx(1)^2 + 2*vx(1)*vx(2) + vx(2)^2 - vx(1) + 2*vx(2) + 3 fy=5*vy(1)^2 + 2*vy(1)*vy(2) + vy(2)^2 - vy(1) + 2*vy(2) + 3 Kanan=lamda*fx + (1-lamda)*fy

Banding=[fu Kanan]

Keluaran program dapat diperoleh dengan mengetik program pada layar MATLAB

>> Studikonveks (Enter)

Pembahasan hasil program: Pada hasil menunjukkan bahwa fungsi

memenuhi kondisi sebagai fungsi konveks. Akan diselidiki selanjutnya untuk berbagai nilai  .

Kegiatan 2.

Membandingkan studi konveks untuk berbagai nilai  , misal nama file adalah Studikonveks2.m

(23)

%studi konveks

lamda=linspace(0,1,10); %memvariasi lamda

%memilih D adalah himpunan titik-titik pada garis x = 0 c=0; y=-5:1:5; n=length(y); x=c*ones(1,n); plot(x,y,'-') axis([-3 3 -3 3]) xy=[x' y'] vx(1)=xy(1,1) vx(2)=xy(1,2) vy(1)=xy(2,1) vy(2)=xy(2,2) pl=length(lamda); fu=zeros(pl,1); Kanan=zeros(pl,1); for i=1:pl u(1)=lamda(i)*vx(1) + (1-lamda(i))*vy(1) u(2)=lamda(i)*vx(2) + (1-lamda(i))*vy(2)

fu(i)=5*u(1)^2 + 2*u(1)*u(2) + u(2)^2 - u(1) + 2*u(2) + 3 fx=5*vx(1)^2 + 2*vx(1)*vx(2) + vx(2)^2 - vx(1) + 2*vx(2) + 3 fy=5*vy(1)^2 + 2*vy(1)*vy(2) + vy(2)^2 - vy(1) + 2*vy(2) + 3 Kanan(i)=lamda(i)*fx + (1-lamda(i))*fy

end

Banding=[lamda' fu Kanan]

figure,plot(1:pl,fu,'*',1:pl,Kanan,'o')

Keluaran Gambar ditunjukkan pada Gambar 1.3.

(24)

Kegiatan 3: Studi Konveks

Selidikilah fungsi-fungsi berikut ini convex atau strictly convex pada himpunan convex yang didefinisikan

2 1 2 2 2 1 2 1, ) /2 3 /2 3 (x x x x x x f    on D = R2

Jawab : Program pada Matlab :

clear close all

%studi konveks

lamda = linspace(0,1,10); %memvariasi lamda

%memilih D adalah himpunan titik-titik pada garis x = 1 y = -5:1:5; n = length (y); for c = 1:10 x = c*ones(1,n); subplot(2,1,1),plot(x,y,'-') axis ([-3 12 -3 3]) hold on xy = [x' y'] vx(1) = xy(1,1) vx(2) = xy(1,2) vy(1) = xy(2,1) vy(2) = xy(2,2) pl = length (lamda); fu=zeros(pl,1); kanan=zeros(pl,1); for i=1:pl

u(1) = lamda(i)*vx(1) + (1-lamda(i))*vy(1) u(2) = lamda(i)*vx(2) + (1-lamda(i))*vy(2)

fu(i) = (u(1).^2 )./2+ (3.*u(2).^2)./2+ (sqrt(3)).*u(1).*u(2) fx = (vx(1).^2 )./2+ (3.*vx(2).^2)./2+ (sqrt(3)).*vx(1).*vx(2) fy = (vy(1).^2 )./2+ (3.*vy(2).^2)./2+ (sqrt(3)).*vy(1).*vy(2) kanan(i) = lamda(i)*fx + (1-lamda(i))*fy

end

banding = [lamda' fu kanan] subplot(2,1,2),plot (1:pl,fu,'*') hold on

subplot(2,1,2),plot (1:pl,kanan,'o') end

(25)

Keluaran ditunjukkan pada Gambar 1.4.

Gambar 1.4. Hasil perbandingan f(x(1)y)danf(x)(1)ydengan

memvariasi  dari [0,1] sebanyak 10 angka untuk

2 1 2 2 2 1 2 1, ) /2 3 /2 3 (x x x x x x f    _. Kesimpulan: 2 1 2 2 2 1 2 1, ) /2 3 /2 3 (x x x x x x

f    adalah strictly convex (konveks tegas) Kegiatan 4.

Kegiatan 4 akan menguji cembung atau cekung untuk fungsi

2 2 1 8 2 1 2 1 ) ( 2 1) ln( ) (xx x x xx f     . Tahap 1. Program clear close all %studi konveks lamda=linspace(0,1,100);%memvariasi lamda

%memilih D adalah himpunan titik-titik pada garis x=0 y=-5:1:5; n=length(y); for c=0:10 x=c*ones(1,n); subplot(2,1,1),plot(x,y,’-‘); axis([-3 3. -3 3]) hold on xy=[x’ y’] vx(1)=xy(1,1) vx(2)=xy(1,2)

(26)

vy(1)=xy(2,1) vy(2)=xy(2,2) pl=length(lamda); fu=zeros(pl,1) kanan=zeros(pl,1) for i=1:pl u(1)=lamda(i)*vx(1) + (1-lamda(i))*vy(1) u(2)=lamda(i)*vx(2) + (1-lamda(i))*vy(2) fu(i)=5*u(1).^2+2*u(1)*u(2)+u(2).^2-u(1)+2*u(2)+3 fx=5*vx(1).^2+2*vx(1)*vx(2)+vx(2).^2-vx(1)+2*vx(2)+3 fy=5*vy(1).^2+2*vy(1)*vy(2)+vy(2).^2-vy(1)+2*vy(2)+3 kanan(i)=lamda(i)*fx + (1-lamda(i))*fy end banding=[lamda’ fu kanan] subplot(2,1,2),plot(1:pl,fu,’*’) hold on subplot(2,1,2),plot(1:pl,kanan,’o’) end hold off

Tahap 2. Keluaran program hanya ditunjukkan dalam Gambar 1.5

Gambar 1.5. Hasil perbandingan f(x(1)y)danf(x)(1)ydengan

memvariasi  dari [0,1] sebanyak 10 angka untuk

2 2 1 8 2 1 2 1 ) ( 2 1) ln( ) (xx x x xx f     _.

(27)

Berdasarkan Gambar 1.5 dan data menunjukkan bahwa fungsi tesebut adalah

strictly convex (0< <1) menurut definisi karena hasil banding untuk setiap  adalah x ≠ y.

1.4 Permasalahan Optimasi dengan Multivariabel

Pada kasus ini akan dipelajari optimasi tak linear dengan lebih dari satu variabel. Tetapi disini hanya akan ditinjau bentuk analog dari (1.1):

minimumkan : z = f( x), (1.7)

dimana x



x₁,x₂,...,x_n



T

merupakan vektor pada D .

Bentuk persamaan (1.7) sebagai optimasi tak berkendala. Selanjutnya, kita akan selalu menganggap optimisasi dalam persamaan (1.7) sebagai maksimisasi; semua hasilnya dapat diterapkan pada program minimisasi jika f( x) diganti dengan -f( x).

1.4.1 Maksimum Lokal dan Global Suatu persekitaran *

x dengan jari-jari  ( neighbourhood,  >0 ) adalah himpunan dari semua vektor x yang sedemikian rupa sehingga: (x -x*)T(x -x*)



 

*



2



*



2 2 3 3 2 * 2 \ 2 2 * 1 1x  x x  x x ... xn xn  x

Dalam istilah geometris, sebuah persekitaran x*adalah bagian dalam (interior) dan batas (boundary) dari sebuah bola berdimensi-n yang berjari-jari dan berpusat di x*.

Sebuah fungsi obyektif f(x) memiliki suatu maksimum lokal di *

x , jika terdapat suatu persekitaran *

x sedemikian hingga f(x) f

 

x* untuk semua x dalam berjarak  dimana fungsinya didefinisikan. Jika persyaratan

(28)

ini dipenuhi untuk setiap  yang positif (cukup kecil), maka f(x) memiliki suatu maksimum global di x*.

Kita akan mengingat kembali syarat maksimum dan minimum global yang ditunjukkan pada kalkulus pada teorema 8-10 berikut ini,

Hasil-hasil dari Kalkulus

Teorema 1.8: Jika f(x) kontinu pada suatu daerah yang tertutup dan terbatas,

maka f( x) memiliki suatu maksimum global ( dan suatu minimum global pada daerah itu ).

Teorema 1.9: Jika f(x) memiliki suatu maksimum lokal ( atau minimum

lokal ) di x* dan jika f terdefinisi pada beberapa persekitaran x*

berjarak  maka f _x= 0.

Teorema 1.10 : Jika f(x) memiliki turunan-turunan kedua pada suatu

persekitaran  sekitar *

x , dan jika  

x

f = 0 dan Hf _x adalah negatif tegas (definite negative), maka f(x) memiliki suatu maksimum lokal di

*

x .

Dari teorema 1.9 dan teorema 1.10 dapat disimpulkan bahwa maksimum global dari suatu fungsi kontinu f(x) tercapai dititik-titik dimana

f

 = 0 (titik stasioner) kecuali jika fungsinya memiliki nilai-nilai yang besar sekali bila xTx  . Untuk keadaan yang terakhir, fungsi tidak memiliki

maksimum global.

Penyelesaian analitik dengan menggunakan kalkulus untuk program multivariabel lebih sulit daripada untuk program satu variabel, karena itu sekali lagi kita gunakan untuk pendekatan maksimum lokal ke dalam toleransi yang diperbolehkan.

(29)

Contoh 1.6 Masalah optimisasi takberkendala:

min f



x₁,x₂

 

 x₁ 2

 

4  x₁ 2x₂



2

Secara jelas f



x₁,x₂



0& f

 

2,1 0; disini (2,1) adalah solusi global minimum. Grad f diberikan oleh:







_



_





             2 1 2 1 3 1 2 1 2 4 2 2 2 4 , x x x x x x x f

Sehingga pada (2,1) didapat f



x1,x2

 

 22

 

4  22(1)



2 0.

1.5 Metode-metode dasar untuk optimasi

1.5.1 Metode penyelesaian untuk masalah optimisasi berkendala persamaan

Secara umum masalah optimisasi yang berkendala persamaan berbentuk: Maksimumkan z = f( x) (1.8) dengan kendala: g1( x  ) = 0 g2( x  ) = 0  gm( x  ) = 0

dengan x



x₁,x₂,...,x_n



T, dan m < n ( jumlah kendala < jumlah variabel). Seperti halnya dalam optimasi linear biasa, program minimisasi dapat diubah ke dalam program maksimisasi dengan mengalikan fungsi obyektif dengan -1. Bentuk standar bagi program-program taklinear yang mengandung kendala-kendala pertidaksamaan adalah:

Maksimumkan z = f( x) (1.9) dengan kendala:

(30)

g1( x  )  0 g2( x  )  0 ... gm( x  )  0 dan x  .0

Program-program taklinear yang tidak dalam bentuk standar (1.9) dipecahkan dengan merubahnya ke bentuk standar atau dengan merubah prosedur-prosedur penyelesaian yang diberikan di bawah ini untuk program-program dalam bentuk standar.

Metode Pengali Lagrange

Untuk memecahkan masalah (1.8), maka pertama kali kita membentuk fungsi

Lagrange



x x x xn m



L ₁, ₂, ₃,...., ,₁,₂,₃,.... f( x) ( ) 1 x g_i m i i 



   (1.10)

dimana _i



i1,2,3,...,m



adalah tetapan-tetapan (yang tidak diketahui) yang disebut pengali Lagrange. Lalu kita pecahkan sistem n+m persamaan

0    j x L (j = 1,2,...,n) (1.11) dan 0    i L  (i = 1,2,...,m). (1.10c)

Teorema 1.11: Jika masalah (1.10) memiliki suatu penyelesaian, maka

penyelesaian ini terdapat diantara penyelesaian-penyelesaian bagi sistem (1.10), asalkan f( x) dan gi( x



) (i = 1,2,...,m) memiliki turunan-turunan parsial pertama yang kontinu dan matriks Jacobi m x n, dengan

(31)

           j i x g J memiliki rank m di x = x*.

Metode pengali Lagrange ini ekuivalen dengan menggunakan persamaan kendala untuk menghilangkan beberapa variabel x tertentu dari fungsi obyektif dan kemudian memecahkan persoalan maksimisasi tanpa kendala dalam variabel-variabel x yang tersisa.

Contoh 1.7. Minimalkan dengan metode pengali Langrange untuk masalah fungsi tujuan dengan kendala persamaan

Min (x) = + (A.a) 0 2 ) (x  x₂ x₁   h (A.b)

Kita bisa menggantikan kendala persamaan x2 = 2 – x1 ke fungsi tujuan

sehingga masalah ini menjadi optimasi tak berkendala sebagai

Min (x) = + (2 − ) = 2 − 4 + 4 (A.c) yang dapat dengan mudah dipecahkan dengan menetapkan turunan dari hal ini.

( ) = 4 − 4 = 0,

Atau, kita dapat menerapkan metode pengali Lagrange sebagai berikut: Mininimumkan (x, λ) = + + ( + − 2)

(32)

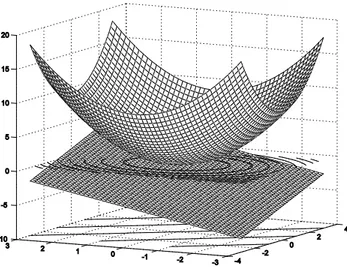
Gambar 1.6 Fungsi obyektif dengan kendala contoh 1.7

Program MATLAB untuk mengilustrasikan Gambar 1.6 ditunjukkan berikut ini clear closeall [X,Y] = meshgrid(-3:.125:3); Z = X.^2 + Y.^2; meshc(X,Y,Z); hold on Z2=X + Y-2; meshc(X,Y,Z2); holdoff

Kondisi ekstrem adalah 2 1 0

1       x x L sehingga = − 2⁄ . Secara sama diperoleh 0 2 ₂ 2       x x L

sehingga x₂ /2. Demikian pula  ₁  ₂ 20

  x x L  . Diperoleh 2 .

Dalam contoh ini, penggantian (linear) kendala persamaan lebih mudah daripada metode pengali Lagrange. Namun, tidak selalu terjadi, seperti yang digambarkan oleh contoh berikut.

(33)

Min f(x₁,x₂)x₁x₂ dimana kendalanya adalah h(x₁,x₂)x₁2 x₂2 2=0. Dengan cara yang sama, kita perlu menyusun fungsi pengali Lagrange yaitu



, ,





22 2



2 1 2 1 2 1 x x x  x x  x L   . Diperoleh x₁  x₂ 1/2 sehingga 1/2_.

Sekarang, dalam rangka untuk memberitahu apakah masing-masing adalah minimum atau maksimum, kita harus menentukan positif atau negatif tegas dari turunan kedua (matriks Hessian).

= ( , λ)

x = ∂ ∂

⁄ ∂ ⁄∂ ∂

∂ ⁄∂ ∂ ∂ ⁄∂ = 20 2λλ 0

Matriks ini positif / negatif tegas (definite negative) jika tanda λ adalah positif / negatif. Oleh karena itu penyelesaian (x1, x2) = (-1, -1) sesuai dengan

λ minimum =(lokal) yang ingin kita dapatkan, sedangkan solusi (x1, x2) =

(1, 1) berkaitan dengan  1/2adalah maksimum (lokal). 1.5.2 Persyaratan Kuhn-Tucker

Secara umum masalah optimisasi yang berkendala persamaan dan pertidaksamaan berbentuk:

minimalkan: f (x)

dengan kendala : h (_i x) = 0; g (_i x)  .0 (1.11) Kita perlu menyusun fungsi pengali Lagrange yang melibatkan kendala persamaan dan kendala pertidaksamaan



x



f

 

x h

 

x g

 

x L _j p j j i m i i      



     1 1 , ,   

untuk i=1,…,m dan j=1,…,p (1.12.a) Perhatikan bahwa banyaknya variabel (n), banyaknya kendala persamaan (m) dan kendala pertidaksamaan (p) tidak harus sama. Secara analog, untuk mendapatkan nilai optimal yaitu * * *

, , 

(34)



, , 



0

L x   . Bentuk ini merupakan bentuk sistem persamaan yang bias taklinear yang terdiri dari (n + m +p) persamaan. Umumnya urutan sistem persamaan dengan menyusun turunan L terhadap masing-masing variabel, kemudian barulah turunan L terhadap masing-masing parameter. Kondisi Karush Kuhn Tucker ditunjukkan berikut ini.

Teorema 1.12 (kondisi Kuhn Tucker): Anggap bahwa fungsi f,h_i,g_i

adalah kontinu dan terdiferensial, dan x* adalah feasible dan memenuhi kendala. Maka syarat cukup untuk optimum lokal pada x*harus ada suatu

0

* 

i

 dan i* 0 sedemikian hingga:

 

x j p g x g x h x f L j j i p j i i m i i ,..., 1 ; 0 ; 0 * * * 1 * * 1 * *          



     (1.12.b) Contoh 1.8 min x₁2 x₂2 dengan kendala: . 4 ; 3 ; 0 ₂ ₁ ₂ 1  x  x x  x

Bentuk kendala belum memenuhi bentuk baku sehingga perlu ditulis dalam bentuk baku (menurut persamaan (1.11) yaitu

. 0 4 ; 0 3 ; 0 ₂ ₁ ₂ 1        x x x x

Langkah pertama disusun pengali Lagrange, yaitu:

L(x,,)  x₁2 x₂2 ₁x₁₂(x₂ 3)



x₁x₂ 4



._. Dengan persyaratan Kuhn-Tucker didapat:

0 2 0 2 2 2 2 1 1 1                 x x L x x L

(35)



3



0, 0 0 , 0 2 2 2 1 1 1                  x L x L

Akan diselesaikan dengan per kasus.

Kasus1:



₁ ₂ 0



. Pada kasus ini, diperoleh sistem persamaan sebagai berikut: . 0 4 0 2 0 2 2 1 2 1        x x x x  

Diperoleh solusi x₁  x₂ 2_{. Hal ini bertentangan dengan kendala}  x₁ 0 dan  x₂30, sehingga tidak memenuhi.

Kasus 2:



₁,₂ 0



. Diperoleh solusi x₁  x0, ₂ 3, juga bertentangan dengan kendala ketiga. Sehingga juga tidak dipenuhi.

Kasus 3:



₁ 0,₂ 0



.Didapat : . 8 8 2 4 0 1 2 2 1             x x x

Tidak memenuhi persyaratan Kuhn-Tucker, karena nilai  adalah₁ negatif. Kasus 4:



₁ 0,₂ 0



.Didapat: . 4 ; 2 ; 3 ; 1 ₂ ₂ 1  x      x

Hasil ini memenuhi persyaratan Kuhn-Tucker, sehingga solusi optimumnya adalahx₁ 1,x₂ 3, 2,₂ 4.

Sekarang dengan memperhatikan kendala yang diberikan, maka pada kasus di atas akan diselesaikan dengan metode pengali Lagrange.

(36)

Contoh 1.9

Dengan fungsi yang diberikan adalah :

minimumkan f



x,y,z



x2  y2 z2 dengan kendala: R z y x z y x g z y x g          , , 12 7 6 9 5 3 2 2 1

Tahap 1: susun fungsi pengali Lagrange:

Ditulis









i i ig z y x f z y x L



   2 1 2 1, , , , , ,    (x)

dimana _i



i1,2,3,...,m



adalah tetapan-tetapan (yang tidak diketahui) yang disebut pengali Lagrange.

Tahap 2: pecahkan sistem 5 persamaan yang telah dibentuk dengan:

0    j x L (j = 1,2,3); 0   i L  (i = 1,2) atau ditulis 0 ,                T i j L x L L  , j=1,2,3 ; i=1,2 .

Sehingga dari masalah contoh 1.8 dapat disusun pengali Lagrange, yaitu:



f,g1,g2, 1, 2



f 1g1 2g2 L     



2 3 5 9



₂



6 7 12



1 2 2 2            x y z  x y z  x y z

Lalu kita pecahkan sistem persamaan di atas dengan:

    0 x L 0 6 2 2x ₁ ₂ 

(37)

    0 y L 2y3₁ ₂ 0     0 z L 2y5₁7₂ 0     0 1  L 2x-3y+5z-9 = 0     0 2  L 6x+y-7z-12 = 0.

Sistem dapat ditulis dalam bentuk sistem persamaan linear Ax = b dengan solusi (bantuan MATLAB)

x= 2.4352 ;y= -0.9907; z= 0.2315



1

 -0.8380 ;₂  -0.5324. 1.5.3 Metode Finalti (Penalty Method)

Metode Finalti digunakan untuk menyelesaikan kasus dimana kasus mula-mula adalah memaksimalkan w (fungsi tujuan) tanpa kendala. Sedangkan Metode Finalti biasa digunakan untuk meminimalkan fungsi dengan kendala. Untuk menggunakan metode ini maka masalah optimasi harus disusun dalam bentuk umum sebagai berikut

Anggap bahwa f(x), g₁(x), …, g_m(x) mempunyai turunan parsial pertama yang kontinu di R . Untuk menyelesaikan masalah optimasin

berkendala yaitu       n m x x R g x g x g x f      , 0 ) ( ),..., ( , 0 ) ( kendala dengan ) ( minimalkan 2 1 (P.1.a)

dilakukan proses sebagai berikut

(1). Untuk setiap bilangan bulat positif k (disebut parameter Finalti), anggap *

k

x adalah peminimum global untuk fungsi Finalti yaitu (Peressini,1988)





2 1 ) ( ) ( ) (



    m i i k x f x k g x P    . (P.1.b)

(38)

Notasi g_i(x) menyatakan bahwa untuk suatu kendala g_i(x) ,0 maka fungsi gi (x)   didefinisikan sebagai ) (x gi   =      0 ) ( jika ) ( 0 ) ( jika 0 x g x g x g i i i    . (P.1.c)

(2). Tunjukkan bahwa subbarisan

 

xk*



konvergen pada suatu penyelesaian

*

x untuk masalah (P.1.a)-(P.1.c).

Oleh karena fungsi kendala dinyatakan dalam bentuk persamaan (P.1.c) maka diperlukan adanya jaminan bahwa h(x) [g(x)]2juga mem-punyai turunan pertama parsial yang kontinu di R . Hal ini ditunjukkann

pada Lemma 1.13 berikut ini.

Lemma 1.13 :

Jika g(x) mempunyai turunan parsial pertama yang kontinu di R , hal inin

berlaku juga 2 )] ( [ ) (x g x

h     . Selain itu turunan parsial tersebut adalah ) ( ) ( 2 ) ( x x g x g x x h i i         

, untuk semua i = 1,2,…,n untuk semua

x





R

n.

Bukti : (Peressini,et.all,1988).

Secara umum metode Finalti ditunjukkan oleh Teorema berikut ini.

Teorema 1.14:

Anggap bahwa f(x), g1(x)



, …, g_m( x) kontinu di Rn dan f(x)

terbatas ke bawah di Rn (yaitu terdapat suatu konstan c sehingga berlaku )

(x

f

c  untuk semua xRn). Jika x_F*suatu penyelesaian pada masalah (P.1.a) yaitu     0, ( ),..., ( ) 0, ) ( kendala dengan ) ( minimalkan 2 1 x g x g x g x f m    

(39)

dan jika setiap bilangan bulat positif k, terdapat suatu n k R x   sehingga ) ( min ) ( P x R x x P_k _k  _ _n _k  , maka (i). Pk(xk) Pk 1(xk 1) f(xF*)    _ _ 

 untuk setiap bilangan bulat positif k

(ii). lim



( )



0 1 2   



  m i k i x g k  .

Sebagai konsekuensi, jika

 

P k

x adalah subbarisan

 

x



_k yang konvergen dan jika * * } { lim x x k kP P    maka **

x adalah penyelesaian untuk problem (P.1.a).

Bukti: (Peressini,et.all,1988) 1.6 Beberapa definisi penting 1.6.1 Tak Bebas Linear dan Bebas Linear

Sebuah himpunan vektor-vektor berdimensi – m,



P₁,P₂,...,P_n



adalah tak bebas linear jika terdapat konstanta-konstanta  ,...,₁ _nyang tidak semuanya nol, sedemikian hingga

0 ... ... 1 1P  nPn   (1.13)

Teorema 1.15: Setiap himpunan vektor berdimensi m + 1 atau lebih dari m

adalah tak bebas linear. Sebuah himpunan vektor berdimensi – m,



P1,P2,...,Pn



adalah bebas linear jika satu-satunya nilai konstanta untuk (1.13) berlaku adalah ₁ ₂ ..._n 0.

(40)

1.6.2 Kombinasi Konveks

Vektor P yang berdimensi – m adalah kombinasi konveks dari vektor berdimensi – m P₁,P₂,...P_n jika terdapat konstanta-konstanta tak negatif

n 

₁,... yang jumlahnya adalah 1, sedemikian rupa sehingga

n nP P

P₁ ₁... (1.14)

1.6.3 Himpunan Konveks

Sebuah himpunan vektor berdimensi – m adalah konveks jika untuk dua vektor yang termasuk dalam himpunan ini berlaku bahwa penggal garis antara kedua vektor juga termasuk dalam himpunan ini.

Contoh 1.10

Piringan yang diarsir pada Gambar 1.8 kiri adalah sebuah himpunan konveks karena penggal garis antara dua buah titik sembarangnya (vektor-vektor berdimensi 2) semuanya berada dalam piringan ini. Gambar 1.8 kanan tidak konveks, karena meskipun R dan S termasuk pada himpunan berbayangan, tetapi terdapat titik-titik seperti T yang terletak pada penggal garis antara R dan S tetapi bukan merupakan bagian dari daerah bintang.

Gambar 1.8 Ilustrasi domain konveks (kiri) dan yang tidak konveks (kanan) Sebuah vektor P adalah titik ekstrim dari sebuah himpunan konveks jika ia tidak dapat dinyatakan sebagai kombinasi konveks dari dua buah vektor lainnya dalam himpunan ini, artinya sebuah titik ekstrim tidak terletak 1.6.2 Kombinasi Konveks

n 

n nP P

P₁ ₁... (1.14)

Contoh 1.10

Gambar 1.8 Ilustrasi domain konveks (kiri) dan yang tidak konveks (kanan) Sebuah vektor P adalah titik ekstrim dari sebuah himpunan konveks jika ia tidak dapat dinyatakan sebagai kombinasi konveks dari dua buah vektor lainnya dalam himpunan ini, artinya sebuah titik ekstrim tidak terletak 1.6.2 Kombinasi Konveks

n 

n nP P

P₁ ₁... (1.14)

Contoh 1.10

Gambar 1.8 Ilustrasi domain konveks (kiri) dan yang tidak konveks (kanan) Sebuah vektor P adalah titik ekstrim dari sebuah himpunan konveks jika ia tidak dapat dinyatakan sebagai kombinasi konveks dari dua buah vektor lainnya dalam himpunan ini, artinya sebuah titik ekstrim tidak terletak

(41)

pada penggal garis yang manapun antara dua buah vektor sembarang dalam himpunan ini.

Teorema 1.14:

Setiap vektor dalam sebuah himpunan konveks tertutup dan terbatas dengan sejumlah berhingga titik ekstrim dapat dinyatakan sebagai gabungan konveks dari titik-titik ekstrim.

Teorema 1.15:

Ruang penyelesaian dari sehimpunan sistem persamaan linear yang serempak (simultan) adalah konveks yang memiliki sejumlah berhingga titik ekstrim.

1.6. 4 Penyelesaian Titik Ekstrim

Misalkan  adalah himpunan dari semua penyelesaian layak dari program linear dalam bentuk standar, yaitu,  adalah himpunan semua vektor

x yang memenuhi Ax b dan x  . Dari teorema 1.15 dan kenyataan0 bahwa irisan dari himpunan-himpunan konveks adalah juga himpunan konveks, maka kesimpulannya adalah bahwa  merupakan himpunan konveks yang memiliki sejumlah berhingga titik ekstrim.

Catatan 1 : Fungsi tujuan mencapai optimumnya (maksimum atau minimum) pada sebuah titik ekstrim dari  , asalkan ada sebuah optimum.

Catatan 2 : Jika A berorde m x n (m baris dan n kolom) dengan mn, maka titik-titik ekstrim dari  memiliki sekurang-kurangnya n – m komponen yang nol.

1.7 Metode Numerik untuk Optimasi tanpa kendala

Masalah optimasi untuk kasus nyata umumnya melibatkan berbagai kendala. Akan tetapi untuk menyusun teori, maka keadaan ideal (tanpa kendala) dapat terlebih dahulu disusun.

(42)

1.7.1 Metode Golden Search (GS)

Metode ini berlaku untuk masalah minimisasi yang dibatasi sedemikian rupa sehingga interval solusi [a, b] diketahui dan f (x) adalah

unimodal dalam interval, yaitu tanda f ‘(x) berubah dalam [a, b] sehingga f

(x) menurun/meningkat monoton untuk [a, ] / [ ,b], dimana adalah solusi yang kita cari. Golden search (GS) dirangkum didalam program "GS". Algoritma GS ini ditunjukkan pada prosedur berikut.

Prosedur G.S Langkah 1.

Ambil dua titik c = a + (1 - r) h dan d = a + rh dalam interval [a,b],dimana =√ dan h = b - a.

Langkah 2.

Jika nilai-nilai f (x) pada dua titik yang hampir sama [yaitu, f (a) ≈ f (b)] dan lebar interval cukup kecil (yaitu, h ≈ 0), kemudian berhenti iterasi untuk keluar dari loop dan menyatakan = c atau = d tergantung pada apakah f (c) < f (d) atau tidak. Jika tidak, lanjutkan ke Langkah 3.

Langkah 3.

Jika f (c) < f (d), biarkan nilai-nilai f(x) baru terbatas pada interval b ← d, jika tidak, biarkan nilai-nilai f(x) baru yang lebih rendah terbatas pada interval a ←

c. Lalu, ke Langkah 1.

Kita akan menggunakan MATLAB Program "UtamaGS.m", yang digunakan untuk menemukan titik minimum.

Contoh 1.11

Fungsi Tujuan untuk meminimumkan persamaan yang diketahui sebagai berikut

(43)

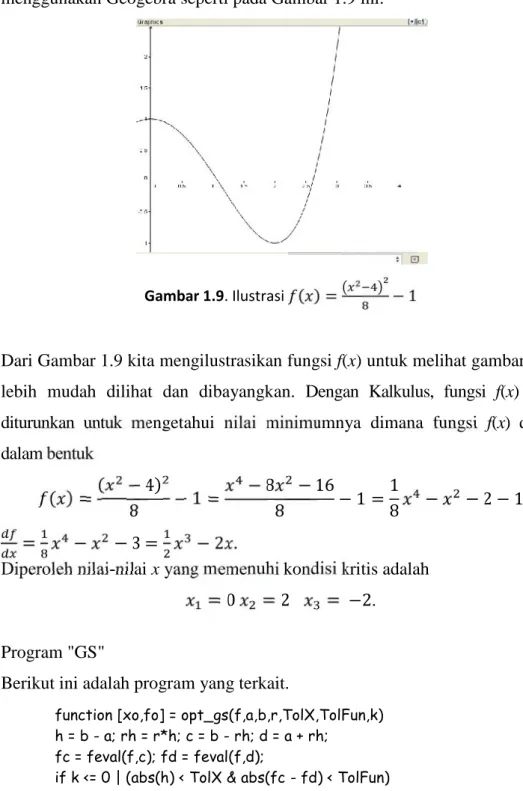
Untuk dapat mengilustrasikan f(x), dalam Gambar 1.9 kita dapat menggunakan Geogebra seperti pada Gambar 1.9 ini.

Gambar 1.9. Ilustrasi ( ) = − 1

Dari Gambar 1.9 kita mengilustrasikan fungsi f(x) untuk melihat gambar agar lebih mudah dilihat dan dibayangkan. Dengan Kalkulus, fungsi f(x) akan diturunkan untuk mengetahui nilai minimumnya dimana fungsi f(x) ditulis dalam bentuk ( ) =( − 4)₈ − 1 = − 8 − 16 8 − 1 = 1 8 − − 2 − 1 = − − 3 = − 2 .

Diperoleh nilai-nilai x yang memenuhi kondisi kritis adalah = 0 = 2 = −2.

Program "GS"

Berikut ini adalah program yang terkait.

function [xo,fo] = opt_gs(f,a,b,r,TolX,TolFun,k) h = b - a; rh = r*h; c = b - rh; d = a + rh;

fc = feval(f,c); fd = feval(f,d);

if k <= 0 | (abs(h) < TolX & abs(fc - fd) < TolFun) if fc <= fd, xo = c; fo = fc;

else xo = d; fo = fd; end

(44)

if k == 0, fprintf('Just the best in given # of iterations'), end else

if fc < fd, [xo,fo] = opt_gs(f,a,d,r,TolX,TolFun,k - 1); else [xo,fo] = opt_gs(f,c,b,r,TolX,TolFun,k - 1); end

end

Program "UtamaGS.m"

f711 = inline('(x.*x-4).^2/8-1','x');

a = 0; b = 3; r =(sqrt(5)-1)/2; TolX = 1e-4; TolFun = 1e-4; MaxIter = 100; [xo,fo] = opt_gs(f711,a,b,r,TolX,TolFun,MaxIter)

Langkah 4: Keluaran pada MATLAB

Xo= 2.0000 fo= -1.0000

Pembahasan : Secara matematis maka

= −20 2 dan Hasil MATLAB

= 2₋₁

Perhatikan hal berikut tentang proses golden search.  Pada setiap iterasi, lebar interval baru

b - c = b - (a + (1 - r) (b - a)) = rh atau d - a = a + rh - a = rh

sehingga menjadi r kali lebar interval lama (b - a = h).

 r rasio golden adalah tetap sehingga titik ₌ _{− ℎ = −} _ℎ diperbaharui pada interval [c, b] sesuai dengan d = a + rh= b - (1 - r)

h, yaitu

(45)

Untuk selanjutnya akan ditunjukkan proses optimasi dimana data diperoleh dari penelitian.

1.8 Optimasi dari penelitian Proyek 1. Kasus Pertanian

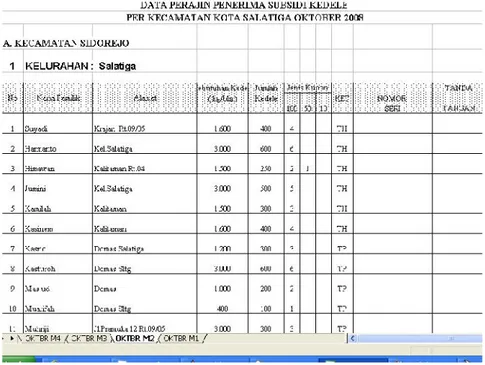
Pada (Parhusip dan Ayunani,2009) telah ditunjukkan bahwa hijauan sebagai variabel dominan untuk berat sapi yang produktif menghasilkan susu. Hal ini dilakukan dengan menggunakan Principal Componen Analysis. Selain hijauan terdapat beberapa variabel lain yang diukur seperti pupuk urea, lingkar dada, garam dapur, ketela untuk mempelajari berat sapi yang optimal dalam menghasilkan produksi susu sapi. Data diobservasi setiap hari selama 1.5 bulan, dari tanggal 15 Juli 2008 sampai dengan 30 Agustus 2008. Data diperoleh dari Peternakan Rakyat Dukuh Belon, Kelurahan Kumpulrejo, Kecamatan Argomulyo, Kota Salatiga. Sebagai salah satu bentuk data hasil survei ditunjukkan pada Tabel 1a-Tabel 1d.

Tabel 1a Contoh data lingkar dada, berat pupuk urea dan berat untuk sapi dari

Peternakan Rakyat Dukuh Belon, Kelurahan Kumpulrejo, Kecamatan Argomulyo, Kota Salatiga dari tanggal 15 Juli 2008 sampai dengan 30 Agustus 2008. Lingkar dada (cm) Pupuk urea (gr) Berat sapi (kg) 104 70 102 106 70 108 108 70 114 110 70 121 112 70 126 115 70 137 118 70 148 120 75 155 122 75 162

(46)

Tabel 1b. Data pupuk urea yang diberikan sesuai dengan berat untuk sapi dari

Peternakan Rakyat Dukuh Belon, Kelurahan Kumpulrejo, Kecamatan Argomulyo, Kota Salatiga dari tanggal 15 Juli 2008 sampai dengan 30 Agustus 2008. 100-150kg 150-200kg 200-250kg 250-300kg 300-350kg 350-400kg >400kg 16 20 25 30 35 40 45 18 22 27 32 37 47 52 20 24 30 34 40 50 55 22 28 33 38 45 55 60 25 32 36 42 50 60 65 30 36 40 46 55 65 70 35 40 45 50 60 70 75 40 45 50 55 65 75 80 45 50 55 60 70 80 85 50 55 60 65 75 83 90 50 55 60 70 80 90 95 55 60 65 70 80 90 100 55 60 65 75 80 95 100 60 65 70 75 85 95 100 60 65 70 80 90 100 100 65 70 75 80 90 100 100 65 70 75 85 95 100 100 70 75 80 85 95 100 100 70 75 80 90 100 100 100 75 80 85 90 100 100 100

(47)

Va ria be l 1 2 3 4 5 6 7 8 9 10 11 12 Ta be l1 c. Da ta be rb ag ai va ria be ly an g di uk ur pa da sa pi da ri Pe te rn ak an Ra ky at Du ku h Be lo n, Ke lu ra ha n Ku m pu lre jo , Ke ca m at an Ar go m ul yo ,K ot a Sa la tig a da ri ta ng ga l1 5 Ju li 20 08 sa m pa id en ga n 30 Ag us tu s2 00 8. N o. ur ut (t ia p ko lo m )m en un ju kk an no .u ru ts ap i Ju m la h hi ja ua n (k g) 40 40 35 35 50 50 50 30 30 30 25 25 ju m la h ka tu l( kg ) 6 6 2 2 10 10 3 4 4 4 3 3 ju m la h te la (k g) 2 2 2 2 10 10 3 2 2 2 2 2 ju m la h ga ra m da pu r( kg ) 0. 1 0. 1 0. 25 0. 2 0. 3 0. 3 0. 5 0. 25 0. 25 0. 25 0. 25 0. 25 Ju m la h ai r/ ha ri (li te r) 40 40 35 30 50 50 30 30 30 30 30 30