vii
PENGARUH SUDUT ANTAR PLANET (θ12) TERHADAP BENTUK LINTASAN SISTEM DUA PLANET
ABSTRAK
viii
INTER PLANET ANGLE (θ12) EFFECT TO THE TRAJECTORY FORM OF TWO
PLANETS SYSTEM
ABSTRACT
i
PENGARUH SUDUT ANTAR PLANET (
θ12) TERHADAP
BENTUK LINTASAN SISTEM DUA PLANET
Skripsi
Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Fisika
Oleh:
THOMAS JOKO KRISMANTO
NIM: 003214016
PROGRAM STUDI FISIKA JURUSAN FISIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
INTER PLANET ANGLE (
θ12) EFFECT ON THE
TRAJECTORY FORM OF TWO
PLANETS SYSTEM
Scription
Presented as Partial Fulfillment of the requirements to obtain the Sarjana Sains Degree
In Physics
By:
THOMAS JOKO KRISMANTO
NIM: 003214016
PHYSICS STUDY PROGRAM PHYSICS DEPARTEMENT FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v K eh i d u p a n i n i a d a l a h b el a ja r
d a r i w a k t u k e w a k t u
sa m p a i k i t a ta k d a p a t m er a sa k a n
p a n a s d i n gi n n y a d u n i a .
Sem u a b egi t u m u d a h b a gi k em a u a n d a n t ek a t
y a n g k u a t .
Ku per sembahkan skr ipsi ini buat bapak dan ibu dan ketiga kakakku
vii
PENGARUH SUDUT ANTAR PLANET (θ12) TERHADAP BENTUK LINTASAN SISTEM DUA PLANET
ABSTRAK
viii
INTER PLANET ANGLE (θ12) EFFECT TO THE TRAJECTORY FORM OF TWO
PLANETS SYSTEM
ABSTRACT
ix
KATA PENGANTAR
Syukur kepada Tuhan Yesus yang selalu membimbing penulis dalam setiap detik kehidupan penulis selama penulisan skripsi ini. Suatu kehormatan yang besar bagi saya dapat memperoleh kesempatan memahami agungnya alam semesta karya tangan Tuhan yang sempurna selama mempelajari ilmu fisika.
Banyak pihak yang telah membantu saya dalam menyelesaikan karya ilmi-ah ini yang membuat saya selalu berdiri dan maju terus. Oleh karena itu dengan rendah hati saya mengucapkan banyak terimakasih kepada:
1. Bapak Drs. Drs. Vet Asan Damanik, M.Si sebagai dosen pembimbing yang dengan sangat sabar dan sepenuh hati serta meluangkan waktu di saat libur untuk membimbing saya dalam menyelesaikan skripsi ini. Saya terkesan dengan jawaban “mudah” setiap saya menanyakan hasil pekerjaan saya dan suatu hal yang tidak saya pahami, itu membuat tak ada yang sulit bagi saya yang ada hanyalah “mau dan maju terus”.
2. Bapak, Ibu, Kakak dan seluruh keluarga besar yang telah memberi dukungan dan semangat penuh, dukungan keluarga tak ternilai bagi saya.
3. Dekan Fakultas Sains dan Teknologi Ir.G.Heliarko,S.J S.S.,BST.,M.Sc.,M.A. beserta staf.
x
Dr. Ign Edi Santoso, M,Si, Bapak Prof. Liek Wilardjo, Bapak Drs.BA. Tjipto Sujitno, M.T, APU, Bapak Drs. Albertus Setyoko, M.Si (almarhum), Bapak Prasetyadi, S.Si, dan Ibu Dwi Nugraheni Rositawati, S.Si.
5. Laboran program studi fisika Bapak Sugito, Mas Agus, Mas Sis yang banyak membantu saya dalam penggunaan laboratorium selama studi. 6. Pegawai Sekretariat Fakultas Sains dan Teknologi.
7. Pegawai Perpustakaan unit kampus III Paingan.
8. Semua teman di Program Studi Fisika angkatan”00 yang sama-sama berjuang serta teman beda angkatan yang sama-sama berjuang dalam menyelesaikan skripsi yang tidak bisa saya sebutkan satu persatu. Terimakasih atas segala dukungan dan smangatnya.
9. Teman-teman MUDIKA yang selalu memberi semangat dan menghibur. 10. Kepada “virtus compusoft” yang telah meminjami saya satu unit
komputer dan hp selama penulisan skripsi serta memberi dukungan baik materi maupun smangat yang tak pernah padam. MAJU dan SUKSES untuk “virtus compusoft” dan menjadi besar untuk menolong sesama. 11.Terima kasih kepada keluarga bapak ibu Wahyudi yang tak henti-henti menanyakan skripsi selama satu tahun ini, itu sangat memberi dukungan dan semangat bagi saya.
xi
Saya menyadari bahwa skripsi ini masih jauh dari sempurna, oleh karena itu kritik dan saran yang membangun diterima dengan senang hati.
Yoyakarta, Januari 2008 Penulis
xii
PERNYATAAN KEASLIAN KARYA
Saya menyatakan sesungguhnya bahwa skripsi yang telah saya tulis ini tidak memuat karya orang lain kecuali yang telah disebutkan dalam Daftar Pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, Januari 2008
Penulis
xiii DAFTAR ISI
HALAMAN JUDUL ………. i
HALAMAN PERSETUJUAN PEMBIMBING ………..….. iii
HALAMAN PENGESAHAN ………..….. iv
HALAMAN MOTTO PERSEMBAHAN ………... v
HALAMAN LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ... vi
ABSTRAK ……….………. vii
ABSTRACT ……… viii
KATA PENGANTAR ………... ix
HALAMAN PERNYATAAN KEASLIAN KARYA ………... xii
DAFTAR ISI ………... xiii
DAFTAR GAMBAR ………... xv
BAB I. PENDAHULUAN ………. 1
1.1. Latar Belakang ……….………....…. 1
1.2. Perumusan Masalah ……….. 2
1.3. Batasan Masalah ………... 2
1.4. Tujuan Penelitian ……….. 3
1.5. Manfaat Penelitian ………… .………... 3
1.6. Sistematika Penulisan Laporan Penelitian ………..………... 3
BAB II. DASAR TEORI ………... 5
2.1. Hukum Kepler ………... 5
2.2. Gerak Benda dengan Gaya Sentral ………... 8
2.3. Hukum Kekekalan Energi dan Persamaan Gerak Planet …….. 13
2.4. Sistem Gerak Dua Planet ... 18
2.5. Polinomial Legendre ………. 20
xiv
3.1. Jenis Penelitian ……….. 22
3.2. Sarana Penelitihan ………. 22
3.3. Langkah-Langkah Penelitihan ……….. 22
BAB IV. HASIL DAN PEMBAHASAN ………….……….... 23
4.1. Sistem Dua Planet ……….. 23
4.2. Bentuk Lintasan Planet ………... 34
4.3. Pembahasan ……….. 41
BAB V. PENUTUP ………... 44
5.1 Kesimpulan ………... 44
5.2 Saran ………... 44
DAFTAR PUSTAKA ………... 45
LAMPIRAN Lampiran A ………. 46
Lampiran B . ………... 55
xv
DAFTAR GAMBAR
Gambar 2.1 Bentuk lintasan (orbit) planet 5
Gambar 2.2 Luas yang disapu planet dalam waktu ∆t 6
Gambar 2.3 Interaksi sistem dua planet 19
Gambar 4.1 Dua planet berinteraksi 23
Gambar 4.2 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudutθ12 =00 35
Gambar 4.3 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudutθ12 =300 35
Gambar 4.4 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut θ12 =600 36
Gambar 4.5 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut 0 12 =90 θ 36
Gambar 4.6 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut 0 12 =120 θ 37
Gambar 4.7 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudutθ12 =1500 37
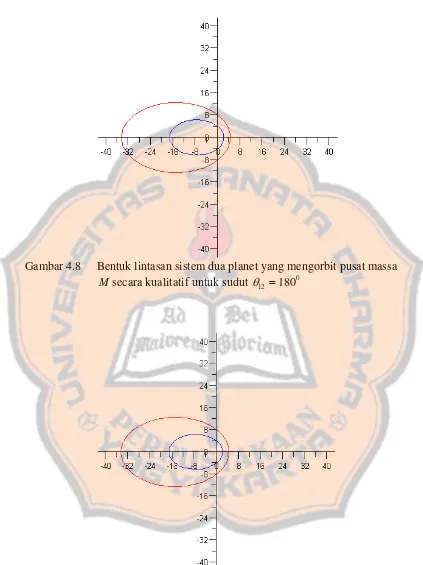
Gambar 4.8 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut 0 12 =180 θ 38
xvi
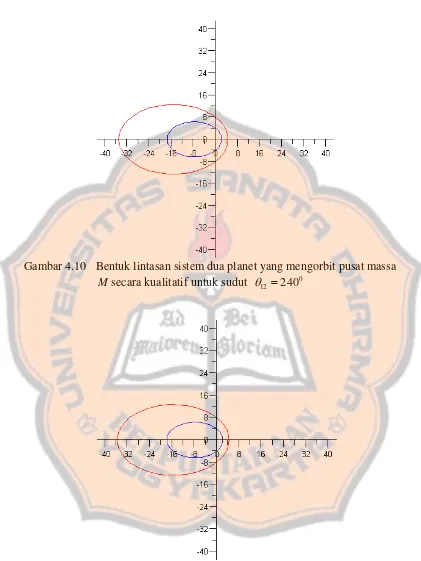
Gambar 4.10 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut 0
12 =240
θ 39
Gambar 4.11 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut 0
12 =270
θ 39
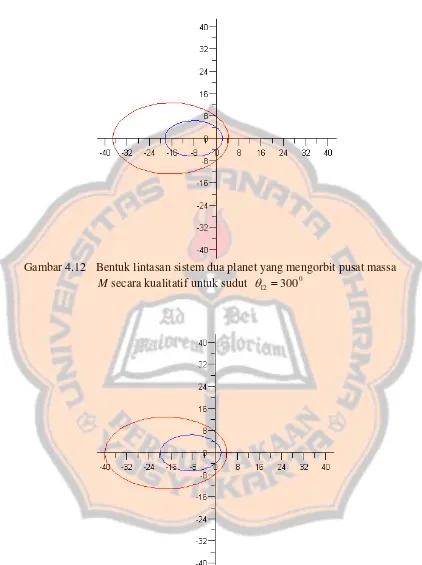
Gambar 4.12 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut θ12 =3000 40 Gambar 4.13 Bentuk lintasan sistem dua planet yang mengorbit pusat massa
M secara kualitatif untuk sudut θ12 =3300 40 Gambar 4.14 Bentuk lintasan sistem dua planet yang mengorbit pusat massa
M secara kualitatif untuk sudut 0 12 =360
BAB I PENDAHULUAN
1.1. Latar Belakang
Dalam pembahasan tentang astronomi khususnya hukum gerak planet sangat
jarang membahas pengaruh interaksi antar planet terhadap bentuk lintasan planet
yang berinteraksi. Pembahasan mengenai gerak planet hanya terbatas pada hukum
Kepler dan hukum Newton secara umum, yaitu bahwa pergerakan planet yang satu
sangat berpengaruh terhadap planet yang lain dan bentuk lintasannya adalah
berbentuk elips (Sears dkk, 1987).
Hukum-hukum yang dapat menjelaskan posisi dan orbit planet dirumuskan
antara tahun 1601 dan 1619 oleh astronom dan ahli matematika Jerman Johanes
Kepler(1571-1630). Kepler sebagai asisten Tycho Brahe (1546-1601) memanfaatkan
data pengamatan yang dikumpulkan oleh Tycho Brahe dan mengolahnya secara
matematis sehingga menghasilkan perumusan matematis gerak planet.
Hukum Kepler menyatakan bahwa semua planet mengorbit matahari dan
gerak semu planet yang terlihat dari bumi dapat digunakan untuk menentukan secara
tepat posisi dari planet. Hukum Kepler menyatakan bahwa kedudukan planet
terhadap matahari selalu berubah secara periodik dengan bentuk lintasan elips
(Suwitra, 2001). Perubahan kedudukan (posisi) planet terhadap matahari
menunjukkan bahwa terjadi interaksi antar planet sehingga setiap planet mempunyai
posisi terjauh dan terdekat dari matahari. Posisi terjauh dari matahari disebut
aphelium, sedangkan posisi terdekat planet dari matahari disebut perihelium.
Karena alasan itulah penulis tertarik untuk mengkaji lebih jauh tentang
interaksi dua planet terhadap gerak planet khususnya pengaruh bentuk lintasan
planet relatif terhadap matahari sebagai fungsi sudut antar planet. Dengan
menggunakan persamaan energi dan sudut yang terbentuk antara dua planet yang
mengorbit matahari akan ditentukan bentuk lintasan sistem dua planet.
1.2. Perumusan Masalah
Berdasarkan latar belakang tersebut bahwa pengaruh interaksi antar planet
yang mengorbit matahari jarang dibahas khususnya terkait dengan pengaruh sudut
antar planet terhadap bentuk lintasan planet, maka yang menjadi permasalahan
dalam penelitian ini adalah bagaimana pengaruh sudut antar planet terhadap bentuk
lintasan (orbit) sistem dua planet yang mengorbit titik pusat (matahari).
1.3. Batasan Masalah
Masalah yang diteliti dibatasi pada
1. Interaksi dua planet yang bergerak mengorbit suatu titik pusat yang sama.
2. Energi total sistem dua planet hanya memperhitungkan energi kinetik dan
energi potensial gravitasi.
3. Sistem dua planet yang berinteraksi.
3
1.4. Tujuan Penelitian
Tujuan penelitian ini adalah untuk
1. Merumuskan persamaan gerak sistem dua planet yang mengorbit titik
pusat massa yang sama.
2. Menyelesaikan persamaan gerak sistem dua planet sehingga diperoleh
bentuk lintasan planet sebagai fungsi sudut yang dibentuk dua planet
dengan menggunakan paket program Maple 10.
1.5. Manfaat Penelitian
Penelitian ini bermanfaat untuk:
Pengembangan ilmu pengetahuan khususnya pengetahuan tentang gerak dua
planet yang mengorbit titik pusat yang sama.
1.6. Sistematika Penulisan Laporan Penelitian
Sistematika laporan penelitian ini adalah sebagai berikut:
BAB I. PENDAHULUAN
Dalam Bab ini dijelaskan uraian mengenai latar belakang masalah, batasan
masalah, tujuan penelitian, manfaat penelitian, sistematika penulisan laporan
penelitian.
BAB II. DASAR TEORI
Dalam Bab II dijabarkan dasar teori yang terkait dengan hukum gerak
hukum kekekalan energi dan persamaan gerak planet, sistem dua planet dan
polinomial Legendre.
BAB III. METODE PENELITIAN
Pada Bab III menjelaskan tentang metode penelitian yang ditempuh dalam
penelitian ini.
BAB IV. HASIL DAN PEMBAHASAN
Dalam Bab IV dibahas tentang sistem dua planet yang berinteraksi, bentuk
lintasan planet dan pembahasan.
BAB V. PENUTUP
BAB II DASAR TEORI
2.1. HUKUM KEPLER
Keteraturan gerak planet dapat dijelaskan oleh mekanika benda langit yang
kemudian dikembangkan untuk menjelaskan gerak dan lintasan planet sehingga
dapat diketahui bentuk orbit planet. Kepler membandingkan data yang dikumpulkan
Tycho Brahe (1546-1601) dengan hasil pengamatannya dan kemudian mengolahnya
secara matematis sehingga menghasilkan tiga buah hukum gerak planet yang
kemudian dikenal sebagai hukum Kepler (Sears dkk, 1987).
Hukum Kepler tersebut adalah:
1. Planet bergerak dalam bidang datar dengan orbitnya berbentuk elips dan
matahari sebagai salah satu titik fokusnya (Gambar 2.1). Ini berarti
kedudukan planet terhadap matahari selalu berubah. Titik terjauh dari
matahari disebut aphelium dan titik terdekat dari matahari disebut
perihelium.
C
A B
D
E
M a b
Gambar 2.1 Bentuk lintasan (orbit) planet
2. Vektor yang menghubungkan matahari dengan planet menyapu luas yang
sama untuk waktu yang sama (Gambar 2.2). Dari Gambar 2.2, jika lintasan
AB ditempuh dengan waktu yang sama dengan lintasan CD, maka luas
AM B sama dengan CMD.
M rr A
∆
A
∆
θ
vr m
r rr+∆r
t
∆
t
∆
Gambar 2.2 Luas yang disapu planet dalam waktu ∆t.
Jika jari-jari lintasan planet adalah rdan sudut yang dibentuk selama waktu
adalah t
∆ ∆θ, maka
∆A= r⋅∆s
2 1
θ ∆ ⋅ ⋅
= r r
2 1
θ ∆
= 2
2 1
r . (2.1)
Jika ∆t →0, maka ∆θ →0, sehingga persamaan (2.1) dapat ditulis menjadi
2
0 2
1
lim A = r
∆ ∆
→
∆θ θ ,
atau
θ
d r
dA 2
2 1
7
3. Rasio kuadrat periode revolusi planet (T) terhadap kubik dari sumbu elips
(r) adalah sama untuk seluruh planet :
C r T =
3 2
. (2.3)
Nilai tetapan Cdapat dijabarkan dari hukum II Newton khususnya tentang
gerak melingkar atau suatu benda bergerak dalam medan atau gaya sentral.
Jika suatu benda bermassa mbergerak melingkar dengan jari-jari r, maka
periode (T ) adalah
v r
T = 2π , (2.4)
dengan adalah kecepatan, dan gaya sentripetal yang bekerja sama dengan
gaya sentrifugal v
r v m F
2
= . (2.5)
Jika 2
r Mm G
F = dimasukkan ke persamaan (2.5), maka diperoleh
v2 r
GM =
, (2.6)
dengan adalah tetapan gaya gravitasi universal. Dari persamaan (2.4) dan
(2.6) akhirnya diperoleh G
GM r
T 2
3 2
4π
= , (2.7)
dengan 2
2 11 10 . 673 , 6
kg Nm
G= − .
GM C
2 4π
= . (2.8)
2.2. Gerak Benda dengan Gaya Sentral
Penggunaan hukum III Newton berbunyi (Goldstein, 1950): untuk sistem
aksi akan selalu ada reaksi yang melawan yang besarnya sama dengan aksi. Jumlah
hukum III Newton diterapkan dalam medan gaya sentral antara dua buah benda
dan , maka aksi yang dilakukan benda pertama terhadap benda kedua
1 m
2
m (Fr12) akan
menimbulkan reaksi pada benda kedua (Fr21) yang besarnya sama dan berlawanan arah dengan (Fr12). Jadi dapat dituliskan
Faksi Freaksi. r r
−
=
Jika aksi tersebut berupa gaya, maka reaksi juga berbentuk gaya. Gaya tarik menarik
antar dua buah benda bermassa dan berbanding lurus dengan massa dan
serta berbanding terbalik dengan kuadrat jarak ( 1
m m2 m1
2
m r) antar m1dan m2.
Jika benda bermassa mmengalami gaya yang arahnya selalu ke suatu titik
yang tetap, maka benda tersebut mangalami gaya sentral. Gaya yang arahnya selalu
menunju suatu titik yang tetap disebut gaya sentral. Contoh gaya sentral adalah gaya
yang dialami oleh suatu benda yang mengorbit benda lain seperti planet yang
mengorbit matahari sebagai pusat orbit planet. Sesuai dengan hukum II Newton,
gaya Fr yang dialami suatu benda bermassa mdengan percepatan adalah ar a
m
Fr = r (2.9)
Vektor posisi dan vektor sudut planet ditulis
r r
9
θ θ
θr= ˆ . (2.11)
Perubahan rˆ dan terhadap waktu di tulis sebagai berikut θˆ
dt d dt
r
dˆ θˆ θ
= , (2.12)
dt d r dt
dθ θ
ˆ ˆ
−
= , (2.13)
Kecepatan radial planet
dt r d r r dt dr dt r d vr ˆ ˆ+ = = r r
. (2.14)
Dari persamaan (2.12) dan (2.14) diperoleh
ˆ θθˆ dt d r r dt dr dt r
dr = +
. (2.15)
Jika persamaan (2.15) diturunkan terhadap waktu (t), maka diperoleh percepatan
planet θ ˆ θ θ θ θˆ 2 2 2 2 2 2 2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = = dt d r dt d dt dr dt d dt dr r dt d r dt r d dt r d ar r r
. (2.16)
Persamaan gerak planet untuk r berubah dalam gaya sentral dapat ditulis sebagai
f(r)rˆ=marr . (2.17)
Jika persamaan (2.16) dimasukkan ke dalam persamaan (2.17), maka diperoleh
⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = θ ˆ θ θ θ θˆ ˆ ) ( 2 2 2 2 2 dt d r dt d dt dr dt d dt dr r dt d r dt r d m r r
f . (2.18)
Dari persamaan (2.18) terikat bahwa
. )
(r m
f = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − 2 2 2 dt d r dt r d θ
dan
0 = ⎥
⎦ ⎤ ⎢
⎣ ⎡
+ +
⋅
2 2
dt d r dt d dt dr dt d dt dr
m θ θ θ . (2.20)
Jadi kalau sebuah benda bergerak dalam medan gaya sentral, sesuai dengan
hukum II Newton, benda tersebut hanya mempunyai percepatan radial (arr)
sedangkan percepatan sudut (arθ) sama dengan nol.
Benda yang bergerak melingkar mempunyai momentum sudut (lr) yang
diberikan oleh
p r
lr = r× r , (2.21)
dengan pr=mvrr adalah momentum linier. Jika persamaan (2.14) dimasukkan ke
persamaan (2.21), maka diperoleh
⎥⎦ ⎤ ⎢⎣
⎡ +
×
= . ˆ θθˆ
dt d r r dt dr m r
lr r
= ˆ×ˆ+ 2 θ ˆ×θˆ
r dt d mr r r dt dr
mr
dt d
mr2 θ
= kˆ , (2.22)
sebab rˆ×rˆ=0 dan rˆ×θˆ=kˆ.
Jika nilai mutlak lr pada persamaan (2.22) dimasukkan ke dalam persamaan
(2.19), maka diperoleh
f(r)=m. ⎥
⎦ ⎤ ⎢
⎣ ⎡
− 22 3
2 2
r m
l dt
r d
. (2.23)
11 dt d d dr dt dr θ θ
= , (2.24)
memasukkan persamaan (2.22) ke persamaan (2.24) menghasilkan
θ d dr mr l dt dr 2
= . (2.25)
Dengan memisalkan
r
u =1, (2.26.a)
maka
du u
dr =− 12 , (2.26.b)
sehingga ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− = θ d du u u m l dt dr 2 2 1 θ d du m l −
= . (2.27)
Jika persamaan (2.27) diturunkan terhadap waktu ( ), maka diperoleh t
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = dt dr dt d dt r d 2 2 θ θ θ d d d du m l dt d ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− = dt d d du m l d d θ θ θ ⎟⎠ ⎞ ⎜ ⎝ ⎛− = 2 2 2 2 2 θ d u d r m l −
= . (2.28)
3 2
2
2 2
2 2
2 )
(
r m
l d
u d r m
l m
r
f =− −
θ . (2.29)
Dengan mengganti u
r = 1, maka diperoleh bentuk persamaan diferensial orde dua
pada persamaan (2.29) menjadi
) 1 ( 2 2 2
2
u f u l
m u
d u d
− = +
θ . (2.30)
Sebuah benda bermassa yang berada dalam medan gravitasi mempunyai
energi potensial
m
r k
V =− , (2.31)
dengan k =GMm.
Turunan energi potensial terhadap posisi r menghasilkan gaya atau secara
matematis
dr dV r
f( )=−
2 r
k
−
= , (2.32)
atau
2 )
1
( ku
u
f =− , (2.33)
memasukkan persamaan (2.33) ke persamaan (2.30) menghasilkan
2 2
2
l mk u d
u d + =
θ . (2.34)
Persamaan diferensial orde dua pada persamaan (2.34) mempunyai penyelesaian
13
cos( 0) 2
l mk A
u = θ −θ + , (2.35)
dengan A tetapan. Karena r
u= 1dan , maka persamaan (2.35) dapat ditulis
menjadi
0 0 =0
θ
θ
cos . 1
2
mk A l
mk l
r
+ =
2
. (2.36)
Jika didefinisikan eksentrisitas
mk A l e
2
= , (2.37)
dan
mk l r
2
0 = , (2.38)
maka
θ
cos 1
0
⋅ + =
e r
r . (2.39)
2.3. Hukum Kekekalan Energi dan Persamaan Gerak Planet
Persamaan gerak dan lintasan (orbit) planet dapat dijabarkan dari hukum
kekekalan energi untuk medan (gaya) sentral menyatakan bahwa jumlah energi
kinetik (T ) dan energi potensial (V ) adalah konstan, secara matematis dituliskan
V T
E= + . (2.40)
Energi kinetik (T ) suatu benda (planet) bermassa ( ) yang mengorbit
benda lain sejauh
m
2 2 2
2 1 2
1
mr l r
m
T = & + , (2.41)
dengan l adalah momentum sudut. Memasukkan persamaan (2.41) ke persamaan
(2.40) menghasilkan
V
mr l r
m
E= + 2 + 2 2
2 1 2
1
& . (2.42)
Jadi kecepatan planet ke arah r adalah
⎟⎟ ⎠ ⎞ ⎜⎜
⎝ ⎛
− − =
2 2
2 2
mr l V E m
r& . (2.43)
Dari kecepatan diperoleh waktu (t)tempuh planet sebagai fungsi dari posisi(r)
2 2
2 2
2
r m
l r
GM m
E
dr dt
− +
= (2.44.a)
2 2 2
2 2
1
m l GMr m
Er r
dr dt
− +
= (2.44.b)
∫
− +
= mak
r
r
m l GMr m
Er
dr r t
min
2 2 2
2 2
.
. (2.44.c)
Dengan menggunakan persamaan Lampiran B (B.1) dan (B.2) penyelesaian untuk
persamaan (2.44.c) dengan memisalkan m
E
a= 2 , b=2GM, dan 2 2
m l
c=− . Hasil
15 ⎢ ⎢ ⎣ ⎡ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − +
= m GM
Er m E GMm m E m l GMr m Er t 2 4 log 2 2 2 2 2 1 2 3 2 1 2 2 2 mak r r m El m EGMr m r E min 2 1 3 2 2 2 2 2 4 4 2 ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎥ ⎦ ⎤ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − +
+ . (2.45)
Perubahan sudut gerak planet sebagai fungsi momentum sudut dapat diperoleh dari
persamaan (2.22), yaitu
2 mr
ldt
dθ = . (2.46)
Dengan mengganti r dr dt
&
= , persamaan (2.46) menjadi
r dr mr l d & 2 =
θ . (2.47)
Jika persamaan (2.43) dimasukkan ke persamaan (2.47) kemudian di integralkan
maka diperoleh
∫
− − = 2 2 22 2 2 1
r l mV l mE r dr
θ . (2.48)
Dengan memasukkan persamaan (2.31), (2.26.a) dan (2.26.b) ke persamaan (2.48),
menjadi
∫
− + − = 2 2 2 2 2 u l mku l mE duθ . (2.49)
Dengan memisalkan y=−1, 2 2 l mk
f = ,
2
2l
mE
g
=
, dan , serta⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + − = − 2 2 2 2 1 1 ) sin( mk El mk ul θ
γ , (2.50)
dengan γadalah tetapan integral (konstanta).
Jika digunakan rumus pada Lampiran B (B.4), maka persamaan (2.50) menjadi
⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + − = 2 2 2 2 1 1 cos mk El mk ul
θ . (2.51)
Dengan mengganti kembali r
u= 1, persamaan (2.51) menjadi
⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + +
= 1 1 2 .cosθ
1 2 2 2 mk El l mk
r , (2.52)
atau θ cos . 2 1 1 . 2 2 2 mk El k m l r + +
= . (2.53)
Mengingat persamaan (2.39), eksentrisitas untuk persamaan (2.53) adalah
2 2 2 1 mk El
e= + . (2.54)
Jika lintasan (orbit) planet berbentuk lingkaran, maka e=0, sehingga
0 2 1 2 2 = + mk El
, (2.55)
17
0 2r
k
E=− . (2.56)
Dengan memasukkan persamaan (2.31) ke persamaan (2.56) diperoleh
V E
2 1
= . (2.57)
Jadi energi total (E) setengah dari nilai energi potensial (V ) untuk planet
yang mengorbit dengan lintasan berbentuk lingkaran.
Dari nilai eksentrisitas persamaan (2.37) dan (2.54) diperoleh
4 2
2 2
2 l Em l
k m
A= + , (2.58)
sehingga nilai eksentrisitas seperti pada persamaan (2.54)
2 2 2 1
mk El e= + .
Untuk lintasan yang berbentuk elips nilai eksentrisitas adalah 0<e<1
(Goldstein, 1950). Sebagai contoh ditinjau lintasan partikel bermassa yang
bergerak melingkar dalam medan sentral dengan gaya sentripetal sama dengan gaya
gravitasi (Alonso, 1994). Energi kinetik partikel tersebut adalah
m
2 2 1
mv
T = . (2.59)
Dengan memasukkan persamaan (2.6) ke persamaan (2.59) diperoleh
r GMm T
2 1
= . (2.60)
Jika persamaan (2.31) dan persamaan (2.60) dimasukkan kedalam persamaan (2.40),
r GMm E
2 1
−
= . (2.61)
Jika energi total berharga negatif pada persamaan (2.61) menyatakan sistem
dalam lintasan tertutup, artinya planet dengan pusat sistem terikat satu sama lain
(Seno dan Sihono, 2007), maka persamaan (2.54) menjadi
2 2 2 1
mk El
e= − . (2.62)
2.4 Sistem Gerak Dua Planet
Dua planet akan saling mempengaruhi. Planet yang satu mempengaruhi
planet yang lain atau sebaliknya. Sesuai dengan hukum III Newton keadaan gaya itu
adalah sama besar dan berlawanan arah. Untuk sistem dua planet dengan massa
dan yang masing-masing planet terletak di
1 m
2
m rr1 dan rr2, dengan matahari sebagai
pusat dengan massa M. Gaya dari masing-masing massa terhadap pusat yaitu
massa m1dan m2terhadap matahari dengan massa M ditulis
21 1 2
1 F
dt r d
m r
r
= , (2.63)
22 2
2
2 F
dt r d
m r
r
= , (2.64)
Untuk gaya interaksi Fr yang memenuhi hukum gravitasi Newton yaitu
berbanding lurus dengan massa planet dan berbanding terbalik dengan kuadrat
jaraknya, untuk masing-masing planet yang berinteraksi dengan pusat massa
M mempunyai gaya sebagai berikut:
1 2 1
1
1 rˆ
r M Gm
19
2 2
2 2
2 rˆ
r M Gm
Fr =− , (2.66)
Jadi momentum sudut gerak relatif massa m1 mengelilingi M (pusat gaya) bernilai
tetap (besar dan arahnya) (Zahara, 1997).
Jika dalam suatu sistem terdapat dua planet maka diantara kedua planet itu
timbul keadaan saling mempengaruhi. Pengaruh mempengaruhi ini juga bergantung
pada jarak masing-masing planet dalam sistem itu. Pengaruh ini berbentuk gaya
yaitu gaya internal untuk membedakan gaya dari luar.
Ditinjau dua planet m1dan m2 yang mengelilingi pusat massa M yang sama,
kedudukan masing-masing adalah rr1 dan rr2, kedudukan relatif terhadap
adalah
1 m
2
m rr21, maka kita dapatkan bentuk koordinat gambar sebagai berikut:
Gambar 2.3 Interaksi sistem dua planet
dengan rr2 =rr1+rr21, θ2 =θ1+θ12, dan
12 1
2 2 1 2 2
21 r r 2r r.cosθ
dari gambar.2.3 dengan hukum II Newton diperoleh 12 1 2 1 2
1 F F
dt r d
m r r
r
+
= , (2.68)
21 2 2
2 2
2 F F
dt r d
m r r
r
+
= , (2.69)
dengan dan adalah gaya ekternal sistem, tanda negatif merupakan arah antara
dengan berlawanan arah maka 12
Fr Fr21
21
F r21 Fr12 =−Fr21, (Halliday dan Resnick, 1984).
2.5 Polinomial Legendre
Polinomial Legendre didefinisikan sebagai
⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⋅⋅ ⋅ − − − ⋅ − − − + − − − ⋅⋅ ⋅ − −
= −2 −4
) 3 2 )( 1 2 ( 4 2 ) 3 )( 2 )( 1 ( ) 1 2 ( 2 ) 1 ( ! 1 ) 3 2 )( 1 2 ( )
( j j j
j x j j j j j j x j j j x j j j x P . (2.70)
Polinomial Legendre sebagai fungsi generator didefinisikan sebagai:
∑
∞=
= +
− 2 0
) ( 2 1 1 j j j x P h h xh
, h <1. (2.71)
Fungsi diatas disebut fungsi generator untuk polinomial Legendre dan berguna
untuk mendapatkan sifat-sifat dari polinomial Legendre. Perhatikan bahwa
adalah polinomial dengan derajat )
(x
Pj j(Boas, 1966). Beberapa polinomial
Legendre pertama ditulis sebagai berikut:
P0(x)=1 , (5 3 ) 2
1 )
( 3
3 x x x
P = − ,
x x
P1( )= , (35 30 3)
8 1 )
( 4 2
4 x = x − x +
21
) 1 3 ( 2 1 )
( 2
2 x = x −
P , (63 70 15 )
8 1 )
( 5 3
5 x x x x
P = − + .
(2.72)
BAB III
METODE PENELITIAN
3.1 Jenis Penelitian
Penelitaan yang dilakukan dalam penulisan sekripsi ini adalah penelitian
studi pustaka dan perhitungan secara numerik dengan paket program Maple 10 .
3.2 Sarana Penelitian
Sarana penelitian ini diambil dari buku yang ada di UPT Sanata Dharma dan
internet yang berhubungan dengan hukum-hukum gerak planet didasari pada hukum
Kepler , hukum Newton dan paket program Maple 10.
3.3 Langkah-Langkah Penelitian
Langkah-langkah yang ditempuh dalam penelitian ini adalah sebagai berikut:
1. Mengelaborasi hukum Kepler dan hukum Newton yang terkait dengan
gerak planet.
2. Merumuskan bentuk lintasan sistem dua planet sebagai fungsi sudut antar
planet.
3. Menggunakan paket program Maple 10 untuk menghitung (jarak
planet ke
2 r
2
m M ).
4. Hasil yang diperoleh ditampilkan dalam betuk Tabel dan Grafik.
5. Menarik kesimpulan.
BAB IV
HASIL DAN PEMBAHASAN
4.1 Sistem Dua Planet
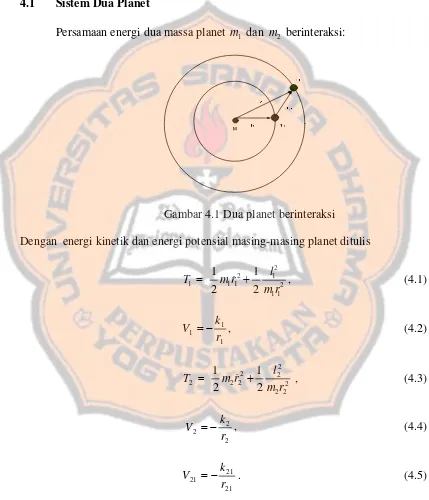
Persamaan energi dua massa planet m1 dan m2 berinteraksi:
Gambar 4.1 Dua planet berinteraksi
Dengan energi kinetik dan energi potensial masing-masing planet ditulis
T1 = 2 1 1
2 1 2
1 1
2 1 2
1
r m
l r
m& + , (4.1)
1 1 1
r k
V =− , (4.2)
T2 = 2
2 2
2 2 2
2 2
2 1 2
1
r m
l r
m & + , (4.3)
2 2 2
r k
V =− , (4.4)
21 21 21
r k
V =− . (4.5)
Energi total sistem dua planet berinteraksi ditulis
21 2 2 1
1 V T V V T
E= + + + + . (4.6)
Dengan memasukkan persamaan (4.1),(4.2),(4.3),(4.4) dan (4.5) ke persamaan (4.6),
maka persamaan energi total sistem dua planet berinteraksi menjadi
21 1 2 2 2 1 1 2 2 2 2 2 2 2 2 2 1 1 2 1 2 1 1 2 1 2 1 2 1 2 1 r m Gm r M Gm r M Gm r m l r m r m l r m
E= & + + & + − − − . (4.7)
Jika jarak relatif antara dengan dari persamaan (2.67) dimasukkan ke
persamaan (4.7), maka diperoleh 1
m m2
2 2 1 1 2 2 2 2 2 2 2 2 2 1 1 2 1 2 1 1 2 1 2 1 2 1 2 1 r M Gm r M Gm r m l r m r m l r m
E= & + + & + − −
12 2 1 2 2 2 1 2 1 cos . 2rr θ r r m Gm − +
− . (4.8)
Dengan mengeluarkan pada energi potensial relatif antara dengan maka
diperoleh
2
r m1 m2
2 2 1 1 2 2 2 2 2 2 2 2 2 1 1 2 1 2 1 1 2 1 2 1 2 1 2 1 r M Gm r M Gm r m l r m r m l r m
E= & + + & + − −
12 2 1 2 2 1 2 2 1 cos . 2 1 θ r r r r r m Gm − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛
− . (4.9)
Jika dimisalkan h r r
=
2
1 , maka persamaan (4.9) menjadi
2 2 1 1 2 2 2 2 2 2 2 2 2 1 1 2 1 2 1 1 2 1 2 1 2 1 2 1 r M Gm r M Gm r m l r m r m l r m
E= & + + & + − −
[
]
12 12 22 2
1 +1−2 .cos −
− h h θ
r m Gm
25
Diperoleh energi potensial relatif dari interaksi massa dan dalam bentuk
polinomial Legendre
1
m m2
2 2 1 1 2 2 2 2 2 2 2 2 2 1 1 2 1 2 1 1 2 1 2 1 2 1 2 1 r M Gm r M Gm r m l r m r m l r m
E= & + + & + − −
(
)
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −∑
= n j j j P h r m Gm 0 12 2 21 cosθ
. (4.11)
Dari memisalkan rasio jarak antara massa m1 dan m2 terhadap pusat massa M
diperoleh
2 1 hr
r = , (4.12)
sehingga
2 1 hr
r& = & , (4.13)
Jika persamaan (4.12) dan persamaan (4.13) dimasukkan ke persamaan (4.11), maka
diperoleh bentuk kekekalan energi
2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 1 2 1 2 2 2 1 2 1 2 1 2 1 2 1 r M Gm hr M Gm r m l r m r h m l r h m
E= & + + & + − −
(
)
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −∑
= n j j j P h r m Gm 0 12 2 2 1cosθ . (4.14)
Dari persamaan (4.14) diperoleh persamaan energi untuk massa dan kita dapat
mencari kecepatan dari planet untuk massa
2 m
⎢⎣ ⎡ + + ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − ⎥⎦ ⎤ ⎢⎣ ⎡ + = 2 1 2 2 2 2 2 2 1 2 1 2 2 1 2 2 1 2 1 2 1 2 1 2 1 1 GMm h GMm r m l h m l E m h m r& ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +
∑
=0 2
12 2 1 1 ) (cos r P h m Gm n j j j θ
. (4.15)
Diperoleh kecepatan planet dengan massa dari persamaan energi yaitu interaksi
antara dua planet dengan persamaan sebagai berikut: 2 m ⎪⎩ ⎪ ⎨ ⎧ ⎢⎣ ⎡ + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − ⎥⎦ ⎤ ⎢⎣ ⎡ + = 2 1 2 2 2 2 2 2 1 2 1 2 1 2 2 1 2 1 2 1 2 1 2 1 2 1 1 GMm h GMm r m l h m l E m h m r& 2 1 2 0 12 2 1 1 ) (cos ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +
∑
= r P h m Gm n j j j θ. (4.16)
Dengan memisalkan p=E,
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + =
∑
= ) (cos 12 0 2 1 2 1 θ j n j j P h m Gm GMm h GMm q , ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + = 2 2 2 2 1 2 1 2 1 2 1 m l h m ls , dan
2 1 2 2 1 2 1 2 1 ⎥⎦ ⎤ ⎢⎣ ⎡ +
= mh m
z , maka bentuk sederhana persamaan
(4.16) menjadi 2 1 2 2 2
2 1 1 1
⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − + = r s r q p z dt dr
. (4.17)
Dari persamaan (4.17) bentuk integral dari waktu t(r) menjadi
∫
− + = rmak
r s qr pr dr r z t min 2 2 2 2 2
27
Dengan menggunakan Lampiran B (B.1) dan (B.2), bentuk penyelesaian persamaan
(4.18) adalah
[
]
mak r r s qr pr p q pr p p q p s qr pr z t min 2 2 2 2 1 2 2 . 2 2 log 1 . 2 ⎪⎭ ⎪ ⎬ ⎫ − + + + − ⎪⎩ ⎪ ⎨ ⎧ + − = .(4.19)Persamaan kecepatan sudut dari momentum untuk planet dengan massa
ditulis 2 m 2 2 2 2 2 r m dt l
dθ = . (4.20)
Dengan mengganti 2 2 r dr dt &
= , persamaan (4.20) menjadi
2 2 2 2 2 2 2 r dr r m l d & =
θ . (4.21)
Persamaan (4.16) dimasukkan ke persamaan (4.21) diperoleh
⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎢⎣ ⎡ + + ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − ⎥⎦ ⎤ ⎢⎣ ⎡ + = 2 1 2 2 2 2 2 2 1 2 1 2 2 2 2 2 2 1 2 2 1 2 1 2 1 2 1 . 2 1 2 1 GMm h GMm r m l h m l E l m r dr m h m dθ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +
∑
= 2 1 2 12 0 2 1 1 ) (cos r P h m Gm n j j j θDengan memisalkan
2 2
1
r
u = , (4.23.a)
maka 2 2 2 2 1 dr r
du =− , (4.23.b)
2 . (4.23.c) 2
2 2 r du dr =−
Jika persamaan (4.23.c) dimasukkan ke persamaan (4.22), maka diperoleh
⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎢⎣ ⎡ + + ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − − ⎥⎦ ⎤ ⎢⎣ ⎡ + = 2 1 2 2 2 2 2 2 2 2 2 2 1 2 1 2 2 2 2 2 2 2 2 2 2 1 2 2 1 2 1 2 1 2 1 . 2 1 2 1 GMm h GMm l m r m l h m l l m l E m du m h m dθ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +
∑
= 2 1 2 12 0 2 1 1 ) (cos r P h m Gm n j j j θ. (4.24)
Jika persamaan (4.23.a) dimasukkan ke dalam persamaan (4.24) kemudian di-
29 ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎢⎣ ⎡ + + ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − ⎥⎦ ⎤ ⎢⎣ ⎡ + − =
∫
2 1 2 2 2 2 2 2 2 2 2 2 1 2 1 2 2 2 2 2 2 2 2 2 2 1 2 2 1 2 2 1 2 1 . 2 1 2 1 Mm h Mm l G m u m l h m l l m l E m du m h m θ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +∑
= 2 1 2 12 0 21m h P (cos ) u m
n
j j
j θ
. (4.25)
Dengan memisalkan ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − = 2 2 2 2 1 2 1 2 2 2 2 2 1 2 1 m l h m l l m A , ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + =
∑
= n j j j P h m m Mm h Mm l G m B 0 12 2 1 2 1 2 2 2 2 )(cosθ ,
dan 2
2 2 2 l E m
C= . Maka bentuk sederhana persamaan (4.25) menjadi
⎪⎩ ⎪ ⎨ ⎧ ⎪⎭ ⎪ ⎬ ⎫ + + ⎥⎦ ⎤ ⎢⎣ ⎡ + − =
∫
C Bu Au du m h m 2 2 2 2 2 1 2 2 1 2 2 1 2 1θ . (4.26)
Jika digunakan Lampiran B (B.3), makapenyelesaian untuk persamaan (4.26) adalah
⎪⎩ ⎪ ⎨ ⎧ ⎭ ⎬ ⎫ + − + − − ⎥⎦ ⎤ ⎢⎣ ⎡ + − = − γ θ AC B B Ax A m h m 4 2 sin 1 2 1 2 1 2 1 2 1 2 2 1
⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎨ ⎧ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎩ ⎨ ⎧ ⎢⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − ⎥⎦ ⎤ ⎢⎣ ⎡ + − = − 2 1 4 2 4 2 2 2 2 2 2 2 1 2 1 2 2 1 2 1 2 2 2 2 1 2 1 2 2 2 1 2 2 1 2 . 2 1 2 1 . 2 sin . 2 1 2 1 1 2 1 2 1 Mm h Mm l m G u m h l m l m m h l m l m m h m θ γ θ θ + ⎪ ⎪ ⎪ ⎭ ⎪⎪ ⎪ ⎬ ⎫ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + +
∑
∑
= = 2 1 2 2 2 2 2 2 2 2 1 2 1 2 2 2 0 12 2 1 0 12 2 1 2 1 2 2 2 2 2 1 2 1 . 4 ) (cos ) (cos l E m m h l m l m P h m m P h m m Mm h Mm l Gm n j j j n j j j, (4.28)
⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎨ ⎧ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎩ ⎨ ⎧ ⎢⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥⎦ ⎤ ⎢⎣ ⎡ + = − 2 1 4 2 4 2 2 2 2 2 2 2 1 2 1 2 2 1 2 1 2 2 2 2 1 2 1 2 2 2 1 2 2 1 2 . 2 1 2 1 . 2 sin . 2 1 2 1 1 2 1 2 1 Mm h Mm l m G u m h l m l m m h l m l m m h m θ γ θ θ + ⎪ ⎪ ⎪ ⎭ ⎪⎪ ⎪ ⎬ ⎫ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + +
∑
∑
= = 2 1 2 2 2 2 1 2 1 2 2 2 2 2 2 2 0 12 2 1 0 12 2 1 2 1 2 2 2 2 . 2 ) (cos ) (cos m h l m l m l E m P h m m P h m m Mm h Mm l Gm n j j j n j j j, (4.29)
⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎪⎩ ⎪ ⎨ ⎧ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + ⎢⎣ ⎡ + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥⎦ ⎤ ⎢⎣ ⎡ + =
∑
= − 2 0 12 2 1 2 1 4 2 4 2 2 2 1 2 2 2 2 2 2 2 2 2 1 2 1 2 2 1 2 1 2 2 2 2 1 2 1 2 2 2 1 2 2 1 2 ) (cos . 2 1 2 1 . 2 sin . 2 1 2 1 2 1 2 1 n j j j P h m m Mm h Mm l m G Mm h Mm l Gm u m h l m l m m h l m l m m h m θ θ γ θ + ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +∑
= 2 1 2 2 2 2 1 2 1 2 2 2 2 2 2 0 12 2 1 . 2 ) (cos m h l m l m l E m P h m m n j j j31 ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎩ ⎨ ⎧ ⎢⎣ ⎡ + ⎢⎣ ⎡ + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥⎦ ⎤ ⎢⎣ ⎡ + = − − 2 1 4 2 4 2 2 2 1 2 2 2 2 2 2 2 2 2 1 2 1 2 2 1 2 1 2 2 2 2 1 2 1 2 2 2 1 2 2 1 2 . 2 1 2 1 . 2 sin . 2 1 2 1 2 1 2 1 Mm h Mm l m G Mm h Mm l Gm u m h l m l m m h l m l m m h m θ γ θ θ − ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +
∑
∑
= = 2 1 2 2 2 2 1 2 1 2 2 2 2 2 2 2 0 12 2 1 0 12 2 1 . 2 ) (cos ) (cos m h l m l m l E m P h m m P h m m n j j j n j j j, (4.31)
⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎩ ⎨ ⎧ ⎢⎣ ⎡ + ⎢⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥⎦ ⎤ ⎢⎣ ⎡ + = − − 2 1 4 2 4 2 2 1 2 2 2 2 2 2 2 2 2 1 2 1 2 2 1 2 1 2 2 2 2 1 2 1 2 2 2 1 2 2 1 2 . 2 1 2 1 . 2 sin . 2 1 2 1 2 1 2 1 Mm h Mm l m G h Mm l Gm u m h l m l m m h l m l m m h m θ γ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎪⎭ ⎪ ⎬ ⎫ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + +
∑
∑
= = 2 1 2 2 2 2 1 2 1 2 2 2 2 2 2 2 0 12 2 1 0 12 2 1 2 . 2 ) (cos ) (cos m h l m l m l E m P h m m P h m m Mm n j j j n j j j θ θ. (4.32)
dengan γadalah tetapan integral (konstanta).
Dengan memisalkan
⎥⎦ ⎤ ⎢⎣
⎡ +
= 2 2
1 2 1 2 1 m h m
α , (4.33)
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +
= 2 2 2
2 1 2 1 2 2 2 1 2 1 m h l m l m
maka persamaan (4.32) menjadi ) (cos . 4 1 1 . ) (cos 2 . ) sin( 2 0 12 2 1 2 1 2 2 2 2 2 2 0 12 2 1 2 1 2 2 2 2 2 ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + − ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎢⎣ ⎡ + = −
∑
∑
= = n j j j n j j j P h m m Mm h Mm m G E l u P h m m Mm h Mm l Gm θ β θ β β α θ γ . (4.35)Jika digunakan rumus pada Lampiran B (B.4), maka persamaan (4.35) menjadi
⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + − ⋅ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + ⋅ =
∑
∑
= = 2 0 12 2 1 2 1 2 2 2 2 2 2 0 12 2 1 2 1 2 2 2 2 2 ) (cos 4 1 1 ) (cos . 2 cos n j j j n j j j P h m m Mm h Mm m G E l u P h m m Mm h Mm l Gm θ β θ β β αθ . (4.36)
Jika
2 2
1
r
u = , maka persamaan (4.36) menjadi
2 2 0 12 2 1 2 1 2 2 2 2 2 0 12 2 1 2 1 2 2 2 2 2 cos ) (cos 4 1 ) (cos 2 θ θ β α β α β θ β ⋅ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + ⋅ + + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + =
∑
∑
= = n j j j n j j j P h m m Mm h Mm m G E l P h m m Mm h Mm Gm l33
Dengan memisalkan
α β =
N , 2
2 2 2 . 2 Gm l
K = β , 2
2 2 2 2 4 m G E l L β α β ⋅
= , 1 Mm2
h Mm
W = + , dan
, diperoleh 2 1m m X = 2 2 0 12 0 12 2 cos ) (cos 1 ) (cos θ θ θ ⋅ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + =
∑
∑
= = n j j j n j j j P h X W L N P h X W Kr , (4.38)
2 2 0 12 2 0 12 2 cos ) (cos 1 1 ) (cos 1 θ θ θ ⋅ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + =
∑
∑
= = n j j j n j j j P h W X W L N P h W X W Kr . (4.39)
Dengan memisalkan W
K
R= , 2
W L
Y = , dan
W X
H = sehingga
2 2 0 12 0 12 2 cos ) (cos 1 1 ) (cos 1 θ θ θ ⋅ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + =
∑
∑
= = n j j j n j j j P h H Y N P h H Rr , (4.40)
dengan eksentrisitas
2
0
12)]] (cos [ 1 [
∑
= + + = n j j j P h H Y N e θ. (4.41)
Mengacu pada persamaan (2.62) untuk bentuk lintasan planet berbentuk elips pada
orbit tertutup dimana energi total sistem (E<0). Maka eksentrisitas diperoleh
2
0
12)]] (cos [ 1 [
∑
= + − = n j j j P h H Y N e θ. (4.42)
Jadi dengan mengganti nilai eksentrisitas sesuai dengan persamaan (4.42), maka
persamaan (4.40) menjadi
2 2 0 12 0 12 2 cos ) (cos 1 1 ) (cos 1 θ θ θ ⋅ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎦ ⎤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + =
∑
∑
= = n j j j n j j j P h H Y N P h H Rr . (4.43)
4.2 Bentuk Lintasan Planet
Dari persamaan (4.43) dan rasio jarak mengacu pada persamaan (4.12), maka
jika dihitung r2dan r1dengan memberi nilai pada konstanta untuk berbagai sudut
12
θ diperoleh hasil pada Lampiran A (Tabel A). Jika Table A digambar grafiknya
35
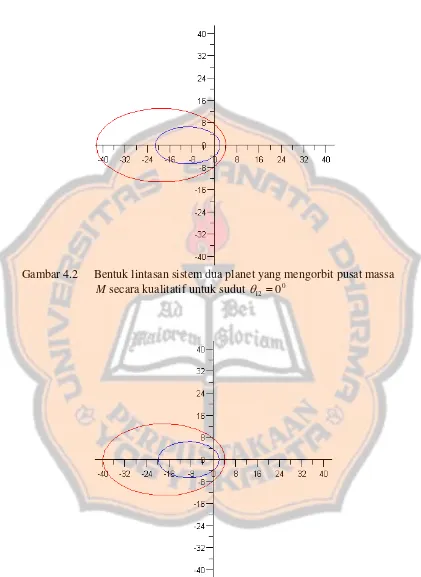
Gambar 4.2 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut θ12 =00
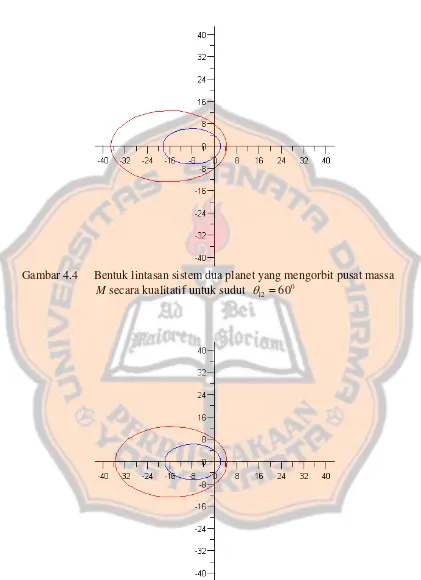
Gambar 4.4 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut θ12 =600
Gambar 4.5 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut 0
12 =90
37
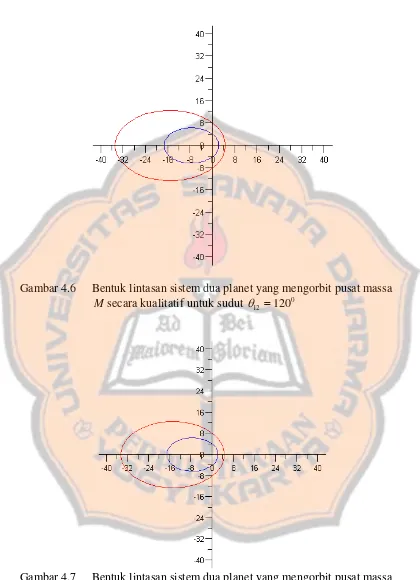
Gambar 4.6 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut θ12 =1200
Gambar 4.7 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut 0
12 =150
Gambar 4.8 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut θ12 =1800
39
Gambar 4.10 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut θ12 =2400
Gambar 4.12 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut θ12 =3000
41
Gambar 4.14 Bentuk lintasan sistem dua planet yang mengorbit pusat massa M secara kualitatif untuk sudut θ12 =3600
4.3 Pembahasan
Berdasarkan rumus (4.43) dan (4.12) dengan menghitung secara numerik
memakai paket program Maple 10 sesuai dengan sintaks program pada Lampiran C
diperoleh nilai pada Lampiran A (Tabel A) dan Grafik pada gambar 4.2 sampai
gambar 4.14 yang menunjukkan perubahan bentuk lintasan untuk dua planet yang
berinteraksi untuk berbagai sudut 2
r
12
θ dengan interval 0. 30
Pada gambar 4.2 dan gambar 4.14 sesuai Tabel A mempunyai bentuk grafik
lintasan planet yang sama dengan nilai sudut dan sudut , nilai
jarak kedua planet yaitu dan mengalami kenaikan untuk sudut 0
12=0
θ 0
12 =360
θ
2
r r1 θ2 dari
sampai dan mengalami penurunan untuk sudut
0 0
0
Pada gambar 4.3 dan gambar 4.13 sesuai Tabel A mempunyai bentuk grafik
lintasan planet yang sama dengan nilai sudut dan sudut , nilai
jarak kedua planet yaitu dan mengalami kenaikan untuk sudut 0
12 =30
θ 0
12=330
θ
2
r r1 θ2 dari
sampai dan mengalami penurunan untuk sudut
0 0
0
180 θ2 dari 0 sampai .
180 3600
Pada gambar 4.4 dan gambar 4.12 sesuai Tabel A mempunyai bentuk grafik
lintasan planet yang sama dengan nilai sudut dan , nilai jarak
kedua planet yaitu dan mengalami kenaikan untuk sudut 0
12 =60
θ 0
12 =300
θ
2
r r1 θ2 dari sampai
dan mengalami penurunan untuk sudut
0 0
0
180 θ2 dari 1800 sampai 3600.
Pada gambar 4.5 dan gambar 4.11 sesuai Tabel A mempunyai bentuk grafik
lintasan planet yang sama dengan nilai sudut dan sudut , nilai
jarak kedua planet yaitu dan mengalami kenaikan untuk sudut 0
12 =90
θ 0
12 =270
θ
2
r r1 θ2 dari
sampai dan mengalami penurunan untuk sudut
0 0
0
180 θ2 dari 1800 sampai 3600.
Pada gambar 4.6 dan gambar 4.10 sesuai Tabel A mempunyai bentuk grafik
lintasan planet yang sama dengan nilai sudut dan sudut , nilai
jarak kedua planet yaitu dan mengalami kenaikan untuk sudut 0
12 =120
θ 0
12 =240
θ
2
r r1 θ2 dari
sampai dan mengalami penurunan untuk sudut
0 0
0
180 θ2 dari 0 sampai .
180 3600
Pada gambar 4.7 dan gambar 4.9 sesuai Tabel A mempunyai bentuk grafik
lintasan planet yang sama dengan nilai sudut dan sudut , nilai
jarak kedua planet yaitu dan mengalami kenaikan untuk sudut 0
12 =150
θ 0
12 =210
θ
2
r r1 θ2 dari
sampai dan mengalami penurunan untuk sudut
0 0
0
180 θ2 dari 0 sampai .
180 0
43
Pada gambar 4.8 sesuai Tabel A dengan nilai sudut , nilai jarak
kedua planet yaitu dan mengalami kenaikan untuk sudut
0 12 =180
θ
2
r r1 θ2 dari sampai
dan mengalami penurunan untuk sudut
0 0
0
180 θ2 dari 1800 sampai 3600.
Pada gambar 4.2, gambar 4.3, gambar 4.4, gambar 4.5, gambar 4.6, gambar
4.7 dan gambar 4.8, sesuai Tabel A, dengan nilai sudut
. Nilai jarak kedua planet yaitu dan
mengalami kenaikan untuk sudut ,
150 , 120 , 90 , 60 , 30 ,
00 0 0 0 0 0
12 =
θ 0
180 r2
1
r θ2 dari sampai dan mengalami
penurunan untuk sudut
0
0 1300
2
θ dari sampai serta mengalami kenaikan
kembali untuk sudut
0
135 2250
2
θ dari 0 sampai .
230 3600
Pada gambar 4.9, gambar 4.10, gambar 4.11, gambar 4.12, gambar 4.13 dan
gambar 4.14, sesuai Tabel A, dengan nilai sudut
. Nilai jarak kedua planet yaitu dan
mengalami penurunan untuk sudut 0 0 0 0 0 0
12 =210 ,240 ,270 ,300 ,330 ,360
θ r2
1
r θ2 dari sampai dan mengalami
penurunan untuk sudut
0
0 1300
2
θ dari sampai serta mengalami kenaikan
kembali untuk sudut
0
135 2300
2
θ dari 2350 sampai 3600.
Pada Lampiran A (Tabel B) diperoleh eksentrisitas dengan lintasan tertutup.
Perubahan sudut (θ12) mempengaruhi nilai eksentrisitas yang akan menyebabkan
BAB V PENUTUP
5.1 Kesimpulan
Kesimpulan yang didapat dari hasil dan pembahasan pada penelitian adalah
sebagai berikut:
1. Sudut (θ12)yang terbentuk antar dua planet dan menyebabkan nilai
eksentrisitas lintasan planet berubah yaitu maksimum saat sudut
( ) dan sudut ( ) dan minimum saat sudut ( ).
1
m m2
0 12 =0
θ 0
12 =360
θ 0
12 =180
θ
2. Jarak planet dengan pusat massa Mterjauh pada sudut ( ) saat
sudut ( ).
0 12 =0
θ
0 2 =180
θ
3. Interaksi antar planet mempengaruhi bentuk lintasan planet.
5.2 Saran
Saran yang dapat diberikan untuk menyempurnakan dan mengembangkan
tulisan ini adalah perlu dilakukan penelitian lebih lanjut bagimana pengaruh sudut
(θ2) terhadap jarak planet (r) dengan pusat massa M terkait dengan perubahan
sudut (θ12).
DAFTAR PUSTAKA
Alonso, M. & Finn, E.J., 1994, Dasar-Dasar Fisika Universitas, Jilid 1, Edisi 2,
Jakarta: Erlangga.
Burington, R.S., 1948, Handbook of Mathematical Table and Formula, New York:
McGraw-Hill Book Company.
Goldstein, H.,1950, Classical Mechanics, New York: Addison-Wesley Publishing Company.
Halliday, D., & Resnick, R., 1984, Fisika, Jilid 1, Edisi 3, Jakarta: Erlangga.
Sears, W.F., Zemansky, M.W., & Young, H.D., 1987, Fisika Universitas, Jilid 1,
Edisi 6, Jakarta: Erlangga.
Seno, D.K., & Sihono, M.Si., 2007, Gravitasi, (Online), (http://dwiseno.fisika.ui.edu /kuliah/gravitasi.ppt, diakses 30 November 2007).
Suwitra, N., 2001, Astronomi Dasar, Jurusan Fisika Institut Keguruan dan Ilmu
Pendidikan Negeri Singaraja.
Zahara, M., 1997, Dinamika Sistem Zarah Dan Benda Tegar, Yogyakarta: Lab Fisika Atom dan Inti Fakultas MIPA UGM.
LAMPIRAN A
TABEL A
No.
1 0 4.078497889 4.208437347 4.376425342
2 5 4.08552778 4.215617006 4.383788355
3 10 4.106709465 4.237248423 4.405970102
4 15 4.142321367 4.273611275 4.443250971
5 20 4.19283564 4.392634147 4.496105975
6 25 4.258930659 4.392634147 4.565216547
7 30 4.34150927 4.476879959 4.651487732
8 35 4.441723511 4.579070706 4.756071355
9 40 4.561006921 4.700639946 4.880396069
10 45 4.701115815 4.843341152 5.026205481
11 50 4.864181381 5.009297949 5.195605802
12 55 5.052775021 5.201066861 5.391124884
13 60 5.269989917 5.421715149 5.615784995
14 65 5.519542733 5.674917308 5.873192085
15 70 5.805900318 5.965074261 6.167644982
16 75 6.134437472 6.29746051 6.504268322
17 80 6.511633281 6.678405247 6.889173728
18 85 6.945314998 7.115514372 7.329653592
19 90 7.444959862 7.617940941 7.834411572
20 95 8.022066026 8.196710803 8.413831682
21 100 8.690602905 8.865107716 9.080283407 22 105 9.467546588 9.639114784 9.848450568 23 110 10.37349329 10.53789332 10.73565313 24 115 11.43331608 11.58424882 11.76209773 25 120 12.67677228 12.80497352 12.95093298 26 125 14.13885817 14.23084654 14.32788652 27 130 15.85950301 15.89588533 15.92010079 28 135 17.88183897 17.83513762 17.75354968 29 140 20.24771642 20.07986057 19.84811939 30 145 22.98835482 22.64840902 22.20917263 31 150 26.10729432 25.53085987 24.81449359 32 155 29.55310351 28.66618983 27.59659831
33 160 33.18285764 31.9143537 30.42350426
34 165 36.72745662 35.03364099 33.08675546 35 170 39.78648761 37.68476523 35.31168511
) ( 12
2θ
r
2
θ r2(0) r2(30) r2(60)
47
No.
36 175 41.89060808 39.48677608 36.8042062 37 180 42.64427177 40.12801694 37.33150826 38 185 41.89060808 39.48677608 36.8042062 39 190 39.78648761 37.68476523 35.31168511 40 195 36.72745662 35.03364099 33.08675546
41 200 33.18285764 31.9143537 30.423