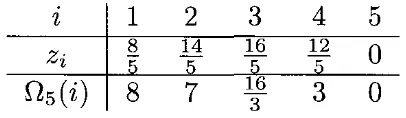Model pergerakan harga saham menggunakan random walk dan gerak brown - USD Repository

(1)

S K R I P S I

Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun Oleh :

GEORGE RIDHO SETYAWAN NIM : 053114010

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(2)

T H E S I S

Presented As a Partial Fulfillment of The Requirements to Obtain The Sarjana Sains Degree

In Mathematics

by :

GEORGE RIDHO SETYAWAN Student Number : 053114010

MATHEMATICS STUDY PROGRAM DEPARTEMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

(3)

RANDOM WALK DAN GERAK BROWN

Oleh:

George Ridho Setyawan NIM : 053114010

Telah disetujui oleh:

Pembimbing

(4)

Dipersiapkan dan ditulis oleh: George Ridho Setyawan

NIM : 053114010

Telah dipertahankan di depan Panitia Penguji Pada tanggal 15 Juli 2009

dan dinyatakan memenuhi syarat

Susunan Panitia Penguji

Ketua Ir. Ig. Aris Dwiatmoko, M.Sc.

Sekertaris Ch. Enny Murwaningtyas, S.Si., M.Si.

Anggota Lusia Krismiyati Budiasih, S.Si., M.Si.

Yogyakarta, 15 Juli 2009 Fakultas Sains Dan Teknologi Universitas Sanata Dharma Dekan

(5)

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 25 Juni 2009 Penulis

(6)

I asked for strength

And God gave me difficulties to make me strong

I asked for wisdom

And God gave me problems to solve

I asked for prosperity

And God gave me a brain and brawn to work

I asked for courage

And God gave me dangers to overcome

I asked for love

And God gave me opportunities

I received nothing I wanted

I received everything I needed

(7)

ABSTRAK

Random walk merupakan sebuah teori dalam probabilitas yang menyatakan bahwa pergerakkan sebuah partikel bersifat random. Dalam random walk, probabilitas untuk bergerak naik maupun turun adalah sama. Random walk yang simetrik merupakan random walk yang mempunyai probabilitas yang sama untuk dua nilai yang berbeda. Random walk termasuk suatu proses stokastik yang bersifat diskret.

Gerak brown merupakan sebuah proses stokastik yang bersifat kontinu dan sering disebut sebagai Proses Wiener. Gerak brown dapat dibentuk dari sebuah random walk yang simetrik yaitu dengan mencari nilai limit dari distribusi random walk tersebut.

(8)

Random Walk and Brownian motion. According to random walk theory, a particle movement is random in nature. This movement whether up or down for two different values has an equal probability called symmetric random walk. Random walk is an example of discrete stochastic process.

On the other hand, Brownian motion is an example of continuous stochastic process which also known as Wiener process. Brownian motion can be formed from a symmetric random walk by counting the limit of its distribution.

(9)

juruselamat dalam hidupku yang oleh karena anugerah dan kemurahanNya sehingga skripsi ini dapat diselesaikan dengan baik. Skripsi ini ditulis untuk memenuhi salah satu syarat memperoleh gelar Sarjana Sains di Program Studi Matematika Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta.

Skripsi ini dapat diselesaikan dengan baik atas bantuan, gagasan, dan dukungan dari berbagai pihak. Oleh karena itu, dalam kesempatan ini perkenankanlah penulis menghaturkan terima kasih kepada :

1. Ch. Enny Murwaningtyas, S.Si., M.Si. selaku dosen pembimbing yang telah banyak meluangkan waktu dan dengan penuh kesabaran membimbing penulis sehingga skripsi ini dapat diselesaikan dengan baik.

2. Yosef Agung Cahyanta, S.T., M.T., selaku Dekan Fakultas Sains dan Teknologi.

3. Lusia Krismiyati Budiasih, S.Si., M.Si., selaku Ketua Program Studi Matematika yang telah banyak membantu.

4. Ir. Ignatius Aris Dwiatmoko, M.Sc., selaku penguji yang telah banyak membantu dan memberi masukan kepada penulis.

5. Prof. Frans Susilo, S.J., selaku dosen pembimbing akademik.

6. Sudi Mungkasi, S.Si., M.Sc., dan Y.G. Hartono, S.Si., M.Sc., yang pernah menjadi dosen pembimbing akademik bagi penulis.

7. Herry Pribawanto Suryawan, S.Si., M.Si., yang memberikan banyak ilmu serta keramahan yang diberikan selama kuliah.

(10)

11.Kedua orang tuaku serta adik dan kakakku yang selalu memberikan dukungan kepadaku.

12.Eko Budi Santoso, S.E., M.Si. dan Irma Dhearni Saragih, S.E. yang sudah banyak membantu penulis serta memberikan dukungan selama penulis menyelesaikan skripsi ini.

13.Keluarga besar Jehovah Nissi dan Full Blast yang sudah memberikan semangat kepada penulis.

14.Teman-teman matematika angkatan 2005 : Ratna, Chris, Luis, Puput, Tyas, Nanin, Priskila,Vincent, Sisiria, Ine, Devi, Septi, Wuri, Susi, Echy, Dedy, Zetho, Yudhi, Sella, Vira.

15.Keluarga besar PMK Oikumene. 16.Keluarga besar Center City on A Hill.

17.Semua pihak yang telah ikut membantu penulis dalam menyelesaikan skripsi ini.

Walaupun penulis telah berusaha menyelesaikan skripsi ini dengan sebaik-baiknya, namun penulis menyadari bahwa dalam skripsi ini masih terdapat kekurangan dan kekeliruan. Oleh karena itu, penulis sangat mengharapkan saran dan kritik yang dapat membangun dan menyempurnakan skripsi ini.

Akhirnya, semoga skripsi ini dapat memberikan wawasan dan pengetahuan bagi pembaca demi perkembangan ilmu pengetahuan, khususnya matematika.

Yogyakarta, 15 Juli 2009

(11)

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma : Nama : George Ridho Setyawan

NIM : 053114010

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma, Karya Ilmiah saya yang berjudul :

MODEL PERGERAKKAN HARGA SAHAM MENGGUNAKAN RANDOM WALK DAN GERAK BROWN

beserta perangkat-perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun member royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini saya buat sebenarnya. Dibuat di Yogyakarta

Pada tanggal : 15 Juli 2009 Yang menyatakan

(12)

i

HALAMAN PERSETUJUAN PEMBIMBING iii

HALAMAN PENGESAHAN iv

HALAMAN KEASLIAAN KARYA v

HALAMAN PERSEMBAHAN vi

ABSTRAK vii

ABSTRACT viii

KATA PENGANTAR ix

DAFTAR ISI xii

DAFTAR TABEL xiv

DAFTAR GAMBAR xv

BAB I PENDAHULUAN

A. Latar Belakang Masalah 1

B. Perumusan Masalah 3

C. Pembatasan Masalah 3

D. Tujuan Penulisan 3

E. Metode Penulisan 4

F. Manfaat Penulisan 4

G. Sistematika Penulisan 4

BAB II LANDASAN TEORI

A. Probabilitas 6

B. Variabel Random dan Distribusinya 9

C. Distribusi Bernoulli dan Binomial 24

(13)

C. Konstruksi Gerak Brown Menggunakan Random Walk Simetrik 70

D. Ito’s Lemma 77

BAB IV MODEL PERGERAKKAN HARGA SAHAM

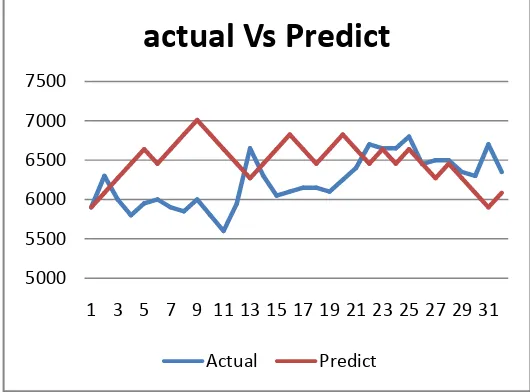
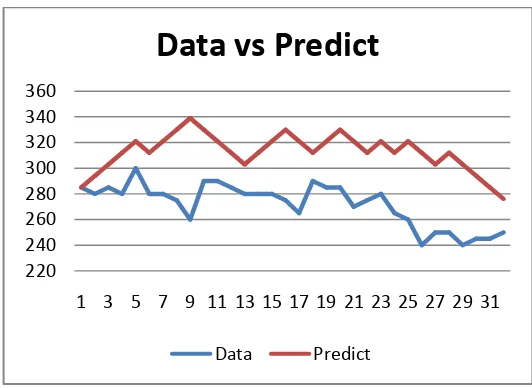
A. Model Random Walk 81

B. Model Gerak Brown 83

C. Perbandingan Model Random walk dengan Model Gerak Brown 88

BAB V PENUTUP

A. Kesimpulan 91

B. Saran 92

DAFTAR PUSTAKA 93

(14)

DAFTAR TABEL

Tabel 2.1 14

Tabel 3.1 61

Tabel 3.2 65

Tabel 4.1 86

(15)

DAFTAR GAMBAR

Gambar 2.1 32

Gambar 2.2 37

Gambar 3.1 39

Gambar 3.2 46

Gambar 3.3 71

Gambar 3.4 73

Gambar 4.1 82

Gambar 4.2 83

Gambar 4.3 87

Gambar 4.4 88

Gambar 4.5 90

(16)

BAB I PENDAHULUAN

A. Latar Belakang Masalah

Dalam bidang ekonomi saham merupakan suatu hal yang sering dibahas dan

diperbicangkan. Saham adalah surat tanda kepemilikan terhadap sebuah

perusahaan. Saham ditransaksikan di sebuah bursa efek melalui proses IPO

(Initial Public Offering). Dengan menerbitkan saham, yang berarti menjual

sebagian kepemilikan perusahaan kepada publik, perusahaan mendapatkan dana

segar yang dapat digunakan untuk tujuan ekspansi, operasional atau yang lainnya.

Dengan menerbitkan saham, nilai sebuah perusahaan menjadi lebih mudah untuk

diukur.

Saham termasuk instrumen investasi yang memiliki resiko tinggi karena

pergerakan harganya yang cepat. Pergerakan harga dari sebuah perusahaan

dipengaruhi oleh banyak hal seperti kinerja perusahaan, laporan keuangan

perusahaan, kondisi ekonomi, estimasi bisnis di masa yang akan datang, dan

banyak lainnya. Hal ini membuat harga saham berfluktuasi secara acak.

Pada interval diskret (misalnya pengamatan per detik), harga dari saham tersebut

diasumsikan dapat berubah menjadi lebih tinggi (meningkat) ataupun lebih

rendah (menurun) satu unit dari harga saham sebelumnya . Dengan kata lain jika

harga saham pada detik ke n adalah , maka harga saham pada detik ke n+1

(17)

Seiring dengan perkembangan zaman, pergerakan harga saham tersebut

kemudian dibawa ke dalam bentuk sebuah model matematika yang dapat

menggambarkan pola pergerakan harga saham tersebut. Salah satu model yang

dikembangkan adalah model random walk dan model gerak Brown.

Secara sederhana, random walk dapat digambarkan sebagai suatu

percobaan dimana perpindahan posisi seseorang ditentukan dengan pelemparan

sebuah koin. Bayangkan seseorang berdiri tepat pada titik asal (titik nol) pada

sebuah garis bilangan real. Orang tersebut akan berpindah tempat berdasarkan

hasil pelemparan sebuah koin yang akan dilemparkan sebanyak n kali

pelemparan. Jika hasil pelemparan koin adalah gambar (k), maka orang tersebut

akan bergerak ke arah kanan (arah positif). Demikian juga sebaliknya, jika hasil

pelemparan koin adalah angka (n-k), maka orang tersebut akan bergerak ke arah

kiri (arah negatif). Apabila peluang orang tersebut untuk berpindah ke arah kanan

adalah p dan peluang orang tersebut berpindah ke arah kiri adalah q, maka

diperoleh persamaan berikut

dan 1

Dalam percobaan tersebut, peluang seseorang bergerak ke kanan akan sama

besarnya dengan peluang orang tersebut bergerak ke kiri. Hal ini menunjukkan

bahwa pergerakan orang tersebut merupakan proses stokastik yang sederhana dan

bersifat random.

Gerak Brown pertama kali ditemukan oleh seorang ahli tanaman dari

Skotlandia yaitu Robert Brown. Gerak Brown merupakan suatu kejadian khusus

(18)

simetrik. Proses gerak Brown sering kali disebut proses Wiener, yaitu salah satu

proses stokastik yang sangat berguna dalam aplikasi teori probabilitas.

B. Rumusan Masalah

1. Apa yang dimaksud dengan Random Walk ?

2. Apa yang dimaksud dengan Gerak Brown ?

3. Bagaimana Random Walk dan Gerak Brown digunakan untuk

memodelkan pergerakan harga saham ?

C. Batasan Masalah

1. Random walk dan gerak Brown yang dibahas hanya yang berdimensi

Satu

2. Deret Taylor dan Maclaurin tidak dibahas secara mendalam

3. Eliminasi Gauss tidak dibahas secara mendalam

4. Sifat spatial homogeneity dari random walk tidak dibahas dan dibuktikan

5. Teorema 2.4.1 tidak dibuktikan

D. Tujuan Penulisan

Tujuan penulisan skripsi ini adalah untuk memenuhi syarat untuk

memperoleh gelar Sarjana Sains dalam matemetika. Selain itu penulisan skripsi

ini juga bertujuan :

1. Mempelajari dan memahami Random Walk.

2. Mempelajari dan memahami Gerak Brown.

(19)

4. Mempelajari hubungan antara random walk dan gerak Brown dalam

model pergerakan harga saham.

E. Manfaat Penulisan

Manfaat yang diperoleh dari penulisan skripsi ini adalah dapat memahami

teori Random Walk dan Gerak Brown serta penggunaanya dalam model harga

saham.

F. Metode Penulisan

Metode penulisan yang digunakan dalam penyusunan skripsi ini adalah

metode studi pustaka, yaitu dengan menggunakan buku-buku, jurnal ilmiah, dan

karangan ilmiah yang telah dipublikasikan. Oleh karena itu dalam karya ilmiah ini

tidak disajikan hal baru dalam bidang matematika. Juga akan digunakan program

Excel, Matlab dan SPSS.

G. Sistematika Penulisan

BAB I: PENDAHULUAN

Dalam bab I dibahas tentang latar belakang, perumusan masalah,

pembatasan masalah, tujuan penulisan, metode penulisan, manfaat

(20)

BAB II LANDASAN TEORI

Dalam bab II dibahas tentang probabilitas, variabel random, fungsi

distribusi probabilitas, nilai harapan dan variansi, fungsi

pembangkit momen, distribusi Bernoulli, distribusi binomial,

distribusi normal serta pendekatan normal terhadap binomial.

BAB III RANDOM WALK dan GERAK BROWN

Dalam Bab III dibahas tentang random walk, gerak Brown, dan

Ito’s Lemma.

BAB IV MODEL PERGERAKAN HARGA SAHAM

Dalam Bab IV dibahas tentang model pergerakan harga saham

menggunakan random walk dan gerak Brown.

BAB V PENUTUP

(21)

BAB II

LANDASAN TEORI A. Probabilitas

Ruang sampel (S) adalah himpunan yang unsur-unsurnya menyatakan semua

kemungkinan hasil suatu percobaan. Setiap unsur dari ruang sampel disebut titik

sampel. Kejadian (event) adalah himpunan bagian dari ruang sampel S.

Definisi 2.1.1

Peluang suatu kejadian A adalah jumlah bobot semua titik sampel yang termasuk

A, sehingga

0 1 , 0 , dan 1

Definisi 2.1.2 Probabilitas klasik

Jika suatu percobaan dapat menghasilkan N titik sampel yang berbeda dan

masing-masing berkemungkinan sama untuk terjadi, dan jika tepat ada sebanyak n

dari titik-titik sampel tersebut merupakan unsur dari kejadian A, maka probabilitas

kejadian A adalah :

P

Teorema 2.1.1 (Aturan Penjumlahan)

Bila A dan B dua kejadian sembarang, maka probabilitas terjadinya kejadian A

atau B adalah

(22)

Bukti :

Pendekatan yang akan digunakan adalah mengekspresikan kejadian dan A

sebagai gabungan dari kejadian yang saling lepas

′

dengan demikian

′

Sehingga

′

■

Jika A dan B adalah kejadian yang saling asing dengan 0, maka

aturan penjumlahan menjadi semakin sederhana yaitu

Probabilitas Bersyarat

Probabilitas terjadinya suatu kejadian B bila diketahui bahwa kejadian A telah

terjadi disebut probabilitas bersyarat dan dinyatakan dengan | . Lambang

| biasanya dibaca ‘probabilitas kejadian B terjadi bila diketahui kejadian A

(23)

Definisi 2.1.3

Probabilitas bersyarat B bila A diketahui, dinyatakan dengan | , ditentukan

oleh

| P A B_{P A} dengan 0 (2.2)

Contoh 2.1.1

Peluang suatu penerbangan yang telah terjadwal teratur berangkat tepat waktu

0,83 ; peluang sampai tepat waktu 0,82 dan peluang berangkat

dan sampai tepat waktu 0,78. Cari peluang bahwa a). pesawat sampai

tepat waktu bila diketahui berangkat tepat waktu, dan b). Pesawat berangkat tepat

waktu jika diketahui sampai tepat waktu.

Jawab :

a) Peluang pesawat sampai tepat waktu jika diketahui berangkat tepat waktu

| ,_, 0,94

b) Peluang pesawat berangkat tepat waktu bila diketahui sampai tepat waktu

| ,_, 0,95

Teorema 2.1.2 (Aturan Perkalian)

Bila kejadian A dan B dapat terjadi pada suatu percobaan, maka

(24)

Bukti :

Bukti teorema ini akan diturunkan dari definisi probabilitas bersyarat (2.1.3)

| P A B_{P A}

| ■

Definisi 2.1.4

Dua kejadian A dan B bebas jika dan hanya jika

B. Variabel Random dan Distribusinya

Gagasan untuk mendefinisikan sebuah fungsi yang dikenal dengan variabel

random timbul karena model-model matematika diekspresikan dalam bentuk

nilai-nilai numeris dari pada hasil percobaan asli seperti sisi, warna, atau yang

lain.

Definisi 2.2.1

Variabel random, misalnya X adalah fungsi yang didefinisikan pada ruang sampel

S, yang memetakan setiap elemen e∈S ke bilangan real.

Notasi : X(e)=x, e∈S

x∈R

Untuk lambang variabel random digunakan huruf-huruf kapital X, Y, Z,

sedangkan untuk melambangkan nilai variabel random yang mungkin, digunakan

(25)

Contoh 2.2.1

Jika seseorang melempar dua buah dadu secara bersamaan maka,

ruang sampel S = {(i,j)}| i,j∈{1, 2, 3, 4, 5, 6}}.

Variabel random X menyatakan jumlah bilangan yang muncul pada kedua buah

dadu maka X(i,j) = i + j, sehingga X(3,5) = 3 + 5 = 8

X(5,2) = 5 + 2 = 7

Konsep variabel random dapat dipahami sebagai sebuah pemetaan dari

himpunan S ke himpunan bilangan real. Kemudian konsep ini dipakai untuk

menghitung peluang timbulnya suatu kejadian.

Dengan mengambil contoh 2.2.1, didefinisikan kejadian memperoleh jumlah

bilangan maksimal adalah 3. Titik-titik sampel kejadian ini dapat dituliskan

sebagai }Y∈{2,3 atau dapat pula dinyatakan dalam interval Y ={y|y≤3}.

Dengan probabilitas :

12 1 36

3 )) 1 , 2 ( ), 2 , 1 ( ), 1 , 1 (( ) 3

(Y ≤ =P = =

P .

Variabel random diskret adalah variabel random yang didefinisikan pada

ruang sampel diskret dan nilainya berhingga atau tak berhingga terbilang.

Contoh 2.2.2

variabel random diskret :

o X = Banyaknya bayi yang lahir dalam waktu satu tahun di Yogyakarta.

(26)

Variabel random kontinu adalah variabel random yang didefinisikan pada

ruang sampel kontinu.

Contoh 2.2.3

Contoh variabel random kontinu adalah M = lamanya permainan catur dalam satu

babak. Meskipun dalam kenyataannya biasa diukur waktu hanya dengan satuan

terdekat seperti menit atau detik, secara teoritik dapat diukur waktu dengan

sembarang satuan kecil.

Definisi 2.2.2

Fungsi f(x) disebut sebagai fungsi probabilitas diskret X bila dan hanya bila

memenuhi syarat :

( i ) f(x)≥0 , untuk semua nilai x real

( ii ) ∑ 1

Definisi 2.2.3

Fungsi f(x) disebut fungsi densitas bagi variabel random kontinu X bila dan hanya

bila memenuhi syarat :

( i ) f(x)≥0 untuk semua nilai x real

( ii )

∫

∞

∞ −

=1 ) (x dx

f

Fungsi Distribusi Kumulatif Diskret Definisi 2.2.4

(27)

F(x) = P(X≤x) untuk semua nilai real x.

Kadang-kadang fungsi F(x) disebut juga fungsi distribusi.

Fungsi Distribusi Kumulatif Kontinu Definisi 2.2.5

Fungsi distribusi kumulatif suatu variabel random X, dengan fungsi densitas f(x)

didefinisikan sebagai :

F(x) =

∫

∞ −

x

dt t

f( )

Fungsi densitas f(x) merupakan derivatif dari F(x).

Fungsi Distribusi Kumulatif Diskret Bersama Definisi 2.2.6

Jika X dan Y adalah variabel random diskret yang didefinisikan pada ruang

probabilitas maka fungsi distribusi bersama X dan Y didefinisikan sebagai

FXY x, y P X x, Y y

Fungsi Distribusi Probabilitas Kontinu Bersama Definisi 2.2.7

Vektor variabel random berdimensi k, X X , X , … , X dikatakan kontinu jika

ada fungsi f X , X , … , X , yang disebut fungsi densitas bersama dari X

(28)

x , x , … , x … f t , … , t d X

t , … , dt

Untuk semua x x , x , … , x

Definisi 2.2.8 Variabel-variabel random saling bebas

Variabel-variabel random X , X , … , X dikatakan saling bebas bila untuk setiap

berlaku

P a X b , … , a X b P a X b

Nilai Harapan dan Variansi

Konsep nilai harapan memegang peranan yang sangat penting dalam

statistika. Contoh yang paling mudah adalah mean dan variansi suatu variabel

random. Keduanya adalah parameter-parameter yang hampir selalu muncul dalam

teknik-teknik analisis statistika elementer maupun lanjut. Nilai harapan

dinyatakan dalam definisi berikut

Definisi 2.2.9

, jika x diskret dengan fungsi probabilitas ∞

∞

(29)

Ditinjau dari segi variabel random yang diskret, maka nilai harapan E(X)

merupakan suatu nilai fungsi linear dari semua unsur di dalam domain fungsi

dengan peluang yang bersesuaian sebagai faktor pembobot.

Contoh 2.2.4

Dalam pelemparan sebuah mata dadu setimbang sebanyak satu kali, kita akan

menerima uang sebanyak titik pada sisi yang tampak. Untuk bermain satu kali

lemparan kita harus membayar c rupiah. Pertama-tama kita perhatikan bahwa

hadiah yang kita terima tiap permainan adalah variabel random dengan distribusi

probabilitas sebagai berikut :

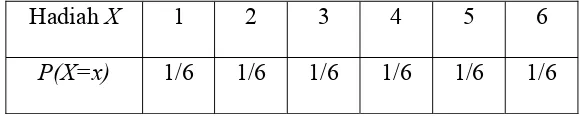
Tabel 2.1 Tabel distribusi probabilitas

Hadiah X 1 2 3 4 5 6

P(X=x) 1/6 1/6 1/6 1/6 1/6 1/6

E(X) = 1.1/6 + 2. 1/6 + 3. 1/6 + 4. 1/6 +5. 1/6 + 6. 1/6 = 3,5 rupiah

Berapa rupiah yang harus kita bayar agar permainan tersebut adil ?

Permainan disebut adil jika 3,5 rupiah. Dengan demikian rata-rata hadiah

yang kita terima sama dengan banyaknya uang yang kita bayarkan untuk bermain.

Nilai harapan 3,5 dapat diinterprestasikan sebagai berikut : “ jika

permainan itu dapat diulang sebanyak-banyaknya, maka perbandingan antara

(30)

Sifat-sifat Nilai Harapan Definisi 2.2.10

Jika X adalah variabel random dan g(x) adalah fungsi dari variabel random X

maka, E[g(X)] =

⎪⎩

⎪

⎨

⎧∑

∫

= ∞ ∞ − n i i

i p x p x

x g x f dx x f x g 1 ) ( as probabilit fungsi dengan diskret X jika ), ( ) ( ) ( densitas fungsi dengan kontinu X jika , ) ( ) ( Teorema 2.2.1

Jika X adalah variabel random dengan fungsi densitas f(x), a dan b konstanta, g(x)

dan h(x) fungsi-fungsi variabel random berharga real, maka

E[ag(x) + bh(x)] = a E[(g(x)] + b E[h(x)]

Bukti

Jika X adalah variabel random kontinu maka menurut definisi nilai harapan

E[ag(x)+bh(x)] =

∫

∞

∞ −

+bh x f x dx x

ag( ) ( )] ( ) [

= a

∫

∞ ∞ − ∞ ∞ −

+b h x f x dx dx

x f x

g( ) ( ) ( ) ( )

= aE[g(x)] + bE[h(x)] ▄

Sifat-sifat lain nilai harapan

Untuk a dan b bilangan konstan maka berlaku

1. E(a) = a

(31)

3. E(X + a) = E(X) + a

4. E(bX + a) = b E(X) + a

Bukti:

1. E(a) = a

Misalkan , maka

2. E(bX) = b E(X)

3. E(X + a) = E(X) + a

(32)

Teorema 2.2.2

Apabila , , … , merupakan variabel random yang saling bebas maka

E X X … X E X E X … E X

Bukti:

Teorema di atas akan dibuktikan menggunakan induksi matematika.

1. Rumus benar untuk 1

Akan ditunjukkan benar untuk 2,

dan merupakan variabel random yang saling bebas dengan dengan fungsi

distribusi gabungan P X , X . Karena variabel random tersebut saling bebas

maka dapat ditulis P X , X P P , sehingga

X ,X

P X , X

P P

2. Diandaikan bahwa rumus benar untuk dimana 2

3. Akan ditunjukkan bahwa rumus benar untuk

… …

(33)

Definisi 2.2.11

Variansi variabel random X adalah :

Var X E X E X (2.4)

Teorema 2.2.3

Apabila X merupakan sebuah variabel random maka variansi dari X adalah

Var X E X E X

Bukti :

Berdasarkan definisi

2

■

Sifat-sifat lain variansi

Untuk a dan b bilangan konstan maka berlaku

1. Var(X + a) = Var(X)

2. Var(bX) = b2 Var(X) 3. Var(bX + a) = b2 Var(X)

Bukti :

(34)

2 2

2

2 2

2. Var(bX) = b2 Var(X)

(35)

2

2 2

Teorema 2.2.4

Apabila , , … , merupakan variabel random yang saling bebas maka

Var X X X Var X Var X Var X

Bukti :

Persamaan di atas benar untuk 1. Selanjutnya akan dibahas untuk 2,

berdasarkan definisi maka diperoleh

Var (X1 + X2) = E [((X1 + X2) - E [X1 + X2])2]

= E [ ( (X1+ X2 ) – E[X1 ] - E [X2 ] )2]

= E [((X1 - E [X1]) + (X2 - E [X2]))2]

= E [(X1- E [X1]) + (X2 - E [X2])2 +2(X1-E[X1])( X2-E[X2 ] )]

= E [(X1 - E [X1])2] + E [(X2 - E [X2])2] +

(36)

= Var (X1) + Var (X2) + 2E [(X1 - E [X1])( X2 - E [X2])]

Karena dan merupakan variabel random yang saling bebas maka

berdasarkan Definisi 2.2.8 diperoleh

E [(X1 - E [X1])( X2 - E [X2])] = E [X1 - E [X1]] E [X2 - E [X2]]

= (E[X1]-E[X1])(E[X2]-E[X2 ])

= 0

Sehingga,

Var (X1 + X2) = Var (X1) + Var (X2)

Diasumsikan bahwa rumus benar untuk k. Selanjutnya akan ditunjukkan bahwa

rumus benar untuk 1.

Var (X1 + … + Xk-1+ Xk ) = Var (X1 + … + Xk-1) + Var (Xk)

= Var (X1) + … + Var (Xk-1)+ Var (Xk) ■

Kovariansi Definisi 2.2.12

Kovariansi antara dua variabel random adalah ukuran sifat asosiasi (hubungan)

antara keduanya. Jika X dan Y merupakan dua variabel random maka kovariansi

dari X dan Y didefinisikan sebagai

Cov X, Y E X E X Y E Y

Sifat-sifat kovariansi 1. Cov X, X Var X

2. Cov X, Y Cov Y, X

(37)

Bukti :

1. Cov X, X Var X

Cov X, X E X E X X E X

E X E X

Var X

2. Cov X, Y Cov Y, X

Cov X, Y E X E X Y E Y

E XY XE Y YE X E X E Y

E YX YE X XE Y E Y E X

E Y E Y X E X

Cov Y, X

3. Cov X Y, Z Cov X, Z Cov Y, Z

Cov X Y, Z E X Y Z E X Y E Z

E XZ E YZ E X E Z E Y E Z

E XZ E X E Z E YZ E Y E Z

Cov X, Z Cov Y, Z

Definisi 2.2.13

Korelasi dari dua variabel random X dan Y ditulis , dan didefinisikan

sebagai

, Cov X, Y

(38)

Fungsi Pembangkit Momen

Salah satu nilai harapan khusus yang sangat berguna dalam teori

probabilitas dan statistika adalah konsep fungsi pembangkit momen.

Definisi 2.2.14

Jika X adalah variabel random, maka nilai harapan disebut

fungsi pembangkit momen dari X jika nilai harapan tersebut ada untuk semua t

dalam interval –h < t < h, untuk h > 0.

Teorema 2.2.5

Andaikan Y1,Y2,...,Yn adalah variabel random yang saling bebas dengan fungsi

pembangkit momen berturut MY1(t), MY2(t),...,MYn(t). Bila

maka fungsi pembangkit momen dari U adalah …

∏ (2.5)

Bukti :

… karena Yi saling bebas maka

…

(39)

C. Distribusi Bernoulli dan Distribusi Binomial

Distribusi Bernoulli didasarkan atas ruang sampel yang dibangkitkan dari

percobaan Bernoulli. Ruang sampel percobaan ini terdiri atas dua unsur yang

biasanya disimbolkan dengan sukses dan gagal masing-masing dengan peluang

timbulnya p dan 1 . Bila sukses disimbolkan dengan 1 dan gagal dengan

0, maka fungsi probabilitas Bernoulli dapat didefinisikan sebagai berikut :

Definisi 2.3.1

Bila X adalah variabel random Bernoulli maka distribusi probabilitas X adalah

x = 0,1 (2.6)

Dari fungsi probabilitas di atas dapat ditentukan nilai harapan dan variansi serta

fungsi pembangkit momen variabel random yang berdistribusi Bernoulli.

Nilai harapan dari distribusi Bernoulli dapat dicari dengan menggunakan Definisi

2.2.6 untuk variabel random yang diskret karena distribusi Bernoulli merupakan

distribusi probabilitas yang diskret.

∑

∑ 1

0 1 1 1

Jadi nilai harapan dari distribusi Bernoulli adalah p. Selanjutnya dengan

menggunakan Definisi 2.2.8 akan dicari variansi dari distribusi Bernoulli yaitu

(40)

Var (X) = E[x2] – (E[x])2

∑

∑ 1

0 1 1 1

0

Var (X) = E[x2] – (E[x])2

1

Selanjutnya untuk mencari Fungsi Pembangkit Momen (FPM) maka akan

digunakan Definisi 2.2.9.

Mx(t) = E[etx]

∑

∑ 1

1 1

1

1 1

Jadi FPM dari distribusi Bernoulli adalah 1 1 .

Distribusi Binomial

Suatu percobaan sering terdiri atas beberapa usaha, tiap usaha dengan dua

kemungkinan hasil yang dapat diberi nama sukses atau gagal. Hal ini dapat

(41)

atau usaha dapat menunjukkan apakah suatu barang cacat atau tidak cacat. Dapat

ditentukan atau dipilih salah satu hasil sebagai sukses. Hal ini juga benar bila

kartu ditarik secara berturutan dari sekotak kartu bridge dan tiap penarikan

disebut sukses atau gagal tergantung pada apakah kartu merah atau hitam yang

terambil. Proses seperti ini disebut proses Bernoulli.

Percobaan binomial merupakan percobaan yang terdiri atas

ulangan-ulangan percobaan Bernoulli. Percobaan binomial adalah percobaan yang

memiliki ciri-ciri berikut:

1. Percobaan terdiri atas n ulangan.

2. Dalam setiap ulangan, hasilnya dapat digolongkan sebagai sukses atau gagal.

3. Peluang sukses, yang dilambangkan dengan p, untuk setiap ulangan adalah

sama, tidak berubah-ubah.

4. Ulangan-ulangan tersebut bersifat bebas satu sama lain.

Banyaknya X yang sukses dalam n usaha bernoulli disebut peubah acak

binomial. Distribusi peluang peubah acak diskret ini disebut distribusi binomial

dan akan dinyatakan dengan ; , , karena nilainya tergantung pada

banyaknya usaha (n) dan peluang sukses dalam suatu usaha (p). Akan dicari

rumus yang akan memberikan peluang x sukses dalam n usaha suatu prcobaan

binomial. Pertama, pandang peluang sukses x dan gagal n-x dalam suatu urutan

tertentu. Karena usaha semuanya bebas maka peluang tiap hasil yang berbeda

dapat diperkalikan. Tiap sukses terjadi dengan peluang p dan tiap kegagalan

(42)

Sekarang harus ditentukan banyaknya semua titik sampel dalam percobaan

tersebut yang menghasilkan x yang sukses dan n-x yang gagal. Banyaknya ini

sama dengan banyaknya cara memisahkan n hasil menjadi dua kelompok

sehingga x hasil berada pada kelompok pertama dan sisanya n-x hasil pada

kelompok kedua. Jumlah ini dapat dinyatakan dengan .

Definisi 2.3.2

Apabila X1,...,Xn masing-masing merupakan variabel random yang saling bebas

dan berdistribusi Bernoulli, maka ∑ merupakan variabel random yang

berdistribusi Binomial yaitu :

; , , x = 0,1,2,...,n (2.7)

Contoh 2.3.1

Suatu suku cadang dapat menahan uji goncangan tertentu dengan peluang ¾.

Hitunglah peluang bahwa tepat 2 dari 4 suku cadang yang diuji tidak akan rusak.

Jawab:

Misalkan tiap pengujian bebas, jadi pengujian yang satu tidak mempengaruhi atau

dipengaruhi yang berikutnya. Jadi, 3 ₄ untuk tiap keempat pengujian,

sehingga

2; 4,

!

! !

Dari fungsi probabilitas di atas dapat ditentukan nilai harapan dan variansi serta

(43)

Nilai harapan dari distribusi binomial dapat dicari dengan menggunakan Definisi

2.2.6 untuk variabel random yang diskret karena distribusi binomial merupakan

distribusi probabilitas yang diskret.

E x ∑ p x

x _! ! _!

!

! !

n 1

Jadi nilai harapan dari distribusi binomial adalah np.

Selanjutnya untuk mencari variansi dari distribusi binomial akan digunakan

definisi 2.2.8

E x x 1 1 p x

1

x x 1 ! _! _!

!

! !

(44)

1

Var (x) = E[x2] – (E[x])2

1

Variansi dari distribusi binomial adalah .

Selanjutnya untuk mencari Fungsi Pembangkit Momen (FPM) maka akan

digunakan Definisi 2.2.9.

Mx(t) = E[etx]

∑

1 1

(45)

Contoh 2.3.2

Buktikan jika 1,2, … , merupakan variabel-variabel random yang

saling bebas dan berdistribusi Bernoulli, maka

merupakan variabel random yang berdistribusi binomial!

Jawab :

Untuk membuktikan bahwa Y berdistribusi binomial maka akan diguakan sebuah

metode dalam menentukan fungsi distribusi variabel random yaitu metode fungsi

pembangkit momen.

Jika berdistribusi bernoulli maka fungsi pembangkit momenya adalah

1 1

, maka fungsi pembangkit momenya adalah

…

1 1 1 1 … 1 1

1 1

Jika diperhatikan, persamaan terakhir yang diperoleh merupakan fungsi

pembangkit momen bagi variabel random Binomial. Jadi terbukti bahwa jika

1,2, … , merupakan variabel-variabel random yang saling bebas

dan berdistribusi Bernoulli, maka merupakan variabel

(46)

Definisi 2.3.3

Fungsi Gamma ditulis Γ(k), untuk semua k>0 didefinisikan sebagai

dt e t k

∫

k t

∞ − − = Γ 0 1 )

( (2.8)

Fungsi Gamma memenuhi sifat-sifat :

π = Γ − = Γ − Γ − = Γ ) 2 / 1 ( )! 1 ( ) ( ) 1 ( ) 1 ( ) ( n n k k k

k>1, dan n = 1, 2, .. (2.9)

D. Distribusi Normal

Distribusi normal sangat penting baik dalam statistika teori maupun

terapan. Distribusi ini pertama kali dipelajari pada abad kedelapan belas, ketika

orang mengamati galat pengukuran berdistribusi simetrik dan berbentuk bel. De

Moivre mengembangkan bentuk matematik distribusi ini pada tahun 1733,

sebagai bentuk limit distribusi binomial. Laplace juga telah mengenal distribusi

ini sebelum tahun 1775. Gauss menurunkan persamaan distribusi ini dari suatu

studi tentang galat dalam pengukuran yang berulang-ulang dari kuantitas yang

sama, dan mempublikasikannya pada tahun 1809. Untuk menghormatinya

distribusi normal juga dikenal sebagai distribusi Gauss. Pada abad kedelapan

belas dan sembilan belas, berbagai usaha telah dilakukan untuk membuat

distribusi ini sebagai hukum probabilitas yang mendasari semua variabel kontinu,

(47)

Definisi 2.4.1

Suatu variabel random kontinu X dikatakan berdistribusi normal dengan mean µ

dan variansi σ2, apabila variabel itu mempunyai fungsi probabilitas yang berbentuk

f(x) =

2 2( ) 2

1

2

1 _σ μ

π σ

− − x

e (2.10)

dengan

∞ < < ∞

− X σ >0 ∞

< < ∞

− μ 718π =3,14dan e=2, .

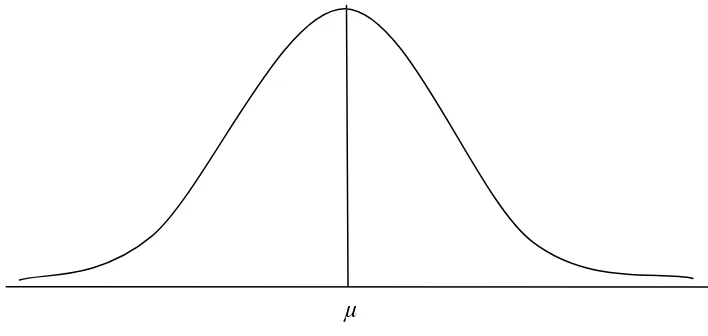
Jika fungsi probabilitas itu digambar, maka kita peroleh grafik seperti dalam

gambar dibawah ini dan dinamakan kurva normal.

Gambar 2.1 : kurva normal dengan mean µ dan variansi σ2

Berikut ini akan ditunjukkan bahwa distribusi normal memenuhi siat-sifat fungsi

densitas.

(48)

Pertama, harus ditunjukkan bahwa integral dari fungsi densitas normal adalah 1.

Kedua, harus ditunjukkan bahwa µ dan σ2 adalah mean dan variansi dari X.

Dengan mensubstitusikan

σ μ

− = x

z dan dx = σdz, didapat :

I = f x dx e z dz e z /2dz

0 2 / 2 2 2 1 2 2 1 ) , ; ( − ∞ − ∞ ∞ − ∞ ∞ −

∫

=

∫

= π π σ μ

Bila dimisalkan w = z2/2, maka z = 2 dan dz = (ww -1/2/ 2)dw, sehingga I = w e−wdw

∞ −

∫

0 2 / 1 π

Dengan menggunakan fungsi Gamma didapat,

I=Γ(1/2) =1

π

Integran yang diperoleh dengan mensubstitusikan

σ μ

− = x

z memegang peranan

yang sangat penting dalam menentukan probabilitas variabel random normal.

Perhitungan menjadi lebih sederhana karena nilai probabilitas telah ditabelkan.

Fungsi densitas hasil transformasi dari X ke Z disebut Distribusi normal standar

yang fungsinya,

φ = − −∞< <∞ z e

z z ,

2 1 )

( 2

π (2.11)

Berikut ini dengan menggunakan Definisi 2.4.1 akan dicari nilai harapan dan

variansi dari variabel random X yang berdistribusi normal.

E(X) = x x dx

(49)

Misal z =

σ μ

− x

maka x = σz + µ dan dx = σdz sehingga diperoleh

E(X) = x e z σdz

π σ 2 2 1 2 1 − ∞ ∞ −

∫

= x e z dz 2 2 1 2 1 − ∞ ∞ −

∫

π

= z e z dz

2 2 1 2 1 ) ( − ∞ ∞ −

∫

+ π μ σ

=

∫

z e z dz

∫

e z dz ∞ ∞ − − − ∞ ∞ − + 2 2 2 1 2 1 2 1 _μ π σ

= 1

2 1 2 2 1 ⋅ + − ∞ ∞ −

∫

μ π

σ z e z dz

jika dimisalkan, -1/2z2 = w maka z = 2 dan z dz = -dw w atau dz =

z dw

= w dw

2 sehingga diperoleh

E(X) = μ

π σ ∞ − + ∞ −

∫

dz e z z 2 2 1 2 1 = μ π σ + −

∫

∞ ∞ − dw ew 2 1 = μ π σ ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + −

∫

∞ − ∞ 0 0 2 e dw e dw

w w =

]

μ π σ ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − − ∞ ∞ − − 0 2 1 0 2

1 2 2

(50)

= 0 + µ

= µ

E(X2) = x x dx

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − −

∫

∞ ∞ − 2 2 2 1 exp 2 1 σ μ π σ

Misal, z =

σ μ

− x

maka x = σz + µ dan σdz = dx sehingga diperoleh

E(X2) =

∫

x e z dz ∞ ∞ − − σ π σ 2 2 1 2 2 1

=

∫

z e z dz ∞ ∞ − − + 2 2 1 2 2 ) ( π μ σ

= z z e z dz

2 2 1 2 2 2 2 ) 2 ( − ∞ ∞ −

∫

+ + π μ μσ σ =

∫

∞ ∞ − − − ∞ ∞ − − ∞ ∞ − +

+ ze dz e dz dz

e

z z2 z2 z2

2 1 2 2 1 2 1 2 2 2 2 2 2 π μ π μσ π σ

=

0

1

2

2 2 1 2 2 2

⋅

+

− ∞ ∞ −

∫

μ

π

σ

dz

e

z

z =

∫

∞ ∞ − − + 2 2 1 2 2 2

2π μ

σ

dz e

z z

misal ½ z2 = w maka z = 2 dan z dz = dw sehingga diperoleh w E(X2) =

w dw e w w 2 2 2 2

∫

∞ ∞ − − π σ

+ µ2

=

∫

w e wdw ∞ ∞ − − 2 1 2 π σ

(51)

=

∫

w e wdw ∞ − 0 2 1 2 2 π σ

+ µ2

dengan menggunakan persamaan (2.8) dan (2.9) didapatkan

E(X2) =

∫

w e wdw

∞ − 0 2 1 2 2 π σ

+ µ2

= 2 (3/2) 2

Γ

π σ

+ µ2

= (1/2) 2 1 2 2 Γ π σ

+ µ2

= π π σ 2 1 2 2

+ µ2

= σ2_{+ µ}2

. (2.12)

Dengan menggunakan persamaan (2.4) maka

Var(X) = E(X2) – [E(X)]2

= (σ2 +μ2) - µ2 = σ2 (2.13)

Hampiran Normal Terhadap Binomial

Peluang yang berkaitan dengan percobaan binomial dengan langsung

dapat diperoleh dari rumus distribusi binomial ; , atau dari tabel distribusi

bila n kecil. Bila n tidak ada dalam daftar tabel yang tersedia, maka peluang

binomial terpaksa dihitung dengan cara hampiran.

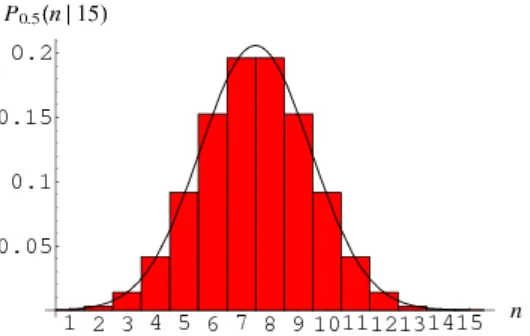
Distribusi normal sering merupakan hampiran yang baik terhadap

distribusi diskret. Distribusi normal merupakan distribusi hampiran yang

(52)

ditabelkan. Distribusi binomial dihampiri dengan baik oleh distribusi normal

dalam praktek bila digunakan fungsi distribusi kumulatif. Berikut ini akan

diberikan sebuah teorema yang memungkinkan penggunaan luas di bawah kurva

normal untuk menghampiri peluang binomial bila n cukup besar.

Teorema 2.4.1

Bila X peubah acak binomial dengan rataan dan variansi maka

bentuk limit distribusi

bila ∞ , adalah distribusi normal standar N z; 0,1 .

(53)

BAB III

RANDOM WALK dan GERAK BROWN

Suatu proses stokastik , merupakan kumpulan dari

variabel-variabel random. Jadi untuk setiap , merupakan variabel random.

Indeks t seringkali menggambarkan waktu dan lebih mengarah kepada hasil

atau keadaan dari proses tersebut pada waktu t.

Dalam bab III ini akan dibahas mengenai Random Walk dan Gerak Brown.

Random walk dan gerak Brown merupakan contoh dari suatu proses stokastik

dan sering digunakan dalam memodelkan pergerakan harga saham. Selain itu juga

akan dibahas mengenai Ito’s Lemma yang juga merupakan lemma yang cukup

penting dan sering digunakan dalam proses stokastik.

A. Random Walk

Secara harafiah random walk berarti langkah random. Suatu percobaan

sederhana dapat menggambarkan dengan jelas mengenai konsep dasar dari

random walk, yaitu pelemparan sebuah mata uang dua sisi. Bayangkan seseorang

yang berada pada titik nol (origin) pada sebuah garis bilangan real dan orang

tersebut akan melemparkan sebuah mata uang dua sisi yang seimbang . Apabila

dalam setiap kali pelemparan mata uang tersebut, muncul sisi gambar maka orang

tersebut akan berpindah satu unit langkah ke arah kanan ( positive direction) dan

jika muncul sisi angka maka orang tersebut akan berpindah satu unit langkah ke

(54)

Kejadian di atas merupakan suatu hal yang mengandung suatu ketidakpastian,

yaitu dalam hal ini peluang memegang peranan yang cukup penting. Bukan

sesuatu hal yang mudah dalam menentukan dengan tepat dan benar apakah orang

tersebut akan bergerak ke arah kanan ataupun sebaliknya, karena dalam situasi ini

orang tersebut mempunyai peluang yang sama besar untuk bergerak ke arah kanan

maupun kiri. Hal ini membuat orang tersebut akan bergerak secara acak

berdasarkan hasil pelemparan sebuah mata uang.

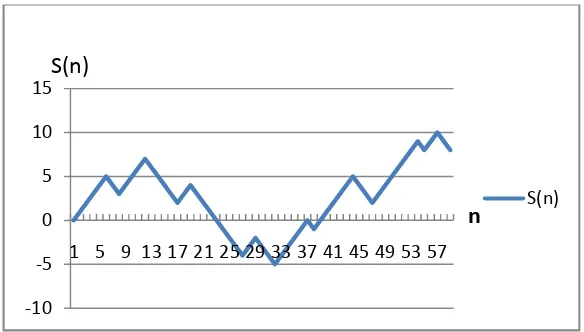
Dapat dikatakan bahwa kejadian perpindahan orang tersebut sebagai sebuah

random walk sederhana atau suatu sistem dinamis stokastik yang diskret yang

akan berkembang menjadi random walk.

Gambar 3.1 gambar random walk pada garis bilangan real

Definisi 3.1.1

Misalkan , , … , merupakan variabel random yang bernilai real dan

0 sehingga,

0 ∑

‐10

‐5 0 5 10 15

1 5 9 13 17 21 25 29 33 37 41 45 49 53 57

S(n)

(55)

maka barisan variabel random ∞ disebut sebagai random walk dengan

0 merupakan keadaan awal.

Apabila definisi ini dipersempit dengan mengasumsikan bahwa hanya bernilai

1 atau -1 dengan peluang yang sama, maka barisan variabel random ∞

disebut sebagai random walk sederhana.

Pembahasan selanjutnya mengenai random walk akan diawali dengan sebuah

aplikasi. Sebuah aplikasi yang cukup sederhana dari random walk adalah dalam

dunia ekonomi, dalam hal ini harga saham, yaitu situasi dimana seseorang yang

mempunyai saham dengan harga tertentu yang dilambangkan dengan S. Pada

interval diskret (misalnya pengamatan per detik), harga dari saham tersebut

diasumsikan dapat berubah menjadi lebih tinggi (meningkat) ataupun lebih

rendah (menurun) satu unit dari harga saham sebelumnya . Dengan kata lain jika

harga saham pada detik ke n adalah , maka harga saham pada detik ke n+1

adalah 1 1 atau 1 1. Sama seperti pada

pembahasan sebelumnya bahwa peluang harga saham tersebut untuk meningkat

akan sama besar dengan peluang harga saham tersebut untuk menurun. Asumsi ini

menghasilkan sebuah sifat yaitu sifat simetrik bagi random walk.

Definisi 3.1.2

Jika distribusi dari random walk mempunyai 1 1 , maka

random walk tersebut disebut sebagai random walk yang simetrik, dan

(56)

i. | 0 | 0 untuk setiap

, , , ( Spatial Homogeneity/ kesamaan tempat).

ii. | 0 | untuk setiap

, , , (Temporal Homogeneity/ kesamaan waktu).

Berdasarkan pembahasan di atas, apabila merupakan sebuah variabel

random yang dapat bernilai 1 atau -1 dengan nilai probabilitas yang sama dan

untuk 0, maka dapat dikatakan bahwa random walk dengan sejumlah n

langkah yang telah diambil sebagai jumlahan parsial dan ditulis

0 (3.1)

Variabel random merupakan bentuk umum dari variabel random

Bernoulli, karena merupakan sebuah variabel random yang menggambarkan

sebuah kejadian dengan dua kemungkinan hasil yaitu 1 dan -1. Apabila

merupakan variabel yang menyatakan harga saham pada hari ke-n dan 1

untuk harga saham pada hari sebelumnya, maka dan 1 dapat

dikurangkan dan diperoleh

0

1 0

1

Secara induksi rumus untuk mencari nilai dari variabel dapat didefinisikan

dengan menggunakan rumus 1 untuk 0, dimana 0

(57)

Apabila keadaan awal dari random walk adalah 0 dan jumlah langkah

yang telah ditempuh sebanyak 0, dimana 0 adalah banyaknya langkah ke

arah kanan (positif) dan 0 adalah banyaknya langkah ke arah kiri

(negatif) maka dapat dicari probabilitas bagi yang menyatakan keadaan atau

posisi dari sebuah random walk setelah menempuh sejumlah n langkah.

0 0 2

Jika diperhatikan dengan baik, 2 merupakan jumlahan dari variabel random

Xi yang saling bebas dan berdistribusi Bernoulli sehingga mengakibatkan variabel

0 berdistribusi binomial (Definisi 2.5.1). Untuk menyatakan posisi

atau tempat dari random walk setelah n langkah ditempuh dapat menggunakan

persamaan 0 2 , dan karena variabel 0 berdistribusi

binomial maka akan dicari peluang k sukses dari n langkah yang ada sehingga

dapat ditulis bahwa

0 2

(3.2)

Jika 0 0 maka variabel 0 dapat ditulis menjadi sebuah

variabel random yang baru yaitu 0 untuk 0,1, … sehingga

diperoleh suatu hubungan yaitu 0 0.

(58)

Lemma 3.1.1

Jika random walk yang didefinisikan seperti pada Persamaan (3.1) dengan

keadaan awal S 0 0, maka

1) 0 jika |m| ,

2) 0 jika n m gasal,

3) _⁄ , selainya.

Bukti :

1) 0

, 0 0

Jika merupakan variabel random yang dapat bernilai 1 atau -1 dengan

peluang yang sama, maka . Dengan demikian sebagai

jumlahan parsial untuk 0 tidak dapat mencapai nilai apabila

| | . Sehingga terbukti benar bahwa

0 | |

2) Berdasarkan Persamaan (3.2) dan 0 0, maka diperoleh 2

sehingga 2 . Hal ini menunjukan bahwa genap dan

kontradiksi dengan asumsi bahwa gasal. Jadi terbukti bahwa

0

3) Diasumsikan bahwa 2 dan genap. Dari asumsi tersebut diperoleh

kemudian dengan menggunakan rumus sebelumnya(Persamaan 3.2)

maka

(59)

■

Pada pembahasan sebelumnya, random walk dapat secara bebas bergerak ke

arah kiri maupun kanan berdasarkan jumlah langkah yang ada. Misalkan sebuah

batas diletakan pada jalur dari random walk. Diasumsikan bahwa keadaan awal

dari random walk adalah positif yaitu 0 0 dan diasumsikan juga bahwa

batas bawah dari random walk adalah 0. Apabila random walk mencapai nilai

batas tersebut dalam jumlah langkah yang berhingga, maka random walk akan

berada pada nilai batas tersebut. Dalam random walk keadaan seperti ini dikenal

sebagai kondisi penyerapan nilai batas ( Absorbing Boundary Condition ).

Sangat perlu untuk diperhatikan setiap nilai terkecil yang dicapai oleh

karena nilai batas pada 0 yang bersifat menyerap (absorbing). Oleh sebab itu

didefinisikan : 0 . Jika j adalah bilangan bulat positif

terkecil sedemikian hingga 0 0 , maka berdasarkan sifat

penyerapan nilai batas 0 untuk semua .

Lemma 3.1.2

Misalkan random walk yang didefinisikan seperti pada Persamaan (3.1) dengan

untuk 1,2, … , merupakan variabel random yang saling bebas dan identik

(60)

bahwa nilai batas pada 0 bersifat menyerap (absorbing). Jika , 0, | |

dan genap juga genap maka

∧ _{0 | 0} _⁄ _⁄ (3.3)

Bukti :

Untuk membuktikan lemma di atas akan diawali dengan pembahasan mengenai

random walk tanpa nilai batas, yaitu variabel random yang mempunyai

keadaan awal 0 0 dan yang dapat bernilai negatif karena tidak

adanya batas. Dalam situasi ini dengan menggunakan aturan penjumlahan

diperoleh

| 0

∧ ₀ ₀ ∧ ₀ ₀ (3.4)

Berdasarkan sifat kesamaan tempat (spatial homogeneity) dari random walk,

maka di dapat

| 0 | 0 0

Menggunakan Lemma 3.1.1 bagian (iii) dengan | | karena akibat dari

| | dan genap maka rumus probabilitas di atas dapat ditulis

menjadi

| 0 0 _⁄ (3.5)

sekarang sifat simetrik dari random walk akan digunakan untuk random walk

yang tidak dibatasi

(61)

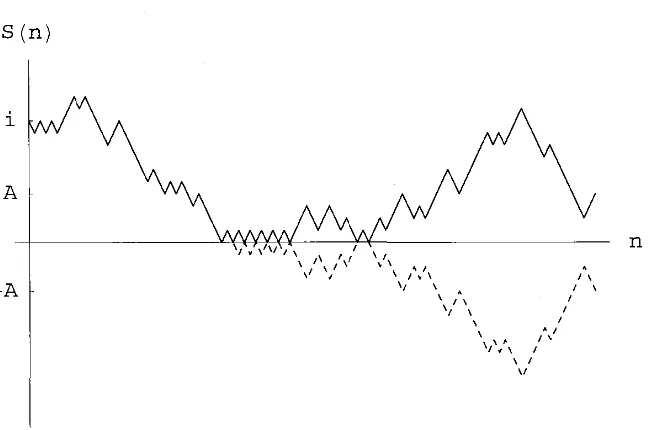
Seperti yang tampak pada Gambar 3.2, realisasi dari random walk yang

memotong sumbu x pada dapat direfleksikan di sekitar sumbu x. Random

walk yang tidak mempunyai batas mengakibatkan bahwa ada kemungkinan untuk

random walk tersebut mencapai daerah bagian bawah yaitu nilai negatif. Garis

putus-putus pada gambar di bawah ini menyatakan bahwa random walk mencapai

nilai negatif dan dapat direfleksikan di sekitar sumbu x sehingga diperoleh

gambar dari random walk yang selalu berada diatas sumbu x meskipun tidak

mempunyai batas.

Gambar 3.2 random walk yang simetri dengan keadaan awal 0

Nilai probabilitas dari random walk di atas sama dengan nilai dari setiap jalur

yang dicapai. Oleh karena itu berdasarkan sifat refleksif dari gambar di atas dan

dengan mengingat syarat bahwa | | dan genap, maka

∧ _{0 | 0} _{| 0}

| 0 0

j j

(62)

_⁄ (3.6)

Berdasarkan hal ini, untuk membuktikan lemma di atas menjadi sedikit lebih

mudah yaitu dengan mensubtitusikan Persamaan 3.6 dan Persamaan 3.5 ke dalam

Persamaan 3.4 sehingga diperoleh

∧ _{0 | 0}

_⁄ _⁄ ■

Contoh 3.1.1

Sebuah random walk yang simetrik dengan keadaan awal 0 10, berapakah

probabilitas bahwa 50 16 dan 0 0,1, … ,50 ?

Jawab :

Diketahui bahwa 50, 16, dan 10.

Untuk menghitung probabilitas di atas maka akan digunakan rumus

∧ 0 | 0

_⁄ _⁄

2

0.0787178

Mengingat bahwa notasi yang digunakan sangat panjang, maka dengan tujuan

mempermudah penulisan maka akan didefinisikan sebuah fungsi baru yaitu

(63)

Sebuah variabel random baru yaitu Ω akan didefinisikan sebagai waktu

penghentian ( stopping time ) jika nilai dari sebuah random walk sama dengan A

dalam kesempatan yang pertama. Selanjutnya akan dibahas mengenai probabilitas

bahwa Ω mempunyai nilai berupa bilangan asli dengan keadaan awal yang

diberikan 0 0 dengan parameter 0 dan nilai batas pada 0 bersifat

menyerap (absorbing). Andaikan bahwa keadaan awal dari random walk adalah

0 0, dengan menggunakan sifat kesamaan tempat (spatial

homegeneity) dari random walk maka diperoleh

0

0 0 0

Misalkan Ω menyatakan bahwa random walk pada langkah ke n mencapai

nilai 0 pada kesempatan yang pertama sehingga jika Ω berarti 0.

Ω jika dan hanya jika 1 1 , 0 dan 1, dimana

1 dan 1 1 , 0 merupakan kejadian yang saling bebas,

sehingga

Ω | 0

1 1 1 0 | 0

1| 0 1 1 0 | 0

1 1 0 | 0

, 1

(64)

Didefinisikan sebuah simbol baru yaitu yang menyatakan sembarang

jalur dalam interval diskret [0,A] dari 0 menuju A dan menjauhi 0. Sedangkan

merupakan sebuah simbol untuk menyatakan probabilitas dari sebuah

random walk yang berawal dari 0 dan melalui jalur . Akhirnya simbol

akan digunakan untuk menyatakan probabilitas dari random walk yang

berawal pada 0 dan akan mencapai nilai dengan menjauhi keadaan

0. Dengan menggunakan aturan penjumlahan pada prinsip probabilitas maka

diperoleh

Setiap pergerakan dari random walk untuk bergerak ke kanan ataupun ke kiri

adalah bebas dan tidak bergantung pada pergerakan sebelumnya, sehingga

keadaan awal 0 dari random walk tersebut dapat dibentuk menjadi dua

keadaan yaitu 1 1 dengan probabilitas dan 1 1 dengan

probabilitas sehingga rumus probabilitas di atas dapat ditulis menjadi

∑

1 1

0 1 2 1 (3.7)

Pada pembahasan sebelumnya dikatakan bahwa random walk hanya

mempunyai satu nilai batas yang bersifat menyerap yaitu 0. Selanjutnya random

(65)

bersifat menyerap yaitu 0 dan A. Karena kedua nilai batas tersebut bersifat

menyerap maka diperoleh 0 0 dan 1.

Teorema 3.1.1

secara distribusi yang dapat bernilai 1 dengan probabilitas . Misalkan juga

bahwa nilai batas pada titik 0 dan A bersifat menyerap. Jika 0 0

maka

1. Probabilitas random walk mencapai nilai A tanpa harus mencapai nilai 0

adalah ⁄ ,

2. Probabilitas random walk mencapai nilai 0 tanpa harus mencapai nilai A

adalah 1 ⁄ .

Bukti

Pembuktian teorema di atas akan dilakukan dengan mencari solusi dari persamaan

linear (Persamaan 3.7).

Persamaan 3.7 di atas merupakan suatu sistem persamaan linear yang mempuyai

solusi yang juga merupakan nilai bagi untuk 1,2, … , 1 dengan nilai

0 0 dan 1. Jika ditulis dalam bentuk matriks maka diperoleh :

1 0 0 0 0 0 0 0

1 2 1 0 0 0 0 0

0 1 2 1 0 0 0 0

0 0 1 2 1 0 0 0

0 0 0 0 0 1 2 1

0 0 0 0 0 0 0 1

0 1 2 3

1

0 0 0 0

(66)

Untuk mempermudah menyelesaikan sistem persamaan linear tersebut akan

dibentuk matriks segitiga atas dengan menggunakan eliminasi Gauss. Eliminasi

Gauss bekerja dengan menambahkan perkalian skalar dengan baris pada baris

dibawahnya yang pada akhirnya akan menghasilkan matris segitiga atas yaitu

matriks dengan semua entri di bawah diagonal utama bernilai nol

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 1 M L L M L L L L

Dengan mengalikan -1 pada baris pertama dan kemudian ditambahkan pada baris

kedua diperoleh ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 1 2 0 0 0 0 0 0 0 0 1 M L L M L L L L

Selanjutnya baris kedua dikalikan dengan kemudian ditambahkan pada baris

(67)

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 2 0 0 0 0 0 0 0 0 1 2 3 M L L M L L L L

Langkah selanjutnya adalah dengan mengalikan pada baris ketiga dan

menjumlahkannya pada baris keempat dan diperoleh

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 2 0 0 0 0 0 0 0 0 1 3 4 2 3 M L L M L L L L

Misalkan bahwa eliminasi Gauss telah dikerjakan sampai pada baris ke i sehingga

bentuk dari matriks tersebut pada baris ke i dan i+1 adalah

0 0 0 0 1 2 1 0 0 0 0 0 1 0 0 1 L L L L − − − i i

Sekali lagi eliminasi Gauss dioperasikan yaitu dengan mengalikan 1 1 ⁄

pada baris ke i kemudian dijumlahkan pada baris ke i+1 sehingga diperoleh

0 0 0 0 1 0 0 0 0 0 0 1 0 0 ) 1 ( 1 L L L L i i i i + − − −

Apabila eliminasi Gauss dikerjakan terus hingga pada baris ke A maka akan

(68)

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 2 0 0 0 0 0 0 0 0 1 1 3 4 2 3 M L L M L L L L A A

Apabila matriks segitiga atas ini ditulis kembali berdasarkan sistem persamaan

linearnya maka diperoleh

1 0 0 0 0 0 0 0

0 2 1 0 0 0 0 0

0 0 1 0 0 0 0

0 0 0 1 0 0 0

0 0 0 0 0 0 1

0 0 0 0 0 0 0 1

0 1 2 3 1 0 0 0 0 0 1

Sistem persamaan linear yang baru ini akan sedikit mempermudah dalam mencari

semua nilai solusi yang mungkin bagi sistem persamaan linear tersebut. Apabila

nilai diketahui maka untuk menentukan nilai 1 dapat ditentukan

dengan menggunakan persamaan berikut

1 0

1 (3.8)

Misalkan diambil , seperti diketahui bahwa nilai batas pada A bersifat

menyerap sehingga 1, kemudian disubstitusikan pada Persamaan 3.8

(69)

Misalkan bahwa nilai diketahui, maka dengan mengambil

dan mensubtitusikannya pada Persamaan 3.8 diperoleh

1

1 (3.9)

Berdasarkan hasil yang sudah diperoleh maka dalam kasus yang lebih umum

dapat dikatakan bahwa . Apabila diambil maka

. Nilai dari solusi ini dapat ditulis dalam bentuk matriks berikut ini

0 1

1

0

1

Variabel menyatakan probabilitas dari sebuah random walk dengan

keadaan awal 0 akan mencapai titik 0 dan menjauhi titik .

Dengan mengganti variabel A pada Persamaan 3.7 dengan 0 maka diperoleh

sebuah persamaan

0 1 2 1 (3.10)

Untuk menyelesaikan sistem persamaan di atas dapat dilakukan sama seperti yang

sebelumnya dilakukan tetapi akan sedikit sulit. Oleh sebab itu akan digunakan

cara yang lebih mudah yaitu dengan menggunakan sifat simetrik dari random

(70)

ke atas akan sama dengan ketika bergerak ke bawah. Mengingat bahwa kedua

nilai batas (0 dan A) bersifat menyerap sehingga mengakibatkan 0 1 dan

0. Berdasarkan hal tersebut dan konsep mengenai probabilitas dari

semua kemungkinan kejadian yang terjadi adalah 1, maka dapat ditulis

1

Berdasarkan hasil terakhir yang diperoleh maka dapat ditulis semua nilai bagi

untuk 1,2, … , 1 dalam sebuah matriks di bawah ini

0 1

1

0

Sehingga diperoleh sebuah kesimpulan yaitu

dan 1 untuk 1,2, … , 1 ■

Misalkan 0, merupakan himpunan nilai batas yang bersifat menyerap dari

random walk berdimensi satu, maka dapat didefinisikan sebuah simbol yang

menyatakan nilai harapan untuk waktu penghentian bagi random walk yang

(71)

: waktu untuk random walk bergerak dari 0 untuk 0 ke B

dan mengikuti jalur .

Ω : nilai harapan .

Berdasarkan definisi nilai harapan maka diperoleh

Ω

Apabila random walk bergerak mulai dari nilai batas 0 maka nilai

harapannya adalah 0, sehingga Ω 0 Ω 0. Jalur dari dapat

dibentuk menjadi jalur yang berbentuk 1 atau 1 dengan

penambahan satu langkah, sehingga diperoleh

Ω ∑ 1 1

∑ ∑

∑

Ω 1 Ω 1 1

2 Ω 1 2Ω Ω 1 (3.11)

Teorema 3.1.2

secara distribusi yang dapat bernilai 1 dengan probabilitas . Misalkan juga

(72)

random walk memotong nilai batas ( S = 0 atau S = A) setelah sejumlah langkah

yang telah ditempuh diberikan oleh rumus

Ω

Bukti

Pembuktian teorema ini akan dilakukan dengan mencari solusi dari persamaan

linear (3.11).

Persamaan 3.11 sering kali disebut sebagai Persamaan Poisson untuk waktu

penghentian. Dari persamaan Poisson ini dapat dibentuk sebuah sistem persamaan

linear untuk waktu penghentian dan ditulis dalam bentuk matriks berikut ini

( )

(

)

( )

⎥⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ Ω − Ω Ω Ω Ω ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − 0 2 2 2 0 1 2 1 0 1 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 1 2 1 0 0 0 0 0 0 1 M M L L M L L L A A B B B B B

Matriks yang dibentuk dari Persamaan Poisson dikenal sebagai matriks

tridiagonal. Jika diperhatikan seluruh entri pada matriks tersebut bernilai nol

kecuali entri-entri pada diagonal utama, sub-diagonal, dan super diagonal. Banyak

metode yang dapat digunakan untuk menyelesaikan sistem persamaan linear,

tetapi metode yang akan digunakan adalah sama dengan yang sudah digunakan di

depan yaitu eliminasi Gauss. Operasi pertama yang dilakukan adalah

memperbesar matriks dengan menambah sebuah kolom pada sisi bagian kanan

(73)

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − 0 2 2 2 0 1 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 1 2 1 0 0 0 0 0 0 1 M L L M L L L

Apabila baris pertama dikalikan dengan -1 dan kemudian dijumlahkan dengan

baris kedua maka diperoleh

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − 0 2 2 2 0 1 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 1 2 0 0 0 0 0 0 0 1 M L L M L L L

Perhatikan sekarang bahwa semua entri pada kolom pertama sudah bernilai nol

kecuali entri pada diagonal utama. Selanjutnya hal yang sama akan dilakukan

untuk kolom yang kedua dengan mengalikan pada baris kedua dan

menjumlahkanya dengan baris ketiga sehingga menjadi

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − 0 2 3 2 0 1 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 2 0 0 0 0 0 0 0 1 2 3 M L L M L L L

Langkah selanjutnya adalah dengan mengalikan pada baris ketiga dan

(74)

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − − 1 0 4 3 2 0 1 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 2 0 0 0 0 0 0 0 0 1 3 4 2 3 M L L M L L L L

Operasi baris elementer ini harus terus dilakukan sampai dua baris terakhir.

Andaikan eliminasi Gauss telah dioperasikan pada baris ke i pada matriks yang

diperbesar tersebut sehingga baris ke i dan i+1 dari matriks tersebut menjadi

seperti berikut 2 0 0 1 2 1 0 0 0 0 0 1 0 0 ₁ − − − − − _i i i L L L L

Dengan mengalikan baris ke i dengan 1 1 ⁄ kemudian dijumlahkan dengan

baris i+1 dan menghasilkan

) 1 ( 0 0 1 0 0 0 0 0 0 1 0 0 ) 1 ( 1 + − − + − − − i i i i i i L L L L

Terlihat bahwa dengan melakukan eliminasi Gauss maka matriks yang diperbesar

ini menjadi matriks segitiga atas dan ditulis

(75)

Proses eliminasi Gauss sama halnya dengan menjumlahkan hasil kali persamaan

linear dengan persamaan linear yang lainya. Jika matriks segitiga atas tersebut

ditulis kembali berdasarkan Persamaan 3.11 maka diperoleh

( )

(

)

( )

⎥⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ Ω − Ω Ω Ω Ω ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − 0 3 2 0 1 2 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 2 0 0 0 0 0 0 0 1 1 2 3 A A A B B B B B A A M M L L M L L L (3.12)

Sekarang sistem persamaan linear ini sudah dapat digunakan untuk mencari solusi

bagi nilai Ω untuk 1,2, … , 1.

Apabila nilai dari Ω diketahui maka dapat ditentukan nilai bagi Ω 1

dengan menggunakan persamaan

Ω 1 Ω

Ω 1 1 Ω (3.13)

Berdasarkan (3.12) nilai Ω 0, nilai ini akan digunakan sebagai substitusi

dalam Persamaan 3.13. Misalkan diambil dan dimasukkan ke dalam

persamaan 3.13, maka

Ω 1 1 Ω

1 0

1