Model matematis dan simulasi pergerakan harga saham - USD Repository

i SKRIPSI

Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun Oleh : RIDWAN RAHADIYANTO

NIM : 033114011

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

i THESIS

Presented As a Partial Fulfillment of The Requirements to Obtain The Sarjana Sains Degree

In Mathematics

by :

Ridwan Rahadiyanto Student Number : 033114011

MATHEMATICS STUDY PROGRAM DEPARTEMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

LAMPIRAN Data Harga Saham

Harga saham IBM harian : Tanggal Harga

28-Sep-01 86.01 30-Jul-01 99.13 4-Jun-01 106.42 6-Apr-01 91.62 9-Feb-01 104.76 27-Sep-01 84.39 27-Jul-01 98.05 1-Jun-01 105.72 5-Apr-01 91.86 8-Feb-01 106.72 26-Sep-01 85.61 26-Jul-01 99.27 31-May-01 104.7 4-Apr-01 86.05 7-Feb-01 109.35 25-Sep-01 88.57 25-Jul-01 98.23 30-May-01 105.49 3-Apr-01 84.55 6-Feb-01 106.69 24-Sep-01 88.89 24-Jul-01 97.87 29-May-01 107.95 2-Apr-01 88.54 5-Feb-01 104.84 21-Sep-01 84.86 23-Jul-01 99.13 25-May-01 110.32 30-Mar-01 89.96 2-Feb-01 103.02 20-Sep-01 87.58 20-Jul-01 98.99 24-May-01 112 29-Mar-01 88.89 1-Feb-01 106.55 19-Sep-01 90.02 19-Jul-01 97.39 23-May-01 109.94 28-Mar-01 88.31 31-Jan-01 104.64 18-Sep-01 90.4 18-Jul-01 97.66 22-May-01 110.51 27-Mar-01 93.07 30-Jan-01 108.95 17-Sep-01 87.53 17-Jul-01 101.64 21-May-01 111.48 26-Mar-01 89.23 29-Jan-01 107.42 10-Sep-01 90.46 16-Jul-01 100.97 18-May-01 109.98 23-Mar-01 87.46 26-Jan-01 106.69 7-Sep-01 90.57 13-Jul-01 101.64 17-May-01 107.76 22-Mar-01 83.34 25-Jan-01 103.47 6-Sep-01 91.9 12-Jul-01 100.44 16-May-01 108.44 21-Mar-01 83.32 24-Jan-01 103.18 5-Sep-01 94.1 11-Jul-01 97.25 15-May-01 106.36 20-Mar-01 82.59 23-Jan-01 101.89 4-Sep-01 95.17 10-Jul-01 95.48 14-May-01 105.41 19-Mar-01 86.61 22-Jan-01 101.43 31-Aug-01 93.72 9-Jul-01 98.07 11-May-01 104.71 16-Mar-01 84.27 19-Jan-01 103.94 30-Aug-01 94.11 6-Jul-01 99.73 10-May-01 107.88 15-Mar-01 89.38 18-Jan-01 101.19 29-Aug-01 97.64 5-Jul-01 104.98 9-May-01 109.55 14-Mar-01 88.82 17-Jan-01 90.34 28-Aug-01 98.41 3-Jul-01 105.8 8-May-01 110.22 13-Mar-01 92.03 16-Jan-01 86.65 27-Aug-01 100.2 2-Jul-01 107.09 7-May-01 108.41 12-Mar-01 89.32 12-Jan-01 87.64 24-Aug-01 100.33 29-Jun-01 106.29 4-May-01 108.37 9-Mar-01 92.87 11-Jan-01 87.53 23-Aug-01 96.58 28-Jun-01 107.79 3-May-01 106.35 8-Mar-01 99.59 10-Jan-01 87.3 22-Aug-01 97.48 27-Jun-01 106.31 2-May-01 107.94 7-Mar-01 100.6 9-Jan-01 86.48 21-Aug-01 95.54 26-Jun-01 105.86 1-May-01 110.85 6-Mar-01 99.15 8-Jan-01 87.41 20-Aug-01 97.62 25-Jun-01 105.49 30-Apr-01 107.7 5-Mar-01 98.13 5-Jan-01 87.82 17-Aug-01 98.07 22-Jun-01 105.7 27-Apr-01 108.69 2-Mar-01 95.69 4-Jan-01 87.07 16-Aug-01 99.16 21-Jun-01 105.45 26-Apr-01 106.39 1-Mar-01 99.19 3-Jan-01 88.4 15-Aug-01 98.47 20-Jun-01 105.91 25-Apr-01 107.42 28-Feb-01 93.44 2-Jan-01 79.24 14-Aug-01 99.58 19-Jun-01 107.54 24-Apr-01 105.38 27-Feb-01 95.96

13-Aug-01 99.27 18-Jun-01 107.01 23-Apr-01 104.76 26-Feb-01 98.49 10-Aug-01 98.41 15-Jun-01 106.38 20-Apr-01 107.41 23-Feb-01 97.28

v

hidup adalah pembelajaran

hidup adalah perjuangan

hidup adalah perbuatan

hidup adalah sebuah perjalanan

hidup adalah pilihan-pilihan

hidup adalah tanggungjawab hidup adalah penantian

hidup adalah menyayangi hidup adalah memahami

hidup adalah mencintai

hidup adalah memberi

hidup adalah menikmati hidup adalah akhir

melalui hidup kita belajar banyak hal dan satu hal yang pasti

“ susahku saiki durung cukup kanggo

mbayar senengku mbesuk, gusti ra bakalan

menehi cobaan sing ora iso dihadapi

hambane ”

vi

Pergerakan harga saham pada dasarnya tidak dapat diprediksi dengan pasti, tetapi pergerakan tersebut dapat diperkirakan. Untuk memperkirakan pergerakan harga saham, maka akan dibuat suatu model matematika yang memanfaatkan pembangkitan bilangan random sebagai sampel data harga sahamnya. Melalui model matematika tersebut dapat diperoleh suatu simulasi pergerakan harga saham.

vii

possible to make some predictions. A mathematical model is designed in order to estimate the movement of asset price. This model uses random numbers as the sample of the asset price and can be used as a simulation model of the movement of asset price.

viii

yang telah diberikan sehingga penulis dapat menyelesaikan skripsi ini.

Dalam penulisan skripsi ini, penulis banyak menemui hambatan dan kesulitan. Namun, berkat bantuan dan dukungan dari banyak pihak, akhirnya skripsi ini dapat terselesaikan. Oleh karena itu, penulis ingin mengucapkan terima kasih kepada :

1. Ibu Ch. Enny Murwaningtyas, S.Si, M.Si, selaku dosen pembimbing skripsi dan dosen pembimbing akademik yang selalu sabar dan memberi semangat kepada penulis selama kuliah dan penyusunan skripsi ini.

2. Bapak Yosef Agung Cahyanta, S.T., M.T, selaku Dekan Fakultas Sains dan Teknologi.

3. Ibu Lusia Krismiyati Budiasih S.Si, M.Si, selaku Ketua Program Studi Matematika yang telah banyak membantu dan memberi saran.

4. Bapak Ir. Ignatius Aris Dwiatmoko, M.Sc, selaku penguji yang telah banyak memberikan masukan kepada penulis.

5. Bapak dan Ibu Dosen Fakultas Sains dan Teknologi yang telah memberikan bekal ilmu yang sangat berguna bagi penulis.

6. Bapak Tukijo dan Ibu Linda yang telah memberikan pelayanan administrasi selama penulis kuliah.

7. Perpustakaan USD yang telah memberikan fasilitas dan kemudahan kepada penulis.

8. Kedua orang tua dan ade’ku yang selalu memberikan dukungan untuk hidupku.

9. Dek ayoe yang telah menemani saat-saat akhir penulisan, Gimbo yang telah memberikan pelajaran hidup yang sangat berharga.

ix

kasih atas keceriaan selama kuliah bareng.

13.Anak-anak kos Pake : Kelik, Asok, Sandex, Mas Jo, Usup, Ijuk, Uduk, Otonx, Mas Wawan yang telah banyak memberikan banyak bantuan selama pengerjaan skripsi ini.

14.Komunitas Kodox Ijo : Didied, Gon-gon, Don Pelikpo, Topan, Tpe, Baiban, yang telah memberikan banyak masukan mengenai pengerjaan skripsi.

15.Personil kos Rafli : Moestapa, Tora, mehonx, Fajar, Briti, dan Kang Moejhi yang selalu memberikan semangat dan juga Anggey n Ana atas nasehat-nasehatnya.

16. Angota-anggota ITI : Gondrong , RT, Betut, Sumin, Gawer, Leo, Ooz, Jaja, dogox, Lili, lia dan anggota-anggota yang lainnya yang telah memberikan banyak pengetahuan tentang sintak-sintak program dan software.

17.Anak-anak KKN : Soesoeh, Poli, Desi, Evi, Lusi, Lian, Helen, Reni makasih untuk kekompakan dan semangatnya.

18.Gank Psycho : Cazanopa, Kotong, Tombir, Antoks, Yanu, Sobir, KampretZ, Gondel, Arex, Gendut (Teman kita yang telah berpulang, moga-moga diterima disisinya), Thika, Imel, Linda, Ling-ling, Utut, terima kasih atas persabatannya.

x

satu disini. Tiada yang sempurna, demikian juga skripsi ini. Masukan dan kritikan yang membangun untuk kesempurnaan skripsi ini menjadi kehormatan bagi penulis.

xi

HALAMAN JUDUL……….. i

HALAMAN JUDUL (INGGRIS)……….. i

HALAMAN PERSETUJUAN PEMBIMBING………... ii

HALAMAN PENGESAHAN………...………. iii

HALAMAN KEASLIAN KARYA………...……… iv

HALAMAN PERSEMBAHAN………... v

ABSTRAK………... vi

ABSTRACT……… vii

KATA PENGANTAR……… viii

DAFTAR ISI……….. xi

DAFTAR TABEL………. xiv

DAFTAR GAMBAR………. xv

BAB I PENDAHULUAN A. Latar Belakang……… 1

B. Perumusan Masalah……… 4

C. Pembatasan Masalah………... 4

D. Tujuan Penulisan………... 4

E. Metode Penulisan………... 5

xii

A. Variabel Random ……….... 7

B. Fungsi Probabilitas 1. Fungsi Distribusi Kumulatif Diskret………. 10

2. Fungsi Distribusi Kumulatif Kontinu……… 10

3. Fungsi Densitas……….. 10

C. Nilai Harapan dan Variansi……… 11

D. Distribusi Normal……… 14

E. Fungsi Variabel Random……… 22

F. Distribusi Lognormal……….. 27

G. Teorema Limit Pusat……….. 31

H. Interval Kepercayaan ……… 32

I. Simulasi Komputer………. 38

J. Penduga Densitas Kernel……… 44

K. Kuantil-Kuantil Plot……… 47

L. Teorema Limit Pusat Dalam Simulasi Komputer……….. 54

BAB III MODEL MATEMATIKA PERGERAKAN HARGA SAHAM A. Pergerakan Harga Saham……… 59

B. Model Matematis Harga Saham 1. Model Saham Diskret……… 68

2. Model Harga Saham Kontinu……… 69

xiii 1. Pola Pergerakan Harga Saham

dengan Skala Waktu yang Berbeda……….. 95

2. Jumlah Kuadrat Return………. 100

BAB IV APLIKASI PADA HARGA SAHAM INDONESIA Analisa harga saham Indonesia……… 108

BAB V PENUTUP A. Kesimpulan ………118

B. Saran………118

DAFTAR PUSTAKA……….119

xiv

Tabel 2.2.1 ………..………... 9

Tabel 2.3.1 ……….………... 12

Tabel 2.9.1 ……….……….. 41

Tabel 2.9.2 ………... 43

Tabel 3.1.1 ………... 65

xv

Gambar 2.4.1 ………... 16

Gambar 2.7.1 ……….. 34

Gambar 2.7.2 ……….. 37

Gambar 2.10.1 ……….………. 45

Gambar 2.10.2 ……….. 45

Gambar 2.10.3 ……….. 46

Gambar 2.10.4 ……….. 47

Gambar 2.11.1 ……….. 51

Gambar 2.11.2 ……….. 52

Gambar 2.11.3 ……….. 54

Gambar 2.12.1 ……….. 56

Gambar 2.12.2 ……….. 57

Gambar 3.1.1 ……….. 60

Gambar 3.1.2 ……….. 61

Gambar 3.1.3 ……….. 63

Gambar 3.1.4 ……….. 64

Gambar 3.1.5 ……….. 64

Gambar 3.1.6 ……….. 67

Gambar 3.1.7 ……….. 68

Gambar 3.2.1 ……….. 82

xvi

Gambar 3.3.3 ……….. 90

Gambar 3.3.4 ……….. 92

Gambar 3.3.5.1 ………... 92

Gambar 3.3.5.2 ……….. 93

Gambar 3.3.6 ………. 94

Gambar 3.3.7 ………. 94

Gambar 3.3.8 ………. 96

Gambar 3.3.9 ………. 101

Gambar 3.3.10 ………. 105

Gambar 3.3.11 ………. 105

Gambar 3.3.12 ………. 106

Gambar 3.3.13 ………. 106

Gambar 3.3.14 ………. 107

Gambar 4.1 ………. 108

Gambar 4.2 ………. 109

Gambar 4.3 ………. 109

Gambar 4.4 ………. 110

Gambar 4.5 ………. 110

Gambar 4.6 ………. 112

Gambar 4.7 ………. 113

xvii

Gambar 4.11 ………. 114

Gambar 4.12 ………. 116

A. Latar Belakang

Dalam kehidupan sehari-hari kadang dijumpai pemberitaan tentang saham,

pergerakan harga saham, investasi dalam bentuk saham, dan jual beli saham.

Tetapi belum tentu setiap orang tahu tentang definisi dan seluk beluk pergerakan

harga saham. Definisi saham itu sendiri adalah suatu obyek finansial yang

nilainya diketahui pada saat ini, tetapi dapat berubah pada masa yang akan datang.

Harga saham pada dasarnya digunakan sebagai ukuran kepercayaan seorang

investor. Hal ini akan dipengaruhi faktor-faktor yang ada seperti berita yang

sedang berkembang, keadaan geografis, desas-desus, spekulasi dan lain

sebagainya. Pergerakan harga saham yang sedang berkembang menggambarkan

semua informasi untuk diketahui investor dan semua perubahan pada harga akan

memberikan informasi baru (hipotesis efisiensi pasar). Menurut hipotesis efisiensi

pasar, jika ingin memprediksi harga saham untuk masa yang akan datang maka

harus diketahui secara lengkap tentang sejarah dari data harga saham sebelumnya

dan faktor-faktor lain seperti keadaan perusahaan, keadaan geografis, spekulasi

dan lain sebagainya. Tetapi pada pembahasan kali ini hanya akan digunakan

sejarah dari data harga saham sebelumnya untuk memprediksi pergerakan harga

saham. Karena pergerakan harga saham pada dasarnya tidak dapat diprediksi

tersebut. Definisi dari model matematika itu sendiri adalah representasi simbolik

yang melibatkan formulasi matematika.

Jika diberikan harga saham S0 pada saat t = 0, tujuannya adalah untuk

membuat model matematika yang mendeskripsikan harga saham S(t) pada waktu t

(0 ≤t ≤T). Seperti yang telah disebutkan diatas, karena pergerakan harga saham

pada dasarnya tidak dapat diprediksi secara pasti, maka S(t) merupakan sebuah

variabel random untuk setiap t. Meskipun harga saham biasanya dibulatkan

menjadi satu atau dua tempat desimal, diasumsikan bahwa harga saham memiliki

nilai ≥ 0. Model harga saham ada dua macam model yaitu model saham diskret

dan model saham kontinu.

Pada perubahan yang tidak dapat diprediksi secara pasti akan ditambahkan

sebuah kenaikan fluktuasi random pada persamaan. Supaya tepat dimisalkan ti =

iδt, dimana δtadalah interval waktu kecil, sehingga harga saham dapat ditentukan

pada titik-titik diskret {t_i}.

Model waktu diskretnya adalah,

S(ti+1) = S(ti) + µ δtS(ti) + σ δtYiS(ti) , dimana

• µ adalah parameter konstan (biasanya µ > 0, sehingga µδtS(ti)

menggambarkan sebuah pergerakan naik pada harga saham).

• σ ≥ 0 adalah parameter konstan yang menentukan kekuatan fluktuasi

random, dan disebut volatilitas.

• Y0,Y1,Y2,…adalah bilangan random yang berdistribusi identik dan

Untuk mendapatkan sebuah model perubahan relatif dalam interval waktu δt,

dimisalkan δt → 0 dengan tujuan untuk mendapatkan sebuah model yang valid

untuk t yang kontinu dalam interval 0 ≤ t ≤ T . Pergerakan harga saham yang

diberikan pada bursa-bursa saham pada dasarnya pergerakan secara diskret tetapi

semakin kecil interval perubahan waktunya, harga saham tidak lagi bersifat

diskret. Oleh karena itu pergerakan harga saham akan didekatkan pada model

saham kontinu.

Misalkan interval waktu [0, t] dengan t = Lδt. Diketahui S(0) = S0, dan dari

model diskret diperoleh S(δt), S(2δt), .., S(Lδt=t).

Maka model waktu kontinunya pada saat t adalah

S(t) = S eµ−2σ )t+σ tZ 1

( 0

2

, dimana Z berdistribusi N(0,1).

Kemudian model matematis tersebut disimulasikan. Pertama-tama akan

digunakan komputer untuk membangkitkan bilangan random dan dari bilangan

random ini digunakan untuk membangkitkan nilai variabel random. Kemudian

akan ditunjukkan bagaimana menggunakan variabel random untuk

B. Perumusan Masalah

Masalah yang akan dibahas pada skripsi ini adalah :

1. Bagaimana menyusun model saham kontinu dari model saham diskret?

2. Bagaimana cara menyimulasikan model matematika dari pergerakan harga

saham?

3. Bagaimana mengaplikasikan model tersebut pada pergerakan harga saham

di Indonesia?

C. Pembatasan Masalah

1. Teorema Limit Pusat tidak dibuktikan.

2. Model yang akan dibahas dalam skripsi ini hanya model return harga

saham, model harga saham diskret dan model harga saham kontinu.

3. Hanya akan digunakan sejarah dari data harga saham untuk menganalisa

pergerakan harga saham.

4. Program yang digunakan adalah Exel, SPSS, dan Matlab.

5. Grafik frekuensi relatif, penduga densitas kernel dan grafik kumulatif pada

bab II dan bab III berupa histogram, tetapi karena keterbatasan Matlab

maka tampak seperti grafik bar.

D. Tujuan Penulisan

Tujuan dari penulisan dari skripsi ini adalah untuk membuat model

simulasi tersebut pergerakan suatu saham dapat dianalisa, sehingga dapat

diperoleh prediksi pergerakannya untuk waktu yang akan datang.

E. Metode Penulisan

Penulisan skripsi ini menggunakan metode studi pustaka, yaitu dengan

menggunakan buku-buku, jurnal, dan makalah yang telah dipublikasikan,

sehingga tidak ditemukan hal baru.

F. Manfaat Penulisan

Manfaat dari penulisan skripsi ini adalah dapat dipahami hubungan model

saham diskret dan model saham kontinu. Selain itu pembaca dapat juga

memperoleh prediksi tentang pergerakan harga saham untuk waktu yang akan

datang.

G. Sistematika Penulisan

BAB I: PENDAHULUAN

Dalam bab I dibahas tentang latar belakang, perumusan

masalah, pembatasan masalah, tujuan penulisan, metode

BAB II: LANDASAN TEORI

Dalam bab II akan dibahas tentang variabel random, fungsi

probabilitas, nilai harapan dan variansi, distribusi normal,

fungsi variabel random, distribusi lognormal, teorema limit

pusat, interval konvidensi, simulasi komputer, penduga

densitas kernel, kuantil-Kuantil plot, dan teorema limit pusat

dalam simulasi komputer.

BAB III: MODEL MATEMATIKA DAN SIMULASI

PERGERAKAN HARGA SAHAM

Dalam bab III ini akan dibahas tentang pergerakan harga

saham, model matematika harga saham dan juga komputasi

aset path.

BAB IV: APLIKASI PADA HARGA SAHAM INDONESIA

Dalam bab IV ini akan diberikan contoh analisa data harga

saham yang ada di Indonesia dengan menggunakan model

harga saham dan komputasi asset path.

BAB V: PENUTUP

Dalam bab V ini akan diberikan tentang kesimpulan dan

A. Variabel Random

Gagasan untuk mendefinisikan sebuah fungsi yang dikenal dengan

variabel random timbul karena model-model matematika diekspresikan dalam

bentuk nilai-nilai numeris daripada hasil percobaan asli seperti sisi, warna, atau

yang lain.

Definisi 2. 1.1:

Variabel random, misalnya X adalah fungsi yang didefinisikan pada ruang sampel

S, yang memetakan setiap elemen e∈S kebilangan real.

Notasi : X(e)=x, e∈S

x∈R

Untuk lambang variabel random digunakan huruf-huruf kapital X, Y, Z,

sedangkan untuk melambangkan nilai variabel random yang mungkin, digunakan

huruf-huruf kecil yang bersesuaian seperti x, y, z.

Contoh 2. 1.1:

Jika seseorang melempar dua buah dadu secara bersamaan maka,

ruang sampel S = {(i,j)}| i,j∈{1, 2, 3, 4, 5, 6}}.

Variabel random X menyatakan jumlah bilangan yang muncul pada kedua buah

dadu maka X(i,j) = i + j, sehingga X(1,2) = 1 + 2 = 3

Konsep variabel random dapat dipahami sebagai sebuah pemetaan dari

himpunan S kehimpunan bilangan bilangan real. Kemudian konsep ini dipakai

untuk menghitung peluang timbulnya suatu kejadian.

Dengan mengambil contoh 2.1.1, didefinisikan kejadian memperoleh jumlah

bilangan maksimal 3. Titik-titik sampel kejadian ini dapat dituliskan sebagai Y =

2,3 atau Y∈{2,3} atau dapat pula dinyatakan dalam interval Y ={y|y≤3}.

Dengan probabilitas :

12 1 36

3 )) 1 , 2 ( ), 2 , 1 ( ), 1 , 1 (( ) 3

(Y ≤ =P = =

P .

Variabel Random Diskret Dan Variabel Random Kontinu Definisi 2. 1.2:

Variabel random diskret adalah variabel random yang nilainya berhingga atau

takberhingga terbilang, selain ini disebut variabel random kontinu.

Contoh 2.1.2:

variabel random diskret :

o X = Banyaknya kecelakaan mobil dalam waktu satu tahun di

Yogyakarta.

o S = Frekuensi denyut jantung permenit. variabel random kontinu :

Contoh variabel random kontinu adalah M = lamanya permainan catur dalam satu

babak. Meskipun dalam kenyataannya biasa diukur waktu hanya dengan satuan

terdekat seperti menit atau detik, seara teoritik dapat diukur waktu dengan

B. Fungsi Probabilitas Definisi 2.2.1:

Fungsi f(xi) = P(X = xi), i = 1, 2, 3,… yang menyatakan probabilitas untuk

semua kemungkinan nilai variabel random diskret X disebut fungsi probabilitas.

Fungsi probabilitas tersebut dapat dinyatakan dalam rumus fungsi atau tabel yang

memuat pasangan nilai variabel random x berikut dengan peluangnya yang

disebut distribusi probabilitas.

Contoh 2.2.1:

Sebuah koin dilemparkan sebanyak 2 kali dan X adalah variabel random yang

menyatakan banyaknya muka yang diperoleh. Variabel random X yang memiliki

distribusi probabilitas sebagai berikut :

Tabel 2.2.1 Tabel distribusi probabilitas

X 0 1 2

P(X=x)

4 1

2 1

4 1

Definisi 2.2.2 :

Probabilitas dari a ≤ X ≤ b ditentukan oleh integral f(x) dengan batas bawah x = a

dan batas atas x = b, dengan X adalah variabel random kontinu dan f adalah fungsi

P(a≤ X ≤b) =

∫

b

a

dx x

f( ) . (2.1)

1. Fungsi Distribusi Kumulatif Diskret Definisi 2.2.3:

Fungsi distribusi kumulatif suatu variabel random diskret X didefinisikan sebagai

F(x) = P(X≤x) untuk semua nilai real x.

Kadang-kadang fungsi F(x) disebut juga fungsi distribusi.

2. Fungsi Distribusi Kumulatif Kontinu Definisi 2.2.4:

Fungsi distribusi kumulatif suatu variabel random X, dengan fungsi densitas f(x)

didefinisikan sebagai :

F(x) =

∫

∞ −

x

dt t

f( ) (2. 2)

Fungsi densitas f(x) merupakan derivatif dari F(x).

3. Fungsi Densitas

Pada fungsi distribusi yang mengandung titik-titik terputus yang berhingga

banyaknya, loncatan yang terdapat pada suatu titik terputus merupakan

probabilitas timbulnya variabel random X pada titik tersebut. Kemudian dapat

pula disimpulkan bahwa pada ruang sampel kontinu, peluang timbulnya variabel

peluang suatu variabel random kontinu selalu dinyatakan dalam peluang bernilai

dalam interval.

Definisi 2.2.5:

Fungsi f(x) disebut fungsi densitas bagi variabel random kontinu X bila dan hanya

bila memenuhi syarat :

( i ) f(x)≥0 untuk semua nilai x real

( ii )

∫

∞ ∞ −

=1 ) (x dx f

C. Nilai Harapan

Konsep nilai harapan memegang peranan yang sangat penting dalam

statistika. Contoh yang paling mudah adalah mean dan variansi suatu variabel

random. Keduanya adalah parameter-parameter yang hampir selalu muncul dalam

teknik-teknik analisis statistika elementer maupun lanjut. Yang dimaksud dengan

nilai harapan dinyatakan dalam definisi berikut,

Definisi 2.3.1:

E(X) =

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧

∫ ∑

∞

∞ −

=

) ( densitas fungsi

dengan kontinu X jika , ) (

) ( as probabilit fungsi

dengan diskret x jika ), (

1

x f dx

x xf

x p x

p x

n

i i i

_(2.3)

Ditinjau dari segi variabel random yang diskret, maka nilai harapan E(X)

merupakan suatu nilai fungsi linear dari semua unsur didalam domain fungsi

Contoh 2.3.1:

Dalam pelemparan sebuah mata dadu setimbang sebanyak satu kali, kita akan

menerima uang sebanyak titik pada sisi yang tampak. Untuk bermain satu kali

lemparan kita harus membayar c rupiah. Pertama-tama kita perhatikan bahwa

hadiah yang kita terima tiap permainan adalah variabel random dengan distribusi

probabilitas sebagai berikut :

Tabel 2.3.1 Tabel distribusi probabilitas

Hadiah X 1 2 3 4 5 6

P(X=x) 1/6 1/6 1/6 1/6 1/6 1/6

E(X) = 1.1/6 + 2. 1/6 + 3. 1/6 + 4. 1/6 +5. 1/6 + 6. 1/6 = 3,5 rupiah

Berapa rupiah yang harus kita bayar agar permainan tersebut adil ?

Permainan disebut adil jika c = 3, 5 rupiah. Dengan demikian rata-rata hadiah

yang kita terima sama dengan banyaknya uang yang kita bayarkan untuk bermain.

Nilai harapan E(X) = 3, 5 dapat diinterprestasikan sebagai berikut : “ jika

permainan itu dapat diulang sebanyak-banyaknya, maka perbandingan antara

jumlah hadiah dengan banyaknya kali permainan adalah 3, 5”.

Sifat-sifat Nilai Harapan Definisi 2.3.2:

Jika X adalah variabel random dan g(x) adalah fungsi dari variabel random X

E[g(X)] =

⎪⎩

⎪

⎨

⎧∑

∫

= ∞

∞ −

n

i

i

i p x p x

x g

x f dx

x f x g

1

) ( as probabilit fungsi

dengan diskret X jika ), ( ) (

) ( densitas fungsi dengan kontinu X jika , ) ( )

( (2.4)

Teorema 2.3.1:

Jika X adalah variabel random dengan fungsi densitas f(x), a dan b konstanta, g(x)

dan h(x) fungsi-fungsi variabel random berharga real, maka

E[ag(x) + bh(x)] = a E[(g(x)] + b E[h(x)] (2. 5)

Bukti :

Jika X adalah variabel random kontinu maka menurut definisi nilai harapan

E[ag(x)+bh(x)] =

∫

∞

∞ −

+bh x f x dx x

ag( ) ( )] ( ) [

= a

∫

∫

∞ ∞ −

∞ ∞ −

+b h x f x dx dx

x f x

g( ) ( ) ( ) ( )

= aE[g(x)] + bE[h(x)] ▄

Definisi 2.3.3:

Variansi variabel random X adalah :

Var(X) = E[(x-µ)2] (2. 6)

Sifat-sifat lain nilai harapan :

Untuk a dan b bilangan konstan maka berlaku

1. E(a) = a

3. E(X + a) = E(X) + a

4. E(bX + a) = b E(X) + a

Sifat-sifat lain variansi :

Untuk a dan b bilangan konstan maka berlaku

1. Var(X) tidak negatif

2. Var(X + a) = Var(X)

3. Var(bX) = b2 Var(X)

4. Var(bX + a) = b2 Var(X)

Definisi 2.3.4:

Fungsi Gamma ditulis Γ(k), untuk semua k>0 didefinisikan sebagai

dt e t k

∫

k t

∞ − −

= Γ

0 1

)

( (2.7)

Fungsi Gamma memenuhi sifat-sifat :

π

= Γ

− = Γ

− Γ − = Γ

) 2 / 1 (

)! 1 ( ) (

) 1 ( ) 1 ( ) (

n n

k k

k

k>1, dan n = 1, 2, .. (2.8)

D. DISTRIBUSI NORMAL

Distribusi normal sangat penting baik dalam statistika teori maupun

terapan. Distribusi ini pertama kali dipelajari pada abad kedelapan belas, ketika

orang mengamati galat pengukuran berdistribusi simetrik dan berbentuk bel. De

sebagai bentuk limit distribusi binomial. Laplace juga telah mengenal distribusi

ini sebelum tahun 1775. Gauss menurunkan persamaan distribusi ini dari suatu

studi tentang galat dalam pengukuran yang berulang-ulang dari kuantitas yang

sama, dan mempublikasikannya pada tahun 1809. Untuk menghormatinya

distribusi normal juga dikenal sebagai distribusi Gauss. Pada abad kedelapan

belas dan sembilan belas, berbagai usaha telah dilakukan untuk membuat

distribusi ini sebagai hukum probabilitas yang mendasari semua variabel kontinu,

maka digunakan nama distribusi normal.

Definisi 2.4.1:

Suatu variabel random kontinu X dikatakan berdistribusi normal dengan mean µ

dan variansi σ2, apabila variabel itu mempunyai fungsi probabilitas yang

berbentuk

f(x) =

2

2( )

2 1

2

1 _σ µ

π σ

−

− x

e (2.9)

dengan

∞ < < ∞

− X σ >0

∞ < < ∞

− µ π =3,14dan e=2,718.

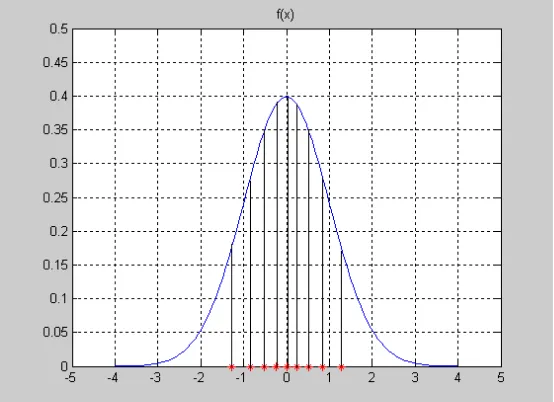
Jika fungsi probabilitas itu digambar, maka kita peroleh grafik seperti dalam

Gambar 2.4.1. : kurva normal dengan mean µ dan variansi σ2

Berikut ini akan ditunjukkan bahwa distribusi normal memenuhi siat-sifat fungsi

densitas.

Pertama, harus ditunjukkan bahwa integral dari fungsi densitas normal adalah 1.

Kedua, harus ditunjukkan bahwa µ dan σ2 adalah mean dan variansi dari X.

Dengan mensubstitusikan σ

µ

− = x

z dan dx = σdz, didapat :

I = f x dx e z dz e z /2dz

0 2

/ 2

2

2 1 2 2

1 )

, ;

( −

∞ −

∞ ∞ −

∞ ∞

−

∫

∫

=

∫

=

π π

σ µ

Bila dimisalkan w = z2/2, maka z = 2w dan dz = (w-1/2/ 2 )dw, sehingga

I = w e−wdw

∞ −

∫

0

2 / 1

π

Dengan menggunakan fungsi Gamma didapat,

I=Γ(1/2)=1 π

Integran yang diperoleh dengan mensubstitusikan σ

µ

− = x

z memegang peranan

yang sangat penting dalam menentukan probabilitas variabel random normal.

Perhitungan menjadi lebih sederhana karena nilai probabilitas telah ditabelkan.

Fungsi densitas hasil transformasi dari X ke Z disebut Distribusi normal standar

yang fungsinya,

φ = − −∞< <∞

z e

z z ,

2 1 )

( 2

π

Berikut ini dengan menggunakan persamaan (2.3) akan dicari nilai harapan dan

variansi dari variabel random X yang berdistribusi normal.

E(X) = x x dx

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − −

∫

∞ ∞ − 2 2 1 exp 2 1 σ µ π σ

Misal z = σ

µ

−

x

maka x = σz + µ dan dx = σdz sehingga diperoleh

E(X) = x e zσdz

π σ 2 2 1 2 1 − ∞ ∞ −

∫

= x e z dz

2 2 1 2 1 − ∞ ∞ −

∫

π

= z e z dz

2 2 1 2 1 ) ( − ∞ ∞ −

∫

+ π µ σ

=

∫

z e z dz

∫

e z dz

∞ ∞ − − − ∞ ∞ − + 2 2 2 1 2 1 2 1 _µ π σ

= 1

2 1 2 2 1 ⋅ + − ∞ ∞ −

∫

µ π

σ z e z dz

jika dimisalkan, -1/2z2 = w maka z = 2w dan z dz = -dw

atau dz = z dw

= w dw

E(X) = µ π σ + −

∫

∞ ∞ − dz e z z 2 2 1 2 1 = µ π σ + −

∫

∞ ∞ − dw ew 2 1 = µ π σ ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + −

∫

∫

∞ − ∞ 0 0

2 e dw e dw

w w =

]

]

µ π σ ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − − ∞ ∞ − − 0 2 1 0 2

1 2 2

2 z z e e =

(

)

µ π σ _{− + − +} − ₍ −∞_{) (} −∞ ₎ 2 0

0 _{e e e}

e

= 0 + µ

= µ (2.10)

E(X2) = x x dx

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − −

∫

∞ ∞ − 2 2 2 1 exp 2 1 σ µ π σ

Misal, z = σ

µ

−

x

maka x = σz + µ dan σdz = dx sehingga diperoleh

E(X2) =

∫

x e z dz

∞ ∞ − − σ π σ 2 2 1 2 2 1

=

∫

z e z dz

∞ ∞ − − + 2 2 1 2 2 ) ( π µ σ

= z z e z dz

2 2 1 2 2 2 2 ) 2 ( − ∞ ∞ −

∫

+ + π µ µσ σ =

∫

∫

∫

∞ ∞ − − − ∞ ∞ − − ∞ ∞ − +

+ ze dz e dz

dz e

z z2 z2 z2

=

0

1

2

2 2 1 2 2 2

⋅

+

+

− ∞ ∞ −

∫

µ

π

σ

dz

e

z

z =

∫

∞ ∞ − − + 2 2 1 2 2 2

2π µ

σ

dz e z z

misal ½ z2 = w maka z = 2w dan z dz = dw sehingga diperoleh

E(X2) =

w dw e w w 2 2 2 2

∫

∞ ∞ − − π σ

+ µ2

=

∫

w e wdw

∞ ∞ − − 2 1 2 π σ

+ µ2

=

∫

w e wdw

∞ − 0 2 1 2 2 π σ

+ µ2

dengan menggunakan persamaan (2.7) dan (2.8) didapatkan

E(X2) =

∫

w e wdw

∞ − 0 2 1 2 2 π σ

+ µ2

= 2 (3/2)

2 Γ

π σ

+ µ2

= (1/2)

2 1

2 2 _Γ

π σ

+ µ2

= π π σ 2 1 2 2

+ µ2

= σ2 + µ2. (2.11)

Dengan menggunakan persamaan (2.6) maka

Var(X) = E(X2) – [E(X)]2

Sekarang akan dicari nilai E(X4)

E(X4) = x x dx

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − −

∫

∞ ∞ − 2 4 2 1 exp 2 1 σ µ π σ

Misal, z = σ

µ

−

x

maka x = σz + µ dan σdz = dx sehingga diperoleh

E(X4) =

∫

x e z dz

∞ ∞ − − σ π σ 2 2 1 4 2 1

=

∫

z e z dz

∞ ∞ − − + 2 2 1 4 2 ) ( π µ σ

= z z z z e z dz

2 2 1 4 3 2 2 2 3 3 4 4 2 ) 4 6 4 ( − ∞ ∞ −

∫

+ + + + π µ µ σ µ σ µσ σ

= z e z dz z e z dz z e z dz

2 2 2 2 1 2 2 2 2 1 3 3 2 1 4 4 2 6 2 4 2 − ∞ ∞ − − ∞ ∞ − − ∞ ∞ −

∫

∫

∫

+ + π µ σ π µσ π σ

∫

∫

∞ ∞ − − − ∞ ∞ − +

+ z e z dz e z dz

2 2 2 1 4 2 1 3 2 2 4 π µ π µ σ ………. *

untuk

∫

∫

∞ ∞ − − − ∞ ∞ − = 2 2 2 1 4 4 2 1 4 4 2 2 z z e z dz e z π σ π σ dz

misal ½ z2 = w maka z = 2w dan z dz = dw maka ruas kanan bagian pertama

persamaan * menjadi

∫

∫

∞ ∞ − − ∞ ∞ − − = w dw e w dz e

z z w

2 4 2 2 2 4 2 1 4 4 2 π σ π σ =

∫

∞ ∞ − − w dw e w2 w

4

=

∫

∞ ∞ − − _dw e w2 w

3 4 2 π σ =

∫

∞ − 0 2 3 4 4 dw e w w π σ

dengan menggunakan persamaan (2.7) dan (2.8) didapatkan

∫

z e z dz

∞ ∞ − − 2 2 1 4 4 2π σ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ 2 5 4 4 π σ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ 2 3 2 3 4 4 π σ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ 2 1 2 1 6 4 π σ

= 4

4 4 3 3 2 1

3 _{π σ}

π σ π σ _{= =} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ

untuk

∫

∫

∞ ∞ − − − ∞ ∞ − = 2 2 2 1 3 3 2 1 3 3 2 4 2

4 z z

e z dz e z π µσ π µσ dz

misal ½ z2 = w maka z = 2w dan z dz = dw maka ruas kanan bagian kedua pada

persamaan * menjadi

( )

∫

∫

∞ ∞ − − ∞ ∞ − − = w dw e w w dz e

z z w

2 2 2 2 4 2 4 2 1 3 2 1 3 3 2 π µσ π µσ =

∫

∞ ∞ − − dw we w π µσ 2 8 3 =

∫

∞ − 0 3 2 16 dw we w π µσ

=

( )

2

2

16 3_Γ

π µσ

= 1

( )

1

2

16 3 _Γ

π µσ

= 0

( )

0

2

16 3 _Γ

π µσ

= 0

untuk z e z dz

2 2 1 2 2 2 2 6 − ∞ ∞ −

∫

π µ σ

misal ½ z2 = w maka z = 2w dan z dz = dw maka ruas kanan bagian

ketiga pada persamaan * menjadi

dz e

z z2

2 1 2 2 2 2 6 − ∞ ∞ −

∫

π µ σ = w dw e w w 2 2 2

6 2 2 ∞ −

∞

−

∫

dz e z z2

2 1 2 2 2 2 6 − ∞ ∞ −

∫

π µ σ

= w e−wdw

∞ ∞ −

∫

2 1 2 2 6 π µ σ

= w e−wdw

∞

∫

0 2 1 2 2 12 π µ σ

dengan persamaan (2.7) dan (2.8) didapatkan

dz e z z2

2 1 2 2 2 2 6 − ∞ ∞ −

∫

π µ σ

= 12 (3/2)

2 2 Γ π µ σ

= (1/2) 2 1

12 2 2 _Γ

π µ σ = π π µ σ 2 1 12 2 2

= 6σ2µ2

untuk z e z dz

2 2 1 3 2 4 − ∞ ∞ −

∫

π µ σ = 0

untuk

∫

∞ ∞ − − dz e z 2 2 1 4 2π µ

= µ4

Jadi E(X4) = z e z dz z e z dz z e z dz

2 2 2 2 1 2 2 2 2 1 3 3 2 1 4 4 2 6 2 4 2 − ∞ ∞ − − ∞ ∞ − − ∞ ∞ −

∫

∫

∫

+ + π µ σ π µσ π σ

∫

∫

∞ ∞ − − − ∞ ∞ − +

+ z e z dz e z dz

2 2 2 1 4 2 1 3 2 2 4 π µ π µ σ

= ₃σ4₊ 2 2

6σ µ +µ4

Sehingga nilai

E(X4) = 3σ4+ 6σ2µ2+µ4. (2.13)

E. Fungsi Variabel Random

Salah satu tujuan dari statistika adalah membuat kesimpulan tentang

populasi berdasarkan informasi yang terdapat dalam sampel dan menentukan

ukuran yang sesuai untuk menarik kesimpulan. Topik fungsi variabel random

yang dipakai untuk menduga dan mengambil kesimpulan tentang parameter

merupakan fungsi dari n buah pengamatan random yang terdapat dalam sampel.

Sebagai gambaran, dalam masalah pendugaan rata-rata populasi, dari

sampel random berukuran n akan didapatkan pengamatan y1, y2, .., yn. Maka akan

digunakan rata-rata sampel

n y y

n

i i

∑

=

= 1 _(2.14)

sebagai penduga rata-rata populasi µ. Pertanyaan yang dapat diajukan adalah

seberapa baikah y sebagai panduga dariµ. Jawabannya tergantung pada sifat

dari variabel random Y1, Y2, .., Yn.

Kebaikan dari suatu penduga dapat diukur, misalnya dengan kesalahan

pendugaan, yaitu selisih antara penduga dan parameter yang diduga (dalam hal ini

y dan µ). Karena Y1, Y2, .., Yn adalah variabel-variabel random dalam sampel

berulang, maka Y adalah juga variabel random yang merupakan fungsi dari Y1,

Y2, .., Yn. Dengan demikian, tidak dapat ditentukan secara pasti bahwa kesalahan

pendugaan akan kurang dari suatu bilangan tertentu, misalnya B. Akan tetapi, jika

dapat ditentukan distribusi probilitas dari Y, maka distribusi ini dapat dipakai

untuk menentukan probabilitas bahwa kesalahan pengukuran kurang dari atau

sama dengan B.

Untuk menentukan distribusi probabilitas dari fungsi suatu variabel Y1,

Y2, .., Yn harus ditemukan terlebih dahulu distribusi probabilitas bersama dari

diperoleh berdasarkan pengambilan sampel secara random. Hal ini berarti bahwa

pengambilan sampel dari populasi berhingga akan menghasilkan percobaan yang

tidak bebas, tetapi percobaan ini secara esensial menjadi percobaan bebas jika

ukuran populasi relatif besar dibandingkan dengan ukuran sampelnya.

Pada pembahasan selanjutnya akan diasumsikan bahwa populasi

berukuran relatif besar terhadap sampel, sehingga variabel random yang terkait

saling bebas satu dengan yang lainnya. Dengan demikian, baik untuk variabel

random diskret maupun kontinu, distribusi probabilitas bersama Y1, Y2, .., Yn yang

berasal dari populasi yang sama adalah

f(y1, y2, .., yn) = p(y1)p(y2)..p(yn)

Selanjutnya pernyataan “Y1, Y2, .., Yn adalah sampel random dari f(y)”

diartikan sebagai “variabel-variabel random Y1, Y2, .., Yn adalah saling bebas

dengan distribusi bersama f(y)”.

Menentukan Distribusi Probabilitas Fungsi Variabel Random

Untuk menentukan distribusi probabilitas suatu fungsi variabel random

dapat ditempuh dengan 3 metode, yaitu metode fungsi distribusi, metode

transformasi, dan metode fungsi pembangkit momen. Dalam skripsi ini akan

digunakan metode transformasi satu-satu untuk menentukan distribusi probabilitas

suatu fungsi variabel random.

Metode Tranformasi satu-satu

Pertama-tama diasumsikan tranformasi variabel-variabel dalam satu

y = u(x) mempunyai persamaan tunggal, misalnya x = w(y), maka tranformasi

tersebut adalah tranformasi satu-satu.

Teorema 2.5.1:

Andaikan X adalah variabel random diskret dengan distribusi probabilitas fx(x)

dan Y = u(x) mendefinisikan trnsformasi satu-satu. Dengan kata lain persamaan Y

= u(x) mempunyai penyelesaian tunggal x = w(y). Maka distribusi probabilitas

dari Y adalah

Fy(y) = fx(w(y)) y∈B = {y|fy(y)>0} (2.15)

Bukti :

Fy(y) = P[Y=y] = P[u(X)=y]=P[X=w(y)]=fx(w(y)) ▄

Contoh 2.5.1:

Andaikan X~GEO(p), yaitu

Fx(x) = pqx-1 x = 1, 2, 3, ..

Tentukan distribusi probabilitas dari Y = X-1

Jawab :

Y = X-1, maka u(x)= x-1, w(y) = y+1, sehingga fy(y) = fx(y+1) = pqy, y = 0, 1, 2, ..

Teorema 2.5.2:

Andaikan X adalah variabel random kontinu dengan fungsi densitas fx(x), dan

Y=u(x) mendefinisikan transformasi satu-satu A = {x| fx(x)>0} ke B = {y|

fy(y)>0} dengan transformasi invers x = w(y). Jika turunan (d/dy)w(y) kontinu

dan tak nol pada B, maka fungsi densitas dari Y adalah

Fy(y) = fx(w(y)) w(y)

dy d

Bukti :

Jika y=u(x) adalah fungsi satu-satu, maka ada dua kemungkinan yaitu monoton

naik atau turun.

Pada kasus monoton naik, u(x) ≤y bila dan hanya bila x≤w(y). Sehingga

FY(y) = P[u(X)≤y] = P[X≤w(y)] = Fx(w(y)), akibatnya

fY(y) = ( ( )) ( )

) ( )) (

( w y

dy d y w F y dw

d y

w F dy

d

x

x =

= fx(w(y)) w(y)

dy d

, karena dalam kasus ini (d/dy)w(y)>0

Pada kasus monoton turun, u(x) ≤y bila dan hanya bila w(y) ≤ x. Sehingga

FY(y) = = P[u(X)≤y] = P[X≥w(y)] = 1-Fx(w(y)), dan

fY(y) = ( ( )) w(y)

dy d y w f_x

−

= ( ( )) w(y)

dy d y w

f_x , karena dalam kasus ini (d/dy)w(y)<0 ▄

Turunan dari w(y) disebut sebagai Jacobian dari transformasi dan disimbolkan

dengan J = (d/dy)w(y). Dapat dilihat pula bahwa mentransformasi variabel

kontinu ekuivalen dengan mengganti variabel dalam integral, sehingga metode

transformasi disebut juga metode penggantian peubah.

Contoh 2.5.2:

Andaikan variabel random X mempunyai distribusi

∞ < < −

= _e− _x

x

F x

x( ) 1 ,0

2

Jawab :

Dapat ditunjukkan bahwa fx(x) = 2e-2x, karena Y = ex maka transformasi inversnya

x = w(y) = ln(y), J = w’(y) = 1/y, sehingga dengan menggunakan persamaan

(2.16) didapatkan

fx(y) = fx(ln y)

y

1

= _⎟⎟ < <∞

⎠ ⎞ ⎜⎜ ⎝ ⎛

−

y y

e y 1 , 1 2 2ln

= 2y-3, y∈B = (1, ∞)

F. Distribusi Lognormal Teorema 2.6.1:

Jika X adalah variabel random yang berdistribusi normal dengan mean µ dan

variansi σ2, dan jika X = ln y, maka fungsi densitas untuk Y adalah

f(y) =

⎪⎩

⎪

⎨

⎧

− − _{, >0}

2 1

, 0

2 2 / 2 )

(ln _y

e y

selainnya

y µ σ

π σ

(2.17)

Bukti :

Fungsi probabilitas dari distribusi normal adalah

f(x) =

2

2( )

2 1

2

1 µ

σ π σ

−

− x

e . ………. **

Dengan menggunakan persamaan (2.16) akan didapatkan fungsi densitas untuk Y.

fx(x) =

2

2( )

2 1

2

1 _σ µ

π σ

−

− x

Jika x = ln Y maka persamaan ** menjadi

fx(ln y) =

2

2(ln )

2 1

2

1 _σ µ

π σ

−

− y

e

X = w(y) = ln y

w’(y) = 1/y

fy(y) = fx(w(y)) w(y)

dy d

fy(y) = fx(ln y)

y

1

=

2

2(ln )

2 1

2

1 _σ µ

π σ − − y e _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ y 1 f(y) = 2

2(ln )

2 1 2 1 µ σ π σ − − y e y ▄

Sekarang akan dicari nilai harapan dan variansi dari distribusi lognormal tersebut.

E(Y) = e dy

y y y 2 ln 2 1 2

1 − ⎜_⎝⎛ − ⎟_⎠⎞ ∞ ∞ −

∫

σ µ π

σ = e dy

y 2 ln 2 1 2 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ∞ ∞ −

∫

σ µ π σ

misal z = σ

µ

−

y

ln

maka y = _eσz+µ _{dan dy =} σ_eσz+µ_{dz sehingga diperoleh}

E(Y) = e z e z dz

2

2 1

2

1 ₊ −

∞ ∞ −

∫

_σ σ µ π σ

= e z e z dz

2

2 1

2

1 ₊ −

∞ ∞ −

∫

σ µ

π

= eµ e z σzdz

π + − ∞ ∞ −

∫

2 2

1

= e e 2(z 2 z)dz 1 2 2 1 σ µ π − − ∞ ∞ −

∫

= e e 2(z ) 2dz

1 2 2

2

1 σ σ

µ π + − − ∞ ∞ −

∫

misal w = z−σ maka z=w+σ dan dz = dw sehingga diperoleh

E(Y) = e e 2w 2dw

1 2 2

2 1 σ µ π + − ∞ ∞ −

∫

= e e w dw

2 2 2 1 2 2 1 − ∞ ∞ − +

∫

_π σ µ

misal v = 2 2 1

w maka w= 2v dan dw

( )

v 2dv

1

2 −

= sehingga diperoleh

E(Y) = dv

v e e v 2 1 2 1 2 0 2 2 − ∞ +

∫

_π σ µ

= e +

∫

∞ v−2e−vdv

1 0 2 1 2 π σ µ

= 2 1 (1/2)

2 Γ + π σ µ e = π π σ µ ₁ 2 2 + e

= 2

2 σ µ+

e (2.18)

E(Y2) = e dy

y y y 2 ) ln ( 2 1 2 2

1 _σ µ

π σ − − ∞ ∞ −

∫

= y e dy

y ₎2

ln ( 2 1

2

1 _σ µ

= x e dy

y ₎2

ln ( 2 1

2

1 _σ µ

π σ − − ∞ ∞ −

∫

misal z = σ

µ −

y

ln

maka y = eσz+µ dan dy = σeσz+µdz sehingga diperoleh

E(Y2) = σeσz µe z eσz µdz

π σ + − ∞ ∞ − +

∫

2 2

1

2 1

= e z e z dz

2 2 1 2 2 2

1 ∞ −

∞ −

+

∫

σ µ

π

= e e ze z dz

2 2 1 2 2 2

1 ∞ −

∞

−

∫

σ µ

π

= e µ e z σz dz

π 2 2 1 2 2 2

1 ∞ − + ∞

−

∫

= e e 2(z 4 z) dz

1 2 2 2 1 σ µ π − − ∞ ∞ −

∫

= e e z dz

2 2 2 ) 2 ( 2 1 2 2

1 σ σ

µ π + − − ∞ ∞ −

∫

misal w = z−2σ maka z = w+2σ dan dw = dz sehingga diperoleh

E(Y2) = e e w dw

2 2 2 2 1 2 2 1 σ µ π + − ∞ ∞ −

∫

= e e w dw

2 2 2 1 2 2 2

1 ∞ −

∞ − +

∫

π σ µ

misal v = 2 2 1

w maka w= 2v dan dv

v dw

2 1

= sehingga diperoleh

E(Y2) = dv

v e e v 2 1 2 1 2 0 2

2 2 −

= dv v e

e 1 v 1

0 2

2 2 −

∞ +

∫

π σ µ

= e e vv 2dv

1

0 2

2 2 1 − −

∞ +

∫

π σ µ

= π

π σ

µ 2 1

2 2 +

e

= e2µ+2σ2 (2.19)

Dengan menggunakan persamaan (2.6) maka didapatkan

Var (Y) = E(Y2) –

[

E

( )

Y

]

2

= e2µ+2σ2 ₍ 2 ₎2

2 σ µ+

− e

= e2µ+2σ2 −e2µ+σ2

= e2µ+σ2(eσ2 −1) (2.20)

G. Teorema Limit Pusat

Teorema berikut menyatakan bahwa rata-rata suatu sampel yang terdiri

dari n buah variabel random yang berdistribusi secara tidak normal tetapi identik

(Y₁,Y₂,...,Y_n memiliki fungsi densitas yang sama) serta bebas stokastik terhadap

sesamanya, distribusinya akan mendekati distribusi normal dengan bertambahnya

Teorema 2.7.1 (Teorema Limit Pusat) :

Andaikan Y₁,Y₂,...,Y_n adalah variabel-variabel random yang berdistribusi

bebas stokastik identik dengan E(Y_i)=µ dan variansinya _{( )}=σ2<∞ i

Y

V , maka

untuk n→∞

n Y Z_n

/

_

σ µ

−

= (2.21)

akan berdistribusi normal standar.

H. Interval Kepercayaan

Nilai pendugaan suatu parameter

^

θ berdasarkan penduga titik, bukanlah

suatu konstanta yang menunjukkan dengan tepat beberapa nilai yang sebenarnya

melainkan suatu variabel random. Apabila penyebaran

^

θ dapat diketahui, maka

dapatlah ditentukan suatu interval dengan peluang tertentu mencakup nilai

parameter

^

θ yang sebenarnya. Interval seperti ini disebut penduga interval atau

lebih dikenal dengan interval kepercayaan. Titik tertinggi dan terendah dari

interval kepercayaan disebut batas kepercayaan atas dan batas kepercayaan bawah.

Probabilitas dari interval kepercayaan disebut koefisien kepercayaan.

Misalkan 1

^

θ dan 2 ^

θ adalah batas kepercayaan bawah dan atas untuk

parameter θ, sehingga jika

α θ

θ

θ ⎟= −

⎠ ⎞ ⎜

⎝

⎛ _{< <}

1

2 ^ 1

^

probabilitas, 1−α adalah koefisien kepercayaan. Interval random yang dihasilkan

oleh 1 ^

θ dan 2 ^

θ dikatakan interval kepercayaan dua sisi.

Sedangkan interval kepercayaan satu sisi dinyatakan dalam

α θ

θ ⎟= −

⎠ ⎞ ⎜

⎝

⎛ <1 1

^

P (2.23)

yang akan menghasilkan interval satu sisi bawah yaitu ⎟

⎠ ⎞ ⎜ ⎝ ⎛ _,∞

1 ^

θ dan

α θ

θ ⎟= −

⎠ ⎞ ⎜

⎝ ⎛ _<

1

2 ^

P (2.24)

yang akan menghasilkan interval satu sisi atas yaitu ⎟

⎠ ⎞ ⎜

⎝ ⎛ ∞− 2

^

,θ .

Salah satu metode yang berguna untuk menentukan interval kepercayaan

adalah metode pivot. Metode ini tergantung pada penentuan besaran pivot yang

memiliki dua karakteristik :

1. Kuantitas pivot merupakan fungsi dari pengukuran sampel dan

parameter θ yang tidak diketahui.

2. Kuantitas pivot memiliki distribusi probabilitas yang tidak tergantung

pada parameter θ .

Contoh 2.8.1:

Misalkan ditentukan suatu pengamatan tunggal Y dari suatu distribusi

eksponensial dengan rata-rata θ . Tentukan interval kepercayaan θ dengan

Jawab :

Fungsi densitas untuk Y adalah :

⎩ ⎨ ⎧

= 1 − , ≥0 , 0

/ )

( e y

selainnya y

y f

θ

θ

Jika U = Y/θ maka Y=Uθ dan Y’ = θ, menggunakan metode transformasi maka

fungsi densitas eksponensial menjadi :

⎩ ⎨ ⎧ = − _, >₀

, 0

)

( e y

selainnya u

y f

Sehingga variabel U = Y/θ adalah fungsi dari Y dan θ , dan distribusi dari U

tidak tergantung dari θ . Maka dapat digunakan U = Y/θ sebagai besaran pivot.

Karena akan ditentukan penduga interval dengan koefisien kepercayaan 0,90,

maka terlebih dahulu ditentukan nilai a dan b sehingga

(

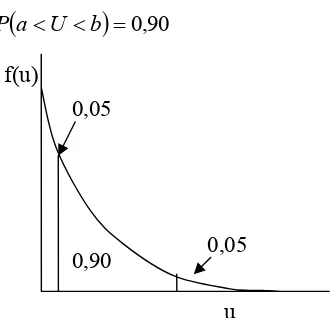
a<U <b

)

=0,90

P

Gambar 2.7.1. Grafik fungsi densitas eksponensial

Salah satu cara untuk menentukan nilai a dan b adalah

∫

=

=

<_a a_e−u_du

U P

0

05 , 0 )

(

f(u)

0,90 0,05

0,05

1−e−a =0,05

kedua ruas dikurangi 1 dan dikalikan 1, maka persamaan menjadi

_e−a=0,95

kedua ruas dilogaritmakan, maka persamaan menjadi

−a=−ln(0,95)

kedua ruas dikalikan 1, maka persamaan menjadi

a=ln(0,95)

a=0,051.

Sedangkan > =

∫

− =

0

05 , 0 )

(

b u_du

e b U P

e−b =0,05

kedua ruas dilogaritmakan, maka persamaan menjadi

−b=−ln(0,05)

kedua ruas dikalikan 1, maka persamaan menjadi

b=ln(0,05)

a=2,996

atau dengan kata lain a = 0,051 dan b = 2,996.

Jadi diperoleh

⎟ ⎠ ⎞ ⎜

⎝

⎛ _{< <} =

< <

= (0,051 2,996) 0,051 2,996 90

, 0

θ

Y P

U P

Karena akan mencari penduga interval untuk θ , maka dengan memanipulasi

⎟ ⎠ ⎞ ⎜

⎝

⎛ _{< <} =

⎟ ⎠ ⎞ ⎜

⎝

⎛ _{< <} =

< < =

051 , 0 996

, 2 996

, 2 1 051 , 0 ) 996 , 2 051

, 0 ( 90 ,

0 P Y Y

Y Y

P Y

P θ

θ θ

Jadi batas bawah dan atas untuk interval kepercayaan θ adalah Y/2,996 dan

Y/0,051. Untuk menentukan nilai numerik dari batas ini, maka perlu dilakukan

pengamatan sehingga dihasilkan nilai Y dan nilai ini disubstitusikan sehingga nilai

itu menghasilkan nilai numerik untuk batas interval kepercayaan θ.

Interval Kepercayaan Sampel Besar

Untuk parameter target θ adalah µ, p,µ₁−µ₂, atau p₁− p₂ maka untuk

sampel besar

^

^

θ σ

θ θ− =

Z (2.25)

akan mendekati distribusi normal standar. Ini berarti bentuk

^

^

θ σ

θ θ− =

Z adalah

suatu besaran pivot, dan metode pivot dapat digunakan untuk menentukan

penduga interval untuk parameter target θ .

Contoh 2.8.2:

Misalkan

^

θ adalah suatu statistik yang berdistribusi normal dengan rata-rata dan

variansi θ dan 2

θ

σ . Tentukan interval kepercayaan untuk θ yang memiliki

koefisien kepercayaan

(

1−α

)

.

Besaran ^ ^ θ σ θ θ− = Z

mempunyai distribusi normal standar. Sehingga nilai dua ekor dari distribusi ini

adalah

2

α

Z

− dan

2

α

Z , sedemikian sehingga P

(

−Z_α/2 <Z <Z_α/2

)

=1−α

Gambar 2.7.2. Grafik fungsi densitas N(0, 1)

Substitusikan Z ke dalam pernyataan probabilitas diatas, maka diperoleh

α σ θ θ α θ α = − ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ < − <

− _/2 1

^ 2 / ^ Z Z P

jika kedua ruas dikalikan dengan ^ θ

σ maka diperoleh

α σ θ θ σ θ α θ α ⎟_⎠⎞= − ⎜ ⎝

⎛_{− < − < 1}

^

^ _/2

^ 2

/ Z

Z P

dan kurangkan kedua sisi dengan

^

θ, maka diperoleh

α σ θ θ σ θ θ α θ α ⎟_⎠⎞= − ⎜ ⎝

⎛_{− − <− <− 1}

^

^ _/2

^ 2 / ^ Z Z P

kalikan kedua ruas dengan -1, maka diperoleh 0 2

/

α α/2

α σ

θ θ σ θ

θ α θ

α ⎟= −

⎠ ⎞ ⎜

⎝

⎛ _{− < < +}

1 ^

^ _/2

^ 2

/ ^

Z Z

P

Jadi diperoleh batas kepercayaan bawah dan atas untuk θ adalah :

Batas kepercayan bawah = _/2 ^

^

θ

α σ

θ−Z dan

Batas kepercayan atas = _/2 ^

^

θ

α σ

θ+Z

Contoh diatas dapat digunakan untuk menentukan interval kepercayaan sampel

besar untuk µ, p,µ₁−µ₂, dan p1 - p2, dengan menggunakan penduga parameter.

I. Simulasi Komputer

Model yang akan dikembangkan untuk penafsiran harga saham akan

meliputi bilangan random dan akan digunakan simulasi komputer untuk

melakukan percobaan, menggambarkan pemikiran dan juga untuk menduga

kuantitas yang tidak dapat ditunjukkan secara analitik. Simulasi disini dapat

diartikan sebagai suatu sistem yang digunakan untuk memecahkan atau

menguraikan persoalan-persoalan dalam kehidupan nyata yang penuh dengan

ketidakpastian dengan tidak atau menggunakan model atau metode tertentu dan

lebih ditekankan pada pemakaian komputer untuk mendapatkan solusinya.

Simulasi menyangkut pembangkitan proses serta pengamatan dari proses untuk

menarik kesimpulan dari sistem yang diwakili. Sedangkan menurut Naylor (1966

dalam Rubinstein & Melamed) simulasi adalah teknik numerik untuk melakukan

eksperimen pada komputer, yang melibatkan jenis matematika dan model tertentu

Menurut Borowsky & Borwein simulasi didefinisikan sebagai teknik untuk

membuat konstruksi model matematika untuk suatu proses atau situasi, dalam

rangka menduga secara karakteristik atau menyelesaikan masalah berkaitan

dengannya dengan menggunakan model yang diajukan.

Beberapa keuntungan simulasi :

o Menghemat waktu

o Dapat melebar-luaskan waktu

o Mengoreksi kesalahan-kesalahan perhitungan

o Dapat dihentikan dan dijalankan kembali

o Mudah diperbanyak

Jika didalam suatu laboratorium simulasi unsur manusianya dikeluarkan maka

yang tertinggal adalah komputer, prosedur operasi, fungsi-fungsi matematis dan

juga distribusi probabilitas, maka akan diperoleh inti dari simulasi komputer.

Simulasi komputer hanya menggunakan komputer untuk memecahkan masalah

sesuai kebutuhan yang kemudian diprogramkan kedalam komputer. Semua

tingkah laku yang dijadikan sebagai persoalan dialihkan kedalam program,

termasuk ketentuan logika pengambilan keputusan dan pelaksanaannya.

Didalam model pergerakan harga saham akan digunakan bilangan random.

Bilangan random itu sendiri adalah suatu bilangan yang diambil dari sekumpulan

bilangan, dimana tiap-tiap elemen dari kumpulan bilangan ini mempunyai peluang

yang sama untuk terambil. Berdasarkan pada tingkat kesulitan untuk memprediksi

bilangan yang akan dibangkitkan selanjutnya maka bilangan random dibagi

random semu (Pseudo-Random). Didalam skripsi ini hanya akan digunakan

bilangan random pseudo .

Bilangan random pseudo adalah kumpulan bilangan yang dihasilkan

menggunakan algoritma yang menerapkan rumus matematika untuk menghasilkan

bilangan yang terlihat acak. Salah satu algoritma untuk pembangkitan bilangan

random pseudo adalah Linear Congruential Generator (LCG). Algoritma LCG

mempunyai bentuk

m b

ax

x_n=( _n−1+ )mod (2.26)

dengan,

n

x = bilangan random ke n

1

− n

x = bilangan random ke n-1

m =angka modulo

a dan b merupakan konstanta dalam LCG, dengan a adalah faktor pengali dan b

adalah increament factor

Contoh 2.9.1:

Membangkitkan bilangan random sebanyak 8 kali dengan a = 2, b = 7, m = 10 dan

x(0) = 2.

Jawab :

X(1) = (2(2) + 7) mod 10 = 1

X(2) = (2(1) + 7) mod 10 = 9

X(3) = (2(9) + 7) mod 10 = 5

X(4) = (2(5) + 7) mod 10 = 7

X(6) = (2(1) + 7) mod 10 = 9

X(7) = (2(9) + 7) mod 10 = 5

X(8) = (2(5) + 7) mod 10 = 7

Bilangan yang dibangkitkan adalah : 1, 9, 5, 7, 1, 9, 5, 7

Didalam komputer bilangan random yang dibangkitkan adalah bilangan random

pseudo. Disini akan digunakan program Matlab untuk membangkitkan bilangan

random pseudo berdistribusi tertentu. Pada Tabel 2.9.1 berikut akan ditunjukkan

dua himpunan yang terdiri dari sepuluh bilangan. Bilangan-bilangan ini diperoleh

dengan membangkitkan bilangan random pseudo dengan menggunakan fungsi

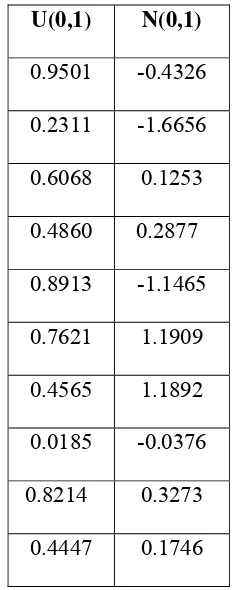
rand dan randn pada Matlab untuk memperoleh sampel U(0,1) dan N(0,1).

Tabel 2.9.1 Sepuluh bilangan random pseudo

berdistribusi U(0,1) dan N(0,1)

U(0,1) N(0,1)

0.9501 -0.4326

0.2311 -1.6656

0.6068 0.1253

0.4860 0.2877

0.8913 -1.1465

0.7621 1.1909

0.4565 1.1892

0.0185 -0.0376

0.8214 0.3273

Dapat dilihat pada Tabel 2.9.1 bahwa dugaan sampel U(0,1) tersebar dalam

interval (0,1), sedangkan dugaan sampel N(0,1) berada disekitar nol.

Berikut ini akan dibandingkan rata-rata dan variansi yang didapat secara

teoritis dari suatu distribusi tertentu dengan rata-rata dan variansi yang didapat

dari pembangkitan bilangan random. Secara teoritis untuk distribusi N(0,1)

dengan menggunakan persamaan (2.3) dan (2.6) nilai harapan dan variansinya

adalah sebagai berikut,

E(X) = x x dx

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − −

∫

∞ ∞ − 2 1 0 2 1 exp 2 1 1

π = 0

Var(X) = E(X2) – [E(X)]2

= 2

2 2 ₁ 1 0 2 1 exp 2 1 1 ₋ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − −

∫

∞ ∞ − dx x x

π = 1

sedangkan untuk U(0,1) nilai harapan dan variansinya,

E(X) = dx

a b x

∫

∞ ∞ − − 1 =

∫

∫

∫

∞ ∞ − + − + b b a a dx dx a b x

dx 1 0

0 = ) ( 2 2 2 a b a b − − = 2 1

Var(X) = E(X2) – [E(X)]2

= 2 2 2 2 ) ( 2 1 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − −

∫

∞ ∞

− b a

a b dx a b

x =

2 2 2 3 3 ) ( 2 ) (

3 ⎟⎟_⎠

⎞ ⎜⎜ ⎝ ⎛ − − − − − a b a b a b a b = 12 1 4 1 3

1_{− =}

.

Sekarang akan digunakan pembangkitan bilangan random dengan M sampel

{ }

M i i =1

ξ untuk mencari rata-rata

∑

= = M i i M M 1 1 _ξ

µ (2.27)

∑

=

− −

= M

i

M i M

M 1

2 2

) (

1

1 _{ξ µ}

σ (2.28)

untuk bilangan random berdistribusi N(0,1) dan U(0,1). Setelah didapat bilangan

random berdistribusi N(0,1) dan U(0,1), kemudian dicari rata-rata dan variansinya

dengan mengetikkan pada ‘command window’ mean(A) dan var(A) (A ada