Pemodelan Dinamika Gelombang Dengan Mengerjakan Persamaan Kekekalan Energi

1. Staf Pengajar KK Kelautan, Fakultas Teknik Sipil dan Lingkungan-ITB.

Catatan : Usulan makalah dikirimkan pada 15 Desember 2006 dan dinilai oleh peer reviewer pada tanggal 13 Pebruari 2007 - 13 Maret 2007. Revisi penulisan dilakukan antara tanggal 6 Maret 2007 hingga 16 Maret 2007.

Abstrak

Paper ini menyajikan pengerjaan hukum kekekalan energi pada pemodelan hidrodinamika gelombang pendek. Pengerjaan hukum kekekalan energi dilakukan dengan mensuperposisikan persamaan kontinuitas yang dihasilkan dari kekekalan masa dengan persamaan kekekalan energi dan menghasilkan persamaan kontinuitas baru yang sesuai dengan hukum kekekalan masa dan kekekalan energi. Penelitian secara numeris menunjukkan bahwa persamaan dapat digunakan untuk memodelkan gelombang dengan tinggi gelombang terbesar pada periodanya. Persamaan juga dapat memodelkan refraksi, difraksi dan shoaling dengan baik.

Kata-kata Kunci:Persamaan kontinuitas, hukum kekekalan masa dan hukum kekekalan energi. Abstract

This paper presents application of energy conservation law for short wave modelling. The application is done by superimposing continuity equation that resulted from mass conservation and the equation of energy tion. The superimposing gives a new form of continuity equation that agree with the mass and energy conserva-tion law. The new equaconserva-tion can model wave with the height as high as the real wave in nature. The model also can simulate other wave dynamic such as refraction-diffraction and shoaling by bathymetry and diffraction in breakwater gap.

Keywords:Continuity equation, mass conservation and energy conservation law.

Pemodelan Dinamika Gelombang dengan Mengerjakan Persamaan

Kekekalan Energi

Syawaluddin H1)

TEKNIK

SIPIL

1. Latar Belakang

Persamaan gelombang Airy, walaupun dikenal sebagai persamaan gelombang panjang dapat digunakan juga untuk memodelkan gelombang pendek, walaupun dengan tinggi gelombang yang sangat kecil (Syawaluddin, H., dkk., 2005).

Persamaan kontinuitas pada persamaan gelombang panjang Airy diperoleh dari pengerjaan hukum kekekalan masa. Walaupun persamaan tersebut diturunkan dari hukum kekekalan masa, tetapi terdapat peristiwa transportasi energi pada persamaan ini, yaitu terjadinya perubahan energi kinetik menjadi energi potensial. Perubahan dari energi potensial dinyatakan pada perubahan elevasi muka air. Jadi persamaan kontinuitas selain mewakili hukum kekekalan masa, juga harus mewakili hukum kekekalan energi.

Dengan persamaan kontinuitas yang bersifat seperti ini maka diharapkan dapat digunakan untuk memodelkan gelombang untuk tinggi gelombang yang besar, sesuai dengan keadaan di alam.

2. Perumusan Persamaan

2.1 Bentuk umum

u

x-δx/2

δ

x

δ

y

v

y-δy/2

v

y+δy/2

u

x+δx/2

w

z-δz/2

w

z+δz/2

δ

z

Energi kinetik pada satu satuan masa air pada aliran

dimana ρ adalah rapat masa air, u, v dan w adalah kecepatan arus pada arah x, y dan z. Pada ruang

tinjauan pada Gambar 2.1, terdapat input-output

energi kinetik pada selang waktu δt, yaitu:

Perubahan energi kinetik pada sistim adalah

Berdasarkan hukum kekekalan, maka IO = ∆E

Dengan membagi ruas kiri dan kanan persamaan kekekalan dengan ρ δx δy δz dan δt serta dengan mengambil δx δy δz dan δt mendekati nol, maka diperoleh persamaan kekekalan energi adalah

Persamaan (1) adalah persamaan kekekalan energi dalam bentuk umum.

2.2 Bentuk terintegrasi terhadap kedalaman

Analisis hidrodinamik akan lebih mudah bila dilakukan dengan analisis terintegrasi terhadap kedalaman, terutama untuk analisis pada perairan dangkal. Pada metoda ini digunakan kecepatan

rata-rata kedalaman dimana kecepatan vertikal (w)

tereliminir sehingga hanya ada dua kecepatan yaitu kecepatan horizontal ara x dan y yaitu ū dan⎯v .

Sebagai contoh dari persamaan yang terintegrasi terhadap kedalaman adalah persamaan gelombang panjang dari Airy (Dean, Robert G., and Dalrymple). Agar persamaan kekekalan energi dapat diaplikasikan pada analisis hidrodinamika yang terintegrasi terhadap kedalaman, maka diperlukan bentuk persamaan kekekalan energi yang juga terintegrasi terhadap kedalaman yang akan dirumuskan pada bagian

berikut. Persamaan (1) diintegrasikan terhadap

kedalaman,

η = fluktuasi muka air terhadap muka air diam

Aturan Leibniz (Dean, Robert G., and Dalrymple),

Berdasarkan persamaan Euler, persamaan pada permukaan adalah

Syarat batas dinamik adalah bahwa tekanan pada permukaan adalah sama pada semua permukaan yaitu bekerja tekanan atmosfir. Fluktuasi muka air memberikan perbedaan tekanan atmosfir yang sangat kecil, sehingga pada seluruh permukaan mempunyai tekanan atmosfir yang sama yaitu pη = patm, sehingga

∂pn/∂x = 0. Dengan demikian persamaan Euler pada permukaan menjadi

Perhitungan dengan persamaan ini akan menghasilkan kecepatan permukaan uη yang sangat kecil, hampir mendekati nol. Oleh karena itu energi kinetik pada permukaan (Ekxη) dikalikan dengan ∂η/∂t.

pada Persamaan (3) adalah bilangan yang sangat

kecil yang dapat diabaikan. Selanjutnya, pada analisis ini kedalaman adalah suatu harga yang konstan terhadap waktu, sehingga

Dengan demikian Persamaan (3) menjadi

Sesuai dengan formulasi persamaan gelombang panjang dari Airy (Dean, Robert G., and Dalrymple),

h

η Muka air diam

Gambar 2.2. Sket muka air akibat gelombang

ρ δx δz δt +

2g

u

E

2 kx

=

ρ

, ,

2g

v

E

2 ky

=

ρ

2g

w

E

2 kz

=

ρ

air adalah IO = ρ δy δz δt

(

x x/2 xkx x/2

)

kx x/2 -x x/2 -x

E

u

E

u

_{δ δ}

−

_{+δ +δ} +

(

ky

)

y/2 y y/2 y ky y/2 -y /2 y -y

E

v

E

v

δ δ

−

+δ +δ ρ δz δz δt

(

w

_{z -δz/2}

E

_zkz_-δz/2

−

w

_z+δz/2

E

_zkz_+δz/2

)

(

δ

E

kx

+

δ

E

ky

+

δ

E

kz

)

∆E = ρ δx δy δz 0 z E w y E v x E u t E t E t Ekx ky kx kx ky _{kz =} ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ (1) 0 dz z E w y E v x E u t E t E t E h -kz ky kx kx ky kx ₌ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂

∫

η

x

f

x

f

-dz

f

x

dz

x

f

∂

∂

+

∂

∂

∂

∂

=

∂

∂

∫

∫

β

α

α

β α β β α (2)

∫

∫

+

∂

_∂

∂

∂

∂

∂

=

∂

∂

η η η

_η

h -h -kx kx kx h -kx

t

(-h)

E

t

E

-dz

E

t

t

E

(3)

x

p

1

-z

u

w

y

u

v

x

u

u

t

u

z

∂

∂

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

+

∂

∂

= η η

ρ

0

z

u

w

y

u

v

x

u

u

t

u

z

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

+

∂

∂

=η

t

(-h)

∂

∂

= 0.

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

t

E

kx

η

η

t

∂

∂

η

_,

∫

∫

∫

= _∂∂ ∂ ∂ = ∂ ∂ η η η h -h -kx h -kx _{u dz} t 2g 1 dz E t t E 2

dimana ū adalah kecepatan rata-rata kedalaman pada arah x, sedangkan α adalah suatu koefisien yang berharga 0.5 – 1, dalam hal ini digunakan α = 1.

dimana adalah energi kinetik pada kecepatan rata-rata kedalaman.

Dengan cara yang sama akan diperoleh

Syarat batas kinematik

Dengan menggunakan anggapan uη dan vη adalah

bilangan yang sangat kecil (seperti telah dibahas pada bagian terdahulu), maka

bilangan yang sangat kecil yang dapat diabaikan, sehingga syarat batas kinematik permukaan menjadi

Selanjutnya didefinisikan

dimana untuk perairan dangkal pendekatan ini masih cukup baik.

Selanjutnya pada bagian berikut diselesaikan

Dengan uη bilangan yang sangat kecil, maka

Dengan cara yang sama akan diperoleh

E

(

)

2 h

-u

h

dz

u

=

+

∫

α

η

η 2 didefinisikan

(

)

2 h -kx

_h

_u

t

2g

1

t

E

+

∂

∂

=

∂

∂

∫

η

η

(

)

(

)

t

E

t

E

h

E

h

t

t

E

kx kx kx h -kx

∂

∂

+

∂

∂

+

=

+

∂

∂

=

∂

∂

∫

η

η

η

η (4a)

(

)

t

E

t

E

h

t

E

ky ky h -ky

∂

∂

+

∂

∂

+

=

∂

∂

∫

η

η

η (4b)

Selanjutnya, akan diselesaikan

∫

∂

_∂

η h -kz

_dz

t

E

∫

∫

−

∂

_∂

∂

∂

=

∂

∂

η η η

_η

h -kz kz h -kz

t

E

dz

E

t

dz

t

E

wη =

t

∂

∂

η

+ uη

x

∂

∂

η

+ vη

y

∂

∂

η

uη

x

∂

∂

η

dan vη

y

∂

∂

η

adalah wη =

t

∂

∂

η

(5)

∫

∫

=

_∂

∂

∂

_∂

∂

∂

η η

_η

h -n kz kz h -kz

t

E

-dz

E

t

dz

t

E

2g

w

E

2 n kz η

=

dengan _{dimana seperti pada persamaan}

(5) wη =

t

∂

∂

η

, maka

∫

∫

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

∂

∂

=

∂

∂

η η

_η

h -k z h -kz

t

2g

1

-dz

E

t

dz

t

E

3

(

h

)

2

w

w

dz

w

h -2 h 2 2

₌

+

₊

∫

−

_η

η η

∫

∫

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

−

∂

∂

=

∂

∂

η η

_η

h -h -kz

t

2g

1

dz

w

t

2g

1

dz

t

E

3 2

(

)

₍

₎

3 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ − + + ∂ ∂ = ∂ ∂

∫

_t 2g 1 E E 2 h t dz t E _-h kz kz h -kz

η

η

η

η

(

)

₊

∂

∂

⎟

⎠

⎞

⎜

⎝

⎛ +

+

∂

∂

+

=

∂

∂

−

∫

E

_t

₂

h

E

_t

₂

2

h

dz

t

E

h kz kz h -kz

η

η

η η

(

)

3

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

∂

∂

+

t

2g

1

-t

E

E

2

1

-h kz kz

η

η

η

∫

∂

_∂

η h -kx

_dz

x

E

u

dan

∫

∂

∂

η h -ky

dz

y

E

v

x E u x E u dz uE x dz x E u -h kx h -h -kx kx h -kx ∂ ∂ − ∂ ∂ − ∂ ∂ = ∂ ∂

∫

∫

η η η η η η

0

x

2g

u

x

E

u

3 kx

≈

∂

∂

=

∂

∂

η

η

η

η η Didefinisikan

(

)

∫

= + η η β h -3 3_{dz h u}

u , dimana β adalah suatu konstanta.

(

)

x

h

E

u

E

u

h

x

dz

x

E

u

-h kx h -kx h -kx

∂

∂

−

+

∂

∂

=

∂

∂

∫

η

η

β

(7a)

(

)

y

h

E

v

E

v

h

y

dz

y

E

v

_-h ky h -ky h -ky

∂

∂

−

+

∂

∂

=

∂

∂

∫

η

η

β

(7b) Selanjutnya

∫

=

∫

∂

∂

∂

η η h -kz h -kz

_dz

_wE

z

E

w

Dari Persamaan-persamaan (4a), (4b), (6), (7a), (7b)

dan (7c), maka

menjadi

Didefinisikan kedalaman total H = η + h dan

persamaan dibagi dengan H, serta ū , , dan

ditulis sebagai u, v, Ekx dan Eky, persamaan menjadi

Penelitian menunjukkan bahwa persamaan akan menjadi lebih baik bila semua suku dibagi dengan β dan diambil harga β = 1/3.

v

E_kx

E

_ky

∫

∂

η h -kz

wE

=

2g

w

-2g

w

3 h -3 η

∫

∂

η h -kz

wE

3 h -3

w

2g

1

-t

2g

1

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

η

= (7c) 0 dz z E w y E v x E u t E t E t E h -kz ky kx kx ky kx ₌ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂

∫

η

(

)

(

)

t

E

t

E

h

t

E

t

E

h

kx _kx ky _ky

∂

∂

+

∂

∂

+

+

∂

∂

+

∂

∂

+

η

η

η

η

(

)

3 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ + − t 2g 1 -t E E 2 1 t E t E 2 h -h kz kz h kz kz η η η η η

(

)

(

)

x h E u -E v h y E u h x h -kx h -ky kx _∂ ∂ + ∂ ∂ + + ∂ ∂ +

β

η

β

η

0

w

2g

1

t

2g

1

y

h

E

v

-

3 h -h kz h

⎟

−

=

⎠

⎞

⎜

⎝

⎛

∂

∂

+

∂

∂

− − 3

η

t

E

2

1

t

E

t

E

t

H

E

H

E

kx ky kx ky kz

₊

∂

∂

+

∂

∂

+

∂

∂

+

∂

∂

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

η

η

y

vHE

H

x

uHE

H

t

E

2

1

kx ky -h kz

∂

∂

+

∂

∂

+

∂

∂

+

β

β

0

w

2g

1

y

h

E

v

-x

h

E

u

-

3 h -h ky h h kx h

−

=

∂

∂

∂

∂

− − − −

t

E

3

t

E

3

t

E

2

1

E

2

1

E

E

H

3

-h kx ky kz 3 kz ky kx

_∂

∂

+

∂

∂

+

∂

∂

⎟

⎠

⎞

⎜

⎝

⎛

₊

₊

₊

η

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

+

∂

∂

y

vHE

H

1

x

uHE

H

1

t

E

2

3

t

E

2

3

kx ky -h kz kz η +

0

w

2g

1

y

h

E

v

3

x

h

E

u

3

H

1

3 h -h -ky h -h -kx h -

⎟⎟

=

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

(8)

Persamaan (8) adalah persamaan kekekalan energi yang terintegrasi terhadap kedalaman.

Syarat batas kinematik dasar perairan

Pada perairan dangkal, dapat dilakukan pendekatan u-h = u dan v-h = v. Pada perairan yang datar atau landai dimana

maka w-h ≈ 0, sehingga suku yang mengandung w-h ataupun

3. Penggunaan Persamaan Kekekalan

Energi

Dengan anggapan Ekzη dan Ekz−η, u-h, v-h serta w-h,

adalah bilangan yang sangat kecil, maka Persamaan (8) menjadi

Dengan mengerjakan diferensial parsial pada

Persamaan (9) akan digunakan untuk analisis hidrodinamika gelombang pendek, dengan mensuper-posisikan dengan persamaan gelombang panjang dari Airy.

t

w

∂

∂

=

η

η dengan maka 2 2 2 kz

t

t

g

1

t

w

w

g

1

w

t

2g

1

t

E

∂

∂

∂

∂

=

∂

∂

=

∂

∂

=

∂

∂

η

η

η

η η η

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

=

y

h

v

x

h

u

-w

-h -h -h

0

y

h

,

x

h

_≈

∂

∂

∂

∂

x

h

∂

∂

atau

y

h

∂

∂

dapat diabaikan.

x

uHE

kx

∂

∂

dan

y

vHE

ky

∂

∂

, maka

(

)

t

E

3

t

E

3

t

E

E

H

3

_kx ky ky kx

+

∂

∂

+

∂

∂

+

∂

∂

+

η

y

vH

H

E

x

uH

H

E

kx ky

∂

∂

+

∂

∂

y

E

v

x

E

u

kx ky

∂

∂

+

∂

∂

+ = 0 (9)

(

)

t

E

3

t

E

3

t

E

E

H

3

kx ky ky kx

+

∂

∂

+

∂

∂

+

∂

∂

+

η

y

vHE

H

1

x

uHE

H

1

kx ky

∂

∂

+

∂

∂

= 0

Persamaan gelombang panjang dari Airy adalah (Dean, Robert G., and Dalrymple),

Keterbatasan persamaan ini adalah bahwa untuk gelombang pendek persamaan hanya dapat digunakan pada amplitudo gelombang yang sangat kecil, A < 0.1 m (Syawaluddin, H., dkk., 2005).

Persamaan kontinuitas, Persamaan (10a), diturunkan berdasarkan hukum kekekalan masa saja. Sementara itu fluktuasi muka air η adalah merupakan perubahan energi potensial. Oleh karena itu pada saat muka air naik ( ∂η / ∂τ > 0 ) diperlukan suplai energi, sedangkan pada saat air turun terjadi pelepasan energi. Pada Persamaan (10a), tidak terlihat adanya suplai energi maupun tempat pelepasan energi. ∂uΗ / ∂x dan

∂uΗ / ∂y hanyalah sumber masa air saja. Oleh karena itu dengan mensuperposisikan Persamaan (9) dengan

Persamaan (10a), akan diperoleh persamaan yang

dapat mensuplai masa dan energi. Persamaan (9)

dijumlahkan dengan Persamaan (10a) diperoleh

Dengan menggunakan persamaan kontinuitas yang

baru Persamaan (11), sedangkan persamaan

momen-tum tetap seperti Persamaan (10b) dan (10c)

dikembangkan model numeris.

4. Metoda Numeris

Metoda numeris yang digunakan untuk diskritisasi ruang adalah metoda selisih hingga berbasis pada poli-nomial Lagrange (Syawaluddin, H., 2006). Sedangkan diferensial waktu diselesaikan dengan metoda inte-grasi atau dapat disebut juga dengan metoda predik-tor-korektor (Syawaluddin, H., dkk., 2005).

Persamaan kontinuitas, Persamaan (11) dapat ditulis dalam bentuk = 0

t

∂

∂

η

x

(uH)

∂

∂

y

(vH)

∂

∂

+ + (10a) + u + v + g = 0

t

u

∂

∂

x

u

∂

∂

y

u

∂

∂

x

∂

∂

η

(10b) + u + v + g = 0

t

v

∂

∂

x

v

∂

∂

y

v

∂

∂

y

∂

∂

η

(10c)

x

uH

H

E

1

t

H

3E

3E

1

kx ky kx

₊

∂

∂

⎟

⎠

⎞

⎜

⎝

⎛ +

+

∂

∂

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

η

t

E

t

E

y

vH

H

E

1

ky kx ky

∂

∂

+

∂

∂

+

∂

∂

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

y

E

v

x

E

u

kx ky

∂

∂

+

∂

∂

+ = 0 (11)

Selanjutnya Persamaan (12a), (12b) dan (12c)

diintegrasikan terhadap waktu, diperoleh

dapat diselesaikan secara numerik dengan mendekati P (t), Q (t) dan R (t) dengan polinomial Lagrange [Syawaluddin, H., dkk., 2005]. Untuk integrasi dari t1

= t - δt sampai t2 = t + δt, dimana terdapat 3 titik

integrasi yaitu t - δt, t dan t + δt, maka

dimana c1 = 1/3, c2 = 4/3 dan c3 = 1/3. Begitu juga

( )

t

E

k

3

t

E

k

3

t

P

t

ky kx

∂

∂

−

∂

∂

=

∂

∂

η

(12a)

( )

_⎜

⎜

⎝

⎛

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

+

∂

∂

⎟

⎠

⎞

⎜

⎝

⎛ +

−

=

y

vH

H

E

1

x

uH

H

E

1

c

1

t

P

kx ky

⎟

⎟

⎠

⎞

∂

∂

+

∂

∂

+

y

E

v

x

E

u

kx ky

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

=

H

E

3

H

E

3

1

k

kx ky

( )

t

Q

t

u

=

∂

∂

_(12b)

( )

t

R

t

v

₌

∂

∂

(12c)

( )

_⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

−

=

x

g

y

u

v

x

u

u

t

Q

η

( )

_⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

−

=

y

g

y

v

v

x

v

u

t

R

η

( )

(

) (

)

∫

−

−

−

−

+

=

t2 t1 t1 ky t2 ky t1 kx t2 kx t1 t2

_E

_E

k

3

E

E

k

3

dt

t

P

η

η

( )

∫

+

=

t2 t1 t1 t2

_u

_Q

_t

_dt

u

( )

∫

+

=

t2 t1 t1 t2

_v

_R

_t

_dt

v

( )

∫

t2 t1

dt

t

P

∫

( )

t2 t1

dt

t

Q

∫

( )

t2 t1

dt

t

R

, _dan

( )

(

)

∫

+ − +

+

+

=

t t t t t t 3 t 2 t -t 1

P

c

P

c

P

c

t

dt

t

P

δ δ δ δ

δ

( )

∫

+ + t t t t

dt

t

Q

δ δ

( )

∫

+ − t t t t

dt

t

R

δ δ dan

Pada saat t = t, dimana ηt+δt, ut+δt dan vt+δt tidak diketahui, maka Pt+δt, Qt+δt dan Rt+δt juga belum diketahui. Oleh karena itu pada tahap awal dilakukan prediksi

Dengan harga-harga hasil prediksi tersebut dapat dihitung harga ηt+δt, ut+δt dan vt+δt prediksi. Karena itu tahap ini dapat disebut dengan tahap prediksi.

Dengan harga (η, u, v) t+ δt yang baru tersebut dihitung lagi harga (P, Q, R) t+ δt yang baru dan dengan menye-lesaikan integrasi diperoleh (η, u, v) t+ δt yang lebih baru lagi dan dilakukan pemeriksaan konvergensi yaitu

Dalam hal syarat konvergensi terpenuhi

adalah hasil yang dicari, bila belum konvergen, maka dengan harga (η, u, v) t+ δt yang baru dilakukan perhitungan (η, u, v) t+ δt yang lebih baru lagi, karena itu tahap ini disebut dengan tahap korektor.

5. Hasil Model

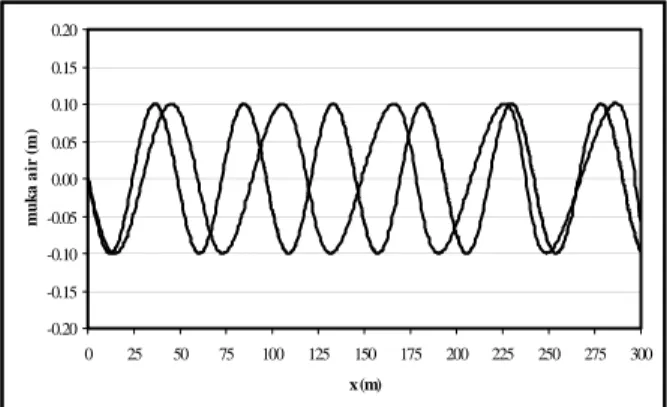
5.1 Panjang gelombang

Pada Gambar (4.1) disajikan perbandingan antara

panjang gelombang dari teori gelombang linier, pan-jang gelombang model dan panpan-jang gelombang dari persamaan gelombang Airy. Hal ini dikarenakan penggunaan tekanan hidrodinamis gelombang panjang

yang dianggap merata pada seluruh kedalaman. Apabila tekanan tersebut dikalikan dengan suatu bilangan yang lebih kecil dari satu, maka akan diperoleh panjang gelombang yang lebih pendek, semakin kecil bilangan pengali tersebut, maka akan semakin kecil panjang gelombangnya. (Syawaluddin, H., 2006). Pt+δt _{= P}t _{+ δt}

t

P

∂

∂

Qt+δt _{= Q}t _{+ δt}

t

Q

∂

∂

Rt+δt _{= R}t _{+ δ} t

t

R

∂

∂

t t new t t oldδ

-

η

δ

η

+ +

= ε begitu juga pada u dan v.

t t new δ

η

+ t t new

u

+δ ,

v

tnewt δ + dan

⎜

⎝

⎛

∂

∂

x

g

η

_⎟⎟

⎠

⎞

∂

∂

y

g

η

dan -0.20 -0.15 -0.10 -0.05 0.00 0.05 0.10 0.15 0.20 0 25 50 75 100 125 150 175 200 225 250 275 300 x (m) mu k a a ir (m )

Gambar 4.1. Perbandingan panjang gelombang

5.2 Tinggi gelombang

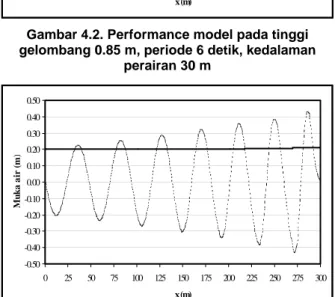
Salah satu tujuan dari pengembangan model adalah agar diperoleh persamaan yang dapat mensimulasikan gelombang pendek dengan tinggi gelombang yang besar. Tinggi gelombang terbesar untuk suatu periode gelombang pada perairan dalam diberikan oleh persamaan Pierson-Moskowitz (Sarpkaya T. and Iseacson, Micheal, 1981), yaitu T2 / 2A = 19.66, dimana 2A = tinggi gelombang. Jadi untuk periode gelombang 6 detik, tinggi gelombang terbesarnya (2A)max = 0.81 m. Pada Gambar (4.2) ditunjukkan

bahwa model dapat mensimulasikan gelombang tersebut dengan baik.

5.3 Shoaling

Pengujian shoaling dilakukan pada perairan dengan kemiringan dasar perairan 0.02, dengan kedalaman mula-mula 10 m. Gelombang yang digunakan adalah gelombang dengan perioda 6 detik, dengan tinggi

gelombang mula-mula 0.2 m. Pada Gambar (4.3)

disajikan perbandingan antara hasil model dengan hasil shoaling dari teori gelombang linier, terlihat bahwa hasil model lebih tinggi dari hasil teori gelombang linier.

Hal ini dikarenakan penggunaan tekanan gelombang

panjang yang bekerja sama

besar pada seluruh kedalaman, sehingga energi gelombang pada persamaan yang digunakan menjadi terlalu besar. Oleh karena itu ketika gelombang (dari model) memasuki perairan yang lebih dangkal terjadi pemampatan energi yang besar baik akibat berkurangnya kedalaman maupun akibat pemendekan gelombang sehingga dihasilkan pembesaran tinggi gelombang yang lebih besar dari yang seharusnya.

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

∂

∂

y

g

x

g

η

dan

η

-1.00 -0.80 -0.60 -0.40 -0.20 0.00 0.20 0.40 0.60 0.80 1.00 0 50 100 150 200 250 300 350 400 450 500 550 600 x (m) mu k a a ir ( m )

Gambar 4.2. Performance model pada tinggi gelombang 0.85 m, periode 6 detik, kedalaman

perairan 30 m

Tekanan pada persamaan momentum diperoleh dengan mengintegrasikan persamaan Euler arah z yaitu

Analisis numerik penyelesaian persamaan Euler (Syawaluddin, H., 2006), memberikan hasil bahwa distribusi kecepatan horizontal terhadap kedalaman adalah seragam. Hal ini dikarenakan tekanan

hidrodinamis yang disebabkan oleh η hasil

bekerja sama besar pada seluruh kedalaman.

Tekanan hidrodinamis dari teori gelombang linier (Dean, Robert G., and Dalrymple) adalah phyd = gη

cosh k (h + z) / cosh kh. Terlihat bahwa tekanan hidrodinamik gηadalah berubah terhadapkedalaman. Oleh karena itu pada model yang dikembangkan

hanya menggunakan tekanan hidrodinamik gη yang

dianggap bekerja pada seluruh kedalaman. Karena itu

-0.50 -0.40 -0.30 -0.20 -0.10 0.00 0.10 0.20 0.30 0.40 0.50 0 25 50 75 100 125 150 175 200 225 250 275 300 x (m) Mu ka a ir ( m )

Gambar 4.3. Perbandingan shoaling antara teori gelombang linier dan model

∫

∫

∫

_⎟⎟

+

∂

+

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

=

η η η

ρ

_-h

y

dz

_-h

ww

_-h

g

dz

w

v

x

w

u

t

w

p

1

panjang gelombang dari model menjadi terlalu panjang dan shoaling yang dihasilkan menjadi terlalu besar karena kelebihan energi.

5.4 Refraksi-difraksi

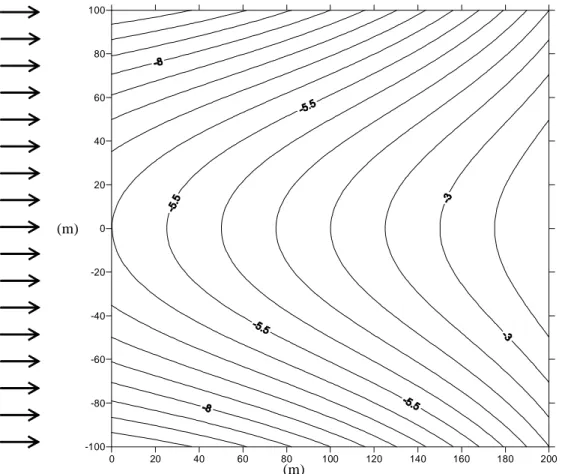
Untuk mengamati kemampuan model dalam mensimulasikan fenomena refraksi-difraksi, model dikerjakan pada suatu kawasan perairan dengan

batimetri berpola seperti tanjung (Gambar 4.4).

Gelombang yang digunakan adalah gelombang dengan perioda 6 detik dengan tinggi gelombang mula-mula 1.2 m.

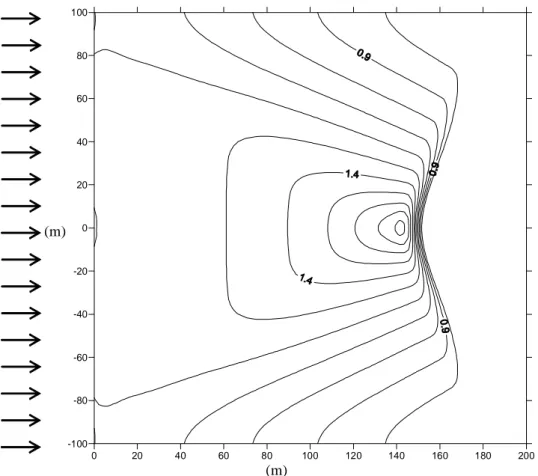
Telah diketahui bahwa pada batimetri seperti ini gelombang akan terefraksi ke arah pusat tanjung, sehingga akibat refraksi yang konvergen ini disertai dengan shoaling, pada pusat tanjung akan terjadi pembesaran gelombang. Kondisi gelombang pada detik ke 24, terlihat bahwa tinggi gelombang pada pusat tanjung jauh lebih besar dari yang lainnya. Pada

Gambar (4.6) diperlihatkan kontur tinggi gelombang terbesar pada daerah yang telah dilewati gelombang. Gambar-gambar tersebut menunjukkan terjadinya refraksi konvergen atau pemusatan energi gelombang pada pusat tanjung.

6. Kesimpulan dan Saran

Berdasarkan hasil model numeris yang dikembangkan, maka dapat disimpulkan bahwa pada pengembangan persamaan hidrodinamika sebaiknya dikerjakan juga persamaan kekekalan energi. Hal ini terbukti bahwa pengerjaan hukum kekekalan energi pada persamaan gelombang panjang dari Airy menjadikan persamaan dapat memodelkan gelombang pendek dengan baik. Contoh lain dari penggunaan hukum kekekalan energi pada pengembangan model hidrodinamika adalah teori gelombang linier, dimana pada formulasinya dikerjakan persamaan kekekalan energi dari Bernoulli (Dean, Robert G., and Dalrymple).

Panjang gelombang yang dihasilkan oleh gelombang lebih panjang dari panjang gelombang dari teori gelombang linier, terlebih lagi terhadap panjang gelombang teori gelombang Stoke. Shoaling yang dihasilkan lebih besar dari pada shoaling dari teori gelombang linier. Kedua hal tersebut dikarenakan penggunaan tekanan gelombang panjang yang bekerja pada seluruh kedelaman. Oleh karena itu untuk mengembangkan model yang lebih baik lagi perlu digunakan tekanan hidrodinamis yang lebih tepat, dimana yang berpotensi digunakan adalah tekanan yang dirumuskan dari persamaan Euler secara lengkap atau dari persamaan Bernoulli.

∫

η h -dz g

(m) (m) 0 20 40 60 80 100 120 140 160 180 200 -100 -80 -60 -40 -20 0 20 40 60 80 100

Gambar 4.4. Batimetri tanjung

(m) (m) 0 20 40 60 80 100 120 140 160 180 200 -100 -80 -60 -40 -20 0 20 40 60 80 100

Gambar 4.6. Kontur tinggi gelombang terbesar setelah detik ke 24

Daftar Pustaka

Dean, Robert G., and Dalrymple, “Water Wave

Mechanics for Engineers and Scientists”.

Prentice-Hall, Englewood Cliffs, New Jersey. Sarpkaya T. and Iseacson, Micheal, 1981, “Mechanics

of Wave Forces on Offshore Structures”, Van Nostrand Reinhold Company.

Shen, S. F., 1977, “Finite Element Method in Fluid

Mechanics”, Ann. Rev. Fluid Mech., Vol. 9. Syawaluddin, H., dkk., 2005, “Model Difraksi dengan

Persamaan Gelombang Airy yang Disempurna-kan”, Thesis S3, Departemen Teknik Sipil, ITB.

Syawaluddin, H., dkk., 2005, “Integrasi Numeris

dengan Manggunakan Polinomial Lagrange”,

Jurnal Teknik Sipil, Vol. 12, No. 2, Departe-men Teknik Sipil, ITB.

Syawaluddin, H., 2006, ”Penyelesaian Persamaan

Differensial dengan Menggunakan Polinomial Lagrange Seri I (1 Dimensi)”, Jurnal Teknik Sipil, Vol. 13, No. 2, Departemen Teknik Sipil, ITB.

Syawaluddin, H., 2006, ”Koefisien pada Persamaan

Euler pada Analisis Gelombang Pendek”,

Jurnal Teknik Sipil, Vol. 13, No. 4, Departemen Teknik Sipil, ITB.