Bab II Tinjauan Pustaka

Bab II Tinjauan Pustaka

II.1 Persilangan Sebidang Jalan dan Jalan Rel

Persilangan sebidang antara jalan dengan jalan rel (perlintasan) merupakan kasus khusus pada suatu ruas jalan raya dengan tanggung jawab untuk pengaturan dan pertimbangan keamanan terbagi pada kepentingan jalan dan jalan rel. Pengemudi kendaraan yang mendekat ke suatu perlintasan harus memiliki pandangan yang tidak terhalang ke jalur masuk yang cukup untuk memungkinkan kontrol terhadap kendaraan. Selain ditinjau dari segi keselamatan, perlintasan juga berdampak terhadap tundaan kendaraan. Tundaan yang terjadi pada persilangan sebidang antara jalan dan jalan rel dipengaruhi oleh faktor-faktor :

(1) pengoperasian kereta yang meliputi kecepatan, panjang kereta, dan frekuensi kereta yang lewat dalam satu hari;

(2) pengoperasian jalan yang meliputi kecepatan kendaraan dan tingkat kepadatan arus;

(3) kondisi geometrik jalan yang meliputi lebar jalan, jumlah lajur, dan keberadaan pemisah arus, keberadaan rumble strips, dan alur jalan rel.

II.2 Karakteristik Lalu Lintas

Lalu lintas merupakan interaksi antara beberapa komponen yang membentuk suatu sistem yang terdiri dari jalan, manusia, dan kendaraan. Untuk keberhasilan pengoperasiannya, ketiga komponen ini harus kompatibel. Dalam kenyataan sehari-hari hal ini tidak pernah terjadi, akibatnya sistem lalu lintas jalan seringkali gagal. Kecelakaan, kemacetan, dan gangguan lalu lintas merupakan contoh kegagalan sistem dan hampir semua kasus disebabkan oleh ketidaksesuaian antar ketiga komponen, atau antar satu komponen dan lingkungan dimana sistem beroperasi.

Ada tiga karakteristik primer dalam teori arus lalu lintas yang saling terkait, secara makroskopik dikenal dengan arus (flow), kecepatan (speed), dan kerapatan

(density), dimana ketiga variabel ini menggambarkan kualitas tingkat pelayanan

A. Arus dan Volume

Arus lalu lintas (flow) adalah jumlah kendaraan yang melintasi satu titik

pengamatan pada penggal jalan tertentu pada periode waktu tertentu, diukur dalam satuan kendaraan per satuan waktu.

Sedangkan volume adalah jumlah kendaraan yang melintasi suatu ruas jalan pada periode waktu tertentu, diukur dalam satuan kendaraan per satuan waktu. Volume biasanya dihitung dalam kendaraan/hari atau kendaraan/jam. Volume dapat juga dinyatakan dalam periode waktu yang lain. Dalam pembahasannya volume dibagi menjadi :

(1) volume harian (daily volumes)

Volume harian ini digunakan sebagai dasar untuk perencanaan jalan dan observasi umum tentang trend. Pengukuran volume harian dibedakan menjadi :

(a) Average Annual Daily Traffic (AADT), dalam satuan vehicle per hour (vph) rata-rata yakni volume yang diukur selama 24 jam

dalam kurun waktu 365 hari.

(b) Average Annual Weekday Traffic (AAWT), dalam satuan vehicle per hour (vph) rata-rata yakni volume yang diukur selama 24 jam

pada hari kerja selama satu bulan dalam kurun waktu 365 hari. (c) Average Daily Traffic (ADT), dalam satuan vehicle per hour (vph)

rata-rata yakni volume yang diukur selama 24 jam penuh dalam periode waktu tertentu yang lebih kecil dari satu tahun, misal enam bulan, satu musim, seminggu.

(d) Average Weekday Traffic (AWT), dalam satuan vehicle per hour

(vph) rata-rata yakni volume yang diukur selama 24 jam pada hari kerja selama satu bulan dalam kurun waktu kurang dari satu tahun. (2) volume jam-an (hourly volumes)

Yakni suatu pengamatan terhadap arus lalu lintas untuk menentukan jam puncak selama periode pagi dan sore yang biasanya terjadi kesibukan akibat orang pergi dan pulang kerja. Dari pengamatan tersebut dapat diketahui arus yang paling besar yang disebut sebagai jam puncak. Arus

pada jam puncak ini dipakai sebagai dasar untuk desain jalan raya dan analisis operasi lainnya.

(3) volume per sub jam (subhourly volumes)

Yakni arus yang disurvei dalam periode waktu lebih kecil dari satu jam.

B. Kecepatan (Speed)

Kecepatan adalah besaran yang menunjukkan jarak yang ditempuh kendaraan dibagi waktu tempuh. Kecepatan umumnya dibagi menjadi tiga jenis :

(1) kecepatan setempat (spot speed)

Adalah kecepatan kendaraan kendaraan pada suatu saat diukur dari suatu tempat yang ditentukan.

(2) kecepatan bergerak (running speed)

Adalah kecepatan kendaraan rata-rata pada suatu jalur pada saat kendaraan bergerak dan didapat dengan membagi panjang jalur dibagi dengan lama waktu kendaraan bergerak menempuh jalur tersebut.

(3) kecepatan perjalanan ( journeyspeed)

Adalah kecepatan efektif kendaraan yang sedang dalam perjalanan antara dua tempat, dan merupakan jarak antara dua tempat dibagi dengan lama waktu bagi kendaraan untuk menyelesaikan perjalanan antara dua tempat tersebut, dengan lama waktu ini mencakup setiap waktu berhenti yang ditimbulkan oleh hambatan (penundaan) lalu lintas.

Panjang lintas pengamatan untuk survai kecepatan setempat dapat dilihat pada Tabel II. 1 berikut ini :

Tabel II.1 Panjang Lintasan Pengamatan yang Dianjurkan Kecepatan rata-rata arus lalu lintas

(km/jam) Panjang lintasan (m) < 40 25 - 30 40 – 65 50 – 60 > 65 75 - 90

Dalam pergerakan arus lalu lintas, tiap kendaraan berjalan pada kecepatan yang berbeda. Dengan demikian dalam arus lalu lintas tidak dikenal kecepatan tunggal tetapi lebih dikenal sebagai distribusi dari kecepatan kendaraan tunggal. Dari distribusi tersebut jumlah rata-rata atau nilai tipikal dapat digunakan untuk mengetahui karakteristik dari arus lalu lintas. Dalam perhitungannya, kecepatan rata-rata dibedakan menjadi :

(1) Time Mean Speed (U ) _t

Adalah kecepatan rata-rata dari seluruh kendaraan yang melewati suatu titik dari jalan selama periode waktu tertentu.

(2) Space Mean Speed (U ) _s

Adalah kecepatan dari seluruh kendaraan yang menempati penggalan jalan selama periode waktu tertentu.

Keduanya dapat dihitung dari serangkaian pengukuran waktu tempuh dan pengukuran jarak menurut rumus di bawah ini (May, 1990) :

n t d U n 1 i i t

∑

= = ... (II.1)

∑

= = n 1 i i s n t d U ... (II.2)

Wadrop memberikan persamaan hubungan umum antara U dan _t U adalah : _s

s 2 s s t U _U U = +σ ... (II.3) dimana : s

U = space mean speed (km/jam , m/dt)

t

U = time mean speed (km/jam , m/dt) σs = simpangan baku dari space mean speed d = jarak tempuh (km, meter)

i

t = waktu tempuh kendaraan (jam, detik) n = jumlah kendaraan yang diamati

Sedangkan untuk menghitung besarnya kecepatan rata-rata ruang dari keseluruhan lalu lintas kendaraan bermotor digunakan rumus (Budiarto,1998) :

sr U = HV LV MC HV s HV LV s LV MC s MC n n n U . n U . n U . n + + + + ... (II.4) dimana : sr

U = kecepatan rata-rata ruang dari seluruh kendaraan (km/jam) nMC = jumlah sampel sepada motor

nLV = jumlah sampel kendaraan ringan

nHV = jumlah sampel kendaraan berat

s

U MC = kecepatan rata-rata ruang sepeda motor (km/jam)

s

U LV = kecepatan rata-rata ruang kendaraan ringan (km/jam)

s

U HV = kecepatan rata-rata ruang kendaraan berat (km/jam)

Selanjutnya, untuk mendapatkan variabel kerapatan (D) dilakukan dengan membagi jumlah arus (V) dalam satuan smp dengan kecepatan rata-rata ruang keseluruhan (U ). _sr

C. Kerapatan (Density)

Kerapatan didefinisikan sebagai jumlah kendaraan yang menempati suatu panjang jalan atau lajur, secara umum diekspresikan dalam vehicle per mile (vpm)

atau vehicle per mile per lane (vpmpl). Kerapatan sulit diukur secara langsung di

lapangan, sehingga nilai kerapatan diperoleh dari hubungan : V = U_s ∗ D Sehingga D = s U V ... (II.5) dimana : V = volume (kend/jam) U_s = space mean speed (km/jam)

II.3 Ekivalensi Mobil Penumpang

Untuk keperluan analisa dan perhitungan dari arus lalu lintas yang terdiri dari berbagai macam tipe maka perlu dikonversikan ke dalam satuan kendaraan ringan, yang dikenal sebagai satuan mobil penumpang (smp) dengan menggunakan faktor ekivalensi mobil penumpang.

DPU (1997) mendefinisikan satuan mobil penumpang dan ekivalen mobil penumpang sebagai berikut :

(1) satuan mobil penumpang (smp) yaitu satuan arus dimana arus dari berbagai tipe kendaraan telah diubah menjadi kendaraan ringan (termasuk mobil penumpang dengan menggunakan emp);

(2) ekivalensi mobil penumpang (emp) yaitu faktor konversi berbagai jenis kendaraan dibandingkan dengan mobil penumpang atau kendaraan ringan lainnya sehubungan dengan dampaknya pada perilaku lalu lintas, dimana untuk mobil penumpang dan kendaraan ringan lainnya nilai emp sama dengan 1,0.

Nilai satuan mobil penumpang pada daerah ruas menggunakan nilai ekivalen jalan perkotaan terbagi pada Bab 5 MKJI 1997.

Tabel II.2 Nilai emp untuk Jalan Perkotaan Terbagi dan Satu Arah

Dimana klasifikasi kendaraan yang dimaksud sebagai berikut :

(1) kendaraan ringan (LV) yaitu kendaraan bermotor beras dua dengan empat roda dengan jarak as 2,0-3,0 meter, meliputi mobil penumpang, mikrobis,

pick up, dan truk kecil sesuai klasifikasi Bina Marga;

(2) kendaraan berat (HV) yaitu kendaraan bermotor dengan lebih dari empat roda yang meliputi bis, truk 2 as, truk 3 as, dan truk kombinasi sesuai sistem klasifikasi Bina Marga;

(3) sepeda motor (MC) yaitu kendaraan bermotor dengan dua atau tiga roda yang meliputi sepeda motor dan kendaraan roda tiga sesuai sistem klasifikasi Bina Marga.

II.4 Kapasitas

Kapasitas didefinisikan sebagai arus maksimum melalui suatu titik di jalan yang dapat dipertahankan per satuan jam pada kondisi tertentu. Untuk jalan dua lajur dua arah, kapasitas ditentukan untuk arus dua arah (kombinasi dua arah), tetapi untuk jalan dengan banyak lajur, arus dipisahkan per arah dan kapasitas ditentukan per lajur.

Persamaan dasar untuk menentukan kapasitas adalah sebagai berikut :

C = Co x FCW x FCSP x FCSF x FCCS ... (II.6)

dimana :

C = kapasitas (smp/jam) Co = kapasitas dasar (smp/jam)

FCW = faktor penyesuaian lebar jalur lalu lintas

FCSP = faktor penyesuaian pemisahan arah (hanya untuk jalan tak terbagi), bernilai

1,0 untuk jalan terbagi dan jalan satu arah

FCSF = faktor penyesuaian hambatan samping dan bahu jalan/kereb

Tabel II.3 Kapasitas Dasar (Co)

Sumber : DPU, 1997

Tabel II.4 Faktor Penyesuaian Kapasitas untuk Lebar Jalur Lalu Lintas (FCW)

Tabel II.5 Faktor Penyesuaian Kapasitas untuk Hambatan Samping dan Jarak Kereb Penghalang (FCSF)

Sumber : DPU, 1997

Tabel II.6 Faktor Penyesuaian Kapasitas untuk Ukuran Kota (FCCS)

Sumber : DPU ,1997

II.5 Model Hubungan Karakteristik Arus Lalu Lintas

Pendekatan teori dari pergerakan kendaraan di jalan sering diambil dari prinsip aliran fluida. Hal ini disebabkan terdapatt kemiripan antara aliran fluida dan pergerakan arus pada kondisi kepadatan tinggi.

Model yang pertama diajukan dengan mengasumsikan fenomena keadaan tunggal (single regime) atas rentang kompleks dari kondisi aliran arus yang

meliputi arus bebas dan kondisi arus macet. Model yang diajukan belakangan berusaha lebih mempresentasikan kondisi sebenarnya di lapangan dengan

mempertimbangkan penggabungan dua keadaan, yaitu keadaan arus bebas dan keadaan arus macet dengan mengenalkan parameter tambahan.

A. Model Linier Greenshields

Model ini adalah model yang paling awal tercatat dalam usaha mengamati perilaku lalu lintas. Greenshields mengadakan studi pada jalur jalan di luar kota Ohio, dimana kondisi lalu lintas memenuhi syarat karena tanpa gangguan dan bergerak secara bebas (steady state condition). Greenshields mendapatkan hasil

bahwa hubungan antara kecepatan dan kerapatan bersifat linier. Berdasarkan penelitian-penelitian selanjutnya terdapat hubungan yang erat antara model linier dengan keadaan data di lapangan. Hubungan linier kecepatan dan kerapatan ini menjadi hubungan yang paling populer dalam tinjauan pergerakan lalu lintas, mengingat fungsi hubungannya adalah yang paling sederhana sehingga mudah diterapkan. Model ini dapat dijabarkan sebagai berikut :

D D U U U j f f s _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = ... (II.7) dimana : s

U = kecepatan rata-rata ruang f

U = kecepatan rata-rata ruang keadaan arus bebas (free flow)

Dj = kerapatan pada saat macet (jam density)

D = kerapatan

Pada saat kecepatan merupakan kecepatan arus bebas (free flow), pengemudi dapat

memacu kendaraannya pada kecepatan yang diinginkannya sedangkan pada saat kondisi kerapatan macet (jam density), kendaraan tidak dapat bergerak sama sekali

atau kondisi kecepatan sangat kecil.

Untuk mendapatkan nilai konstanta U dan Df j, maka persamaan (II.7) diubah

menjadi persamaan linier y = a + bx, dengan memisalkan : y = U s x = D a = U b f = j f D U −

Hubungan antara arus dan kerapatan diperoleh dari substitusi U = s D V

ke persamaan (II.7) didapat :

D D U U U j f f s _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = D V = D D U U j f f _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − 2 j f f D D U U D V _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = ... (II.8)

Hubungan antara arus dan kecepatan diperoleh dari substitusi D = s U

V ke persamaan (II.7) didapat :

D D U U U j f f s _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = s U = s j f f U V D U U _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − 2 s f j j s U U D - D U V _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ... (II.9) Harga arus maksimum dapat dicari dengan menurunkan persamaan (II.8) terhadap kerapatan (D) dan nilai arus maksimum terjadi pada saat nilai kerapatan maksimum yakni pada saat nilai turunan pertama (diferensial ke-1) tersebut sama dengan nol. V = D 2 j f f D D U U _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = ∂ ∂ j f m f 2D U_D U D V Untuk nilai 0 D V = ∂ ∂ maka : 0 = _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − j f m f 2D U_D U

2 D

D_m = j ... (II.10)

Nilai Dm disubstitusikan ke dalam persamaan (II.8) dengan kondisi V berubah

menjadi Vm dan D menjadi Dm , diperoleh :

4 U D V_m = j f ... (II.11) dimana :

Vm = arus maksimum (kend/jam)

Dm = kerapatan pada saat arus maksimum (kend/km)

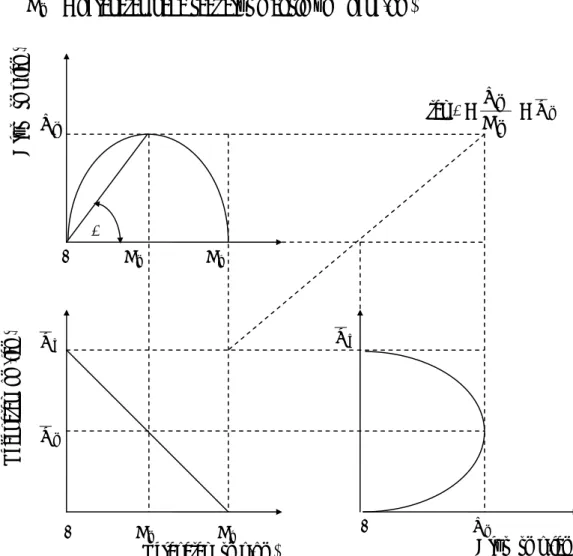
Gambar II.1 Hubungan Antara Kecepatan, Arus dan Kerapatan Model Greenshields 0 Vm Arus (smp/jam) f U tan θ = m m D V = U m θ m V m U f U 0 Dm Dj 0 Dm Dj Kerapatan (smp/km) Kece patan (km/ jam ) Arus (sm p/ jam )

Selanjutnya hubungan antara ketiga kecepatan, volume dan kerapatan digambarkan pada Gambar II.1. Gambar ini menunjukkan bentuk umum hubungan antara arus dengan kecepatan, arus dengan kerapatan dan kecepatan dengan kerapatan. Hubungan antara kecepatan dengan kerapatan adalah monoton ke bawah yang artinya apabila kerapatan naik, maka kecepatan akan turun. Arus menjadi nol ketika kerapatan sangat tinggi sehingga tidak memungkinkan kendaraan untuk bergerak lagi. Ketika kerapatan nilainya nol, maka tidak terdapat kendaraan di jalan sehingga arus juga nol. Antara kedua nilai-nilai ekstrim tersebut dikembangkan hubungan antara kedua parameter tersebut.

Gambar II.1 menunjukkan beberapa titik penting, yaitu tingkat volume nol terjadi pada dua kondisi berbeda. Pertama, jika tidak ada kendaraan di fasilitas, kerapatan adalah nol dan tingkat arus adalah nol. Secara teoritis, kecepatan pada saat kondisi ini ditentukan oleh pengemudi pertama (diasumsikan pada nilai yang tinggi). Kecepatan ini dinyatakan dalam U . Kedua, jika kerapatan menjadi begitu f tinggi sehingga semua kendaraan harus berhenti, kecepatan adalah nol dan tingkat arus adalah nol. Karena tidak ada pergerakan dan kendaraan tidak dapat melintas pada suatu titik di potongan jalan. Kerapatan dimana semua kendaraan berhenti disebut kerapatan macet dinyatakan sebagai Dj.

Di antara kedua ekstrim tersebut, dinamika arus lalu lintas menghasilkan pengaruh maksimum. Dengan meningkatnya arus dari nol, kerapatan juga meningkat karena lebih banyak kendaraan di jalan. Jika hal ini terjadi, kecepatan menurun karena interaksi antar kendaraan. Penurunan ini diabaikan pada kerapatan dan arus rendah dan sedang. Dengan meningkatnya kerapatan, kurva ini menganjurkan bahwa kecepatan menurun cukup berarti sebelum kapasitas dicapai.

Apabila kerapatan naik dari nol, maka arus juga naik. Namun apabila kerapatan terus naik akan dicapai suatu titik dimana akan menyebabkan penurunan kecepatan dan arus. Titik maksimum ini dinamakan kapasitas.

B. Model Logaritma Greenberg

Hubungan karakteristik arus lalu lintas pada model ini dibuat dengan mengasumsikan bahwa arus lalu lintas mempunyai kesamaan dengan arus fluida. Pada tahun 1959 Greenberg mengadakan studi yang dilakukan di terowongan

Lincoln dan menganalisa hubungan antara kecepatan dan kerapatan dengan menggunakan asumsi persamaan kontinuitas dari persamaan gerakan benda cair/fluida. Rumus dasar dari Greenberg adalah :

D = _{c e}bUs _{... (II.12)} dimana c dan b merupakan nilai konstanta

Dengan menggunakan asumsi di atas Greenberg mendapatkan hubungan antara kecepatan dan kerapatan berbentuk logaritma sebagai berikut :

D D ln U

U_s = _m j ... (II.13) Untuk mendapatkan nilai konstanta U dan Dm j, maka persamaan (II.13) diubah menjadi persamaan linier y = a + bx sebagai berikut :

s

U = U . ln Dm j - U . ln D ... (II.14) m

Dengan memisalkan variabel-variabelnya : y = U x = ln D s a = U . ln Dm j b = - U m

Untuk mendapatkan hubungan antara arus dan kerapatan maka U = s D V disubstitusikan ke persamaan (II.11) :

s U = U . ln Dm j - U . ln D m D V = U . ln Dm j - U . ln D m D V = U (ln Dm j – ln D) D V = U . ln m D D_j D D ln D U V = _m j ... (II.15)

Hubungan antara arus dan kecepatan didapat dari substitusi D = s U

V ke persamaan (II.13) didapat :

s U = U . ln m ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ s U V j D s U = U . ln m _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ V U D_{j s} ln _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ V U D_{j s} = m s U U m U s U e U D V= _{j s} − ... (II.16)

Nilai kerapatan pada saat arus maksimum untuk model Greenberg dapat dicari dengan menurunkan persamaan (II.15) terhadap kerapatan (D) dan menyamakan hasil diferensial tersebut dengan nol sehingga diperoleh :

V = U . D . ln m D D_j ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∂ ∂ D DD D m j m _j 2 j D U D D ln U D V m j m _D U D ln U D V − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∂ ∂ Untuk nilai 0 D V = ∂ ∂ maka : 0 = _m j U_m D D ln U _⎟⎟− ⎠ ⎞ ⎜⎜ ⎝ ⎛ 0 = 1 D D ln j_⎟⎟− ⎠ ⎞ ⎜⎜ ⎝ ⎛

0 = _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ D D ln j e D D_m = j ... (II.17) Sedangkan nilai kecepatan pada saat volume maksimum dicari dengan menurunkan persamaan (II.16) terhadap kecepatan (U ) dan menyamakan hasil _s diferensial tersebut dengan nol sehingga diperoleh :

V = Um s U e U D_{j s} − ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + = ∂ ∂ − − m U s U m U s U e U 1 U D e D U V m s j j s ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ − = ∂ ∂ − − m U s U m U s U e D U U e D U V j m s j s ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ = ∂ ∂ − m s j s U U 1 e D U V U_m s U Untuk 0 U V s = ∂ ∂ maka : 0 = _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ ₋ m s je 1 _UU D Um s U 0 = _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − m s U U 1 m s U U = ... (II.18) Arus maksimum pada metode Greenberg dihitung dengan menggunakan rumus dasar : m m m D x U V = = e D_j x U_m e U D V_m = j m ... (II.19)

C. Model Eksponensial Underwood

Underwood mengemukakan suatu hipotesis bahwa hubungan antara kecepatan dan kerapatan merupakan hubungan eksponensial dengan bentuk persamaan sebagai berikut :

m D D f s U U − = e ... (II.20)

Untuk mendapatkan nilai konstanta U dan Df m, maka persamaan (II.20) diubah menjadi persamaan linier y = a + bx sebagai berikut :

ln (U ) = ln (s U . ef Dm D − ) ln (U ) = ln (s U ) - f m D D ... (II.21) Dengan memisalkan variabel-variabelnya :

y = ln U x = D s a = ln U b = - f

m D

1

Untuk mendapatkan hubungan antara volume dan kerapatan maka U = s D V

disubstitusikan ke persamaan (II.20) :

s U = U ef Dm D − D V = U ef Dm D − m D D f U D V − = e ... (II.22) Selanjutnya dengan mengganti U = ef B dan Dm =

A 1 − didapat : V = D U . ef Dm D − V = D . eB . e-D/(-1/A) V = D . eB+AD

Hubungan antara arus dan kecepatan didapat dengan substitusi D = s U V ke persamaan (II.20) : s U = U . ef Dm D − s U = U . e f UsDm V −

Apabila kedua ruas dinyatakan dalam fungsi logaritma naturalis, maka diperoleh persamaan : ln (U ) = ln (s U . ef UsDm V − ) ln (U ) = ln (s U ) - f m s .D U V V = U . Ds m . ln (U ) - f U . Ds m . ln (U ) s U U ln D U V s f m s = ... (II.23)

Nilai kerapatan pada saat arus maksimum dicari dengan menurunkan persamaan (II.22) terhadap kerapatan (D) dan menyamakan hasil diferensial tersebut dengan nol sehingga diperoleh :

V = D U ef Dm D − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + = ∂ ∂ − − m DD m DD _e D 1 D U e U D V m f f ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = ∂ ∂ − − m DD m DD _e D D U e U D V m f f D D 1 e U D V m f Dm D ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = ∂ ∂ −

Untuk 0 D V ₌ ∂ ∂ maka diperoleh : 0 = D D 1 e U m f Dm D ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − 0 = D D 1 m ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − D_m = D ... (II.24)

Sedangkan nilai kecepatan pada saat arus maksimum dicari dengan menurunkan persamaan (II.23) terhadap kecepatan (U ) dan menyamakan hasil _s diferensial tersebut dengan nol sehingga diperoleh :

V = U Ds m ln U U s f ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∂ ∂ s f 2 s f U U U U s m s f m s U D U U ln D U V m s f m s D -U U ln D U V ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∂ ∂ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∂ ∂ 1 -U U ln D U V s f m s Untuk 0 U V s = ∂ ∂ maka : 0 = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 -U U ln D s f m 0 = -1 U U ln s f ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ s f U U = e ... (II.25) Karena terjadi pada kondisi maksimum maka U adalah _s U . _m

Arus maksimum pada metode Underwood dihitung dengan menggunakan rumus dasar : m m m D x U V = = D_m x e U_f e U D V_m = m f ... (II.26) D. Model Northwestern

Model hubungan volume, kecepatan dan kerapatan yang keempat ini diusulkan oleh sekelompok peneliti dari Universitas Northwestern. Mereka melakukan observasi lapangan dan mendapatkan model hubungan kecepatan dan kerapatan mendekati bentuk kurva S terbalik. Model ini kemudian diberi nama Model Northwestern. Bentuk persamaannya merupakan hubungan eksponensial kuadratis sebagai berikut :

2 D D 2 1 f s U m U ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − = e ... (II.27) Model ini hampir sama dengan model yang dikembangkan oleh Underwood, hanya besaran nilai parameternya berbeda. Untuk mendapatkan nilai konstanta U f dan Dm maka persamaan (II.27) diubah menjadi persamaan linier y = a + bx sebagai berikut : s U = U . e f 2 D D 2 1 m⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − ln U = ln (s U . e f 2 D D 2 1 m⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − ) ln U = ln s U - f 2 m D D 2 1 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ... (II.28) Dengan memisalkan variabel-variabelnya :

y = ln U s x = D2 a = ln U f b = - ₂ m D 2 1

Untuk mendapatkan hubungan antara arus dan kerapatan maka U = s D V disubstitusikan ke persamaan (II.27) :

s U = U . e f 2 D D 2 1 m⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − D V = U . e f 2 D D 2 1 m⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − 2 D D 2 1 f m U D V ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − = e ... (II.29)

Hubungan antara arus dan kecepatan didapat dengan substitusi

s U V D= ke persamaan (II.27) : s U = U . e f 2 D D 2 1 m⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − s U = U . e f 2 D 2 1 m s U V ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ −

Apabila kedua ruas dinyatakan dalam fungsi logaritma naturalis, maka diperoleh persamaan : ln (U ) = ln (s U . e f 2 D 2 1 m s U V ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − ) ln (U ) = ln (s U ) – f 2 m U V D 2 1 s ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ V 2 = 2 (U Ds m)2 . ln (U ) – 2 (f U Ds m)2 ln (U ) s s f s f m s D 2ln U_U lnU_U U V 2 1 ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ... (II.30)

Nilai kerapatan pada saat arus maksimum dicari dengan menurunkan persamaan (II.29) terhadap kerapatan (D) dan menyamakan hasil diferensial tersebut dengan nol sehingga diperoleh :

V = D U . e f 2 D D 2 1 m⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − 2 f Dm D 2 1 e U D V ₌ − ⎜_⎝⎛ ⎟_⎠⎞ ∂ ∂ + ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − ⎜⎝⎛ ⎟⎠⎞ 2 m f Dm D 2 1 e D 2D U 2 1 2 f Dm D 2 1 e U D V ₌ − ⎜_⎝⎛ ⎟_⎠⎞ ∂ ∂ - ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − 2 m f Dm D 2 1 e D D U ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = ∂ ∂ − ⎜_⎝⎛ ⎟_⎠⎞ m 2 f e 1 _DD U D V 21 DD_m Untuk 0 D V ₌ ∂ ∂ maka diperoleh : 0 = _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − m 2 f e 1 _DD U Dm D 2 1 0 = D D 1 m ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − 1 = D D m D_m = D ... (II.31)

Sedangkan nilai kecepatan pada saat arus maksimum dicari dengan menurunkan persamaan (II.30) terhadap kecepatan (U ) dan menyamakan hasil _s diferensial tersebut dengan nol sehingga diperoleh :

V = U Ds m ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 21 s f U U 2ln

⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∂ ∂ 2 / 1 U U U U s m s f m s s f s 2 / 1 f 2 1 2 U D U U 2ln D U V m 2 / 1 s f m s D 2 U U ln D 2 U V − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∂ ∂ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∂ ∂ 1 -U U ln D 2 U V 1/2 s f m s Untuk 0 U V s = ∂ ∂ maka : 0 = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 -U U ln D 2 1/2 s f m 0 = -1 U U ln 1/2 s f ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 0 = 1/2 s f U U ln _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ s f U U 2 = e ... (II.32) Karena terjadi pada kondisi maksimum maka U adalah _s U . _m

Arus maksimum pada metode Underwood dihitung dengan menggunakan rumus dasar : V_m =D_m x U_m = D_m x e U 2 _f = m V e U D 2 _{m f} ... (II.33)

II.6 Model Antrian

Ketika permintaan melebihi kapasitas untuk suatu periode waktu atau pada suatu waktu antar kedatangan yang lebih rendah dibandingkan dengan waktu pelayanan (pada tingkat mikroskopik) di suatu lokasi tertentu, maka terbentuklah antrian. Antrian bisa berupa antrian yang bergerak (moving queue) atau antrian

yang berhenti (stopped queue). Pada dasarnya kelebihan kendaraan disimpan pada

daerah upstream dari bottleneck atau daerah pelayanan, dan kedatangannya ditunda

selama periode waktu berikutnya.

Ada dua teknik analisis yang bisa dipakai dalam mempelajari proses antrian, yaitu shock wave analysis dan queueing analysis. Shock wave analysis dapat

digunakan ketika proses permintaan-kapasitas adalah deterministic, dan terutama

cocok untuk evaluasi jarak yang diperlukan untuk proses antrian dan untuk interaksi proses antrian. Queueing analysis dapat digunakan baik untuk proses deterministic maupun proses stochastic, dan kendaraan yang berada di dalam

proses dianggap disimpan dalam antrian vertikal.

A. Shock Wave Analysis

Salah satu bagian dalam studi mengenai fenomena lalu lintas ialah sifat-sifat dari gelombang kejut pada arus lalu lintas. Gelombang kejut didefinisikan sebagai batas kondisi berbasis ruang dan waktu ditandai dengan diskontinuitas antara arus padat dan tak padat (May, 1990). Sedangkan Lighthill dan Whitham seperti dikutip dari Wohl dan Martin (1967) menjelaskan bahwa gelombang kejut terbentuk ketika pada sebuah ruas jalan terdapat arus dengan kerapatan rendah yang diikuti oleh arus dengan kerapatan tinggi, dimana kondisi ini mungkin diakibatkan oleh kecelakaan, pengurangan jumlah lajur, atau jalur masuk ramp. Misalnya saja perilaku lalu lintas pada saat memasuki jalan menyempit, pada simpang bersinyal ketika nyala lampu merah, atau pada perlintasan kereta api. Pada perlintasan kereta api, diskontinuitas terjadi saat kereta melintas (pintu perlintasan ditutup) dan adanya perlambatan sebagai akibat pengurangan kecepatan oleh kendaraan di depannya karena adanya hambatan berupa pengendali kecepatan (rumble strips)

Kondisi pada saat pintu perlintasan ditutup dapat digambarkan sebagai berikut :

(1) Kondisi jalan tertutup total

Kondisi ini terjadi saat kereta melintas dan pintu perlintasan ditutup. Akibatnya nilai kerapatan pada kondisi arus yang masuk (volume kebutuhan = demand) berangsur-angsur menjadi kerapatan macet. Kendaraan yang

berada di depan kelompoknya mengurangi kecepatannya saat mendekati perlintasan, dan akhirnya berhenti sehingga terbentuk antrian di belakangnya. (2) Pada saat pintu perlintasan dibuka, kerapatan pada kondisi macet berangsur-angsur kembali sampai pada keadaan dimana kerapatan menuju ke kondisi maksimum.

(3) Pada tahap ini kecepatan gelombang kejut 2 (ω_BC) akan menyusul kecepatan gelombang kejut 1 (ω_AB), dimana kerapatan saat kondisi macet akan hilang dan arus akan kembali pada kondisi normal sebelum adanya penutupan.

Tiga gelombang kejut mulai pada saat t₁ di garis henti : ω_AD( gelombang kejut bentukan maju), ω_DB (gelombang kejut diam depan), dan ω_AB (gelombang kejut bentukan mundur). Kecepatan dari ketiga gelombang kejut ini dinyatakan pada diagram Gambar II.2 (a) dan dapat dihitung dengan menggunakan rumus-rumus berikut : A A D A D DA _DV _DV μ ω =+ − − = ... (II.34) 0 D D V V ω B D B D DB = ₋− = ... (II.35) A B A B A B A AB _DV _DV _D V _D ω − − = − − = ... (II.36) dimana : DA

ω = gelombang kejut dari kondisi titik awal D (VD = 0 dan DD = 0) ke titik A (VA ,DA)

DB

ω = gelombang kejut pada saat pintu perlintasan ditutup selama kendaraan berhenti sehingga VB = 0 dan DB = kerapatan saat macet)

AB

ω = gelombang kejut saat nilai kerapatan arus pada kondisi volume kendaraan sama dengan volume kebutuhan (V = VA) berangsur-angsur menjadi kerapatan macet (DB).

Kondisi arus A, B, dan D ini tetap sampai waktu t2 pada saat pintu perlintasan dibuka.

Gambar II. 2 Gelombang Kejut Pada Perlintasan Kereta Api Saat Pintu Ditutup D B D A V C V A ω DB D U A U C Arus (s mp/jam/laj ur) ω AC • • • • ω DC ω BC t 0 t 1 t 2 t 3 t 4 Jarak Waktu D C

Ruas yang ditinjau

A B C ω AB ω DC ω AC ω AB ωBC

Kondisi arus baru C pada waktu t₂ di garis henti meningkat dari nol sampai arus jenuh. Ini menyebabkan dua gelombang kejut baru, ω_DC(gelombang kejut pemulihan maju) dan ω_BC (gelombang kejut pemulihan mundur) , sedangkan gelombang kejut akhir adalah ω_DB (gelombang kejut diam di. Kecepatan dua gelombang kejut baru ini dapat secara grafis dilihat pada Gambar II.2 (a) dan dihitung dengan persamaan berikut ini :

C C D C D DC _DV _DV μ ω =+ − − = ... (II.37) C B C C B C B BC _DV _DV _D V _D ω − − = − − = ... (II.38) dimana : DC

ω = gelombang kejut pada saat pintu perlintasan dibuka, kondisi ruas di depan pintu perlintasan dari kondisi arus dan kerapatan nol perlahan bergerak searah dengan lalu lintas ke arah hilir sampai pada kondisi titik C (VC = volume maksimum = kapasitas, DC = kerapatan maksimum)

BC

ω = gelombang kejut dari kendaraan yang mengalami kondisi berhenti saat pintu ditutup mulai bergerak disusul oleh kendaraan dibelakangnya sampai kendaraan terakhir yang tidak mengalami antrian tetapi kecepatannya terpengaruh oleh kecepatan arus di depannya.

Kondisi arus D, C, B, dan A tetap sampai ω_AB dan ω_BC memotong waktu t3. Interval waktu antara t₂ dan t3 dapat dihitung sebagai berikut :

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = AB BC AB a ω ω ω r t ... (II.39)

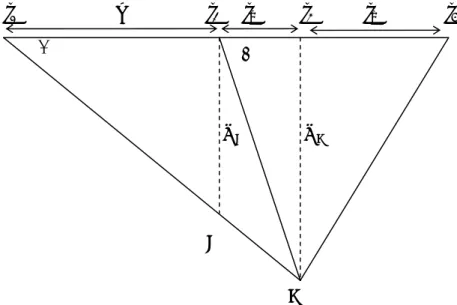
Gambar II.3 Lokasi Antrian dan Lokasi Hilangnya Antrian

Lokasi antrian dari garis henti pada waktu t₂ dapat dihitung sebagai berikut :

XA = r . tan α ... (II.40) tan α = A j A D D V − ... (II.41)

Lokasi hilangnya antrian dari garis henti pada waktu t3 dapat dihitung dengan rumus berikut : ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = AB BC AB BC B ω ω ω . ω 3600 r X ... (II.42) dimana r = lamanya waktu penutupan pintu perlintasan = t₂−t₁

Respon lalu lintas yang tidak bisa bergerak dengan segera begitu pintu perlintasan dibuka mengakibatkan beberapa kendaraan mungkin masih mengalami tundaan walaupuntidak mengalami antrian.

Pada saat t gelombang kejut gerak maju baru ₃ ω_AC terbentuk, dan dua gelombang kejut gerak mundur ω_AB dan ω_BC berakhir. Gelombang kejut ω_AC

dapat dihitung dengan rumus :

C A C A AC _DV _DV ω − − = ... (II.43) A B XB XA α _β r ta t1 t2 t3 tb t4

Kondisi arus D, C, dan A tetap sampai waktu tertentu sampai pintu perlintasan ditutup kembali, tetapi sebebelumnya pada saat waktu t₄, gelombang kejut bentukan maju ω_AC memotong garis henti dan arus di garis henti menurun dari arus maksimum V menjadi _C V_A. Periode waktu dari mulai pintu perlintasan dibuka sampai tingkat pelepasan garis henti turun dibawah nilai maksimum (t₂

sampai t₄) dapat dihitung sebagai berikut :

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − = 1 ω ω ω ω ω . r t AC BC AB BC AB b ... (II.44) Jumlah kendaraan yang mengalami antrian :

N = (r + ta ) x VA ... (II.45) Tundaan yang terjadi :

T = ½ x r x N ... (II.46)

Pada saat pintu dibuka kondisi yang terjadi dapat disamakan dengan kasus

bottleneck, dimana ruas yang belum terpengaruh perlintasan sebagai daerah upstream dan ruas dengan perlintasan sebagai downstream. Dalam Wohl (1967)

dijelaskan jika volume pada ruas tanpa hambatan lebih kecil daripada volume maksimum pada bottleneck, maka akan terjadi penurunan kecepatan dan kenaikan

kerapatan dari D1 ke D2 selama kendaraan memasuki perlintasan. Walaupun terjadi tundaan pada kendaraan tetapi shock wave tidak terjadi.

Kenaikan volume pada upstream masih dapat ditampung oleh bottleneck

sampai pada tingkat volume maksimum bottleneck. Kecepatan gelombang kejut

pada downstream adalah nol. Jika volume maksimum ini terlampaui maka

timbullah antrian. Pada suatu titik masuk bottleneck arus yang diberikan oleh

diagram dasar harus sebanding. Sehingga untuk jalan tanpa hambatan, kerapatan akan meningkat mencapai titik E. Kecepatan gelombang di E adalah negatif pengaruhnya terhadap jalan utama, dan dari sini akan dipantulkan ke bawah ke jalan pendekat dari bottleneck. Pengaruh dari gelombang ini akan bertemu dengan

gelombang yang datang bergabung pada kemiringan di C dan gelombang kejut dari kecepatan negatif relatif terhadap jalan. Pengaruh dari bottleneck akan

Ini dapat dijelaskan bahwa antrian tidak dapat dikurangi selama arus masuk kurang dari kapasitas bottleneck.

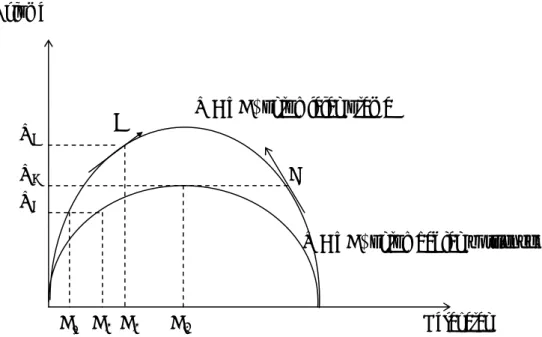
Gambar II.4 Hubungan Antara Volume dan Kerapatan Pada Jalan dengan Bagian Bottleneck

Gambar II.5 Hubungan Antara Volume dan Kerapatan dan Hubungan Shock Wave Pada Situasi Bottleneck

Kecepatan dari gelombang yang dipantulkan

Volume

Kerapatan Kecepatan dari

gelombang yang mendekat

Space Mean Speed dari kendaraan dalam antrian

Kecepatan gelombang kejut Space Mean Speed dari

kendaraan yang mendekati antrian VC VB VA C E D1 D3 D3 D4

V = f(D) untuk jalan utama

V = f(D) untuk bagian bottleneck

Volume

B. Analisis Antrian (Queueing Analysis)

Data masukan yang dibutuhkan pada analisis antrian adalah :

(1) nilai kedatangan rata-rata (mean arrival value), nilai ini menggambarkan

rata-rata arus (kendaraan per jam) atau time headway (detik per

kendaraan), istilah permintaan (demand) atau masukan (input) biasanya

menggantikan istilah kedatatangan (arrival);

(2) distribusi kedatangan (arrival distribution), dapat berupa distribusi deterministic atau distribusi probabilistic;

(3) nilai pelayanan rata-rata (mean service value), istilah kapasitas

(capacity), keberangkatan (depature), atau keluaran (output) biasanya

menggantikan istilah pelayanan (service);

(4) distribusi pelayanan (service distribution);

(5) disiplin antrian (queue dicipline).

Dalam analisis antrian perlu dilakukan terlebih dahulu klasifikasi masukan karakteristik, yaitu :

(1) Apabila distribusi kedatangan dan/atau distribusi pelayanan bersifat

probabilistic dan waktu kedatangan serta pelayanan tiap individu tidak

diketahui maka menggunakan stochasticqueueing analysis

(2) Apabila distribusi kedatangan dan distribusi pelayanan bersifat

deterministic dan waktu kedatangan serta pelayanan diketahui maka

digunakan deterministic queueing analysis

Deterministic queueing anaylsis dapat dibedakan menjadi dua level yang

berbeda. Pada level mikroskopik, pola kedatangan dan pelayanan dianggap menerus sedangkan pada level makroskopik hal ini dianggap acak. Level mikroskopik biasanya dipilih ketika rata-rata kedatangan dan pelayanan tinggi dan level makroskopik sering dipilih ketika kedatangan dan pelayanan rendah.

Pada persilangan sebidang jalan raya dan jalan rel adalah salah satu contoh analisis antrian deterministic pada tingkat makroskopik, dimana kedatangan dan

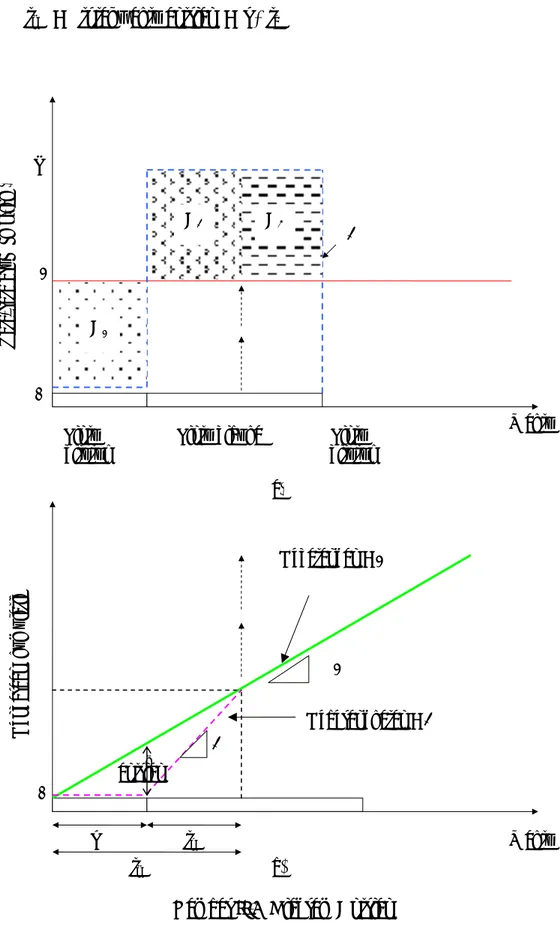
pola pelayanan dianggap menerus. Pada Gambar II.6 a menggambarkan rata-rata kedatangan (λ) yang konstan selama periode studi. Rata-rata pelayanan (μ) mempunyai dua kondisi : nol ketika pintu perlintasan ditutup dan meningkat sampai nilai rata-rata arus jenuh (s) ketika pintu dibuka. Nilai rata-rata pelayanan

akan sebanding dengan arus jenuh ketika terjadi antrian. Dengan kata lain, rata-rata pelayanan sebanding dengan rata-rata kedatangan jika kondisi pintu terbuka. Disiplin antrian yang dipakai adalah sistem FIFO.

Durasi waktu antrian dimulai dari awal pintu ditutup sampai antrian berakhir (tq). Durasi waktu antrian ini berguna untuk mengetahui apakah ada kendaraan di dalam antrian yang tersisa atau bisa dilepaskan seluruhnya.

Area A1 menggambarkan jumlah kendaraan yang disimpan selama periode waktu pintu ditutup. Saat pintu mulai dibuka, area A2 mulai meluas dan menggambarkan jumlah kendaraan yang dilepaskan. Ketika luasan A2 sama dengan luasan A1 maka antrian hilang. Sedangkan luasan A3 menggambarkan jumlah kendaraan yang dilayani selama pintu terbuka sampai saat pintu ditutup kembali karena ada kereta yang lewat.

Jumlah kendaraan yang mengalami antrian digambarkan oleh proyeksi vertikal segitiga antrian. Kendaraan pertama yang mengalami antrian adalah kendaraan yang datang setelah pintu ditutup. Semua kendaraan yang datang selama pintu ditutup sama seperti yang datang pada saat pintu dibuka tetapi sebelum terjebak antrian mengalami proses antrian dan dipaksa untuk berhenti atau menurunkan kecepatannya.

Panjang antrian digambarkan oleh jarak vertikal melalui segitiga. Pada saat awal pintu ditutup, panjang antrian meningkat dari nol sampai nilai maksimum di akhir waktu penutupan. Kemudian panjang antrian berkurang sampai garis kedatangan berpotongan dengan garis pelayanan (panjang antrian menjadi nol). Hal ini berlangsung sampai periode waktu penutupan pintu perlintasan kembali.

Tundaan individu digambarkan oleh jarak horisontal yang memotong segitiga. Kendaraan pertama yang datang setelah awal penutupan mengalami tundaan individu terbesar. Setiap kendaraan yang datang setelah itu mengalami lebih kecil dan semakin kecil tundaan individu sampai antrian menghilang.

May memakai teknik dari arus menerus untuk masalah pada bottleneck sementara (misalnya suatu ruas jalan yang bersilangan dengan jalan rel, atau jalan satu lajur yang tertutup karena adanya kecelakaan). Kondisi ini dapat dijelaskan dengan perilaku antrian selama satu siklus sinyal lalu lintas, dimana durasi tundaaan atau

penutupan sebanding dengan interval panjang waktu penutupan r dan waktu yang dibutuhkan oleh antrian untuk habis setelah pelepasan adalah ta.

May dalam Gerlough (1975) merumuskan model persamaan matematis untuk kondisi jalan dengan kondisi arus menerus yang secara prinsip bisa disamakan dengan kasus bottleneck seperti pada kasus perlintasan kereta api ini.

Durasi antrian : ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = A S B S q V V V V r t ... (II.47) Waktu pelepasan antrian :

ta = tq – r ... (II.48) Jumlah kendaraan yang mengalami tundaan :

N = VA . tq ... (II.49) Jumlah maksimum kendaraan dalam antrian :

Nm = r (VA – VB) ... (II.50) Jumlah rata-rata kendaraan dalam antrian :

N = Nm /2 ... (II.51) Total kendaraan dalam satu waktu antrian :

M = 2 t ) V -(V r _{A B q} ... (II.52) Waktu rata-rata kendaraan tertunda :

Tr _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = A B V V 1 2 r ... (II.53) Tundaan maksimum per kendaraan :

T _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = A B m V V 1 r ... (II.54) dimana :

VA = rata-rata kedatangan lalu lintas pada bagian hulu (upstream) VS = rata-rata arus jenuh atau kapasitas dari arus tak terganggu

VB = arus rata-rata pada bagian hilir (downstream) selama r (VB < VA < VS) r = durasi waktu tinjauan , pada saat pintu perlintasan ditutup r adalah

ta = waktu pelepasan antrian setelah awal pembukaan pintu perlintasan tq = total waktu antrian = r + ta

Waktu 0 λ μ λ 0 S Rata-rat a arus (sm p/ jam )

Pintu Pintu dibuka Pintu ditutup ditutup

μ

(a) A2 A3

A1

Kendaraan kumulatif Keberangkatan = μ

Kedatangan = λ

Gambar II.6 Diagram Antrian

Waktu (b) r to antrian N tq Nm

II.7 Tundaan

Tundaan menurut MKJI 1997 disebut sebagai waktu tempuh tambahan yang diperlukan untuk melewati suatu simpang dibandingkan terhadap situasi tanpa simpang. Berdasarkan definisi di atas, dapat diturunkan ke dalam persamaan matematis sebagai berikut :

W = W0 + T ... (II.55) dimana :

W = waktu tempuh total

W0 = waktu tempuh pada kondisi arus bebas, merupakan waktu minimum yang diperlukan untuk menempuh suatu ruas jalan tertentu

T = tundaan

Tundaan terdiri dari Tundaan Lalu Lintas (TT) yaitu tundaan yang disebabkan oleh pengaruh kendaraan lain, dan Tundaan Geometrik (TG) yaitu tundaan yang disebabkan oleh perlambatan dan percepatan untuk melewati fasilitas seperti pada persimpangan dan terhenti karena lampu merah. Secara matematis dapat dinyatakan sebagai berikut :

T = TT + TG ... (II.56) dimana :

TT = tundaan lalu lintas rata-rata TG = tundaan geometri rata-rata

Tundaan merupakan ukuran kinerja kritis dari interrupted flow. Menurut

Taylor (1996), ada dua definisi tundaan :

(1) Tundaan berhenti (stopped delay), yaitu tundaan yang dialami oleh

kendaraan yang benar-benar berhenti, yang merujuk pada tundaan antrian. (2) Tundaan kemacetan (congestion delay), yaitu tundaan yang meliputi

tundaan akibat antrian dan yang disebabkan oleh kendaraan yang mengurangi kecepatan karena interaksi dengan kendaraan lainnya. Tundaan ini dapat diukur dengan menghitung selisih antara journey time

Dalam studi ini, tundaan didefinisikan sebagai tambahan waktu perjalanan saat melalui pertemuan sebidang jalan dan jalan rel. Komponen tundaan terdiri dari perlambatan kendaraan, berhentinya kendaraan, dan percepatan kembali pada kondisi kecepatan semula, yang terjadi akibat penutupan pintu perlintasan saat kereta lewat dan pada saat pintu dibuka (akibat kondisi geometrik daerah perlintasan). Sehingga nilai tundaan total dapat dicari dari persamaan berikut : Ttotal = TL1 + TL2 + TL3 ... (II.57) Sehingga waktu tempuh total menjadi :

W = W0 + TL1 + TL2 + TL3 ... (II.58) dimana :

Ttotal = nilai tundaan total (det/smp)

TL1 = tundaan kendaraan dimana pengemudi berjalan dengan kecepatan .

yang diinginkan

TL2 = tundaan kendaraan akibat penurunan kecepatan TL3 = tundaan kendaraan akibat penutupan pintu perlintasan

Waktu Jarak Ttotal Wo Sta 1 Sta 2 TL1 TL2 TL3 Kendaraan dengan arus bebas Kendaraan dengan kecepatan yang diinginkan

Gambar II.7 Tundaan Yang Dialami Kendaraan Pada Perlintasan A

Pada kondisi dimana arus yang masuk bottleneck menurunkan

kecepatannya maka tundaan yang terjadi diakibatkan oleh perbedaan kecepatan pada saat memasuki bottleneck (kecepatan awal) dan saat berada pada daerah akhir bottleneck (kecepatan akhir). Waktu yang diperlukan bagi kendaraan untuk

menaikkan atau memperlambat pada rata-rata percepatan atau perlambatan dari kecepatan awal sampai kecepatan akhir adalah :

a U U

w ₌ A− B _{... (II.59)}

Sedangkan jarak yang diperlukan bagi kendaraan untuk menaikkan atau memperlambat pada rata-rata percepatan atau perlambatan a dari kecepatan awal sampai kecepatan akhir adalah :

2 B w 0,733a w U 1,47 x = + ... (II.60) dimana :

UA = kecepatan pada permulaan perlambatan

UB = kecepatan pada akhir perlambatan

a = rata-rata perlambatan

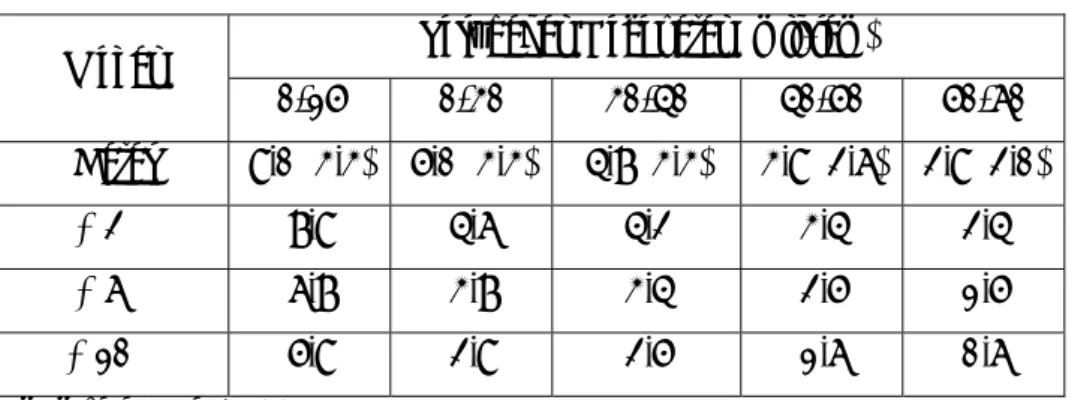
Nilai percepatan atau perlambatan bervariasi tergantung pada pengemudi, kendaraan, situasi lalu lintas, situasi jalan, dan untuk berbagai tingkat kecepatan yang berbeda. Maksimum dan normal rata-rata percepatan atau perlambatan untuk mobil penumpang pada perubahan kecepatan dan kondisi medan yang bervariasi dapat dilihat pada Tabel II.7 berikut ini :

Tabel II.7 Maksimum dan Normal Percepatan Atau Perlambatan Untuk Mobil Penumpang (Mil per jam/detik)

Perubahan Kecepatan (mil/jam) Medan 0-15 0-30 30-40 40-50 50-60 Datar 8,0 (3,3) 5,0 (3,3) 4,7 (3,3) 3,8 (2,6) 2,8 (2,0) + 2% 7,8 4,6 4,2 3,4 2,4 + 6% 6,7 3,7 3,4 2,5 1,5 + 10% 5,8 2,8 2,5 1,6 0,6 Sumber : May, 1990

II.8 Analisis Statistik

A. Perkiraan Jumlah Sampel

Dari data pengamatan yang diambil sebagai sampel dapat kita hitung nilai ratanya dan perkiraan yang paling baik terhadap rata populasi adalah rata-rata sampel. Walaupun jumlah sampel yang besar dapat memberikan hasil perkiraan yang lebih baik dari nilai rata-rata populasi tetapi jumlah sampel yang besar membutuhkan lebih banyak waktu dan usaha dalam pengumpulan dan analisisnya. Apabila nilai rata sampel ( x ) dipakai untuk menaksir nilai rata-rata populasi (μ), maka besarnya jumlah sampel adalah sebagai berikut :

n = 2 ε ts ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{... ( II.61)} dimana :

n = jumlah sampel yang dibutuhkan s = simpangan baku yang diharapkan

ε = limit kesalahan tertentu (galat) yang diperbolehkan dan ditetapkan sebelumnya oleh pengguna

t = koefisien standar kesalahan dari rata-rata yang dipakai sebagai acuan untuk tingkat kepercayaan tertentu

Besarnya nilai t untuk berbagai tingkat kepercayaan dapat dilihat pada Tabel II.8.

Tabel II.8 Nilai t Untuk Berbagai Tingkat Kepercayaan Tingkat kepercayaan yang

diharapkan (%) t Persamaan 68,3 1,00 n = σ₂2 e 95,0 1,96 n = 3,84σ₂2 e 95,5 2,00 n = 4σ₂2 e 99,7 3,00 n = 9σ₂2 e Sumber : Pignataro, 1973

Apabila kita tidak mempunyai data awal mengenai kondisi lokasi penelitian sehingga sukar untuk menentukan nilai simpangan baku maka kita dapat menggunakan nilai simpangan baku pada Tabel II.8. Tabel ini memperlihatkan beberapa simpangan baku untuk fasilitas dan lokasi yang berbeda. Nilai-nilai ini bisa digunakan untuk perkiraan pendahuluan dari jumlah sampel yang dibutuhkan jika tidak diketahui data sebelumnya.

Tabel II.9 Simpangan Baku Kecepatan Sesaat Untuk Perkiraan Jumlah Sampel Area Lalu Lintas Tipe Jalan Raya Simpangan Baku

(mil per jam)

Rural 2 lajur 4 lajur 5,3 4,2 Intermediate 2 lajur 4 lajur 5,3 5,3 Urban 2 lajur 4 lajur 4,8 4,9 Sumber : McShane, 1990

B. Mean, Median, dan Modus

Rata-rata sampel (mean) didapat dari perhitungan seluruh sampel dibagi dengan jumlah data. n x x n 1 i i

∑

= = ... (II.62) Sedangkan untuk data berkelompok rata-ratanya adalah :

∑ ∑ = i i i f x f x ... (II.63) dimana :

x = rata-rata sampel (mean) xi = sampel ke-i

n = jumlah sampel

Median menentukan letak data setelah data itu disusun menurut urutan nilainya. Jika banyak data ganjil, median merupakan data paling tengah setelah data diurutkan. Sedangkan jika jumlah data genap, median adalah rata-rata hitung dua data tengah. Jika data telah disusun dalam daftar distribusi frekuensi maka mediannya : Me = b + p _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − f F n 2 1 ... (II.64) dimana : Me = median

b = batas bawah kelas median, ialah kelas dimana median akan terletak p = panjang kelas median

F = jumlah semua frekuensi dengan tanda lebih kecil dari tanda kelas median

f = frekuensi kelas median

Modus menyatakan fenomena yang paling banyak terjadi, yaitu data yang mempunyai frekuensi terbanyak. Jika data telah disusun dalam daftar distribusi frekuensi maka modusnya :

Mo = b + p _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ₂ 1 1 b b b ... (II.65) dimana : Mo = modus

b = batas bawah kelas median, ialah kelas dimana median akan terletak p = panjang kelas modal

b1 = frekuensi kelas modal dikurangi frekuensi kelas interval dengan tanda kelas yang lebih kecil sebelum tanda kelas modal

b2 = frekuensi kelas modal dikurangi frekuensi kelas interval dengan tanda kelas yang lebih besar sesudah tanda kelas modal

Dalam membuat daftar distribusi frekuensi ada beberapa hal yang perlu diperhatikan :

- Rentang : adalah data terbesar dikurangi data terkecil - Banyak kelas interval = 1 + 3,3 log (n)

dimana n = jumlah sampel - Panjang kelas interval p =

kelas banyak

rentang

C. Variansi dan Simpangan Baku Sampel

Variansi dan simpangan baku sampel adalah suatu ukuran yang menyatakan penyebaran dari sampel, dirumuskan sebagai berikut :

(

)

1 -n x x s n 1 i 2 i 2

∑

= − = ... (II.66)

(

)

1 -n x x s n 1 i 2 i

∑

= − = ... (II.67) Untuk data sampel yang telah disusun dalam daftar frekuensi maka :

(

)

1 -n x x f s2 = ∑ i i− 2 ... (II.68) dimana : s2 = variansi sampel

s = simpangan baku sampel

D. Analisis Regresi Linier

Pada pasangan variabel (xi,yi), apabila yi merupakan variabel yang diamati (diukur setelah xi ditentukan) maka analisis penentuan y sebagai fungsi x disebut analisis regresi. Apabila rataan dari peubah acak Y yang berkaitan linier dengan suatu nilai tetap x, maka persamaan linier populasi dinyatakan sebagai :

μY|x = α + βx ... (II.69) Koefisien regresi linier α dan β merupakan dua parameter yang ditaksir dari data sampel. Bila taksiran untuk kedua parameter tersebut masing-masing dinyatakan dengan a dan b, maka μY|x dapat ditaksir dengan yˆ dari bentuk garis regresi berdasarkan sampel atau garis kecocokan regresi. Hubungan antara variabel bebas x dan variabel tidak bebas y yang dicocokkan pada data percobaan ditandai dengan persamaan prediksi yang disebut persamaan regresi.

yˆ = a + bx ... (II.70) Besarnya konstanta a dan b dapat dicari dari persamaan-persamaan di bawah ini :

∑

∑

∑

∑

∑

= 2 i 2 i i i i i ) x ( - x n y x - y x n b ... (II.71) i i bx y a= − ... (II.72) dimana : n y y_i =

∑

i n x x_i =

∑

i n = jumlah sampel

Sedangkan untuk menaksir parameter σ2 _{yang menggambarkan variasi acak} atau variasi galat percobaan di sekitar garis regresi dapat dicari sebagai berikut :

Jxx = 2 n 1 i i ) x x (

∑

= − ... (II.73) Jyy = 2 n 1 i i ) y y (

∑

= − ... (II.74) Jxy = ( x - x ) (y y) n 1 i i i

∑

= − ... (II.75) JKG = Jyy + b Jxy ... (II.76) 2 n JKG s2 − = ... (II.77) dimana :

JKG = jumlah kuadrat galat

Jxx = total jumlah kuadrat x terkoreksi Jyy = total jumlah kuadrat y terkoreksi Jxy = jumlah kuadrat regresi = JKR

E. Analisis Korelasi

Analisis korelasi dilakukan untuk mengukur eratnya hubungan antara variabel y dan x dengan menggunakan suatu bilangan yang disebut koefisien korelasi. Nilai koefisien korelasi dihitung dengan persamaan di bawah ini:

{

n x - ( x )

}{

n y - ( y )

}

y x - y x n r 2 i 2 i 2 i 2 i i i i i ∑ ∑ ∑ ∑ ∑ ∑ ∑ = ... (II.78) Besarnya nilai r terletak antara -1 < r < +1, jika harga r mendekati -1 atau +1 maka hubungan antara variabel y dan variabel x kuat, tetapi jika r mendekati 0 maka hubungan yang dihasilkan lemah dan berarti bahwa baik variabel x maupun variabel y adalah variabel bebas. Tanda (-) menyatakan pertambahan nilai x menyebabkan penurunan y, dan tanda (+) menyatakan pertambahan nilai x menyebabkan kenaikan nilai y.

Pengukuran untuk mengetahui sejauh mana ketepatan fungsi regresi adalah dengan melihat nilai koefisien determinasi (r2_{) yang didapat dengan} mengkuadratkan nilai koefisien korelasi. Nilai koefisien determinasi menyatakan proporsi variasi keseluruhan dalam nilai peubah y yang dapat diterangkan atau diakibatkan oleh hubungan linier dengan nilai peubah acak x.

F. Uji Signifikansi

Uji signifikansi digunakan untuk menentukan linier atau tidaknya hubungan antara variabel bebas dan tidak bebas. Uji signifikasi yang digunakan biasanya adalah Uji- t ( student’s t test) dan Uji- F (variance ratio test /The F test).

Uji-t memungkinkan untuk pengujian dengan tandingan satu arah sementara uji-F terbatas pada pengujian dengan tandingan dua arah.

(a) Uji - t

Ho : β = βo → variasi dalam y diakibatkan oleh fluktuasi acak yang tidak tergantung pada nilai x

H1 : β≠βo t = xx o J s/ β - b ... (II.79) T mempunyai distribusi-t dengan derajat kebebasan n-2.

(b) Uji- F

Misal kita ingin menguji hipotesis :

Ho : β = 0 → variasi dalam y diakibatkan oleh fluktuasi acak yang tidak tergantung pada nilai x

H1 : β≠ 0

Untuk menguji hipotesis di atas kita hitung :

f = ₂ s JKR 2) JKG/(n JKR/1 ₌ − ... (II.80)

dan menolak Ho pada taraf keberartian α bila f > f αˆ (1, n-2)

Jika hipotesis nol ditolak, yaitu bila nilai statistik f hitungan melebihi nilai kritis f αˆ (1,n-2) maka dapat disimpulkan bahwa terdapat jumlah variasi yang berarti dalam respon y yang disebabkan atau model merupakan fungsi linier. Bila statistik f berada dalam daerah penerimaan maka disimpulkan bahwa data tidak memberikan cukup dukungan kepada model sehingga model tersebut bukan merupakan fungsi linier.

G. Distribusi Normal

Distribusi normal standar adalah distribusi normal dengan rata-rata μ=0 dan simpangan baku σ = 1. Fungsi densitasnya berbentuk :

f(z) = e 1/2z2 2π

1 ₋

− ... (II.81) Mengubah distribusi normal umum menjadi distribusi normal baku ditempuh dengan menggunakan transformasi :

Z =

σ μ

X−

μ-3σ μ-2σ μ-σ μ μ+σ μ+2σ μ+3σ -3 -2 -1 0 1 2 3 rata-rata = μ≠ 0

simpangan baku = σ≠ 1 Kurva Normal Umum

Kurva Normal Standar