BAB 2
LANDASAN TEORI
2.1 Evaporasi
2.1.1 Pengertian
Evaporasi adalah salah satu komponen siklus hidrologi, yaitu peristiwa menguapnya air dari permukaan air, tanah,dan bentuk permukaan bukan dari vegetasi lainnya.Evaporasi merupakan proses penguapan air yang berasal dari permukaan bentangan air atau dari bahan padat yang mengandung air (Lakitan, 1994). Sedangkan menurut Manan dan Suhardianto (1999), evaporasi (penguapan) adalah perubahan air menjadi uap air. Air yang ada di bumi bila terjadi proses evaporasi akan hilang ke atmosfer menjadi uap air. Evaporasi dapat terjadi dari permukaan air bebas seperti bejana berisi air, kolam, waduk, sungai ataupun laut. Proses evaporasi dapat terjadi pada benda yang mengandung air, lahan yang gundul atau pasir yang basah. Pada lahan yang basah, evaporasi mengakibatkan tanah menjadi kering dan dapat memengaruhi tanaman yang berada di tanah itu. Mengetahui banyaknya air yang dievaporasi dari tanah adalah penting dalam usaha mencegah tanaman mengalami kekeringan dengan mengembalikan sejumlah air yang hilang karena evaporasi.
2.1.2 Faktor-Faktor yang Memengaruhi Evaporasi
sangat tergantung pada masukan energi yang diterima. Semakin besar jumlah energi yang diterima, maka akan semakin banyak molekul air yang diuapkan. Sumber energi utama untuk evaporasi adalah radiasi matahari. Oleh sebab itu, laju evaporasi yang
tinggi tercapai pada waktu sekitar tengah hari (solar noon). Selain masukan energi, laju
evaporasi juga dipengaruhi oleh kelembaban udara di atasnya. Laju evaporasi akan semakin terpacu jika udara diatasnya kering (kelembaban rendah), sebaliknya akan terhambat jika kelembaban udaranya tinggi (Lakitan, 1994). Evaporasi sangat bergantung kepada karakteristik lokasi sehingga faktor-faktor meteorologi yang berperan dalam proses evaporasi dapat berbeda dari tempat ke tempat lainnya.
Faktor-faktor utama yang berpengaruh terhadap evaporasi adalah (Ward, 1967) : 1. Faktor-faktor meteorologi
a. Radiasi Matahari
b. Temperatur udara dan permukaan c. Kelembaban
d. Angin
e. Tekanan Barometer 2. Faktor-faktor Geografi
a. Kualitas air (warna, salinitas dan lain-lain) b. Jeluk tubuh air
c. Ukuran dan bentuk permukaan air 3. Faktor-faktor lainnya
a. Kandungan lengas tanah b. Karakteristik kapiler tanah c. Jeluk muka air tanah d. Warna tanah
e. Tipe, kerapatan dan tingginya vegetasi f. Ketersediaan air (hujan, irigasi dan lain-lain
2.1.2.1 Radiasi matahari (%)
Pada setiap perubahan bentuk zat; dari es menjadi air (pencairan), dari zat cair menjadi gas (penguapan) dan dari es lengsung menjadi uap air (penyubliman) diperlukan panas
laten (laten heat). Panas laten untuk penguapan berasal dari radiasi matahari dan tanah.
Radiasi matahari merupakan sumber utama panas dan memengaruhi jumlah evaporasi di atas permukaan bumi, yang tergantung letak pada garis lintang dan musim.
Radiasi matahari di suatu lokasi bervariasi sepanjang tahun, yang tergantung pada letak lokasi (garis lintang) dan deklinasi matahari. Pada bulan Desember kedudukan matahari berada paling jauh di selatan, sementara pada bulan Juni kedudukan matahari berada palng jauh di utara. daerah yang berada di belahan bumi selatan menerima radiasi maksimum matahari pada bulan Desember, sementara radiasi terkecil pada bulan Juni, begitu pula sebaliknya. Radiasi matahari yang sampai ke permukaan bumi juga dipengaruhi oleh penutupan awan. Penutupan oleh awan dinyatakan dalam persentase dari lama penyinaran matahari nyata terhadap lama penyinaran matahari yang mungkin terjadi.
2.1.2.2 Temperatur udara (°C)
Temperatur (suhu) udara pada permukaan evaporasi sangat berpengaruh terhadap evaporasi. Semakin tinggi suhu semakin besar kemampuan udara untuk menyerap uap air. Selain itu semakin tinggi suhu, energi kinetik molekul air meningkat sehingga molekul air semakin banyak yang berpindah ke lapis udara di atasnya dalam bentuk uap air. Oleh karena itu di daerah beriklim tropis jumlah evaporasi lebih tinggi, di banding dengan daerah di kutub (daerah beriklim dingin). Untuk variasi harian dan bulanan suhu udara di Indonesia relatif kecil.
Tekanan udara adalah tenaga yang bekerja untuk menggerakkan massa udara dalam setiap satuan luas tertentu. Diukur dengan menggunakan barometer. Satuan tekanan udara adalah milibar (mb).
Tekanan udara akan berbanding terbalik dengan ketinggian suatu tempat sehingga semakin tinggi tempat dari permukaan laut semakin rendah tekanan udarannya. Kondisi ini disebabkansemakin tinggi tempat akan semakin berkurang udara yang menekannya.
2.1.2.4 Kelembaban udara (%)
Pada saat terjadi penguapan, tekanan udara pada lapisan udara tepat di atas permukaan air lebih rendah di banding tekanan pada permukaan air. Perbedaan tekanan tersebut menyebabkan terjadinya penguapan. Pada waktu penguapan terjadi, uap air bergabung dengan udara di atas permukaan air, sehingga udara mengandung uap air.
Udara lembab merupakan campuran dari udara kering dan uap air. Apabila jumlah uap air yang masuk ke udara semakin banyak, tekanan uapnya juga semakin tinggi. Akibatnya perbedaan tekanan uap semakin kecil, yang menyebabkan berkurangnya laju penguapan. Apabila udara di atas permukaan air sudah jenuh uap air tekanan udara telah mencapai tekanan uap jenuh, di mana pada saat itu penguapan terhenti. Kelembaban udara dinyatakan dengan kelembaban relatif (RH).
Indonesia yang merupakan negara kepulauan dengan perairan laut cukup luas mempunyai kelembaban udara tinggi. Kelembaban udara tergantung pada musim, di mana nilainya tinggi pada musim penghujan dan berkurang pada musim kemarau. Di daerah pesisir kelembaban udara akan lebih tinggi daripada di daerah pedalaman.
Penguapan yang terjadi menyebabkan udara di atas permukaan evaporasi menjadi lebih lembab, sampai akhirnya udara menjadi jenuh terhadap uap air dan proses evaporasi terhenti. Agar proses penguapan dapat berjalan terus lapisan udara yang telah jenuh tersebut harus diganti dengan udara kering. Penggantian tersebut dapat terjadi apabila ada angin. Oleh karena itu kecepatan angin merupakan faktor penting dalam evaporasi. Di daerah terbuka dan banyak angin, penguapan akan lebih besar daripada di daerah yang terlindung dan udara diam.
Di Indonesia, kecepatan angin relatif rendah. Pada musim penghujan angin dominan berasal dari barat laut yang membawa banyak uap air, sementara pada musim kemarau angin berasal dari tenggara yang kering.
2.2 Aljabar Matriks
2.2.1 Definisi
Matriks
Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga berbentuk persegi panjang, dimana panjang dan lebarnya ditunjukkan oleh banyaknya kolom dan baris serta dibatasi tanda “[ ]” atau “( )”.
Suatu matriks dinotasikan dengan symbol huruf besar seperti A, X, atau Z dan
sebagainya. Sebuah matriks A yang berukuran m baris dan n kolom dapat ditulis sebagai
berikut:
𝐴𝐴𝑚𝑚𝑚𝑚𝑚𝑚 = �
𝑎𝑎11 𝑎𝑎12 … 𝑎𝑎1𝑚𝑚
𝑎𝑎21 𝑎𝑎22 … 𝑎𝑎2𝑚𝑚
⋮ 𝑎𝑎𝑚𝑚1
⋮ 𝑎𝑎𝑚𝑚2
⋱ …
⋮ 𝑎𝑎𝑚𝑚𝑚𝑚
�
𝐴𝐴 = �𝑎𝑎𝑖𝑖𝑗𝑗� ; 𝑖𝑖= 1, 2, … ,𝑚𝑚;𝑗𝑗 = 1, 2, … ,𝑚𝑚
Skalar
Skalar adalah besaran yang hanya memiliki nilai, tetapi tidak memiliki arah.
Vektor Baris
Suatu matriks yang terdiri dari satu baris dan n kolom disebut vektor baris.
𝑋𝑋 = �𝑋𝑋𝑖𝑖𝑗𝑗�
𝑚𝑚𝑚𝑚𝑚𝑚disebut vektor baris m = 1
Vektor Kolom
Suatu matriks yang hanya terdiri dari m baris dan satu kolom disebut vektor kolom.
𝑋𝑋 = �𝑋𝑋𝑖𝑖𝑗𝑗�
𝑚𝑚𝑚𝑚𝑚𝑚disebut vektor kolom n = 1
Kombinasi Linier
Vektor w merupakan kombinasi linier dari vektor-vektor 𝑣𝑣1,𝑣𝑣2, … ,𝑣𝑣𝑚𝑚 jika terdapat
skalar 𝑘𝑘1,𝑘𝑘2, … ,𝑘𝑘𝑚𝑚 sehingga berlaku:
𝑤𝑤 = 𝑘𝑘1𝑣𝑣1+ 𝑘𝑘2𝑣𝑣2+ … + 𝑘𝑘𝑚𝑚𝑣𝑣𝑚𝑚 (2.1)
Jika vektor w = 0, maka disebut persamaan homogen dan 𝑣𝑣1,𝑣𝑣2, … ,𝑣𝑣𝑚𝑚 disebut
vektor yang bebas linier, yang mengakibatkan 𝑘𝑘1 =𝑘𝑘2= ⋯= 𝑘𝑘𝑚𝑚 = 0, tetapi jika ada
bilangan 𝑘𝑘1,𝑘𝑘2, … ,𝑘𝑘𝑚𝑚 yang tidak semuanya sama dengan nol, maka 𝑣𝑣1,𝑣𝑣2, … ,𝑣𝑣𝑚𝑚disebut
vektor yang bergantung linier.
2.2.2 Jenis-jenis Matriks
Matriks Kuadrat
Matriks kuadrat adalah matriks yang memiliki baris dan kolom yang sama banyak.
Dalam suatu matriks kuadrat, elemen-elemen 𝑎𝑎11,𝑎𝑎22, … ,𝑎𝑎𝑚𝑚𝑚𝑚 disebut elemen diagonal
𝐴𝐴𝑚𝑚𝑚𝑚𝑚𝑚 = �
di bawah diagonal utama merupakan cermin dari elemendi atas diagonal utama. Matriks
𝐴𝐴𝑇𝑇 =𝐴𝐴 artinya 𝑎𝑎
Matriks A disebut matriks identitas dan biasa diberi simbol I.
𝐴𝐴 =�𝑎𝑎𝑖𝑖𝑗𝑗� = 1 𝑖𝑖= 1, 2, … ,𝑚𝑚 <=>𝑚𝑚= 𝑚𝑚dan untuk
𝑎𝑎𝑖𝑖𝑗𝑗 = 1 → 𝑖𝑖 =𝑗𝑗
𝑎𝑎𝑖𝑖𝑗𝑗 = 1 → 𝑖𝑖 ≠ 𝑗𝑗
Matriks nol suatu matriks dengan semua elemennya mempunyai nilai nol. Biasanya diberi simbol 0, dibaca nol.
Matriks Elementer
Suatu matriks nxn dikatakan matriks elementer jika matriks tersebut dapat diperoleh
dari matriks identitas nxn yakni Indengan melakukan operasi baris elementer tunggal.
Matriks Segitiga
Matriks 𝐿𝐿 =�𝑎𝑎𝑖𝑖𝑗𝑗� suatu matriks bujur sangkar dikatakan segitiga bawah (lower
triangular) jika 𝑎𝑎𝑖𝑖𝑗𝑗 = 0 untuk i < j dan matriks 𝑈𝑈= �𝑎𝑎𝑖𝑖𝑗𝑗� suatu matriks bujur sangkar
Matriks kuadrat 𝐴𝐴 = �𝑎𝑎𝑖𝑖𝑗𝑗� dikatakan singular jika semua elemen pada salah satu baris
atau kolom adalah nol atau jika semua kofaktor dari elemen suatu baris atau kolom sama dengan nol. Untuk melihat kesigularan suatu matriks adalah dengan menghitung determinan matriks tersebut. Apabila determinannya sama dengan nol, maka matriks tersebut singular.
Matriks Ortogonal
Matriks kuadrat 𝐴𝐴 = �𝑎𝑎𝑖𝑖𝑗𝑗� dikatakan dapat didiagonalisasi secara ortogonal jika
terdapat matriks ortogonal P sehingga berlaku 𝑃𝑃−1𝐴𝐴𝑃𝑃= 𝑃𝑃−1AP. Matriks ortogonal
didefinisikan sebagai matriks kuadrat yang inversnya sama dengan transposenya, sehingga:
𝑃𝑃−1 =𝑃𝑃
2.2.3 Operasi Matriks
Perkalian Matriks dengan Skalar
Jika 𝐴𝐴= �𝑎𝑎𝑖𝑖𝑗𝑗� adalah matriks mxn dan k adalah suatu skalar, maka hasil kali A dengan
k adalah 𝐵𝐵= �𝑏𝑏𝑖𝑖𝑗𝑗� matiks mxn dengan 𝑏𝑏𝑖𝑖𝑗𝑗 =𝑘𝑘𝑎𝑎𝑖𝑖𝑗𝑗(1≤ 𝑖𝑖 ≤ 𝑚𝑚, 1≤ 𝑗𝑗 ≤ 𝑚𝑚).
Perkalian Matriks dengan Matriks
Jika 𝐴𝐴 = �𝑎𝑎𝑖𝑖𝑗𝑗� adalah matriks mxp dan 𝐵𝐵 = �𝑏𝑏𝑖𝑖𝑗𝑗� adalah matriks pxn maka hasil kali
dari matriks A dan matriks B yang ditulis dengan AB adalah C matriks mxn. Secara
matematik dapat ditulis sebagai berikut:
𝑐𝑐𝑖𝑖𝑗𝑗 = 𝑎𝑎𝑖𝑖1𝑏𝑏1𝑗𝑗 + 𝑎𝑎𝑖𝑖2𝑏𝑏2𝑗𝑗 + … + 𝑎𝑎𝑖𝑖𝑝𝑝𝑏𝑏𝑝𝑝𝑗𝑗
= ∑𝑝𝑝𝑘𝑘=1𝑎𝑎𝑖𝑖𝑘𝑘𝑏𝑏𝑘𝑘𝑗𝑗 (1≤ 𝑖𝑖 ≤ 𝑚𝑚, 1≤ 𝑗𝑗 ≤ 𝑚𝑚) (2.2)
Penjumlahan Matriks
Jika 𝐴𝐴= �𝑎𝑎𝑖𝑖𝑗𝑗� adalah matriks mxn dan 𝐵𝐵= �𝑏𝑏𝑖𝑖𝑗𝑗� adalah matriks mxn maka
penjumlahan matriks dari matriks A dan matriks B yang ditulis dengan 𝐶𝐶 = �𝑐𝑐𝑖𝑖𝑗𝑗�
dengan: 𝑐𝑐𝑖𝑖𝑗𝑗 = 𝑎𝑎𝑖𝑖𝑗𝑗 + 𝑏𝑏𝑖𝑖𝑗𝑗(𝑖𝑖 = 1, 2, … ,𝑚𝑚;𝑗𝑗 = 1, 2, … ,𝑚𝑚).
Pengurangan Matriks
Jika 𝐴𝐴= �𝑎𝑎𝑖𝑖𝑗𝑗� adalah matriks mxn dan 𝐵𝐵= �𝑏𝑏𝑖𝑖𝑗𝑗� adalah matriks mxn maka
pengurangan matriks dari matriks A dan matriks B yang ditulis dengan 𝐶𝐶 = �𝑐𝑐𝑖𝑖𝑗𝑗�
dengan: 𝑐𝑐𝑖𝑖𝑗𝑗 = 𝑎𝑎𝑖𝑖𝑗𝑗 − 𝑏𝑏𝑖𝑖𝑗𝑗(𝑖𝑖 = 1, 2, … ,𝑚𝑚;𝑗𝑗= 1, 2, … ,𝑚𝑚).
Transpose Suatu Matriks
Jika 𝐴𝐴= �𝑎𝑎𝑖𝑖𝑗𝑗� adalah matriks mxn maka matriks nxm dengan 𝐴𝐴′ = �𝑎𝑎𝑖𝑖𝑗𝑗′ � dan 𝑎𝑎𝑖𝑖𝑗𝑗′ =
𝑎𝑎𝑗𝑗𝑖𝑖(1≤ 𝑖𝑖 ≤ 𝑚𝑚, 1≤ 𝑗𝑗 ≤ 𝑚𝑚) disebut dengan transpose dari matriks A. Matriks secara umum dapat ditulis:
𝐴𝐴𝑚𝑚𝑚𝑚𝑚𝑚 = �
𝑎𝑎11 𝑎𝑎12 … 𝑎𝑎1𝑚𝑚
𝑎𝑎21 𝑎𝑎22 … 𝑎𝑎2𝑚𝑚
⋮ 𝑎𝑎𝑚𝑚1
⋮ 𝑎𝑎𝑚𝑚2
⋱ …
⋮ 𝑎𝑎𝑚𝑚𝑚𝑚
maka𝐴𝐴′𝑚𝑚𝑚𝑚𝑚𝑚 = 𝐴𝐴𝑚𝑚𝑚𝑚𝑚𝑚 = �
𝑎𝑎11 𝑎𝑎12 … 𝑎𝑎1𝑚𝑚
𝑎𝑎21 𝑎𝑎22 … 𝑎𝑎2𝑚𝑚
⋮ 𝑎𝑎𝑚𝑚1
⋮ 𝑎𝑎𝑚𝑚2
⋱ …
⋮ 𝑎𝑎𝑚𝑚𝑚𝑚
�
Determinan Matriks
Misalkan 𝐴𝐴 = �𝑎𝑎𝑖𝑖𝑗𝑗� adalah matriks nxn. Fungsi determinan dari A ditulis dengan det(A)
atau |𝐴𝐴| . Secara matematis ditulis:
Det(A) = |𝐴𝐴| = ∑(±)𝑎𝑎1𝑗𝑗1𝑎𝑎2𝑗𝑗2…𝑎𝑎𝑚𝑚𝑗𝑗𝑚𝑚 dengan 𝑗𝑗1,𝑗𝑗2, … ,𝑗𝑗𝑚𝑚 merupakan himpunan S =
{1, 2, ..., n}.
Invers Matriks
Misalkan A matiks nxn disebut matriks non singular (invertible) jika terdapat matriks B
sehinga menyebabkan: 𝐴𝐴𝐵𝐵= 𝐵𝐵𝐴𝐴 =𝐼𝐼, maka matriks B disebut invers matriks A. Jika
tidak terdapat matriks B yang menyebabkan kejadian tersebut, maka matriks A disebut
matriks singular (non-invertible).
Secara umum invers matriks A adalah:
𝐴𝐴−1 = 1
det(𝐴𝐴)𝐴𝐴𝐴𝐴𝑗𝑗 (𝐴𝐴)
Adjoint matriks A adalah suatu matriks yang elemen-elemmennya terdiri dari
semua elemen-elemen kofaktor matriks A, dengan 𝐾𝐾𝑖𝑖𝑗𝑗adalah kofaktor elemen-elemen
𝑎𝑎𝑖𝑖𝑗𝑗, 𝑖𝑖,𝑗𝑗 = 1, 2, … ,𝑚𝑚. Sehingga dapat ditulis dalam bentuk matriks sebagai berikut:
𝑎𝑎𝐴𝐴𝑗𝑗(𝐴𝐴) = �
𝐾𝐾11 𝐾𝐾12 … 𝐾𝐾𝑚𝑚1
𝐾𝐾21 𝐾𝐾22 … 𝐾𝐾𝑚𝑚2
⋮ 𝐾𝐾1𝑚𝑚
⋮ 𝐾𝐾2𝑚𝑚
⋮ …
⋮ 𝐾𝐾𝑚𝑚𝑚𝑚
�
dengan:
𝐾𝐾𝑖𝑖𝑗𝑗 = (−1)𝑖𝑖+𝑗𝑗det�𝑀𝑀𝑖𝑖𝑗𝑗� Sifat-sifat Invers:
a. Jika A adalah matriks non singular, maka (A-1)-1adalah non singuar dan
(A-1)-1 = A
b. Jika A dan B adalah matriks non singular, maka AB adalah non singular dan
c. Jika A adalah matriks singular, maka (AT)-1 = (A-1)
2.3 Nilai Eigen dan Vaktor Eigen
Jika A adalah matriks nxn, maka vektor tak nol X di dalam Rn dinamakan vektor eigen
(eigen vector) dari A jika AX adalah kelipatan skalar dari X, yakni:
AX = λX (2.3)
untuk suatu skalar λ. Skalar λ ini dinamakan nilai eigen (eigen value) dari A dan X
dinamakan vektor eigen yang bersesuaian dengan λ.
Untuk mencari nilai eigen matriks A yang berukuran nxn, dari persamaan (2.3)
dapat ditulis kembali sebagai suatu persamaan homogen:
(A – λI) X = 0 (2.4)
Dengan I adalah matriks identitas yang berordo sama dengan matriks A, dalam catatan
mariks:
Untuk memperoleh nilai λ,
Jadi apabila matriks𝐴𝐴𝑚𝑚𝑚𝑚𝑚𝑚 mempunyai akar karakteristik λ1,λ2, … ,λn dan ada kemungkinan bahwa diantaranya mempunyai nilai yang sama, bersesuaian dengan akar-akar karakteristik ini adalah himpunan vektor-vektor karakteristik yang ortogonal (artinya masing-masing nilai akar karakteristik akan memerikan vektor karakteristik) X1,X2, … ,Xn sedemikian sehingga:
𝑋𝑋𝑖𝑖′𝑋𝑋𝑗𝑗 = 0;𝑖𝑖 ≠ 𝑗𝑗𝑖𝑖,𝑗𝑗 = 1,2, … ,𝑚𝑚
Tanpa menghilangkan sifat umum, vektor-vektor tersebut dapat dibuat normal (standard) sedemikian rupa sehingga 𝑋𝑋𝑖𝑖′𝑋𝑋𝑗𝑗 = 𝐼𝐼 untuk semua i, suatu himpunan
vektor-vektor ortogonal yang telah dibuat normal (standard) disebut ortogonal set.
Apabila X merupakan matriks nxn, dimana kolom-kolomnya terdiri dari
vektor-vektor 𝑋𝑋𝑖𝑖 dan kemudian bisa ditulis dengan dua syarat berikut:
1. 𝑋𝑋𝑖𝑖′𝑋𝑋𝑗𝑗 = 0, jika 𝑖𝑖 ≠ 𝑗𝑗
𝑋𝑋𝑖𝑖′𝑋𝑋𝑗𝑗 = 1, jika 𝑖𝑖= 𝑗𝑗
2. 𝑋𝑋′𝑋𝑋= 𝐼𝐼𝑚𝑚 sehingga 𝑋𝑋′ = 𝑋𝑋−1
Matriks yang mempunyai sifat demikian dinamakan matriks ortogonal.
Definisi:
Misalkan 𝐴𝐴 = �𝑎𝑎𝑖𝑖𝑗𝑗� matriks nxn.
Determinan 𝑓𝑓(𝜆𝜆) =det(𝐴𝐴 − 𝜆𝜆𝐼𝐼𝑚𝑚) = �
𝑎𝑎21− 𝜆𝜆 … 𝑎𝑎1𝑚𝑚
⋮ ⋮ ⋮
𝑎𝑎𝑚𝑚1 … 𝑎𝑎𝑚𝑚𝑚𝑚 − 𝜆𝜆
�
dikatakan karakterisitik polinom dari A.
Persamaan 𝑓𝑓(𝜆𝜆) =det(𝐴𝐴 − 𝜆𝜆𝐼𝐼𝑚𝑚) = 0 dikatakan persamaan karakterstik dari A.
Matriks korelasi adalah matriks yang di dalamnya terdapat korelasi-korelasi Andaikan X
adalah matriks data, 𝑚𝑚̅ adalah matriks rata-rata dan Σ adalah matriks ragam pragam.
Dengan:
𝑚𝑚̅dihitung dari matriks yang dikalikan dengan vektor 1 dan kostanta 1
𝑚𝑚.
Selanjutnya persamaan (2.7) dikalikan dengan vektor 1’, sehingga dihasilkan
matriks 𝑚𝑚̅1’.
Kurangkan matriks X dengan persamaan matriks (2.8) yang menghasilkan matriks baku
pxn yang dinotasikan dengan V.
Matriks (𝑚𝑚 −1)𝑆𝑆 adalah perkalian silang antara matriks (2.9) dengan matriks
Karena
Sehinga didapat
𝑆𝑆= 1
𝑚𝑚−1𝑋𝑋 �1− 1
𝑚𝑚11′� 𝑋𝑋′ (2.10)
Persamaan (2.10) menunjukkan dengan jelas hubungan operasi perkalian
matriks data dengan �1−𝑚𝑚111′� dan transpose matriks data. Jika S telah diketahui dari
persamaan (2.10), maka S dapat dihubungkan ke matriks korelasi ρ dengan cara:
1. menghitung matriks Σ
𝑆𝑆𝑖𝑖𝑘𝑘 =
2. menghitung matriks baku yang isinya adalah simpangan baku, dengan asumsi
2.5 Analisis Regresi Linier Berganda
Dalam perkembangannya, terdapat dua jenis regresi yang sangat terkenal, yaitu regresi linier sederhana dan regresi linier berganda. Regresi linier sederhana digunakan untuk
menggambarkan hubungan antara suatu variabel bebas (X) dengan satu variabel tak
bebas (Y) dalam bentuk persamaan linier sederhana.
𝛽𝛽0+ 𝛽𝛽1𝑋𝑋1i = 1,2, …, n (2.12)
Regresi linier berganda merupakan perluasan dari regresi linier sederhana. Perluasannya terlihat dari banyaknya variabel bebas pada model regresi tersebut. Bentuk umum persamaan regresi linier berganda dapat dinyatakan secara statistik sebagai berikut:
𝑌𝑌𝑖𝑖 = 𝛽𝛽0+ 𝛽𝛽1𝑋𝑋1𝑖𝑖+𝛽𝛽2𝑋𝑋2𝑖𝑖 + ⋯+ 𝛽𝛽𝑘𝑘𝑋𝑋𝑘𝑘𝑖𝑖 +ɛ𝑖𝑖 (2.13)
dengan:
𝑌𝑌𝑖𝑖 = variabel tak bebas
𝑋𝑋𝐼𝐼 = variabel bebas
𝛽𝛽0, ⋯, 𝛽𝛽𝑘𝑘= parameter regresi
ɛ𝑖𝑖 = variabel gangguan
2.5.1 Asumsi Regresi Linier Berganda
Dalam model regresi linier berganda ada beberapa asumsi yang harus dipenuhi, asumsi tersebut adalah:
1. Nilai rata-rata kesalahan pengganggu nol, yaitu E(𝜀𝜀𝑖𝑖) = 0,
untuk i= 1, 2, …, n
2. Varian (𝜀𝜀𝑖𝑖) = E(𝜀𝜀𝑖𝑖2) = 𝜎𝜎2, sama untuk semua kesalahan pengganggu (asumsi
heterokedastisitas)
3. Tidak ada autokorelasi antara kesalahan pengganggu, berarti kovarian (𝜀𝜀𝑖𝑖,𝜀𝜀𝑗𝑗) =
4. Variabel bebas 𝑋𝑋1,𝑋𝑋2, … ,𝑋𝑋𝑘𝑘, konstan dalam sampling yang terulang dan bebas
terhadap kesalahan pengganggu 𝜀𝜀𝑖𝑖.
5. Tidak ada multikolinieritas dalam variabel bebas X.
6. 𝜀𝜀𝑖𝑖 ~ 𝑁𝑁 (0; 𝜎𝜎2, artinya kesalahan pengganggu mengikuti distribusi normal
dengan rata-rata 0 dan varian 𝜎𝜎2.
2.5.2 Metode Kuadrat Terkecil (MKT)
Metode kuadrat terkecil merupakan suatu metode yang paling banyak digunakan untuk menduga parameter-parameter regresi. Pada model regresi linier berganda juga digunakan metode kuadrat terkecil untuk menduga parameter. Biasanya metode kuadrat terkecil ini diperoleh dengan meminimumkan jumlah kuadrat galat. Misalkan model
yang akan diestimasi adalah parameter dari persamaan dengan n pengamatan, maka
diperoleh:
𝑌𝑌𝑖𝑖 = 𝛽𝛽0+ 𝛽𝛽1𝑋𝑋1𝑖𝑖 +𝛽𝛽2𝑋𝑋2𝑖𝑖 + ⋯+ 𝛽𝛽𝑘𝑘𝑋𝑋𝑘𝑘𝑖𝑖 +ɛ𝑖𝑖
𝑌𝑌𝑖𝑖 = 𝛽𝛽0+ 𝛽𝛽1𝑋𝑋1𝑖𝑖 +𝛽𝛽2𝑋𝑋2𝑖𝑖 + ⋯+ 𝛽𝛽𝑘𝑘𝑋𝑋𝑘𝑘𝑖𝑖 +ɛ𝑖𝑖
⋮
𝑌𝑌𝑖𝑖 = 𝛽𝛽0+ 𝛽𝛽1𝑋𝑋1𝑖𝑖 +𝛽𝛽2𝑋𝑋2𝑖𝑖 + ⋯+ 𝛽𝛽𝑘𝑘𝑋𝑋𝑘𝑘𝑖𝑖 +ɛ𝑖𝑖
Persamaan-persamaan di atas dapat ditulis dalam bentuk matriks:
𝑌𝑌 =𝑋𝑋𝛽𝛽+ ɛ (2.14)
dengan:
𝑌𝑌=� 𝑦𝑦1
𝑦𝑦2
𝑦𝑦3
𝑦𝑦4
� 𝑋𝑋 =�
1 𝑋𝑋11 𝑋𝑋11 ⋯ 𝑋𝑋11
1 𝑋𝑋11 𝑋𝑋11 ⋯ 𝑋𝑋11
⋮ 1
⋮ 𝑋𝑋11
⋮ ⋯ ⋮ 𝑋𝑋11 ⋯ 𝑋𝑋11
� 𝛽𝛽 =� 𝛽𝛽0
𝛽𝛽0
𝛽𝛽0
𝛽𝛽0
� ɛ= � ɛ1
ɛ1
ɛ1
ɛ1
�
Untuk mendapatkan penaksir-penaksir MKT bagi 𝛽𝛽, maka dengan asumsi klasik
𝛽𝛽̂ =� 𝛽𝛽1
𝛽𝛽1
𝛽𝛽1
𝛽𝛽1
� 𝑒𝑒̂= � 𝑒𝑒1
𝑒𝑒1
𝑒𝑒1
𝑒𝑒1
�
Persamaan hasil estimasi dari persamaan (2.14) dapat ditulis sebagai:
𝑌𝑌=𝑋𝑋𝛽𝛽̂+ ɛ
atau
𝑒𝑒 =𝑌𝑌 − 𝑋𝑋𝛽𝛽̂ (2.15)
Karena tujuan MKT adalah meminimumkan jumlah kuadrat dari kesalahan, yaitu ∑𝑘𝑘 𝑒𝑒𝑖𝑖2
𝑖𝑖=1 = minimum, maka:
� 𝑒𝑒𝑖𝑖2 = 𝑒𝑒
𝑖𝑖2 𝑘𝑘
𝑖𝑖=1
+𝑒𝑒𝑖𝑖2+⋯+𝑒𝑒𝑖𝑖2
= [𝑒𝑒1 𝑒𝑒1 … 𝑒𝑒1]�
𝑒𝑒1
𝑒𝑒1
𝑒𝑒1
𝑒𝑒1
�= 𝑐𝑐 (2.16)
jadi,
� 𝑒𝑒𝑘𝑘 𝑖𝑖2
𝑖𝑖=1
=𝑒𝑒′𝑒𝑒
= (𝑌𝑌 − 𝑋𝑋𝛽𝛽̂)′(𝑌𝑌 − 𝑋𝑋𝛽𝛽̂ )
= 𝑌𝑌′𝑌𝑌 − 𝛽𝛽̂′𝑋𝑋′𝑌𝑌 − 𝑌𝑌′𝑋𝑋𝛽𝛽̂+𝛽𝛽̂′𝑋𝑋′𝑋𝑋𝛽𝛽̂
Oleh karena 𝛽𝛽̂′𝑋𝑋′𝑌𝑌 adalah skalar, maka matriks transposenya adalah:
�𝛽𝛽̂′𝑋𝑋′𝑌𝑌�′ = 𝑌𝑌′𝑋𝑋𝛽𝛽̂ jadi,
𝑒𝑒′𝑒𝑒=𝑌𝑌′𝑌𝑌 −2𝛽𝛽̂′𝑋𝑋′𝑌𝑌+𝛽𝛽̂′𝑋𝑋′𝑋𝑋𝛽𝛽̂ (2.17)
Untuk menakar parameter 𝛽𝛽̂,maka 𝑒𝑒′𝑒𝑒 harus diminimumkan terhadap 𝛽𝛽̂, maka:
� 𝑒𝑒𝑖𝑖2 𝑘𝑘
𝑖𝑖=1
𝜕𝜕
𝜕𝜕𝛽𝛽̂′�� 𝑒𝑒𝑖𝑖
2
𝑘𝑘
𝑖𝑖=1 �
=𝑌𝑌′𝑌𝑌 −2𝛽𝛽̂′𝑋𝑋′𝑌𝑌+𝛽𝛽̂′𝑋𝑋′𝑋𝑋𝛽𝛽̂= 0
atau:
𝑋𝑋′𝑋𝑋𝛽𝛽̂ =𝑋𝑋′𝑌𝑌
𝛽𝛽̂ = (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝑌𝑌 dengan ketentuan det (𝑋𝑋′𝑋𝑋) ≠ 0 (2.18)
2.5.3 Sifat Penduga Kuadrat Terkecil
Menurut Sembiring (2003), metode kuadrat terkecil memiliki beberapa sifat yang baik. Untuk menyelidiki sifatnya, pandang kembali model umum regresi linier pada persamaa
(2.14). Dalam hal ini, dianggap bahwa 𝜀𝜀 bebas satu sama lain dan E(𝜀𝜀) = 0, var = 𝜕𝜕2.
Dengan demikian, maka 𝐸𝐸(𝑌𝑌) =𝑋𝑋𝛽𝛽̂ dan 𝑐𝑐𝑐𝑐𝑣𝑣(𝑌𝑌) =𝜎𝜎2𝐼𝐼.
Jadi sifat penduga kuadrat terkecil adalah:
1. Tak bias
Jika 𝐸𝐸�𝛽𝛽̂�= 𝛽𝛽 maka 𝛽𝛽̂ adalah penduga tak bias dari 𝛽𝛽. Dari persamaan (2.15)
diketahui:
𝛽𝛽̂= (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝑌𝑌
= (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′(𝑋𝑋𝛽𝛽+ 𝜀𝜀)
= (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝑋𝑋𝛽𝛽+ (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′ 𝜀𝜀
= 𝛽𝛽+ (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′ (2.19)
dengan (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝑋𝑋= 1
𝐸𝐸�𝛽𝛽̂�=𝐸𝐸[(𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝑌𝑌]
= (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′ 𝐸𝐸(𝑌𝑌)
= (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′(𝑋𝑋𝛽𝛽)
= (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝑋𝑋𝛽𝛽
= 𝐼𝐼𝛽𝛽 = 𝛽𝛽
Jika 𝑐𝑐𝑐𝑐𝑣𝑣(𝑌𝑌) =𝜎𝜎2𝐼𝐼 maka matriks kovarian untuk 𝛽𝛽̂ diberikan oleh 𝜎𝜎2 =
(𝑋𝑋′𝑋𝑋)−1. Jika 𝐸𝐸(𝑌𝑌) =𝑋𝑋𝛽𝛽 dan 𝑐𝑐𝑐𝑐𝑣𝑣(𝑌𝑌) =𝜎𝜎2𝐼𝐼, maka penduga kuadrat terkecil 𝛽𝛽̂
mempunyai varian minimum diantara semua variabel penduga tak bias linier. Bukti:
𝑐𝑐𝑐𝑐𝑣𝑣�𝛽𝛽̂�= 𝐸𝐸 ���𝛽𝛽̂ − 𝐸𝐸�𝛽𝛽̂�� �𝛽𝛽̂ − 𝐸𝐸�𝛽𝛽̂���
′
�
= 𝐸𝐸[( 𝛽𝛽+ (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝜀𝜀 − 𝛽𝛽)(𝛽𝛽+ (𝑋𝑋′𝑋𝑋)−1(𝑋𝑋′)𝜀𝜀)− 𝛽𝛽′]
=𝐸𝐸[((𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝜀𝜀)((𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝜀𝜀)′]
= 𝐸𝐸[(𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝜀𝜀𝜀𝜀′𝑋𝑋(𝑋𝑋′𝑋𝑋)−1]
= (𝑋𝑋′𝑋𝑋)−1𝑋𝑋′𝑋𝑋(𝑋𝑋′𝑋𝑋)−1𝐸𝐸(𝜀𝜀′𝜀𝜀)
= (𝑋𝑋′𝑋𝑋)−1𝐼𝐼𝜎𝜎2
= (𝑋𝑋′𝑋𝑋)−1𝜎𝜎2 (2.20)
2.6 Uji Regresi Linier
Pengujian nyata regresi adalah sebuah pengujian untuk menentukan apakah ada
hubungan linier antara varaiabel tak bebas Y dan variabel bebas 𝑋𝑋1,𝑋𝑋2, … ,𝑋𝑋𝑘𝑘.
Uji yang digunakan adalah uji mengggunakan statistik F berbentuk:
𝐹𝐹𝐻𝐻𝑖𝑖𝑡𝑡𝐻𝐻𝑚𝑚𝐻𝐻 = 𝐽𝐽𝐾𝐾𝐽𝐽
𝑘𝑘 � 𝐽𝐽𝐾𝐾𝑆𝑆
(𝑚𝑚−𝑘𝑘−1)
� (2.21)
dengan:
JKR = Jumlah Kuadrat Regresi
JKS = Jumlah Kuadrat Sisa
k = Derajat kebebasan JKR
(n– k- 1) = Derajat kebebasan JKS
Dalam uji hipotesis, digunakan daerah kritis:
𝐻𝐻0 ditolak jika 𝐹𝐹𝐻𝐻𝑖𝑖𝑡𝑡𝐻𝐻𝑚𝑚𝐻𝐻 >𝐹𝐹𝑇𝑇𝑎𝑎𝑏𝑏𝑒𝑒𝑇𝑇
dengan:
Selanjutnya, jika model regresi layak digunakan akan dilakukan lagi uji terhadap koefisien-koefisien regresi secara terpisah untuk mengetahui apakah koefisien tersebut layak dipakai dalam persamaan atau tidak.
Rumusan hipotesis untuk menguji parameter regresi secara parsial adalah sebagai berikut:
𝐻𝐻0 ∶ 𝛽𝛽𝑗𝑗 = 0 artinya koefisien regresi ke-𝑗𝑗 tidak signifikan atau variabel bebas ke-𝑗𝑗 tidak
berpengaruh nyata terhadap 𝑌𝑌.
𝐻𝐻1 ∶ 𝛽𝛽𝑗𝑗 ≠0 artinya koefisien regresi ke-𝑗𝑗 signifikan atau variabel bebas ke-𝑗𝑗
berpengaruh nyata terhadap 𝑌𝑌.
Statistik uji yang digunakan untuk menguji parameter regresi secara parsial adalah:
𝑡𝑡𝐻𝐻𝑖𝑖𝑡𝑡𝐻𝐻𝑚𝑚𝐻𝐻 �𝛽𝛽̂𝑗𝑗�= 𝛽𝛽�𝑗𝑗 �𝑣𝑣𝑎𝑎𝑡𝑡 �𝛽𝛽�𝑗𝑗�
(2.23)
Jika �𝑡𝑡𝐻𝐻𝑖𝑖𝑡𝑡𝐻𝐻𝑚𝑚𝐻𝐻 �𝛽𝛽̂𝑗𝑗��> 𝑡𝑡(𝑚𝑚−𝑝𝑝−1);𝛼𝛼/2, maka 𝐻𝐻0 ditolak yang artinya variabel bebas ke-𝑗𝑗
berpengaruh nyata terhadap 𝑌𝑌.
2.7 Analisis Klaster
2.7.1 Konsep Dasar
Analisis klaster merupakan suatu kelas teknik, dipergunakan untuk mengklasisfikasi objek atau kasus (responden) ke dalam kelompok yang relatif homogen, yang disebut
klaster (cluster). Objek/ kasus/ variabel dalam satu klaster cenderung mirip satu sama
lain dan berbeda jauh (tidak sama) dengan objek dari klaster lainnya. Analisis klaster
disebut juga analisis klasifikasi atau taksonomi numerik (numerical taxonomy). Setiap
objek hanya masuk ke dalam 1 klaster saja, tidak terjadi tumpang tindih (overlapping)
(Supranto, 2010).
(X2)
(X1)
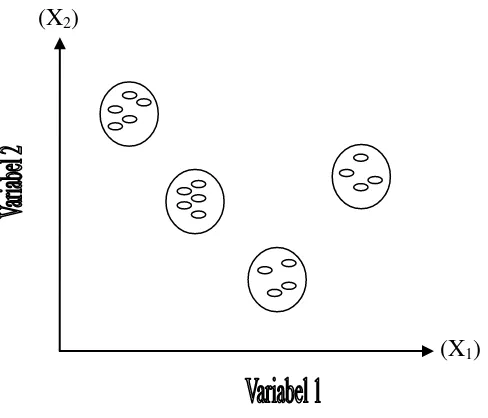
Gambar 2.1 menunjukkan hasil pengklasteran yang ideal, di mana setiap objek/ variabel/ kasus hanya masuk atau menjadi anggota dari salah satu klaster (tidak mungkin menjadi anggota dari dua klaster atau lebih). Gambar 2.1 menunjukkan situasi
di mana klaster dipisahkan secara berbeda (distincly separated) pada dua variabel.
Perhatikan bahwa setiap objek/ kasus/ variabel hanya masuk ke dalam1 klaster dan tidak
terjadi tumpang tindih, kalster saling meniadakan (mutually exclusive).
Sebaliknya pada gambar 2.2 menunjukkan hasil pengklasteran yang sering terjadi dalam praktik, yaitu terjadi tumpang tindih, artinya objek/ variabel yang seharusnya menjadi anggota klaster 1, menjadi anggota klaster 2, dan sebaliknya.
Gambar 2.2: Pengklasteran dalam praktik
(X2)
2.7.2 Melakukan Analisis Klaster
Adapaun langkah-langkah yang diperlukan untuk melakukan analisis klaster adalah:
1. Merumuskan Masalah
Hal yang paling penting dalam perumusan masalah analisis klaster ialah pemilihan variabel-variabel yang akan digunakan untuk pengklasteran Memasukkan satu atau dua varaiebel yang tidak relevan akan mendistorsi hasil pengklasteran yang kemungkinan besar sangat bermanfaat.
Pada dasarnya set variabel yang dipilih harus menguraikan kemiripan (similarity),
yang memang benar-benar relevan dengan permasalahn yang akan dibahas.
2. Memilih Ukuran Jarak
Oleh karena tujuan analisis klaster adalah untuk mengelompokkan objek/ variabel yang mirip dalam klaster yang sama, maka beberapa ukuran diperlukan untuk mengakses seberapa mirip atau berbeda objek/ objek atau varaiabel/ varaiabel tersebut.Pendekatan yang paling biasa ialah mengukur kemiripan dinyatakan dalam
jarak (distance) antara pasangan objek.
Ukuran kemiripan yang yang paling biasa dipakai ialah jarak euclidean (euclidean
distance) atau nilai kuadratnya yang merupakan akar dari jumlah kuadrat perbedaan/ deviasi di dalam nilai untuk setiap variabel. Rumusnya adalah sebagai berikut:
𝐷𝐷(𝑋𝑋,𝑌𝑌) =�(∑ 𝑋𝑋𝑖𝑖 − 𝑌𝑌𝑖𝑖)2 (2.25)
3. Memilih Suatu Prosedur Pengklasteran
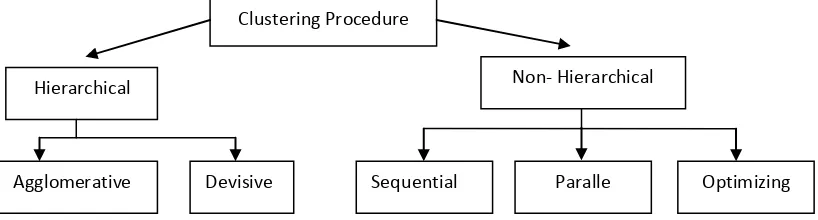
Gambar 2.3: Klasifikasi Prosedur Pengklasteran
Clustering Procedure
Hierarchical
Devisive
Prosedur pengklasteran bisa hierarki dan bisa juga non hierarki. Pengklasteran hierarki ditandai dengan pengembangan suatu hierarki atau struktur mirip pohon (tree like structure). Metode hierarki bisa aglomeratif atau devisif (agglomerative or divisive).
Pengklasteran agglomeratif dimulai dengan setiap objek dalam suatu klaster yang terpisah. Klaster dibentuk dengan mengelompokkan objek/ variabel ke dalam klaster yang semakin membesar., yaitu semakin banyak elemen atau objek yang menjadi anggotanya. Proses ini dilanjutkan sampai semua objek menjadi anggota dari suatu klaster tunggal. Sebaliknya pengklasteran devisif dimulai dari semua objek dikelompokkan menjadi klaster tunggal. Kemudian klaster dibagi atau dipisah, sampai setiap objek berada di dalam klaster yang terpisah.
Hasil dari kedua metode agglomeratif dan devisif bisa disajikan dalam bentuk dendogram, sebagai suatu diagram dua dimensi. Di sini akan dibahas
prosedur agglomerasi hierarkis, khususnya metode pertalian (linkage method), yaitu
single linkage method (metode pertalian tunggal), complete linkage method (metode
pertalian lengkap), average linkage method (metode pertalian rata-rata).
Berikut adalah langkah-langkah di dalam pengklasteran agglomeratif hierarkis untuk mengelompokkan N objek (responden/ kasus/ variabel).
a. Mulai dengan N kelompok (klaster), masing-masing kelompok suatu objek
tunggal dan matriks simetris N x N berjarak D = {dik}.
Centroid Variance
Linkage
Ward’s Method
Average Linkage Complete Linkage
b. Selidiki jarak matriks untuk pasangan kelompok yang paling mirip atau
paling dekat. Misalkan jarak yang paling mirip yaitu U dan V = duv.
c. Gabungkan kelompok atau klaster U dan V.
Klaster ini disebut klaster (UV). Perbaharui entry di dalam matriks jarak
dengan:
i. Menghapus/ menghilangkan baris dan kolom, sesuai dengan klaster
U dan V.
ii. Tambah satu baris dan kolom memberikan jarak antara klaster (UV)
dan sisa klaster.
d. Ulangi langkah (2 dan 3) sebanyak (N-1) kali.
Seluruh objek akan berada dalam 1 klaster/ kelompok setelah algoritma
selesai. Catat identitas klaster yang digabung dan tingkatan (distance or
similarities) pada saat mana penggabungan terjadi.
Jenis prosedur pengklasteran yang kedua yaitu metode nonhierarki atau
yang sering disebut K-means clustering sangat berbeda dengan metode hierarki.
Dalam metode ini, kita terlebih dahulu menentukan jumlah klaster dan pusat klaster
sembarang, sehingga hasil klaster bergantung pada bagaimana pusat (center) dipilih.
4. Menentukan Banyaknya Klaster
Isu utama dalam analisis klaster ialah menetukan berapa banyaknya klaster. Dalam kenyataannya, tidaka ada aturan baku untuk menentukan berapa sebetulnya banyaknya klaster, namun demikian ada beberapa petunjuk yang bisa dipergunakan, yaitu:
a. Pertimbanngan teoritis, konseptual, praktis, mungkin bisa diusulkan/ disarankan
untuk menetukan berapa banyaknya klaster yang sebenarnya.
b. Di dalam pengklasteran hierarki, jarak dimana klaster digabung bisa
dipergunakan sebagai kriteria. Hal paling mudah adalah dengan melihat dendogram.
c. Di dalam pengklasteran nonhierarki, rasio jumlah varian dalam klaster dengan
jumlah varian antarklaster dapat diplotkan melawan banyaknya klaster, di luar titik ini biasanya tidak perlu.
5. Menginterpretasi dan Memprofil Klaster
2.8 Analisis Komponen utama
Analisis komponen utama merupakan teknik statsistik yang dapat digunakan untuk mereduksi sejumlah variabel bebas menjadi beberapa variabel baru yang bersifat orthogonal dan tetap mempertahankan total keragaman dari variabel asalnya.
Analisis komponen utama bertujuan untuk mengubah dari sebagian besar variabel asli yang digunakan yang saling berkorelasi menjadi satu set variabel baru yang lebih kecil saling bebas dan merupakan kombinasi linier dari variabel asalnya.
Selanjutnya variabel baru ini dinamakan komponen utama (principal component).
Secara umum tujuan dari analisis komponen utama adalah mereduksi dimensi data sehingga lebih mudah untuk menginterpretasikan data tersebut.
2.8.1 Menentukan Komponen Utama
Komponen utama ditentukan melalui matriks kovarian (Ʃ) dan matriks korelasi (𝜌𝜌) dari
𝑚𝑚1,𝑚𝑚2, … ,𝑚𝑚𝑝𝑝. Matriks kovarian Ʃdigunakan untuk membentuk komponen utama apabila
semua variabel yang diamati mempunyai satuan pengukuran yang sama. Sedangkan
matriks korelasi 𝜌𝜌 digunakan apabila variabel yang diamati tidak mempunyai satuan
pengukuran yang sama. Variabel tersebut perlu dibakukan, sehingga komponen utama berdasarkan matriks korelasi ditentukan dari variabel baku.
2.8.1.1 Komponen Utama Berdasarkan Matriks Kovarian (Ʃ)
Dipunyai matriks kovarianƩdari 𝑝𝑝 buah variabel, 𝑚𝑚1,𝑚𝑚2, … ,𝑚𝑚𝑝𝑝. Total varian dari
variabel-variabel tersebut didefinisikan sebagai 𝑡𝑡𝑡𝑡(Ʃ) =𝑡𝑡𝑡𝑡𝑎𝑎𝑐𝑐𝑒𝑒(Ʃ) yaitu penjumlahan
cirinya, yaitu: 𝜆𝜆1 ≥ 𝜆𝜆2 ≥ ⋯ ≥ 𝜆𝜆𝑝𝑝 ≥0 dan vektor ciri-vektor cirinya 𝛼𝛼1,𝛼𝛼2, … ,𝛼𝛼𝑝𝑝.
Komponen utama dari vektor berukuran 𝑝𝑝× 1,𝑚𝑚=�𝑚𝑚1,𝑚𝑚2, … ,𝑚𝑚𝑝𝑝�
′
adalah kombinasi linier terbobot dari variabel asal yang dapat menerangkan keragaman terbesar.
Komponen utama pertama dapat dituliskan sebagai:
𝑌𝑌1 = 𝛼𝛼11𝑋𝑋1+𝛼𝛼12𝑋𝑋2+⋯+𝛼𝛼1𝑝𝑝𝑋𝑋𝑝𝑝
𝑌𝑌1 =𝛼𝛼1′𝑋𝑋 (2.29)
dengan:
𝛼𝛼1′𝑋𝑋=�𝛼𝛼11,𝛼𝛼12, … ,𝛼𝛼1𝑝𝑝�
′
dan 𝛼𝛼1′𝛼𝛼1 = 1
Varian dari komponen utama pertama adalah:
𝜎𝜎2𝑌𝑌
1 =� � 𝛼𝛼𝑖𝑖1𝛼𝛼𝑗𝑗1𝑠𝑠𝑖𝑖𝑗𝑗
𝑝𝑝
𝑗𝑗=1
𝑝𝑝
𝑖𝑖=1
= 𝛼𝛼1′ ∑ 𝛼𝛼1 (2.30)
Vektor pembobot 𝛼𝛼′ adalah vektor normal, koefisisen 𝛼𝛼𝑖𝑖1 adalah unsur-unsur
dari vektor ciri yang berhubungan dengan akar ciri terbesar 𝜆𝜆1 yang diturunkan dari
matriks kovarian Ʃ dipilih sedemikian sehingga 𝜎𝜎2𝑌𝑌
1 mencapai maksimum dengan
kendala 𝛼𝛼1′𝛼𝛼1 = 1. Menggunakan teknik pemaksimuman berkendala Lagrange
diperoleh persamaan:
𝑓𝑓(𝛼𝛼1,𝜆𝜆1) =𝜎𝜎2𝑌𝑌
1− 𝜆𝜆1(𝛼𝛼1′𝛼𝛼1−1) =𝛼𝛼1′ � 𝛼𝛼1− 𝜆𝜆1(𝛼𝛼1′𝛼𝛼1−1)
Fungsi ini mencapai maksimum jika turunan parsial pertama 𝑓𝑓(𝛼𝛼1,𝜆𝜆1) terhadap
𝛼𝛼1 sama dengan nol.
𝜕𝜕𝑓𝑓(𝛼𝛼1,𝜆𝜆1)
𝜕𝜕𝛼𝛼1 = 2∑ 𝛼𝛼1 −2𝜆𝜆1𝛼𝛼1 = 0 atau ∑ 𝛼𝛼1 = 𝜆𝜆1𝛼𝛼1 (2.31)
Persamaan (2.31) dipenuhi oleh 𝜆𝜆1 dan 𝛼𝛼1 yang merupakan pasangan akar ciri
varian 𝑌𝑌1 = 𝜎𝜎2𝑌𝑌1 =𝛼𝛼1′ ∑ 𝛼𝛼1 = 𝜆𝜆1 harus maksimum, maka 𝜆𝜆1 adalah akar ciri yang
terbesar dari matriks Ʃdan𝛼𝛼1 adalah vektor ciri yang bersesuaian dengan 𝜆𝜆1.
Komponen utama kedua adalah kombinasi linier terbobot variabel asal yang tidak berkorelasi dengan komponen utama pertama, serta memaksimumkan sisa kovarian data setelah diterangkan oleh komponen utama pertama. Komponen utama kedua dapat dituliskan sebagai:
𝑌𝑌2 = 𝛼𝛼21𝑋𝑋1+𝛼𝛼22𝑋𝑋2+⋯+𝛼𝛼2𝑝𝑝𝑋𝑋𝑝𝑝
𝑌𝑌2 = 𝛼𝛼2′𝑋𝑋 (2.32)
dengan:
𝛼𝛼2′𝑋𝑋= �𝛼𝛼21,𝛼𝛼22, … ,𝛼𝛼2𝑝𝑝�
′
dan 𝛼𝛼2′𝛼𝛼2 = 1
Vektor pembobot 𝛼𝛼′ adalah vektor normal yang dipilih sehingga keragaman
komponen utama kedua maksimum, serta orthogonal terhadap vektor pembobot 𝛼𝛼1′ dari
komponen utama pertama. Agar varian dari komponen utama kedua maksimum, serta antara komponen utama kedua tidak berkorelasi dengan komponen utama pertama,
maka vektor pembobot 𝛼𝛼2 dipilih sedemikan sehingga 𝑌𝑌2 =𝛼𝛼2′𝑋𝑋 tidak berkorelasi
dengan 𝑌𝑌1= 𝛼𝛼1′𝑋𝑋. Varian komponen utama kedua (𝑌𝑌2) adalah:
𝜎𝜎2𝑌𝑌
2 = � � 𝛼𝛼𝑖𝑖2𝛼𝛼𝑗𝑗2𝑠𝑠𝑖𝑖𝑗𝑗
𝑝𝑝
𝑗𝑗=1
𝑝𝑝
𝑖𝑖=1
= 𝛼𝛼2′ ∑ 𝛼𝛼2 (2.33)
Varian tersebut akan dimaksimumkan dengan kendala 𝛼𝛼2′𝛼𝛼2 = 1 dan
𝑐𝑐𝑐𝑐𝑣𝑣(𝑦𝑦1,𝑦𝑦2) =𝑐𝑐𝑐𝑐𝑣𝑣(𝛼𝛼1𝑚𝑚,𝛼𝛼2𝑚𝑚) =𝛼𝛼1′ ∑ 𝛼𝛼2 = 0. Karena 𝛼𝛼1 adalah vektor ciri dari Ʃ dan Ʃ
adalah matriks simetris, maka: 𝛼𝛼1′Ʃ= (Ʃ𝛼𝛼1)′ = (𝜆𝜆𝛼𝛼1)′ = 𝜆𝜆𝛼𝛼1′.
Kendala 𝛼𝛼1′ ∑ 𝛼𝛼2 =𝜆𝜆𝛼𝛼1′𝛼𝛼2 = 0 dapat dituliskan sebagai 𝛼𝛼1′𝛼𝛼2 = 0. Jadi fungsi
Lagrange yang dimaksimumkan adalah:
Fungsi ini mencapai maksimum jika turunan parsial pertama 𝑓𝑓(𝛼𝛼2,𝜆𝜆2,𝜆𝜆)
terhadap 𝛼𝛼2 sama dengan nol, sehingga diperoleh:
𝜕𝜕𝑓𝑓(𝛼𝛼1,𝜆𝜆1,𝜆𝜆)
𝜕𝜕𝛼𝛼2 = 2∑ 𝛼𝛼2−2𝜆𝜆2𝛼𝛼2− 𝜆𝜆 ∑ 𝛼𝛼1 = 0 (2.35)
Jika persamaan (2.35) dikalikan dengan 𝛼𝛼1′ maka diperoleh:
2𝛼𝛼1′ ∑ 𝛼𝛼2 −2𝜆𝜆2𝛼𝛼1′𝛼𝛼2− 𝜆𝜆𝛼𝛼1′ ∑ 𝛼𝛼1 = 0 (karena ∑ 𝛼𝛼1 = 𝜆𝜆1𝛼𝛼1)
2𝛼𝛼1′ � 𝛼𝛼2−2𝜆𝜆2𝛼𝛼1′𝛼𝛼2− 𝜆𝜆𝜆𝜆1𝛼𝛼1′𝛼𝛼1 = 0
2𝛼𝛼1′ � 𝛼𝛼2 −0− 𝜆𝜆𝜆𝜆1 = 0
Oleh karena 2𝛼𝛼1′ ∑ 𝛼𝛼2 = 0 maka 𝜆𝜆= 0. Dengan demikian persamaan (2.35) setelah
diturunkan terhadap 𝛼𝛼2 menjadi
𝜕𝜕𝑓𝑓(𝛼𝛼1,𝜆𝜆1,𝜆𝜆)
𝜕𝜕𝛼𝛼2
= 2� 𝛼𝛼2−2𝜆𝜆2𝛼𝛼2 = 0
∑ 𝛼𝛼2− 𝜆𝜆2𝛼𝛼2 = 0 (2.36)
Jadi 𝜆𝜆2 dan 𝛼𝛼2 merupakan pasangan akar ciri dan vektor ciri dari matriks varian
kovarian Ʃ. Seperti halnya penurunan pada pencarian 𝛼𝛼1, akan diperoleh bahwa 𝛼𝛼1
adalah vektor yang bersesuaian dengan akar ciri terbesar kedua dari matriks Ʃ.
Secara umum komponen utama ke-j dapat dituliskan sebagai berikut:
𝑌𝑌𝑗𝑗 =𝛼𝛼1𝑗𝑗𝑋𝑋1+𝛼𝛼2𝑗𝑗𝑋𝑋2+⋯+𝛼𝛼𝑝𝑝𝑗𝑗𝑋𝑋𝑝𝑝
𝑌𝑌𝑗𝑗 = 𝛼𝛼𝑗𝑗′𝛼𝛼 (2.37)
dengan:
𝛼𝛼𝑗𝑗′ = �𝛼𝛼𝑗𝑗1,𝛼𝛼𝑗𝑗2, … ,𝛼𝛼𝑗𝑗𝑝𝑝�
′
dan 𝛼𝛼𝑗𝑗′𝛼𝛼𝑗𝑗 = 1
vektor pembobot 𝛼𝛼𝑗𝑗′ diperoleh dengan memaksimumkan keragaman komponen utama
ke-j, yaitu:
𝜎𝜎2𝑌𝑌
𝑗𝑗 =𝛼𝛼𝑗𝑗′∑ 𝛼𝛼𝑗𝑗 (2.38)
dengan kendala:
𝛼𝛼𝑗𝑗′𝛼𝛼
Dengan kendala ini, maka akar ciri 𝜆𝜆𝑗𝑗 dapat diinterpretasikan sebagai ragam komponen
utama ke-j sesama komponen utama tidak berkorelasi.
Vektor pembobot 𝛼𝛼𝑗𝑗′ yang merupakan koefisien pembobot variabel asal bagi
komponen utama ke- j diperoleh dari matriks peragam Ʃ yang diduga dengan matriks S
berikut:
𝑆𝑆= 1
𝑚𝑚−1∑ (𝑚𝑚ℎ− 𝑚𝑚̅)(𝑚𝑚ℎ− 𝑚𝑚̅)
′ 𝑚𝑚
ℎ=1 (2.39)
2.8.1.2 Komponen Utama Berdasarkan Matriks Korelasi (𝝆𝝆)
Jika variabel yang diamati tidak mempunyai satuan pengukuran yang sama, maka varaiabel tersebut perlu dibakukan sehingga komponen utama ditentukan dari variabel baku (Vincent Gasperz, 1991). Variabel asal perlu ditransformasi ke dalam variabel
baku Z, dalam catatan matriks adalah:
𝑍𝑍 =𝑋𝑋−µ
𝜎𝜎 (2.40)
dengan:
Z = variabel baku
X = variabel asal
µ = rata-rata variabel asal
σ = standard deviasi
Komponen utama dari Z dapat ditentukan dari vektor ciri yang diperoleh melalui
matriks korelasi yang diduga dengan matriks 𝜌𝜌, dimana vektor pembobot 𝛼𝛼𝑗𝑗′ diperoleh
dengan memaksimumkan keragaman komponen utama ke- j dengan kendala: 𝛼𝛼𝑗𝑗′𝛼𝛼𝑗𝑗 = 1,
serta 𝛼𝛼𝑗𝑗′𝛼𝛼𝑗𝑗 = 0, untuk 𝑖𝑖 ≠ 𝑗𝑗.
Semua formula yang telah diturunkan berdasarkan variabel-variabel 𝑚𝑚1,𝑚𝑚2, … ,𝑚𝑚𝑝𝑝
dengan matriks Ʃ akan berlaku untuk peubah-peubah 𝑧𝑧1,𝑧𝑧2, … ,𝑧𝑧𝑝𝑝 dengan nilai matriks
Sehingga diperoleh komponen utama ke- jdengan menggunakan variabel baku yaitu:
𝑌𝑌𝑗𝑗 = 𝛼𝛼𝑗𝑗′𝑍𝑍 dengan:
𝑌𝑌𝑗𝑗 = komponen utama ke- j
𝛼𝛼𝑗𝑗′ = vektor ciri ke- j
𝑍𝑍 = variabel baku
2.8.2 Kriteria Pemilihan Komponen Utama
Salah satu tujuan dari analisis komponen utama adalah mereduksi dimensi data asal
yang semula terdapat p variabel bebas menjadi k komponen utama (dimana 𝑘𝑘< 𝑝𝑝).
Kriteria pemilihan k didasarkan pada akar ciri yang lebih besar dari satu, dengan kata
lain hanya komponen utama yang memiliki akar ciri lebih besar dari satu yang dilibatkan dalam analisis.
2.9 Analisis Regresi Komponen Utama
Aroef, M. A. (1991) mengatakan bahwa analisis komponen utama bertujuan untuk menyederhanakan variabel yang diamati dengan cara menyusutkan dimensinya. Hal ini dilakukan dengan menghilangkan korelasi variabel melalui transformasi variabel asal ke
variabel baru yang tidak berkorelasi. Variabel baru (y) disebut komponen utama yang
merupakan hasil transformasi dari variabel asal x yang modelnya dalam catatan matriks
adalah:
y= Ax
dimana A adalah matriks yang melakukan transformasi terhadap variabel asal x,
sehingga diperoleh vektor komponen y. Secara umum komponen utama ke-j dapat
𝑌𝑌𝐽𝐽 = 𝑎𝑎1𝑗𝑗𝑋𝑋1+ 𝑎𝑎2𝑗𝑗𝑋𝑋2… + 𝑎𝑎𝑝𝑝𝑗𝑗𝑋𝑋𝑝𝑝
Regresi komponen utama adalah teknik yang digunakan untuk meregresikan komponen utama dengan variabel tak bebas melalui metode kuadrat terkecil. Tahap pertama pada prosedur regresi komponen utama yaitu menentukan komponen utama
yang merupakan kombinasi linier dari beberapa variabel X, dan tahap kedua adalah
variabel tak bebas diregresikan pada komponen utama dalam sebuah model regresi linier.
Persamaan regresi komponen utama berdasarkan matriks kovarian pada dasarnya hampir sama dengan persamaan regresi komponen utama berdasarkan matriks
korelasi yaitu variabel X1, X2, …, Xp diganti dengan variabel baku Z1, Z2, …, Zp. Kedua
persamaan tersebut digunakan sesuai dengan pengukuran variabel-variabel yang diamati.
Apabila diberikan notasi W1, W2, …, Wksebagai banyaknya komponen utama
yang dilibatkan dalam analisis regresi komponen utama, dimana k lebih kecil daripada
banyaknya variabel penjelas asli X, yaitu sejumlah p(k<p). Maka bentuk umum
persamaan regresi komponen utama adalah:
𝑌𝑌 = 𝛿𝛿0 + 𝛿𝛿1𝑊𝑊1+ 𝛿𝛿2𝑊𝑊2 + … + 𝛿𝛿𝑘𝑘𝑊𝑊𝑘𝑘 (2.41) dengan:
Y = variabel tak bebas
Wi = variabel komponen utama
δi = parameter model regresi komponen utama
Komponen utama merupakan kombinasi linier dari variabel Z:
𝑊𝑊1 = 𝛼𝛼11𝑍𝑍1+ 𝛼𝛼21𝑍𝑍2+ … + 𝛼𝛼𝑃𝑃1𝑍𝑍𝑃𝑃
𝑊𝑊2 = 𝛼𝛼12𝑍𝑍1+ 𝛼𝛼22𝑍𝑍2+ … +𝛼𝛼𝑃𝑃2𝑍𝑍𝑃𝑃
. . . … .
. . . … .
𝑊𝑊𝐾𝐾 = 𝛼𝛼1𝐾𝐾𝑍𝑍1+ 𝛼𝛼2𝐾𝐾𝑍𝑍2+ … + 𝛼𝛼𝑃𝑃𝐾𝐾𝑍𝑍𝑃𝑃
dengan:
Wi = komponen utama
αij =koefisien komponen utama
Zi = variabel baku
Komponen utama W1, W2, …, Wkdalam persamaan di atas disubstitusikan ke dalam
persamaan bentuk umum regresi komponen utama, kemudian diselesaikan secara aljabar, maka diperoleh:
Ŷ = 𝛽𝛽0+ 𝛽𝛽1𝑍𝑍1+ 𝛽𝛽2𝑍𝑍2+ … + 𝛽𝛽𝑃𝑃𝑍𝑍𝑝𝑝 (2.42)
dengan:
β0 = δ0 = Ŷ
β1 = δ1α11+ δ2α12+ … + δkα1k
. . . … .
. . . … .
. . . … .