p-ISSN : 2550-0384; e-ISSN : 2550-0392
GEOMETRI TRANSFORMASI DALAM MOTIF BATIK KAWUNG YOGYAKARTA
Paskalia Pradanti
Universitas Sanata Dharma [email protected]
Maria Rettian Anggita Sari
Universitas Sanata Dharma
ABSTRACT. Batik is one of Yogyakarta cultural element and one of known batik motif in Yogyakarta named kawung. Ethnomathematics is a research field that studies the relation between mathematics and culture. Mathematical aspects found in kawung motif could be studied in the field of ethnomathematics and the mathematical aspect studied in this research is transformation geometry. Making processes of kawung motif were described in this paper using transformation geometry concepts. From this research results, it could be showed that mathematics is found in Yogyakarta cultural element, especially in the making of kawung batik motif.
Keywords: ethnomathematics, yogyakarta batik, kawung, transformation geometry ABSTRAK. Salah satu unsur budaya yang berkembang di Yogyakarta adalah batik. Motif batik yogyakarta yang banyak dikenal oleh masyarakat. Suatu bidang ilmu yang mempelajari hubungan antara budaya dan matematika adalah etnomatematika. Melalui etnomatematika dapat dikaji berbagai aspek matematis yang dapat ditemukan dalam motif kawung, termasuk aspek goemetri transformasi. Proses penyusunan motif kawung dijelaskan dalam makalah ini dengan menggunakan konsep goemetri transformasi. Dari penelitian ini dapat ditunjukkan bahwa matematika ditemukan dalam unsur budaya yogyakarta khususnya digunakan pada penyusunan motif batik kawung.
Kata Kunci: etnomatematika, batik yogyakarta, kawung, geometri transformasi
1. PENDAHULUAN
Yogyakarta memiliki berbagai macam budaya dengan berbagai konteks atau unsur budaya, seperti bahasa, kebiasaan, mitos, serta simbol. Batik merupakan salah satu unsur budaya yang berkembang di Yogyakarta. Batik ditetapkan oleh UNESCO sebagai Masterpieces of the Oral and Intangibel
Heritage of Humanity pada tanggal 2 Oktober 2009 dan tanggal 2 Oktober
ditetapkan sebagai Hari Batik Nasional oleh Pemerintah Indonesia. Dengan demikian, batik semakin dikenal oleh masyarakat Indonesia, termasuk
Purwokerto, 3 Desember 2016
Yogyakarta. Berbagai motif batik yang berkembang di Yogyakarta juga semakin dikenal oleh masyarakat Yogyakarta.
Motif batik dari berbagai daerah yang merupakan representasi dari lingkungan dan filosofi kehidupan suatu daerah memiliki ciri khas masing-masing. Motif batik yang berkembang di Yogyakarta memiliki ciri khas latar atau warna dasar kain hitam dan putih dengan warna batik putih, biru tua kehitaman, dan cokelat soga. Kawung merupakan salah satu motif batik yang berbentuk geometris dan banyak dikenal oleh masyarakat Yogyakarta.
Istilah etnomatematika diperkenalkan oleh Ubiratan D’Ambrosio (1985: 45) yang menyatakan bahwa etnomatematika merupakan matematika yang digunakan dalam kelompok-kelompok budaya yang dapat diidentifikasi. Etnomatematika dapat dipahami sebagai suatu bidang ilmu yang mempelajari hubungan antara matematika dan budaya. Melalui etnomatematika, dapat dikaji berbagai aspek matematis yang terdapat dalam unsur penyusun motif kawung. Bishop (1988) mengelompokkan aspek matematika berdasarkan enam aktivitas matematika fundamental, yaitu menghitung (counting), menempatkan (locating), mengukur (measuring), mendesain (designing), bermain (playing), menjelaskan (explaining). Aspek matematis yang akan dikaji dalam artikel ini yaitu aspek geometri transformasi yang digunakan dalam menyusun unsur penyusun motif kawung.
2. HASIL DAN PEMBAHASAN 2.1 Motif Batik Kawung Yogyakarta
Motif kawung dipakai oleh raja dan keluarga dekatnya sebagai lambang keadilan dan keperkasaan. Unsur motif kawung berupa empat bulatan dengan sebuah titik pusat. Titik pusat pada unsur ini melambangkan seorang raja dan para pembantu
yang mendampingi dilanbangkan oleh empat bulatan. Motif kawung khas Yogyakarta dapat dilihat pada Gambar 1.
Purwokerto, 3 Desember 2016 Gambar 1. Motif batik kawung Yogyakarta.
Unsur motif kawung yang berupa empat bulatan dapat didekati dengan bangun datar elips. Satu unsur motif kawung dapat disusun dari satu elips yang ditransformasikan berdasarkan konsep transformasi seperti translasi, refleksi, atau rotasi. Proses penyusunan satu unsur motif kawung dapat dilakukan dengan berbagai cara dan urutan transformasi tertentu. Transformasi yang digunakan pada artikel ini yaitu rotasi dan refleksi. Cara penyusunan unsur motif kawung dijelaskan pada bagian berikutnya.
2.2 Penyusunan Motif Batik Kawung Yogyakarta
Menurut Rosa dan Orey (2010) dalam Rosa dan Orey (2011),
ethnomodeling adalah pendekatan pedagogis yang menghubungkan aspek budaya
dari matematika dengan aspek akademis. Bassanezi (2002) dan D’Ambrosio (2000) dalam Rosa dan Orey (2012: 12) menyatakan bahwa ethnomodeling merupakan proses elaborasi masalah dan pertanyaan yang tumbuh dari situasi nyata yang membentuk suatu gambaran atau makna dari versi matematika yang teridealisasi. Penyelidikan-penyelidikan yang dilakukan dalam pemodelan berguna dalam penerjemahan konteks-konteks etnomatematika (Bassanezi, 2002; Biembengut, 2000; Ferreira, 2004; Rosa dan Orey, 2007; Rios, 2000 dalam Rosa dan Orey, 2012:12). Ethnomodeling yang dilakukan pada artikel ini yaitu penyusunan unsur motif kawung menggunakan konsep-konsep pada geometri transformasi.
Purwokerto, 3 Desember 2016
Transformasi yang digunakan untuk menyusun satu unsur motif kawung dalam artikel ini adalah rotasi. Elips yang dirotasikan adalah elips yang diperoleh dengan merotasikan elips terhadap pusat putaran dengan sudut putar . Elips merupakan elips yang sumbu mayornya sejajar dengan . Persamaan elips yang yaitu
dengan syarat , , dan .
Berdasarkan persamaan elips dan syarat-syarat tersebut, diperoleh: (( * ( * ) (( * ( * ) ( * ( * ( * ( * ( * ( * ( * ( * ( * ( * (1) dengan ( ) ( ) .
Persamaan (1) dapat ditulis:
( * ( * ( ) ( ) ( ) ( ) (2) dengan dan .
Persamaan (2) merupakan persamaan elips dengan titik pusat ( ), panjang sumbu mayor , panjang sumbu minor , dan jarak fokus di mana
Purwokerto, 3 Desember 2016
√ . Puncak elips terletak pada titik ( ), ( ), ( ), dan ( ). Sedangkan koordinat fokus elips adalah ( ) dan ( ).
Rotasi titik terhadap pusat putaran dan sudut putar dilakukan dengan langkah sebagai berikut:
( * ( ) ( ) ( * ( √ √ √ √ ) ( ) ( * ( √ √ √ √ ) ( * ( √ √ √ √ ) dengan titik merupakan hasil rotasi titik .
Rotasi elips dapat dilakukan cukup dengan merotasikan titik puncak terhadap pusat putaran dan sudut putar untuk dan .
Hasil rotasi titik puncak ( ) yaitu
( * ( √ ( * √ ( *
)
Sedangkan hasil rotasi titik puncak ( ) yaitu
( * ( √ ( * √ ( *
Purwokerto, 3 Desember 2016
Hasil rotasi titik puncak ( ) yaitu
( * ( √ ( * √
√ ( * √
)
Sedangkan hasil rotasi titik puncak ( ) yaitu
( * ( √ ( * √
√ ( * √
)
Sehingga diperoleh elips yang melalui , , , dan .
Satu unsur motif kawung disusun dengan merotasikan titik puncak elips terhadap pusat putaran secara berturut-turut dengan sudut putar dan . Rotasi titik terhadap pusat putaran dan sudut putar dilakukan dengan langkah sebagai berikut
( * ( ) ( * ( * ( ) ( *
( * ( *
Hasil rotasi titik puncak ( √ ( ) √ ( ) ) yaitu
( * ( √ ( * √ ( *
)
Hasil rotasi titik puncak ( √ ( ) √ ( ) ) yaitu
( * ( √ ( * √ ( *
Purwokerto, 3 Desember 2016
Hasil rotasi titik puncak ( √ ( ) √ √ ( ) √ ) yaitu
( * ( √ ( * √
√ ( * √
)
Hasil rotasi titik puncak ( √ ( ) √ √ ( ) √ ) yaitu
( * ( √ ( * √
√ ( * √
)
Sehingga diperoleh elips yang melalui , , , dan .
Rotasi titik terhadap pusat putaran dan sudut putar dilakukan dengan langkah sebagai berikut
( * ( ) ( * ( * ( ) ( * ( * ( *
Hasil rotasi titik puncak ( √ ( ) √ ( ) ) yaitu
( * ( √ ( * √ ( *
)
Hasil rotasi titik puncak ( √ ( ) √ ( ) ) yaitu
( * ( √ ( * √ ( *
Purwokerto, 3 Desember 2016
Hasil rotasi titik puncak ( √ ( ) √ √ ( ) √ ) yaitu
( * ( √ ( * √
√ ( * √
)
Hasil rotasi titik puncak ( √ ( ) √ √ ( ) √ ) yaitu
( * ( √ ( * √
√ ( * √
)
Sehingga diperoleh yang melalui , , , dan .
Rotasi titik terhadap pusat putaran dan sudut putar dilakukan dengan langkah sebagai berikut
( * ( ) ( * ( * ( ) ( *
( * ( *
Hasil rotasi titik puncak ( √ ( ) √ ( ) ) yaitu
( ) ( √ ( * √ ( *
)
Hasil rotasi titik puncak ( √ ( ) √ ( ) ) yaitu
( ) ( √ ( * √ ( *
Purwokerto, 3 Desember 2016
Hasil rotasi titik puncak ( √ ( ) √ √ ( ) √ ) yaitu
( ) ( √ ( * √
√ ( * √
)
Hasil rotasi titik puncak ( √ ( ) √ √ ( ) √ ) yaitu
( ) ( √ ( * √
√ ( * √
)
Sehingga diperoleh persamaan elips yang melalui ( ), ( ), ( ), dan ( ).
Jadi, diperoleh elips , , , dan sebagai penyusun satu unsur motif kawung. Titik-titk puncak elips , , dan dapat ditentukan tanpa harus melakukan rotasi secara berurutan mulai dari sudut putar , , dan karena titik-titik puncak tersebut merupakan hasil rotasi titik puncak .
2.3 Contoh Penyusunan Motif Batik Kawung Yogyakarta
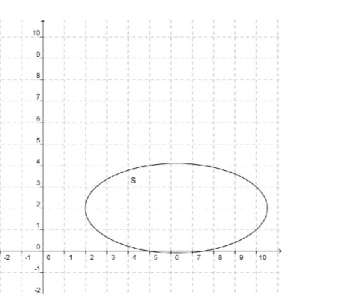
Pada contoh penyusunan satu unsur motif batik kawung digunakan persamaan elips . Dari persamaan tersebut
diperoleh , , , , , , , , , , titik puncak , , ,dan .
Purwokerto, 3 Desember 2016
Gambar 2. Sketsa elips
Rotasi titik puncak elips terhadap pusat putaran dan sudut putar adalah sebagai berikut. Hasil rotasi titik puncak yaitu
( * ( √ √
) ( √ √
) Hasil rotasi titik puncak yaitu
( * ( √ √
) ( √ √
) Hasil rotasi titik puncak yaitu
( * ( √ √ √ √
) ( √ √
) Hasil rotasi titik puncak yaitu
( * ( √ √ √ √
) ( √ √
)
Sehingga diperoleh elips yang melalui , , , dan .
Purwokerto, 3 Desember 2016
Rotasi titik terhadap pusat putaran dan sudut putar adalah sebagai berikut. Hasil rotasi titik puncak ( √ √ ) yaitu
( * ( √ √
)
Hasil rotasi titik punca( √ √ )k yaitu
( * ( √ √
) Hasil rotasi titik puncak ( √ √ ) yaitu
( * ( √ √
)
Hasil rotasi titik puncak ( √ √ ) yaitu
( * ( √ √
)
Sehingga diperoleh elips yang melalui , , , dan .
Rotasi titik terhadap pusat putaran dan sudut putar adalah sebagai berikut. Hasil rotasi titik puncak ( √ √ ) yaitu
( * ( √ √
)
Hasil rotasi titik puncak ( √ √ ) yaitu
( * ( √ √
Purwokerto, 3 Desember 2016
Hasil rotasi titik puncak ( √ √ ) yaitu
( * ( √ √
)
Hasil rotasi titik puncak ( √ √ ) yaitu
( * ( √ √
)
Sehingga diperoleh elips yang melalui , , , dan .
Rotasi titik terhadap pusat putaran dan sudut putar adalah sebagai berikut. Hasil rotasi titik puncak ( √ √ ) yaitu
( ) ( √ √
) ( *
Hasil rotasi titik puncak ( √ √ ) yaitu
( ) ( √ √
)
Hasil rotasi titik puncak ( √ √ ) yaitu ( ) ( √
√ )
Hasil rotasi titik puncak ( √ √ ) yaitu
( ) ( √ √
Purwokerto, 3 Desember 2016
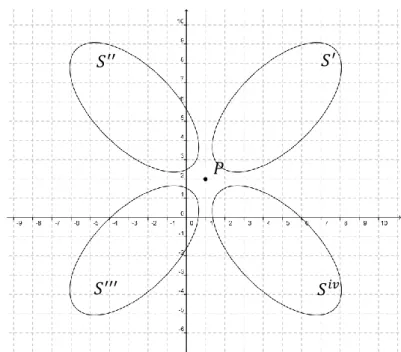
Sehingga diperoleh elips yang melalui ( ), ( ), ( ), dan ( ).
Gambar 3. Sketsa hasil contoh penyusunan satu unsur motif batik kawung. 3. KESIMPULAN DAN SARAN
Bentuk unsur motif kawung Yogyakarta dapat didekati dengan bangun datar elips. Elips yang digunakan untuk menyusun satu unsur elips merupakan elips horizontal. Hasil rotasi elips tersebut terhadap suatu titik pusat dengan sudut putar kemudian dirotasikan dengan sudut putar , , dan untuk menyusun unsur motif kawung. Dengan demikian dapat ditunjukkan bahwa terdapat aspek matematis yang digunakan dalam unsur budaya Yogyakarta yaitu motif batik kawung. Aspek matematis yang digunakan termasuk dalam kategori aktivitas matematika fundamental mendesain (designing).
Persamaan umum elips hasil rotasi belum dirumuskan dalam artikel ini. Oleh karena itu, dapat dilakukan penelitian untuk menentukan persamaan umum elips yang digunakan dalam menyusun motif batik kawung. Selain itu dapat pula dilakukan penelitian tentang penyusunan unsur motif batik kawung atau motif lainnya menggunakan jenis transformasi yang lain.
DAFTAR PUSTAKA
Bishop, Alan J., Mathematical Enculturation, Kluwer, 1988. 𝑆𝑖𝑣 𝑆
𝑆 𝑆
Purwokerto, 3 Desember 2016
D’Ambrosio, Ubiratan, Ethnomathematics and its Place in the History and
Pedagogy of Mathematics, For the Learning of Mathematics, 5(1) (1985),
44-48.
Martin, G. E., Transformation Geometry: An Introduction to Symmetry, Springer-Verlag, New York, 1982
Rosa, M. dan Orey, D. C., Ethnomathematics: The Cultural Aspects of
Mathematics, Revista Latinoamericana de Etnomatemática, 4(2) (2011),
32-54.
_______________________________, An Ethnomathematical Study of the
Symmetrical Freedom Quilts, Symmetry: Culture and Science, 23(2) (2012),
191-220.
_______________________________, Ethnomathematics: Connecting Cultural
Aspects of Mathematics through Culturally Relevant Pedagogy, Proceedings
of the Eighth International Mathematics Education and Society Conference Volume 3, Portland, Oregon, Amerika Serikat, 21-26 Juni 2015.
Susanta, Geometri Transformasi, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Gadjah Mada, 1990.
Kebermaknaan Batik Kraton Motif Batik Larangan, Nusantaraku, 27 Januari
2014, http://akucintanusantaraku.blogspot.co.id/2014/01/kebermaknaan-batik-kraton-motif-batik.html, diakses pada 25 November 2016.