Numerik
3.1. Rasionalisasi
Mendapatkan nilai dari f’(3) atau
10 ) (x dx
f secara analitik
dari fungsi f(x) = x2 atau f(x) = sin (3x) bukanlah pekerjaan
sulit, karena formula fungsi tersebut cukup sederhana dan dengan mudah dapat ditentukan secara anlitik. Akan tetapi
mendapatkan g’(3) dan
10 ) (x dx
g secara analitik dari
x x
x x
xe x
e x
xe e
x x g
4 sin ln
) ln(
tan ) cos( 2 ) (
3 2 sin 2
sin 3
bukanlah pekerjaan
mudah, karena bentuk fungsinya cukup kompleks sehingga membutuhkan multi subtitusi fungsi untuk mendapatkan nilai
dari f’(3) maupun
10 ) (x dx
g . Penyelesaian secara numerik
menjadi alternatif yang epektif dan efesien untuk
mendapatkan penyelesaian f’(3) dan
10 ) (x dx
g .
Demikian juga halnya apabila ingin mendapatkan luas daerah seperti pada peta pada gambar 3.1 di bawah.
Gambar 3.1 Peta wilayah kota Mataram NTB
Ripai, S.Pd., M.Si
BAB
III
Numerik
Penyelesaian secara analitik dengan konsep integral tentunya tidak dapat dilakukan, karena fungsi dari kurva peta tersebut tidak diketahui. Melakukan rekontruksi fungsi dengan interpolasi kemungkinan akan menjadi proses yang cukup panjang. Penyelesaian dengan teknik inegrasi secara numerik menjadi alternatif solusi pendekatan yang efektif dan efesien.
3.2 Turunan Numerik
Turunan berasal dari kata turun yang dalam konsep matematika dapat dipandang sebagai ukuran kemiringan pada suatu titik permukaan kurva. Untuk memahami aksioma turunan tersebut, pandanglah suatu tanjakan pada permukaan bumi atau tanah. Pada tanjakan tersebut akan memuat kondisi
menurun. Ukuran menurunya sangat tergantung dari tingkat keterjalannya. Keterjalan atau kemiringan tanjakan tersebut ditentukan dari besarnya sudut yang dibentuk atau raiso antara perubahan tinggi tanjakan dengan lebar dasar tanjakan.
Gambar 3.2 Kemiringan garis
Tanjakan 1 lebih terjal atau lebih miring dari tanjakan 2. Hal ini dapat diketahui dari fakta bahwa jika kita mendaki tankan 1 akan lebih membutuhkan energi atau tenaga yang lebih banyak dari tanjakan 2. Kenyataan ini memberikan rumusan matematika yang dapat menyatakan keterjalan atau kemiringan suatu tanjakan adalah dengan menentukan besarnya sudut yang dibentuk atau nilai perbandingan ∆y dengan ∆x. Misalkan ukuran kemiringan disimbolkan m (awal hurup dari kata miring) maka alternatif perbandingannya adalah sebagai berikut:
1.
x y m
bernilai bernilai benar, karena
1 2 1 1
x y x y
sesuai dengan fakta alam yang menyatakan bahwa tanjakan 1 lebih terjal/miring dari tanjakan 2.
2. m yx
bernilai bernilai salah, karena
1 2 1 1
y x y x
tidak sesuai dengan fakta alam yang menyatakan bahwa tanjakan 1 lebih terjal/miring dari tanjakan 2.
Tanjakan 1
α ∆y1
Tanjakan 2 ∆y2
∆x1 ∆x2
1 2 1 1
x y x y
Numerik
Definisi 3.1 Kemiringan suatuu garis
Misalkan suatu garis melalui titik (xi, yi) dan (xi+1,yi+1) maka
ukuran kemiringan dari garis tersebut adalah
x y m
dengan
∆y = yi+1 – yi dan ∆x = xi+1 - xi
Lebih lanjut defnisi turunan dalam konsep matematika yang didasari dari defnisi kemiringan tersebut diuraiakan secara singkat berikut ini.
3.2.1 Turunan Pertuama
Defnisi turunan dalam konsep matematika dikontruksi dari tiga aksioma yaitu beda maju, beda mundur dan beda tengah/ pusat.
3.2.1.1 Beda Maju
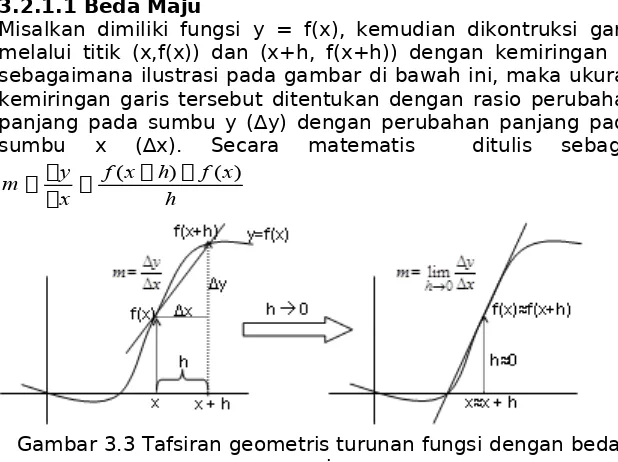
Misalkan dimiliki fungsi y = f(x), kemudian dikontruksi garis melalui titik (x,f(x)) dan (x+h, f(x+h)) dengan kemiringan m sebagaimana ilustrasi pada gambar di bawah ini, maka ukuran kemiringan garis tersebut ditentukan dengan rasio perubahan panjang pada sumbu y (∆y) dengan perubahan panjang pada sumbu x (∆x). Secara matematis ditulis sebagai
h x f h x f x y
m ( ) ( )
Gambar 3.3 Tafsiran geometris turunan fungsi dengan beda maju
Jika nilai h diambil sedekat mungkin dengan 0, maka x+h akan mendekati x dan f(x+h) akan mendekati f(x). Kondisi ini akan menciptakan suatu garis singgung pada kurva tersebut pada titik (x,f(x)) dengan kemiringan
Numerik
Karena posisis titik x+h berada di depan titik x, maka nilai h = ∆x = (x+h) – x dan ∆y = f(x+h) – f(x) disebut sebagai selisih maju atau beda maju.
Berdasarkan uraian sebelumnya, bahwa persamaan umum fungsi polinomial adalah f(x) = a0 + a1x + a2x2+ … + anxn
dimana fungsi tersebut dapat menghampiri semua jenis fungsi, maka evaluasi nilai dari
x
lim diperoleh sebagai berikut:
f(x+h) = a0 + a1(x+h) + a2(x+h)2 +a3(x+h)3 +…+ an(x+h)n
Perolehan fungsi yang menyatakan kemiringan garis singgung kurva ini memberikan fakta bahwa derajatu fungsi polinomial akan tuurun satu tingkatan apabila diambil nilai dari
. Kenyataan ini memberikan
definisi tuurunan fungsi sebagai kemiringan garis singgung pada kurva yang secara anlitik memberikan dampak terhadap penurunan derajatu fungsi tersebut 1 (satu) tingkat.
Numerik terhadap x
b. Defnisi Numerik
i
Teladan 3.1
Dapatkan turunan f’(3) dari f(x) = x3+3x+6 dengan
mengunakan cara analitik dan numerik.
Solusi:
a. Penyelesaian analitik
h
b. Penyelesaian numeric dengan beda maju
h=0.1
Numerik
01 . 0
6 3 3 3 6 01 . 3 3 01 .
3 3 3
30.0901
Error relatif = 100%
30 30 0901 . 30
x 0.30033%
Pemeriksaan lebih lanjut menggunakan pemograman komputer sebagaimana di bawah untuk h lebih mendekati 0 (nol) menunjukkan nilai f’(3) = 30 untuk h=10-6. Nilai ini sesuai
dengan nilai eksak dari f’(3)=30 yang diperoleh dari penyelesaian anlitik sebelumnya.
f=inline('x^3+3*x+6'); x=3;
h=[0.1 0.01 0.001 0.0001 0.00001 0.000001 0.0000001]; for i=1:7
df(i)=(f(x+h(i))-f(x))/h(i); end
df =
30.9100 30.0901 30.0090 30.0009 30.0001 30.0000 30.0000
Teladan 3.2
Tentukan secara analitik dan numerik f’(x) pada domain
0.8≤x≤ 0.8000001 dari fungsi
x x
x x
xe x
e x
xe e
x x f
4 sin ln
) ln(
tan ) cos( 2 ) (
3 2 sin 2
sin 3
.
Solusi
Penyelesaian secara analitik memerlukan konsep turunan berantai yang cukup banyak sehingga akan menajdi proses yang cukup rumit. Hasil evaluasi turunan analitik mengunakan komputer dengan kode program
syms x
f1=2*x*cos(exp(3*x))-tan(log(x*exp(sqrt(sin(x))))); f2=(x^2)*exp(sin(2*x-3))+log(x)*sin(4*x*exp(-x)); f=f1/f2;
diff(f,x);
diperoleh hasil sebagai berikut:
f'(x) = ((tan(log(x*exp(sin(x)^(1/2)))) -
Numerik
cos((4*x)/exp(x))*log(x)*(4/exp(x) - (4*x)/exp(x)) + 2*x^2*exp(sin(2*x - 3))*cos(2*x -
3)))/(x^2*exp(sin(2*x - 3)) + sin((4*x)/exp(x))*log(x))^2 -
(6*x*exp(3*x)*sin(exp(3*x)) - 2*cos(exp(3*x)) + ((tan(log(x*exp(sin(x)^(1/2))))^2 +
1)*(exp(sin(x)^(1/2)) +
(x*exp(sin(x)^(1/2))*cos(x))/(2*sin(x)^(1/2))))/(x *exp(sin(x)^(1/2))))/(x^2*exp(sin(2*x - 3)) + sin((4*x)/exp(x))*log(x))
Turunan anlitik dari f(x) memiliki formula yang jauh lebih rumit dari fungsi f(x) sendiri. Kenyataan ini akan memberikan kesulitan dalam memeriksa atau mengunakan f’(x) tersebut dalam penyelesaian matematika. Penyelesaian secara numerik menjadi alternatif yang baik dengan mengambil nilai h sedekat mungkin dengan 0 (nol).
Misalkan dipilih h = 0.0001, maka perhitungan turunan pertama dari f(x) secara numerik sebagai berikut:
0.8000001
= 6875.231517
Perhitungan dengan kode komputer di bawah memberikan output komputasi sebagai:
i
xi fi+1 fi f'Numerik Analitik Error Relatif I = (fi+1
-26 6948.388423 6948.462441 0.001065238 %
1 0.8000001
-38.123656 6
-38.124351
42 6948.240407 6948.314419 0.001065181 %
2 0.8000002
-38.122961 79
-38.123656
6 6948.092393 6948.166402 0.001065161 %
Numerik
3 0.8000003 -38.122267
-38.122961
79 6947.944378 6948.018389 0.00106522 %
4 0.8000004
-38.121572
22 -38.122267 6947.796378 6947.870382 0.001065126 %
5 0.8000005
-38.120877 45
-38.121572
22 6947.648378 6947.722379 0.001065117 %
6 0.8000006
-38.120182 7
-38.120877
45 6947.500376 6947.574381 0.001065184 %
7 0.8000007
-38.119487 97
-38.120182
7 6947.35239 6947.426387 0.001065111 %
8 0.8000008
-38.118793 25
-38.119487
97 6947.204404 6947.278399 0.001065097 %
9 0.8000009
-38.118098 54
-38.118793
25 6947.056422 6947.130415 0.001065085 %
1
0 0.800001
-38.117403 85
-38.118098
54 6946.908445 6946.982436 0.001065077 %
Hasil komputasi sebagaimana pada tabel di atas, menunjukkan kesalahan relatif perhitungan f’(x) secara numerik berada pada toleransi kesalahan. Hal ini terlihat dari prosentase kesalahan relatif hingga ketelitian 0.001%.
syms x
f1=2*x*cos(exp(3*x))-tan(log(x*exp(sqrt(sin(x))))); f2=(x^2)*exp(sin(2*x-3))+log(x)*sin(4*x*exp(-x)); f=f1/f2;
h=0.0000001;
d=[0.8:h:0.800001]; n=length(d);
for i=1:n
fh(i)=subs(f,d(i)+h); fx(i)=subs(f,d(i)); df(i)=(fh(i)-fx(i))/h;
end
g=diff(f,x); dF=subs(g,d);
Numerik
xlswrite('Hasil',H) subplot(3,1,1) ezplot(f,[0.8 1.8]) subplot(3,1,2) plot(d,df,'-r') hold on
plot(d,dF) xlabel('x') ylabel('df(x)')
title('Grafik turunan numerik beda maju pada domain [0.8 0.800001]')
subplot(3,1,3) plot(d,error) xlabel('xi')
ylabel('error ke-i')
title('Error relatif pada domain [0.8 0.800001]')
0.8 0.9 1 1. 1 1.2 1.3 1.4 1.5 1.6 1.7 1.8
-12 -10 -8 -6 -4 -2 0 2 4 6
x -(tan(log(x ex p(s in(x )1/2
))) - 2 x c os (ex p(3 x )))/(x2
ex p(s in(2 x - 3)) + s in((4 x )/ exp(x )) log(x))
Numerik
0.8 0.8 0.8 0. 8 0.8 0.8 0. 8
6946.8 6947 6947.2 6947.4 6947.6 6947.8 6948 6948.2 6948.4 6948.6 6948.8
x
d
f
(
x
)
Grafik turunan numerik beda maju pada domain [0. 8 0. 800001]
Numerik
A nalitik
0. 8 0.8 0.8 0. 8 0.8 0.8 0. 8
1. 0651 1. 0651 1. 0651 1. 0651 1. 0651 1. 0652 1. 0652 1. 0652 1. 0652 1. 0652 1. 0653
x 10
-3
x i
e
r
r
o
r
k
e
-i
Error relat if pada dom ain [ 0. 8 0.800001]
Gambar 3.4 Grafk fungsi f(x), turunan f(x) secara analitik dan numerik dengan beda maju dan error relative
3.2.1.2 Beda Mundur
Numerik
Gambar 3.5 Tafsiran geometris turunan fungsi dengan beda mundur
Pada gambar 3.5 di atas, kemiringan garis singing pada kurva diberikan oleh
)
memberikan defnisi turuna fungsi berdasarkan beda mundur.
Definisi 3.3 Turunan fungsi beda mundur
a. Defnisi Analitik
)
disebut sebagai turunan analitik beda mundur dari f(x) terhadap x
b. Defnisi Numerik
i
Disebut sebagai turunan numerik beda mundur dari fi
terhadap xi.
Teladan 3.3
Selesaikan teladan 3.1 di atas dengan mengunakan beda mundur!
Solusi
Diketahui fungsi analitik pada teladan 3.1 yaitu f(x) = x3+3x+6, maka dengan cara analitik mengunakan defnisi
beda mundur diperoleh
h
Numerik
Sehingga untuk x = 3 , maka (3) 3 3 2 3 30
f
Penyelesaian numerik dengan beda mundur diperoleh sebagai berikut:
Untuk h = 0.1, maka
1 . 0
) 1 . 0 3 ( ) 3 ( ) 3
(
f f
f
1 . 0
6 9 . 2 3 9 . 2 6 3 3
33 3
29.11
Error relatif = 100%
30 30 11 . 29
x 2.97%.
Untuk h = 0.01, maka
01 . 0
) 01 . 0 3 ( ) 3 ( ) 3
(
f f
f
01 . 0
6 99 . 2 3 99 . 2 6 3 3
33 3
29.9101
Error relatif = 100%
30 30 9101 . 29
x 0.2997%.
Untuk meperkecil kesalahan maka disimulasikan dengan mengambil nilai h lebih mendekati 0 (nol).
f=inline('x^3+3*x+6'); x=3;
h=[0.1 0.01 0.001 0.0001 0.00001 0.000001]; for i=1:6
df(i)=(f(x)-f(x-h(i)))/h(i); end
df =
29.1100 29.9101 29.9910 29.9991 29.9999 30.0000
Hasil komputasi di atas menunjukkan bahwa semakin dekat h dengan nol, nilai f’(3) semakin dekat denngan 30, dan untuk h = 10-6 diperoleh f’(3) = 30. Nilai turunan numerik ini sama
dengan nilai turunan analitik.
Teladan 3.4
Selesaikan teladan 3.2 di atas dengan mengunakan defnisi beda mundur!
Numerik
Diketahui fungsi analitik pada teladan 3.2 adalah
x
, maka penerapan beda
mundur untuk mendapatkan f’(x) pada domain [0.8 0.800001] dengan h=0.0000001 adalah
h
= 6948.536451
Pemeriksaan nilai f’(x) pada domain [0.8 0.8000001] lebih lanjut dilakukan dengan computer sebagaimana kode program di bawah. Hasil komputasi yang diperoleh disajikan dalam table berikut:
i
xi fi-1 fi
Numerik Analitik Error Relatif f'I = (fi - f
i-63 6948.536451 6948.462 0.0010651 %
1 0.8000001
-38.12504 6
-38.12435
14 6948.388423 6948.314 0.0010651 %
2 0.8000002
-38.12435 1
-38.12365
66 6948.240407 6948.166 0.0010651 %
3 0.8000003
-38.12365 7
-38.12296
18 6948.092393 6948.018 0.0010651 %
4 0.8000004
-38.12296 2
-38.12226
7 6947.944383 6947.87 0.0010651 %
5 0.8000005
-38.12226 7
-38.12157
22 6947.796378 6947.722 0.0010651 %
6 0.8000006 38.12157- 38.12087- 6947.648378 6947.574 0.0010651 %
Numerik
i
xi fi-1 fi
Numerik Analitik Error Relatif f'I = (fi - f
i-1)/h f'(xi) |f'I - f'(xi)|/|f'(xi)|
2 75
7 0.8000007
-38.12087 7
-38.12018
27 6947.500381 6947.426 0.0010651 %
8 0.8000008
-38.12018 3
-38.11948
8 6947.35239 6947.278 0.001065 %
9 0.8000009
-38.11948 8
-38.11879
32 6947.204404 6947.13 0.001065 %
1
0 0.800001
-38.11879 3
-38.11809
85 6947.056422 6946.982 0.001065 %
Numerik
0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 -10
-5 0 5
x
-(tan(log(x exp(sin(x)1/2))) - 2 x cos(exp(3 x)))/(x2 exp(sin(2 x - 3)) + sin((4 x)/exp(x)) log(x))
0.8 0.8 0.8 0.8 0.8 0.8 0.8
6946 6948 6950
x
d
f
(
x
)
Grafik turunan numerik beda mundur pada domain [0.8 0.800001]
0.8 0.8 0.8 0.8 0.8 0.8 0.8
1.065 1.0651 1.0652
x 10
-3
xi
e
r
r
o
r
k
e
-i
Error relatif pada domain [0.8 0.800001]
Gambar 3.5 Turunan f(x) dengan beda mundur dan error relatif syms x
f1=2*x*cos(exp(3*x))-tan(log(x*exp(sqrt(sin(x))))); f2=(x^2)*exp(sin(2*x-3))+log(x)*sin(4*x*exp(-x)); f=f1/f2;
h=0.0000001; d=[0.8:h:0.800001]; n=length(d);
for i=1:n
fh(i)=subs(f,d(i)-h); fx(i)=subs(f,d(i)); df(i)=(fx(i)-fh(i))/h;
end
g=diff(f,x);
Numerik
dF=subs(g,d);
error=(abs(dF-df)./dF)*100; H=[d;fh;fx;df;dF;error]'; xlswrite('Hasil',H) subplot(3,1,1) ezplot(f,[0.8 1.8]) subplot(3,1,2) plot(d,df,'-r') hold on
plot(d,dF) xlabel('x') ylabel('df(x)')
title('Grafk turunan numerik beda mundur pada domain [0.8
0.800001]')
subplot(3,1,3) plot(d,error) xlabel('xi')
ylabel('error ke-i')
title('Error relatif pada domain [0.8 0.800001]')
3.2.1.3 Beda Tengah
Pada uraian sebelumnya telah di bahas defnisi turunan fungsi berdasarkan beda maju dan mundur. Dengan mengambil nilai beda tengah yakni ∆x = (x+h) –(x-h) dan ∆f = f(x+h) – f(x-h). Untuk mendapatkan tafsiran geometris dari beda tengah, maka dari suatu fungsi f(x) dapat dikontruksi suatu kemiringan garis yang melalui titik ((x+h),f(x+h)) dan titik ((x-h),f(x-h)).
Numerik
Pada gambar 3.6 di atas, dari titik x, ditentukan titik ke kanan sejauh h yang disebut x+h dan kekiri sejauh h yang disebut x-h. Jika jika h tersebut dibuat sedekat mungkin dengan 0 (nol) , maka akan diperoleh titik x, x-h dan x+h akan berdempetan dan titik f(x), f(x-h) dan f(x+h) akan berdempetan. Kondisi ini akan menyebabkan garis yang melalui titik (x-h,f(x-h)) dan (x+h,f(x+h)) akan menjadi garis singgung pada kurva f(x) di titik (x,f(x)). Kemiringan garis singgung tersebut ditentukan dengan beda tengah/pusat.
Defnisi 3.4 Turunan fungsi beda tengah/pusat a. Defnisi Analitik
) terhadap x
b. Defnisi Numerik
i
Teladan 3.5
Selesaikan teladan 3.1 di atas dengan mengunakan defnisi turunan beda tengah!
Solusi
Fungsi yang didefnisikan pada teladan 3.1 di atas adalah f(x) = x3 + 3x + 6. Dengan konsep beda tengah, maka turunan
analitiknya adalah
Numerik
Sehingga untuk x = 3 diperoleh nilai (3) 3 3 2 3 30
f
Penyelesaian secara numerik diberikan sebagai berikut:
Untuk h = 0.1
) 1 . 0 ( 2
) 1 . 0 3 ( ) 1 . 0 3 ( ) 3
(
f f
f
) 1 . 0 ( 2
6 9 . 2 3 9 . 2 6 1 . 0 3 3 0.1)
(3 3 3
= 30.01
Error relatif = 100%
30 30 01 . 30
x 0.033%. Untuk meperkecil
kesalahan maka disimulasikan dengan mengambil nilai h lebih mendekati 0 (nol).
h = 0.01
) 01 . 0 ( 2
) 01 . 0 3 ( ) 01 . 0 3 ( ) 3
(
f f
f
) 01 . 0 ( 2
6 99 . 2 3 99 . 2 6 01 . 0 3 3 0.01)
(3 3 3
= 30.0001
Eror relative = 100%
30 30 0001 . 30
x 0.00033%
Pemeriksaan lebih lanjut dengan kode komputer untuk h lebih dekat dengan 0 (nol) sebagai berikut:
f=inline('x^3+3*x+6'); x=3;
h=[0.1 0.01 0.001 0.0001 0.00001 0.000001]; for i=1:6
df(i)=(f(x+h(i))-f(x-h(i)))/(2*h(i)); end
df =
30.0100 30.0001 30.0000 30.0000 30.0000 30.0000
Hasil komputasi di atas menunjukkan bahwa untuk h = 0.001, sudah dapat memberikan nilai f’(3) = 30 sesuai dengan nilai eksaknya.
Teladan 3.6
Numerik
Solusi:
Diketahui fungsi analitik dari pada teladan 3.2 di atas adalah
x dengan mengunakan beda tengah/pusat sebagai berikut:
x , sehingga
h
= 6948.462437
Pemeriksaan dengan komputer nilai eksak dari f’(0.8) = 6948.4624. Error relatif dari nilai numerik tersebut adalah er =
5.51 x 10-8 % = 0.00000005.51%. Nilai ini cukup kecil dan
berada pada toleransi kesalahan. Hasil komputasi numerik dengan kode program di bawah diperoleh sebagai berikut:
i
xi fi+1 fi-1
Numerik Analitik Error Relatif f'I = (fi+1 -
fi-41 6948.462437 6948.4624 5.51E-08 %
1 0.8000001
-38.1236 57
-38.1250
46 6948.314415 6948.3144 5.75E-08 %
2 0.8000002
-38.1229 62
-38.1243
51 6948.1664 6948.1664 2.48E-08 %
3 0.8000003
-38.1222 67
-38.1236
57 6948.018385 6948.0184 6.13E-08 %
4 0.8000004
-38.1215 72
-38.1229
62 6947.870381 6947.8704 1.78E-08 %
5 0.8000005
-38.1208 77
-38.1222
67 6947.722378 6947.7224 1.52E-08 %
6 0.80000 - - 6947.5743 6947.57 5.53E- %
Numerik
i xi fi+1 fi-1
Numerik Analitik Error Relatif f'I = (fi+1 -
fi-1)/2h f'(xi)
|f'I - f'(xi)|/| f'(xi)|
06 38.120183 38.121572 77 44 08
7 0.8000007
-38.1194 88
-38.1208
77 6947.426385 6947.4264 3.01E-08 %
8 0.8000008
-38.1187 93
-38.1201
83 6947.278397 6947.2784 3.21E-08 %
9 0.8000009
-38.1180 99
-38.1194
88 6947.130413 6947.1304 2.97E-08 %
1 0
0.80000 1
-38.1174 04
-38.1187
93 6946.982434 6946.9824 3.16E-08 %
0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 -10
-5 0 5
x
-(tan(log(x exp(sin(x)1/2))) - 2 x cos(exp(3 x)))/(x2 exp(sin(2 x - 3)) + sin((4 x)/exp(x)) log(x))
0.8 0.8 0.8 0.8 0.8 0.8 0.8
6946.5 6947 6947.5 6948 6948.5
x
d
f(
x
)
Grafik turunan numerik beda mundur pada domain [0.8 0.800001]
0.8 0.8 0.8 0.8 0.8 0.8 0.8
0 2 4 6 8
x 10-8
xi
e
rr
o
r
k
e
-i
Numerik
Gambar 3.6. Garif f(x) dan turunan dengan beda tengah/pusat
syms x
f1=2*x*cos(exp(3*x))-tan(log(x*exp(sqrt(sin(x))))); f2=(x^2)*exp(sin(2*x-3))+log(x)*sin(4*x*exp(-x)); f=f1/f2;
h=0.0000001;
d=[0.8:h:0.800001]; n=length(d);
for i=1:n
fh1(i)=subs(f,d(i)+h); fh2(i)=subs(f,d(i)-h);
df(i)=(fh1(i)-fh2(i))/(2*h);
end
g=diff(f,x); dF=subs(g,d);
error=(abs(dF-df)./dF)*100; H=[d;fh1;fh2;df;dF;error]'; xlswrite('Hasil',H)
subplot(3,1,1) ezplot(f,[0.8 1.8]) subplot(3,1,2) plot(d,df,'-r') hold on
plot(d,dF) xlabel('x') ylabel('df(x)')
title('Grafik turunan numerik beda mundur pada domain [0.8 0.800001]')
subplot(3,1,3) plot(d,error) xlabel('xi')
ylabel('error ke-i')
title('Error relatif pada domain [0.8 0.800001]')
3.2.2 Turunan Kedua
Pendefnisian turunan kedua secara numerik dihampiri dengan pendekatan aproksimasi deret taylor.
! 2
) ( ) ( ) ( )
( )
( 0 2 0
0 0 0
x f x x x f x x x f x f
Jika f(x) ≈ P2(x), maka f(x) =
( ) ( )2! ( ))
( 0 2 0
0 0 0
x f x x x f x x x
f
Numerik Dari (a) dan (b) diperoleh hasil jumlah sebagai berikut:
2
diperoleh rumusan turunan kedua adalah
2
Definisi 3.5 Turunan kedua
Jika f(x) fungsi kontinu, maka turunan kedua dari f(x) adalah a. Defnisi analitik
2
b. Defnisi Numerik
2
Teladan 3.7
Numerik
Sehingga diperoleh f’’(3) = 6(3) = 18.
Penyelesaian secara numerik Untuk h=0.1
2 1 1 2
h f f f
fi i i i = ( ) 2 2( ) ( )
h
h x f x f h x
f
1 . 0
) 1 . 0 3 ( ) 3 ( 2 ) 1 . 0 3 ( ) 3
(
f f f
f
1 . 0
6 ) 9 . 2 ( 3 9 . 2 6 ) 3 ( 6 ) 3 ( 2 6 1 . 3 3 1 .
3 3 3 3
=
18
Jadi penyelesaian secara analitik dan numerik dengan h= 0.1 memberikan nilai f’’(3) =18.
Teladan 3.8
Dapatkan f’’(x) pada domain [0.8 0.800001] secara analitik dan numerik dari fungsi pada teladan 3.2, yakni
x x
x x
xe x
e x
xe e
x x f
4 sin ln
) ln(
tan ) cos( 2 ) (
3 2 sin 2
sin 3
.
Solusi:
Penentuan turunan kedua mengunakan cara analitik sangat tidak efesien. Hal ini disebabkan karena formula dari fungsi f(x) sangan kompleks. Pemeriksaan dengan mengunakan computer untuk turunan analitik kedua dari f(x) adalah
f'’(x) = (2*(6*x*exp(3*x)*sin(exp(3*x)) - 2*cos(exp(3*x)) + ((tan(log(x*exp(sin(x)^(1/2))))^2 + 1)*(exp(sin(x)^(1/2)) + (x*exp(sin(x)^(1/2))*cos(x))/(2*sin(x)^(1/2))))/(x*exp(sin(x)^(1 /2))))*(sin((4*x)/exp(x))/x + 2*x*exp(sin(2*x - 3)) +
cos((4*x)/exp(x))*log(x)*(4/exp(x) - (4*x)/exp(x)) +
2*x^2*exp(sin(2*x - 3))*cos(2*x - 3)))/(x^2*exp(sin(2*x - 3)) + sin((4*x)/exp(x))*log(x))^2 - (12*exp(3*x)*sin(exp(3*x)) + 18*x*exp(6*x)*cos(exp(3*x)) + 18*x*exp(3*x)*sin(exp(3*x)) - ((tan(log(x*exp(sin(x)^(1/2))))^2 + 1)*(exp(sin(x)^(1/2)) + (x*exp(sin(x)^(1/2))*cos(x))/(2*sin(x)^(1/2))))/(x^2*exp(sin(x) ^(1/2))) + ((tan(log(x*exp(sin(x)^(1/2))))^2 +
1)*((exp(sin(x)^(1/2))*cos(x))/sin(x)^(1/2) - (x*exp(sin(x)^(1/2))*sin(x)^(1/2))/2 + (x*exp(sin(x)^(1/2))*cos(x)^2)/(4*sin(x)) -
(x*exp(sin(x)^(1/2))*cos(x)^2)/(4*sin(x)^(3/2))))/(x*exp(sin(x) ^(1/2))) +
(2*tan(log(x*exp(sin(x)^(1/2))))*(tan(log(x*exp(sin(x)^(1/2))))
Numerik
^2 + 1)*(exp(sin(x)^(1/2)) +
(x*exp(sin(x)^(1/2))*cos(x))/(2*sin(x)^(1/2)))^2)/(x^2*exp(2*s in(x)^(1/2))) - (cos(x)*(tan(log(x*exp(sin(x)^(1/2))))^2 + 1)*(exp(sin(x)^(1/2)) +
(x*exp(sin(x)^(1/2))*cos(x))/(2*sin(x)^(1/2))))/(2*x*exp(sin(x)^ (1/2))*sin(x)^(1/2)))/(x^2*exp(sin(2*x - 3)) +
sin((4*x)/exp(x))*log(x)) + ((tan(log(x*exp(sin(x)^(1/2)))) - 2*x*cos(exp(3*x)))*(2*exp(sin(2*x 3)) sin((4*x)/exp(x))/x^2 -sin((4*x)/exp(x))*log(x)*(4/exp(x) - (4*x)/exp(x))^2 +
4*x^2*exp(sin(2*x - 3))*cos(2*x - 3)^2 + 8*x*exp(sin(2*x - 3))*cos(2*x - 3) + (2*cos((4*x)/exp(x))*(4/exp(x) -
(4*x)/exp(x)))/x - cos((4*x)/exp(x))*log(x)*(8/exp(x) - (4*x)/exp(x)) - 4*x^2*exp(sin(2*x - 3))*sin(2*x -
3)))/(x^2*exp(sin(2*x - 3)) + sin((4*x)/exp(x))*log(x))^2 - (2*(tan(log(x*exp(sin(x)^(1/2)))) -
2*x*cos(exp(3*x)))*(sin((4*x)/exp(x))/x + 2*x*exp(sin(2*x - 3)) + cos((4*x)/exp(x))*log(x)*(4/exp(x) - (4*x)/exp(x)) +
2*x^2*exp(sin(2*x - 3))*cos(2*x - 3))^2)/(x^2*exp(sin(2*x - 3)) + sin((4*x)/exp(x))*log(x))^3.
Penyelesaian secara numerik akan sangat memberikan efesiensi dalam perhitungan. Dengan mengambil h = 0.0000001 maka analisis numeris f’’(x) pada domain [0.8 0.800001] adalah
Numerik
Pemeriksaan lebih lanjut dengan pemograman komputer sebagaimana kode program dibawah diperoleh hasil turunan kedua dari f(x) secara analitik dan numerik adalah
Numerik
Pada table di atas diketahui bahwa beda hasil analitik dengan numerik memeiliki galat relatif hingga 0.0001%. Kesalahan ini masih berada pada tingkat toleransi kesalahan. Model grafs f(x) dan f’’(x) serta error relatif diberikan sebagai berikut:
0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8
-10 -5 0 5
x
-(tan(log(x exp(sin(x)1/2))) - 2 x cos(exp(3 x)))/(x2 exp(sin(2 x - 3)) + sin((4 x)/exp(x)) log(x))
0.8 0.8 0.8 0.8 0.8 0.8 0.8
-1.4805 -1.48 -1.4795
x 10
6
x
d
f
(
x
)
Grafik turunan numerik beda mundur pada domain [0.8 0.800001]
0.8 0.8 0.8 0.8 0.8 0.8 0.8
-4 -2 0
x 10
-3
xi
e
r
r
o
r
k
e
-i
Error relatif pada domain [0.8 0.800001]
Gambar 3.7 Grafk f(x) dan f’’(x) pada domain [0.8 0.00001]
syms x
f1=2*x*cos(exp(3*x))-tan(log(x*exp(sqrt(sin(x))))); f2=(x^2)*exp(sin(2*x-3))+log(x)*sin(4*x*exp(-x)); f=f1/f2;
h=0.0000001;
d=[0.8:h:0.800001]; n=length(d);
Numerik
fh1(i)=subs(f,d(i)+h); fh2(i)=subs(f,d(i)); fh3(i)=subs(f,d(i)-h);
df(i)=(fh1(i)-2*fh2(i)+fh3(i))/(h^2);
end
g=diff(f,x,2); dF=subs(g,d);
error=(abs(dF-df)./dF)*100; H=[d;fh1;fh2;fh3;df;dF;error]'; xlswrite('Hasil',H)
subplot(3,1,1) ezplot(f,[0.8 1.8]) subplot(3,1,2) plot(d,df,'-r') hold on
plot(d,dF) xlabel('x') ylabel('df(x)')
title('Grafik turunan numerik beda mundur pada domain [0.8 0.800001]')
subplot(3,1,3) plot(d,error) xlabel('xi')
ylabel('error ke-i')
title('Error relatif pada domain [0.8 0.800001]')
3.2.3 Turunan Polinomial Newtuon Gerigory
Turunan fungsi tingkat satu, dua hingga ke-n dapat ditentukan dengan mengunakan polynomial Newtuon Gregory.
3.2.3.1 Turunan Polinomial Newtuon Gregory Maju
Berdasarkan defnisi polynomial Newton Gregory Maju yang dapat digunakan untuk menghampiri fungsi f(x) yang secara matematis dirumuskan sebagai
! 4
) 3 )( 2 )( 1 ( !
3 ) 2 )( 1 ( !
2 ) 1 ( ! 1 ! 0 ) ( )
(x P x f0 s f0 s s 2f0 s s s 3f0 s s s s 4f0
f n
dengan
h x x
s 0 , maka turunan pertama dari f(x) ditentukan
sebagai berikut:
h dx ds h
x x
s 0 1
s(s-1) = s2-s;
Numerik
3.2.2.2 Turunan Polinomial Newtuon Gregoriy Mundur
Berdasarkan defnisi polynomial Newton Gregory Mundur
mengan
h x x
s 0
maka analisis turunan pertama dari polynomial tersebut adalah
Untuk
Jadi fomula turunan pertama dengan mengunakan pendekatan polynomial Newton Gregori mundur adalah
Numerik
Dapatkan f’(3) dari f(x) = x3 pendekatan polynomial newton
gregori mundur dan evaluasi nilai sejatinya dengan cara analitik!
Solusi:
Tabel beda hingga dari f(x) diberikan sebagai berikut:
i xi fi ∆fi ∆2fi ∆3fi
-4 2.8 21.952 2.43
7
-3 2.9 24.389 0.174 2.61
1
0.00 6
-2 3 27 0.18
2.79
1 0.006
-1 3.1 29.791 0.186 2.97
7
0 3.2 32.768
Dengan memilih nilai awal x0 = 3.2, maka diperoleh solusi
numerik
s = (x-x0)/h = (3-3.2)/0.1 = -2
0.006
6
2 ) 2 ( 6 ) 2 ( 3 186 . 0 2
1 2 2 977 . 2 1 . 0
1 ) (
2 x
f
2.977 0.279 0.002
27 1. 0
1
Penyelesaian secara analitik diperoleh f’(x) = 3x2 = 3(32) = 27.
Teladan 3.10
Dapatkan kemiringan tiap titik pada model tebing yang di ilustrasikan pada teladan 2.10
Solusi:
Pada teladan tersebut diketahui
Numerik
Gambar 3.8 Model pelukir dan gritisasi sebuh tebing
i 0 1 2 3 4 5 6 7 8 9 10 11
x 1 2 3 4 5 6 7 8 9 10 11 12
f 0.
5 1.1 1.6 2.7 5.3 6.3 7.8 10 10.3 10.5 10.6 10.7
Tabel beda hingga dari data di atas adalah xi fi ∆fi ∆2fi ∆3fi ∆4fi
1 0.5 0.6 2 1.1
0.5
3 1.6 0.6
1.1 0.9
4 2.7 1.5 -4
2.6 -3.1
5 5.3 -1.6 5.2
1 2.1
6 6.3 0.5 -1.9
1.5 0.2
7 7.8 0.7 -2.8
2.2 -2.6
8 10 -1.9 4.4
0.3 1.8
Numerik sebagai berikut
Pada interval 1x2 f(x)1hf0 (karena modelnya cendrung linier)
0.6
0.6cendrung linier)
0.5
0.5karena modelnya cendrung terkontruksi daripolinomial berderajat 3 (tiga)
1
Numerik
Pada interval
merupakan polinomial berderajat 3 (tiga).2
(karena model kurva cendrung kuadrat)
1
(karena model kurva cendrung kuadrat)
0
Numerik
12 10
1 . 0
10 8
15 . 1 1 . 0
8 5
8167 . 1 7 . 0 1 . 0
5 3
4333 . 28 9 . 13 5501
. 1
3 2
5 . 0
2 1
6 . 0
)
( 2
2
x x x
x x
x
x x
x
x x
x f
Hasil ini tidak berbeda signifkan dengan hasil dengan cara melakukan interpolasi untuk mendapatkan persamaanya kemudian dilakukan penentuan kemiringannya secara analitik. Jika dibandingkan dengan metode Newton Gregory, tentunya lebih mudah karena tidak dituntut unutk menyelesaikan system persamaan linier dari koefesien polinomila dalam upaya rekontruksi fungsi interpolasinya.
Teladan 3.11
Selesaikan permasalahan teladan dengan metode Newton Gregory Mundur
Solusi:
Penyelesaian secara numerik dengan metode Newton Gregori Mundur sebagai memiliki konsep yang sama.
Pada domain [1 2] dan [2 3] digunakan pendekatan derajat 1 (satu) dengan persamaan f(x)1hf1 .
Domain [1 2] ==> x0 = 2 ==> ∆f-1 = 0.6 ==> f’(x) = 0.6
………(a)
Domain [2 3] ==> x0 = 3 ==> ∆f-1 = 0.5 ==> f’(x) = 0.5
………(b)
Numerik
Pada domain
5 3x pola
grafk cendung
mengikuti pola polinomial derajat 3 (tiga) sehingga persamaan Newton Gregori Mundur yang digunakan adalah
6
2 6 3 2
1 2 1
)
( 3
3 2
2 2
1 s f s s f
f h x f
Agar mendapatkan nilai ∆3f
-3 yang terkontruksi dari batas-batas
interval 3x5, maka haruslah dipilih x0 = 6.
1 . 3 6
. 1 ;
1 ;
6
6 0 1 2 2 3 3
0 x f f dan f x
x s x
xi fi ∆fi ∆2fi ∆3fi ∆4fi
1 0.5 0.6 2 1.1
0.5
3 1.6 0.6
1.1 0.9
4 2.7 1.5 -4
2.6 -3.1
5 5.3 -1.6 5.2
1 2.1
6 6.3 0.5 -1.9
1.5 0.2
7 7.8 0.7 -2.8
2.2 -2.6
8 10 -1.9 4.4
0.3 1.8
9 10.3 -0.1 -1.8
0.2 0
1
0 10.5 -0.1 0.1
0.1 0.1
1
1 10.6 0
0.1 1
Numerik
Pada domain [8 10] dengan pendekatan polinomial derajat 2 (dua), maka persamaan yang digunakan
Pada domain [10 12] dengan pendekatan polinomial berderajat 2 (dua)
Dari (a), (b), (c), (d), (e) dan (f) diperoleh menurut polinomial Newton Gregory Mundur
Numerik
12 10
1 . 0
10 8
15 . 1 1 . 0
8 5
8167 . 1 7 . 0 1 . 0
5 3
4333 . 28 9 . 13 5501
. 1
3 2
5 . 0
2 1
6 . 0
)
( 2
2
x x x
x x
x
x x
x
x x
x f
Hasil yang diperoleh sama dengan cara-cara sebelumnya. Hal ini menunjukkan bahwa sangat banyak alternatif yang dapat digunakan untuk mendapatkan nilai turunan dari suatu fungai yang terdefnisi tidak secara analitik, tetapi dalam sebuah kurva aatau data pemetaan.
3.3. Intuegral Numerik
Integral berasal dari kata integrasi yang berarti penyatuan. Integral disimbolkan dengn ∫ merupakan dibentuk dari hurup S awal huruf kata SUM yang berarti Jumlah. Dalam konsep matematika integral merupakan jumlah dari penyatuan pias-pias yang sangat kecil dari sutau kurva tertutup.
Gambar 3.9 Model integrasi suatu kurva f(x)
Pada gambar di atas, luas daerah yang dibatasi oleh kurva y = f(x), garis x = a, x = b dan y = 0 dapat dihitung dengan menyatukan luas daerah 1, 2, 3, 4, 5 dan 6. Kenyataan ini secara matematis disebut sebagai integrasi dari fungsi y = f(x) dengan batas bawah x= a dan batas atas x = b. Secara
matematis ditulis sebagai
6 5 3 2 1
, f(x)dx LD LD LD LD LD
LD
b
a b
a
dengan LD =Luas Daerah. Penyelesaian secara analitik ditentukan dengan
b
a
dx x
Numerik
f(x). Penyelesaian secara numrik integrasi tersebut dapat dilakukan dengan beberapa metode, diantaranya metode Deret Reimant, Metode Tropezoidal Newton Cotes dan lainnya. Peruntukan metode ini dalam upaya memecahkan permasalahan integrasi dari formula fungsi yang sangat sulit untuk ditentukan anti turunannya atau fungsinya dinyatakan dalam data dimana fungsi analitiknya tidak diketahui.
3.3.1 Metuode Deretu Reimantu
Metode integrasi klasik yang dikembangan oleh Reimant yang selanjutnya disebut integral Reimant diberikan oleh formula
n
i i b
a
f h dx x f
0 )
( dengan h diambil sedekat mungkin dengan 0 (nol).
Gambar 3.10 Model integrasi dengan Metode Deret Reimant
Pada gambar di atas, luas daerah di bawah kurav y = f(x) dengan batas garis x = x0, x = xn dan y = 0 adalah jumlah dari
luas tiap pias pada kurva tersebut:
Luas = hf1 + hf2 + hf3 + … + hfn = h(f1 + f2 + f3 + … + fn)
n
i i x
x
f h dx x f
n
1 0
) (
Teladan 3.12
Selesaikan
1
0
2 2 )
(x x dx dengan cara analitik dan numerik .
Solusi:
a. Cara analitik
33 . 1 3 4 1 3 1 3
1 )
2 (
1 0 2 3 1
0 2
x x dx x xb. Cara Numerik
Numerik
xi
fi = xi2 +
2xi xi
fi = xi2 + 2xi xi
fi = xi2 + 2xi xi
fi = xi2 + 2xi
0 0 0.25 0.5625 0.5 1.25 0.75 2.0625
0.0
1 0.0201 0.26 0.5876 0.51 1.2801 0.76 2.0976 0.0
2 0.0404 0.27 0.6129 0.52 1.3104 0.77 2.1329 0.0
3 0.0609 0.28 0.6384 0.53 1.3409 0.78 2.1684 0.0
4 0.0816 0.29 0.6641 0.54 1.3716 0.79 2.2041 0.0
5 0.1025 0.3 0.69 0.55 1.4025 0.8 2.24
0.0
6 0.1236 0.31 0.7161 0.56 1.4336 0.81 2.2761 0.0
7 0.1449 0.32 0.7424 0.57 1.4649 0.82 2.3124 0.0
8 0.1664 0.33 0.7689 0.58 1.4964 0.83 2.3489 0.0
9 0.1881 0.34 0.7956 0.59 1.5281 0.84 2.3856
0.1 0.21 0.35 0.8225 0.6 1.56 0.85 2.4225 0.1
1 0.2321 0.36 0.8496 0.61 1.5921 0.86 2.4596 0.1
2 0.2544 0.37 0.8769 0.62 1.6244 0.87 2.4969 0.1
3 0.2769 0.38 0.9044 0.63 1.6569 0.88 2.5344 0.1
4 0.2996 0.39 0.9321 0.64 1.6896 0.89 2.5721 0.1
5 0.3225 0.4 0.96 0.65 1.7225 0.9 2.61
0.1
6 0.3456 0.41 0.9881 0.66 1.7556 0.91 2.6481 0.1
7 0.3689 0.42 1.0164 0.67 1.7889 0.92 2.6864 0.1
8 0.3924 0.43 1.0449 0.68 1.8224 0.93 2.7249 0.1
9 0.4161 0.44 1.0736 0.69 1.8561 0.94 2.7636
0.2 0.44 0.45 1.1025 0.7 1.89 0.95 2.8025 0.2
1 0.4641 0.46 1.1316 0.71 1.9241 0.96 2.8416 0.2
2 0.4884 0.47 1.1609 0.72 1.9584 0.97 2.8809 0.2
3 0.5129 0.48 1.1904 0.73 1.9929 0.98 2.9204 0.2
Numerik
xi
fi = xi2 +
2xi xi
fi = xi2 + 2xi xi
fi = xi2 + 2xi xi
fi = xi2 + 2xi
∑ = 6.49 ∑ = 22.0525 ∑ = 40.74 ∑ = 62.5525
Berdasarkan table di atas, maka diperoleh
6.49 22.0525 40.74 62.5525 1.31835 01
. 0 01
. 0 ) 2 (
100 1 1
0 2
x x dx i fiNilai ini memiliki error relatif =
1.12375% %
100 33333
. 1
33333 . 1 31835 . 1
Untuk memperkecil kesalahan, dapat dilakukan dengan mengambil nilai h diperoleh lebih dekat dengan 0 (nol). Komputer program yang dapat digunakan untuk mengevaluasi nilai untuk h = 0.000001 tersebut adalah
syms x f=x^2+2*x; h=0.000001; d=[0:h:1];
p=subs(f,d);format long Luas=h*sum(p)
Luas =
1.333334833333463
Hasil komputasi tersebut diperoleh
333463 3333334833
. 1 ) 2 ( 1
0 2
x x dx . Nilai tersebut sudah mendekati nilai sebenarnya 4/3.Teladan 3.14
Gunakan integral Reimant unutk memeriksa apakah data berikut terdistribusi Normal dengan tingkat kesalahan maksimal 5%.
65 72 67 82 72 91 67 73 71 70 85 87 68 86 83 90 74 89 75 61 65 76 71 65 91 79 75 69 66 85 95 74 73 68 89 90 70 71 88 68
Solusi:
Suatu data disebut terdistribusi Normal apabila distribusi data
tersebut memenuhi fungsi peluang
2
2 1 2
2 1 )
(
x
e x
f .
Berdasarkan data diperoleh parameter statistik E
X =76.33 dan E
S 9.32 sehingga bentuk khusus fungsiNumerik
normal dari data di atas adalah
2 32 . 9
33 . 76 2 1 2
32 . 9 2
1 )
(
x
e x
f
.
Dengan menerapkan aturan Struges dan Cumulatif Distribusi Funaction (CDF), serta penyelesainya secara numerik dengan kode program komputasi dibawah adalah sebagai berikut:
b b
b
a fo
5 . 0
5 . 0
) (
bb
bb
h n f x dx
f
h h o
f f f 2
6
1 - 65 4 3.12 0.25
6
6 - 70 9 5.73 1.87
7 1
-7 5
1 1
7.95 1.17
7
6 - 80 2 8.33 4.81
8
1 - 85 4 6.59 1.02
8
6 - 90 7 3.93 2.39
9
1 - 95 3 1.77 0.85
∑ 12.35
Kode komputasi numerik dengan deret Reimant untuk
menghitung nilai dari
5 . 0
5 . 0
) (
bb
bb
h n f x dx
f .
syms x
f1=exp(-0.5*(((x-76.33)/9.32)^2)); f2=1/sqrt(2*pi*(9.32)^2);
f=f1*f2; h=0.00001;
Numerik
bahwa probability Distribusi Function (PDF) chi kuadrat adalah
Sehingga fungsi peluang ditribusi chi kuadrat untuk data yang diketahui adalah
Andaikan data tersebut tidak terdistribusi normal, maka
haruslah
Kode program komputasi dengan metode deret Reimant yang digunakan untuk mengevaluasi integral tersebut adalah
syms x h=0.00001;
g=(1/16)*(x^2)*exp(-x/2); format long
alpa=1-h*sum(subs(g,[0:h:12.35])) alpa =
0.054600898347735
Numerik
Hasil yang diperoleh ini menunjukkan bahwa kesalahan menyatakan Data tersebut tidak normal adalah α = 0.054600898347735 > 0.05 = 5%.
Kesalahan ini tidak bisa diterima karena nilai errornya melebihi batas maksimum 5%. Jika kondisi Tidak Normal tidak diterima, maka seharusnya yang diterima adalah Data tersebut InsyaAllah berasal dari Distribusi Normal.
3.3.2 Metuode Tropezoidal
Tinjau kembali ilustrasi gambar integral di atas
Gambar 3.11 Model integrasi dengan metode Tropezoidal
Luas di bawah kurva y = f(x), di atas garis y=0, dibatas kiri x= x0 dan batas kanan x=xn dapat ditentukan dengan integrasi
dari luas tiap pias-pias. Luas tiap pias dapat ditentukan dengan luas trapezium sebagai berikut:
Luas =
f f
h
f f
h
f f
h
f fn
hdx x
f n
x
x
n
( ) 2 0 1 2 1 2 2 2 3 2 10
f f f f f f f f f fn
h
n n
n
2 0 1 1 2 2 3 2 1 1
f f f f f fn
h
n
2 0 2 1 2 3 1
Jadi berdasarkan rumus luas trapezium, diperoleh nilai dari
f f f f f fn
hdx x
f n
x
x
n
0 2 1 2 3 12 ) ( 0
Numerik
Tentukan nilai dari
21 1 dx
x mengunakan metode TraTropeziodal dengan h=0.1 dan bandingkan akurasinya secara analitik.
Solusi:
Dengan mengambil nilai h = 0.1 maka diperoleh
Penyelesaian secara analitik
0559945
Error relatif = 0.090055829059348 %.
3.3.3 Newtuon Cotues
Inetgrasi dengan metode Newton Cotes didasari dari integrasi dapi polinomial Newton Gregory
3.3.3.1 Pendekatuan Polinomial Newtuon Gregory Maju
Tinjau kembali formula umum polinomial Newton Gregory Maju sebagai berikut:
Numerik
Teladan 3.16
Tentukan nilai dari
x
dx 2. 0
0
2 2 dengan mengunakan cara analitik dan numerik
Solusi:
a. Cara Analitik
0.2
2(0.2) 0.4027b. Cara Numerik
Ambil h = 0.1, maka diperoleh x0 = 0 f0 = 2 nilai h lebih dekat dengan 0 (nol). Misalkan unutk h = 0.01 maka diperoleh hasil integrasi sebagai berikut:
Numerik
x1 = 0.01 f1 = (0.01)2 + 2 = 2.0001 (0.01/2)( f1 + f2 ) =
0.0200025
x2 = 0.02 f2 = (0.02)2 + 2 = 2.0004 (0.01/2)(f2 + f3 ) =
0.0200065
x3 = 0.03 f3 = (0.03)2 + 2 = 2.0009 (0.01/2)(f3 + f4 ) =
0.0200125
x4 = 0.04 f4 = (0.04)2 + 2 = 2.0016 (0.01/2)(f4 + f5 ) =
0.0200205
x5 = 0.05 f5 = (0.05)2 + 2 = 2.0025 (0.01/2)(f5 + f6 ) =
0.0200305
x6 = 0.06 f6 = (0.06)2 + 2 = 2.0036 (0.01/2)(f6 + f7 ) =
0.0200425
x7 = 0.07 f7 = (0.07)2 + 2 = 2.0049 (0.01/2)(f7 + f8 ) =
0.0200565
x8 = 0.08 f8 = (0.08)2 + 2 = 2.0064 (0.01/2)( f8 + f9 ) =
0.0200725
x9 = 0.09 f9 = (0.09)2 + 2 = 2.0081 (0.01/2)( f9 + f10) =
0.0200905
x10 = 0.1 f10 = (0.10)2 + 2 = 2.0100 (0.01/2)(f10 + f11) =
0.0201105
x11 = 0.11 f11 = (0.11)2 + 2 = 2.0121 (0.01/2) (f11 + f12) =
0.0201325
x12 = 0.12 f12 = (0.12)2 + 2 = 2.0144 (0.01/2) (f12 + f13) =
0.0201565
x13 = 0.13 f13 = (0.13)2 + 2 = 2.0169 (0.01/2) (f13 + f14) =
0.0201825
x14 = 0.14 f14 = (0.14)2 + 2 = 2.0196 (0.01/2) (f14 + f15) =
0.0202105
x15 = 0.15 f15 = (0.15)2 + 2 = 2.0225 (0.01/2) (f15 + f16) =
0.0202405
x16 = 0.16 f16 = (0.16)2 + 2 = 2.0256 (0.01/2) (f16 + f17) =
0.0202725
x17 = 0.17 f17 = (0.17)2 + 2 = 2.0289 (0.01/2) (f17 + f18) =
0.0203065
x18 = 0.18 f18 = (0.18)2 + 2 = 2.0324 (0.01/2) (f18 + f19)=
0.0203425
x19 = 0.19 f19 = (0.19)2 + 2 = 2.0361 (0.01/2) (f19 + f20) =
0.0203805
x20 = 0.2 f20 = (0.20)2 + 2 = 2.0400
04 . 0
03 . 0
2 03
. 0
02 . 0
2 02
. 0
01 . 0
2 01
. 0
0 2 2
. 0
0
2 2dx x 2dx x 2dx x 2dx x 2dx
x
Numerik Error Relatif
%
Komputer program yang dapat digunakan untuk mencari
nilai
x
dxfor i=1:length(d)-1
H(i+1)=(h/2)*(p(i)+p(i+1));
end
hasil = sum(H)
Teladan 3.17
Tentukan luas daerah yang dibatasi oleh garis x = 0, x=1 dan
Numerik
Solusi
Dengan mengambil nilai h = 0.01
Luas daerah yang diminta dapat dinyatakan dengan
i i
x x
x x
f f f
f f f h dx xe x e
x
xe e
x
0 1 1 2 11
0 2 sin 2 3
sin 3
2 4
sin ln
) ln(
tan ) cos( 2
Evaluasi dengan mengunakan kode komputasi dibawah diperoleh hasil
i xi fi x0∫
x1 f(x) dx = (0.01/2)(f 0
+f1)
0 1 1.505048744 0.028356885
1 1.01 4.166328184 0.052032601
2 1.02 6.240191996 0.065771556
3 1.03 6.914119263 0.063990794
4 1.04 5.884039509 0.047181489
5 1.05 3.552258346 0.02246199
6 1.06 0.940139591 0.008306523
7 1.07 0.721165049 0.006577636
8 1.08 0.594362051 0.009234554
9 1.09 1.252548692 0.025058808
1
0 1.1 3.759212885 0.04571821
1
1 1.11 5.384429122 0.052125197
1
2 1.12 5.040610212 0.039734506
1
3 1.13 2.906290937 0.016898222
1
4 1.14 0.473353562 0.004469333
1
5 1.15 0.42051307 0.006883446
1 1.1 0.9561761 0.021997813
Numerik
i xi fi x0∫
x1 f(x) dx = (0.01/2)(f 0
+f1)
6 6 52
1
7 1.17 3.443386429 0.041147696
1
8 1.18 4.786152728 0.04221755
1
9 1.19 3.657357304 0.023960326
2
0 1.2 1.134707808 0.006335683
2
1 1.21 0.13242877 0.00708346
2
2 1.22 1.28426329 0.025042261
2
3 1.23 3.724188982 0.039260381
2
4 1.24 4.127887284 0.030225034
2
5 1.25 1.917119474 0.010155481
2
6 1.26 0.113976646 0.007281934
2
7 1.27 1.342410099 0.025339312
2
8 1.28 3.72545229 0.035655252
2
9 1.29 3.405598143 0.021513542
3
0 1.3 0.897110304 0.007726807
3
1 1.31 0.648251113 0.018815311
3
2 1.32 3.114811157 0.032854125
3
3 1.33 3.456013828 0.022154761
3
4 1.34 0.974938278 0.009885607
3
5 1.35 1.002183217 0.022240428
3
6 1.36 3.445902337 0.030050866
3
7 1.37 2.564270849 0.015663078
Numerik
i xi fi x0∫
x1 f(x) dx = (0.01/2)(f 0
+f1)
3
9 1.39 2.545179653 0.028665579
4
0 1.4 3.187936121 0.019944519
4
1 1.41 0.800967644 0.015404955
4
2 1.42 2.28002327 0.027092517
4
3 1.43 3.13848004 0.019937142
4
4 1.44 0.848948282 0.01809099
4
5 1.45 2.769249651 0.026332567
4
6 1.46 2.497263746 0.018309223
4
7 1.47 1.164580918 0.02276532
4
8 1.48 3.388483154 0.023287256
4
9 1.49 1.268967995 0.020217058
5
0 1.5 2.774443551 0
Jumlah 1.247023204
syms x
f1=2*x*cos(exp(3*x))-tan(log(x*exp(sqrt(sin(x))))); f2=(x^2)*exp(sin(2*x-3))+log(x)*sin(4*x*exp(-x)); f=f1/f2;
h=0.01; d=[1:h:1.5]; p=abs(subs(f,d));
for i=1:length(d)-1
H(i)=(h/2)*(p(i)+p(i+1));
end
H(end+1)=0; S=[d;p;H]'
xlswrite('Simpan',S)
disp(['Hasil = ',num2str(sum(H))]); area(d,subs(f,d))
text(1.3,-6,['Luas = ',num2str(sum(H))])
Numerik
Gambar 3.12 Luas daerah
Dar hasil perhitungan tersebut, dapat diketahui luas daerah yang diarsir adalah
4
Teladan. 3.18
Buktikan bahwa untuk
2
0 4 1 2
Dengan pendekatan polynomial newton gergori maju hingga beda ke-2, maka diperoleh
Numerik
Teladan. 3.19
Dapatkan luas daerah di bawah ini
Gambar 3.13 Model sembarang suatu kurva tertutup
Solusi:
Gambar disamping dapat di pandang sebagai kurva yang dibatasi oleh dua buah fungsi f(x) dan g(x). f(x) adalah sisi kurva bagian bawah dan g(x) adalah kurva pada sisi bagian atas. Hasil Gridtisasi diperoleh sebagai berikut:
Numerik
Gambar 3.14 Model gritisasi suatu semabarang kurva tertutup
Berdasarkan gritisasi di atas, maka dapat ditentukan nilai i, xi,
fi dan gi sebagaimana pada tabel dibawah dan perhitungan
integrasinya berdasarkan formula Newton Cotes unutk n =1 dan n = 2. Hasil yang diperoleh luas daerah tersebut menurut n = 1 adalah 81.45 satuan luas dan untuk n = 2 adalah 81.78333333 satuan luas. Terdapat perbedaan sebesar 0.3333. Perbedaan ini disebabkan karena ukuran derajat yang digunakan, semakin tinggi derajat polynomial Newton Gregory yang dipakai, maka hasilnya juga lebih akurat. Pada contoh ini hasil sebesar 81.78333333 satuan luas unutk n= 2 lebih direkomendasikan. Akan tetapi jika ingin mengambil tengahnya, maka nilai luas pendekatan yang diperoleh adalah (81.78333333+81.45)/2 = 81.6167 satuan luas menjadi lebih bijaksana. Pehitungan detailnya sebagai berikut:
i xi fi gi hi
n = 1 n=2
hi + hi+1
(0.5/2)(hi + hi+1)
h0 + 4h1 + h2
(0.5/3)*(h0 + 4h1 + h2)
0 0 2 2 0 1.8 0.45
10.2 1.7
1 0.5 1.2 3 1.8 4.8 1.2
2 1 1 4 3 6.9 1.725
23.5 3.916666667
3 1.5 1 4.9 3.9 8.8 2.2
4 2 1.1 6 4.9 10.8 2.7
34.5 5.75
5 2.5 1.1 7 5.9 11.9 2.975
6 3 1.2 7.
Numerik
i xi fi gi hi
n = 1 n=2
hi + hi+1
(0.5/2)(hi + hi+1)
h0 + 4h1 + h2
(0.5/3)*(h0 + 4h1 + h2)
7 3.5 1.3 7.3 6 11.8 2.95
8 4 1.4 7.2 5.8 11.4 2.85
33.6 5.6
9 4.5 1.5 7.1 5.6 11 2.75
1
0 5 1.6 7 5.4 10.6 2.65
31.2 5.2
1
1 5.5 1.7 6.9 5.2 10.2 2.55 1
2 6 1.8 6.8 5 9.8 2.45
28.75 4.791666667 1
3 6.5 1.9 6.7 4.8 9.35 2.3375 1
4 7 1.95 6.5 4.55 9 2.25
27.05 4.508333333 1
5 7.5 1.95 6.4 4.45 9.15 2.2875 1
6 8 1.8 6.5 4.7 9.8 2.45
30.6 5.1
1
7 8.5 1.6 6.7 5.1 10.6 2.65 1
8 9 1.3 6.8 5.5 11.4 2.85
35.2 5.866666667 1
9 9.5 1 6.9 5.9 12 3
2
0 10 0.9 7 6.1 12.5 3.125
38.5 6.416666667 2
1 10.5 0.6 7 6.4 13.2 3.3
2
2 11 0.3 7.1 6.8 13.8 3.45
41.6 6.933333333 2
3 11.5 0.2 7.2 7 13.8 3.45 2
4 12 0.2 7 6.8 13.5 3.375
40.1 6.683333333 2
5 12.5 0.3 7 6.7 13.2 3.3
2
6 13 0.3 6.8 6.5 12.5 3.125
35.9 5.983333333 2
7 13.5 0.4 6.4 6 11.4 2.85 2
8 14 0.6 6 5.4 10.1 2.525
28.2 4.7
2
9 14.5 0.8 5.5 4.7 8.7 2.175 3
0 15 1 5 4 7 1.75
16 2.666666667
3 15. 1.1 4. 3 3 0.75
Numerik
Luas Daerah = Jumlah = 81.45 Luas Daerah 81.78333333
3.2.3.32 Pendekatuan Polinomial Newtuon Gregory Mundur
Tinjau kembali polinomial Newton Gregory Mundur
Teladan. 3.20
Terapkan formula integrasi dengan polinomial Newton Gregory
Mundur di atas untuk memeriksa nilai
005 . 1Numerik
bandingkan hasilnya dengan cara analitik untuk melihat akurasinya serta tentukan error relatifnya.
Solusi:
Evaluasi nili f(x) pada interval [1 1.005] dengan h = 0.001 serta nilai integrasinya sebagai berikut:
xi fi 2fo-f-1
1.002 1.004004 1.008014 0.001008014
1.003 1.006009 1.010023 0.001010023
1.004
1.005 1.010025 ∑ 0.00504008
Formula integrasi numerik dengan metode Newton Gregori Mundur derajat 1 (satu) adalah
0.001012= 0.00504
Numerik
Nilai error relatifnya adalah
%
berada di bawah 1% sehingga masih bias ditoleransi.
3.4 Rangkuman
1. Turunan merupakan ukuran yang menyatakan kemiringan garis singgung pada suatu kurva.
2. Defnisi turunan pertama menurut beda maju adalah
3. ( ) lim ( ) ( ) 1 , 0
4. Defnisi turunan pertama menurut beda mundur adalah 0
5. Defnisi turunan pertama menurut beda tengah
0
6. Defnisi turunan kedua menurut beda hingga
2
7. Defnisi turunan pertama menurut polinomial Newton Gregory Maju
8. Defnisi turunan pertama menurut Polinomial Newton Gregory Mundur
Numerik
11.Defnisi integral menurut metode Tropzoidal adalah
f f f f f fn
h dx x
f n
x
x
n
( ) 2 0 2 1 2 3 10
12.Defnisi integral menurut metode Newton Cotes yang dihampiri dari polinomial Newton Gregory Maju hingga
derajat n = 1 adalah
1
0 1
2 ) ( 1
0 1
0
f f h dx x P dx x f
x
x x
x
13.Defnisi integral menurut metode Newton Cotes yang dihampiri dari polinomial Newton Gregory Maju hingga
derajat n = 2 adalah
2
3
0 4 1 2
22
0
f f f h dx x P dx x f
x
x x
x o
.14.Integral numerik dengan Metode Newton Cotes yang dihampiri dengan polinomial Newton Gregori Mundur
derajat n =1 adalah 2 0 1 1
0
f xdx h f fx
x
dan untuk n =
2 adalah 3
19f0 20f17f2
h.
3.5 Latuihan
Untuk menguji tingkat penguasaan metri integrasi dan diferensial numerik, kerjakan dengan benar dan baik soal-soal di bawah ini.
1. Dapatkan formula integrasi
0 3 1 3 2 3
8 3 ) ( 3
0
f f f f h dx x f
x
x
dengan pendekatanpolinomial Newton Gregori Maju
2.
Apabila diberikan data sebagai berikut :
x Y
Ripai, S.Pd., M.Si
a. Hitung luas yang dibentuk oleh fungsi y(x) dengan garis-garis x = 0.2 dan x = 0.6
Numerik
0.2 1.221403
0.3 1.349859
0.4 1.491825
0.5 1.648721
0.6 1.822119
3. Tentukan nilai dari f’(x) dan f’’(x) pada domain [0 0.1]
dengan h = 0.001 dari
) 4
tan(
)) sin( 2 ln( 5 cos
2 )
( 5x
x
e x
x x e
x x f
.
4. Lakukan gritisasi dan hitung luas daerahPulau Moyo berdasarkan peta di bawah dengan metode yang sesuai.
Numerik
6. Diketahui data sebagaimana tabel beda hingga di bawah ini
x y ∆y ∆2y ∆3y ∆4y
1.3 3.669
0.813
1.5 4.482 0.179
0.992 0.041
1.7 5.474 0.22 0.007
1.212 0.048
1.9 6.686 0.268 0.012
1.480 0.060
2.1 8.166 0.328 0.012
1.808 0.072
2.3 9.974 0.4
2.208 2.5 12.182
Tentukan nilai f’(1.7) dengan pendekatan polinomial derajat I, II, III dan IV.
![Grafik turunan numerik beda maju pada domain [0.8 0.800001]](https://thumb-ap.123doks.com/thumbv2/123dok/2244060.1624262/10.420.32.335.460.563/grafik-turunan-numerik-beda-maju-domain.webp)

![Grafik turunan numerik beda mundur pada domain [0.8 0.800001]](https://thumb-ap.123doks.com/thumbv2/123dok/2244060.1624262/15.420.76.370.65.367/grafik-turunan-numerik-beda-mundur-domain.webp)
![Grafik turunan numerik beda mundur pada domain [0.8 0.800001]](https://thumb-ap.123doks.com/thumbv2/123dok/2244060.1624262/20.420.55.352.240.536/grafik-turunan-numerik-beda-mundur-domain.webp)

![Gambar 3.7 Grafk f(x) dan f’’(x) pada domain [0.8 0.00001]](https://thumb-ap.123doks.com/thumbv2/123dok/2244060.1624262/26.420.30.345.107.411/gambar-grafk-f-x-f-x-domain.webp)

