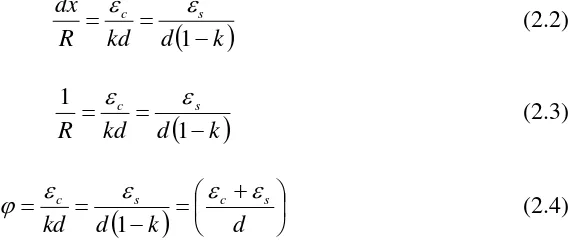BAB II TINJAUAN PUSTAKA - Studi Parameter Pilar Jembatan Beton Bertulang dengan Metode Pushover

BAB II

TINJAUAN PUSTAKA

2.1 Pendahuluan Pilar Jembatan

Pilar jembatan merupakan struktur yang memberikan dukungan vertikal untuk

rentang di antara dua poin.Pilar jembatan memiliki dua fungsi utama yaitu; mentransfer

beban bangunan atas vertikal ke pondasi dan menahan kekuatan horisontal yang bekerja

pada jembatan. Meskipun pilar secara umum dirancang untuk menahan beban vertikal,

lebih dari pada itu pilar juga didesain untuk menahan beban lateral tinggi disebabkan

oleh peristiwa seismik. Bahkan untuk beberapa daerah seismik yang rendah, biasanya

perencanajuga memperhitungkan aspek daktilitas desain terhadap gempa.Pilar

merupakan bagian dari jembatan yang dibangun menggunakan beton bertulang. Untuk

kondisi tertentu biasanya material bajajuga digunakanuntuk sebagai pilar. Material baja

yang didesain berbentuk silinder yang kemudian diisi campuran beton disebut dengan

struktur komposit digunakan juga sebagai pilar jembatan atau pun kolom dari suatu

struktur bangunan (Chen, 2000).

Pilar atau pier biasanya digunakan sebagai istilah umum untuk semua jenis

substruktur terletak antara rentang horizontal dan pondasi. Namun, dari waktu ke waktu,

juga digunakan terutama untuk dinding yang solid dalam rangka untuk membedakannya

dari kolom atau bents. Dari sudut pandang struktural, kolom adalah anggota yang menolak gaya lateral terutama oleh aksi lentur sedangkan pilar adalah anggota yang

menolak gaya lateral terutamadengan mekanisme geser. Sebuah pilar yang terdiri dari

beberapa kolom sering disebut bentsAda beberapa cara untuk mendefinisikan jenis pilar. Salah satunya adalah dengan konektivitas struktural ke bangunan atas Gambar 2.1

monolitik atau kantilever. Lain adalah dengan penampangnya Gambar 2.2 padat atau

berongga, bulat, segi delapan, heksagonal, atau persegi panjang. Hal ini juga dapat

dibedakan dengan konfigurasi framingnya; bengkok pilar tunggal atau ganda, martil

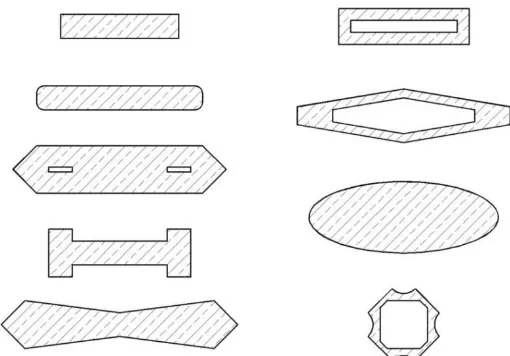
Gambar 2.1 Bentuk typical cross-sectionpilar untuk overcrossings atau viaducts di darat (Chen, 2000)

Gambar 2.2 Bentuk typical cross-sectionpilar untuk sungai dan penyeberangan jalur air (Chen, 2000)

2.2 Pemilihan Kriteria Pilar Jembatan

Pemilihan jenis pilar untuk jembatan harus didasarkan pada fungsional,

struktural, danpersyaratangeometris. Estetika juga merupakan faktor yang sangat

penting didalam pemilihan kriteria sejakjembatan jalan raya di era modernmerupakan

bagian dari lanskap kota. Gambar 2.1 menunjukkan koleksi khas bentuk cross section

untukovercrossings dan viaducts di darat dan Gambar 2.2 menunjukkan beberapa

bentuk bagian khas jembatan untukpilar sungai dan penyeberangan jalur air. Seringkali,

jenis atau bentuk pilarbiasanya ditentukan oleh instansi pemerintah atau pihak swasta

seperti PTPN dalam hal ini pemilik struktur jembatan. Di beberapa negara biasanya

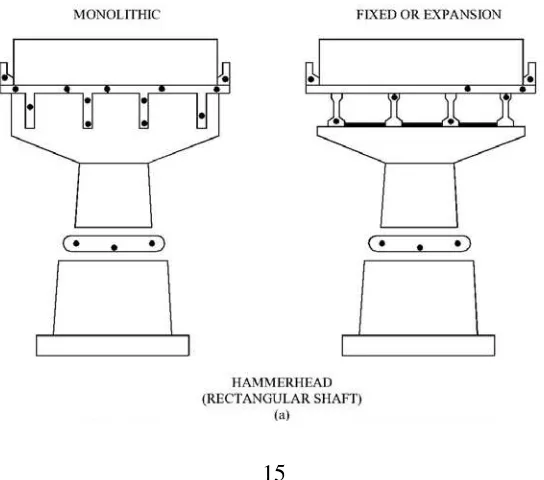
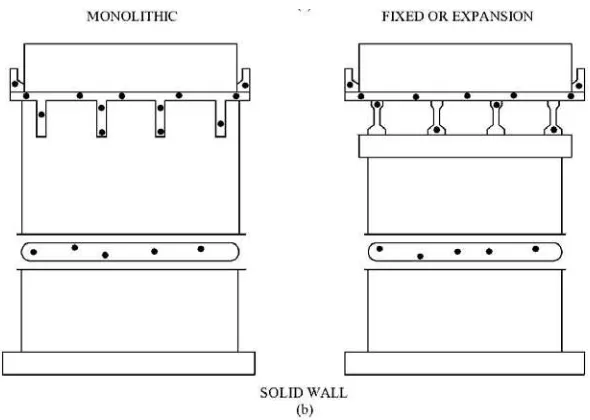
Bentuk pilar berdinding padat, seperti yang ditunjukkan pada Gambar 2.3 dan

2.4, yang sering digunakan di perlintasan air dapat didesain untuk proporsi yang baik,

ramping dan efisien. Bentuk-bentuk seperti ini memberikan resistensi minimal terhadap

aliran banjir.Hammerhead pilar, seperti yang ditunjukkan pada Gambar 2.3.b, sering

ditemukan di daerah perkotaan di mana keterbatasan pada ruang sering terjadi.

Pilar-pilar tersebut digunakan untuk mendukung gelagar baja atau beton pratekan

pracetaksuperstruktur. Mempunyai nilai estetika yang menarik. Umumnya pilar tersebut

memerlukan ruang yang sedikit, sehingga memberikan ruang lainnya untuk lalu lintas di

bawahnya (Chen,2000).

Gambar 2.4 Jenis pilar dan konfigurasi untuk penyeberangan sungai dan jalur air (Chen, 200)

Sebuahkolom pilar bents terdiri dari balok dan kolom topi pendukung membentuk bingkai. Kolompilar bents, seperti yang ditunjukkan pada Gambar 2.3.c dan Gambar 2.5, dapat digunakan untuk mendukung gelagar bajabangunan atas atau

digunakan sebagai pilaruntuk konstruksi yang cor ditempat.Kolom pilar dapat berupa

bentuk lingkaran atau empat persegi panjang. Bentuk pilar tersebut adalah bentuk yang

paling populerdi sistem jalan raya modern.Sebuah pilar dengan perpanjangan tumpuan

terdiri dari poros yang dibor sebagai dasar dan kolom melingkar diperpanjangdari poros

untuk membentuk substruktur. Keuntungan yang jelas dari jenis pilar ini adalah bahwa

hal itu menempatijumlah minimal ruang. Pelebaran jembatan yang ada dalam beberapa

kasus mungkin memerlukan tumpuan ekstensi karena ruang terbatas menghalangi

penggunaan jenis lain dari pondasi.

Dalam menyeleksi jenis pilar yang tepat tergantung pada banyak faktor.

Pertama-tama, itu tergantung pada jenissuprastruktur. Misalnya, baja girder

superstruktur biasanya didukungoleh kantileverpilar, sedangkan cor dtempat

pierdisukai pada jembatan penyeberangan sungai,hal ini disebabkan kekhawatiran jika

sampah menyangkut dipilar jembatan. Bents ekstensi biasanya digunakan pada jembatan slab. Terakhir, ketinggian pilar juga menentukan jenispemilihan pilar. Bentuk pilar

tinggi sering membutuhkan penampang berongga untuk mengurangi berat badandari

substruktur. Hal ini kemudian mengurangi tuntutan beban pada pondasi mahal.

Gambar 2.5 Jenis pilaruntuk Jembatan Beton

2.3 Konsep Perencanaan Struktur Tahan Gempa

Indonesia yang diantara 4 lempeng benua merupakan salah satu negara

dikawasan rawan gempa. Akibat gempa yang sering terjadi mengakibatkan struktur

bangunan yang ada mengalami pergerakan secara vertikal maupun secara lateral.

Sehingga dalam perencanaan perhitungan struktur bangunannya harus menggunakan

faktor keamanan yang cukup aman untuk menahan gaya vertikal daripada gaya gempa

lateral. Gaya gempa lateral langsung bekerja pada bagian-bagian struktur yang tidak

kuat sehingga menyebabkan keruntuhan elemen struktur.

Dalam merencanakan struktur jembatan beton yang harus diperhitungkan adalah

struktur tersebut, seperti beban gravitasional dan beban lateral. Beban gravitasi adalah

beban mati struktur sendiri dan beban hidup, sedangkan yang termasuk beban lateral

adalah beban angin dan beban gempa.

Mengacu kepada kode perencanaan bangunan tahan gempa amerika UBC 1997

perencanaan desain struktur bangunan tahan gempa adalah untuk mencegah terjadinya

kegagalan pada setiap elemen struktur dan timbulnya korban jiwa. Tiga kriteria yang

harus dipenuhi adalah:

1. Ketika terjadi gempa kecil, tidak terjadi kerusakan sama sekali,

2. Ketika terjadi gempa sedang, diperbolehkan terjadi kerusakan arsitektural

tetapi bukan merupakan kerusakan struktural,

3. Ketika terjadi gempa kuat, diperbolehkan terjadinya kerusakan struktural

dan nonstruktural, namun kerusakan yang terjadi tidak sampai menyebabkan

bangunan runtuh.

Jadi, dalam perencanaan struktur bangunan tahan gempa harus diperhitungkan

efek dari gaya lateral yang bersifat siklis (bolak-balik) yang dialami oleh elemen

struktur selama terjadinya gempa bumi. Agar struktur dapat memikul gaya lateral yang

terjadi, maka diperlukan beberapa kriteria seperti daktilitas yang memadai di daerah

joint dan penggunaan elemen struktur yang tahan gempa. Oleh karenanya didalam

merencanakan suatu struktur dapat dilakukan dengan mengetahui skenario keruntuhan

dari struktur tersebut dalam memikul beban-beban ekstrim yang bekerja.

Pelaksanaan konsep desain kapasitas struktur adalah memperkirakan urutan

kejadian dari kegagalan suatu struktur berdasarkan beban maksimum yang dialami

struktur. Sehingga kita merencanakan bangunan dengan elemen-elemen struktur tidak

dibuat sama kuat terhadap gaya yang direncanakan, tetapi ada elemen-elemen struktur

atau titik pada struktur yang dibuat lebih lemah dibandingkan dengan yang lain dengan

harapan di elemen atau titik itulah kegagalan struktur terjadi pada saat beban gempa

maksimum bekerja (Wibisono, 2008).

Berdasarkan hal tersebut, perencanaan struktur dapat direncanakan dengan

maksimum yang bekerja. Pelaksanaan konsep desain kapasitas struktur adalah

memperkirakan urutan kejadian dari kegagalan suatu struktur berdasarkan beban

maksimum yang dialami struktur. Sehingga kita merencanakan bangunan dengan

elemen-elemen struktur tidak dibuat sama kuat terhadap gaya yang direncanakan, tetapi

ada elemen-elemen struktur atau titik pada struktur yang dibuat lebih lemah

dibandingkan dengan yang lain dengan harapan di elemen atau titik itulah kegagalan

struktur terjadi pada saat beban gempa maksimum bekerja.

Berdasarkan konsep mekanisme keruntuhan ini, pertama kali terbentuk sendi

plastis pada struktur balok, baru pada tahap-tahap akhir plastis terjadi pada ujung-ujung

bawah kolom (strong column weak beam). Hal ini dimaksudkan agar sejumlah besar sendi plastis yang terjadi pada struktur secara daktail. Struktur yang daktail dapat

memencarkan energi melalui proses pelelehan struktur dan diharapkan dapat menyerap

beban gempa. Secara matematis konsep “strong column weak beam” dapat dituliskan dalam bentuk persamaan sebagai berikut;

kolom

balok Mn

Mn

6 5

∑

∑

< (2.1)

Bangunan tahan gempa didesain berdasarkan zona gempa, karakter lokasi, jenis

tanah, okupansi bangunan, faktor kegunaan bangunan, periode natural struktur, dan lain-

lain. UBC 1997 mensyaratkan seluruh elemen struktur didesain dengan tahanan yang

sesuai untuk menahan perpindahan lateral yang terjadi akibat ground motion dengan memperhatikan respon inelastis struktur, faktor redundan, kuat lebih dan daktilitas

struktur.

Dalam melakukan analisa perencanaan suatu struktur bangunan tahan gempa

terdapat berbagai metode dalam memodelkan gaya lateral akibat gempa. Respons suatu

bangunan akibat beban gempa yang terjadi adalah sangat kompleks, sehingga

metode-metode baru terus berkembang untuk mengetahui perilaku struktur akibat gempa yang

terjadi. Analisis dinamik merupakan cara yang paling tepat saat ini untuk mengetahui

(time history analysis), dapat diketahui respons struktur akibat gempa seperti simpangan, kecepatan dan percepatan untuk setiap segmen waktu yang ditentukan.

Perencanaan struktur dapat pula dilakukan dengan menggunakan deformasi

maksimum struktur akibat beban gempa rencana. Metode ini dikenal dengan cara

spektrum respons. Gempa kuat yang pernah terjadi dibuat spektrum responsnya untuk

struktur dengan satu derajat kebebasan. Sedangkan untuk struktur dengan banyak

derajat kebebasan, respon maksimumnya diperoleh dengan menggunakan metode SRSS

(Square Root of the Sum of Squares), yaitu menguadratkan respon maksimum dari masing-masing ragam, kemudian dijumlahkan semuanya, lalu diakarkan.

Menurut UBC 1997, gedung-gedung yang diklasifikasikan sebagai gedung yang

beraturan dapat dianalisis dengan menggunakan analisis statik ekivalen, cara yang jauh

lebih mudah dibandingkan dengan analisis dinamik. Analisis ini mentransfer pergerakan

tanah pada level fondasi menjadi beban-beban statik lateral yang bekerja pada setiap

pusat massa lantai. Hasil perencanaan struktur yang diperoleh harus diverifikasi melalui

analisis dinamik, yaitu dengan menggunakan time history analysis dan respon spektrum, untuk mendapatkan respon nyata struktur ketika terkena beban gempa. Tetapi, analisis

dinamik bukanlah persoalan yang mudah sehingga para ahli mengembangkan metode

yang lebih sederhana melalui analisis statik, yaitu dengan konsep desain kinerja struktur

(Performance Based Design).

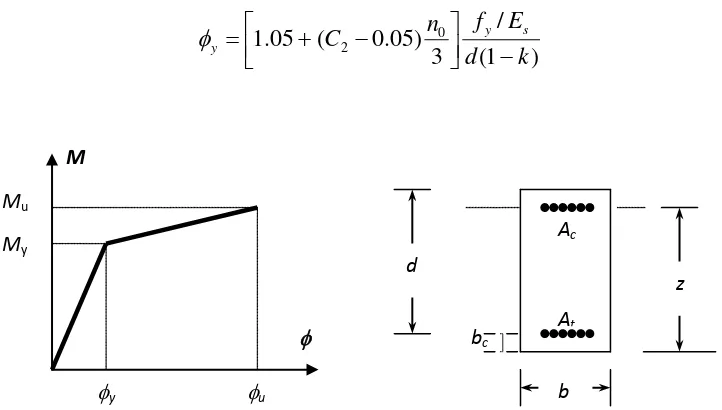
2.4 Hubungan Momen-Kurvatur

Analisis momen kurvatur diperlukan untuk mengetahui daktilitas dari suatu

elemen struktur yang erat kaitannya dengan redistribusi momen. Redistribusi momen

ini berpengaruh dalam sebuah desain, yaitu dapat mengurangi besarnya tulangan baja

yang diperlukan pada sebuah perletakan menerus. Hal ini dikarenakan dengan

melakukan redistribusi momen, akan dapat mengurangi besarnya momen maksimum

Hal yang penting dalam suatu desain dengan beban gempa adalah daktilitas

dari struktur, karena filosofi desain yang ada saat ini berdasarkan pada konsep

penyerapan energi dan disipasi oleh deformasi plastis untuk bertahan terhadap sebuah

gempa. Sehingga sebuah struktur yang tidak memiliki kemampuan daktilitas yang

mencukupi harus didesain dengan beban gempa yang lebih besar untuk menghindari

keruntuhan dari struktur tersebut.

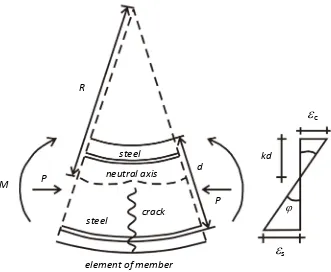
Gambar 2.6 berikut ini memperlihatkan potongan sebuah elemen dari sebuah

struktur beton bertulang dengan momen ujung dan gaya aksial yang sama besarnya.

Jari-jari dari kurvatur R diukur sampai dengan garis netral dari penampang. Jari-jari

dari kurvatur R, kedalaman garis netral kd, regangan beton pada serat tekan terluar εc dan regangan tarik dari baja εs akan bervariasi sepanjang elemen struktur tersebut

karena diantara retak yang terjadi, beton akan mengalami tegangan akibat dari retak

tersebut (Wigan, 2001).

Dengan meninjau sebuah potongan kecil sepanjang dx dari sebuah elemen struktur, serta menggunakan notasi dari Gambar 2.6, maka putaran diantara kedua ujung

dari potongan tersebut adalah seperti berikut ini;

(

k

)

Maka 1/R adalah kurvatur pada potongan (putaran per satuan panjang dari

elemen struktur) dan diberikan notai ϕ. Sehingga terlihat bahwa kurvatur ϕ adalah

Gambar 2.6 Deformasi dari sebuah elemen lentur struktur

Kurvatur tersebut sebenarnya akan bervariasi sepanjang elemen karena

fluktuasi dari kedalaman garis netral dan regangan diantara retak-retak yang terjadi.

Bila panjang dari elemen adalah kecil pada sebuah retakan, maka kurvaturnya adalah

seperti yang terlihat pada Persamaan 2.2, dengan εc dan εs adalah regangan pada

penampang yang retak (Wigan, 2001).

Bila regangan pada penampang yang kritis dari sebuah balok beton bertulang

diukur secara teliti dengan momen lentur terus dinaikkan hingga runtuh, maka kurvatur

dapat dihitung dari Persamaan 2.2, sehingga pada akhimya dapat diperoleh hubungan

momen kurvatur dari penampang tersebut. Hubungan momen kurvatur pada sebuah

balok beton bertulang tunggal yang mengalami keruntuhan pada tarik dan tekan dapat

dilihat seperti pada Gambar 2.7. Pada tahap awal, kurva adalah linier dan hubungan

antara momen M dan kurvatur ϕ diberikan oleb Persamaan 2.5 berikut ini; neutral axis

steel

steel crack

element of member R

P

P M

d

kd

ϕ

ε

c

ϕ

M R M

EI = × = (2.5)

dengan El adalah kekakuan lentur dari penampang tersebut.

Gambar 2.7 Hubungan momen kurvatur untuk beton dengan tulangan tunggal (a) Penampang runtuh akibat tarik ρ<ρbalance

(b) Penampang runtuh akibat tekan ρ>ρbalance

Seiring dengan meningkatnya momen, maka retak yang terjadi pada beton akan

mengurangi kekakuan lentur dari penampang tersebut. Pengurangan kekakuan tersebut

akan semakin besar pengaruhnya pada penampang beton dengan tulangan yang sedikit

bila dibandingkan dengan penampang beton dengan tulangan yang lebih banyak. Sifat

dari penampang setelah mengalami retak akan lebih banyak bergantung dari baja

tulangannya.

section

unit length

M

M

ϕ ϕ

M

first yield of steel

first crack _{first crack}

ϕ

unconfined concrete crushing of concrete commemce

b f l ld

curvature curvature

moment

Seperti pada Gambar 2.7.a mcnunjukkan hubungan momcn kurvatur untuk

penampang dengan tulangan yang lebih sedikit. Kurva tersebut dapat dikatakan

hampir bersifat linier sampai dengan titik di mana baja mulai leleh. Setelah baja mulai

leleh, maka kurvatur akan bertambah secara besar untuk suatu nilai momen lentur yang

hampir sama, kemudian momen akan terus bertambah hingga maksimum akibat dari

pertambahan pada jarak lengan momen, dan pada akhimya menurun kcmbali (Wigan,

2001).

Sebaliknya, pada Gambar 2.7.b, hubungan momen kurvatur menjadi tidak

linier (nonlinier) setelah titik di mana baja mulai memasuki keadaan plastis dari

hubungan tegangan-regangannya. Akibat dari hal ini, maka keruntuhan dapat terjadi

secara tiba-tiba, kecuali apabila beton tersebut diberikan perkuatan dengan sengkang

pada bagian tengah atau intinya. Bila beton tersebut tidak diberikan sengkang, maka

beton akan mengalami kehancuran pada kurvatur yang relatif kecil sebelum baja mulai

leleh, yang tentunya akan menurunkan kapasitas momennya secara singkat.

Untuk memastikan sifat daktilitas dari sebuah penampang dalam prakteknya,

rasio dari baja tulangan dibuat agar kurang dari nilai rasio seimbang (ρbalance) pada

sebuah balok beton. Hubungan momen kurvatur sccara praktisnya dapat diidealisasikan

menjadi tiga macam kurva seperti yang terlihat pada Gambar 2.8. Kurva yang pertama

menunjukkan adanya tiga fase; yaitu fase pertama pada saat beton mulai retak, fase

kedua pada saat baja mulai leleh dan fase ketiga adalah pada saat baja sudah mencapai

batas dari nilai regangan gunanya (Wigan, 2001).

Pada Gambar 2.8.b dan Gambar 2.8.c menunjukkan kurva yang bilinier, yang

pada umumnya cukup akurat untuk dapat dipergunakan. Setelah beton mengalami

retak, maka hubungan antara momen kurvatur hampir linier dari titik awal nol sampai

dengan titik di mana baja mulai leleh. Sehingga kedua kurva ini merupakan idealisasi

Gambar 2.8 Idealisasi hubungan momen kurvatur untuk penampang beton dengan tulangan tunggal akibat kegagalan tarik.

2.5 Daktilitas Struktur Global (μ)

Daktilitas adalah kemampuan suatu struktur untuk mengalami simpangan dalam

kondisi pasca elastik hingga terjadinya keruntuhan (UBC 1997). Perlu digarisbawahi

bahwa perilaku ini sangatlah penting, sebab selama proses pelelehan, elemen struktur M

Mu

ϕu

ϕy

ϕ

(c) (b)

M

Mu

ϕu

ϕy

ϕ

My

M

(a) Mu

ϕu

ϕy

ϕ

My

first yielding

tersebut mengalami proses dissipasi energi gempa. Selama terjadi gempa, daktilitas

akan mempertahankan kekuatan dan kekakuan yang cukup, sehingga struktur gedung

tersebut dapat tetap berdiri meskipun telah berada pada kondisi di ambang keruntuhan.

Terkait dengan desain rancangan untuk suatu struktur bangunan, akan menjadi

tidak ekonomis apabila desain struktur bangunan tersebut direncanakan memiliki respon

elastis terhadap gempa kuat. Hal ini dikarenakan gempa kuat tersebut jarang sekali

terjadi. Oleh sebab itu, agar ekonomis, struktur bangunan yang direncanakan diharapkan

berespon inelastis dengan tingkat daktilitas tertentu (Wibisono, 2008).

Struktur dengan tingkat daktilitas tertentu akan memungkinkan terjadinya sendi

plastis secara bertahap pada elemen-elemen struktur yang telah ditentukan. Dengan

terbentuknya sendi plastis pada elemen struktur, maka struktur akan mampu menahan

beban gempa maksimum tanpa memberikan kekuatan yang berlebihan pada elemen

struktur sebab energi kinetik akibat gerakan tanah dasar yang diterima akan dipencarkan

pada sendi plastis tersebut. Semakin banyak terbentuk sendi plastis pada elemen

struktur, semakin besar pula energi gempa yang dipencarkan. Setelah terjadi sendi

plastis pada suatu elemen, defleksi struktur serta rotasi plastis masih terus bertambah.

Pada stuktur rencana, daktilitas struktur tersebut digambarkan dengan faktor

modifikasi respon yang turut mewakili faktor kuat lebih (overstrenght factor) serta kapasitas komponen struktur secara keseluruhan dalam kondisi daktail. Faktor

modifikasi respon ini dilambangkan dengan simbol μ. Batasan-batasan terkait dengan

kriteria perencanaan desain daktilitas bangunan dengan menggunakan faktor modifikasi

respon dipaparkan sebagaimana berikut (Wibisono, 2008):

a. Kekakuan dan kekuatan struktur ketika direncanakan untuk memenuhi

kondisi di atas pun perlu direncanakan agar dapat memberikan kemampuan

yang cukup kepada struktur bangunan untuk melakukan deformasi

(simpangan) yang bersifat elastoplastik tanpa runtuh, bila mengalami gempa

rencana maksimum.

b. Untuk memperoleh daktilitas yang tinggi pada struktur gedung tinggi yang

akibat beban gempa maksimum hanya terjadi di dalam balok-balok dan

tidak terjadi dalam kolom-kolom, kecuali pada kaki kolom yang paling

bawah dan pada bagian atas kolom penyangga atap. Hal ini dapat terpenuhi

apabila kapasitas (momen leleh) kolom lebih tinggi dibandingkan dengan

kapasitas (momen leleh) balok yang bertemu pada kolom tersebut.

c. Perlu dilakukan pembatasan terkait besarnya perpindahan (displacement) yang terjadi. Hal ini tidak lain untuk menjaga integritas bangunan serta

untuk menghindari jatuhnya korban jiwa pada saat gempa rencana

maksimum terjadi.

Faktor daktilitas ( μ ) adalah merupakan rasio antara simpangan maksimum struktur

(Xmax) terhadap simpangan struktur pada saat terjadinya sendi plastis yang pertama (Xy).

Faktor daktilitas maksimum yang digunakan untuk bangunan beton bertulang adalah 5,3

dan untuk bangunan baja adalah 8.0.

2.6 Konsep Dasar Metoda Analisa Pushover

2.6.1 Umum

Metoda analisa statik tidak linear (pushover analysis) adalah metoda tidak linear yang sangat popular digunakan dalam perencanaan atau penilaiaan bangunan yang

terletak di daerah rawan gempa. Seperti yang dijelaskan oleh (Kunnath, 2005), ide yang

mendasari metoda ini adalah untuk menjelaskan keadaan beban gempa yang bekerja

pada rangka struktur. Respon rangka struktur terhadap berbagai beban dinamis adalah

sebuah kombinasi ragam getar dinamis dari system yang bergetar. Sehingga metode ini

juga didasarkan kepada konsep dasar analisa ragam getar pada struktur. Penjelasan teori

2.6.2 Dasar Teori

Seperti pada umumnya sebuah vector berorde n dapat dinyatakan melalui suatu kumpulan vector n yang berdiri sendiri. Dalam hal ini nilai vector-Eigen dihasilkan melalui masalah nilai Eigen yang berperan sebagai vector-vektor yang menjelaskan

simpangan-simpangan yang terjadi pada setiap lantai pada sebuah bangunan bertingkat.

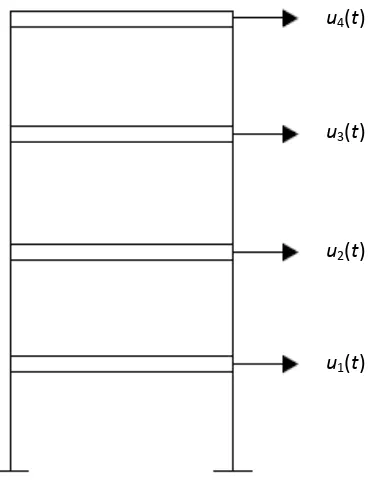
Variabel n ini mengacu kepada derajat kebebasan (DOF) yang pada metode ini adalah jumlah lantai pada bangunan bertingkat (Gambar 2.9) atau jumlah titik kumpul

(idealisasi) pada system berderajat kebebasan tunggal (SDOF) seperti kolom kantilever.

Simpangan ini dapat didefinisikan dengan persamaan berikut;

{ }

u qm

[ ]

{ }

q

N

m m m

i =

∑

Φ = Φ

=1

(2.6)

dimana {ui} adalah vector simpangan, {q} adalah koordinat ragam, [Φ] adalah matrik

ector Eigen, m adalah nomor ragam getar dan i adalah nomor tingkat.

Gambar 2.9 Model struktur rangka bertingkat dengan DOF yang disederhanakan. u4(t)

u3(t)

u2(t)

Berikut ini adalah hubungan keseimbangan untuk system berderajat kebebasan

banyak (MDOF);

[ ]

m

{ }

u +

[ ]

c

{ }

u +

[ ]

k

{ }

u =−

[ ]

m

{}

ι u_g(t) (2.7)

dimana [m] adalah matriks massa, [c] adalah matriks redaman, dan [k] adalah matriks kekakuan, sedangkan {u} adalah vector simpangan, { }u adalah vector kecepatan dan ( )u

adalah vector percepatan. Parameter {}ι adalah vector nilai unit dan ug(t)adalah

percepatan getaran tanah yang diberikan.

Persamaan kesetimbangan dapat disederhanakan seperti berikut setelah

menerapkan dekomposisi ragam getar yang diberikan pada Pers. (2.6) dan menerapkan

hubungan-hubungannya secara ortogonal;

) (

2 q 2 u t

q_{n n}_{n n n}_g

 + ζω +ω =−Γ (2.8)

Dimana;

[ ] [ ]

{}

(

T

)

/ _n,

n = Φ m ι M

Γ dan

[ ] [ ][ ]

Φ Φ

= m

M_n T

Untuk lebih memudahkan pemahaman maka bagian sebelah kanan dari Pers.

(2.7) dapat dianggap sebagai kontribusi ragam getar yang berdiri sendiri seperti

dijelaskan Chopra (2001) sebagai berikut;

[ ]

{ }

[ ]

{ }

[ ]

{ }

g

N

n nu R u

k u c u

m  

∑



=

− = +

+

1

(2.9)

Dengan membagi Pers. (2.9) dengan Pers. (2.7) dan menyelesaikannya melalui

transformasi nilai ragam getar seperti yg dihasilkan pada Pers. (2.8), maka dapat

ditentukan bahwa;

Setiap bagian dari persamaan di atas mengandung kontribusi nilai ragam getar

untuk setiap ragam getarnya. Cara lain untuk menjelaskan Pers. (2.10) adalah dengan

menganggap vector beban pada bagian kanan Pers. (2.7) seperti berikut ini;

{ }{}

m ι u_g =

{ } ( )

R f t (2.11)

dimana {R} adalah vector distribusi beban. Untuk fungsi pembebanan yang umum {p(t)}={r}f(t), vektor {r} adalah vector transformasi simpangan yang dihasilkan akibat adanya satu unit simpangan pada bagian perletakan. Pada pembebanan akbat gempa hal

ini dapat disederhanakan menjadi sebuah vector dengan nilai-nilai per unit.

Pemmbebanan dari luar tentunya dapat divariasikan sebagai sebuah fungsi waktu dalam

hal amplitude dan distribusi ruang (spatial distribution). Tujuan menguraikan persamaan dalam bentuk seperti Pers. (2.11) adalah untuk memisahkan distribusi ruang

dari fungsi amplitude yang bervariasi terhadap waktu. Konsep ini dijelaskan secara

lebih mendalam pada banyak buku-buku dinamika seperti (Chopra, 2001).

Langkah berikutnya adalah memasukkan kondisi pembebanan gempa. Karena

prosedur ini merupakan prosedur analisa static maka bentuk pembebanan gempa yang

dapat dianggap paling layak adalah bentuk spectrum respon. Distribusi gaya-gaya

lateral yang akan digunakan di dalam analisa static tidak linear dapat didekati dalam

bentuk kontribusi ragam getar puncak (peak modal contributions) seperti berikut ini;

{ }

fn =Γn

[ ]

m

{ } (

Φn Sa ζn,Tn

)

(2.12)

di mana Sa adalah spectrum percepatan untuk pembebanan gempa pada sebuah perioda

T dan rasio redaman ζ pada ragam getar ke-n.

Gaya-gaya modal yang didapat dengan menggunakan Pers. (2.12) hanya akan

menjelaskan kontribusi-kontribusi sampai ke ragam getar ke-n. Pers. (2.12) mewakili bentuk vector gaya lateral yang sangat umum yang akan dipakai dalam analisa static

tidak linear. Jika n=1, maka hanya kontribusi ragam getar pertama yang ditinjau.

Untuk memahami konsep spectrum kapasitas adalah perlu untuk meninjau

getaran gempadapat diperoleh melalui sebuah spectrum respon getaran gempa. Pers.

(2.8) menjelaskan satu set ragam getar n pada sistem SDOF yang mana setiap ekspresi persamaan memberikan jawaban terhadap sebuah ragam getar tertentu. Respon total

diperoleh melalui transformasi yang terdapat pada Pers. (2.6).

Dengan menganggap Sd(ζn,ωn) sebagai simpangan maksimum dari sebuah

sistem SDOF dengan frekuensi ωn dan rasio redaman ζn, yang dibebani getaran gempa

) (t

u_g , respon simpangan puncak dari system pada Pers. (2.8) diberikan oleh;

{ }

qn max =ΓnSd

( )

ζn,ω_n (2.13)

Simpangan puncak pada setiap tingkat (lantai) dapat diperoleh dengan Pers. (2.6) seperti

berikut ini;

(

)

(

)

(

)

Persamaan di atas mengandung kontribusi-kontribusi yang terdapat pada semua

ragam getar. Dengan menganggap hanya simpangan puncak pada sebuah DOF tertentu

yang diperlukan, contohnya jika DOF ke-n adalah level atap (level tertinggi sebuah struktur), dan hanya kontribusi ragam getar pertama yang ditinjau, maka persamaan

berikut akan diperoleh;

(

1, 1

)

1

Persamaan ini dipakai untuk mengubah simpangan atap, hasil dari sebuah

analisa static tidak linear, menjadi spectrum simpangan ragam getar pertama di dalam

prosedur spectrum kapasitas.Untuk membentuk spectrum percepatan ragam getar

pertama ekivalen maka simpangan puncak dapat diperoleh melalui

persamaan-persamaan berikut;

{ }

2

[ ]

{ }

_max

max n n

n m u

{ }

f_{n max} =ω_n2

[ ]

mΓ_nS_d

(

ζ_n,ω_n

)

[ ]

Φ (2.17)

Jika hanya kontribusi ragam getar pertama yang ditinjau maka

{ }

(

)

Gaya geser dasar Vbdiperoleh dengan menjumlahkan gaya-gaya geser tingkat,

maka kontribusi ragam getar pertama terhadap gaya geser dasar diberikan melalui

persamaan berikut ini;

(

)

₁

2.6.3 Prosedur Perhitungan Analisa Pushover

Dalam menjalankan analisa static tidak linear berdasarkan teori yang dijelaskan

pada bagian sebelumnya, diperlukan sejumlah langkah yang berulang. Langkah ini telah

diformalisasi ke dalam peraturan ATC-40 yang kemudian dipakai juga ke dalam

peraturan-peraturan lain di USA. Penjelasan berikut ini adalah didasarkan kepada

analisa static tidak linear (pushover analysis) yang direkomendasikan oleh ATC-40: 1. Buat model struktur dan pembebanan tetap.

2. Analisa struktur menggunakan metode analisa static linear biasa untuk

mendapatkan gaya-gaya aksial yang bekerja pada kolom.

momen batas (Mu) dan kurvaturnya (φy dan φu) beserta interaksi gaya aksial

dan momen. Masukkan kondisi batas ini ke dalam model struktur.

Penjelasan kondisi batas untuk struktur beton dibuat setelah bagian ini.

4. Distribusikan gaya geser dasar menjadi gaya-gaya geser lateral pada setiap

tingkat dengan mengacu secara proporsional kepada massa dan bentuk

ragam getar alami. Dalam hal ini pendistribusian gaya geser dapat dibuat ke

dalam beberapa bentuk seperti:

a. Gaya geser tingkat tunggal pada puncak bangunan struktur (umumnya

dibuat pada struktur bertingkat satu).

b. Gaya geser dasar didistribusikan ke setiap tingkat secara proporsional

mengacu kepada prosedur peraturan gempa seperti Fx= [wxhx/Σwxhx]Vb.

c. Gaya geser dasar didistribusikan ke setiap tingkat secara proporsional

mengacu kepada hasil perkalian dari massa pada setiap tingkat dan

bentuk ragam getar pertama kondisi elastic seperti Fx=

[wxφx>/Σwxφx]Vb.

d. Gaya geser dasar didistribusikan sama dengan kondisi 3 di atas tetapi

dibuat sampai mendapati kondisi leleh awal.

e. Pendistribusian gaya geser dasar sama dengan 3 dan 4, tetapi

melibatkan pengaruh ragam getar yang lebih tinggi (bukan hanya ragam

getar pertama).

5. Lakukan analisa static akibat pembebanan tetap dan lateral dan catat

gaya-gaya pada elemen struktur seperti momen dan rotasi beserta gaya-gaya aksial.

6. Catat gaya geser dasar dan simpangan pada puncak struktur yang terjadi.

7. Naikkan beban lateral secara bertahap dan lakukan kembali analisa statis.

Catat hasil seperti langkah 5 dan 6 di atas. Pada tahap ini gaya-gaya dan

perpindahan yang telah dihasilkan (momen dan rotasi) pada analisa

sebelumnya harus ditambahkan.

8. Perbaiki model struktur menggunakan kekakuan nol (mendekati nol) pada

9. Naikkan secara bertahap beban lateral lagi seperti pada langkah 7 dan

perbaiki model struktur seperti langkah 8. Peningkatan beban lateral secara

bertahap umumnya sangat memadai bila dilakukan sebanyak 10 kali.

10. Tambahkan setiap peningkatan yang terjadi pada gaya geser dasar dan

simpangan pada puncak struktur (akumulasi).

11. Lakukan langkah 7 sampai dengan langkah 10 sampai model struktur secara

global mengalami kondisi batas (ultimate) yang umumnya ditandai dengan telah terjadinya kondisi leleh pada semua elemen struktur dan kondisi batas

pada sebagian elemen utama struktur (seperti kolom-kolom dasar). Pada

kondisi ini umumnya elemen balok telah mengalami kondisi batas. Kondisi

batas ini juga dapat ditandai dengan terjadinya penurunan (degradasi)

kekuatan global struktur mencapai 20%. Kondisi batas juga dapat diukur

dengan simpangan antar tingkat (interstory drift ratio) yang ditentukan oleh peraturan-peraturan yang ada seperti ATC-40 atau FEMA356.

2.7 Kondisi Batas Pada Struktur Beton

Penentuan kondisi batas pada setiap elemen struktur sangat memegang peranan

penting dalam analisa tidak linear, baik itu untuk analisa static tidak linear maupun

analisa dinamik tidak linear. Dalam sebuah proses analisa berbasis kinerja

(performance-based design), penentuan kondisi batas ini dibuat setelah analisa static linear akibat beban gravitasi (beban tetap) dilakukan. Dengan kata lain, keadaan tidak

linear dan tidak elastis sebuah elemen struktur, mulai dari segi bahannya, penampang

dan elemen itu sendiri, adalah merupakan alasan utama kenapa sebuah analisa dikatakan

linear elastis atau tidak linear dan tidak elastis.

Hal ini dikarenakan kondisi batas akan mensuplai informasi tentang keadaan

kekakuan dan fleksibilitas secara local dan global.Penentuan kondisi batas ini dapat

(displacement)seperti momen-kurvatur, gaya aksial-simpangan aksial, gaya geser-simpangan geser, dan interaksi antara gaya-gaya tersebut. Sedangkan secara mikro

maksudnya kondisi batas ditentukan dengan memakai parameter yg lebih detail seperti

tegangan (stress) dan regangan (strain) untuk lentur, geser, dan aksial. Kondisi batas secara mikro ini umumnya disebut dengan model serat (fiber model). Penentuan kondisi batas secara makro dapat dilakukan dengan bantuan program BIAX, CUMBIA, dan

KSU_RC, sedangkan secara mikro dapat dilakukan dengan program XTRACT atau

secara langsung melalui program SAP2000. Pada bagian berikut ini akan dijelaskan

penentuan kondisi batas elemen struktur beton (kolom) berdasarkan keadaan makro

(gaya-perpindahan) dan juga model fiber (tegangan-regangan).

2.7.1 Kondisi Batas Makro untuk Elemen Kolom Beton

Model elemen kolom yang ditinjau adalah memperkirakan pengaruh lentur,

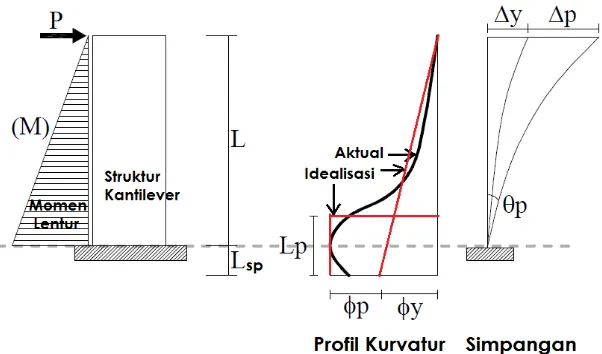
geser, deformasi aksial dan zona panjang kaku (rigid length zone). Kondisi batas yang ditinjau adalah keadaan leleh (yield) dan runtuh (ultimate). Panjang zona kaku (Lp) pada

sebuah elemen adalah panjang dimana kondisi sendi plastis terjadi. Panjang ini dapat

ditentukan menggunakan persamaan usulan (Priestley, 1996) untuk kondisi elemen

struktur kantilever seperti pilar jembatan (Gambar 2.10.).

Lp = kLc+ Lsp≥ 2Lsp (2.21)

dimana

Lsp= 0,0022 fsdbluntukfs ≤fy (2.22)

k = [0.02 (fsu / fy)] – 1 (2.23)

Lc = panjang dari penampang kritis ke titik dimana terjadi lenturan balik.

fs = tegangan tarik besi tulangan memanjang (lentur).

fsu = tegangan tarik runtuh (fracture) besi tulangan memanjang (lentur).

fy = tegangan leleh besi tulangan memanjang (lentur).

dbl = diameter tulangan lentur.

2.7.1.1 Penampang Persegi

Nilai-nilai momen-kurvatur untuk kondisi batas kolom beton bertulang, seperti

yang ditunjukkan pada Gambar 2.11 dapat diperkirakan secara perhitungan manual.

Untuk kurvatur pada keadaan leleh φy dapat diperkirakan dengan menggunakan

persamaan usulan (Park, 1976) yang dimodifikasi oleh (Kunnath, 1992);

)



k = faktor ketinggian sumbu netral, yang dihitung melalui persamaan berikut;

dimana Acadalah luasan baja tulangan tekan; dcadalah tebal selimut beton pada tulangan

tekan, εy dan ε0 adalah regangan pada tegangan maksimum untuk baja tulangan dan

selimut beton.

Momen lentur pada keadaan leleh (My) dapat diperkirakan dengan persamaan

berikut (Park, 1987);



Sedangkan momen lentur pada keadaan runtuh atau batas (Mu) dapat

diperkirakan dengan persamaan berikut (Park dkk., 1987);

y

Kurvatur elemen kolom beton bertulang dapat diperkirakan dengan menganggap

kolom berperilaku sama dengan elemen balok sebagaimana persamaan yang diusulkan

oleh(Park, 1976);

y berterusan sebesar 0.05 untuk setiap 1000 psi bila melebihi 4000 psi; sedangkan εc

adalah regangan beton pada penampang kolom bagian serat tekan.

2.7.1.2 Penampang Lingkaran

Dalam menentukan hubungan momen dan kurvatur yang terjadi pada

penampang kolom lingkaranmenggunakan metode sendi plastis yang ditemukan oleh

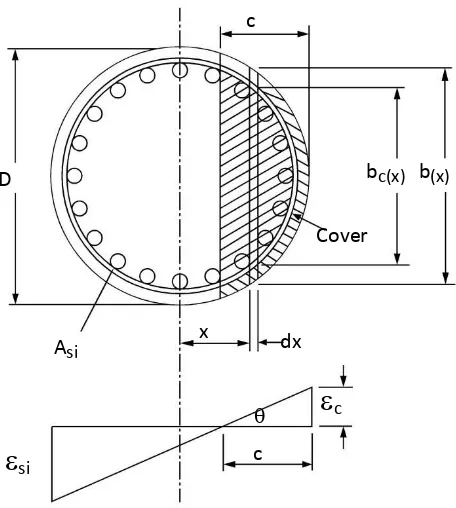
Gambar 2.12 Ilustrasi analisa momen-kurvatur penampang kolom bulat berdasarkan metode sendi plastis (Priestley, 1996)

Momen-kurvatur diperoleh melalui regangan tekan serat𝜀𝜀_𝑐𝑐yaitu melalui keseimbangan gaya aksial dan momen lentur yang terjadi pada sistem. Keseimbangan gaya aksial

ditentukan melalui persamaan (2.31) berikut;

𝑃𝑃 =∫𝐷𝐷 �𝑏𝑏_𝑐𝑐(𝑥𝑥)𝑓𝑓𝑐𝑐(𝜀𝜀_𝑥𝑥)+�𝑏𝑏(𝑥𝑥)− 𝑏𝑏𝑐𝑐(𝑥𝑥)�𝑓𝑓𝑐𝑐𝑐𝑐(𝜀𝜀_𝑥𝑥)� /2

𝑥𝑥=(𝐷𝐷/2)−𝑐𝑐 𝑑𝑑𝑥𝑥+∑ 𝐴𝐴𝑛𝑛_𝑠𝑠=𝑙𝑙 𝑠𝑠𝑠𝑠𝑓𝑓𝑠𝑠(𝜀𝜀𝑥𝑥𝑠𝑠) (2.31) Dimana;

𝑓𝑓𝑠𝑠 =𝑓𝑓𝑦𝑦𝑦𝑦 �1.5−0.5�0.12 _0.112−𝜀𝜀𝑠𝑠�

2

� ; tegangan saatstrain hardening pd hubungan tegangan-regangan baja (Gambar 2.13)

diasumsikan ; 𝜀𝜀_𝑠𝑠ℎ = 0.008 dan 𝜀𝜀_{𝑠𝑠𝑐𝑐} = 0.12

Besaran 𝑓𝑓_𝑐𝑐(𝜀𝜀), 𝑓𝑓_{𝑐𝑐𝑐𝑐}(𝜀𝜀)dan 𝑓𝑓_𝑠𝑠(𝜀𝜀) secara berurutan adalah hubungan tegangan-regangan pada bagian selimut beton (beton tanpa ikatan) dan bagian inti kolom (beton dengan

ikatan) yang ditunjukkan pada Gambar 2.14 dan hubungan tegangan-regangan tulangan

D

c

c

Cover

x _dx

θ

A_si

b_c(x) b_(x)

ε

si

baja (Gambar 2.15). 𝐴𝐴_{𝑠𝑠𝑠𝑠}adalah luasan sebuah tulangan longitudinal dengan jarak 𝑥𝑥_𝑠𝑠ke garis sumbu netral penampang.𝜀𝜀_{𝑥𝑥𝑠𝑠}adalah regangan tarik tulangan yag terletak sejauh𝑥𝑥_𝑠𝑠dari sumbu garis normal penampang.

Gambar 2.13 Hubungan tegangan-regangan tulangan baja

dimana regangan tekan ekstrimpada serat;

𝜀𝜀𝑥𝑥 = 𝜀𝜀_𝑐𝑐𝑐𝑐(𝑥𝑥 −0.5𝐷𝐷+𝑐𝑐) (2.32)

Melalui keseimbangan momen lentur makahubungan momen-kurvatur dapat dihitung

dengan;

𝑀𝑀 = ∫𝐷𝐷 �𝑏𝑏_𝑐𝑐(𝑥𝑥)𝑓𝑓𝑐𝑐(𝜀𝜀_𝑥𝑥)+�𝑏𝑏(𝑥𝑥)− 𝑏𝑏𝑐𝑐(𝑥𝑥)�𝑓𝑓𝑐𝑐𝑐𝑐(𝜀𝜀_𝑥𝑥)� /2

𝑥𝑥=(𝐷𝐷/2)−𝑐𝑐 𝑑𝑑𝑥𝑥+∑ 𝐴𝐴𝑛𝑛_𝑠𝑠=𝑙𝑙 𝑠𝑠𝑠𝑠𝑓𝑓𝑠𝑠(𝜀𝜀𝑥𝑥𝑠𝑠)𝑥𝑥𝑠𝑠 (2.33) dimana kurvaturnya dapat diperoleh melalui persamaan;

𝜙𝜙 =𝜀𝜀𝑐𝑐

𝑐𝑐 (2.34)

nilai regangan tekan beton𝜀𝜀_𝑥𝑥sampai dengan regangan tekan ultimit, yang dibuat naik secara bertahap, menggunakanPersamaan (2.32) sampai denganpersamaan (2.34).

Nilaitegangan 𝑓𝑓_𝑐𝑐saat mengalami regangan tekan beton 𝜀𝜀_𝑐𝑐sampai dengan regangan tekan ultimit diperoleh melalui hubungan tegangan-regangan selimut beton

danhubungan tegangan-regangan inti beton. Hubungan ini dapat ditentukan melalui

model Mander yang dimodifikasi (Montejo dan Kowalsky, 2007).Sedangkan nilai

tegangan tarik tulangan baja𝑓𝑓_𝑠𝑠saat mengalami regangan tarik𝜀𝜀_𝑠𝑠sampai dengan regangan tarik ultimit𝜀𝜀_{𝑠𝑠𝑠𝑠}diperoleh melalui Gambar 2.15. Hubungan tegangan-regangan tulangan baja model King (Montejo dan Kowalsky, 2007).

Gambar 2.14 Hubungan tegangan-regangan model Mander untuk beton yang dimodifikasi (Montejo dan Kowalsky, 2007).

Tegangan normal tekan pada beton𝑓𝑓_𝑐𝑐dihitung berdasarkan regangan normal tekan𝜀𝜀_𝑐𝑐,mulaidari nilai regangan normal tekan terkecilsampai dengan regangan normal tekan ultimit 𝜀𝜀_{𝑐𝑐𝑐𝑐}, melalui persamaan berikut ini;

𝑓𝑓𝑐𝑐 = _{𝑥𝑥 −}𝑓𝑓′ _{1 +}𝑐𝑐𝑐𝑐𝑥𝑥𝑥𝑥_𝑥𝑥𝑥𝑥

𝑥𝑥= 𝜀𝜀𝑐𝑐

𝜖𝜖𝑐𝑐𝑐𝑐 : rasio regangan tekan longitudinal beton tanpa

ikatan dan beton dengan ikatan.

𝜀𝜀𝑐𝑐 : regangan normal tekan longitudinal.

𝜀𝜀𝑐𝑐𝑐𝑐 =𝜀𝜀𝑐𝑐𝑐𝑐�1 + 5�𝑓𝑓′_𝑓𝑓′𝑐𝑐𝑐𝑐

𝑐𝑐𝑐𝑐 −1�� : regangan normal tekan longitudinal maksimum.

𝜀𝜀𝑐𝑐𝑐𝑐 : regangan normal tekan beton tanpa ikatan.

𝑓𝑓′𝑐𝑐𝑐𝑐 : tegangan normal tekan beton tanpa ikatan.

𝑥𝑥= 𝐸𝐸𝑐𝑐

𝐸𝐸𝑐𝑐−𝐸𝐸sec : rasiomodulus elastisitas beton tanpa ikatanEcdan

beton dengan ikatan.

𝐸𝐸sec = 𝑓𝑓′_𝜀𝜀𝑐𝑐𝑐𝑐

𝑐𝑐𝑐𝑐 : modulus elastisitas beton dengan ikatan.

𝜀𝜀𝑐𝑐𝑐𝑐 = 1.4�0.004 +1.4𝜌𝜌𝑠𝑠_𝑓𝑓′𝑓𝑓_{𝑐𝑐𝑐𝑐}𝑦𝑦ℎ𝜀𝜀𝑠𝑠𝑐𝑐� : regangan batas (ultimit) beton dengan ikatan,

dimana 𝜀𝜀_{𝑠𝑠𝑐𝑐}adalah regangan tulangan longitudinal

𝑓𝑓′𝑐𝑐𝑐𝑐 = 𝑓𝑓′𝑐𝑐𝑐𝑐�−1.254 + 2.254�1 +7.94_{𝑓𝑓′𝑐𝑐𝑐𝑐}𝑓𝑓′𝑙𝑙−2_𝑓𝑓′𝑓𝑓′_{𝑐𝑐𝑐𝑐}𝑙𝑙 � : tegangan maksimum beton

dengan ikatan.

𝑓𝑓′𝑙𝑙 =

1

2𝑘𝑘𝑦𝑦𝜌𝜌𝑠𝑠𝑓𝑓𝑦𝑦ℎ

𝑓𝑓𝑦𝑦ℎ : teganganleleh tulangan geser.

𝜌𝜌𝑠𝑠 = 4_𝑑𝑑𝐴𝐴𝑠𝑠𝑠𝑠

𝑠𝑠𝑠𝑠 : rasio tulangan geser dan penampang geser.

𝐴𝐴𝑠𝑠𝑠𝑠 : luaspenampang tulangan geser spiral atau cincin.

𝑑𝑑𝑠𝑠 : panjangdiameter inti di dalamtulangan geser spiral.

𝑘𝑘𝑦𝑦 = �1−𝑠𝑠′

2_{𝑑𝑑𝑠𝑠}� 2

1−𝜌𝜌_{𝑐𝑐𝑐𝑐} : koefisien tulangan untuk tulangan geser cincin .

𝑘𝑘𝑦𝑦 =

1−𝑠𝑠′

2𝑑𝑑𝑠𝑠

𝑠𝑠′ : jarak bersih antara tulangan geser spiral atau cincin.

𝜌𝜌𝑐𝑐𝑐𝑐 : rasio luasan tulangan longitudinaldan luasan penampang bagian inti

Nilai-nilai berikut adalah diketahuiuntuk menyelesaikan persamaan di atas;

𝑓𝑓𝑐𝑐𝑐𝑐 =𝑓𝑓′𝑐𝑐 : (tegangan tekan beton (tanpa ikatan) karakteristik umur 28 hari

dalamMPa)

𝐸𝐸𝑐𝑐 = 4700�𝑓𝑓′𝑐𝑐 : (modulus elastisitas beton dalam MPa)

𝑓𝑓𝑦𝑦 : tegangan leleh tulangan longitudinal (MPa)

𝑓𝑓𝑦𝑦ℎ : tegangan leleh tulangan sengkang (MPa)

𝜀𝜀𝑐𝑐𝑐𝑐= 0,002 : regangan tekan beton(tanpa ikatan) saat mengalami𝑓𝑓𝑐𝑐𝑐𝑐

𝜀𝜀𝑠𝑠𝑐𝑐= 0,12 : regangan ultimit tulangan longitudinal

Tegangan tarik fsberdasarkan regangan tarik tulangan baja𝜀𝜀𝑠𝑠,mulai dari yg terkecil

sampai dengan regangan tarik ultimit𝜀𝜀_{𝑠𝑠𝑠𝑠},dihitung dengan persamaan berikut ini;

𝑓𝑓𝑠𝑠 =𝐸𝐸𝑠𝑠𝜀𝜀𝑠𝑠 untuk 𝜀𝜀𝑠𝑠 ≤ 𝜀𝜀𝑦𝑦

𝑓𝑓𝑠𝑠 =𝑓𝑓𝑦𝑦 untuk 𝜀𝜀𝑦𝑦 < 𝜀𝜀𝑠𝑠 <𝜀𝜀𝑠𝑠ℎ

𝑓𝑓𝑠𝑠 =𝑓𝑓𝑦𝑦�₆₀₍𝑠𝑠(𝜀𝜀_𝜀𝜀𝑠𝑠_𝑠𝑠−𝜀𝜀_−𝜀𝜀𝑠𝑠ℎ_𝑠𝑠ℎ)+2₎₊₂+(𝜀𝜀𝑠𝑠−𝜀𝜀₂₍₃₀𝑠𝑠ℎ_𝑥𝑥)(60₊₁₎−𝑠𝑠2 )� untuk 𝜀𝜀𝑠𝑠ℎ < 𝜀𝜀𝑠𝑠 ≤ 𝜀𝜀𝑠𝑠𝑐𝑐

dimana

𝑠𝑠=

�𝑓𝑓𝑠𝑠𝑐𝑐

𝑓𝑓𝑦𝑦�(30𝑥𝑥+ 1)

2_{−60𝑥𝑥 −1}

15𝑥𝑥2

𝑥𝑥= 𝜀𝜀_{𝑠𝑠𝑐𝑐} − 𝜀𝜀_𝑠𝑠ℎ

Nilai-nilai berikut adalah diketahuiuntuk menyelesaikan persamaan di atas;

𝐸𝐸𝑠𝑠 : 200000 MPa

𝑓𝑓𝑦𝑦 : tegangan leleh tulangan longitudinal (MPa)

𝑓𝑓𝑦𝑦ℎ : tegangan leleh tulangan sengkang (MPa)

𝜀𝜀𝑠𝑠ℎ= 0,008 : regangan tulanganlongitudinal saat mengalami strain hardening

𝜀𝜀𝑠𝑠𝑐𝑐= 0,12 : regangan maksimumtulangan longitudinal

2.7.2 Kondisi Batas Elemen Struktur Umum Memakai Model Fiber

Elemen balok multifiber sudah dikembangkan lebih dari 20 tahun yang lalu. Elemen ini didasarkan kepada diskretisasi penampang melintang dalam bentuk

lapisan-lapisan yang tersusun (untuk balok 2-D) atau serat-serat tersusun (untuk balok 3-D)

Gambar 2.16Model fiber pada penampang elemen struktur (Ceresa, 2007)

Dengan menganalisa penampang menggunakan model konstitusi uniaksial

sederhana (simple uniaxial constitutive models), perilaku struktur 3 dimensi akibat gaya aksial dan gaya lentur dapat diperoleh melalui integrasi tegangan-tegangan yang terjadi

pada serat di seluruh penampang melintang Gambar 2.17.

Pendekatan model serat atau model fiber sangat sesuai menggunakan teori balok Euler-Bernoulli dengan meninjau penampang sebuah balok secara umum (generic). Menurut Ceresa dkk. (2007), berdasarkan deformasi aksial εo(x) pada sumbu balok dan kurvatur penampang χy(x) dan χz(x), maka aksial deformasi setiap serat pada sebuah penampang εixx

( )

x dapat diperoleh melalui persamaan berikut ini;

( )

x

(

( )

x zi _y

( )

x yi _z

( )

x

)

xx

i ε χ χ

ε = ₀ + − (2.35)

Gambar 2.17Ilustrasi model fiber pada elemen struktur beton bertulang

Berdasarkan hukum material uniaksial maka tegangan arah memanjang

(longitudinal) serat dapat diperoleh secara langsung melalui persamaan berikut;

( )

x EiT ixx

( )

x

xx ε

σ' = (2.36)

dimana EiT adalah modulus tangent serat ke-i.

Sehingga gaya-gaya total untuk aksial dan momen pada penampang balok dapat

secara mudah dihitung melalui penjumlahan kontribusi-kontribusi setiap serat ke-i seperti berikut ini;

∑

tetapi merupakan momen lentur yang terjadi akibat rotasi pada sumbu y.

ditunjukkan pada Gambar 2.18. Material beton bertulang harus dibedakan kepada 2

jenis aturan konstitusi yaitu beton tanpa ikatan (unconfined) tulangan dan beton dengan ikatan (confined) tulangan. Aturan konstitusi beton tanpa ikatan mewakili daerah penampang selimut beton, sedangkan aturan konstitusi beton dengan ikatan adalah

mewakili daerah inti pada penampang beton (daerah di dalam tulangan geser).

Aturan konstitusi yang paling umum dipakai adalah model Mander (1988)

seperti yang ditunjukkan pada Gambar 2.17. Dimana tegangan tekan akibat adanya

tulangan lentur dan ikatan tulangan geser (f’cc) beserta regangannya (εcc) akan lebih

besar dari tegangan tekan normal beton tanpa ikatan (f’c) dan regangannya (εc).

Gambar 2.18Model Mander (1988) untuk beton tanpa ikatan dan dengan ikatan

Regangan tekan beton dengan ikatan saat runtuh (εcu) juga jauh lebih besar dari

regangan runtuh beton tanpa ikatan (εsp). Nilai-nilai tegangan-regangan model Mander

untuk beton tanpa ikatan (unconfined) adalah dihitung melalui persamaan-persamaan berikut;

fc = 0 untuk ε< 2 εt (2.38)

r

ε = regangan tekan beton yang dihitung

fc = tegangan tekan beton yang dihitung

f’c = tegangan tekan karakteristik beton umur 28 hari

fcp = tegangan tekan beton pasca keruntuhan

εc = regangan tekan beton tanpa ikatan pada saat tegangan tekan maksimum = 0.002

εsp = regangan tekan maksimum beton tanpa ikatan = 0.0064

εt = kapasitas regangan tarik beton tanpa ikatan = ft / Ec

ft = tegangan tarik beton tanpa ikatan =0,5 f'c

Nilai-nilai tegangan-regangan model Mander untuk beton dengan ikatan

(confined) adalah dihitung melalui persamaan-persamaan berikut;

dimana

Sedangkan parameter-parameter lainnya dapat dihitung secara sama dengan beton tanpa

ikatan.Nilai-nilai tegangan-regangan model Mander untuk tulangan baja lentur beton

bertulang adalah seperti yang ditunjukkan Gambar 2.19 berikut ini.

Gambar 2.19Hubungan tegangan-regangan sebagai aturan konstitusi untuk tulangan baja lentur

Hubungan tegangan-regangan untuk tulangan baja lentur dapat dihitung melalui

persamaan-persamaan berikut;

dimana

fs = tegangan tulangan lentur yang dihitung ε = regangan yang ditinjau

fy = tegangan leleh tulangan lentur

fsu = tegangan tulangan lentur saat mengalami kegagalan εy = regangan leleh tulangan lentur = fy / Es

εsh = regangan tulangan lentur saat mengalami pengerasan (hardening) = 0,008

εsu = regangan tulangan lentur saat mengalami kegagalan = 0,10 s/d 0,15

Es = modulus elastisitas tulangan lentur = 200x103 MPa

Seperti telah dijelaskan pada bagian sebelumnya bahwa hubungan

tegangan-regangan sebagai aturan konstitusi beton bertulang ini dapat dimasukkan secara

langsung ke dalam program SAP2000 sebagai kondisi batas dalam menganalisa

struktur. Kondisi batas ini diberikan kepada luasan-luasan kecil penampang beton

bertulang yang dibagi seperti lapisan-lapisan serat atau fiber (Gambar 2.16 dan 2.17)di dalam program SAP2000. Beberapa program lain dapat melakukan proses ini secara

otomatis seperti program SeismoStruct dan ZeusNL.

Kelemahan metode fiber yang ada pada kebanyakan program analisa struktur seperti SAP2000, SeismoStruct dan ZeusNL adalah terletak pada kemampuannya dalam

menganalisa gaya-gaya yang bekerja pada struktur. Dalam hal ini hanya gaya momen

lentur (M2-M3) dan interaksi momen lentur dan gaya aksial (P-M2-M3) yang dapat

dianalisa. Namun demikian, keadaan ini sudah sangat memadai untuk mensimulasikan