ADAPTIVE GENETIC ALGORITHM (AGA) RADIAL BASIS FUNCTION (RBF) NEURAL NETWORK

(1)

commit to user

i

ADAPTIVE GENETIC ALGORITHM (AGA) RADIAL

BASIS FUNCTION (RBF) NEURAL NETWORK

UNTUK KLASIFIKASI

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Mencapai Gelar Strata Satu

Jurusan Informatika

Disusun oleh :

Muh Aziz Nugroho

NIM. M0508053

JURUSAN INFORMATIKA

FAKULTAS MATEMATIKA & ILMU PENGETAHUAN ALAM

UNIVERSITAS SEBELAS MARET

SURAKARTA

2012

(2)

commit to user

ii

(3)

commit to user

iii

(RBF) NEURAL NETWORK UNTUK KLASIFIKASI

MUH AZIZ NUGROHO

Jurusan Informatika.Fakultas Matematika dan Ilmu Pengetahuan Alam. Universitas Sebelas Maret.

ABSTRAK

Jaringan Syaraf Tiruan (JST) merupakan salah satu metode yang dapat digunakan untuk melakukan klasifikasi. Salah satu model jaringan syaraf tiruan adalah Radial basis function (RBF). Dengan berkembangnya penelitian, muncul beberapa penelitian yang bertujuan meningkatkan akurasi hasil pelatihan JST RBF dengan cara optimasi bobot hasil pelatihan JST RBF. Salah satu algoritma yang dapat digunakan untuk optimasi tersebut adalah algoritma genetika. Sementara itu dari beberapa penelitian mengenai algoritma genetika, muncul beberapa modifikasi untuk meningkatkan performa algoritma genetika. Salah satunya adalah Adaptive Genetic Algorithm (AGA) yaitu dengan pendekatan baru untuk penentuan probabilitas crossover dan probabilitas mutasi yang adaptif sesuai dengan fungsi

fitness. Oleh karena itu, penelitian ini melakukan evaluasi tentang penggabungan RBF dengan AGA untuk klasifikasi data untuk mengetahui akurasi AGA RBF.

Penelitian ini dilakukan dengan melakukan simulasi pada data tumbuhan iris. Penentuan center RBF menggunakan algoritma clustering K-Means. Setelah RBF dilatih dan didapatkan bobot selanjutnya bobot diubah dengan AGA. Fungsi

fitness AGA adalah akurasi RBF untuk data training dimana proses training

menggunakan 70 % data dan proses testing dengan 30 %. Efektifitas klasifikasi diukur dari hasil akurasi. Skenario yang dijalankan adalah melakukan simulasi untuk mendapatkan variabel RBF yang terbaik untuk masing-masing arsitektur, kemudian kombinasi variabel terbaik dari variabel RBF dari masing-masing arsitektur dikombinasikan dengan variabel AGA RBF untuk mendapatkan variabel AGA RBF yang terbaik untuk masing-masing arsitektur. Arsitektur yang digunakan adalah JST dengan 2 hidden layer sampai 10 hidden layer.

Evaluasi dari simulasi menunjukkan bahwa JST AGA RBF (Adaptive Genetic Algorithm Radial Basis Function) dapat memperbaiki akurasi untuk arsitektur JST RBF yang sederhana yaitu pada arsitektur dengan hidden layer 2, 3, 4 dan 5, sedangkan untuk arsitektur yang lebih kompleks yaitu pada arsitektur dengan

hidden layer 6, 7, 8, 9 dan 10, akurasi AGA RBF relatif sama dengan akurasi RBF, namun cenderung menurun dengan presentase penurunan akurasi yang relatif kecil. Dari seluruh simulasi yang dilakukan dapat direkomendasikan bahwa algoritma yang paling tepat untuk melakukan klasifikasi tumbuhan iris adalah algoritma RBF dengan arsitektur 6 hidden layer.

(4)

commit to user

iv

ADAPTIVE GENETIC ALGORITHM (AGA) RADIAL BASIS FUNCTION (RBF) NEURAL NETWORK FOR CLASSIFICATION

MUH AZIZ NUGROHO

Department of Informatic. Mathematic and Science Faculty. Sebelas Maret University

ABSTRACT

Artificial Neural Network (ANN) is one method that can be used to perform classification. One model of neural network is a radial basis function (RBF). With the development of research, there is some research that aims to improve the accuracy of the RBF ANN training by optimization of RBF ANN weight training results. One algorithm that can be used for optimization is the genetic algorithm. Meanwhile, from some research on the genetic algorithm, it has been appeared some few modifications to improve the performance of genetic algorithms. One is the Adaptive Genetic Algorithm (AGA) is a new approach for determining the probability of crossover and mutation probabilities are adaptive according to the fitness function. Therefore, this study evaluates the incorporation of RBF with the AGA for the classification of data to determine the accuracy of AGA RBF.

The research was done by performing simulations on data of iris plants. Determination of RBF's centers using K-Means clustering algorithm. After the RBF trained and gained weight then weight is converted by AGA. AGA's fitness function is the RBF accuracy for training data where the training process uses 70% of the data and testing process by 30%. Effectiveness is measured by classification accuracy results. The Scenario is run simulation to get the best RBF variables for each architecture, then the best RBF variables from each of the architecture combined with a AGA RBF variable to get the best AGA RBF variable for each architecture. ANN's architecture used is a ANN with 2 hidden layer to 10 hidden layer.

Evaluation of the simulation show that the ANN AGA RBF (Radial Basis Adaptive Genetic Algorithm Function) can improve the accuracy for the RBF ANN simple architecture is the architecture with 2, 3, 4 and 5 hidden layer , while for the more complex architecture with 6, 7, 8, 9 and 10 hidden layer, accuracy of AGA RBF relatively equal to the accuracy of RBF, but tends to decrease with the percentage decrease in accuracy which is relatively small. From all the simulations carried out can be recommended that the most appropriate algorithm to classify iris plants are RBF algorithm with 6 hidden layer architecture.

(5)

commit to user

v

“Karena sesungguhnya sesudah kesulitan itu ada kemudahan, sesungguhnya sesudah kesulitan itu ada kemudahan, Maka apabila kamu telah selesai (dari sesuatu

urusan), kerjakanlah dengan sungguh-sungguh (urusan) yang lain”

(Q.S Alam Nasyrah : 5-7)

“Ingatlah, sesungguhnya pertolongan Allah itu amat dekat”

(Q.S Al-Baqarah : 214)

“Sesuatu yang belum dikerjakan, seringkali tampak mustahil, kita baru yakin kalau kita telah berhasil melakukannya dengan baik”

(Evelyn Underhill)

“Banyak kegagalan dalam hidup ini dikarenakan orang-orang tidak menyadari betapa dekatnya mereka dengan keberhasilan saat mereka menyerah”

(Thomas Alva Edison)

“Kita berdoa kalau kesusahan dan membutuhkan sesuatu, mestinya kita juga berdoa dalam kegembiraan besar dan saat rezeki melimpah”

(6)

commit to user

vi

PERSEMBAHAN

Kupersembahkan karya ini kepada :

Ibu, Bapak serta kedua kakak tercinta Mas M

a’ruf dan Mbak Iim

Semua teman Informatika UNS khsusnya angkatan 2008

(7)

commit to user

vii

Bismillahirrahmaanirrahiim

Puji syukur penulis panjatkan kehadirat Allah Subhanahu Wa Ta’ala yang senantiasa memberikan nikmat dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi dengan judul AdaptiveGenetic Algorithm (AGA) Radial Basis Function (RBF) Neural Network Untuk Klasifikasi, yang menjadi salah satu syarat wajib untuk memperoleh gelar Sarjana Informatika di Universitas Sebelas Maret (UNS) Surakarta.

Penulis menyadari akan keterbatasan yang dimiliki, begitu banyak bimbingan, bantuan, serta motivasi yang diberikan dalam proses penyusunan skripsi ini. Oleh karena itu, ucapan terima kasih penulis sampaikan kepada :

1. Bapak Wiharto, S.T., M.Kom. selaku Dosen Pembimbing I yang penuh kesabaran membimbing, mengarahkan, dan memberi motivasi kepada penulis selama proses penyusunan skripsi ini,

2. Ibu Bapak Drs. YS. Palgunadi, M.Scselaku Dosen Pembimbing II yang penuh kesabaran membimbing, mengarahkan, dan memberi motivasi kepada penulis selama proses penyusunan skripsi ini,

3. Ibu Umi Salamah,S.Si.,M.Kom. selaku Ketua Jurusan S1 Informatika,

4. Bapak Wisnu Widiarto, S.Si., M.T. selaku Pembimbing Akademik yang telah banyak memberi bimbingan dan pengarahan selama penulis menempuh studi di Jurusan Informatika FMIPA UNS,

5. Bapak dan Ibu dosen serta karyawan di Jurusan Informatika FMIPA UNS yang telah mengajar penulis selama masa studi dan membantu dalam proses penyusunan skripsi ini,

6. Ibu, Bapak, dan kakak-kakakku, serta teman-teman yang telah memberikan bantuan sehingga penyusunan skripsi ini dapat terselesaikan.

Penulis berharap semoga skripsi ini dapat bermanfaat bagi semua pihak yang berkepentingan.

Surakarta, Agustus 2012

(8)

commit to user

viii

DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN PENGESAHAN ... ii

ABSTRAK ... iii

ABSTRACT ... iv

MOTTO ... v

PERSEMBAHAN ... vi

KATA PENGANTAR ... vii

DAFTAR ISI ... viii

DAFTAR TABEL ... x

DAFTAR GAMBAR ... xi

DAFTAR LAMPIRAN ... xiii

DAFTAR SIMBOL ... xiv

BAB I PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Rumusan Masalah ... 3

1.3 Batasan Masalah ... 3

1.4 Tujuan Penelitian ... 3

1.5 Manfaat Penelitian ... 3

1.6 Sistematika Penulisan ... 4

BAB II TINJAUAN PUSTAKA ... 5

2.1 Landasan Teori ... 5

2.1.1 Jaringan Syaraf Tiruan ... 5

2.1.2 Jaringan Radial Basis Function ... 7

2.1.3 Algoritma K-Means Clustering ... 11

2.1.4 Algoritma Genetika ... 13

2.1.5 Adaptive Genetic Algorithm (AGA) ... 20

2.2 Penelitian Sebelumnya ... 21

(9)

commit to user

ix

3.1 Studi Literatur ... 31

3.2 Perancangan ... 31

3.2.1 Data ... 31

3.2.2 Algoritma AGA RBF ... 31

3.2.3 Implementasi ... 40

3.2.4 Analisa... 42

BAB IV HASIL DAN PEMBAHASAN ... 43

4.1 Variasi Simulasi Pada Variabel RBF ... 44

4.2 Variasi Simulasi Pada Variabel AGA RBF ... 53

4.3 Perbandingan JST RBF dan AGA RBF ... 62

BAB V KESIMPULAN DAN SARAN ... 67

5.1 Kesimpulan ... 67

(10)

commit to user

x

DAFTAR TABEL

Tabel 2.1 Probabilitas seleksi dan nilai fitness ... 18

Tabel 3.1 Deskripsi atribut data iris ... 31

Tabel 3.2 Variasi Simulasi Pada Variabel RBF ... 40

Tabel 3.3 Variasi Simulasi Pada Variabel AGA RBF ... 41

Tabel 4.1 Simulasi RBF Dengan 2 Hidden Layer ... 44

Tabel 4.10 Simulasi AGA RBF Dengan 2 Hidden Layer ... 53

Tabel 4.19 Perbandingan Akurasi RBF dan AGA RBF ... 62

Tabel 4.20 Rumus Empiris Penentuan Jumlah Neuron Hidden Layer ... 63

Tabel 4.21 Perbaikan Akurasi Untuk Hidden Layer 2, 3, 4, 5 dan 6 ... 65

(11)

commit to user

xi

Gambar 2.1 Struktur unit jaringan syaraf tiruan ... 6

Gambar 2.2 Topologi Jaringan Radial Basis Function ... 8

Gambar 2.3 Flowchart K-Means Clustering ... 13

Gambar 2.4 Seleksi roda roullet ... 18

Gambar 2.5 Topologi JST RBF ... 23

Gambar 2.6 Kromosom GA-RBF ... 24

Gambar 2.7 Flowchart ANN-AG ... 25

Gambar 2.8 Model jaringan syaraf tiruan (neuromodel). ... 26

Gambar 2.9 Diagram alir penelitian ... 28

Gambar 3.1 Algoritma AGA RBF ... 32

Gambar 3.2 Tahapan pembangunan jaringan radial basis function ... 33

Gambar 3.3 Algoritma K-Means ... 34

Gambar 3.4 Arsitektur jaringan radial basis function ... 36

Gambar 3.5 Algoritma AGA RBF ... 38

Gambar 4.1 Grafik Simulasi RBF 2 Hidden Layer ... 44

Gambar 4.6 Grafik RBF Simulasi Dengan 7 Hidden Layer ... 49

Gambar 4.7 Grafik Simulasi RBF Dengan 8 Hidden Layer ... 50

Gambar 4.9 Grafik Simulasi RBF Dengan 10 Hidden Layer ... 52

Gambar 4.10 Grafik Simulasi AGA RBF 2 Hidden Layer ... 53

Gambar 4.11 Grafik Simulasi AGA RBF Dengan 3 Hidden Layer ... 54

Gambar 4.12 Grafik Simulasi AGA RBF 4 Hidden Layer ... 55

(12)

commit to user

xii

(13)

commit to user

xiii

LAMPIRAN A ... 70

LAMPIRAN B ... 72

LAMPIRAN C ... 76

(14)

commit to user

xiv

DAFTAR SIMBOL

p : Konstanta pada fungsi aktivasi JST

f(x) : fungsi variabel x

wk+1 : Bobot JST pada cacah ke k-1

wk : Bobot JST pada cacah ke k

wji : Bobot dari unit hidden layer j ke output i α : Laju konvergensi (learning rate) (0 < α < 1) v : Masukan yang diboboti

Xm : Vector input RBF ke-m

tj : Vector data yang dianggap sebagai center ke-j.

yj : Output JST ke-j

q : Jumlah hidden layer

MSE : Mean Square Error

φj : Output fungsi basis ke j

exp : natural number

d(x,c) : Hasil jarak eucledian dari vector data xyang ke vector center c

r : Jarak eucledian antara vector data dengan vectorcenter

cj : Vector center ke-j

d : Lebar fungsi Gaussian

σ : nilai spread

x : Vector input data

k : Urutan cluster

𝑀𝑘(𝑚) : Center ke-k pada iterasi ke-m 𝑀𝑖(𝑚) : Center ke-i pada iterasi ke-m

D : Jumlah dimensi pada algoritma K-Means

Clk : Cluster ke-k

Nk : Jumlah data-data pada cluster k

Jk : Error data-data terhadap masing-masing center

Pk : Subset yang berisi data-data untuk cluster ke -k

(15)

commit to user

xv

pm : Probabilitas mutasi

fmax : Fitness maksimal

f : Fitness terbesar dari solusi yang dimutasi

f’ : Fitness terbesar dari solusi yang disilangkan

𝑓 : Fitness rata-rata

k1 : Konstanta pertama untuk update probabilitascrossover

k2 : Konstanta pertama untuk update probabilitasmutasi

k3 : Konstanta kedua untuk update probabilitascrossover

k4 : Konstanta kedua untuk update probabilitasmutasi

Zn : Nilai gen ke n pada kromosom yang merepresentasikan bobot RBF

Zn+1 : Nilai gen ke n+1 pada kromosom yang merepresentasikan bobot bias

(16)

commit to user

1

BAB I

PENDAHULUAN

1.1 Latar Belakang

Jaringan Syaraf Tiruan (JST) merupakan sistem komputasi dimana

arsitektur dan operasinya diilhami dari sistem otak manusia. JST dapat digunakan

untuk belajar dan menghasilkan aturan atau operasi dari beberapa contoh yang

diberikan. Dengan kemampuannya ini JST dapat digunakan untuk klasifikasi, dimana

sebuah kelas data dapat diketahui dari variabel yang dimasukkan sehingga walaupun

data yang diklasifikasi memiliki jumlah variabel yang cukup besar, JST bisa

memetakan input menjadi output yang akurat dari hasil belajarnya.

Salah satu model jaringan syaraf tiruan adalah Radial basis function, Model

ini melakukan pembelajaran secara hybrid yaitu menggabungkan antara

pembelajaran terbimbing dan pembelajaran tidak terbimbing. Beberapa penelitian

tentang radial basis function diantaranya adalah penelitian yang dilakukan oleh

Venkatesan & Anitha (2006) yang memaparkan penggunaan model RBF (radial

basis function) untuk melakukan diagnosis penyakit diabetes mellitus. Artsitekur

jaringan yang dipakai menggunakan satu hidden layer dengan penentuan center

menggunakan metode clustering K-Means. Dari hasil penelitian tersebut, diagnosis

menggunakan RBF (radial basis function) lebih baik dari pada menggunakan logistic

regression dan MLP (Multi Layer Perceptron) dengan tingkat akurasi mencapai

98%. Selain itu waktu yang dibutuhkan untuk melakukan pelatihan pada jaringan

RBF lebih cepat dari pada MLP.

Senada dengan penelitian tersebut, penelitian yang dilakukan oleh

Jayawardena & Fernando (1998) memaparkan perbandingan antara penggunanan

model RBF dengan metode clustering data noniterative clustering, RBF dengan

metode clustering K-Means dan model MLP (Multi Layer Perceptron) dengan

training menggunakan backpropagation. Pada model RBF dengan metode clustering

data noniterative clustering mempunyai tingkat error terkecil dengan 6 node pada

(17)

commit to user

model RBF memiliki tingkat akurasi yang lebih baik dan waktu yang lebih cepat

dalam trainingnya.

Dari penelitian di atas bobot neuron model RBF hasil pelatihan langsung

digunakan untuk melakukan testing. Namun dengan berkembangnya penelitian,

muncul beberapa penelitian yang bertujuan meningkatkan akurasi hasil pelatihan

dengan cara optimasi bobot hasil pelatihan jaringan RBF. Salah satu algoritma yang

dapat digunakan untuk optimasi tersebut adalah algoritma genetika. Algoritma ini

mengadopsi mekanisme evolusi biologis. Salah satu penelitian yang melakukan

optimasi pada radial basis function dengan algoritma genetika adalah penelitian yang

dilakukan oleh Zhangang, Yanbo, & Cheng (2007). Pada penelitian ini dipaparkan

penggabungan antara radial basis function dan algoritma genetika untuk model

peramalan. Dari hasil penelitian diperoleh hasil bahwa AG-RBF mempunyai tingkat

akurasi peramalan yang lebih tinggi dan kecepatan konvergensi yang lebih cepat dari

pada RBF biasa.

Sementara itu dari beberapa penelitian mengenai algoritma genetika,

muncul beberapa modifikasi untuk meningkatkan performa algoritma genetika. Salah

satu penelitian mengenai modifikasi algoritma adalah penelitian yang dilakukan oleh

Srinivas & Patnaik (1994). pada penelitian ini dipaparkan pendekatan baru untuk

penentuan probabilitas crossover dan probabilitas mutasi yang adaptif sesuai dengan

fungsi fitness. Pada penelitian ini dilakukan pengujian Adaptive Genetic Algorithm

(AGA) untuk penyelesaian TSP, optimasi jaringan syaraf tiruan dan kasus VLSI

sirkuit. Dari hasil percobaan dapat disimpulkan bahwa kemampuan AGA lebih baik

dari pada Algorima genetika standar.

Dari penjelasan di atas dapat diketahui bahwa model RBF lebih baik dari

pada MLP ditinjau dari tingkat akurasi maupun waktu pelatihan, sementara model

RBF yang sudah dimodifikasi juga didapatkan hasil jauh lebih baik. Salah satu

modifikasi model RBF adalah dikombinasi dengan algoritma genetika. Oleh karena

itu pada penelitian ini, peneliti akan melakukan penelitian mengenai Adaptive

Genetic Algorithm Radial Basis Function Neural Network (AGA RBF) Untuk

(18)

commit to user

1.2 Rumusan Masalah

Berdasarkan latar belakang masalah tersebut, dapat dirumuskan

permasalahan yaitu bagaimana akurasi Adaptive Genetic Algorithm Radial Basis

FunctionNeural Network (AGA RBF) untuk melakukan klasifikasi tumbuhan iris.

1.3 Batasan Masalah

Batasan masalah pada penelitian ini adalah :

1. Penelitian ini hanya menganalisa mengenai Adaptive Genetic Algorithm Radial

Basis Function Neural Network (AGA RBF) untuk melakukan klasifikasi dengan

studi kasus klasifikasi tumbuhan iris dengan Radial Basis Function Neural

Network sebagai pembanding.

2. Jumlah node di hidden layer adalah dari 2 node sampai 10 node.

3. Nilai θ (threshold) adalah 0.5.

4. Nilai k1, k2, k3 dan k4 pada AGA berturut-turut adalah 1.0, 0.5, 1.0 dan 0.5.

5. Probabilitas elitism adalah 0.2.

6. Metode crossover pada AGA adalah crossover menengah dengan nilai alpha

dipilih secara random dengan interval [-d. 1+d] dengan d adalah 0.25.

7. Metode mutasi pada AGA adalah mutasi random.

1.4 Tujuan Penelitian

1. Mengetahui bagaimana akurasi Adaptive Genetic Algorithm Radial Basis

Function Neural Network (AGA RBF) untuk melakukan klasifikasi tumbuhan

iris.

2. Merekomendasikan algoritma yang tepat untuk melakukan klasifikasi tumbuhan

iris.

1.5 Manfaat Penelitian

Manfaat penelitian ini adalah mengetahui pengaruh Adaptive Genetic

Algorithm yang dikombinasikan dengan Radial Basis Function Neural Network

untuk melakukan klasifikasi tumbuhan iris, sehingga dapat direkomendasikan

(19)

commit to user

Sistematika penulisan penelitian ini terdiri dari beberapa bab yaitu BAB I

PENDAHULUAN, berisi mengenai latar belakang masalah, rumusan masalah,

pembatasan masalah, tujuan, dan sistematika penulisan. BAB II TINJAUAN

PUSTAKA, berisi mengenai teori yang menjadi dasar dalam penelitian ini, yaitu

teori mengenai jaringan syaraf RBF, Algoritma genetika dan dasar teori lain yang

mendukung penelitian ini dan penelitian-penelitian terdahulu yang mendukung

penelitian yang dilakukan sekarang. BAB III METODE PENELITIAN, berisi

tentang metode atau langkah–langkah dalam pemecahan masalah, meliputi

penyusunan formula serta algoritma yang digunakan dalam penelitian. BAB IV

HASIL DAN PEMBAHASAN, Berisi tentang pelatihan dan pengujian algoritma

AGA RBF untuk klasifikasi yang diimplementasikan pada sampel data iris yang ada,

serta menghitung akurasi algoritma AGA RBF dan dibandingkan dengan algoritma

RBF biasa. BAB V PENUTUP, berisi tentang kesimpulan tugas akhir dan

(20)

commit to user

5

BAB II

TINJAUAN PUSTAKA

2.1 Landasan Teori

2.1.1 Jaringan Syaraf Tiruan

Jaringan Syaraf Tiruan (Artificial Neural Networks) atau disingkat JST

adalah sistem komputasi dimana arsitektur dan operasi diilhami dari

pengetahuan tentang sel syaraf biologi di dalam otak. JST dapat digambarkan

sebagai model matematis dan komputasi untuk fungsi aproksimasi nonlinear,

klasifikasi data, cluster dan regresi non parametric atau sebagai sebuah simulasi

dari koleksi model syaraf biologi. (Kristanto, 2004).

Model syaraf ditunjukkan dengan kemampuannya dalam emulasi, analisa,

prediksi, dan asosiasi. Berdasarkan kemampuan yang dimiliki, JST dapat

digunakan untuk belajar dan menghasilkan aturan atau operasi dari beberapa

contoh, untuk menghasilkan output yang sempurna dari contoh atau input yang

dimasukkan dan membuat prediksi tentang kemungkinan output yang akan

muncul atau menyimpan karakteristik dari input yang disimpan kepadanya.

a. Struktur Jaringan Syaraf Tiruan

Seperti halnya otak manusia, jaringan syaraf juga terdiri dari beberapa

neuron dan ada hubungan antara neuron-neuron tersebut. Beberapa neuron akan

mentransformasikan informasi yang diterimanya melalui sambungan keluaran

menuju neuron-neuron yang lain. Dengan kata lain, neuron / sel syaraf adalah

sebuah unit pemroses informasi yang merupakan dasar operasi jaringan syaraf

tiruan. Neuron ini dimodelkan dari penyederhanaan sel syaraf manusia yang

(21)

commit to user

X1

X2

Xn

W1

W2

Wn

Fungsi

Aktivasi Y

Gambar 2.1 Struktur unit jaringan syaraf tiruan

Gambar 2.1 memperlihatkan struktur unit pengolah jaringan syaraf tiruan.

Pada sisi sebelah kiri terlihat beberapa masukan yang menuju ke unit pengolah

yang masing-masing datang dari unit yang berbeda x(n). Setiap sambungan

mempunyai kekuatan hubungan terkait (bobot) yang disimbolkan dengan w(n).

Unit pengolah akan membentuk penjumlahan berbobot dari tiap masukkannya

dan menggunakan fungsi ambang nonlinear (fungsi aktivasi) untuk menghitung

keluarannya. Hasil perhitungan akan dikirimkan melalui hubungan keluaran

seperti tampak pada gambar sisi sebelah kanan (Hermawan, 2006).

b. Fungsi Aktivasi

Operasi dasar dari jaringan syraf tiruan meliputi penjumlahan bobot sinyal

input dan menghasilkan suatu output atau fungsi aktivasi. Beberapa fungsi

aktivasi yang digunakan dalam jaringan syaraf tiruan adalah (Hermawan, 2006) :

1. Fungsi identitas

𝑓 𝑥 =𝑥, untuk semua x (2.1)

2. Fungsi undak biner (dengan batas ambang)

𝑓 𝑥 = 1 untuk x ≥ θ

0 untuk x < 𝜃 (2.2)

3. Fungsi sigmoid

𝑓 𝑥 = 1

1 + exp −px (2.3)

(22)

commit to user 4. Fungsi sigmoid bipolar

𝑔 𝑥 = 2𝑓 𝑥 −1 = 2

1 + exp −𝑝𝑥 (2.5)

𝑔 𝑥 =1−exp −𝑝𝑥

1 + exp −𝑝𝑥 (2.6)

𝑔′_𝑥₌ 𝑐

2 1 +𝑔 𝑥 1− 𝑔 𝑥 (2.7)

2.1.2 Jaringan Radial Basis Function

Metode pelatihan jaringan syaraf tiruan terdiri dari 3 macam yaitu, metode

pelatihan terbimbing, metode pelatihan tidak terbimbing dan metode pelatihan

hibrida. (Hermawan, 2006). Algoritma pelatihan terbimbing memanfaatkan

informasi keanggotaan kelas dari setiap contoh pelatihan, dengan informasi ini

algoritma pelatihan terbimbing dapat mendeteksi kesalahan klasifikasi pola

sebagai umpan balik jaringan sementara algoritma pelatihan tak terbimbing

menggunakan contoh yang tidak diklasifikasikan jenisnya, sistem akan dengan

sendirinya (heuristacally) memprosesnya. Penggabungan metode pelatihan

terbimbing dengan metode pelatihan tak terbimbing disebut metode pelatihan

hibrida.

Jaringan Syaraf Tiruan Radial Basis Function merupakan salah satu contoh

jaringan syaraf tiruan dengan metode pelatihan hibrida yaitu menggabungkan

metode pelatihan terbimbing dan metode pelatihan tak terbimbing.

Seperti halnya jaringan saraf tiruan yang lain, Radial Basis Function

(RBF) juga memiliki topologi jaringan. Topologi milik RBF terdiri atas unit

lapisan masukan (input), unit lapisan tersembunyi (hidden), dan unit lapisan

keluaran (output) (Haryono, 2005). Topologi Jaringan RBF digambarkan

(23)

commit to user

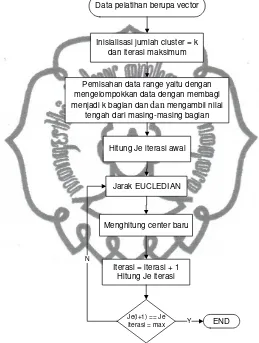
Gambar 2.2 Topologi Jaringan Radial Basis Function

1. Struktur Jaringan Radial Basis Function

1. Input layer

Input layer adalah bagian dari rangkaian jaringan syaraf tiruan

radial basis function sebagai masukan untuk melakukan proses pertama.

Input layer ini membaca data dari faktor luar yaitu keluaran plant (unit

sensor) dan nilai yang kita kehendaki (referensi) (Kusaedi, 2004).

2. Hidden layer

Pada bagian ini terjadi aktifitas perumusan dalam pembentukan

sistem algoritma yang digunakan dalam jaringan RBF. Layer (lapisan)

kedua adalah lapisan tersembunyi dari dimensi yang lebih tinggi, yang

melayani suatu tujuan pada fungsi basis dan bobotnya dengan nilai yang

berbeda.

Algoritma LMS (Least Means Square) merupakan salah satu

algoritma yang digunakan untuk pembelajaran atau update bobot

jaringan. Algoritma ini banyak digunakan karena kesederhanaan

prosesnya dan kemudahan dalam komputasi. Algoritma LMS akan

meminimalkan fungsi rata – rata kuadrat error. Secara matematis

algoritma LMS dituliskan sebagai berikut (Kusaedi, 2004)

(24)

commit to user

Pada hidden layer ini selain memuat bobot juga memuat fungsi

basis. Pada jaringan RBF fungsi basis ini identik dengan dengan Fungsi

gaussian yang diformulasikan sebagai berikut (Haryono, 2005) :

𝜑( 𝑋_𝑚 − 𝑡_𝑗 ) = exp⁡(−1

Hasil dari penjumlahan dari perkalian antara bobot dengan fungsi

basis akan menghasilkan keluaran yang disebut output layer. Output

layer merespon dari jaringan sesuai pola yang diterangkan pada input

layer. Transformasi dari ruang masukan ke ruang hidden unit adalah

non linier, sedang transformasi dari ruang hiddenunit ke ruang keluaran

adalah linier (Kusaedi, 2004).

Menurut Haryono (2005), hal yang khusus pada RBF ialah

berbasis radial, misalnya fungsi Gaussian.

c. Pada output unit, sinyal dijumlahkan seperti biasa

d. Sifat jaringannya ialah feed-forward.

2. Strategi Pembelajaran Jaringan Radial Basis Function

Berdasarkan rumus fungsi gaussian dan topologi jaringan dapat di

usulkan beberapa strategi pembelajaran pada jaringan RBF ini antara lain

(Kusaedi, 2004) :

1. Mengubah posisi center pada fungsi basis dengan lebar fungsi basis

(25)

commit to user

basis dan bobot keluaran setiap fungsi basis diset tetap.

3. Mengubah bobot keluaran setiap fungsi basis dengan posisi center

pada fungsi basis dan lebar fungsi basis diset tetap.

3. Algoritma Pelatihan Jaringan Radial Basis Function

Jaringan Radial Basis Function memiliki algoritma pelatihan yang

agak unik karena terdiri atas cara terbimbing dan tak terbimbing

sekaligus. Pelatihan Jaringan Radial Basis Function terdiri atas dua

tahap (Haryono, 2005).

1. Tahap Clustering Data

Pada tahap pertama, data di-cluster atau dikelompokkan

berdasarkan kedekatan tertentu, misalnya: kedekatan warna antara 2

pixel, kedekatan jarak antar 2 titik, dan seterusnya. Penentuan

cluster dengan sendirinya akan menghasilkan center atau pusat dari

kelompok data. Jumlah cluster menentukan hidden unit yang dipakai.

Dalam menentukan center, ada dua cara yang bisa dipakai.

Cara yang mudah ialah menentukan center secara acak dari

kelompok data. Cara yang lebih sulit, tetapi lebih baik ialah dengan

menggunakan algoritma clustering. Algoritma yang paling mudah

ialah algoritma K-means. Dengan algoritma tersebut, jaringan saraf

tiruan mampu mencari sendiri center-center yang terbaik bagi data.

Dengan melihat tahap pertama dari pelatihan Jaringan Radial Basis

Function tersebut, dapat disimpulkan bahwa, pada tahap ini, pelatihan

bersifat unsupervised.

2. Tahap Pembaharuan Bobot

Jaringan saraf tiruan menyimpan pengetahuannya dalam bobot

neuron-neuronnya. Pelatihan tahap berikutnya berfungsi mendapatkan

nilai bobot neuron-neuronnya. Pada tahap ini, ada serangkaian

perhitungan yang diperlukan untuk memperbaharui bobot. Pada tahap

ini juga, dibutuhkan data training beserta targetnya. Jadi, dapat

(26)

commit to user

Algoritma Pelatihan Jaringan Radial Basis Function secara Iteratif

(Kusaedi, 2004)

Langkah 1 : Menentukan fungsi basis yang akan digunakan

Langkah 2 : Menentukan center tiap node pada hidden layer

Langkah 3 : Menyediakan bobot sebanyak node pada hidden layer

Langkah 4 : Inisialisasi bobot w = [0 0 0 . . . 0]

Set laju konvergensi ( 0 < α <1) , Menentukan maksimal epoch dan

MSE maksimal.

Langkah 5 : Untuk setiap sinyal latih, selama epoch <= maksimal

epoch dan atau MSE <= MSE maksimal, kerjakan langkah 6 – 11.

Langkah 6 : Hitung keluaran node pada hidden layer

Langkah 7 : Hitung keluaran jaringan RBF

Langkah 8 : Hitung kesalahan (error) antara sinyal terhadap (d)

dengan keluaran RBF y.

error = d – y

Langkah 9 : Update bobot-bobot tiap fungsi basis dan bobot basis

dengan metode LMS.

Langkah 10 : Hitung MSE = akar dari jumlahan kuadrat error

Langkah 11 : epoch = epoch + 1

2.1.3 Algoritma K-Means Clustering

Penghitungan center pada penelitian ini menggunakan K-Means

Clustering. Terdapat n data-data training yang memiliki ukuran dimensi d dalam

lingkungan Rd, yang terbagi dalam k bagian. Permasalahan dalam clustering

adalah cara untuk menentukan nilai k yang merupakan jumlah center yang

bertujuan untuk meminimumkan mean square distance dari masing-masing

data pada center - center yang terdekat. Penghitungan ini sering kali disebut

squared-error.

Misalkan n data-data vektor diasumsikan sebagai Xj = {x1, x2, x3, …, xN,

j=1,2, ..,N} yang akan di pisahkan berdasarkan kemiripannya menjadi k bagian

(27)

commit to user

cluster satu dengan yang lain bersifat disjoint (tidak terdapat interseksi antara

cluster).

Algoritma k-means clustering sebagai berikut: (Ririd, 2008)

Menentukan K inisialisasi cluster centers, yaitu M1(1), M2(1), ... , MK(1).

Nilai K merupakan jumlah center dimulai dengan nilai terkecil. Nilai center

yang diinisialisasi dihitung dengan membagi data menjadi K bagian dan

mengambil nilai tengah dari masing-masing bagian.

1. Eucledian

pembelajaran terhadap center, pemindahan pengelompokan jika jarak data

terhadap center k lebih kecil daripada jarak ke center i .

2. Penghitungan nilai center baru

𝑀𝑘 𝑚+ 1 =

1

𝑁𝑘_𝑥 𝑥𝑗

𝑗∈𝐶𝑙𝑘(𝑚)

(2.13)

Penghitungan center yang baru setelah dikelompokkan dengan eucledian.

3. Penghitungan kesalahan dengan Je

𝐽𝑒 = 𝑥𝑗 − 𝑀𝑘

𝑥∈𝑃𝑘 𝐾

𝑘=1

(2.14)

Dapat dipisah menjadi 2 bagian yaitu :

𝐽𝑘 = 𝑥𝑗 − 𝑀𝑘

Dengan langkah ini maka dapat dinilai penghitungan center telah konvergen

(28)

commit to user 4. Pembahasan iterasi

5. Pemeriksaan penghitungan sudah konvergen atau belum

Jika telah mendapatkan penghitungan yang konvergen maka dapat ditemukan

jumlah cluster yang tepat untuk penghitungan aktivasi.

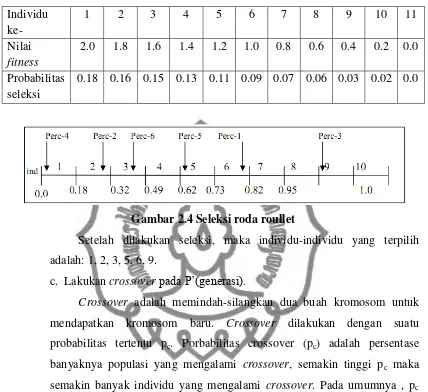
Berikut adalah flowchart dari K-Means Clustering :

Data pelatihan berupa vector

Inisialisasi jumlah cluster = k dan iterasi maksimum

Pemisahan data range yaitu dengan mengelompokkan data dengan membagi menjadi k bagian dan dan mengambil nilai

tengah dari masing-masing bagian

Jarak EUCLEDIAN Hitung Je iterasi awal

Menghitung center baru

Iterasi = iterasi + 1 Hitung Je iterasi

Je(i+1) == Je

Iterasi = max Y END

N

Gambar 2.3 Flowchart K-Means Clustering

2.1.4 Algoritma Genetika

Pengertian Algoritma Genetika menurut beberapa sumber :

1. Dalam bukunya, DE Golderg mendefinisikan Algoritma genetika sebagai

algoritma pencarian yang didasarkan pada mekanisme seleksi alamiah dan

genetika alamiah. (Suyanto, 2005) .

2. Menurut Kusumadewi (2003) , Algoritma genetika adalah algortima

(29)

commit to user

mekanisme seleksi alam dan genetika. Algoritma genetika merupakan salah

satu algoritma yang sangat tepat digunakan dalam menyelesaikan masalah

optimasi kompleks, yang sulit dilakukan oleh metode konvensional (Desiani

& Arhami, 2006).

Jadi dapat dikatakan bahwa Algoritma genetika adalah algoritma pencarian

yang mengadopsi mekanisme seleksi genetika alamiah. Algoritma genetika

pertama kali dikembangkan oleh John Holland dari Universitas Michigan pada

tahun 1975. John Holland menyatakan bahwa setiap masalah yang berbentuk

adaptasi (alami maupun buatan) dapat diformulasikan ke dalam terminologi

genetika. Algoritma genetika adalah simulasi dari proses evolusi Darwin dan

operasi genetika atas kromosom. (Kusumadewi, 2003).

Menurut Kusumadewi (2003), misalkan P(generasi) adalah populasi dari

suatu generasi, secara sederhana algoritma genetika terdiri dari langkah-langkah

sebagai berikut :

1. Generasi = 0 (generasi awal).

2. Inisialisasi populasi awal, P(generasi), secara acak.

3. Evaluasi nilai fitness pada setiap individu dalam P(generasi).

4. Kerjakan langkah-langkah berikut hingga generasi mencapai maksimum

generasi :

a. Generasi = generasi + 1 (tambah generasi).

b. Seleksi populasi tersebut untuk mendapatkan kandidat induk, P’(generasi)

c. Lakukan crossoverpada P’(generasi).

d. Lakukan mutasi pada P’(generasi).

e. Lakukan evaluasi fitnesssetiap individu pada P’(generasi).

(30)

commit to user

Adapun algoritma genetika tersebut adalah sebagai berikut :

Generasi dapat dikatakan sebagai kumpulan solusi dari masalah yang akan

diselesaikan. Pada satu generasi berisi kumpulan solusi yang disebut populasi.

Untuk menyatakan solusi tersebut diperlukan pengkodean masalah. Pengkodean

adalah suatu teknik untuk menyatakan populasi awal sebagai calon solusi suatu

masalah ke dalam suatu kromosom sebagai suatu kunci pokok persoalan ketika

menggunakan algoritma genetika (Desiani & Arhami, 2006). Teknik

pengkodean ini meliputi pengkodean gen dan kromosom. Gen merupakan

bagian dari kromosom. Satu gen bisanya akan mewakili satu variabel.

Terdapat 3 skema yang paling umum digunakan dalam pengkodean

(Suyanto, 2005), yaitu :

a. Real number encoding. Pada skema ini, nilai gen berada dalam interval

[0,R], dimana R adalah bilangan real positif dan biasanya R = 1. Real

number encoding biasanya digunakan untuk permasalah pencarian rute

terpendek, perbaikan bobot JST dan lain sebagainya. Contoh real

number encoding adalah gen pada kromosom berisi 0.3 , 0.4 , 0.7 dan

seterusnya.

b. Discrete decimal encoding. Setiap gen bisa bernilai satu bilangan bulat

dalam interval [0,9].

c. Binary encoding. Setiap gen hanya bernilai 0 atau 1.

Ukuran populasi tergantung pada masalah yang akan dipecahkan dan jenis

operator genetika yang akan diimplementasikan. Misalnya untuk penyelesaian

kasus TSP dengan jumlah lokasi yang sedikit maka ukuran populasinya juga

kecil karena solusi yang dimungkinkan juga sedikit, selain itu penentuan ukuran

populasi juga tergantung operator genetika yang diimplementasikan misalnya

untuk nilai probabilitas mutasi yang kecil maka ukuran populasi dapat diset

besar karena dengan ukuran yang besar kemungkinan terjadi mutasi masih ada

walaupun dengan probabilitas yang kecil. Setelah ukuran populasi ditentukan,

(31)

commit to user

harus tetap memperhatikan domain solusi dan kendala permasalahan yang ada.

Fungsi fitness merupakan ukuran kinerja suatu individu agar tetap bertahan

hidup (Desiani & Arhami, 2006). Pada masalah optimasi, jika solusi yang dicari

adalah memaksimalkan sebuah fungsi 𝑕 (dikenal sebagai masalah maksimasi),

maka nilai fitness yang digunakan adalah nilai fungsi 𝑕 tersbut, yakni 𝑓= 𝑕

(dimana 𝑓 adalah nilai fitness). Tetapi jika masalahnya adalah meminimalkan

fungsi 𝑕 (masalah minimasi), maka fungsi 𝑕 tidak bisa digunakan secara

langsung. Hal ini disebabakan adanya aturan bahwa individu yang memiliki nilai

fitness tinggi lebih mampu bertahan hidup pada generasi berikutnya. Oleh karena

itu nilai fitness yang bisa digunakan adalah

𝑓= 1 _𝑕 (2.17)

Yang artinya semakin kecil nilai 𝑕, semakin besar nilai 𝑓. Tetapi hal ini

menjadi masalah jika 𝑕 bisa bernilai 0, yang mengakibatkan 𝑓 bisa bernilai tak

hingga. Untuk mengatasinya, 𝑕 perlu ditambah sebuah bilangan yang dianggap

sangat kecil sehingga nilai fitnessnya menjadi :

𝑓= 1

𝑕+𝑎 (2.18)

Dimana 𝑎 adalah bilangan yang dianggap sangat kecil dan bervariasi

sesuai dengan masalah yang akan diselesaikan. (Suyanto, 2005). Misalnya untuk

kasus meminimalkan fungsi h dengan nilai fungsi h berkisar pada angka 0.01

maka nilai a dapat diset 1x10-6 , namun jika nilai fungsi h berkisar pada angka

yang besar misalnya 100 maka nilai dapat diset 1 dan seterusnya.

generasi :

b. Seleksi populasi tersebut untuk mendapatkan kandidat induk, P’(generasi)

Seleksi akan menentukan individu-individu dari P’ (generasi ) yang

(32)

commit to user

seleksi yang umum dipakai adalah Seleksi Roda Roulette (Roulette Wheel

Selection). Pada metode ini, individu-individu dipetakan dalam suatu

segmen garis secara berurutan sedemikian hingga tiap-tiap segmen individu

memiliki ukuran yang sama dengan ukuran fitnessnya. Kemudian sebuah

bilangan random dibangkitkan dan individu yang memiliki segmen dalam

kawasan bilangan random tersebut akan terseleksi. Proses ini akan diulang

hingga diperoleh sejumlah individu yang diharapkan.

Contoh metode Roulette Wheel Selection dapat dilihat pada Tabel 2.1.

Misalnya ada 11 individu dalam populasi. Individu pertama memiliki nilai

fitness terbesar yaitu 2.0, individu kedua memiliki nilai fitness 1.8 dan

seterusnya. Kemudian dihitung probablilitas seleksi dengan cara membagi

nilai fitness dengan jumlah total fitness. Misalnya untuk probabilitas seleksi

individu pertama, diperoleh dari perhitungan sebagai berikut :

Total fitness = 2.0 + 1.8 + 1.6 + 1.4 + 1.2 + 1.0 + 0.8 + 0.6 + 0.4 + 0.2 = 11

𝑃𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑎𝑠𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢𝑝𝑒𝑟𝑡𝑎𝑚𝑎_{= 2.0 11}= 0.18

Setelah semua probabilitas dihitung maka ditentukan kumulatif

probabilitasnya untuk mengetahui ukuran segmen individu tersebut.

Misalnya untuk individu kedua, segmen tersebut diperoleh dengan cara

sebagai berikut Segmen individu 2 = kumulatif sebelumnya + probabilitas

seleksi individu 2

Segmen individu 2 = 0.18 + 0.16 = 0.32

Pembagian segmen pada Roulette Wheel Selection dapat dilihat pada

Gambar 2.4. Setelah semua segmen dipetakan, kemudian dibangkitkan

bilangan random antara 0-1 sebanyak individu yang akan diseleksi,

misalnya akan menyeleksi 6 individu maka dibangkitkan 6 bilangan

random. Sebagai contoh dapat dilihat pada Gambar 2.4, misalnya bilangan

random pertama adalah 0.8 maka individu yang terpilih adalah individu ke-6

(33)

commit to user Individu

ke-

1 2 3 4 5 6 7 8 9 10 11

Nilai

fitness

2.0 1.8 1.6 1.4 1.2 1.0 0.8 0.6 0.4 0.2 0.0

Probabilitas seleksi

0.18 0.16 0.15 0.13 0.11 0.09 0.07 0.06 0.03 0.02 0.0

Gambar 2.4 Seleksi roda roullet

Setelah dilakukan seleksi, maka individu-individu yang terpilih

adalah: 1, 2, 3, 5, 6, 9.

c. Lakukan crossoverpada P’(generasi).

Crossover adalah memindah-silangkan dua buah kromosom untuk

mendapatkan kromosom baru. Crossover dilakukan dengan suatu

probabilitas tertentu pc. Porbabilitas crossover (pc) adalah persentase

banyaknya populasi yang mengalami crossover, semakin tinggi pc maka

semakin banyak individu yang mengalami crossover. Pada umumnya , pc

diset mendekati 1, misalnya 0.8. Probabilitas crossover merupakan Adapun

nilai pc ditetapkan di awal dan tidak mengalamai perubahan.

Salah satu jenis crossover adalah Crossover menengah. Crossover

menengah merupakan metode crossover yang hanya dapat digunakan untuk

variabel real. Nilai variabel anak dipilih di sekitar dan antara nilai-nilai

variabel induk. anak dihasilkan menurut aturan sebagai berikut:

Anak = induk 1 + alpha (induk 2 – induk 1)

Dengan alpha adalah faktor skala yang dipilih secara random pada

interval [-d,1+d], biasanya d = 0,25. tiap-tiap variabel pada anak merupakan

hasil crossover variabel-variabel menurut aturan di atas dengan nilai alpha

(34)

commit to user

Misalkan ada 2 individu dengan 3 variabel, yaitu:

Induk 1 : 12 25 5

Induk 2 ; 123 4 34

Misalkan nilai alpha yang terpilih adalah;

Sampel 1 : 0.5 1.1 -0,1

Sample 2 : 0.1 0.8 0.5

Kromosom baru yang terbentuk:

Anak 1 : 67.5 1.9 2.1

Anak 2 : 23.1 8.2 19.5

Crossover disebut juga perkawinan atau penyilangan dua individu

untuk menghasilkan anak. Dari aturan di atas dapat digambarkan misalnya

induk 1 adalah ayah dan induk 2 adalah ibu maka aturan tersebut

menggambarkan bahwa ayah memiliki pengaruh yang lebih besar dari pada

ibu. Pada kondisi lain sesuai dengan proses perkawinan pada manusia dapat

juga terjadi ibu lebih dominan, sehingga dari aturan di atas dapat berubah

menjadi sebagai berikut

Anak = induk 2 + alpha (induk 1 – induk 2)

Namun untuk aturan crossver menengah di sini digunakan aturan

pertama dengan ayah lebih dominan dari pada ibu.

Mutasi berperan untuk menggantikan gen yang hilang dari populasi

akibat proses seleksi yang memungkinkan munculnya kembali gen yang

tidak muncul pada inisialisasi populasi. Proses mutasi ditentukan oleh

probabiltias mutasi (pm). Probabilitas mutasi (pm) didefinisikan sebagai

presentasi dari jumlah total gen pada populasi yang mengalami mutasi.

Adapun nilai pm ditetapkan di awal dan tidak mengalamai perubahan.

Salah satu contoh mutasi adalah dengan mengubah gen yang dimutasi

dengan bilangan random antara nilai tertinggi dan terendah gen dari

kromosom yang dimutasi. (F.Herrera, Lozano, & Vergeday, 1998). Contoh

(35)

commit to user Anak = 23.1 8.2 14.5

Dari contoh tersebut gen ke-3 dengan nilai 19.5 terkena mutasi. Nilai

mutasi diperoleh dengan membangkitkan bilangan random dari 8.2 (nilai

terendah kromosom) sampai 23.1 misalnya diperoleh 14.5, maka nilai 14.5

(nilai tertinggi kromosom) tersebut menggantikan gen yang termutasi

tersebut.

f. Bentuk populasi baru : P(generasi) = {P(generasi-1) yang survive, P’(generasi)}.

P(generasi-1) yang survive diperoleh dengan proses elitism. Proses

elitism adalah proses penyalinan beberapa kromosom terbaik dari

P(Generasi - 1), kemudian dimasukkan pada P(Generasi) untuk menggantikan kromosom pada P’(Generasi) yang buruk. Dimana P’(Generasi) adalah populasi hasil proses crossover dan mutasi.

2.1.5 Adaptive Genetic Algorithm (AGA)

Adaptive Genetic Algorithm pada dasarnya sama dengan algoritma

genetika, perbedaannya adalah pada probabilitas crossover dan mutasi yang

adaptif sehingga diperlukan Update probabilitas crossover dan probailitas

mutasi setiap satu generasi sedangkan untuk proses yang lainnya sama dengan

algoritma genetika biasa. Secara sederhana algoritma genetika terdiri dari

langkah-langkah sebagai berikut :

generasi :

(36)

commit to user c. Lakukan crossover pada P’(generasi).

f. Bentuk populasi baru : P(generasi) = {P(generasi-1) yang survive, P’(generasi)}.

g. Update probabilitas crossover dan probailitas mutasi dengan rumus :

(Srinivas & Patnaik, 1994)

𝑝𝑐 =𝑘1 𝑓𝑚𝑎𝑥 − 𝑓′ 𝑓𝑚𝑎𝑥 − 𝑓 , 𝑘1 ≤ 1.0 (2.19)

𝑝𝑚 = 𝑘2 𝑓𝑚𝑎𝑥 − 𝑓 𝑓𝑚𝑎𝑥 − 𝑓 , 𝑘2 ≤ 1.0 (2.20)

Dengan batasan

𝑝𝑐 =𝑘3, 𝑓′ ≤ 𝑓 (2.21)

𝑝𝑚 = 𝑘4, 𝑓 ≤ 𝑓 (2.22)

Dengan k3, k4≤ 1.0

2.2 Penelitian Sebelumnya

Beberapa penelitian mengenai Radial Basis Function diantaranya adalah

penelitian yang dilakukana oleh Venkatesan & Anitha (2006). Pada penelitiannya

Venkatesan & Anitha (2006) memaparkan penggunaan model RBF (radial basis

function) untuk melakukan diagnosis penyakit diabetes mellitus. Arsitekur jaringan

yang dipakai menggunakan satu hidden layer dengan penentuan center menggunakan

metode clusteringK-Means. Pada penelitian tersebut dilakukan perbandingan antara

metode RBF (radial basis function), logistic regression dan MLP (Multi Layer

Perceptron).

Venkatesan & Anitha (2006) menggunakan database test dan database

eksternal untuk pengujian. Pada database test perancangan model RBF yang

digunakan menggunakan center sebanyak 10 buah dan untuk MLP digunakan 4 node

di hidden layer. Adapun hasil akurasi ketiga model tersebut dengan data dari

database test adalah 73.7 % untuk model LOGISTIK, 91.3 % untuk model MLP dan

untuk model RBF mencapai 97.0 %.

Sedangkan untuk database external perancangan model model RBF yang

(37)

commit to user

database external adalah 77.0 % untuk model LOGISTIK, 94.3 % untuk model MLP

dan untuk model RBF mencapai 98.0 %.

Dari hasil penelitian tersebut, Venkatesan & Anitha (2006) menyimpulkan

bahwa diagnosis menggunakan RBF (radial basis function) lebih baik dari pada

menggunakan logistic regression dan MLP (Multi Layer Perceptron) dengan tingkat

akurasi mencapai 98%. Selain itu waktu yang dibutuhkan untuk melakukan pelatihan

pada jaringan RBF lebih cepat dari pada MLP. Namun jika dibandingkan dengan

metode logistic, model RBF dan MLP membutuhkan waktu yang lebih lama untuk

melakukan training. (Venkatesan & Anitha, 2006).

Penelitian lainnya adalah penelitian yang dilakukan oleh Jayawardena &

Fernando (1998) yang memaparkan perbandingan antara penggunanan model RBF

dengan metode clustering data noniterative clustering, RBF dengan metode

clustering K-Means dan model MLP (Multi Layer Perceptron) dengan training

menggunakan backpropagation. Pada model RBF dengan metode clustering data

noniterative clustering mempunyai tingkat error terkecil dengan 6 node pada hidden

layer sedangkan RBF dengan metode clustering K-Means mempunyai tingkat error

terkecil dengan 11 node pada hidden layer. Jika dibandingkan dengan MLP, model

RBF memiliki tingkat akurasi yang lebih baik dan waktu yang lebih cepat dalam

trainingnya.

Sementara itu, penelitian yang dilakukan oleh Haryono (2005) memaparkan

penggunaan RBF untuk pengenalan huruf abjad dari A sampai Z. Arsitektur JST

RBF pada hidden layer digunakan menggunkan fungsi Gaussian sebagai berikut

𝜃 𝑟 =𝑒𝑥𝑝 − 𝑟

2

2𝜎2 (2.23)

Dimana 𝜎 adalah nilai spread yang didefinisikan sebagai berikut :

𝜎= 𝑗𝑎𝑟𝑎𝑘𝑚𝑎𝑘𝑠𝑖𝑚𝑢𝑚𝑎𝑛𝑡𝑎𝑟𝑎 2 𝑝𝑢𝑠𝑎𝑡

𝑏𝑎𝑛𝑦𝑎𝑘𝑝𝑢𝑠𝑎𝑡 =

𝑑𝑚𝑎𝑥

𝑚𝑖 (2.24)

Sementara untuk menentukan bobot di hidden layer digunakan metode

(38)

commit to user

Cluster Decision. Dari hasil penelitian kekakuratan jaringan syaraf tiruan dalam

pengenalan huruf abjad mencapai 97 %. (Haryono, 2005)

Penelitian lain tentang penggunan JST RBF adalah penelitian yang

dilakukan oleh Kusaedi. Rancangan JST RBF yang digunakan oleh Kusaedi (2004)

dalam Perancangan Kendali Kecepatan Motor DC pada penelitian tersebut

menggunakan fungsi Gaussian sebagai berikut :

𝜑𝑗 =𝑒−

Dari hasil penelitian dapat disimpulkan bahwa dengan menggunakan

pelatihan (penggunaan bobot) memberikan hasil yang lebih bagus, walaupun sering

terjadi overshoot terlebih dahulu. (Kusaedi, 2004)

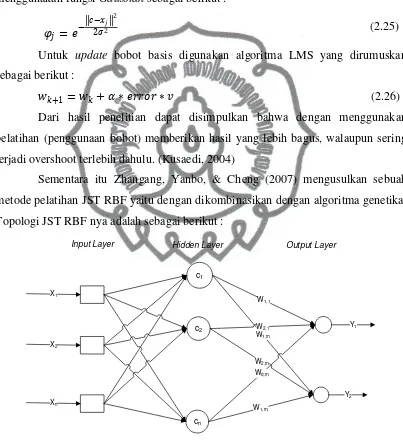
Sementara itu Zhangang, Yanbo, & Cheng (2007) mengusulkan sebuah

metode pelatihan JST RBF yaitu dengan dikombinasikan dengan algoritma genetika.

Topologi JST RBF nya adalah sebagai berikut :

X1

Input Layer Hidden Layer Output Layer

Gambar 2.5 Topologi JST RBF

Pemetaan dari data input sampai ke layer output digunakan rumus sebagai

(39)

commit to user

𝑦𝑖 = 𝑤𝑗,𝑖𝜑 𝑥 − 𝑐𝑗 𝑗=1

(2.27)

Radial basis function didefinisikan sebagai fungsi Gaussian sebagai

berikut :

𝜑 𝑟 =𝑒𝑥𝑝 −𝑟2_/2_𝜎2 𝜎_{> 0,} _{𝑟 ≥}₀ _(2.28)

Kromosom dikodekan dalam bentuk string real. Adapun kromosomnya

adalah sebagai berikut :

The right to export unit The basic center position The variance of RBF A chromosome string

Order by number of node in hidden layer

Gambar 2.6 Kromosom GA-RBF

Dari Gambar 2.6 dapat diketahui bahwa kromosom merupakan representasi

dari export unit, posisi center dan variance RBF. Sementara fungsi fitness

didefiniskan sebagai 1

𝑀𝑆𝐸. Dari hasil penelitian diperoleh hasil bahwa AG-RBF mempunyai tingkat akurasi peramalan yang lebih tinggi dan kecepatan konvergensi

yang lebih cepat dari pada RBF biasa. (Zhangang, Yanbo, & Cheng, 2007).

Senada dengan penelitian Zhangang, Yanbo, & Cheng (2007), Ahmed,

Nordin, Sulaiman, & Fatimah (2009) membahas mengenai pelatihan jaringan syaraf

tiruan MLP (Multi Layer Perceptron) dengan 1 hidden layer yang dioptimasi

menggunakan algoritma genetika. Model MLP yang digunakan adalah

back-propagation dengan algoritma training Lavenberg Marquant (LM). Adapun

(40)

commit to user

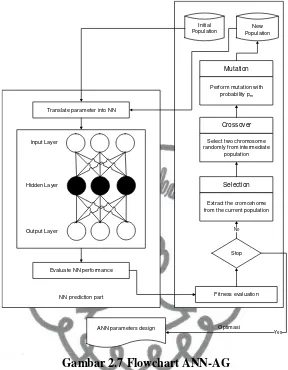
Gambar 2.7 Flowchart ANN-AG

Mean Square Error (MSE), Root Mean Square Error (RMSE), dan

Determination Coefficients (R²) digunakan untuk mengevaluasi performa ANN-GA.

Semakin kecil MSE dan RMSE serta nilai R² mendekati 1 maka ANN-AG

menunjukan performa yang bagus dan ketepatan akurasi yang tinggi. Adapun rumus

untuk menghitung MSE, RMSE dan R2 adalah sebagai berikut :

(41)

commit to user

MSE dan RMSE yang lebih sedikit serta nilai R2 yang lebih besar daripada model

ANN dengan trial-error procedure. (Ahmed, Nordin, Sulaiman, & Fatimah, 2009)

Penelitian lain yang menggabungkan JST dan algoritma genetika adalah

penelitian yang dilakukan oleh Yasin Fahmi. Pada penelitiannya Fahmi (2011)

memaparkan penggabungan antara jaringan syaraf tiruan backpropagation dengan

optimasi menggunakan algoritma genetika untuk peramalan harga saham. Adapun

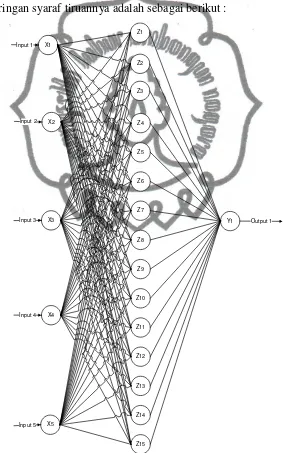
arsitektur jaringan syaraf tiruannya adalah sebagai berikut :

X1

(42)

commit to user

Pada penelitiannya dipilih lima indeks saham perusahaan yang memiliki

index saham yang sehat yaitu :

a. Index saham individual Astra International.

b. Index saham individual Gudang Garam.

c. Index saham individual Indosat.

d. Index saham individual Telkom.

e. Index saham individual Unilever.

Kelima index tersebut menjadi input pada jaringan syaraf tiruan. Sedangkan

pada hidden layer terdapat 15 neuron. Fungsi aktivasi yang digunakan adalah

sigmoid biner dan metode normalisasi data yang digunakan adalah Min-max

normalization. Adapun rumus yang digunakan untuk penskalaan adalah sebagai

berikut :

𝑆𝑘𝑎𝑙𝑎 = 𝑛𝑖𝑙𝑎𝑖𝑦𝑎𝑛𝑔𝑑𝑖𝑠𝑘𝑎𝑙𝑎 − 𝑛𝑖𝑙𝑎𝑖𝑚𝑖𝑛𝑖𝑚𝑢𝑛𝑑𝑎𝑡𝑎

𝑛𝑖𝑙𝑎𝑖𝑚𝑎𝑥𝑖𝑚𝑢𝑛𝑑𝑎𝑡𝑎 − 𝑛𝑖𝑙𝑎𝑖𝑚𝑖𝑛𝑖𝑚𝑢𝑛𝑑𝑎𝑡𝑎 (2.32)

Pada proses optimasi dengan algoritma genetika, fungsi fitness didefinisikan

dengan rumus 1

𝑀𝑆𝐸 , dimana MSE merupakan Mean Square Error. Kromosom direpresentasikan sebagai kumpulan 15 neuron di hidden layer, karena pada

penelitian ini hanya bobot output yang dioptimasi. Adapun representasi

kromosomnya adalah sebagai berikut :

Z1 Z2 ….. Z14 Z15

Z1, Z2, Z3, Z4, Z5, Z6, Z7, Z8 Z9, Z10, Z11, Z12, Z13, Z14, Z15.

Z = berisi locus yang merupakan nilai neuron 1 sampai 15, pada hidden layer.

(43)

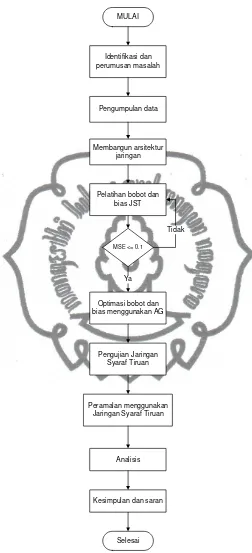
commit to user Identifikasi dan perumusan masalah

Pengumpulan data

Membangun arsitektur jaringan

Pelatihan bobot dan bias JST

MSE <= 0.1

Optimasi bobot dan bias menggunakan AG

Pengujian Jaringan Syaraf Tiruan

Peramalan menggunakan Jaringan Syaraf Tiruan

Analisis

Kesimpulan dan saran

Selesai Ya

Tidak

Gambar 2.9 Diagram alir penelitian

Dari hasil penelitian menunjukan bahwa pada saat inisialisasi bobot dan bias

jaringan syaraf tiruan, nilai MSE yang didapatkan adalah 0.0297. Setelah bobot dan

(44)

commit to user

sebesar 0,004490 dan nilai fitness sebesar 222.70. Nilai MSE sebelum dan setelah

optimasi bobot ini mengalami penurunan sebesar 567.455%. (Fahmi, 2011).

Di sisi lain, seiring perkembangan penelitian mengenai algoritma genetika,

muncul berbagai macam modifikasi algoritma genetika untuk meningkatkan kualitas

algoritma genetika, salah satunya adalah penelitian yang dilakukan oleh Srinivas &

Patnaik (1994). Pada penelitiannya Srinivas & Patnaik (1994) memaparkan sebuah

pendekatan baru pada algoritma genetika yaitu probabilitas crossover dan mutasi

yang adaptif. Selama ini pada Algoritma genetika standar nilai probabilitas crossover

dan mutasi selalu diset tetap untuk setiap iterasi pada proses optimasi dengan

algoritma genetika.

Srinivas & Patnaik (1994) mengusulkan nilai probabilitas crossover dan

mutasi tidak tetap namun berubah sesuai dengan nilai fitness. Adapun rumus

probabilitas crossover dan mutasi yang diusulkan adalah sebagai berikut :

𝑝𝑐 =𝑘1 𝑓𝑚𝑎𝑥 − 𝑓′ 𝑓𝑚𝑎𝑥 − 𝑓 , 𝑘1 ≤ 1.0 (2.33)

𝑝𝑚 = 𝑘2 𝑓𝑚𝑎𝑥 − 𝑓 𝑓𝑚𝑎𝑥 − 𝑓 , 𝑘2 ≤ 1.0 (2.34)

Dengan batasan

𝑝𝑐 =𝑘3, 𝑓′ ≤ 𝑓 (2.35)

𝑝𝑚 = 𝑘3, 𝑓 ≤ 𝑓 (2.36)

Dimana k3, k4≤ 1.0

𝑘1,𝑘2,𝑘3,𝑘4 ≤ 0

Agar rumus di atas dapat berjalan dengan optimal maka dasarankan untuk

nilai k1, k2, k3 dan k4 berturut-turut adalah 1.0, 0.5, 1.0 dan 0.5.

Srinivas & Patnaik (1994) melakukan pengujian Adaptive Genetic

Algorithm (AGA) untuk penyelesaian TSP, optimasi jaringan syaraf tiruan dan kasus

VLSI sirkuit. Dari hasil percobaan dapat disimpulkan bahwa kemampuan AGA lebih

baik dari pada Algorima genetika standar.

Dari hasil penelitian penentuan nilai pc dan pm yang adaptif sesuai dengan

nilai fitness sesuai dengan yang diusulkan tersebut, tidak hanya meningkatkan

konvergensi algoritma genetika tetapi juga mencegah terjadinya local optimum.

(45)

commit to user

Rismawan & Kusumadewi (2008) yang memaparkan penggunaan metode clustering

K-Means Untuk Pengelompokkan Mahasiswa Berdasarkan Nilai Body Mass Index

(Bmi) & Ukuran Kerangka. Pada penelitian ini telah dibangun sistem yang dapat

digunakan untuk mengklasifikasi mahasiswa menurut BMI dan ukuran kerangkanya

berdasarkan data kondisi fisik dari mahasiswa yang bersangkutan yang telah diambil

terlebih dahulu. Data kondisi fisik yang digunakan adalah tinggi badan, berat badan

dan lingkar lengan bawah. Dari data tersebut dikelompokkan menjadi 3 dengan

menggunakan metode K-Means.

Dari hasil penelitian, dapat disimpulkan bahwa algoritma klasifikasi

K-Means dapat digunakan untuk mengelompokkan mahasiswa berdasarkan status gizi

dan ukuran kerangka. Dari data yang dilatih, diperoleh 3 kelompok berdasarkan BMI

dan ukuran kerangka, yaitu : (Rismawan & Kusumadewi, 2008)

1. BMI normal dan kerangka besar, dengan pusat cluster (19,53; 11,52).

2. BMI obesitas sedang dan kerangka sedang, dengan pusat custer (25,44;

10,22).

3. BMI obesitas berat dan kerangka kecil, dengan pusat cluster (43,25;

8,95).

2.3 Rencana penelitian

Dengan melihat tinjauan pustaka di atas, penelitian ini akan berkonsentrasi

pada penggabungan jaringan syaraf tiruan Radial Basis Function (RBF) dengan

algoritma genetika untuk klasifikasi. Algoritma genetika yang digunakan pada

penelitian ini adalah Adaptive Genetic Algortihm (AGA). Hasil penelitian ini adalah

(46)

commit to user

31

BAB III

METODE PENELITIAN

3.1StudiLiteratur

Studi literatur dilakukan untuk mendapatkan pengetahuan dari

literatur-literatur yang berkaitan dengan objek yang dikaji. Pengetahuan yang diperlukan

didapatkan dengan mempelajari Algoritma Genetika, Jaringan Syaraf Tiruan,

Adaptive Genetic Algorithm, Algoritma K-Means Clustering dan Jaringan Radial

Basis Function.

3.2Perancangan

3.2.1 Data

Database iris diperoleh dari UCI Machine Learning Repository dengan

alamat di http://archive.ics.uci.edu/ml/. Total data sebanyak 150 data, 50 data

(33.3%) untuk masing masing class yaitu iris setosa, iris versicolour dan iris

virginica, dengan deskripsi atribut ditunjukkan pada tabel 3.1 :

Tabel 3.1 Deskripsi atribut data iris

No Atribut Domain

1 Panjang sepal Bilangan real dalam cm

2 Lebar sepal Bilangan real dalam cm

3 Panjang petal Bilangan real dalam cm

4 Lebar petal Bilangan real dalam cm

5 Class iris setosa, iris versicolour dan iris virginica

Sumber : (Blak, 1988)

3.2.2 Algoritma AGA RBF

Pada tugas akhir ini akan dibuat algoritma penggabungan jaringan radial

(47)

commit to user

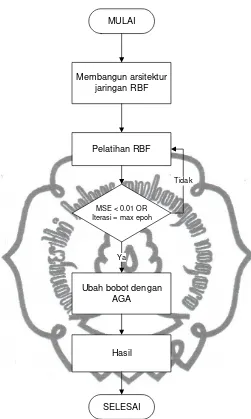
MULAI

Membangun arsitektur jaringan RBF

Pelatihan RBF

MSE < 0.01 OR Iterasi = max epoh

Ubah bobot dengan AGA

SELESAI

Ya

Tidak

Hasil

Gambar 3.1 Algoritma AGA RBF

Algoritma AGA RBF tersebut adalah sebagai berikut :

1. Membangun arsitektur jaringan RBF (Radial Basis Function)

Tahapan dalam membangun jaringan radial basis function ditunjukkan

(48)

commit to user

MULAI

Menentukan fungsi basis

Menentukan banyaknya center

Menyusun arsitektur RBF

SELESAI Menentukan center

dengan algoritma K-Means

Gambar 3.2 Tahapan pembangunan jaringan radial basis function

a. Menentukan fungsi basis. Fungsi basis ini akan digunakan untuk aktivasi

fungsi di hidden layer. Fungsi yang digunakan adalah fungsi berbasis

radial yaitu fungsi Gaussian. Adapun fungsi Gaussian adalah sebagai

berikut :

𝜃 𝑟 =𝑒𝑥𝑝 − 𝑟

2

2𝜎2 (3.1)

Dimana 𝜎 adalah nilai spread yang didefinisikan sebagai berikut :

𝜎= 𝑗𝑎𝑟𝑎𝑘𝑚𝑎𝑘𝑠𝑖𝑚𝑢𝑚𝑎𝑛𝑡𝑎𝑟𝑎 2 𝑝𝑢𝑠𝑎𝑡

𝑏𝑎𝑛𝑦𝑎𝑘𝑝𝑢𝑠𝑎𝑡 =

𝑑𝑚𝑎𝑥

𝑛 (3.2)

Menetukan banyaknya center. Banyaknya center akan mempengaruhi

arsitektur jaringan radial basis function karena banyaknya center akan

(49)

commit to user

yang akan dicari centernya menggunakan algoritma K-Means.

b. Menentukan center dengan algoritma K-Means. Adapun algoritma

K-Means ditunjukkan pada Gambar 3.3 :

Data berupa vektor MULAI

SELESAI Inisialisasi jumlah cluster = k dan iterasi

maksimum

Inisialisasi center

Hitung Je iterasi awal

Hitung eucledian

Hitung center baru

Iterasi = iterasi + 1 Hitung Je iterasi

Je(i+1) == Je Iterasi = max

Ya

Tidak

Gambar 3.3 Algoritma K-Means

1) Loaddata