PEDOMAN PRAKTIKUM FISIKA DASAR. Berperilaku dan berpakaian sopan. Jika tidak dipenuhi maka sekurangkurangnya

PEDOMAN PRAKTIKUM FISIKA DASAR

1. Kehadiran

Praktikum harus diikuti sekurang-kurangnya 80 % dari jumlah total praktikum yang diberikan. Jika syarat tersebut tidak dipenuhi maka praktikum dinyatakan tidak lulus, yang akan mengakibatkan ketidaklulusan pada mata kuliah Fisika Dasar.

Ketidakhadiran karena sakit harus disertai surat keterangan resmi yang diserahkan ke LFD paling lambat dua minggu sejak ketidak-hadirannya. Jika tidak dipenuhi maka dikenakan SANKSI 3.

Keterlambatan kurang dari duapuluh menit dikenai SANKSI 1.

Keterlambatan lebih dari duapuluh menit dikenai SANKSI 3.

Data kehadiran akan dirujuk pada data absensi yang ada pada komputer absensi. Setiap mahasiswa diwajibkan melakukan dan mengkonfirmasi absensinya dengan benar.

2. Persyaratan Mengikuti Praktikum

Berperilaku dan berpakaian sopan. Jika tidak dipenuhi maka sekurang-kurangnya dikenakan SANKSI 1.

Mengenakan Jas Lab dan memakai

Name Tag

(dengan code bar) Jika

tidak dipenuhi maka dikenakan SANKSI 2 atau SANKSI 1 plus SANKSI ADMINISTRASI.

Mengerjakan tugas-tugas pendahuluan jika ada.

Menyiapkan diri dengan materi praktikum yang akan dilakukan. Mahasiswa yang kedapatan tidak siap untuk praktikum bisa tidak diijinkan mengikuti praktikum (dapat dikenai Sanksi 3).

3. Pelaksanaan Praktikum

Mentaati tata tertib yang berlaku di Laboratorium Fisika Dasar.

Mengikuti petunjuk yang diberikan oleh Asisten dan Dosen Penanggung Jawab Praktikum.

Memelihara kebersihan dan bertanggung jawab atas keutuhan alat-alat praktikum.

Pedoman Praktikum Fisika Dasar ii 4. Penilaian

Nilai praktikum ditentukan dari nilai Tugas Awal, Test Awal, Aktivitas dan Laporan.

Nilai akhir praktikum (AP) dihitung dari rata-rata nilai praktikum, yaitu jumlah nilai seluruh modul praktikum dibagi jumlah praktikum yang wajib dilaksanakan.

Kelulusan praktikum ditentukan berdasarkan nilai akhir praktikum (AP ≥≥≥≥ 50) dan keikutsertaan praktikum ( ≥≥≥≥ 80 %).

5. Sanksi nilai

SANKSI 1 : Nilai Modul yang bersangkutan dikurangi 10. SANKSI 2 : Nilai Modul yang bersangkutan dikurangi 50% SANKSI 3 : Tidak diperkenankan praktikum, sehingga Nilai Modul

yang bersangkutan = NOL.

6. Sanksi Administrasi

Sanksi administrasi diberikan bagi praktikan yang selama praktikum berlangsung menimbulkan kerugian, misalnya memecahkan/ merusakkan alat, menghilangkan/tertinggal

Name Tag

dsb. Nilai denda dan tata cara penggantian dapat dilihat pada papan pengumuman kolektif.

7. Praktikum susulan dan ulangan

Secara umum tidak diadakan praktikum susulan, kecuali bagi yang berhalangan praktikum karena sakit. Praktikum susulan akan dilaksanakan setelah praktikum reguler berakhir. Persyaratan lengkap dan jadwalnya akan diatur kemudian (lihat informasi di papan pengumuman kolektif LFD). Bagi mahasiswa yang mengulang praktikum, diwajibkan mengikuti

praktikum sebanyak jumlah total praktikum. Mahasiswa diwajibkan mengikuti praktikum regular yang berjalan dengan mendaftarkan lebih dahulu waktu praktikum yang sesuai dengan jadwalnya masing-masing. Pendaftaran dilakukan di kantor Tata Usaha LFD sebelum praktikum berjalan.

8. Lain-lain

Praktikum reguler dilaksanakan pada waktu yang dijadwalkan yaitu Pagi

Praktikum yang tidak dapat dilaksanakan karena hari libur, kegagalan arus listrik PLN dsb., akan diberikan praktikum pengganti setelah seluruh sesi praktikum reguler selesai.

Tata tertib berperilaku sopan di dalam laboratorium meliputi di antaranya larangan makan, minum, merokok, menggunakan walkman, handphone dan sejenisnya. Selama praktikum tidak diperkenankan menggunakan handphone untuk bertelepon maupun ber-SMS.

Tata tertib berpakaian sopan di dalam laboratorium meliputi di antaranya larangan memakai sandal dan sejenisnya.

Informasi praktikum Fisika Dasar dapat dilihat pada papan pengumuman di luar gedung LFD. Pengumuman yang sifatnya kolektif

(untuk seluruh mahasiswa) ditulis pada kertas merah muda. Pengumuman

per kelompok (Senin Pagi s.d. Jumat Sore) ditulis pada kertas kuning dan

biru.

Informasi praktikum dan tugas-tugas praktikum dapat dilihat di halaman website http://lfd.fmipa.itb.ac.id. Mahasiswa wajib mengakses sendiri halaman website tersebut dan dianggap telah mengetahui atas informasi dan tugas-tugas yang telah ditampilkan pada halaman website tersebut.

Juli 2011

Pedoman Praktikum Fisika Dasar iv

Kontributor

Buku modul praktikum ini ditulis oleh Dosen-dosen Program Studi Fisika:

M. Hamron Hendro

R. Hamron R. Soegeng

Soejoto Suprapto A.

Rustan Rukmantara Umar Fauzi

Moerjono Doddy S.

Hasbuna Kifli M. Birsyam

Suparno Satira Neny K.

Euis Sustini Daniel K.

Pepen Arifin Triyanta

Agoes S.

Revisi

Buku modul ini telah beberapa kali mengalami revisi pada saat LFD dikoordinir oleh Hendro, MSi, Dr. Daniel Kurnia dan Dr. Euis Sustini, khususnya dengan penambahan beberapa modul praktikum yang terintegrasi dengan komputer. Revisi minor terakhir dilakukan pada bulan Juli 2011 (oleh Dr. Rahmat Hidayat dan Dr. Khairul Basar dengan dibantu para Koordinator Asisten LFD periode 2011/12)

DAFTAR ISI

Pedoman Praktikum Fisika Dasar i

Daftar Isi v

Modul 01. Dasar Pengukuran dan Ketidakpastian 1

Modul 02. Osilasi Harmonik Sederhana (Pegas) 10

Modul 03. Osilasi Harmonik Sederhana (Bandul Matematis) 15

Modul 04. Bandul Fisis 18

Modul 05. Momen Inersia 23

Modul 06. Modulus Young 29

Modul 07. Modulus Puntir 32

Modul 08. Pesawat Atwood 36

Modul 09. Dinamika, Usaha, dan Energi 40

Modul 10. Resonansi Gelombang Bunyi 46

Modul 11. Gelombang Berdiri Pada Tali 49

Modul 12. Kalorimeter 51

Modul 01 Dasar Pengukuran dan Ketidakpastian 1

MODUL 01

DASAR PENGUKURAN DAN KETIDAKPASTIAN

TUJUAN

1. _{mampu menggunakan dan memahami alat-alat ukur dasar}

2. _{mampu menentukan ketidakpastian pada pengukuran tunggal dan berulang} 3. _{dapat mengaplikasikan konsep ketidakpastian dan angka berarti dalam}

pengolahan hasil pengukuran

ALAT DAN BAHAN

• Penggaris plastik • Amperemeter • Voltmeter • Thermometer • Mikrometer sekrup • Jangka sorong • Stopwatch • Busur derajat • Bola besi • Balok kuningan/almunium • Hidrometer • Barometer laboratorium • Neraca teknis TEORI DASAR A. Alat ukur dasar

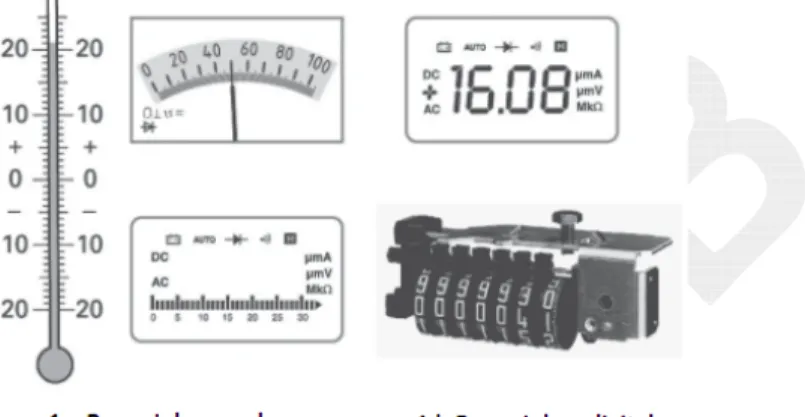
Alat ukur adalah perangkat untuk menentukan nilai atau besaran dari suatu kuantitas atau variabel fisis. Pada umumnya alat ukur dasar terbagi menjadi dua jenis, yaitu alat ukur analog dan digital. Ada dua sistem pengukuran yaitu sistem analog dan sistem digital. Alat ukur analog memberikan hasil ukuran yang bernilai kontinyu, misalnya penunjukan temperatur dalam ditunjukkan oleh skala, penunjuk jarum pada skala meter, atau penunjukan skala elektronik (Gambar 1.a). Alat ukur digital memberikan hasil pengukuran yang bernilai diskrit. Hasil pengukuran tegangan atau arus dari meter digital merupakan sebuah nilai dengan jumlah digit tertentu yang ditunjukkan pada panel display-nya (Gambar 1.b).

Suatu pengukuran selalu disertai oleh ketidakpastian. Beberapa penyebab ketidakpastian tersebut antara lain adanya Nilai Skala Terkecil (NST), kesalahan kalibrasi, kesalahan titik nol, kesalahan paralaks, fluktuasi parameter pengukuran dan ling-kungan yang saling mempengaruhi serta keterampilan pengamat. Dengan demikian amat sulit untuk mendapatkan nilai sebenarnya suatu besaran melalui pengukuran. Beberapa panduan akan disajikan dalam modul ini bagaimana cara

memperoleh hasil pengukuran seteliti mungkin serta cara melaporkan ketidakpastian yang menyertainya.

Beberapa alat ukur dasar yang akan dipelajari dalam praktikum ini adalah jangka sorong, mikrometer sekrup, barome

derajat, stopwatch dan beberapa alat ukur besaran listrik. Masing

memiliki cara untuk mengoperasikannya dan juga cara untuk membaca hasil yang terukur.

Gambar 1. Penunjukan me

Nilai Skala Terkecil

Pada setiap alat ukur terdapat suatu nilai skala yang tidak dapat lagi dibagi bagi, inilah yang disebut Nilai Skala Terkecil (

pada NST ini. Pada Gambar 2 di bawah ini tampak bahwa

Gambar 2. Skala utama suatu alat ukur dengan

Nonius

Skala nonius akan meningkatkan ketelitian pembacaan alat ukur. Umumnya terdapat suatu pembagian sejumlah skala utama dengan sejumlah skala nonius yang akan menyebabkan garis skala titik nol dan titik maksimum skala nonius berimpit dengan skala utama. Cara membaca skalanya adalah sebagai berikut:

1. baca posisi 0 dari skala nonius pada skala utama,

2. angka desimal (di belakang koma) dicari dari skala nonius yang berimpit dengan skala utama.

memperoleh hasil pengukuran seteliti mungkin serta cara melaporkan

Beberapa alat ukur dasar yang akan dipelajari dalam praktikum ini adalah jangka sorong, mikrometer sekrup, barometer, neraca teknis, penggaris, busur dan beberapa alat ukur besaran listrik. Masing-masing alat ukur memiliki cara untuk mengoperasikannya dan juga cara untuk membaca hasil yang

. Penunjukan meter analog dan meter digital.

Pada setiap alat ukur terdapat suatu nilai skala yang tidak dapat lagi dibagi-bagi, inilah yang disebut Nilai Skala Terkecil (NST). Ketelitian alat ukur bergantung

ini. Pada Gambar 2 di bawah ini tampak bahwa NST = 0,25 satuan.

Skala utama suatu alat ukur dengan NST = 0,25 satuan.

Skala nonius akan meningkatkan ketelitian pembacaan alat ukur. Umumnya terdapat suatu pembagian sejumlah skala utama dengan sejumlah skala nonius yang akan menyebabkan garis skala titik nol dan titik maksimum skala nonius berimpit

membaca skalanya adalah sebagai berikut: baca posisi 0 dari skala nonius pada skala utama,

Modul 01 Dasar Pengukuran dan Ketidakpastian

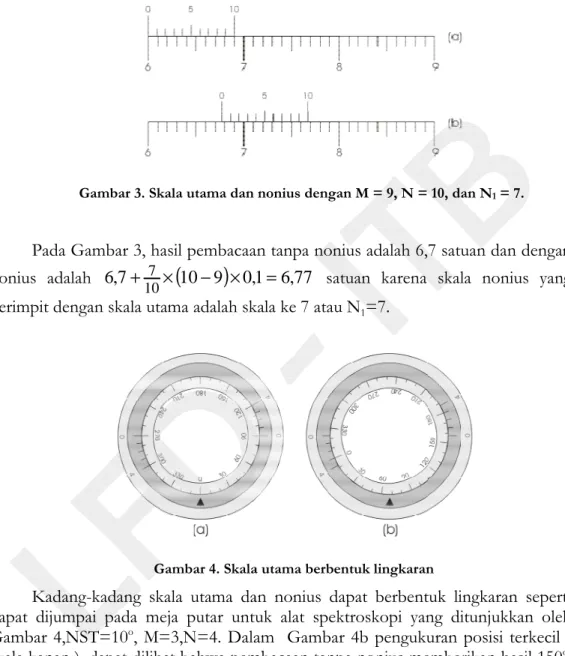
Di bawah ini contoh alat ukur dengan NST utama 0,1 satuan dan 9 skala utama M menjadi 10 skala nonius N.

Gambar 3. Skala utama dan nonius dengan M = 9, N = 10, dan N

Pada Gambar 3, hasil pembacaan tanpa nonius adalah 6,7 satuan dan dengan nonius adalah 6,7

(

10 9

)

0,1

10

7 _{× − ×}

+

berimpit dengan skala utama adalah skala ke 7 atau N

Gambar 4. Skala utama berbentuk lingkaran

Kadang-kadang skala utama dan nonius dapat berbentuk lingkaran seperti dapat dijumpai pada meja putar untuk alat

Gambar 4,NST=10o_{, M=3,N=4. Dalam}

skala kanan ), dapat dilihat bahwa pembacaan tanpa nonius membe sedangkan dengan menggunakan nonius hasilnya adalah

157,5o_.

B. Parameter alat ukur

Ada beberapa istilah dan definisi dalam pengukuran yang harus dipahami, diantaranya :

odul 01 Dasar Pengukuran dan Ketidakpastian 3 Di bawah ini contoh alat ukur dengan NST utama 0,1 satuan dan 9 skala

. Skala utama dan nonius dengan M = 9, N = 10, dan N1 = 7.

, hasil pembacaan tanpa nonius adalah 6,7 satuan dan dengan

77 , 6 1

, = satuan karena skala nonius yang berimpit dengan skala utama adalah skala ke 7 atau N1=7.

Gambar 4. Skala utama berbentuk lingkaran

kadang skala utama dan nonius dapat berbentuk lingkaran seperti dapat dijumpai pada meja putar untuk alat spektroskopi yang ditunjukkan oleh Dalam Gambar 4b pengukuran posisi terkecil ( dapat dilihat bahwa pembacaan tanpa nonius memberikan hasil 150o_,

sedangkan dengan menggunakan nonius hasilnya adalah 150+₄3×

(

4−3

)

×10=

a) Akurasi, kedekatan alat ukur membaca pada nilai yang sebenarnya dari variabel yang diukur.

b) Presisi, hasil pengukuran yang dihasilkan dari proses pengukuran, atau derajat untuk membedakan satu pengukuran dengan lainnya.

c) Kepekaan, ratio dari sinyal output atau tanggapan alat ukur perubahan input atau variabel yang diukur.

d) Resolusi, perubahan terkecil dari nilai pengukuran yang mampu ditanggapi oleh alat ukur.

e) Kesalahan, angka penyimpangan dari nilai sebenarnya variabel yang diukur.

C. Ketidakpastian

Suatu pengukuran selalu disertai oleh ketidakpastian. Beberapa penyebab ketidakpastian tersebut antara lain adanya Nilai Skala Terkecil (NST), kesalahan kalibarasi, kesalahan titik nol, kesalahan pegas, adanya gesekan , kesalahan paralaks, fluktuasi parameter pengukuran dan lingkungan yang sangat mempengaruhi hasil pengukuran. hal ini disebabkan karena sistem yang diukur mengalami suatu gangguan. Dengan demikian sangat sulit untuk mendapatkan nilai sebenarnya suatu besaran melalui pengukuran. oleh sebab itu, setiap hasil pengukuran harus dilaporkan dengan ketidakpastiannya.

Ketidakpastian dibedakan menjadi dua, yaitu ketidakpastian mutlak dan relatif. Masing-masing ketidakpastian dapat digunakan dalam pengukuran tunggal dan berulang.

Ketidakpastian mutlak

Suatu nilai ketidakpastian yang disebabkan karena keterbatasan alat ukur itu sendiri. Pada pengukuran tunggal, ketidakpastian yang umumnya digunakan bernilai setengah dari NST. Untuk suatu besaran X maka ketidakpastian mutlaknya dalam pengukuran tunggal adalah:

NST x 2 1 = ∆ (1)

dengan hasil pengukurannya dituliskan sebagai

x x

X = ±∆ (2)

Melaporkan hasil pengukuran berulang dapat dilakukan dengan berbagai cara, diantaranya adalah menggunakan kesalahan ½- rentang atau bisa juga menggunakan standar Deviasi.

Modul 01 Dasar Pengukuran dan Ketidakpastian 5 Pada pengukuran berulang, ketidakpastian dituliskan tidak lagi seperti pada pengukuran tunggal. Kesalahan ½ - Rentang merupakan salah satu cara untuk menyatakan ketidakpastian pada pengukuran berulang. Cara untuk melakukannya adalah sebagai berikut :

a) Kumpulkan sejumlah hasil pengukuran variabel x, misalnya n buah, yaitu n

x x x₁, ₂,...,

b) Cari nilai rata-ratanya yaitu

x

n x x

x

x = 1 + 2 +...+ n (3)

c) Tentukan x_maxdan x_min dari kumpulan data x tersebut dan ketidakpastiannya dapat dituliskan

(

)

2 min max x x x= − ∆ (4)

d) Penulisan hasilnya sebagai

x x

x= ±∆ (5)

Untuk jelasnya sebuah contoh dari hasil pengukuran (dalam mm) suatu besaran x yang dilakukan empat kali yaitu : 153,2 ; 153,6 ;152,8; 153,0. Rata-ratanya adalah 2 , 153 4 0 , 153 8 , 152 6 , 153 2 , 153 = + + + = x mm

Nilai terbesar dalam hasil pengukuran tersebut adalah 153,6 mm dan nilai terkecilnya adalah 152,8 mm. Maka rentang pengukuran adalah

(

153,6−152,8

)

=0,8 mm

sehingga ketidakpastian pengukuran adalah

4 , 0 2 8 , 0 = = ∆x mm

maka hasil pengukuran yang dilaporkan adalah

(

153,2±0,4

)

=

x mm

Standar Deviasi

Bila dalam pengamatan dilakukan n kali pengukuran dari besaran x dan terkumpul data x1, x2, ... xn, maka nilai rata-rata dari besaran ini adalah

x n x x xn n j xj n = + + + = =

∑

1 1 1 2 1 ( L ) ₍₆₎

Kesalahan dari nilai rata-rata ini terhadap nilai sebenarnya besaran x (yang tidak mungkin kita ketahui nilai benarnya x0) dinyatakan oleh standar deviasi.

(

)

s x x n n x x n n x j j n j _j j n j n = − − = − − = = =

∑

( )

∑

∑

( ) ( ) 2 1 2 1 2 1 1 1 (7).

Standar deviasi diberikan oleh persamaan (7), sehingga kita hanya dapat menyatakan bahwa nilai benar dari besaran x terletak dalam selang (x- sx) sampai (

x + sx). Jadi penulisan hasil pengukurannya adalah x = x±sx

Ketidakpastian relatif

Ketidakpastian relatif adalah ketidakpastian yang dibandingkan dengan hasil pengukuran. terdapat hubungan hasil pengukuran terhadap KTP yaitu :

x x

KTP relatif = ∆ (8).

Apabila menggunakan KTP relatif maka hasil pengukuran dilaporkan sebagai ) % 100 relatif ( × ± = x KTP X _(9).

Ketidakpastian pada Fungsi Variabel (Perambatan Ketidakpastian)

Jika suatu variabel merupakan fungsi dari variabel lain yang disertai oleh ketidakpastian, maka variabel ini akan disertai pula oleh ketidakpastian. Hal ini disebut sebagai perambatan ketidakpastian. Untuk jelasnya ketidakpastian variabel yang merupakan hasil operasi variabel-variabel lain yang disertai oleh ketidakpastian akan disajikan dalam Tabel 1 berikut ini.

Misalkan dari suatu pengukuran diperoleh

(

a±∆a

)

dan

(

b±∆b

)

. Kepada kedua hasil pengukuran tersebut akan dilakukan operasi matematik dasar untuk memperoleh besaran baru.

Modul 01 Dasar Pengukuran dan Ketidakpastian 7

Tabel 1. Contoh perambatan ketidakpastian. Variabel

yang dilibatkan

Operasi Hasil Ketidakpastian

b b a a ∆ ± ∆ ± Penjumlahan p =a+b ∆p =∆a+∆b Pengurangan q=a−b ∆q =∆a+∆b Perkalian r =a×b b b a a r r ∆ + ∆ = ∆ Pembagian b a s= b b a a s s ∆ + ∆ = ∆ Pangkat n a t= a a n t t ∆ = ∆

Angka Berarti (

Significant Figures

)

Angka berarti (AB) menunjukkan jumlah digit angka yang akan dilaporkan pada hasil akhir pengukuran. AB berkaitan dengan KTP relatif (dalam %). Semakin kecil KTP relatif maka semakin tinggi mutu pengukuran atau semakin tinggi ketelitian hasil pengukuran yang dilakukan. Aturan praktis yang menghubungkan antara KTP relatif dan AB adalah sebagai berikut:

) log(

1 KTPrelatif

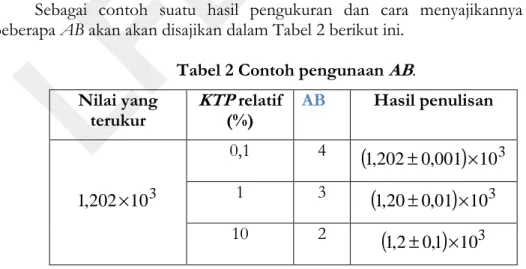
AB= − (10) Sebagai contoh suatu hasil pengukuran dan cara menyajikannya untuk beberapa AB akan akan disajikan dalam Tabel 2 berikut ini.

Tabel 2 Contoh pengunaan

AB.

Nilai yang terukur

KTP

relatif (%) AB Hasil penulisan 3 10 202 , 1 × 0,1 4

(

_1,202±0,001

)

_×103 1 3

(

_1,20±0,01

)

_×103 10 2

(

_1,2±0,1

)

_×103

PERCOBAAN

Di dalam laboratorium Anda akan diberikan alat-alat ukur dasar seperti penggaris, stopwatch, jangka sorong dan lain-lain seperti tertulis pada bagian alat-alat yang digunakan. Percobaan yang dilakukan yaitu menentukan massa jenis suatu bahan dengan keteraturan dimensi, seperti balok dan bola.

Prosedur percobaan

NST alat ukur

Menentukan NST alat ukur seperti : mikrometer sekrup, amperemeter, voltmeter, jangka sorong, penggaris plastik, busur derajad, termometer, stopwatch.

Catatan : Perhatikan nonius pada jangka sorong dan mikrometer sekrup. Ten-tukan NST alat ukur tersebut tanpa dan dengan nonius. Katupkan jangka sorong Anda rapat-rapat tetapi jangan dipaksa keras-keras dan catat kedudukan skala dalam keadaan ini. Bahas mengenai kedudukan titik nolnya.

Dimensi dan massa bahan

Balok kuningan/alumunium : pengukuran panjang, lebar dan tinggi sebanyak 5 kali untuk masing-masing parameter untuk tempat yang berbeda pada bahan tersebut menggunakan jangka sorong.

Bola besi : pengukuran diameter sebanyak 10 kali untuk tempat yang berbeda pada bahan tersebut menggunakan micrometer sekrup.

Massa balok dan bola dukur menggunakan neraca teknis dan NST alat ukur pun diambil sebagai data.

Data fisis keadaan laboratorium

Pengukuran suhu menggunakan thermometer raksa yang ada di bagian depan pintu masuk laboratorium dalam skala Celsius (o_{C) dengan penyajian}

menggunaakan KTP pengukuran tunggal (mutlak dan relatif). Pengukuran kelembaban menggunakan hydrometer (di depan pintu masuk dan di depan ruang modul 3) dengan penyajian menggunakan KTP pengukuran tunggal. Pengukuran tekanan menggunakan barometer (depan ruang modul 3), data meliputi nilai P dan NST alat ukur. Nilai factor koreksi untuk P karena pengaruh suhu yang terukur.

Modul 01 Dasar Pengukuran dan Ketidakpastian 9

LAPORAN

1. Tabulasi data dimensi untuk balok (p, l, t) dan bola (d), karena menggunakan pengukuran berulang digunakan standar deviasi (hasil hanya disajikan menggunakan KTP mutlak).

2. Tentukan volum untuk balok dan bola dan KTPnya menggunakan perambatan ketidakpastian (nilai volum dengan KTP mutlaknya). Nilai volum disajikan dengan KTP relatifnya (gunakan konsep angka berarti).

3. Tentukan massa bahan (pengukuran tunggal dengan KTP mutlak ; ½ NST ). 4. Tentukan rapat massa (ρ =m/v) bahan dan gunakan perambatan

ketidakpastiannya. Jangan lupa konversi nilai KTP massa ke bentuk KTP relatif. (dilakukan karena berbeda metode dalam pengukurannya).

Standar deviasi (volum) 66 % sedangkan mutlak (massa) 50%.

5. Tekanan terkoreksi, dibuat grafik factor koreksi terhadap P lalu tentukan persamaan garisnya. Tentukan nilai koreksi untuk tekanan ruang yang terukur. Nilai koreksi tersebut mengurangi nilai P yang terukur dalam penyajian datanya yang dilengkapi KTP mutlaknya.

Gunakan regresi dan standar deviasi menggunakan kalkulator.

6. Kenapa ada faktor koreksi dalam pembacaan nilai P, kenapa dipengaruhi oleh suhu, serta mengapa nilai P terbaca harus dikurangi dalam koreksinya.

7. Ketidakcocokan nilai rapat massa bahan yang diperoleh dari eksperimen terhadap referensi.

8. Bagaimana menentukan NST dari alat ukur digital ?

PUSTAKA

1. Darmawan Djonoputro, B., Teori Ketidakpastian, Penerbit ITB, 1984.

MODUL 02

OSILASI HARMONIK SEDERHANA: OSILASI PEGAS

TUJUAN

1. Menentukan tetapan pegas dan massa efektif pegas dengan melaksanakan percobaan ayunan pegas yang dibebani.

2. Menentukan percepatan gravitasi dengan mengukur perpanjangan pegas yang dibebani.

ALAT DAN BAHAN

1. Statif

2. Skala pelengkap statif 3. Pegas spiral

4. Tabung tempat menaruh beban 5. Beban tambahan

6. Stopwatch

TEORI DASAR

Dalam modul ini, kita akan mempelajari suatu jenis gerak yang sering kita temui sehari-hari yaitu getaran atau gerak osilasi atau gerak harmonik sederhana. Gerak harmonik sederhana adalah gerak bolak-balik suatu benda disekitar posisi seimbangnya, yang disebabkan oleh adanya gaya restorsi (gaya Hooke), umpamanya gerak yang terjadi pada pegas atau bandul.

Hukum Hooke dan Getaran

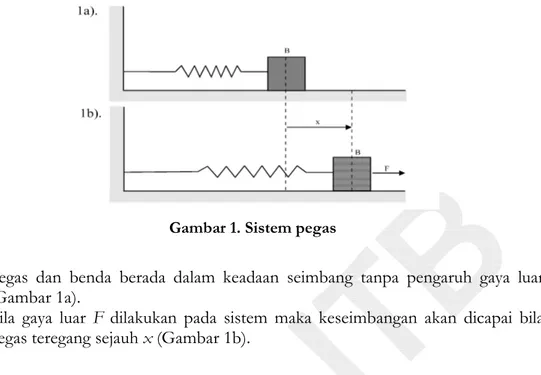
Setiap sistem yang memenuhi hukum Hooke akan bergetar dengan cara yang unik dan sederhana yang disebut gerak harmonik sederhana. Sebagai contoh, tinjau perilaku pegas seperti pada Gambar 1.

Bila kita tinjau benda B saja, yang berada dalam kesetimbangan tentulah ada gaya F' yang dilakukan oleh pegas pada benda B, gaya F' ini sama besar tapi berlawanan arah dengan gaya F. Untuk simpangan x kecil maka gaya luar berbanding lurus dengan x. Andaikan gaya luar F ditiadakan maka benda akan ditarik oleh gaya F’ sehingga benda akan bergerak ke kiri sejauh x pula. Jika tidak ada gaya lain (umpamanya gaya gesek) maka benda ini akan terus menerus bergerak ke kiri dan kekanan sejauh x dari keseimbangan semula. Ini yang disebut getaran atau gerak harmonis sederhana, dan F' adalah gaya Hooke.

Modul 02. Osilasi Harmonik Sederhana (Pegas) 11 Gambar 1. Sistem pegas

a. Pegas dan benda berada dalam keadaan seimbang tanpa pengaruh gaya luar (Gambar 1a).

b. Bila gaya luar F dilakukan pada sistem maka keseimbangan akan dicapai bila pegas teregang sejauh x (Gambar 1b).

Jika beban bermassa m kita gantungkan pada pegas dalam posisi vertikal, maka keseimbangan akan dicapai setelah pegas mengalami perpanjangan

x

o

.

Bila beban ditarik dari kedudukan setimbangnya lalu dilepaskan maka benda di ujung pegas ini akan bergetar (berosilasi). Anda sudah sering melihat getaran benda di ujung pegas sepeti itu. Perilaku benda secara umum terlihat pada gambar di bawah ini. Dalam Gambar 2 di bawah ini diperlihatkan massa di ujung pegas meninggalkan jejak kertas yang memperlihatkan bagaimana massa itu berosilasi ke atas dan ke bawah.

Gambar 2. Gerak periodik atau getaran

Gerak getar sistem yang memenuhi hukum Hooke seperti sistem pegas dan benda di atas disebut gerak harmonik sederhana. Akan kita lihat nanti bahwa kurva yang dibentuk oleh massa di atas selama bergetar berbentuk sinusoidal.

Gerak Harmonik Sederhana

Kita terapkan hukum II Newton pada benda yang mengalami ghs (gerak harmonik sederhana) ini, dengan F adalah gaya Hooke, yakni

F = ma (1) 2 2 dt x d m kx = − (2)

Persamaan ini menyatakan hubungan x dan t tetapi mengandung suku dalam bentuk difrensial dan disebut persamaan diferensial. Jika kita ingin mencari solusinya, artinya kita ingin mencari suatu fungsi yang menyatakan kedudukan benda (x) dan memenuhi persamaan diferensial di atas. Jelas bahwa x adalah fungsi waktu yang bila diturunkan (dideferensialisasikan) dua kali terhadap t menghasilkan -k/m kali fungsi yang sama (sebelum diturunkan). Disamping itu fungsi tersebut bila dibuat grafiknya terhadap waktu mestilah berbentuk seperti pada Gambar 2. Dari bentuk grafik tersebut dan sifat diferensial fungsi sinus atau cosinus, solusinya dapat dituliskan sebagai :

( )

t A

(

t

)

a

( )

t b

( )

t

x = cos ω −ϕ = cos ω + sin ω (2)

dengan a= Acosϕ dan b= Asinϕ.

Konstanta a dan b memungkinkan solusi ini diungkapkan dalam bentuk kombinasi sinus dan cosinus, dengan tetapan A,

ω

, dan

ϕ

yang belum diketahui. Jika kita solusi umum tersebut ke dalam persamaan diferensial di atas, kita peroleh

ω = k

m (3)

dan

( )

t = A

(

ωt+ϕ

)

x cos (4)

yang merupakan solusi dari persamaan gerak harmonis sederhana tersebut di atas dengan tetapan A dan

ϕ

masih belum tertentu. Ini berarti ada berbagai kemungkinan macam gerak harmonik sederhana ini yang bergantung pada nilai A dan

ϕ

.

PERCOBAAN

A. Penentuan tetapan pegas a. Prinsip percobaan

Telah kita lihat di atas

ω

dan perioda getaran pegas bergantung pada massa beban dan tetapan pegas sebagai berikut:

Modul 02. Osilasi Harmonik Sederhana (Pegas) 13 T m k π ω = = 2 (5) k m T =2π atau m k T 2 2 ₌4π . (6)

Jadi bila kita gantungkan beban yang telah diukur massanya (ditimbang) pada pegas lalu kita getarkan dan diukur pula periodanya, kita dapat me-nentukan tetapan pegas k. Ketelitian yang lebih tinggi dapat diperoleh bila percobaan seperti itu dilakukan berulang-ulang untuk beban yang berbeda-beda.

b. Prosedur percobaan

Pegas yang dibebani digantungkan pada statif, simpangkan sedikit ke bawah lalu lepaskan agar terjadi gerak harmonik sederhana dan tentukan periodanya. Untuk mendapatkan hasil yang teliti percobaan ini dilakukan untuk beberapa beban. Setiap beban yang digunakan ditimbang begitu juga pegasnya.

Langkah percobaannya adalah sebagai berikut :

1. Gantungkanlah pegas pada statif lalu gantungkan tabung kosong di bawahnya. Tariklah tabung itu sedikit ke bawah dan kemudian lepaskan. a. Catatlah waktu yang diperlukan untuk 10, 20 dan 30 getaran. (petunjuk: besar amplitudo simpangan sebaiknya hampir sama selama getaran)

b. Amati berapa jumlah getaran yang dapat memberikan hasil yang paling teliti ?

c. Ulangi pengukuran itu dengan menambahkan 2 keping beban setiap kali, hingga terakhir 5 keping beban digunakan.

2. Timbanglah masing-masing beban dan juga pegas, olahlah data Anda itu dengan merujuk pers. (6) !

B. Penentuan percepatan gravitasi a. Prinsip percobaan

Dengan membebani pegas (yang telah diketahui tetapan pegasnya) dengan beban (yang telah ditimbang massanya) dan mengukur perpanjang-an pegas yperpanjang-ang dihasilkperpanjang-annya kita dapat menentukperpanjang-an besar percepatperpanjang-an gravitasi. Untuk mendapatkan hasil yang lebih tinggi ketelitiannya, pem-bebanan ini dilakukan beberapa kali, mula-mula dengan cara menambahkan beban satu per satu dan kemudian dengan cara mengurangi beban satu per satu. Dengan demikian untuk setiap beban kita mengukur perpanjangan pegas dua kali. Untuk itu kita ambil nilai rata-ratanya dan nilai rata-rata seluruh percobaan ditentukan dengan grafik.

Mula-mula dibaca dan dicatat posisi tabung kosong pada skala. Ska-la diatur sedemikian rupa hingga jarum penunjuk pada bagian atas skaSka-la itu tepat dengan jarum penunjuk. Beban dimasukkan ke dalam tabung dan tunggu kira-kira 10 detik, baru dibaca posisinya. Penambahan beban ini di-lakukan hingga 10 kali dan setiap kali menambahkan beban dicatat posisi jarum penunjuk, kurangi beban tersebut satu per satu dan baca pula posisi jarum penunjuk untuk setiap pengurangan beban. Dari data yang diperoleh dapat dibuat grafik antara simpangan terhadap beban, lalu tentukan percepatan gravitasi.

Aturlah skala sedemikian rupa hingga jarum menunjuk pada bagian skala itu. Catatlah berturut-turut penunjukan jarum ketika tabung kosong, kemudian ditambah beban satu per satu hingga beban ke-5 lalu dikurangi satu persatu hingga tabung kosong kembali.

LAPORAN

A. Penentuan tetapan pegas

1. Buatlah grafik antara

T

2terhadap massa total beban yang digunakan 2. Tentukanlah nilai rata-rata tetapan pegas dari grafik di atas !

3. Dalam perumusan di atas tidak disinggung tentang massa pegas, seperti penurunan persamaan dalam buku referensi umumnya yang mengabaikan massa pegas. Dalam gerak pegas ini, sistem sebenarnya merasakan bahwa pegas tersebut bermassa, meski tidak sebesar massa sesungguhnya. Massa pegas efektif dapat ditentukan dari grafik antara

T

2terhadap massa total beban yang digunakan. Tentukanlah massa efektif pegas itu !

4. Selayaknya massa efektif pegas lebih besar atau lebih kecil dari massa sebenarnya ? Bagaimanakah hasil dari percobaan Anda ?

5. Berikanlah analisa Anda mengenai percobaan ini.

B. Penentuan percepatan gravitasi

1. Buatlah grafik antara simpangan dengan massa beban. 2. Tentukan percepatan gravitasi dari grafik di atas.

3. Percepatan gravitasi di Bandung menurut pengukuran yang teliti adalah 9,78 m/s2_{, bandingkanlah hasil Anda dengan data tersebut !}

4. Berikanlah analisa Anda jika terjadi perbedaan !

PUSTAKA

1. Halliday, D., Resnick, R., Walker, J., Fundamentals of Physics, John Wiley & Sons, 1997.

Modul 03. Osilasi Harmonik Sederhana: Bandul Matematis 15

MODUL 03

BANDUL MATEMATIS

TUJUAN

1. Menentukan percepatan gravitasi dengan metode ayunan bandul sederhana. 2. Memahami pengaruh panjang tali, massa beban dan besar sudut simpangan

pada hasil pengukuran.

ALAT DAN BAHAN

1. Komputer PC dan program aplikasi

Logger Pro

(1 set) 2. LabPro Interface / antar muka (1 buah)

3. Sistem bandul (1 set) 4. Photogate (1 buah)

5. Neraca Ohauss (digunakan bersama)

TEORI DASAR

Sebuah bandul yang diikat dengan tali ringan(massanya dapat diabaikan) dengan panjangnya l mempunyai persamaan gerak osilasi:

2

2 sin 0

d g

dt l

θ _{+ θ = (1)}

Jika sudut θ sangat kecil, maka geraknya adalah gerak harmonik sederhana dengan perioda:

g l

T₀ =2π (2)

Jika panjang tali dan periodanya diketahui, maka dapat ditentukan percepatan gravitasinya, yaitu: 2 0 2 4 T l g= π (3)

Jika sudut simpangan cukup besar, gerak bandul tidak lagi harmonik sederhana dan periodanya merupakan suatu deret yang tergantung pada sudut simpangan. Penguraian sampai orde ke 3 diperoleh perioda osilasi T:

)

sin

sin

1

(

4 ₂1 _max 64 9 max 2 1 2 4 1 0

+

θ

+

θ

=

T

T

(4)

dimana

θ

max adalah amplitudo sudut simpangan maksimum dari arah vertikal dan T0

adalah perioda ayunan sederhana, seperti ditunjukkan pada persamaan (2).

Tabel 1 Nilai 0

T T

untuk θθθθmax tertentu

θmax (derajat) 0 T T θ_max (derajat) 0 T T 0 1 50 1,049138 10 1,001907 60 1,071289 20 1,007666 70 1,097468 30 1,017378 80 1,127301 40 1,031169 90 1,160156 PERCOBAAN

a. Setup awal percobaaan

1. Hubungkan sensor photogate ke antarmuka LabPro pada Channel 1. Atur posisi sensor dengan baik (tanyakan asisten).

2. Pasang bandul pada tali dan gantungkan pada tempat yang telah disediakan. 3. Hidupkan komputer dan buka file eksperimen“osilasi bandul sudut kecil”

jika amplitudo sudut simpangannya adalah kecil.

4. Ada 2 buah tampilan window. Window1 melukiskan grafik percepatan gravitasi g terhadap waktu. Window2 merupakan tabel data pengukuran. 5. Coba ayunkan bandul sehingga talinya menutupi bagian sensor photogate.

Perhatikan, lampu photogate akan berkedip saat tali melewati sensornya. Jika sudah demikian, berarti pengukuran sudah bisa dimulai.

b.

Prosedur percobaan

1. Timbanglah bandul yang disediakan dan catat nilainya.

2. Timbanglah tali dengan panjang tertentu dan catatlah rapat massa talinya. 3. Pasang bandul pada tali dengan panjang tertentu (lihat tabel).

4. Buka file eksperimen“osilasi bandul sudut kecil” jika sudut ayunan yang akan dilakukan adalah kurang dari 10 derajat. Buka file “osilasi bandul sudut 10” jika amplitudo sudut simpangannya adalah 10 derajat, dst.

5. Atur posisi sensor photogate sesuai dengan sudut ayunan yang akan dipilih. Buat ayunan dengan sudut tertentu (perhatikan langkah 2). Perhatikan ayunannya.

6. Dengan mouse, klik

Collect

untuk mulai mengambil data. Amati nilai gravitasi g pada grafik atau tabel.

7. Jika nilai gravitasi g sudah konstan, segera klik

Stop

. Catat nilai gravitasinya. 8. Ulangi langkah (4) s/d (7) di atas untuk sudut yang makin besar.

Modul 03. Osilasi Harmonik Sederhana: Bandul Matematis 17 Tabel 2 Percobaan Ayunan Bandul Sederhana

m1 = (gr) m2= (gr)

No. l (cm) θmax(o) g No. l(cm) θmax(o) g

1 120,0 5,0 1 120,0 5,0 2 10,0 2 10,0 . . . . . . . . 6 30,0 8 30,0 1 100,0 5,0 1 100,0 5,0 2 10,0 2 10,0 . . . . . . . . 6 30,0 8 30,0 1 70,0 5,0 1 70,0 5,0 2 10,0 2 10,0 . . . . . . . . 6 30,0 8 30,0

LAPORAN

Ambillah data dan buatlah analisis untuk percobaan ini !

PUSTAKA

Halliday, D., Resnick, R., Walker, J., Fundamentals of Physics, John Wiley & Sons, 1997.

MODUL 04

OSILASI HARMONIK SEDERHANA: BANDUL FISIS

TUJUAN

1. Mengamati ayunan bandul fisis,

2. Menentukan momen inersia sistem bandul dan hubungannya dengan perioda osilasi,

3. Menentukan percepatan gravitasi bumi.

ALAT DAN BAHAN

• Bandul fisis yang terdiri dari:

dua keping logam S berbentuk silinder yang dapat dieratkan pada batang logam yang berlubang-lubang (lihat Gambar 2).

• Meteran

• Stopwatch

• Neraca Olland dan batu timbangan

TEORI DASAR

Dalam modul ini kita akan meninjau kasus yang lebih umum, dengan sistem ataupun benda yang terdiri dari banyak partikel (titik partikel) maupun benda yang terdiri dari partikel-partikel yang dianggap tersebar secara kontinyu pada benda yang disebut dengan sistem partikel. Dalam suatu sitem partikel dikenal titik pusat massa, yang didefinisikan sebagai berikut

= ∑ (1)

dengan adalah posisi partikel ke-i di dalam sistem dan M adalah massa total sistem.

Dalam modul ini akan dipelajari gerak suatu bandul yang bentuknya sembarang yang lazim disebut sebagai bandul fisis. Bandul fisis adalah bandul yang berosilasi secara bebas pada suatu sumbu tertentu dari suatu benda rigid (kaku) sembarang. Berbeda dengan bandul matematis, bentuk, ukuran dan massa benda pada bandul fisis tidak bisa diabaikan dengan menganggapnya sebagai sebuah benda titik.

Jika sebuah benda digantungkan pada suatu poros O, kemudian diberi simpangan θ dan dilepaskan, maka benda itu akan berosilasi karena adanya torka

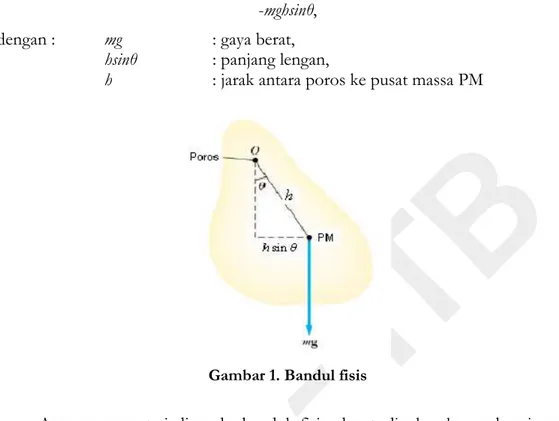
Modul 04. Bandul Fisis 19 pemulih/momen gaya pemulih (suatu momen gaya yang selalu mengembalikan bandul pada kedudukan kesetimbangannya) sebesar

-mghsinθ, dengan : mg : gaya berat,

hsinθ : panjang lengan,

h : jarak antara poros ke pusat massa PM

Gambar 1. Bandul fisis

Ayunan yang terjadi pada bandul fisis dapat digolongkan sebagai gerak harmonik sudut (angular harmonic motion), jika momen gaya pulih sebanding dengan simpangan sudutnya. Maka dapat dianalogikan dengan gerak harmonis sederhana.

Jika redaman diabaikan, maka persamaan gerak dari sistem bandul fisis ini adalah:

= −ℎ (2)

dengan I : momen inersia benda rigid dihitung terhadap titik poros. Jika simpangan kecil, maka sin θ≈ θ, sehingga persamaan gerak berubah menjadi:

+ = 0 (3)

Solusi dari persamaan ini adalah: = sin "#, dengan " = $

atau perioda

osilasi adalah sebesar :

Bandingkan kemiripan dengan persamaan serupa untuk osilasi harmonik pegas yang memiliki bentuk

₎

+ *+ = 0 (5)

dan solusinya yang berbentuk

+ = +sin "# (6)

dengan perioda

% = 2'$₍ (7)

Gambar 2 menunjukkan bandul fisis dengan pusat massanya di C dan poros horizontalnya melalui P. Sebagai acuan untuk simpangan sudut θ kita ambil sumbu z yang vertikal melalui P sehingga dalam kesetimbangan.

Gambar 2. Bandul fisis pada percobaan

Momen inersia terhadap sumbu ayunan dapat ditentukan dengan meng-gunakan dalil sumbu sejajar. Jika momen inersia terhadap sumbu melalui pusat massa (C) adalah I_odan l_{adalah jarak C terhadap P, maka momen inersia terhadap} sumbu yang melalui P adalah:

= + ,- (5)

maka perioda ayunan bandul fisis di atas menjadi :

% = 2'$./0

(6)

Jika T1 adalah perioda ayunan dengan jarak antara C terhadap P adalah l1 dan T2 adalah perioda ayunan dengan jarak antara C terhadap P adalah l2, maka

Modul 04. Bandul Fisis 21 percepatan gravitasi dapat kita tentukan dengan mengeliminasi I_o dari T1 dan T2

hasilnya adalah sebagai berikut:

= 4'- 203045

260364045 (7) Dengan mengunakan persamaan (1) dapat diperoleh koordinat pusat massa bandul fisis dengan bentuk seperti pada Gambar 2 adalah :

∑

∑

= i i i m m x x_pm (8)

dengan x_iadalah posisi pusat massa benda ke-i yang massanya m_i.

PERCOBAAN

1. Ukur massa batang dan keping silinder logam pada bandul fisis secara terpisah,

2. Ukur panjang batang logam (L),

3. Tangkupkan keping-keping logam pada batang logam, ukurlah jarak pusat keping terhadap ujung batang logam O (OA), lihat Gambar2,

4. Tentukan jarak OP (jarak ujung batang O terhadap titik poros putar/titik gantung bandul fisis),

5. Ayunkan bandul fisis dengan simpangan sudut kecil, catatlah waktu yang diperlukan untuk 50 ayunan pertama t,

6. Ayunkan bandul fisis dengan simpangan sudut kecil sekali lagi, catatlah waktu yang diperlukan untuk 50 ayunan ke dua t',

7. Catatlah jumlah ayunan n untuk waktu t ditambah t’. 8. Tentukan pusat massa sistem melalui persamaan (8), 9. Dapatkan nilai l yaitu jarak pusat massa – OP,

10. Ulangi percobaan pengukuran waktu untuk menentukan perioda dan jumlah ayunan untuk jarak OP yang berbeda.

LAPORAN

1. Hitunglah posisi pusat massa (x_pm) bandul fisis terhadap ujung batang O. 2. Hitunglah jarak l_{1, yaitu jarak antara titik P1 yang dipilih sebagai titik gantung}

dengan titik pusat massa bandul fisis tersebut.

3. Hitung perioda sementara (Tsementara) dari percobaan 5 dan 6 dengan cara

100 ' sementara t t T = +

4. Hitunglah perioda T₁, yaitu perioda yang lebih teliti dengan cara ' " 1 n t T =

5. Hitunglah perioda sementara (Tsementara) dan T2 untuk jarak OP yang berbeda. 6. Hitunglah harga percepatan gravitasi g menggunakan pers. (7).

7. Bandingkan nilai yang didapat dengan percepatan gravitasi universal g = 9.8 m/s2_{, dan jelaskan mengapa terdapat perbedaan nilai !}

8. Mengapa harus menentukan pusat massa sistem tersebut dulu dalam eksperimen ini ?

9. Mengapa dalam percobaan ini digunakan simpangan bersudut kecil ? 10. Bagaimana pengaruh peletakan titik poros putar dalam percobaan ini ?

PUSTAKA

Modul 05. Momen Inersia 23

MODUL 05

MOMEN INERSIA

TUJUAN

1. Memahami peran momen inersia pada gerak rotasi benda tegar

2. Menentukan momen inersia dari benda tegar secara teori dan eksperimen.

ALAT DAN BAHAN

• Statif dilengkapi kawat untuk ayunan torsi,

• Keping logam berbentuk piringan silinder dan segiempat

• Jangka sorong dan mikrometer sekrup

• Stopwatch

• Nerca teknis

TEORI DASAR

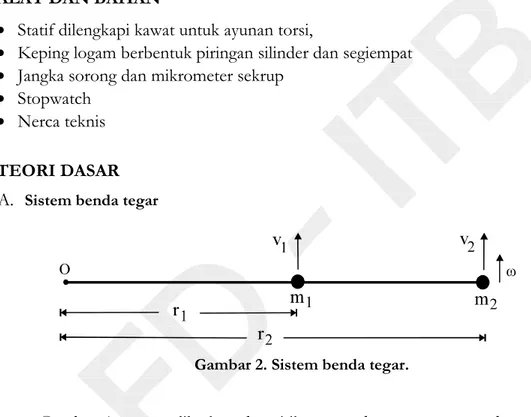
A. Sistem benda tegar

Gambar 2. Sistem benda tegar.

Gambar 1 memperlihatkan dua titik massa dengan massa m1 dan m2 yang

dihubungkan oleh batang ringan (tak bermassa), sehingga m1 dan m2membentuk

suatu benda tegar.

Ujung kiri batang di O diberi sumbu yang tegak lurus pada bidang gambar sehingga batang dapat berotasi pada sumbu tersebut. Jika jarak m1 dan m2 ke sumbu

di O masing-masing adalah r1 dan r2 dan batang mengalami gerak rotasi dengan

kecepatan sudut ω, maka kecepatan tangensial adalah m1

78 = "8 (1)

7- = "- (2)

dan v2kecepatan tangensial m2. Energi kinetik dari kedua titik massa adalah

dengan = :₈₈-+ _---; disebut momen inersia dari m1 dan m2 terhadap

sumbu rotasi di O.

Energi kinetik dari m1 dan m2 yang disebabkan oleh gerak rotasinya disebut

energi kinetik rotasi dan dinyatakan dengan :

8

-"- (4)

B. Penentuan momen inersia secara teori

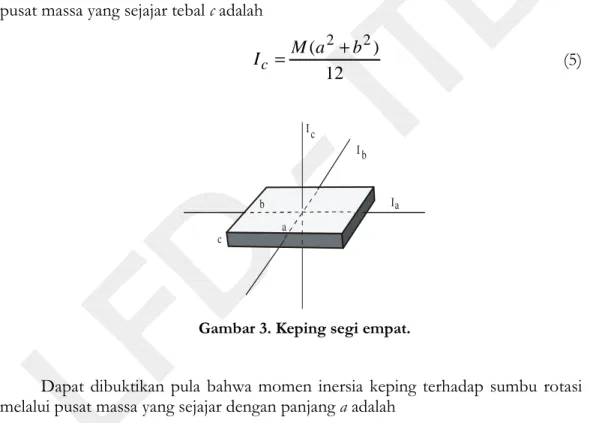
Untuk menentukan momen inersia dari keping logam berbentuk segi empat secara teori, dapat dilakukan dengan cara mengukur panjang, lebar dan tebal dari keping dan juga menimbang massanya. Jika panjang keping a, lebar b, tebal c, dan massanya M (Gambar 2), momen inersia keping terhadap sumbu rotasi melalui pusat massa yang sejajar tebal c adalah

12 ) (a2 b2 M I_c = + (5) I I I c c b b a a

Gambar 3. Keping segi empat.

Dapat dibuktikan pula bahwa momen inersia keping terhadap sumbu rotasi melalui pusat massa yang sejajar dengan panjang a adalah

12 ) (b2 c2 M

I_a = + (6) Terhadap sumbu rotasi melalui pusat massa dan sejajar lebar b, momen inersianya adalah 12 ) (a2 c2 M Ib = + (7) Momen inersia keping lingkaran terhadap sumbu rotasi yang berimpit dengan sumbu silinder (Gambar 3) adalah

Modul 05. Momen Inersia 25 2 2 1 MR I_s = (8)

Gambar 4. Keping lingkaran.

M massa silinder dan R jari-jari silinder. Jadi secara statis momen inersia si-linder dapat ditentukan, jika massa dan jari-jari sisi-linder diketahui.

Momen inersia batang berbentuk silinder terhadap sumbu rotasi melalui pusat massa yang sejajar dengan diameter silinder (Gambar 3), adalah

        + = 4 12 2 2 R L M I_d (9)

M massa silinder, R jari-jari silinder dan L panjang silinder. Jadi secara statis momen inersianya dapat ditentukan jika M, R dan L diketahui.

C. Penentuan momen inersia secara eksperimen

Momen inersia benda juga dapat ditentukan secara dinamis, yaitu dengan menggantungkan benda pada kawat, dan ujung kawat yang lain dieratkan pada statif (Gambar 4).

Jika benda diberi sedikit simpangan dari posisi setimbangnya dengan cara memutar benda (dengan sudut kecil), maka kawat akan terpuntir. Jika benda dilepaskan maka benda akan mengalami gerak harmonik anguler (sudut), disebabkan oleh momen gaya puntir dari kawat. Perioda T dari gerak harmonik anguler benda ini adalah

K I

Gambar 5. Pengukuran momen inersia dalam eksperimen.

K : tetapan momen gaya puntiran dari kawat K

B I

I

I = +

B

I : momen inersia dari benda

K

I : momen inersia dari kawat

Jika dua buah benda dengan momen inersia masing-masing I₁ dan I₂ secara berturut-turut digantungkan pada kawat yang sama, maka perioda gerak harmonik angulernya masing-masing dinyatakan dengan

K I I T₁=2π 1+ k (11) K I I T₂ =2π 2+ k (12) Dari kedua persamaan ini jika I₁, T₁, I₂dan T₂diketahui, maka

I

_kdan K dapat ditentukan. Sebaliknya jika

I

_k dan K telah diketahui, cara ini dapat dipakai untuk menentukan momen inersia benda yang lain secara dinamis dengan mengukur perioda dari gerak harmonik angulernya.

Modul 05. Momen Inersia 27

PERCOBAAN

A. Persiapan percobaan

1. Ukurlah panjang dan lebar keping segi empat masing-masing 5 kali pada tempat yang berbeda dengan menggunakan jangka sorong.

2. Ukurlah tebal keping segi empat 5 kali pada tempat yang berbeda dengan menggunakan mikrometer sekrup.

3. Ukurlah diameter silinder 5 kali pada tempat yang berbeda dengan jangka sorong dan juga ukurlah tebalnya 5 kali pada tempat yang berbeda dengan mikrometer sekrup.

4. Timbanglah masing-masing keping dengan neraca teknis untuk menentukan massa masing-masing keping.

B. Tahapan percobaan

1. Gantungkan keping segi empat pada kawat sehingga garis lurus per-panjangan kawat melalui pusat massa keping dan sejajar panjang kepingnya (Gambar 4b)

2. Berilah simpangan sudut pada keping dan kemudian lepaskan. Catatlah waktu yang diperlukan untuk melakukan 10 getaran penuh (10T).

3. Gantungkan keping segi empat kepada kawat sehingga garis lurus perpanjangan kawat melalui pusat massa keping dan sejajar dengan lebar b. Kemudian lakukanlah seperti pada tugas 2.

4. Lakukan seperti pada tugas 1 dan tugas 2 dengan kawat sejajar tebal c dari keping (Gambar 4a).

5. Gantungkan keping silinder sehingga sumbu silinder berimpit dengan kawat, dan lakukanlah kemudian seperti pada tugas 2 (Gambar 4d).

6. Gantungkan keping silinder sehingga diameternya berimpit dengan kawat, dan kemudian lakukanlah seperti pada tugas 2 (Gambar 4c).

LAPORAN

1. Hitung momen inersia secara teoritis menggunakan persamaan yang ada untuk masing-masing benda dan posisi.

2. Hitung periode getaran masing-masing percobaan

3. Tentukan nilai Ik dan K dengan cara substitusi/eliminasi dari 2 persamaan

4. Pergunakan persamaan T untuk mendapatkan momen inersia segiempat untuk semua posisi dengan menggunakan nilai Ik dan K yang telah diperoleh

sebelumnya.

5. Bandingkan nilai momen inersia I untuk segiempat hasil eksperimen terhadap nilai teori.

6. Selidiki keberlakuan teorema sumbu tegak untuk keping segiempat !

7. Jelaskan faktor yang menyebabkan perbedaan antara nilai eksperimen dan teori dan manakah yang lebih presisi atau valid antara perhitungan secara teori atau eksperimen. Jelaskan !

8. Jelaskan pengaruh momen inersia terhadap rotasi benda tegar !

PUSTAKA

Modul 07. Modulus Puntir 29

MODUL 06

MODULUS YOUNG

TUJUAN

1. Memahami sifat elastis bahan di bawah pengaruh tarikan 2. Menentukan modulus Young suatu bahan.

ALAT DAN BAHAN

1. Dua utas kawat,

2. Perangkat baca skala utama dan nonius,

3. Seperangkat beban (dasar beban dan 5 beban masing-masing 0.5 kg), 4. Mistar panjang/tiang,

5. Meteran,

6. Mikrometer sekrup.

TEORI DASAR

Sifat elsatisitas suatu bahan biasa dinyatakan dalam hubungan antara besaran-besaran tegangan dan regangan. Sebatang logam berada dalam kesetimbangan bila ditarik oleh gaya-gaya F1 dan F2 yang sama besar (F1=F2=F) seperti pada Gambar

1.

Gambar 6. Batang logam dalam pengaruh gaya tarik F1 dan F2.

Bayangkan batang dipotong sejajar salah satu sisinya. Bagian ini mula-mula dalam keadaan setimbang. Jika pada bagian ini bekerja gaya F yang tersebar merata (uniform) di seluruh permukaan penampang yang dinyatakan oleh anak-anak panah (Gambar 2) maka benda akan mulur/bertambah panjang sebesar ∆L.

Gambar 7. Elemen batang logam dalam pengaruh gaya F.

Bila luas penampang adalah A, maka tegangan tarik adalah F/A, panjang batang mula-mula adalah L_o dan akibat gaya tarik F panjang batang menjadi L maka regangan tarik adalah :

<3< <=

Batang disebut elastis bila gaya F batang kembali ke panjang asal (L_o). Pada

dan regangan tarik bentuknya linier dan dalam daerah ini berlaku hukum Hooke. Perbandingan tegangan terhadap re

atau modulus elastisitas.

regangan tegangan E =

Bahan mempunyai batas elastisitas

ditambah hingga ke suatu harga tertentu atau melebihinya, kemudian gaya berhenti bekerja maka panjang bahan tidak kembali ke panjang asal.

Gambar 3. Kurva elastisitas suatu bahan.

PERCOBAAN

Untuk mencatat pertambahan panjang suatu kawat yang ditarik dengan suatu beban, diperlukan kawat lain yang sejenis dan sama panjangnya. Panjang asal dari kedua kawat itu dapat dilihat pada kedudukan skala non

kemudian salah satu kawat diberi beban, sehingga kedudukan nonius akan berubah terhadap skala utama. Perubahan kedudukan ini menun

panjang yang terjadi. Dengan mengubah

pertambahan panjang yang ditimbulkannya dan didapatkan gra massa beban tarikan dan pertambahan panjang kawat.

<=

₌

∆<

<= (1)

F berhenti bekerja pada batang maka panjang . Pada bahan elastis hubungan antara tegangan dan regangan tarik bentuknya linier dan dalam daerah ini berlaku hukum Hooke.

Perbandingan tegangan terhadap regangan tarik disebut modulus Young (E)

o L L A F tarik regangan tarik tegangan / / ∆ = (2)

Bahan mempunyai batas elastisitas tertentu,yang berarti bila tegangan tarik ditambah hingga ke suatu harga tertentu atau melebihinya, kemudian gaya berhenti bekerja maka panjang bahan tidak kembali ke panjang asal.

. Kurva elastisitas suatu bahan.

Untuk mencatat pertambahan panjang suatu kawat yang ditarik dengan suatu beban, diperlukan kawat lain yang sejenis dan sama panjangnya. Panjang asal dari pat dilihat pada kedudukan skala nonius dan skala utama, kemudian salah satu kawat diberi beban, sehingga kedudukan nonius akan berubah rubahan kedudukan ini menunjukkan pertambahan di. Dengan mengubah-ubah massa beban, dapat dicatat panjang yang ditimbulkannya dan didapatkan grafik hubungan antara massa beban tarikan dan pertambahan panjang kawat.

Modul 07. Modulus Puntir 31 Dalam mengubah-ubah massa beban harus diperhatikan beban tak melebihi batas elastisitas. Bila beban melebihi batas elastisitas, kawat tidak kembali ke asal dan hubungan antara tegangan dan regangan tarik tidak lagi linier.

Prosedur percobaan

1. Gantungkanlah kedua kawat dan lengkapi dengan perangkat baca. Agar kawat lurus, bebani kedua kawat dengan beban yang tak terlalu berat.

a. Ukur panjang salah satu kawat yang akan ditentukan modulus Young nya dengan tiang lalu ukur menggunakan meteran.

b. Ukur diameter kawat menggunakan mikrometer sekrup.

c. Gantungkan kedua dasar beban pada kedua utas kawat. Catat kedudukan skala nonius saat gelembung pada waterpas berada di tengah fluidanya. 2. Tambahkan beban setiap kali 0.5 kg pada salah satu utas kawat. Pada setiap

penambahan beban setelah kira-kira 10 detik,

a. Catatlah kedudukan nonius, nilai skala yang terbaca merupakan pertambahan panjang oleh penambahan beban yang diberikan pada kawat. Lakukan penambahan sampai 5 kali (berarti sampai penambahan beban 2.5 kg),

b. Hitung pertambahan panjang. Ingat bahwa nilai skala yang dibaca merupakan nilai akibat pertambahan beban setiap 0.5 kg.

3. Ambil beban setiap kali 0.5 kg sehingga beban habis. Setiap kali beban diambil, setelah kira-kira 10 detik lakukan sesuai prosedur penambahan beban.

a. Catatlah kedudukan nonius, b. Hitung pengurangan panjang.

LAPORAN

1. Hitung tegangan dan regangan tarik pada setiap langkah penambahan dan pengurangan beban.

2. Buatlah grafik hubungan antara tegangan dan regangan tarik. Tentukan persamaan garis dari grafik tersebut lalu tentukan modulus Young bahan yang diuji menggunakan hasil grafik.

3. Jelaskan daerah-daerah dalam elastisitas suatu bahan melalui grafik yang diperoleh yang mengacu pada Hukum Hooke !

4. Bandingkan nilai modulus Young yang diperoleh dari percobaan dengan literatur ! Jelaskan faktor apa saja yang mempengaruhi hal tersebut ?

5. Selain menggunakan metode ini, metode seperti apa yang dapat digunakan untuk menentukan nilai modulus Young dan jelaskan jawaban Anda ?

PUSTAKA

Halliday, D., Resnick, R., Walker, J., Fundamentals of Physics, John Wiley & Sons, 1997.

MODUL 07

MODULUS PUNTIR

TUJUAN

1. Memahami sifat elastis bahan di bawah pengaruh puntiran. 2. Menentukan modulus puntir suatu bahan

ALAT DAN BAHAN

1. Kit modulus puntir,

2. Batang silinder logam besi dan kuningan, 3. Meteran,

4. Satu set beban (5 buah beban masing-masing ±0.5 kg dan dasar beban), 5. Mikrometer sekrup,

6. Jarum penunjuk 2 buah.

TEORI DASAR

Batang yang ditarik oleh suatu gaya dikatakan berada di bawah tegangan merenggang (tensile stress). Bentuk tegangan lainnya adalah tegangan menekan (compressive stress), yang merupakan lawan dari tensile stress, dan tegangan memuntir (shear stress) yang terdiri dari dua gaya yang sama tetapi arahnya berlawanan dan tidak segaris (lihat Gambar 1).

Gambar 1. Tipe-tipe tegangan (a) merenggang (b) menekan (c) memuntir

Untuk tegangan memuntir kita dapat tulis persamaannya sebagai berikut :

0

FL L

GA

Modul 07. Modulus Puntir

dimana ∆L adalah pertambahan panjang, L

adalah luas dari permukaan dimana gaya F itu bekerja. Dalam regangan geser dan memuntir, gaya F bekerja sejajar dengan permukaan A, sedangkan

terhadap L0. Tetapan G adalah modulus puntir (

sebagai konstanta proposionalitas (1/G).

Gambar 2. Suatu batang silinder dengan ujung tetap A dipuntir di C

Gambar 2 mengilustrasikan kasus batang silinder yang diberi puntiran. batang silinder yang salah satu ujungnya dijepit tetap pada posisi gambar, sedangkan ujung lainnya di

geser/modulus puntir batang tersebut

G

dengan R adalah jari-jari batang silinder dan A) ke tempat sudut puntir α (titik C yang digantungkan pada ujung bebas. Jika jari

yang digantungkan adalah sebesar m maka torsi yang dihasilkan adalah sebesar

T

PERCOBAAN

Sebatang logam silindris diteguhkan di salah satu ujungnya (di titik dipuntir di ujung lainnya (di titik B) oleh sebuah gaya torsi. Be

α

ditunjukkan oleh suatu alat penunjuk yang dilekatkan pada batang pada posisi tertentu. Dari besarnya

α

, modulus puntir G batang logam dapat ditentukan.

33

dimana ∆L adalah pertambahan panjang, L0 adalah panjang mula-mula dan A

adalah luas dari permukaan dimana gaya F itu bekerja. Dalam regangan geser dan memuntir, gaya F bekerja sejajar dengan permukaan A, sedangkan ∆L tegak lurus . Tetapan G adalah modulus puntir (share modulus), atau juga dikenal sebagai konstanta proposionalitas (1/G).

. Suatu batang silinder dengan ujung tetap A dipuntir di C

Gambar 2 mengilustrasikan kasus batang silinder yang diberi puntiran. Jika suatu batang silinder yang salah satu ujungnya dijepit tetap pada posisi A seperti dalam gambar, sedangkan ujung lainnya dipuntir dengan torsi T, maka modulus geser/modulus puntir batang tersebut dapat ditentukan dari hubungan:

α π 4 2 R LT G= (2)

jari batang silinder dan L adalah jarak antara ujung tetap (titik C). Gaya torsi T di sini dihasilkan dari beban yang digantungkan pada ujung bebas. Jika jari-jari roda pemutar adalah r dan beban

maka torsi yang dihasilkan adalah sebesar

rmg

T = (3)

Sebatang logam silindris diteguhkan di salah satu ujungnya (di titik A) dan ) oleh sebuah gaya torsi. Besarnya sudut puntir ditunjukkan oleh suatu alat penunjuk yang dilekatkan pada batang pada posisi

Gambar 3. Gambar alat untuk menentukan modulus puntir

Prosedur percobaan

1. Ukurlah diameter batang logam yang akan ditentukan modulus puntirnya dan ukur pula diameter roda pemutar.

2. Masukkan satu ujung batang ke dalam penjepit diam dan ujung lain ke dalam penjepit pemuntir. Kemudian pasanglah jarum pengamat su

jarak tertentu dari penjepit diam. Catat jarak terse

3. Bebani roda pemutar dengan dasar beban (penggantung beban) dan buat jarum penunjuk skala pada posisi 0o_.

4. Bebanilah roda pemutar berturut

penambahan beban adalah 0,5 kg. Setelah beberapa saat ca

yang ditunjukkan oleh jarum penunjuk pada setiap penambahan beban untuk α dan α2. Nilai α1 dan α2 dibaca dengan melihat jarum penunjuk yang menandakan

nilai simpangan pada busur derajat. Lakukan penamba (berarti sampai 2,5 kg).

5. Setelah semua beban digantungkan, kurangilah berturut dengan 0,5 kg setiap kali pengurangan. Tunggu beberapa sa kedudukan jarum pengamat sudut puntir untuk se

LAPORAN

1. Buatlah grafik α terhadap massa beban lalu regresi dan dapatkan persamaan garisnya. Data yang diolah adalah sebagai berikut :

a) Logam besi : nilai α1 dan α

beban,

b) Logam kuningan : nilai α1

dan pengurangan beban.

2. Tentukan nilai modulus puntir untuk masing menggunakan hasil regresi.

3. Bagaimana pengaruh α1 dan α

modulus puntir tiap bahan ?

4. Apakah terdapat perbedaan antara pengurangan dan penambahan beban pada percobaan ini ? Jelaskan jawaban Anda dan apa maksud dilakukann penambahan/pengurangan beban pada percobaan ini.

Gambar 3. Gambar alat untuk menentukan modulus puntir

Ukurlah diameter batang logam yang akan ditentukan modulus puntirnya dan

Masukkan satu ujung batang ke dalam penjepit diam dan ujung lain ke dalam penjepit pemuntir. Kemudian pasanglah jarum pengamat sudut puntir pada

Catat jarak tersebut.

Bebani roda pemutar dengan dasar beban (penggantung beban) dan buat jarum

Bebanilah roda pemutar berturut-turut dengan beban yang tersedia. Setiap 0,5 kg. Setelah beberapa saat catatlah sudut puntir yang ditunjukkan oleh jarum penunjuk pada setiap penambahan beban untuk α1

dibaca dengan melihat jarum penunjuk yang menandakan nilai simpangan pada busur derajat. Lakukan penambahan beban sampai 5 kali

Setelah semua beban digantungkan, kurangilah berturut-turut beban tersebut dengan 0,5 kg setiap kali pengurangan. Tunggu beberapa saat, kemudian catat kedudukan jarum pengamat sudut puntir untuk setiap pengurangan beban.

Buatlah grafik α terhadap massa beban lalu regresi dan dapatkan persamaan garisnya. Data yang diolah adalah sebagai berikut :

dan α2 terhadap massa beban dengan penambahan

terhadap massa beban dengan penambahan

Tentukan nilai modulus puntir untuk masing-masing bahan dengan

dan α2 dalam pengukuran untuk penentuan

rbedaan antara pengurangan dan penambahan beban pada percobaan ini ? Jelaskan jawaban Anda dan apa maksud dilakukannya

Modul 07. Modulus Puntir 35

PUSTAKA

Halliday, D., Resnick, R., Walker, J., Fundamentals of Physics, John Wiley & Sons, 1997.

MODUL 08

PESAWAT ATWOOD

TUJUAN

1. Memahami Hukum Newton dalam konsep kinematika dan aplikasinya 2. Menentukan momen inersia katrol.

ALAT DAN BAHAN

1. Pesawat Atwood yang terdiri dari (Gambar 1).

a. tiang berskala R yang pada ujung atasnya terdapat katrol P

b. genggaman G dengan pegas S, penahan beban B, penahan beban tambahan A yang berlubang.

2. Stopwatch. 3. Neraca teknis. 4. Jangka sorong 5. Meteran

6. Satu set massa beban tambahan 1

m

dan

m

₂( 2 gram dan 4 gram) 7. Satu set beban gantung bertali

dengan massa M1 san M2..

Gambar 1. Ilustrasi pesawat Atwood

TEORI DASAR

Bila suatu katrol hanya dapat berotasi murni pada porosnya yang diam, maka geraknya dapat dianalisis dengan menggunakan Gambar 2.

0

2 1

−

−

+

=

−

T

Mg

T

N

(1)

α

I

R

T

R

T

₁

−

₂

=

(2) R a = α (3)

Modul 08. Pesawat Atwood 37

Gambar 2. Gaya-gaya pada katrol Gambar 3. Katrol dan beban

dimana a adalah percepatan tangensial tepi katrol, dan percepatan ini sama dengan percepatan tali penggantung yang dililitkan pada katrol tanpa slip. Bila suatu benda digantungkan pada tali seperti Gambar 3, maka percepatan benda adalah:

g R I M M m M M m a 2 2 1 2 1 / ) ( + + + − + = (4)

dengan I adalah momen inersia katrol.

Perhatikan Gambar 3. Jika massa beban tak sama maka sistem akan bergerak lurus dipercepat beraturan. Dengan mengukur jarak yang ditempuh serta mengukur waktu yang diperlukan kita dapat menentukan percepatan beban dari percobaan. Jika percepatan telah diketahui maka dengan menggunakan Pers. (4) kita dapat menghitung momen inersia katrol. Jika massa beban sama, maka sistem akan bergerak lurus beraturan atau diam (hukum I Newton). Jika pada awalnya sistem telah mempunyai kecepatan (dalam keadaan bergerak), maka kecepatan awal tersebut dapat ditentukan dengan mengukur jarak tempuh dan waktu tempuh benda.

PERCOBAAN

a. Persiapan percobaan

1. Ukur massa beban tambahan dan massa beban bertali agar lebih presisi dalam perhitungan data.

2. Periksa apakah pesawat Atwood telah siap untuk digunakan. Lihat Gambar 1.

a. tulis data mengenai massa dan jari-jari katrol yang akan digunakan. b. pastikan bahwa tiang tidak miring.

d. gantungkan

M

₁ dan

M

₂ pada ujung-ujung tali dan kemudian pasang tali pada katrol.

e. pastikan bahwa tali sejajar dengan tiang.

f. pasang

M

₁pada genggaman G dan tambahkan beban

m

₁ pada

M

₂. Lepaskan

M

₁ dengan menekan pegas S. Pastikan bahwa beban

M

₂ dapat melalui A tanpa terganggu dan hanya beban

M

₁ saja yang tertahan di A.

b. Prosedur percobaan 1. GLB :

a. Ukur jarak dari pusat katrol ke ujung atas beban bertali 1 (M2) dan buat

jarak tersebut tetap( tidak dirubah).

b. Variasikan jarak A ke B (XAB) dan hitung waktu yang diperlukan beban

M1 dari A ke B setelah beban tambahan tertahan pada titik A (tAB).

c. Koreksi jarak AB dengan ditambah tinggi beban M2 untuk dimasukan dalam

perhitungan.

d. Lakukan percobaan ini sebanyak 5 kali dengan nilai massa beban tambahan yang berbeda (terdapat 5 pasang data untuk massa tambahan m1 dan m2).

2. GLBB :

a. Variasikan jarak C ke A (titik ujung atas beban M2 terhadap titik A atau

XCA) dan hitung waktu yang diperlukan beban M2+m dari C ke A

setelah benda mulai bergerak (tCA).

b. Lakukan percobaan ini sebanyak 5 kali dengan nilai massa beban tambahan yang berbeda (terdapat 5 pasang data untuk massa tambahan m1 dan m2).

LAPORAN

1. Percobaan 1 (GLB) :

a) Buat grafik tAB terhadap XAB yang telah dikoreksi untuk kedua massa

tambahan.

b) Tentukan persamaan regresi dari grafik tersebut lalu tentukan nilai kecepatan GLB sistem menggunakn persamaan yang diperoleh (kecepatan pada daerah AB konstan, sehingga pergunakan rumusan hubungan jarak dan waktu untuk kecepatan konstan),

c) Bandingkan kecepatan untuk kedua massa tambahan.

d) Mengapa kecepatan di daerah AB konstan dan jarak AB harus dikoreksi terhadap tinggi beban M1.

2. Percobaan 2 (GLBB) :