BAB II LANDASAN TEORI

BAB II

LANDASAN TEORI

2.1. Sistem Kendali Lup[1]

Sistem kendali dapat dikatakan sebagai hubungan antara komponen yang membentuk sebuah konfigurasi sistem, yang akan menghasilkan tanggapan sistem yang diharapkan. Sistem kendali yang sederhana biasanya terdiri dari empat bagian yaitu masukan (input), pengendali (controller), kendalian (plant), keluaran (output). Sistem kendali lup merupakan suatu rangkaian simpul proses yang digunakan untuk mengendalikan suatu plant, agar diperoleh keluaran sesuai dengan yang diiinginkan. Sistem kendali lup dapat dibedakan menjadi dua, yaitu :

1. Sistem kendali lup terbuka (open loop control system) 2. Sistem kendali lup tertutup (close loop control system) 2.1.1 Sistem Kendali Lup Terbuka

Sistem kendali lup terbuka (open loop control system) adalah suatu sistem kendali dimana keluarannya tidak berpengaruh pada nilai masukan (input) dan pengendali. Pada setiap sistem kendali lup terbuka, nilai keluaran tidak dibandingkan dengan nilai masukan, seperti tampak pada gambar 2.1.

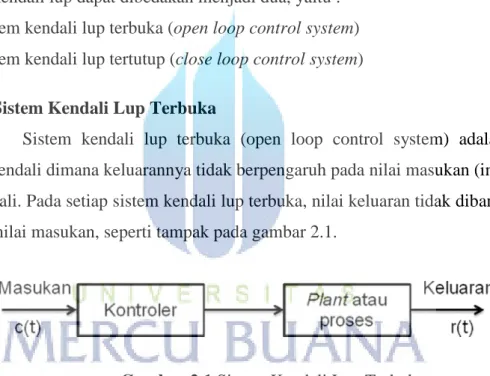
Gambar 2.1 Sistem Kendali Lup Terbuka

Berdasarkan gambar di atas terlihat bahwa setiap masukan langsung diproses untuk menghasilkan nilai keluaran. Apabila terdapat gangguan, maka keluaran sistem r(t) tidak akan dapat dikendalikan untuk menjadi sama dengan masukan (referensi) yang diinginkan. Sistem kendali lup terbuka ini digunakan apabila hubungan antara masukan dan keluaran sudah diketahui dan tidak terdapat gangguan internal maupun eksternal.

2.1.2 Sistem Kendali Lup Tertutup

Sistem kontrol lup tertutup adalah suatu sistem kontrol yang sinyal keluarannya memiliki pengaruh langsung pada aksi pengontrolan. Sinyal keluaran akan dibandingkan dengan sinyal masukan yang membentuk selisih dan akan diumpankan ke kontroler untuk memperkecil kesalahan sehingga menghasilkan keluaran sistem yang sesuai atau mendekati harga yang diinginkan. Hubungan antara masukan-keluaran dari sistem kontrol lup tertutup diperlihatkan pada Gambar 2.2.

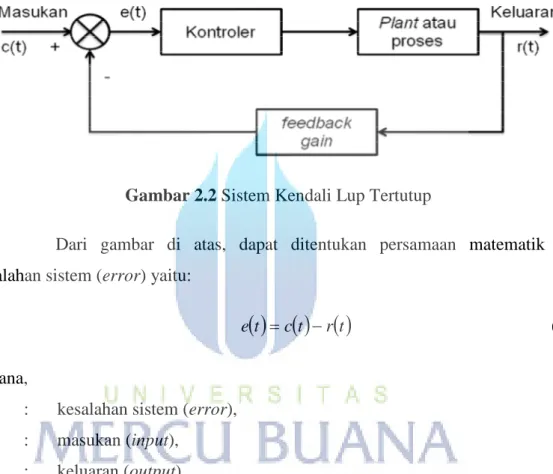
Gambar 2.2 Sistem Kendali Lup Tertutup

Dari gambar di atas, dapat ditentukan persamaan matematik dari kesalahan sistem (error) yaitu:

     

t c t r t

e   (2.1)

dimana,

e(t) : kesalahan sistem (error), c(t) : masukan (input),

r(t) : keluaran (output).

2.2. Kalman Filter[3]

Kalman Filter merupakan sebuah algoritma matematika yang

mengoptimalkan penggunaan data tak jelas (imprecise data) pada sebuah sistem linier dengan kesalahan Gaussian yang secara terus menerus memperbaharui estimasi atau perkiraan terbaik dari keadaan (state) sistem tersebut. Kalman Filter mengestimasi keadaan proses pada satu waktu dan kemudian mengambil umpan balik dalam bentuk keluaran berderau.

Dalam Kalman Filter terdapat time update (persamaan prediksi) yang memprediksikan nilai vektor keadaan yang selanjutnya dipakai untuk umpan balik.

Measurement update atau observation update merupakan sebuah persamaan koreksi

yang digunakan untuk mengkoreksi vektor keadaan. Jadi dalam Kalman Filter terjadi proses prediksi dan koreksi. Kalman Filter akan memprediksi suatu ruang keadaan dan akan mengkoreksi apakah keluaran sistem telah sama seperti masukan yang diinginkan.

Gambar 2.3 Hubungan antara Predictor dengan Corrector

2.2.1 Algoritma Kalman Filter Diskrit[3]

Kalman Filter menunjukkan masalah umum dari estimasi sebuah

keadaan (state) suatu proses kontrol waktu diskrit yang diatur oleh persamaan dari perubahan linier stokastik.

Secara umum hal tersebut dapat dinyatakan dalam persamaan keadaan :

(2.2) dengan suatu pengukuran z m

(2.3) dan persamaan output

k k k Cx z y   (2.4) Dimana : A : matriks keadaan (n x n),

B : matriks (n x 1) yang menghubungkan input kontrol ke sebuah keadaan,

Time Update (Predictor) Measurement Update (Corrector) k k k Hx v z   k k k k Ax Bu w x_k1  Ax_k Bu_k w_k x _1   

k

x : vektor keadaan proses (n x 1) saat waktu t ,_k

k

w : vektor derau proses yang diasumsikan sebagai sebuah deret putih dengan struktur kovarian diketahui,

k

v : vektor derau pengukuran yang diasumsikan sebagai sebuah deret putih dengan struktur kovarian diketahui dan mempunyai korelasi silang nol dengan deret w ,_k yk : vektor keluaran,

uk : vektor masukan,

k

z : vektor pengukuran saat waktu t ,_k

k

H : matriks (m x n) yang memberikan hubungan ideal antara pengukuran dan vektor keadaan saat waktu t ._k

Variabel acak w_k dan v_k menjelaskan derau proses dan pengukuran. Variabel – variabel tersebut diasumsikan berdiri sendiri antara yang satu dengan yang lainnya, white (putih) dan dengan distribusi kemungkinan normal.

Persamaan Kalman Filter terbagi menjadi dua bagian yaitu persamaan time

update dan persamaan measurement update. Persamaan – persamaan time update

bertanggung jawab atas rencana yang akan datang dari sebuah keadaan yang sekarang dan kovarian kesalahan mengestimasi untuk memperoleh estimasi a priori untuk langkah selanjutnya. Persamaan – persamaan measurement update digunakan sebagai umpan balik, menyatukan sebuah pengukuran baru ke dalam estimasi a priori untuk memperoleh sebuah estimasi a posteriori yang telah diperbaharui.

Q A AP Pk  k T   1 1 1 ˆ ˆ _{   } k k k Ax Bu x

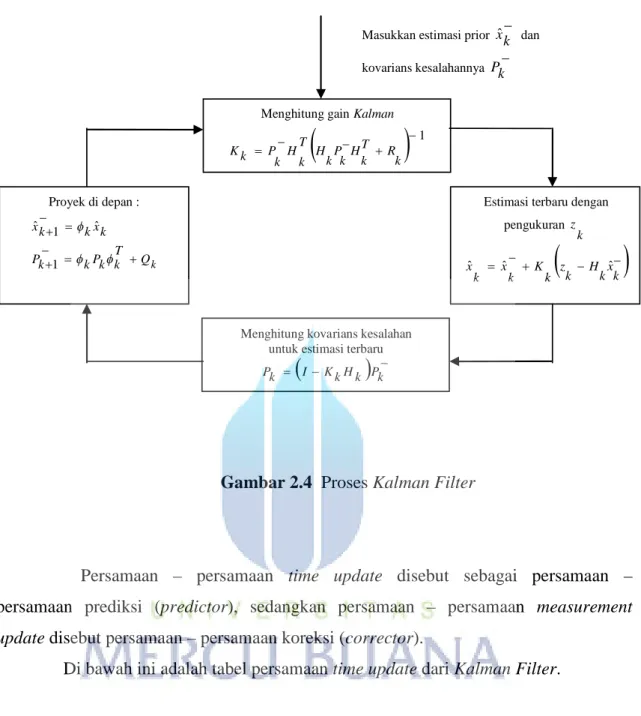
Gambar 2.4 di bawah ini menjelaskan proses Kalman Filter

Masukkan estimasi prior xˆ_k dan kovarians kesalahannya P_k

Menghitung gain Kalman





1     k R T k H k P k H T k H k P k K

Estimasi terbaru dengan pengukuran k z



_ 



   k x k H k z k K k x k xˆ ˆ ˆ Proyek di depan : k Q T k k P k k P k x k k x           1 ˆ 1 ˆ

Menghitung kovarians kesalahan untuk estimasi terbaru









 I K_kH_k P_k k

P

Gambar 2.4 Proses Kalman Filter

Persamaan – persamaan time update disebut sebagai persamaan – persamaan prediksi (predictor), sedangkan persamaan – persamaan measurement

update disebut persamaan – persamaan koreksi (corrector).

Di bawah ini adalah tabel persamaan time update dari Kalman Filter.

Tabel 2.1 Persamaan – Persamaan Time Update Kalman Filter

Estimasi a priori



_



1  _  P H HP H R K k T T k k







_{ }  k k k k k x K z Hx xˆ ˆ ˆ



_



  _{k k} k I K H P P Keterangan :  k

xˆ : estimasi a priori saat tk,

1 ˆ_k

x : estimasi a posteriori saat tk-1,

1 

k

u : vektor masukan saat tk-1, A : matriks keadaan,

B : matriks yang menghubungkan input kontrol ke sebuah keadaan,

AT : matriks transpose A, 

k

P : kovarian kesalahan estimasi a priori saat tk,

1 

k

P : kovarian kesalahan estimasi a posteriori saat tk-1, Q : kovarian derau proses.

Di bawah ini adalah tabel dari persamaan measurement update dari Kalman

Filter.

Tabel 2.2 Persamaan – Persamaan Measurement Update Kalman Filter

Gain Kalman

Estimasi a posteriori

Kovarian kesalahan estimasi a posteriori

Keterangan :

k

K : gain Kalman, 

k

P : kovarian kesalahan estimasi a priori saat tk,

R : kovarian derau pengukuran,

k

xˆ : estimasi a posteriori saat tk,



k

xˆ : estimasi a priori saat tk,

k

z : vektor pengukuran saat tk,

H : matriks yang memberikan hubungan ideal antara pengukuran dan vektor keadaan saat waktu t ,_k

HT : matriks transpose H,

k

P : kovarian kesalahan estimasi a posteriori saat tk, I : matriks identitas.

2.2.2 Kalman Filter Sebagai Estimator

Kalman Filter dapat berfungsi sebagai estimator. Maksudnya adalah Kalman Filter mampu melakukan estimasi ruang keadaan suatu plant yang dipengaruhi

oleh disturbansi.

Kalman Filter Estimator dapat dinyatakan sebagai :



n n



Ax



nn



Bu

 

n L



y

 

n Cx



nn



Du

 

n



xˆ 1  ˆ 1   _v  ˆ 1  (2.5)

 

 













 

 

                               n y n u M MD CM D CM I n n x MC I MC I C n n x n n y v 1 ˆ . ˆ ˆ (2.6)

  

nn xnn



M



y

 

n Cx



nn



Du

 

n



xˆ  ˆ 1  _v  ˆ 1  (2.7) Keterangan :

 

nn

xˆ : estimasi keadaan saat t = n,

 

nn

yˆ_v : estimasi keluaran saat t = n,



n n



xˆ 1 : estimasi keadaan saat t = n+1 dari t = n,



1



ˆnn

x : estimasi keadaan saat t = n dari t = n-1,

 

n u : masukan,

 

n y_v : keluaran, L : gain pengukuran, M : gain inovasi.

Di bawah ini merupakan diagram blok Kalman Filter Estimator

KALMAN

FILTER

PLANT

y

w

υ

xˆ yˆ

y

υ

Gambar 2.5 Diagram Blok Kalman Filter Estimator

Keterangan :

c : masukan (input),

w : vektor derau proses,

υ : vektor derau sensor atau pengukuran, r : keluaran (output),

yυ : respon terukur (jumlah antara keluaran dengan vektor derau sensor),

xˆ : estimasi ruang keadaan,

yˆ : estimasi keluaran.

Gambar 2.5 di atas menjelaskan tentang proses estimasi ruang keadaan dari

Kalman Filter. Sebelum masuk ke plant, sinyal masukan (c) yang berupa sinyal kotak

akan mendapatkan gangguan berupa derau proses (w). Derau proses bersifat acak. Setelah melakukan proses, plant akan menghasilkan keluaran (r). Keluaran dari plant akan dibandingkan dengan setpoint agar diperoleh hasil yang sesuai dengan setpoint yang diinginkan.

Saat proses pengukuran terjadi gangguan berupa derau sensor (υ) yang bersifat acak. Derau tersebut bercampur dengan keluaran plant dan menghasilkan respon terukur (yυ). Respon terukur bersama dengan sinyal masukan akan dijadikan

Pada Kalman Filter terjadi proses prediksi dan koreksi. Kalman Filter akan memprediksi ruang keadaan yang diberikan oleh plant dan akan mengkoreksi apakah keluaran sistem telah sama seperti masukan yang diinginkan sesuai dengan itersi yang telah ditentukan. Keluaran dari Kalman Filter berupa estimasi ruang keadaan

 

xˆ dan

estimasi keluaran

 

yˆ . Hasil estimasi ruang keadaan akan dijadikan penalaan untuk

kontroler.

Untuk mencari besarnya estimasi ruang keadaan, plant akan diparalelkan dengan Kalman Filter, sehingga Gambar 2.5 dapat disederhanakan. Gambar 2.6 merupakan penyederhanaan dari Gambar 2.5.

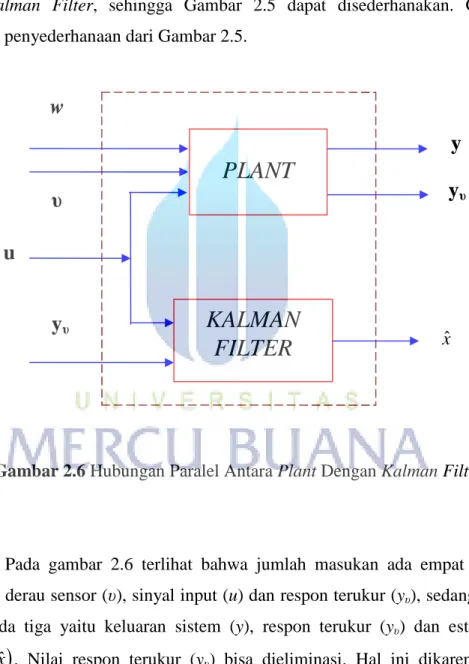
Gambar 2.6 Hubungan Paralel Antara Plant Dengan Kalman Filter

Pada gambar 2.6 terlihat bahwa jumlah masukan ada empat yaitu derau proses (w), derau sensor (υ), sinyal input (u) dan respon terukur (yυ), sedangkan jumlah

keluaran ada tiga yaitu keluaran sistem (y), respon terukur (yυ) dan estimasi ruang

keadaan

 

xˆ . Nilai respon terukur (yυ) bisa dieliminasi. Hal ini dikarenakan selain menjadi keluaran plant, respon terukur juga berfungsi sebagai masukan Kalman Filter. Sehingga Gambar 2.6 dapat disederhanakan seperti Gambar 2.7 di bawah ini :

u

y

υ

KALMAN

FILTER

w

υ

y

υ xˆ

y

PLANT

Gambar 2.7 Penyederhanaan Gambar 2.6

Jika terdapat estimasi ruang keadaan

 

xˆ yang bernilai negatif, maka nilainya akan dimutlakkan sehingga bernilai positif.

2.3. Kontroler[6]

Suatu kontroler harus mendeteksi sinyal kesalahan penggerak dan menghilangkan sinyal tersebut untuk mencapai keadaan mantap. Kontroler – kontroler yang biasa digunakan untuk pengontrolan otomatis adalah kontroler proportional (P), kontroler proportional integral (PI) dan kontroler proportional integral derivatif (PID).

2.3.1 Proportional (P)

Untuk kontroler dengan aksi kontrol proportional, hubungan antara keluaran kontroler m

 

t dan sinyal kesalahan penggerak e

 

t adalah

(2.8)

u

KALMAN

FILTER

w

υ

xˆ

y

PLANT

 

t m K e

 

t m   _c

 

t m K



r

   

t c t



m   c 

dimana :

 

t e : kesalahan (error),

 

t r : set point,

 

t

c : variabel proses yang akan dikontrol,

m : nilai bias kontrol,

Nilai bias adalah nilai keluaran yang tetap pada kontrol dalam keadaan error bernilai nol,

c

K : gain control.

Bentuk transformasi Laplace kontrol proportional :

 

 

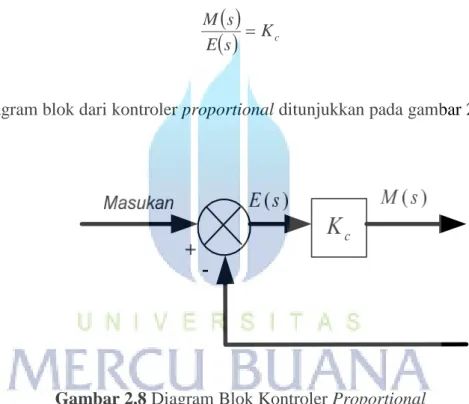
Kc s E s M 

Bentuk diagram blok dari kontroler proportional ditunjukkan pada gambar 2.8 di bawah ini.

Gambar 2.8 Diagram Blok Kontroler Proportional

Pada kontroler proportional hanya ada satu parameter yang ditala yaitu gain kontrol (K ). Kelemahan kontrol proportional adalah pada kontrol proportional terjadic

offset pada keadaan steady state. Yang dimaksud offset disini adalah bila nilai kesalahan

 

t

2.3.2 Proportional Integral (PI)

Pada kontrol proportional, untuk menghilangkan offset yaitu kesalahan

     

t r t ct

e   tidak dapat mencapai nilai nol pada saat steady state perlu ditambahkan komponen pada kontrol tersebut yaitu integral time atau aksi reset time, sehingga kontrol proportional menjadi Propotional Integral (PI). Pada kontrol PI ini ada dua parameter yang perlu ditala yaitu K dan_c T ._i

Aksi kontrol dari kontroler Proportional Integral didefinisikan dengan persamaan berikut : (2.9) dimana m = nilai bias,

 

t e = error, c K = gain kontrol, i T = integral time.

Bentuk transformasi Laplace kontrol Proportional Integral :

(2.10)

Gambar 2.9(a) menunjukkan diagram blok kontroler Proportional

Integral. Jika sinyal kesalahan penggerak e

 

t adalah fungsi tangga satuan (unit step), seperti ditunjukan pada Gambar 2.9(b), maka keluaran kontroler m

 

t menjadi seperti yang ditunjukan pada Gambar 2.9 (c).

2.3.3 Proportional Integral Derivative (PID)

Komponen kontrol Proportional Integral (PI) ditambahkan dengan aksi kontrol derivative akan menjadi kontrol Proportional Integral Derivative (PID).

Derivative berfungsi untuk mengantisipasi kesalahan yang mendahului proses. Pada

kontrol PID ini ada tiga parameter yang perlu ditala yaitu K ,c T , dani T .d

 

 

 



_

t

 

i c c e t dt T K t e K m t m 0

 

 

        s T K s E s M i c . 1 1

(a)

(b)

(c) Gambar 2.9

(a) Diagram Blok Kontroler Proportional Integral (b) Diagram Masukan Tangga Satuan (Unit Step)

(c) Keluaran Kontroler Proportional Integral.

0 Kp 2 i T Kp t Aksi kontrol PI (Hanya proportional)

 

t m

 

t e t 0 1 Unit step

Persamaan kontroler dengan aksi gabungan PID ini diberikan oleh :

(2.11) dalam transformasi Laplace

(2.12) dimana, m : nilai bias,

 

t e : kesalahan (error), c K : gain kontrol, d T : derivative time, i T : integral time.

Blok kontroler Proportional Integral Derivative ditunjukan pada Gambar 2.10(a). Jika

 

t

e adalah fungsi ramp satuan (unit ramp) seperti yang ditunjukan pada Gambar 2.10(b), maka keluaran kontroler m

 

t menjadi seperti yang ditunjukan pada Gambar 2.10(c).

2.3.4 Penalaan Parameter pada PID

Penalaan parameter-parameter bertujuan untuk mendapatkan suatu sistem kendali yang baik. Penalaan ini hanya dilakukan untuk pengendali P, PI, dan PID. Parameter-parameter tersebut adalah Kc, Ti, dan Td.

Parameter-parameter tersebut di dapatkan dengan metode Routh’s test dan dengan metode quarter decay ratio response.

 

 

 

e

 

tdt T K dt t de T K t e K m t m t i c d c c  



  0

 

 

         s T s T K s E s M i d c . 1 . 1

(a)

(b)

(c) Gambar 2.10

(a) Diagram Blok Kontroler Proportional Integral Derivative (b) Diagram Masukan Ramp Satuan (Unit Ramp) (c) Keluaran Kontroler Proportional Integral Derivative

2.3.4.1 Metode Routh’s Test

Dengan metode Routh’s test didapatkan KC atau ultimate gain, yaitu gain

maksimum pada umpan balik lup kendali yang mengakibatkan sistem kendali PID tidak stabil.

Routh’s test merupakan prosedur untuk menentukan kondisi stabilitas sistem

persamaan polinominal yang mempunyai konstanta positif. Jika kestabilan dari sistem yang dianalisa tidak memerlukan akar kuadrat persamaan dari sistem dan mempunyai bagian yang positif, sehingga Routh’s test merupakan cara yang tepat untuk menentukan kestabilan.

Metode Routh’s test sesuai untuk menyelesaikan masalah dalam menentukan batas-batas sebuah parameter lup, terutama kontrol gain yang stabil.

Untuk melaksanakan metode Routh’s test ditentukan persamaan karakteristik lup, yaitu : 0 ... ) ( ) ( ) ( 1 1 0 1 1          s a s a a s a s G s G s H n n n n V C (2.13)

dimana an, an-1, …., a1, a0 merupakan koefisien polinominal, menyatakan kebanyakan

akar positif bagian real.

Untuk melakukan test pertama, harus dipersiapkan array sebagai berikut :

Baris 1 an an-2 an-4 ……. a1 0 Baris 2 an-1 an-3 an-5 ……. a0 0 Baris 3 b1 b2 b3 ……. 0 0 Baris 4 c1 c2 c3 ……. 0 0 …….. ……. ……… ……… . ……. …… ……. Baris n d1 d2 0 ……… 0 0 Baris n+1 e1 0 0 ……… 0 0

Dimana baris ke tiga sampai baris n +1 dihitung dengan : 1 3 2 1 1       n n n n n a a a a a b (2.14) 1 5 4 1 2       n n n n n a a a a a b 1 2 1 3 1 1 b b a a b c  n  n 1 3 1 5 1 2 b b a a b c  n  n

dan seterusnya. Proses diteruskan sampai pada suatu baris baru semuanya bernilai nol.

2.3.4.2 Metode Substitusi Langsung

Dari persamaan (2.13) yang merupakan persamaan karakteristik di substitusikan s = ui, dan kontrol proportional saja. Hasil substitusi akan diperoleh ultimate gain (KC).

Dariuakan diperoleh perioda ultimate yaitu :

u U T   2  (2.15)

2.3.4.3 Metode Quarter Decay Ratio Response

Metode ini dikenal sebagai metode lup tertutup ( closed loop ) atau on line

tuning, diilhami oleh Zieger dan Nichols tahun 1942. Penalaan parameter PID

dilakukan dengan mencari ultimate gain ( KCU) dan periodanya ( TU).

Untuk menala parameter PID dengan metode ini dilakukan langkah – langkah sebagai berikut :

1. menentukan karakteristik atau jenis lup kendali.

2. melakukan pendekatan dari parameter kendali yang ditala yang menghasilkan respons untuk jenis lup kendali pada langkah pertama.

Pada metode ini karakteristik dari proses diwakilkan dengan adanya ultimate

Prosedur untuk metode quarter decay ratio adalah :

1. set waktu kendali integral dan derivative pada posisi off, sehingga pengendali hanya

proportional. Pada beberapa metode integral time tidak dimatikan, tetapi diatur

pada nilai maksimum.

2. naikan nilai gain proportional (atau kurangi nilai proportional band) sehingga c(t) berosilasi dengan amplitudo konstan, catat gain yang menghasilkan osilasi dengan amplitudo konstan sebagai KCU( Ultimate gain ).

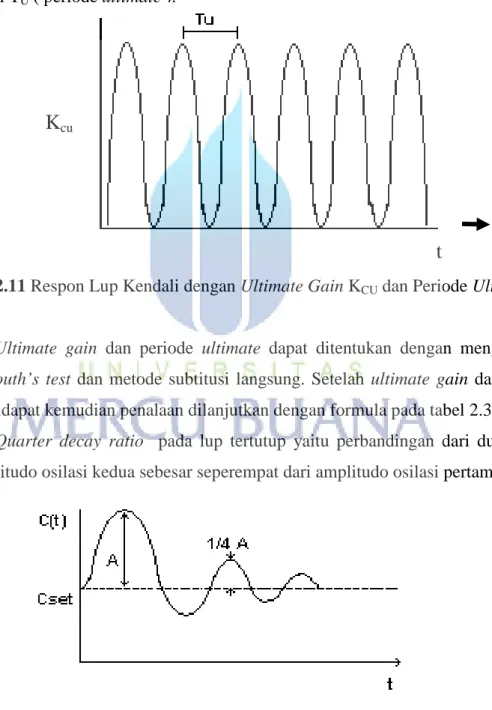
3. dari hasil rekorder variabel yang dikendalikan diukur periode osilasi dan dinyatakan sebagai TU( periode ultimate ).

K

cu

t

Gambar 2.11 Respon Lup Kendali dengan Ultimate Gain KCUdan Periode Ultimate TU

Ultimate gain dan periode ultimate dapat ditentukan dengan menggunakan

metode Routh’s test dan metode subtitusi langsung. Setelah ultimate gain dan periode

ultimate didapat kemudian penalaan dilanjutkan dengan formula pada tabel 2.3.

Quarter decay ratio pada lup tertutup yaitu perbandingan dari dua osilasi,

yaitu amplitudo osilasi kedua sebesar seperempat dari amplitudo osilasi pertama

Gambar 2.13 Respon Quarter Decay Ratio terhadap Setpoint

Gambar 2.12 mengilustrasikan respon quarter decay ratio terhadap disturbance dan setpoint, parameter kendali diatur sehingga terjadi osilasi pada Gambar 2.13. Keuntungan quarter decay ratio dapat mencegah deviasi yang besar dari setpoint tanpa terlalu osilasi.

Tabel 2.3 Quarter Decay Tuning Formula

Tipe kendali Proportional Gain,

KC Integral Time, Ti Derivative Time, Td Proportional P Kcu/2 - -Proportional integral PI Kcu/2,2 Tu/1,2 -Proportional integral derivative PID Kcu/1,7 Tu/2 Tu/8