DINAMIKA MODEL INTERAKSI TIGA SPESIES PREY-PREDATOR-
MUTUALISTIK PADA POPULASI KONSTAN
S K R I P S I
Untuk memenuhi sebagian persyaratan
mencapai derajat sarjana
(S-1)
HASRUN
F1A1 11 030
PROGRAM STUDI MATEMATIKA
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS HALU OLEO
KENDARI
2016
iii
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Allah SWT, karena atas limpahan
rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi yang
berjudul “Dinamika Model Interaksi Tiga Spesies Prei-Predator-Mutualistik Pada
Populasi Konstan”. Penulisan skripsi ini dimaksudkan untuk memenuhi salah satu
persyaratan akademik Program Studi Matematika (S1) Fakultas Matematika dan
Ilmu Pengetahuan Alam Universitas Halu Oleo Kendari.
Penulis sepenuhnya menyadari bahwa dalam penyelesaian Skripsi ini,
dihadapkan dengan berbagai macam kendala dan hambatan, namun dengan
bantuan dari berbagai pihak akhirnya penyusunan Skripsi ini dapat terselesaikan
juga. Oleh karena itu, penulis mengucapkan terima kasih dan penghargaan yang
setinggi-tinggiya kepada
Bapak Drs. Asrul Sani, M.Sc., Ph.D selaku
Pembimbing I dan Bapak La Gubu, S.Si., M.Si selaku Pembimbing II yang telah
meluangkan waktunya, memberikan petunjuk, arahan dan bimbingan sejak awal
penyusunan hingga selesainya penulisan Skripsi ini. Penulis juga mengucapkan
terima kasih kepada Bapak Drs. Jufra, M.S, Bapak Rasas Raya, S.Si., M.Si, dan
Bapak Dr. Mukhsar, M.Si, selaku tim Penguji yang telah memberikan saran dan
kritik sehingga Skripsi ini menjadi lebih baik.
Ungkapan rasa cinta dan terima kasih yang dalam penulis tujukan kepada
ayahanda
Haeruddin
dan ibunda tercinta
Hasnawati
yang telah memberikan
dorongan, pengorbanan dan do’a yang tulus, demi kesuksesan penulis. Tak
iv
terlupa, terima kasih kepada saudaraku tercinta, kakak-kakaku (Hasrida
Anggraini, muhammad alimin, dayat) dan adikku
(ekis), serta seluruh
keluargaku atas segala dukungan, motivasi dan doa selama penulis melaksanakan
studi.
Ucapan terima kasih dan penghargaan penulis ucapkan pula kepada semua
pihak yang telah banyak membantu penulis baik secara langsung maupun tidak
langsung, utamanya kepada:
1.
Bapak Prof. Dr. Ir. H. Usman Rianse, M.S., selaku Rektor Universitas Halu
Oleo.
2.
Bapak Dr. Muh. Zamrun F., S.Si., M.Si., M.Sc, selaku Dekan Fakultas
Matematika dan Ilmu Pengetahuan Alam Universitas Halu Oleo
3.
Bapak La Gubu, S.Si, M.Si, selaku Ketua Jurusan Matematika Fakultas
Matematika dan Ilmu Pengetahuan Alam Universitas Halu Oleo.
4.
Kepala Laboratorium Komputasi Matematika FMIPA Universitas Halu Oleo,
Ibu Norma Muchtar, S.Si, M.Si.
5.
Kepala Perpustakaan FMIPA Universitas Halu Oleo, Ibu Dra. Hj. Indrawati,
M.Si.
6.
Bapak dan Ibu Dosen dalam lingkup FMIPA Universitas Halu Oleo, dimana
atas bimbingan dan ilmunya yang telah diberikan selama masa perkuliahan
penulis.
7.
Sahabat-sahabatku The Vooh: muh. Izharul prianda, hardiati, liza tanzil,
nuraini, miadi, asarudin terima kasih atas dukungan, motivasi, dan do’anya.
v
8.
Kepada keluarga Bapak kos leni’s, khususnya Bapak La Lera selaku Bapak
kos dan Ibu kos serta putra putrinya, Jafar, Ayu, Leny, Arif dan Fadila yang
selalu memberikan dukungan dan motifasi serta selalu bertanya kapan wisuda.
9.
Sahabat-sahabat dan teman-temanku di Asrama Leni’s: bang rajab, bang awal
S.Sos, bang carli S.Pd, bang arbin S.H, bang nasrun S.Sos,bang darman S.P,
bang aspin S.Sos, om dodi hartono syahrir S.T, kanda rasnan A.Md.ars, kanda
david A.Md.ars, kanda amran S.pd, kanda rahmat S.Sos, Asri, Rosnawati,
sarina, riska, siti harsia S.pd, fanto, fandi, oda, saban, boni, gafar, komang,
amir, la gamsir, ayu lestary, rida, nursia, heli, wa feti, azrat, susi, awal.
10.
Sahabat-sahabat seperjuangan mahasiswa (i) angakatan 2011 kelas genap:
arfan, amal syahrin S.Mat, asran, nisfa wardiana, agus noviar riyanto S.Mat,
I wayan ignasius S.Mat, randy S.Mat, jefrianto, muh. khoirul amin, gafur
asrima al azubait sadiah, muh. safar kasim, muh. samsir abd. samad, S.Mat,
usman, ahmad tahir, risnawati, nur hayati, uly hidayati, S.Mat, rina arsani,
S.Mat, citrawan fitri, S.Mat, mayan sari putri, S.Mat, eka rahmi syamsudin
S.Mat, siti sartina, cici trisnawati S.Mat, silfie elisa gauzan, elfisah, juriati,
siti erna linda, tendri sompa, yeni rahmawati, salfina.
11.
Teman-teman mahasiswa (i) angkatan 2011 kelas ganjil, senior-senior
angkatan 2010 dan Adik-adik angkatan 2012 terima kasih atas dukungan dan
do’anya
Penulis menyadari bahwa penyusunan tugas akhir ini masih jauh dari
kesempurnaan. Oleh karena itu, kritik dan saran yang sifatnya membangun
vi
penulis terima dengan tangan terbuka. Akhir kata, semoga Skripsi ini bermanfaat
dan memberikan sumbangan yang berharga serta bernilai amal kebaikan.Amin.
Kendari, April 2016
Penulis
vii
DAFTAR ISI
Halaman
HALAMAN JUDUL ………...
i
HALAMAN PENGESAHAN...
ii
KATA PENGANTAR ...
iii
DAFTAR ISI ...
vii
DAFTAR GAMBAR ...
x
DAFTAR TABEL ...
xi
DAFTAR LAMPIRAN ...
xii
ABSTRAK ...
xiii
ABSTRACT ...
xiv
BAB I
PENDAHULUAN
1.1
Latar Belakang ...
1
1.2
Rumusan Masalah ...
3
1.3
Tujuan Penelitian ...
4
1.4
Manfaat Penelitian ...
4
BAB II
TINJAUAN PUSTAKA
2.1
Interaksi Antar Spesies ...
5
2.2
Model Dasar Prey-Predator ...
6
2.3
Persamaan Diferensia ...
8
2.4
Persamaan Differensial Autonomous ...
9
2.5
Matriks Jakobi ...
10
viii
2.7
Linearisasi Di Sekitar Titik Kesetimbangan ...
11
2.8
Sifat Sifat Kestabilan Titi Kesetimbangan ...
12
2.9
kriteria kestabilan routh-hurwitz ...
14
2.10
Solusi Numerik ...
15
BAB III
METODE PENELITIAN
3.1
Waktu Dan Tempat ...
18
3.2
Prosedur Penelitian ...
18
BAB 1V HASIL DAN PEMBAHASAN
4.1.
Model Interaksi Tiga Spesies Prey-Predator-Mutualistik 19
4.1.1
Asumsi...
19
4.1.1.
Skema Model ...
20
4.1.2.
Model ...
21
4.2.
Titik Kesetimbangan ...
21
4.3.
Analisis Kestabilan Titik Kesetimbangan ...
23
4.3.1
Model Kestabilan sistem di titik kesetimbangn
𝐸
1..
23
4.3.2
Kestabilan sistem di titik kesetimbangn
𝐸
2...
24
4.3.3
Kestabilan sistem di titik kesetimbangn
𝐸
3...
26
4.4.
Simulasi Numerik ...
28
4.4.1
Kasus I ...
28
4.4.2.
Kasus II ...
30
BAB V
PENUTUP
4.1.
Kesimpulan ...
34
ix
4.2.
Saran ...
34
DAFTAR PUSTAKA
x
DAFTAR GAMBAR
Halaman
Gambar 2.1
skema model dasar prey-predator
6
Gambar 2.2 skema
model
dasar
prey-predator
&
prey
bersimbiosis mutualisme dengan spesies lain
7
Gambar 4.1
Skema model interaksi tiga spesies
prey-predator-mutualistik.
20
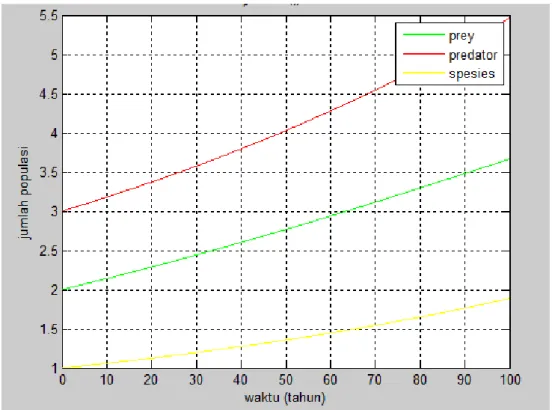
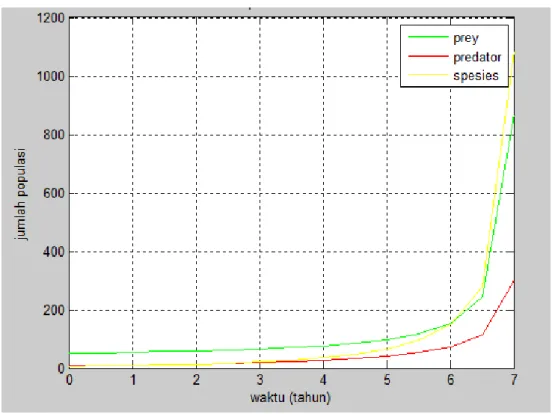
Gambar 4.2
Grafik laju perubahan populasi prey , predator dan
mutualistik
29
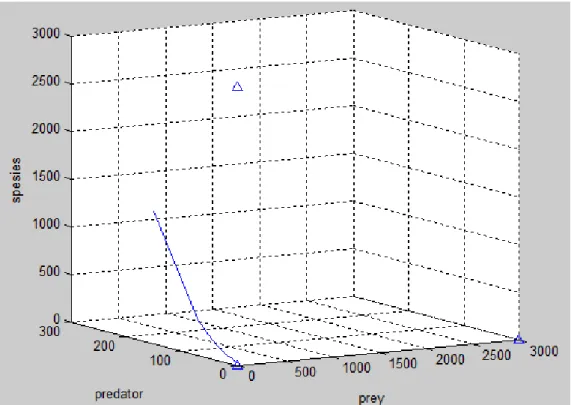
Gambar 4.3
Phase potret untuk ketiga populasi pada setiap titik
kesetimbangan Kasus I
30
Gambar 4.4
Grafik laju perubahan populasi prey , predator dan
mutualistik (Kasus II)
32
Gambar 4.5
Phase potret untuk ketiga populasi pada setiap titik
xi
DAFTAR TABEL
Halaman
Tabel 2.1
Array Routh persamaan (2.13)
15
Tabel 4.1
Sifat kestabilan sistem di titik kesetimbangan
𝐸
124
Tabel 4.2
Sifat kestabilan sistem di titik kesetimbangan
𝐸
226
Tabel 4.3
Titik kesetimbangan, nilai eigen, dan sifat kestabilan
sistem (Kasus I)
28
Tabel 4.4
Titik kesetimbangan, nilai eigen, dan sifat kestabilan
xii
DAFTAR LAMPIRAN
Halaman
Lampiran 1.
Penentuan titik kesetimbangan dengan Maple 13
37
Lampiran 2.
Script Maple 13 untuk menetukan nilai eigen umum
38
Lampiran 3.
Script
Maple
13
untuk
menentukan
titik
kesetimbangan Kasus I
39
Lampiran 4.
Nilai eigen Kasus I
40
Lampiran 5.
Script
Maple
13
untuk
menentukan
titik
kesetimbangan Kasus II
41
Lampiran 6.
Nilai eigen Kasus II
42
Lampiran 7.
Skrip Mfile Matlab Kasus I
43
Lampiran 8.
Script Matlab untuk menentukan Phase Potret Kasus I
44
Lampiran 9.
Skrip Mfile Matlab Kasus II
45
xiii
DINAMIKA MODEL INTERAKSI TIGA SPESIES PREY-PREDATOR-
MUTUALISTIK PADA POPULASI KONSTAN
OLEH
HASRUN
F1A1 11 030
Abstrak
Penelitian ini dilakukan untuk menentukan model interaksi tiga spesies pada
populasi konstan. yang kemudian dilakukan analisis kestabilan dari titik
kesetimbangan yang diperoleh. Proses pemodelan dilakukan dalam tiga tahap
yaitu perumusan masalah, dilakukan untuk mencari relasi antar variabel sehingga
terbentuk asumsi-asumsi yang nantinya akan digunakan dalam penbentukan
model. Tahap selanjutnya adalah membuat skema dan model matematika dengan
cara membentuk persamaan matematika yang sesuai dengan asumsi-asumsi yang
dibentuk sebelumnya. Tahap terakhir adalah mencari perilaku selesaian model
dengan cara mencari titik kesetimbangan, menganalisis kestabilan titik
kesetimbangan, dan melakukan simulasi numerik menggunakan sofware matlab.
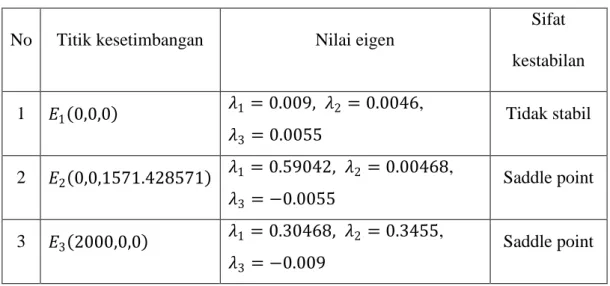
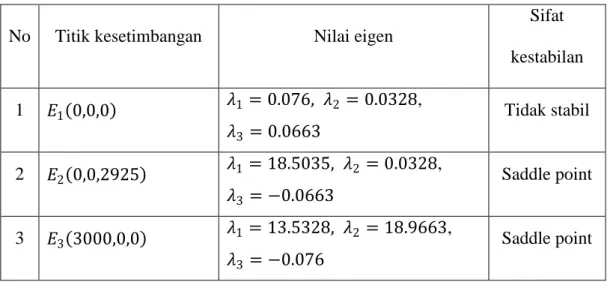
Terdapat tiga titik kesetimbangan yang diperoleh dari model.
𝐸
10,0,0
mempunyai dua kemungkinan yaitu tidak Stabil atau saddle point,
𝐸
20,0,
𝐾 𝑎𝑎𝑧−𝜇𝑧𝑧
mempunyai dua kemungkinan yaitu saddle point atau tidak
stabil,
𝐸
3𝐾, 0,0
memberikan nilai eigen yang cukup kompleks. Pada simulasi
numerik kasus I di mana
𝜃
1> 𝛾
1dan
(𝜃
2> 𝛾
2)
dengan
𝐸
10,0,0
tidak stabil,
𝐸
20,0,1571.428571
saddle point,
𝐸
3200,0,0
saddle point. Selanjutnya pada
simulasi numerik kasus II di mana
𝜃
1= 𝛾
1dan
(𝜃
2= 𝛾
2)
dengan
𝐸
10,0,0
tidak stabil,
𝐸
2, 0,0,2925
saddle point,
𝐸
33000,0,0
saddle point.
xiv
DYNAMICS OF INTERACTION MODEL OF THREE SPECIES
PREY-PREDATOR- MUTUALISTIC IN CONSTANT POPULATION
By
HASRUN
F1A1 11 030
Abstract
This study sought to determine the model of the three species interaction in the
constant population which analyzed the stability of the equilibrium point
obtained. Modeling process is done in three phases, namely the formulation of the
problem, made to look for relationships between variables that formed the
assumptions that will be used in models building. The next stage is made the
scheme and a mathematical model by forming a mathematical equation in
accordance with the assumptions that formed earlier. The last stage is search for
behavioral solution models by finding the equilibrium point, analyze the stability
of the equilibrium point, and showing numerical simulations by using matlab
software. There are three equilibrium point which obtained from the model. E
1(0,0,0)
has
two
possibilities
namely
not
stable
or
saddle
point,
𝐸
20,0,
𝐾 𝑎𝑎𝑧−𝜇𝑧𝑧
has two possibilities, namely saddle point or unstable,
𝐸
3𝐾, 0,0
gives a fairly complex eigen values. In the numerical simulation of
case I in which
𝜃
1> 𝛾
1and
(𝜃
2> 𝛾
2)
with E
1(0,0,0) unstable, E
2(0,0,1571.428571) saddle point, E
3(200,0,0) saddle point. Furthermore, the
numerical simulation of case II in which (θ
1= γ
1) and (θ
2= γ
2) with E
1(0,0,0)
unstable, E
2(, 0,0,2925) saddle point, E
3(3000,0,0 ) saddle point.
1
BAB I
PENDAHULUAN
1.1
Latar Belakang
Peranan matematika telah memberikan pengaruh yang sangat besar
terhadap kemajuan pengetahuan dan teknologi. Model matematika termasuk salah
satu bagian dari perkembangan tersebut. Pemodelan matematika merupakan salah
satu cabang dari matematika terapan yang cukup penting dan bermanfaat. Salah
satu bentuk pemodelan yang dapat diterapkan yaitu pada masalah ekologi.
Di alam terdapat banyak makhluk hidup. Makhluk hidup tersebut akan
menjalani seleksi alam di mana yang kuat yang akan bertahan. Salah satu kejadian
yang dapat diamati adalah persaingan untuk memperoleh makanan dalam
peristiwa makan dan dimakan. Makhluk hidup pemakan atau yang dikenal sebagai
prey akan mencari buruan atau yang dikenal dengan predator guna
mempertahankan hidup (Hasibuan, 1998).
Interaksi antar makhluk hidup dikaji jauh dalam ekologi. Ekologi
merupakan cabang dalam ilmu biologi yang mempelajari tentang hubungan
makhluk hidup dengan habitatnya. Pada dasarnya makhluk hidup bergantung pada
makhluk hidup lainnya ataupun habitatnya sehingga terjadi hubungan timbal balik
antara suatu makhluk hidup dengan makhluk hidup lainnya ataupun dengan
habitatnya. Interaksi yang terjadi antar makhluk hidup ataupun dengan habitatnya
dalam suatu lingkungan hidup, antara lain berupa simbiosis mutualisme,
kompetisi (persaingan) dan predasi.
2
Dalam ekologi, dikenal istilah rantai makanan. Rantai makanan
merupakan lintasan konsumsi makanan yang terdiri dari beberapa spesies
organisme. Dalam rantai makanan pada suatu ekosistem dikenal istilah
keseimbangan ekosistem yang harus dipenuhi agar lingkungan hidup tersebut
dapat terus berlangsung dalam periode generasi yang cukup lama. Bagian paling
sederhana dari suatu rantai makanan berupa interaksi dua spesies yaitu interaksi
antara spesies prey dengan predator. Banyak faktor yang mempengaruhi jumlah
populasi suatu spesies, selain kematian alami, yaitu predasi, pemanenan,
pencemaran, dan lain sebagainya. Predasi merupakan salah satu faktor yang sering
dibahas dalam interaksi antar spesies. Kehadiran predator memberikan pengaruh
pada jumlah prey. Oleh karena itu, pada interaksi tiga spesies, kehadiran spesies
lain berpengaruh pada jumlah prey dan predator sehingga dalam rantai makanan
tiap komponennya saling memberikan pengaruh (Dwidjoseputro, 1991).
Dalam masalah ekologi, terjadi interaksi antar spesies yang saling
berhubungan satu sama lain. Pemodelan matematika berperan penting dalam
mempelajari masalah ekologi, sehingga dari proses tersebut jumlah populasi dapat
diketahui, bahkan mengusulkan strategi pemodelan yang berbeda dengan
asumsi-asumsi yang berbeda pula untuk menguraikan perilaku-perilaku tertentu dari suatu
populasi. Untuk mempelajari interaksi antar spesies diperlukan suatu model
matematika. Walaupun model matematika yang melibatkan interaksi dua spesies
tidak dapat menggambarkan hubungan yang kompleks antar spesies sebagaimana
kejadian nyata di alam, tetapi dari model sederhana tersebut merupakan langkah
awal untuk mengetahui perilaku hubungan antar spesies (Murray, 1989).
3
Model yang mendiskripsikan interaksi dua spesies yang terdiri dari prey
dan predator adalah model rantai makanan dua spesies, sedangkan model yang
mendiskripsikan interaksi tiga spesies yang terdiri dari prey, predator , dan
spesies lain adalah model rantai makanan tiga spesies. Model ini terdiri dari
model laju perubahan populasi prey, spesies lain dan model laju perubahan
populasi predator (Murray, 1989).
Salah satu model prey predator yang menyajikan lebih dari dua populasi
adalah model populasi prey – predator dan prey yang bersimbiosis mutualisme
dengan spesies lain. Model ini diasumsikan mengikuti model populasi prey –
predator
Lotka Voltera,
dengan asumsi bahwa tidak hanya predator dan prey
saling berinteraksi, akan tetapi terdapat hubungan predasi yang mana prey
bersimbiosis mutualisme dengan spesies lain. Dengan demikian, jika tidak ada
prey, maka populasi predator akan puna dengan sendirinya. Diasumsikan juga
bahwa makanan prey dari sumber daya alam lainnya, yang tidak dimasukkan
dalam model (Toaha dan Budin, 2005).
Berdasarkan uraian di atas, penelitian ini akan mengembangkan
Dinamika Model Interaksi Tiga Spesies Prey-Predator-Mutualistik Pada Populasi
Konstan.
1.2
Rumusan Masalah
Pada uraian latar belakang, permasalahan yang akan dibahas pada
penelitian ini adalah sebagai berikut:
1.
Bagaimana model matematika interaksi tiga spesies prey-predator-mutualistik
pada populasi konstan?
4
2.
Bagaimana perilaku selesaian dari model interaksi tiga spesies
prey-predator-mutualistik pada populasi konstan?
3.
Bagaimana simulasi model matematika interaksi tiga spesies
prey-predator-mutualistik pada populasi konstan?
1.5
Tujuan Penelitian
Tujuan penelitian ini adalah sebagai beikut:
1.
Merumuskan model matematika interaksi tiga spesies
prey-predator-mutualistik pada populasi konstan.
2.
Mengetahui perilaku selesaian dari model interaksi tiga spesies
prey-predator-mutualistik pada populasi konstan.
3.
Mengetahui simulasi model matematika interaksi tiga spesies preypredator
-mutualistik pada populasi konstan.
1.6
Manfaat Penelitian
Manfaat penelitian ini adalah sebagai berikut:
1.
Memberikan informasi mengenai Dinamika Model Interaksi Tiga Spesies
Prey-Predator-Mutualistik Pada Populasi Konstan
2.
Dapat menjadi informasi bagi mereka yang terkait dengan manajemen
ekosistem
3.
memperkaya wawasan, khususnya pada model matematika pada bidang biologi
yang berhubungan dengan interaksi tiga spesies pada populasi konstan
4.
memberi manfaat bagi matematikawan dan matematikawati yang berkenan
untuk membahas yang berhubungan dengan model matematika.
5
BAB II
TINJAUAN PUSTAKA
2.1
Interaksi Antar Spesies
Secara singkat dapat dikemukakan bahwa interaksi dapat berdampak
positif, tidak berpengaruh atau berdampak negatif bagi spesies-spesies atau salah
satu spesies yang berinteraksi. Ada beberapa kemungkinan interaksi antar spesies
yang terjadi, sebagai berikut:
1.
Interaksi positif atau kooperatif yang terdiri atas:
a.
Mutualisme atau simbiosis yaitu kedua spesies yang berinteraksi
memperoleh keuntungan dari interaksi.
b.
Komensalisme yaitu salah satu spesies memperoleh keuntungan sedangkan
yang lain tidak berpengaruh.
2.
Interaksi tanpa dampak (indiferens)
yaitu interaksi antara dua atau lebih
spesies yang masing-masing tidak terpengaruh oleh adanya interaksi.
3.
Interaksi negatif.
a.
Amensalisme yaitu salah satu spesies memproduksi dan mengeluarkan
sejenis bahan yang merugikan spesies kedua.
b.
Pemangsaan atau predasi yaitu suatu spesies memangsa spesies lainnya
sehingga satu spesies memperoleh keuntungan dan yang lainnya dirugikan.
c.
Persaingan atau kompetisi yaitu kedua spesies yang berinteraksi saling
dirugikan
6
2.2
Model Dasar Prey-Predator
Misalkan dalam suatu habitat terdapat suatu hubungan atau peristiwa
prey-predator, dimana
𝑥(𝑡)
dan
𝑦(𝑡)
berturut-turut menyatakan kepadatan populasi
prey dan predator pada waktu
𝑡
. Untuk mempersingkat penulisan,
𝑥(𝑡)
dan
𝑦(𝑡)
akan ditulis sebagai
𝑥
dan
𝑦
saja. Selanjutnya, dalam mengkonstruksi suatu model
prey predator dibuat asumsi-asumsi sebagai berikut:
1.
Jika populasi predator diabaikan maka populasi prey akan tumbuh dengan laju
intrinsik
𝑟
secara eksponensial hingga mendekati
𝐾
(carryng capacity),
sedangkan apabila jumlah populasi prey semakin mendekati
𝐾
, maka
jumlahnya akan tumbuh secara logistik, yakni:
𝑑𝑥
𝑑𝑡
= 𝑟𝑥 1 −
𝑥𝐾
,
jika
𝑦 = 0
(2.1)
2.
Jika populasi prey diabaikan maka laju pertumbuhan populasi predator
berkurang yang dapat dinyatakan sebagai fungsi kematian dari populasi
predator, yakni:
𝑑𝑦
𝑑𝑡
= −𝜇𝑦
, jika
𝑥 = 0
(2.2)
3.
Pada setiap pertemuan kedua populasi, predator dapat mengkonsumsi prey
dengan jumlah yang tak terhingga.
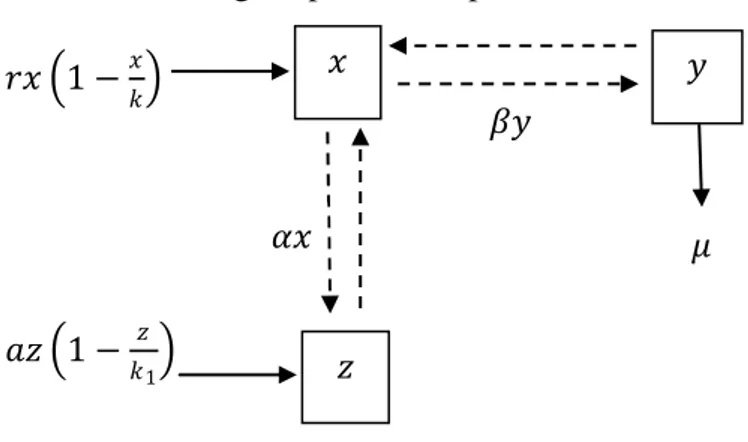
Dapat digambarkan skema model dasar prey-predator pada Gambar 2.1:
𝑟𝑥 1 −
𝑥𝑘Gambar 2.1 skema model dasar prey-predator
𝑥
𝑦
𝜇
𝛽𝑦
7
4. perubahan jumlah populasi spesies lain dipengaruhi oleh ada atau tidak adanya
interaksi dengan populasi prey. Saat tidak terjadi interaksi dengan populasi
prey, maka pertumbuhan populasi spesies lain mengikuti model logistik dengan
daya dukung lingkung
𝐾
dan tingkat pertumbuhan intrinsik spesies lain sebesar
𝑎
. Dengan demikian, populasi spesies lain akan bertambah dengan laju:
𝑑𝑧
𝑑𝑡
= 𝑎𝑧 1 −
𝑧𝐾
,
jika
𝑥 = 0
(2.3)
Dapat digambarkan skema model dasar prey-predator dan prey bersimbiosis
mutualisme dengan spesies lain pada Gambar 2.2:
𝑟𝑥 1 −
𝑥𝑘𝑎𝑧 1 −
𝑘𝑧1
Gambar 2.2
skema model dasar prey-predator & prey bersimbiosis mutualisme
dengan spesies lain
Berdasarkan asumsi-asumsi dan skema model, maka diperoleh sistem
persamaan sebagai berikut:
𝑑𝑥 𝑑𝑡
= 𝑟𝑥 1 −
𝑥 𝐾− 𝜃𝑥𝑦
𝑑𝑦 𝑑𝑡
= 𝛾𝑥𝑦 − 𝜇𝑦
𝑑𝑧
𝑑𝑡
= 𝑎𝑧 1 −
𝑧
𝐾
+ 𝛼𝑧𝑥 , 𝑟, 𝑎. 𝑘, 𝑘
2, 𝛼, 𝛾 > 0.
(2.4)
(Tarumingkeng, 1994).
𝑧
𝑥
𝑦
𝛽𝑦
𝜇
𝛼𝑥
8
dengan:
𝑟
:
laju pertumbuhan pada populasi prey.
𝜃
:
angka penurunan kepadatan populasi prey karena terjadinya
interaksi antara prey dan predator.
𝛾
:
angka pertumbuhan kepadatan populasi predator karena
terjadinya interaksi antara prey dan predator.
𝛼
:
angka pertumbuhan kepadatan populasi spesies lain karena
terjadinya interaksi antara prey dan spesies lain.
𝐾 ∶
Menyatakan kapasitas batas atau daya dukung lingkungan.
𝜇
:
laju kematian alami pada populasi predator.
2.3
Persamaan Diferensial
Persamaan diferensial seringkali muncul dalam model matematika yang
mencoba menggambarkan keadaan kehidupan nyata. Sebagai contoh, dalam
biologi yaitu laju pertumbuhan populasi. Diberikan sistem persamaan diferensial
nonlinear orde 1, dapat dinyatakan dalam bentuk matriks yakni:
𝑑𝑥
𝑑𝑡
= 𝒇 𝒙, 𝑡 , 𝒙
𝟎= 𝒙 𝑡
0,
(2.5)
dimana
𝒙
=
𝑥
1, 𝑥
2, … , 𝑥
𝑛 𝑇dan
𝒇 = 𝑓
1, 𝑓
2, … , 𝑓
𝑛 𝑇, 𝑇
adalah transpose.
Sistem (2.5) dikatakan nonlinear apabila fungsi
𝒇(𝒙)
taklinear dan
kontinu, yang dapat berbentuk:
9
𝑑𝑥
1𝑑𝑡
= 𝑓
1𝑡, 𝑥
1, 𝑥
2, … , 𝑥
𝑛𝑑𝑥
2𝑑𝑡
= 𝑓
2𝑡, 𝑥
1, 𝑥
2, … , 𝑥
𝑛⋮
𝑑𝑥
𝑛𝑑𝑡
= 𝑓
𝑛𝑡, 𝑥
1, 𝑥
2, … , 𝑥
𝑛(2.6)
Dengan kondisi awal
𝑥
𝑖𝑡
0= 𝑥
0𝑖, 𝑖 = 1,2, … , 𝑛
. Selanjutnya sistem (2.6)
dikatakan sistem autonomous apabila fungsi
𝒇(𝒙)
tidak bergantung terhadap
waktu, yakni:
𝑑𝒙
𝑑𝑡
= 𝒇 𝒙 ,
(2.7)
dengan
𝒇(𝒙)
merupakan fungsi linear maupun nonlinear (Arrowsmith & Place,
1987).
2.4
Persamaan Differensial
Autonomous
Sistem persamaan differensial orde pertama interaksi tiga spesies dapat
dinyatakan sebagai:
𝑑𝑥
𝑑𝑡
= 𝑃 𝑥, 𝑦, 𝑧 ,
𝑑𝑦
𝑑𝑡
= 𝑄 𝑥, 𝑦, 𝑧 ,
𝑑𝑧
𝑑𝑡
= 𝑆 𝑥, 𝑦, 𝑧 ,
(2.8)
𝑃, 𝑄,
dan
𝑆
adalah fungsi kontinu bernilai real dari
𝑥, 𝑦,
dan
𝑧
, dan mempunyai
turunan parsial kontinu. Sistem persamaan differensial (2.8) disebut sistem
persamaan diferensial
autonomous,
karena secara eksplisit
𝑃, 𝑄,
dan
𝑆
tidak
mengandung
𝑡
didalamnya.
10
2.5
Matriks Jakobian
Jika
𝐹(𝑢, 𝑣, 𝑤)
,
𝐺(𝑢, 𝑣, 𝑤)
dan
𝐻(𝑢, 𝑣, 𝑤)
terdiferensialkan dalam sebuah
daerah, maka determinan jakobi, atau singkatnya Jakobi,
𝐹
,
𝐺
, dam
𝐻
terhadap
𝑢
,
𝑣
dan
𝑤
adalah determinan fungsional orde ketiga yang didefinisikan sebagai
berikut:
𝜕(𝐹, 𝐺, 𝐻)
𝜕(𝑢, 𝑣, 𝑤)
=
𝜕𝐹
𝜕𝑢
𝜕𝐺
𝜕𝑢
𝜕𝐹
𝜕𝑣
𝜕𝐺
𝜕𝑣
𝜕𝐹
𝜕𝑤
𝜕𝐺
𝜕𝑤
𝜕𝐻
𝜕𝑢
𝜕𝐻
𝜕𝑣
𝜕𝐻
𝜕𝑤
=
𝐹
𝑢𝐹
𝑣𝐹
𝑤𝐺
𝑢𝐺
𝑣𝐺
𝑤𝐻
𝑢𝐻
𝑣𝐻
𝑤.
(2.9)
Persamaan (2.9) disebut matriks Jakobi
𝐹, 𝐺,
dan
𝐻
dan
𝑢, 𝑣,
dan
𝑤
.
2.6
Nilai Eigen dan Vektor Eigen
Definisi 2.1 Jika
𝐴
adalah matriks berukuran
𝑛 × 𝑛
maka vektor taknol
𝒙
didalam
𝑅
𝑛dikatakan vektor eigen (eigenvector)
dari
𝐴
jika
𝑨𝒙
adalah kelipatan
skalar dari
𝑥
yakni:
𝐴𝑥 = 𝜆𝑥
Untuk suatu skalar
𝜆
. Skalar
𝜆
dikatakan nilai eigen dari
𝐴
dan vektor
𝒙
dikatakan vektor eigen yang bersesuaian dengan
𝜆
.
Untuk mencari nilai eigen matriks
𝐴
yang berukuran
𝑛 × 𝑛
maka bentuk
𝑨𝒙 = 𝝀𝒙
dituliskan sebagai berikut:
𝑨𝒙 = 𝝀𝑰𝒙 ≡ 𝝀𝑰 − 𝑨 𝒙 = 𝟎
(2.10)
Dengan
𝐼
adalah matriks identitas berukuran
𝑛 𝑥 𝑛.
11
Agar
𝜆
dikatakan nilai eigen dari
𝐴
maka harus ada selesaian tak nol
(nontrivial) dari (2.10). persamaan (2.10) mempunyai selesaian tak nol (nontrivial)
jika dan hanya jika:
(
𝜆𝐼 − 𝐴) = 0.
(2.11)
Persamaan (2.11) dikatakan persamaan karakteristik dari
𝐴
. Skalar yang
memenuhi persamaan ini disebut nilai eigen (eigenvalue)
2.7
Linearisasi Di Sekitar Titik Kesetimbangan
Definisi 2.2 Titik
𝒙
∗= 𝑥
01, 𝑥
02, … , 𝑥
0𝑛∈ 𝑅
𝑛disebut titik kesetimbangan
(equilibrium) dari
𝑑𝑥𝑑𝑡= 𝒇 𝒙 ,
jika
𝒇(𝒙
∗) = 0
. Titk kesetimbangan
𝒙
∗disebut titk
kesetimbangan
hiperbolik
dari
𝑑𝑥𝑑𝑡= 𝒇(𝒙)
jika semua nilai eigen dari matriks
𝐷𝒇(𝒙
∗)
tidak nol bagian realnya (Panfilov, 2004).
Perilaku selesaian sistem nonlinear
𝑑𝑥𝑑𝑡
= 𝒇(𝒙)
di sekitar
titik
kesetimbangan
𝒙
∗dapat didekati dengan meninjau sifat solusi linear
𝑑𝑥𝑑𝑡
= 𝑨𝒙
,
dimana
𝐴
matriks Jakobian,
𝐴 = 𝐷𝒇(𝒙
∗)
.
Deret taylor
𝑓
𝑖𝒙 , 𝒊 = 1,2, … , 𝑛
dan di sekitar titik kesetimbangan
𝒙
∗adalah
𝑓1 𝑥1, 𝑥2, … , 𝑥𝑛 = 𝑓1 𝑥∗ + 𝜕𝑓1(𝑥∗) 𝜕𝑥𝑖 𝑥𝑖− 𝑥0𝑖 + 𝜕2𝑓 1(𝑥∗) 𝜕𝑥𝑖2 𝑥𝑖− 𝑥0𝑖 2+ 𝑘 𝑖=1 𝑘 𝑖=1 … + 𝜕𝑛𝑓1(𝑥∗) 𝜕𝑥𝑖𝑛 𝑥𝑖 − 𝑥0𝑖 𝑛 𝑘 𝑖=1 𝑓2 𝑥1, 𝑥2, … , 𝑥𝑛 = 𝑓2 𝑥∗ + 𝜕𝑓2(𝑥∗) 𝜕𝑥𝑖 𝑥𝑖− 𝑥0𝑖 𝑘 𝑖=1 + 𝜕2𝑓 2(𝑥∗) 𝜕𝑥𝑖2 𝑥𝑖− 𝑥0𝑖 𝑘 𝑖=1 … + 𝜕𝑛𝑓 2(𝑥∗) 𝜕𝑥𝑖𝑛 𝑥𝑖 − 𝑥0𝑖 𝑛 𝑘 𝑖=1 𝑓𝑛 𝑥1, 𝑥2, … , 𝑥𝑛 = 𝑓𝑛 𝑥∗ + 𝜕𝑓𝑛(𝑥∗) 𝜕𝑥𝑖 𝑥𝑖− 𝑥0𝑖 𝑘 𝑖=1 + 𝜕2𝑓 𝑛(𝑥∗) 𝜕𝑥𝑖2 𝑥𝑖− 𝑥0𝑖 𝑘 𝑖=1 … + 𝜕𝑛𝑓 𝑛(𝑥∗) 𝜕𝑥𝑖𝑛 𝑥𝑖− 𝑥0𝑖 𝑛 𝑘 𝑖=1Karena di titik kesetimbangan
𝒇
𝑖(𝒙
∗) = 0
, dimana
𝑖 = 1,2, … , 𝑛
dan di
sekitar titik kesetimbangan
𝒙
∗dianggap cukup dekat dengan
𝒙
, maka suku-suku
12
yang memuat pangkat dua atau lebih seperti
(𝑥
1− 𝑥
01)
2, (𝑥
2− 𝑥
02)
2dan
seterusnya, nilainya sangat kecil dan dapat diabaikan sehingga diperoleh:
𝒇 𝒙 ≈ 𝑨𝒙,
(2.12)
dimana:
𝒇 𝒙 =
𝑓
𝟏(𝑥
𝟏, … , 𝑥
𝑛⋮
𝑓
𝑛(𝑥
𝟏, … , 𝑥
𝑛, 𝐴 =
𝜕𝑓
1(𝒙
∗)
𝜕𝑥
1⋯
𝜕𝑓
1(𝒙
∗)
𝜕𝑥
𝑛⋮
⋱
⋮
𝜕𝑓
𝑛(𝒙
∗)
𝜕𝑥
1⋯
𝜕𝑓
𝑛(𝒙
∗)
𝜕𝑥
𝑛, 𝒙 =
𝑥
1− 𝑥
𝟎𝟏⋮
𝑥
𝒏− 𝑥
0𝑛Hal ini menunjukkan bahwa fungsi linear
𝐷𝒇 𝒙
∗𝒙
merupakan
aproksimasi untuk fungsi non linear
𝒇(𝒙)
di sekitar titik kesetimbangan
𝒙
∗,
sehingga tafsiran solusi dari sistem nonlinear
𝑑𝑥𝑑𝑡
= 𝒇(𝒙)
di sekitar titik
kesetimbangan
𝒙
∗dapat didekati dengan mencari solusi
𝑑𝑥𝑑𝑡= 𝑨𝒙
dengan
𝐴
matriks turunan parsial pertama yang disebut matriks Jakobian. Nilai eigen
matriks
𝐴
memberikan informasi kestabilan lokal di sekitar titik kesetimbangan
𝒙
∗(Nayfeh & Balachandra, 1995).
2.8
Sifat Sifat Kestabilan Titik Kesetimbangan
Definisi 2.3. Titik kesetimbangan
𝒙
∗dari sistem
𝑑𝑥𝑑𝑡= 𝑨𝒙
dikatakan stabil jika
∀ 𝜀 > 0, ∃ 𝜀
′> 0, 𝜀
′≤ 𝜀
sedemikian hingga
∀ 𝑡
dan
𝑡
′dengan
𝑡 ≤ 𝑡
′berlaku jika
𝑥 𝑡 ∈ 𝑁
𝜀(𝒙
∗)
maka
𝑥(𝑡
′) ∈ 𝑁
𝜀
(𝒙
∗)
.
Definisi 2.4. Titik kesetimbangan
𝒙
∗dari sistem
𝑑𝑥𝑑𝑡= 𝑨𝒙
dikatakan stabil
asimtotik jika
𝒙
′stabil dan terdapat persekitaran
𝑵
dari
𝒙
∗sedemikian rupa
sehingga setiap trayektori yang melalui
𝑵
kemudian
𝒙
∗dimana
𝑡
menuju tak
hingga.
13
Definisi 2.5. Titik kesetimbangan
𝑥
∗dari sistem
𝑑𝑥𝑑𝑡
= 𝐴𝑥
yang stabil tetapi tidak
stabil asimtotik disebut sebagai netral stabil.
Definisi 2.6. Titik kesetimbangan
𝑥
∗dari sistem
𝑑𝑥𝑑𝑡= 𝐴𝑥
yang tidak stabil disebut
unstable.
(Arrowsmith & place, 1992).
Bentuk-bentuk umum dan tipe-tipe kesetimbangan sistem linear dengan
sifat kestabilannya yaitu:
1.
Kedua nilai eigen positif, menghasilkan trayektori simpul tak stabil
(unstablenode).
2.
Nilai eigen positif, yang lainnya negatif, menghasilkan titik pelana (saddle
point).
3.
Kedua nilai eigen negatif, menghasilkan simpul stabil (stable node).
4.
Bagian positif, menghasilkan spiral tak stabil (unstable spiral).
5.
Bagian real nol, menghasilkan trayektori pusat sentral atau stabil netral
(neutral center atau neutral stable).
6.
Bagian real negatif, menghasilkan spiral stabil (stable spiral).
(Tarumingkeng, 1994)
Kestabilan suatu sistem kesetimbangan dapat diperiksa berdasarkan nilai
eigen dengan menyelesaikan
𝜆𝐼 − 𝐴 = 0
dengan
𝐴
adalah matriks dari (2.12)
yang berukuran
𝑛 × 𝑛
, menghasilkan polynomial dengan derajat yang sama
dengan ukuran matriks
𝐴
yang mempunyai bentuk umum
𝑎
𝑛𝜆
𝑛+ 𝑎
14
Stabilitas titik kesetimbangan
𝒙
∗ditentukan berdasarkan tanda bagian real pada
nilai eigen yang dibagi menjadi tiga, yaitu:
1. Stabil
Titik kesetimbangan
𝒙
∗dikatakan stabil jika dan hanya jika nilai eigen
𝜆
adalah
real dan negatif atau mempunyai bagian real tak positif.
2. Stabil Asimtotik
Titik kesetimbangan
𝒙
∗dikatakan stabil asimtotik jika dan hanya jika nilai
eigen
𝜆
adalah real dan negatif atau mempunyai bagian real negatif.
3. Tidak Stabil
Titik kesetimbangan
𝒙
∗dikatakan tidak stabil jika dan hanya jika nilai eigen
𝜆
adalah real dan positif atau mempunyai paling sedikit satu nilai eigen dengan
bagian real positif.
(Tarumingkeng, 1994).
2.9
Kriteria Kestabilan Routh-Hurwitz
Kestabilan Routh-Hurwitz menyatakan bahwa banyaknya perubahan tanda
dalam kolom pertama pada tabel
Routh
sama dengan banyaknya akar-akar
polinomial
𝑝(𝑠)
yang bagian realnya positif. Jadi, bila pada kolom pertama dalam
tabel tidak ada perubahan tanda (semuanya bertanda positf atau semuanya
bertanda negatif), maka semua akar polinomial
𝑝(𝑠)
bagian realnya adalah negatif,
bila polinomial ini merupakan polinomial akar-akar karakteristik dari matriks
𝐴
dimana
𝑑𝑥𝑑𝑡= 𝐴𝑥
, maka sistem ini adalah stabil. Nilai-nilai karakteristik dari
matriks
𝐴
adalah akar-akar karakteristik dari polinomial:
15
𝑝 𝑠 = 𝑎
𝑛𝑠
𝑛+ 𝑎
𝑛−1
𝑠
𝑛−1+ ⋯ + 𝑎
1𝑠 + 𝑎
0.
(2.14)
Dari persamaan (2.14) disusun Tabel Routh pada Tabel 2.1.
Tabel 2.1. Array Routh persamaan (2.13)
𝑠
𝑛𝑎
𝑛𝑎
𝑛−2𝑎
𝑛−4…
𝑎
0𝑠
𝑛−1𝑎
𝑛−1𝑎
𝑛−3𝑎
𝑛−5…
0
𝑠
𝑛−2𝑏
𝑛−2𝑏
𝑛−4…
𝑠
𝑛−3𝑐
𝑛−3𝑐
𝑛−5⋮
⋮
⋮
⋮
⋮
⋮
𝑠
00
Kolom-kolom yang berasal dari polinomial persamaan karakteristik, diletakkan
sesuai dengan Array Routh di atas. Sedangkan variabel lainnya, mengikuti aturan
sebagai berikut:
𝑏𝑛−2= − 1 𝑎𝑛−1 𝑎𝑛 𝑎𝑛−2 𝑎𝑛−1 𝑎𝑛−3 𝑏𝑛−4 = − 1 𝑎𝑛−1 𝑎𝑛 𝑎𝑛−4 𝑎𝑛−1 𝑎𝑛−5 … 𝑏𝑛−𝑖= − 1 𝑎𝑛−1 𝑎𝑛 𝑎𝑛−𝑖 𝑎𝑛−1 𝑎𝑛−𝑖−1dimana
𝒊 = 𝒏, 𝒊 = 𝟐, 𝟒, 𝟔, …
𝑐𝑛−3= − 1 𝑏𝑛−2 𝑎𝑛−1 𝑎𝑛−3 𝑏𝑛−1 𝑏𝑛−4 𝑐𝑛−5= − 1 𝑏𝑛−2 𝑎𝑛−1 𝑎𝑛−5 𝑏𝑛−1 𝑏𝑛−6 … 𝑐𝑛−𝑖 = − 1 𝑏𝑛−2 𝑎𝑛−1 𝑎𝑛−𝑖 𝑏𝑛−1 𝑏𝑛−𝑖−1dimana
𝒊 ≥ 𝒏, 𝒏 = 𝟑, 𝟓, 𝟕, …
(2.15)
(Subiono, 2010).
2.10
Solusi Numerik
Metode Runge-Kutta merupakan alternatif lain dari metode deret Taylor
yang tidak membutuhkan perhitungan turunan yang lebih tinggi, yakni dengan
mengevaluasi fungsi pada titik yang dipilih dalam setiap langkah interval. Bentuk
umum metode Runge-Kutta ialah:
16
Fungsi
Φ 𝑥
𝑖, 𝑦
𝑖, ℎ ℎ
menyatakan fungsi yang dapat diinterpretasikan sebagai
suatu kemiringan (slope) rata-rata sepanjang interval, Fungsi tersebut dapat
dituliskan dalam bentuk umum:
Φ = 𝛼
1𝑘
1+ 𝛼
2𝑘
2+ ⋯ + 𝛼
𝑛𝑘
𝑛(2.17)
dengan
𝛼
1, 𝛼
2, … , 𝛼
𝑛adalah konstanta, dan
𝑘
adalah:
𝑘
1= 𝑎(𝑥
𝑖, 𝑦
𝑖)
𝑘
2= 𝑎(𝑥
𝑖+ 𝑝
1ℎ, 𝑦
𝑖+ 𝑞
11𝑘
1ℎ)
𝑘
3= 𝑎(𝑥
𝑖+ 𝑝
2ℎ, 𝑦
𝑖+ 𝑞
21𝑘
1ℎ + 𝑞
22𝑘
2ℎ
⋮
𝑘
𝑛= 𝑎(𝑥
𝑖+ 𝑝
𝑛−1ℎ, 𝑦
𝑖+ 𝑞
𝑛−1,1𝑘
1ℎ + 𝑞
𝑛−1,2𝑘
2ℎ + ⋯ + 𝑞
𝑛−1,𝑛−1𝑘
𝑛−1ℎ)
Nilai
𝛼
𝑖, 𝑝
𝑖, 𝑞
𝑖𝑗dipilih sedemikian sehingga meminimumkan galat per langkah.
Dalam penelitian ini digunakan metode runge-kutta orde 4 yakni:
𝒚
𝒊+𝟏= 𝒚
𝒊+
ℎ
6
𝑘
1+ 2𝑘
𝟐+ 2𝑘
𝟑+ 𝑘
𝟒,
(2.18)
dimana:
𝑘
1= 𝑎(𝑡
𝑖, 𝑦
𝑖)
𝑘
2= 𝑎 𝑡
𝑖+
ℎ
2
, 𝑦
𝑖+
ℎ
2
𝑘
1𝑘
3= 𝑎 𝑡
𝑖+
ℎ
2
, 𝑦
𝑖+
ℎ
2
𝑘
2𝑘
4= 𝑎 𝑡
𝑖+ ℎ, 𝑦
𝑖+ 𝑘
3.
Metode Runge-Kutta untuk persamaan diferensial biasa tunggal dapat
dikembangkan untuk solusi persamaan diferensial majemuk. Berikut adalah
pengembangan metode Runge-Kutta untuk solusi sistem persamaan diferensial
biasa dengan tiga persamaan yang dinyatakan sebagai berikut:
17
𝑑𝑥
𝑑𝑡
= 𝑎(𝑡, 𝑥, 𝑦, 𝑧)
𝑑𝑦
𝑑𝑡
= 𝑏 𝑡, 𝑥, 𝑦, 𝑧
𝑑𝑧
𝑑𝑡
= 𝑐 𝑡, 𝑥, 𝑦, 𝑧 ,
(2.19)
dimana
𝑎, 𝑏
dan
𝑐
merupakan fungsi
𝑡, 𝑥, 𝑦,
dan
𝑧
yang telah diketahui.
Selanjutnya didefinisikan sebaga
ℎ = 𝑡
𝑖+1− 𝑡
𝑖, 𝑥
𝑖= 𝑥(𝑡
𝑖), 𝑦
𝑖= 𝑦(𝑡
𝑖), 𝑧
𝑖= 𝑧(𝑡
𝑖)
.
Dengan parameter-parameter metode Runge-Kutta orde 4 sebagai berikut:
𝑘1= 𝑎(𝑡𝑖, 𝑥𝑖, 𝑦𝑖, 𝑧𝑖) 𝑘2= 𝑎 𝑡𝑖+ℎ2, 𝑥𝑖+ℎ2𝑘1, 𝑦𝑖+ℎ2𝑙𝑖, 𝑧𝑖+ℎ2𝑚1 𝑘3= 𝑎 𝑡𝑖+ℎ2, 𝑥𝑖+ℎ2𝑘2, 𝑦𝑖+ℎ2𝑙2, 𝑧𝑖+ℎ2𝑚2 𝑘4= 𝑎(𝑡𝑖+ ℎ, 𝑥𝑖+ ℎ𝑘3, 𝑦𝑖+ ℎ𝑙3, 𝑧𝑖+ ℎ𝑚3 𝑙1= 𝑏(𝑡𝑖, 𝑥𝑖, 𝑦𝑖, 𝑧𝑖) 𝑙2= 𝑏 𝑡𝑖+ℎ2, 𝑥𝑖+ℎ2𝑘1, 𝑦𝑖+ℎ2𝑙𝑖, 𝑧𝑖+ℎ2𝑚1 𝑙3 = 𝑏 𝑡𝑖+ℎ2, 𝑥𝑖+ℎ2𝑘2, 𝑦𝑖+ℎ2𝑙2, 𝑧𝑖 +ℎ2𝑚2 𝑘4= 𝑎(𝑡𝑖+ ℎ, 𝑥𝑖+ ℎ𝑘3, 𝑦𝑖+ ℎ𝑙3, 𝑧𝑖+ ℎ𝑚3 𝑚1= 𝑐(𝑡𝑖, 𝑥𝑖, 𝑦𝑖, 𝑧𝑖) 𝑚2= 𝑐 𝑡𝑖+ℎ2, 𝑥𝑖+ℎ2𝑘1, 𝑦𝑖+ℎ2𝑙𝑖, 𝑧𝑖+ℎ2𝑚1 𝑚3= 𝑐 𝑡𝑖+ ℎ 2, 𝑥𝑖+ ℎ 2𝑘2, 𝑦𝑖+ ℎ 2𝑙2, 𝑧𝑖+ ℎ 2𝑚2 𝑚4= 𝑐(𝑡𝑖+ ℎ, 𝑥𝑖+ ℎ𝑘3, 𝑦𝑖+ ℎ𝑙3, 𝑧𝑖+ ℎ𝑚3
Nilai
𝑥, 𝑦
dan
𝑧
pada
𝑡
𝑖+1adalah:
𝑥
𝑖+1= 𝑥
𝑖+
ℎ
6
(𝑘
1+ 2𝑘
2+ 2𝑘
3+ 𝑘
4)
𝑦
𝑖+1= 𝑦
𝑖+
ℎ
6
(𝑙
1+ 2𝑙
2+ 2𝑙
3+ 𝑙
4)
𝑧
𝑖+1= 𝑧
𝑖+
ℎ
6
𝑚
1+ 𝑚𝑙
2+ 𝑚𝑙
3+ 𝑙
4.
(2.20)
(Raymond, et al., 1991).
18
BAB III
METODE PENELITIAN
3.1
Waktu Dan Tempat
Penelitian ini akan berlangsung pada bulan Desember 2015. Penelitian ini
bertempat di Laboratorium penelitian mahasiswa dan Matematika terapan Jurusan
Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Halu
Oleo.
3.2
Prosedur Penelitian
Penelitian ini adalah studi kepustakaan (library research) dengan urutan
kerja sebagai berikut:
1)
Penelusuran pustaka yang berkaitan dengan model prey dan predator, serta
prey yang bersimbiosis mutualisme dengan spesies lain,
2)
Mengkonstruksi model prey dan predator, serta prey yang bersimbiosis
mutualisme dengan spesies lain,
3)
Menganalisa perilaku selesaian model prey dan predator, serta prey yang
bersimbiosis mutualisme dengan spesies lain,
4)
Melakukan simulasi numerik dengan menggunakan software matlab,
5)
Menginterpretasikan hasil yang diperoleh.
19
BAB IV
HASIL DAN PEMBAHASAN
Dalam bab ini akan dibahas mengenai asumsi, skema, dan formulasi model
dinamika interaksi tiga spesies prey-predator-mutualistik pada populasi konstan.
Model tersebut akan dianalisis dan ditentukan sifat kestabilannya.
4.1
Model Interaksi Tiga Spesies Prey-Predator-Mutualistik
Model interaksi tiga spesies prey-predator-mutualistik dalam sistem ini
sangat kompleks, sehingga diperlukan beberapa asumsi agar menjadi sederhana.
4.1.1 Asumsi
Asumsi yang digunakan dalam penelitian ini dipaparkan sebagai berikut:
1.
Populasi prey
𝑥
dan populasi spesies lain
𝑧
secara berturut-turut akan tumbuh
secara logistik dengan carring capacity (
𝐾 > 0
) dinyatakan sebagai:
𝑑𝑥
𝑑𝑡
= 𝑟
𝑥𝑥 1 −
𝑥
𝐾
𝑑𝑧
𝑑𝑡
= 𝑎
𝑧𝑧 1 −
𝑧
𝐾
dengan:
𝑟
𝑥merupakan laju pertumbuhan intrinsik populasi
𝑥
.
𝑎
𝑧merupakan laju pertumbuhan intrinsik populasi
𝑧
2.
Laju kematian alami populasi
𝑥
diabaikan. Kematian prey hanya diakibatkan
oleh pemangsaan.
3.
Pertemuan antara populasi
𝑥
dan
𝑦
akan menyebabkan populasi
𝑥
berkurang
sebesar
𝜃
1𝑦𝑥
dan populasi
𝑦
bertambah sebesar
𝛾
1𝑦𝑥
sedangkan pertemuan
populasi
𝑥
dengan
𝑧
akan menyebabkan populasi
𝑥
bertambah sebesar
𝜃
2𝑧𝑥
dan populasi
𝑧
bertambah sebesar
𝛾
2𝑧𝑥
.
20
4.
Adanya laju pertumbuhan intrinsik
𝑏
𝑦pada populasi
𝑦
.
5.
Laju kematian alami untuk populasi
𝑦
dan
𝑧
secara berturut-turut sebesar
𝜇
𝑦dan
𝜇
𝑧.
6.
Terjadi interaksi sesama spesies pada kelompok populasi
𝑦
sebesar
𝛽𝑦
.
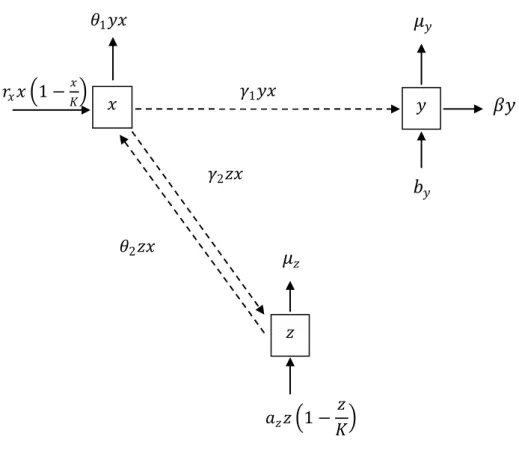
4.1.2 Skema Model
Berdasarkan asumsi di atas, maka diperoleh skema model interaksi tiga
spesies prey-predator-mutualistik pada Gambar 4.1.
𝑟
𝑥𝑥 1 −
𝑥𝐾Gambar 4.1. Skema model interaksi tiga spesies prey-predator-mutualistik.
𝜃
1𝑦𝑥
𝑥
𝑦
𝑧
𝛾
1𝑦𝑥
𝛾
2𝑧𝑥
𝜃
2𝑧𝑥
𝑏
𝑦𝜇
𝑦𝛽𝑦
𝜇
𝑧𝑎
𝑧𝑧 1 −
𝑧
𝐾
21
4.1.3 Model
Berdasarkan Asumsi dan skema di atas, maka diperoleh model interaksi
tiga spesies prey-predator-mutualistik sebagai berikut:
𝑑𝑥
𝑑𝑡
= 𝑟
𝑥𝑥 1 −
𝑥
𝐾
+ 𝜃
2𝑧𝑥 − 𝜃
1𝑦𝑥
𝑑𝑦
𝑑𝑡
= 𝛾
1𝑦𝑥 + 𝑏
𝑦− 𝜇
𝑦+ 𝛽𝑦 ,
𝑑𝑧
𝑑𝑡
= 𝑎
𝑧𝑧 1 −
𝑧
𝐾
+ 𝛾
2𝑧𝑥 − 𝜇
𝑧,
(4.1)
Keterangan:
𝑟
𝑥: Laju pertumbuhan pada prey
𝑏
𝑦: Laju pertumbuhan pada predator
𝑎
𝑧: Laju pertumbuhan pada spesies lain
𝜃
1: Angka penurunan kepadatan populasi prey karena terjadinya interaksi
antara prey dan predator
𝜃
2: Angka penambahan kepadatan populasi prey karena terjadinya interaksi
antara prey dan spesies lain.
𝛾
1: Laju pertumbuhan kepadatan populasi predator karena terjadinya
interaksi antara prey dan predator.
𝛾
2: Laju pertumbuhan kepadatan populasi spesies lain karena terjadinya
interaksi antara prey dan spesies lain.
𝛽
: Pengaruh kerapatan suatu spesies terhadap laju pertumbuhan spesies
yang bersangkutan.
22
𝜇
𝑦: Laju kematian predator.
𝜇
𝑧: Laju kematian spesies lain.
dengan:
𝑟
𝑥, 𝑏
𝑦, 𝑎
𝑧, 𝜃
1, 𝜃
2, 𝛾
1, 𝛾
2, 𝛽, 𝜇
𝑦, 𝜇
𝑧> 0
Selanjutnya akan ditentukan titik kesetimbangan untuk sistem (4.1)
kemudian akan dibahas analisis kestabilan di sekitar titik kesetimbangan tersebut,
orbit dan dinamika populasinya.
4.2
Titik Kesetimbangan
Analisis titik kesetimbangan pada sistem persamaan diferensial digunakan
untuk menentukan suatu selesaian yang tidak berubah terhadap waktu
𝑡
. Sistem
(4.1) titik kesetimbangannya dinyatakan ke dalam bentuk
𝐸 𝑥, 𝑦, 𝑧 .
titik
kesetimbangan dari (4.1) akan diperoleh dengan menyelesaikan:
𝑑𝑥
𝑑𝑡
=
𝑑𝑦
𝑑𝑡
=
𝑑𝑧
𝑑𝑡
= 0.
(4.2)
Sehingga sistem (4.1) menjadi:
𝑟
𝑥𝑥 1 −
𝑥
𝐾
+ 𝜃
2𝑧𝑥 − 𝜃
1𝑦𝑥 = 0
𝛾
1𝑦𝑥 + 𝑏
𝑦− 𝜇
𝑦+ 𝛽𝑦 = 0
𝑎
𝑧𝑧 1 −
𝑧
𝐾
+ 𝛾
2𝑧𝑥 − 𝜇
𝑧= 0
(4.3)
Terdapat
tiga
titik
kesetimbangan
pada
sistem
(4.3)
yaitu
𝐸
10,0,0 , 𝐸
20,0,
𝐾 𝑎𝑎𝑧−𝜇𝑧𝑧
, dan 𝐸
3𝐾, 0,0
Titik kesetimbangan ini diperoleh dengan software Maple 13, selanjutnya dapat
dilihat pada lampiran 1.
23
4.3
Analisis Kestabilan Sistem di sekitar Titik Kesetimbangan
Pada bagian ini akan dianalisis kestabilan titik kesetimbangan dari sistem
(4.3). selanjutnya digunakan deret Taylor (lihat bagian 2.7 halaman 11), sehingga
diperoleh:
𝑓
1𝑥, 𝑦, 𝑧 = 𝑟
𝑥𝑥 1 −
𝑥
𝐾
+ 𝜃
2𝑧𝑥 − 𝜃
1𝑦𝑥
𝑓
2𝑥, 𝑦, 𝑧 = 𝛾
1𝑦𝑥 + 𝑏
𝑦− 𝜇
𝑦+ 𝛽𝑦
𝑓
3𝑥, 𝑦, 𝑧 = 𝑎
𝑧𝑧 1 −
𝑧
𝐾
+ 𝛾
2𝑧𝑥 − 𝜇
𝑧(4.4)
Kemudian dilakukan pelinearan pada sistem (4.4) dengan
𝑑𝒙𝑑𝑡= 𝐴𝒙
,
dimana
𝐴
adalah matriks jakobi:
𝐴 =
𝜕𝑓
1𝜕𝑥
𝜕𝑓
1𝜕𝑦
𝜕𝑓
1𝜕𝑧
𝜕𝑓
2𝜕𝑥
𝜕𝑓
2𝜕𝑦
𝜕𝑓
2𝜕𝑧
𝜕𝑓
3𝜕𝑥
𝜕𝑓
3𝜕𝑦
𝜕𝑓
3𝜕𝑧
=
𝑎
11−𝜃
1𝑥 𝜃
2𝑥
𝛾
1𝑦
𝑎
220
𝛾
2𝑧
0
𝑎
33,
(4.5)
dengan:
𝑎
11= 𝑟
𝑥1 −
𝑥
𝐾
−
𝑟
𝑥𝑥
𝐾
+ 𝜃
2𝑧 − 𝜃
1𝑦
𝑎
22= 𝛾
1𝑥 + 𝑏
𝑦− 𝜇
𝑦− 𝛽
𝑎
33= 𝑎
𝑧1 −
𝑧
𝐾
−
𝑎
𝑧𝑧
𝐾
+ 𝛾
2𝑥 − 𝜇
𝑧.
4.3.1 Kestabilan Sistem di Titik Kesetimbangan
𝑬
𝟏Jika titik kesetimbangan
𝐸
1= 0,0,0
disubtitusikan pada (4.5), maka
diperoleh:
24
𝐴
1=
𝑟
𝑥0
0
0 𝑏
𝑦− 𝜇
𝑦− 𝛽
0
0
0
𝑎
𝑧− 𝜇
𝑧.
Selanjutnya nilai eigen dari
𝐴
1diperoleh dengan menyelesaikan persamaan
𝜆𝐼 − 𝐴
1= 0
, yaitu,
𝜆 − 𝑟
𝑥0
0
0
𝜆 − (𝑏
𝑦− 𝜇
𝑦− 𝛽)
0
0
0
𝜆 − (𝑎
𝑧− 𝜇
𝑧)
= 0,
dengan nilai eigen pada
𝐴
1, yaitu
𝜆
1= 𝑟
𝑥,
𝜆
2= 𝑏
𝑦− 𝜇
𝑦− 𝛽
, atau
𝜆
3= 𝑎
𝑧− 𝜇
𝑧.
Berdasarkan nilai eigen yang diperoleh pada
𝐴
1diketahui bahwa
𝜆
1selalu
bernilai real positif, jika
𝑏
𝑦− 𝜇
𝑦≥ 𝛽
maka
𝜆
2bernilai real positif . Sedangkan
jika
𝑏
𝑦− 𝜇
𝑦< 𝛽
maka
𝜆
2bernilai negatif. Hal ini menunjukan bahwa
𝜆
2memiliki dua kemungkinan, yaitu
𝜆
2dapat bernilai positif atau negatif.
Sedangkan untuk
𝜆
3memiliki dua kemungkinan yaitu
𝜆
3bernilai real positif jika
𝑎
𝑧≥ 𝜇
𝑧.
dan bernilai negatif jika
𝑎
𝑧< 𝜇
𝑧. Secara umum, berdasarkan sifat
kestabilan sistem dapat ditentukan bahwa pada titik
𝐸
1memiliki dua
kemungkinan sifat kestabilan yaitu tidak stabil atau titik sadel . Untuk lebih
jelasnya dapat di lihat pada Tabel 4.1.
Tabel 4.1. Sifat kestabilan sistem di titik kesetimbangan
𝐸
1Titik
𝜆
1𝜆
2𝜆
3Sifat Kestabilan
𝐸
1Positif
Positif
Positif
Tidak stabil
Positif
Negatif
Negatif
Saddle point
4.3.2 Kestabilan Sistem di Titik kesetimbangan
𝑬
𝟐Jika titik kesetimbangan
𝐸
2= 0,0,
𝐾(𝑎𝑎𝑧−𝜇𝑧)𝑧