Bab VI. Konduksi Transient

Bab VI

Konduksi Transient

Analisi temperatur suatu titik yang berubah setiap waktu adalah tanggung jawab transient analysis

Pada bab-bab sebelumnya kita hanya fokus pada pembahasan dimana waktu tidak mempengaruhi temperatur, artinya temperatur hanya fungsi dari posisi, biasa dituliskan T(x,y,z). Kasus-kasus seperti inilah yang disebut steady. Jika faktor waktu diperhitungkan sehingga temperatur merupakan fungsi dari posisi dan waktu, T(x,y,z,t) maka akan disebut transient. Misalnya, temperatur sebuah logam yang baru dikeluarkan dari cetakan dan diletakkan di luar (udara lingkungan), maka temperaturnya akan bervariasi tergantung setelah berapa lama logam tersebut diletakkan. Jika dibandingkan dengan kondisi steady, analysis transient memerlukan usaha ekstra. Metode-metode menganalisis perpindahan panas konduksi transient akan menjadi tanggung jawab bab ini. Pada bagian awal akan diperkenalkan kenapa kita membutuhkan analyisis transient. Kemudian teknik analysis yang biasa digunakan seperti analysis seragam (lumped analysis system) dan metode grafik akan dibahas. Selamat membaca.

I. Analisis Seragam

Ada kalanya perubahan temperatur dalam suatu materi dapat diasumsikan seragam. Misalnya sebuah bola besi yang berukuran kecil (ball bearing) awalnya mempunyai temperatur 200oC saat dikeluarkan dari cetakan dan diletakkan di suatu ruangan. Setelah beberapa menit temperaturnya akan turun, misalnya menjadi 100oC. Dapat dipastikan temperatur didalam besi tidak semuanya 100oC, dipermukaan bisa saja 98oC, di bawah permukaan bisa saja 100oC, dan di dalam intinya malah masih 102oC. Dalam analysis temperatur bola ini bisa dianggap seragam dan diwakili oleh satu angka, yaitu 100oC. Sebaran temperatur ini sangat tergantung pada konduktivitas bahan bola tersebut. Jika konduktivitasnya sangat besar, maka temperatur di permukaan bola akan segera sama dengan temperatur di permukaan. Sebaliknya jika konduktivitas nya rendah sebarannya akan semakin lebar. Bayangkan jika bola tersebut terbuat dari batu bata. Temperatur di permukaan batu bisa saja sudah 100oC, tetapi temperatur di dalam intinya masih bertahan 200oC.

Analysis yang membuat asumsi bahwa temperatur di dalam benda yang dibahas adalah seragam disebut lumped system analysis (saya menerjemahkannya sebagai analysis seragam). Sejujurnya tidak ada benda yang bersifat seperti ini, karena untuk bisa segera seragam maka dibutuhkan tahanan termal nol atau konduktivitas tak terhingga. Tetapi perbedaan temperatur yang dianggap kecil bisa diasumsikan seragam. Asumsi ini hampir mirip dengan analisis transient. Untuk menghilangkan variabel waktu dari analysis, maka diasumsikan steady. Di sini untuk menghilangkan variabel posisi (x, y, z) dari persamaan, maka asumsi seragam dipergunakan. Apakah hal ini tidak menyalahi aturan. Jawabnya selama batasan masalah dipenuhi maka nilai pendekatan bisa dipergunakan. Misalnya untuk benda-benda yang kecil dan mempunyai

konduktivitas tinggi. Koefisien konveksi di permukaan juga turut berpengaruh. Sejauh mana asumsi seragam ini dapat diterima akan dibahas lagi nantinya.

Misalkan sebuah benda yang mempunyai temperatur T

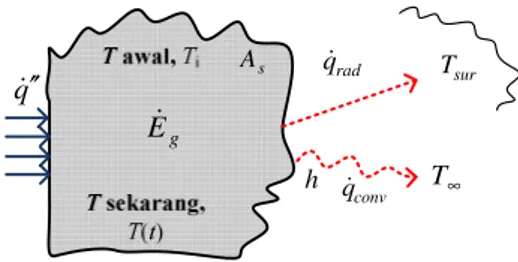
diletakkan di ruangan yang temperaturnya T∞ , untuk memudahkan analisis anggap T_∞ <T , maka temperatur benda akan turun seiring dengan bertambahnya waktu atau benda mengalami pendinginan. Temperatur benda, sifat fisik dan konveksi dengan lingkungan ditampilkan pada Gambar 1. Pada gambar As bukanlah luas penampang, tetapi luas permuakaan benda yang berbatasan dengan udara lingkungan. ∞ T s A h Q

Gambar 1 Proses pendinginan sebuah benda di udara lingkangan

Energi panas akan berpindah dari bagian luar benda yang bersentuhan dengan udara luar secara konveksi dengan koefisien h . Pada analisis ini karena koefisien konduksi benda tinggi dianggap temperatur benda akan turun dari keadaan awal sampai temperatur temperatur tertentu yang besarnya seragam untuk seluruh benda. Jika asumsi ini dipenuhi maka dapat disebutkan bahwa:

pada satuan waktu tertentu, panas yang berpindah dari permukaan benda ke lingkungan akan sama dengan

penurunan energi di dalam benda.

Fakta ini dapat dirumuskan dengan persamaan berikut: t T mc T T hA_{s p} ∆ ∆ = − − ( _∞) (1)

Tanda minus menyatakan benda mengalami penurunan energi. Jika limit perbedaan waktunya mendekati dibuat mendekati nol, maka persamaan (1) dapat ditulis menjadi:

dT mc dt T T hA_s − = _p − ( ∞) (2)

Untuk memudahkan analisis diajukan parameter berikut: ∞

−

=T T

θ , akan membuat dθ =dT (3) Substitusi persamaan (3) ke dalam persamaan (2) akan memberikan: θ θ d dt mc hA p s ₌ − (4)

Persamaan (4) dapat diintegralkan untuk waktu dari 0

=

i

t sampai waktu t dimana temperatur awal

∞

−

=T_i T

i

θ dan temperatur saat itu θ =T(t)−T_∞.

∫

∫

− = _θθ θ θ i d dt mc hA t p s 0 (5)

Jika semua parameter beriku h,A_s,m dan c_p adalah konstant atau tidak berubah meskipun waktu dan temperatur benda berubah, maka hasil pengintegralan persamaan (5) adalah: i p s _t mc hA θ θ ln = − (6)

Atau dapat dimodifikasi menjadi:                 − = − − = ∞ ∞ _t mc hA T T T T p s i i exp θ θ (7) Bagian yang didalam kurung (masih didalam kurung kurawal) bias disederhakan lagi dengan mengajukan satu parameter yang biasa disebut konstanta waktu (time constant): s p s p hA Vc hA mc ρ τ = = (8)

Dengan menggunakan konstanta ini, maka persamaan (7) dapat ditulis menjadi:

τ t i e T T T T ₋ ∞ ∞ ₌ − − (9)

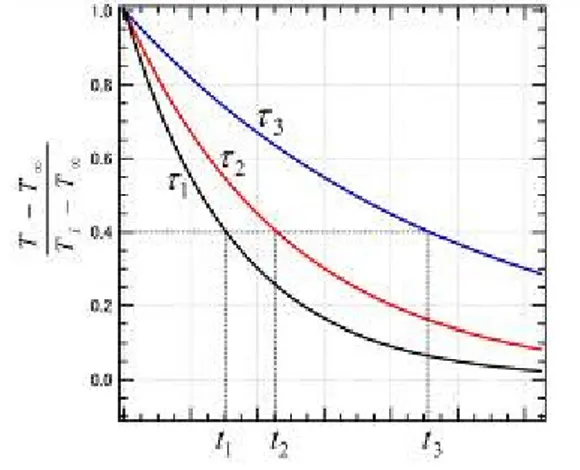
Untuk menjelaskan persamaan ini akan dibuat grafik perubahan suhu terhadap waktu dari tiga buah benda yang mempunyai τ yang berbeda.

Gambar 2 Grafik penurunan suhu

Pada gambar ditampilkan grafik penurunan suhu benda yang ditempatkan pada suhu lingkungan. Benda pertama mempuyai massa yang lebih kecil dari benda kedua dan ketiga, atau m1<m2 <m3maka jika besaran lainnya sama konstanta waktu masing-masing benda menjadi

3 2 1 τ τ

τ < < . Dari grafik dapat dilihat semakin besar konstanta waktu maka semakin lama waktu yang dibutuhkan untuk mendinginkannya.

Sementara total energi yang dipindahkan selama proses pendinginan ini dapat dihitung dengan menggunakan persamaan:

∫

∫

= − − ∞ = t s t dt T T hA dt q Q 0 0 ) ( (10)

Gunakan persamaan (9) untuk mengganti (T−T_∞) pada persamaan ini.

∫

− ∞ − − = t t i s T T e dt hA Q 0 ) ( τ (11)

Jika diintegralkan akan didapat persamaan berikut:

[

tτ

]

i

p T T e

mc

Q= ( − _∞)1− − (12)

I.1. Keabsahan Analisis Seragam

Perhatikan Gambar 3 berikut ini, yang menunjukkan proses perpindahan panas konduksi di dalam sebuah benda dan perpindahan panas konveksi kelingkungan.

Gambar 3 Perpindahan panas dari solid ke lingkungan Pada bagian (a), perpindahan panas konveksi ke lingkungan lebih kecil daripada konduksi di dalam benda. Panas dari dalam benda akan tertahan dipermukaan, akibatnya perbedaan temperatur di dalam benda padat akan kecil. Analisis temperatur seragam akan dapat diterima di

sini. Pada bagian (b) perpindahan panas konveksi di permukaan jauh lebih besar daripada konduksi di dalam benda, akibatnya akan terjadi gradient tempertur yang besar. Maka analisis seragam tidak berlaku untuk kasus ini. Parameter yang digunakan untuk membandingkan besar konduksi dan konveksi pada kasus ini disebut bilangan Biot (Biot number), yaitu perbandingan tahanan kondukdi dan tahanan konveksi:

k hL hA kA L R R Bi c c conv cond _{= =} = ) 1 ( ) ( (13) Dimana Lc =Vol As disebut panjang karakteristik. Jika bilangan Biot kecil maka konduksi akan lebih kuat dari konveksi. Tetapi sebaliknya jika bilangan Biot besar konduksi lebih lemah dari konveksi. Analisis seragam disarankan untuk digunakan jika memenuhi persamaan berikut: 1 , 0 ≤ Bi (14)

Sebelum menggunakan persamaan (9) untuk menghitung temperature sebuah benda, maka persamaan (14) harus dipastikan dulu terpenuhi.

Contoh 1

Sebagai seorang konsultan, anda diminta oleh sebuah industri yang memproduksi bola-bola besi bantalan luncur untuk menentukan lama pendinginan yang dibutuhkan bola tersebut setelah keluar dari cetakan. Bola yang diproduksi adalah terbuat dari stainless steel dengan diameter 1cm, dengan sifat fisik sebagai berikut ρ=7854kg/m3 ,

J/kgK 434

=

p

c , k=60W/mK . Temperatur bola saat dikeluarkan dari cetakan adalah 300oC. Begitu bola keluar proses pendinginan dimulai dengan menghembuskan udara luar 30oC dengan kecepatan 5m/s. Berdasarkan buku perpindahan panas konveksi kecepatan ini akan menghasilkan koefisien konveksi 17,9 W/m2K. Karena industri tersebut ingin membeli konveyor yang sesuai, maka anda diminta menghitung waktu yang dibutuhkan bola-bola tersebut mencapai temperatur 50oC.

Penyelesaian:

Asumsi yang digunakan sifat fisik konstan. Data yang diberikan soal adalah: ρ=7854kg/m3, c_p =434J/kgK,

W/mK 60

=

k , h=17,9W/m2K.T_i =300oC, T_∞ =30oC, dan D=1×10−2m.

Ditanya: t=?untuk mencapai temperatur akhir T =50oC

Langkah yang dilakukan adalah:

1. Hitung Lc untuk menghitung bilangan Bi

m 10 67 , 1 4 2 3 1 2 3 3 4 − × = = = = r r r A Vol L s c π π 3 2 10 96 , 4 60 10 67 , 1 9 , 17 × × − _{= ×} − = = k hL Bi c

Karena lebih kecil dari 0,1 maka analisis seragam bias digunakan.

2. Hitung konstanta waktu dengan persamaan (8). Persamaan ini bias diubah dengan menggunakan Lc.

s 3180 = = = h c L hA Vc _{c p} s p ρ ρ τ

3. Hitung waktu pendinginan dengan menggunakan persamaan (9): τ τ t T T T T e T T T T i t i − =       − − ⇒ = − − ∞ ∞ − ∞ ∞ _ln s 8008 ) 6 , 2 ( 3180 30 300 30 50 ln 3180 =− − =      − − × − = t

Atau sekitar 2 jam 14 menit

Catatan: Analisis waktu ini diperlukan untuk menentukan panjang dan kecepatan konveyor yang dibutuhkan. Jika masih terlalu lama, maka anda bias mengusulkan kecepatan angin yang sesuai untuk mencapai tujuan yang diinginkan.

II. Persamaan Umum Analisis Seragam

Bagian pertama dari bab ini, yang menjelaskan analisis seragam adalah merupakan fase pemanasan dari masalah yang sebenarnya di bidang engineering. Alasannya adalah: pada bagian tersebut hanya pengaruh konveksi yang diperhitungkan sebagai “pelarian” panas dari dalam benda padat. Maka dengan hanya konveksi yang diperhitungkan terbentuklah persamaan (9). Pada kasus yang sebenarnya ada tiga faktor yang mungkin mengubah persamaan (9), yaitu: (1) adanya sumber panas di dalam benda, (2) aliran flux panas melalui permukaan benda dan (3) efek radiasi yang menjadi pelarian panas dari permukaan benda ke lingkungannya. Jika semua faktor ini diperhitungakan, maka mekanisme yang terjadi pada Gambar 1 akan berubah menjadi seperti pada Gambar 4 berikut ini:

∞ T s A h conv q rad q q′′ g E sur T

Gambar 4 Aliran panas pada sebuah benda

Selisih energi yang masuk dan yang dibangkitkan dengan energi yang keluar dari benda tersebut akan digunakan untuk menaikkan temperatur benda tersebut. Kalimat ini dapat dituliskan dalam bentuk persamaan berikut: dt dT Vc q q E A q′′ _f + _g− _conv− _rad =ρ _{p (15)}

Jika perpindahan panas konveksi dan radiasi dijabarkan dengan menggunakan rumus masing-masing maka persamaan ini menjadi:

dt dT Vc T T A T T hA E A q′′ _f + _g − _s( − _∞)−εσ _s( 4− _s4)=ρ _p (16) Perhatikan bahwa luas permukaan untuk flux dan luas permukaan utuk radiasi dan konveksi dibedakan. Persamaan (16) dikategorikan sebagai persamaan differensial biasa orde pertama yang bersifat non-linier dan tidak homogen. Masalahnya sekarang adalah persamaan ini

belum bisa diselesaikan secara analitik. Untuk saat ini hanya ada satu cara menyelesaiakannya yaitu dengan cara numerik yang akan dijelaskan di Bab 7.

Seandainya dilakukan penghilangan beberapa komponen dari persamaan (16), maka persamaan ini akan mungkin diselesaiakan secara analitik. Misalnya tidak ada flux, tidak ada panas yang dibangkitkan, dan tidak ada konveksi (atau sangat kecil dibandingkan radiasi), maka persamaan (16) berubah menjadi:

dt dT Vc T T A_{s sur} ρ _p εσ − = − ( 4 4 ) (17)

Jika persamaan ini diintegralakan dan dilakukan modifikasi akan menjadi:         −       − − + = − A T T T T T T T A Vc t sur sur sur sur s p 1 4 ln 2tan 4ε σ ρ (18) Dimana _      + − + = − sur i i sur i sur T T T T T T A ln 2tan 1

Penyederhanaan lain yang mungkin dari persamaan (16) adalah jika perpindahan panas radiasi yang diabaikan. Kasus penyederhanaan seperti bisa dilakukan jika temperatur benda yang dianalisis cukup rendah. Maka persamaan (16) dapat disederhanakan menjadi:

0 = − +a b dt d θ θ (19) Dimana θ=T−T_∞ , b=

[

(q′′Af +Eg) ρVcp

]

, dan

(

hAs Vcp

)

a= ρ . Persamaan (19) ini dapat diselesaikan dengan teknik transformasi, hasilnya adalah:

[

1 exp( )

]

) exp( at T T a b at T T T T i i − − − + − = − − ∞ ∞ ∞ ₍₂₀₎

Perhatikan, jika seandainya tidak ada panas yang dibangkitkan di dalam benda dan juga flux dianggap nol, maka parameter b akan sama dengan 0. Maka persamaan (20) akan kembali menjadi persamaan (7).

Contoh 2

Jika pada soal yang ada pada contoh 1 efek flux panas akibat persentuhan permukaan bola dengan lantai tidak diabaikan dan dianggap 1% permukaan bola melepas flux 1W/m2 ke lantai maka tentukalah waktu yang dibutuhkan bola sekarang untuk mencapai suhu 50oC.

III. Persamaan dengan pengaruh ruang (Spatial effects)

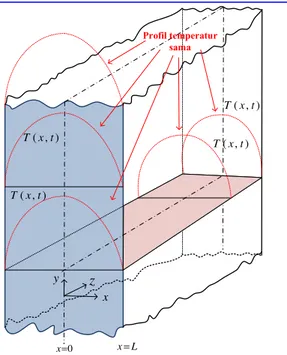
Pada pembahasan masalah transient di bagian sebelumnya kita telah mengeliminasi pengaruh ruang dengan memanfaatkan bilangan Biot. Adakalanya kasus pengaruh ruang tidak dapat diabaikan lagi. Pada bagian ini kita akan memasukkan pengaruh ruang ke dalam analisis. Seperti yang sudah diketahui pengaruh ruang mempunyai tiga dimensi, dalam kordinat kartesian disimbolkan x, y, dan z. Tetapi hal ini tidak dilakukan sekaligus, tetapi hanya memasukkan satu dimensi saja, misalnya hanya x. Kasus seperti ini mungkin saja terjadi, misalnya untuk kasus plat yang sangat panjang dan sangat lebar, seperti yang ditampilkan pada Gambar 5.

x 0 = x x=L ) , (x t T ) , (x t T ) , (x t T ) , (x t T y _z Profil temperatur sama

Gambar 5 Distribusi temperatur transient 1 dimensi Pada gambar plat dianggap sangat panjang (arah-y), akibatnya pada waktu kapanpun profil temperaturnya akan diasumsikan sama untuk setiap nilai y. Demikian juga jika plat sangat lebar sehingga profil temperatur akan sama pada nilai z berapapun. Oleh karena itu, temperatur benda di setiap posisi pada waktu tertentu hanya merupakan fungsi dari x dan waktu t atau T(x,t). Dengan asumsi ini maka persamaan energi (yang diturunkan pada Bab II) dapat disederhakan menjadi:

t T x T ∂ ∂ = ∂ ∂ α 1 2 2 (21) Nilai awal dan nilai batas (pada pertengahan konduksi nol dan pada permukaan konduksi sama dengan konveksi ke lingkungan) untuk persamaan ini dapat dirumuskan:

i T x T( ,0)= (22) 0 0 = ∂ ∂ = x x T dan

(

_∞

)

= − = ∂ ∂ − hT L t T x T k L x ) , ( (23)

Bilangan Tanpa Dimensi

Untuk mempermudah langkah-langkah analysis, biasanya persamaan differensial diubah ke dalam bentuk tanpa dimensi. Pada tulisan ini bilangan tanpa dimensi yang digunakan adalah:

∞ ∞ − − = T T T T i * θ , L x x* = , dan Fo L t t*= α₂ = (24) Semua bilangan ini tidak lagi memiliki dimensi tetapi hanya konstanta. Khusus bagian terakhir waktu tanpa dimensi ini disebut bilangan Fourier. Jika persamaan (24) didifferensialkan dan disubstitusi ke persamaan (21), akan didapat persamaan: Fo x ∂ ∂ = ∂ ∂ * 2 * * 2_{θ θ} (25) Nilai awal dan kondisi batas pada persamaan (22) dan persamaan (23) menjadi:

1 ) 0 , ( * * _{x =} θ (26) 0 0 * * * = ∂ ∂ = x x θ dan _* *(1, *) * * t Bi x _{x L} θ θ − = ∂ ∂ = (27) Persamaan (25) dengan nilai awal dan nilai batas pada persamaan (26) dan persamaan (27) akan diselesaiakan secara eksak pada bagian berikutnya.

III.1 Plat datar dengan konveksi

Penyelesaian eksak dengan menyelesaiakan persamaan (25) untuk bentuk-bentuk geometri yang sederhana dapat dijumpai pada buku-buku perpindahan panas. Pada bagian ini akan ditulis kembali penyelesaian utuk bidang seperti yang ditampilkan pada Gambar 6. Sebuah plat dengan temperatur awal Tiditempatkan di daerah yang mengalami konveksi h dengan temperatur lingkungan T_∞ . Untuk kasus ini penyelesian eksak persamaan (25) adalah:

) cos( ) exp( 2 * 1 * _{C Fo x} n n n n ξ ξ θ =

∑

∞ − = (28)

Dimana koefisien C_ndihitung dengan persamaan berikut:

) 2 sin( 2 sin 4 n n n n C ξ ξ ξ + = (29) * x ) , (x t T 0 *₌ x x*=1 h ∞ T ∞ T h

Gambar 6 Konveksi transien 1D pada plat datar Dan parameter ξ_n (eigenvalue) adalah akar-akar positif dari persamaan karakteristiknya:

Bi

n

n ξ =

ξ tan (30)

Penyelesaian yang dinyatakan dalam bentuk deret, seperti pada persamaan (28) masih jauh dari praktis untuk digunakan. Oleh karena itu diperlukan pendekatan.

Pada kasus khusus dengan bilangan Forier Fo>0,2, persamaan (28) dapat diwakili dengan suku pertama deretnya, dengan kesalahan kurang dari 2% .

) cos( 1 * * 0 * _{θ ξ x} θ = (31) * 0

θ adalah temperatur bagian tengah plat datar, yang dirumuskan dengan: ) exp( 12 1 * 0 C ξ Fo θ = − (32)

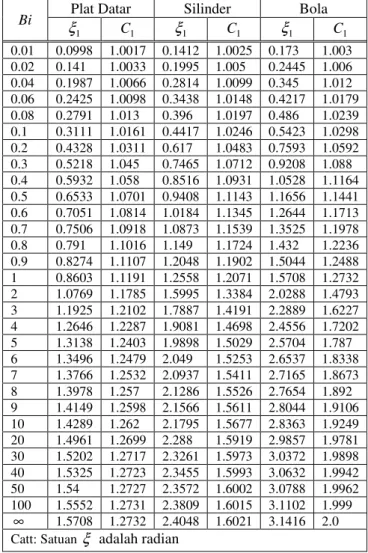
Dimana C₁ dapat dihitung dengan menggunakan persamaan (29). Nilai C₁ dan akar pertama persamaan karakteristik ξ₁ adalah fungsi dari bilangan Biot, seperti yang ditampilkan pada Tabel 1.

Plat Datar Silinder Bola

Bi 1 ξ C1 ξ1 C1 ξ1 C1 0.01 0.0998 1.0017 0.1412 1.0025 0.173 1.003 0.02 0.141 1.0033 0.1995 1.005 0.2445 1.006 0.04 0.1987 1.0066 0.2814 1.0099 0.345 1.012 0.06 0.2425 1.0098 0.3438 1.0148 0.4217 1.0179 0.08 0.2791 1.013 0.396 1.0197 0.486 1.0239 0.1 0.3111 1.0161 0.4417 1.0246 0.5423 1.0298 0.2 0.4328 1.0311 0.617 1.0483 0.7593 1.0592 0.3 0.5218 1.045 0.7465 1.0712 0.9208 1.088 0.4 0.5932 1.058 0.8516 1.0931 1.0528 1.1164 0.5 0.6533 1.0701 0.9408 1.1143 1.1656 1.1441 0.6 0.7051 1.0814 1.0184 1.1345 1.2644 1.1713 0.7 0.7506 1.0918 1.0873 1.1539 1.3525 1.1978 0.8 0.791 1.1016 1.149 1.1724 1.432 1.2236 0.9 0.8274 1.1107 1.2048 1.1902 1.5044 1.2488 1 0.8603 1.1191 1.2558 1.2071 1.5708 1.2732 2 1.0769 1.1785 1.5995 1.3384 2.0288 1.4793 3 1.1925 1.2102 1.7887 1.4191 2.2889 1.6227 4 1.2646 1.2287 1.9081 1.4698 2.4556 1.7202 5 1.3138 1.2403 1.9898 1.5029 2.5704 1.787 6 1.3496 1.2479 2.049 1.5253 2.6537 1.8338 7 1.3766 1.2532 2.0937 1.5411 2.7165 1.8673 8 1.3978 1.257 2.1286 1.5526 2.7654 1.892 9 1.4149 1.2598 2.1566 1.5611 2.8044 1.9106 10 1.4289 1.262 2.1795 1.5677 2.8363 1.9249 20 1.4961 1.2699 2.288 1.5919 2.9857 1.9781 30 1.5202 1.2717 2.3261 1.5973 3.0372 1.9898 40 1.5325 1.2723 2.3455 1.5993 3.0632 1.9942 50 1.54 1.2727 2.3572 1.6002 3.0788 1.9962 100 1.5552 1.2731 2.3809 1.6015 3.1102 1.999 ∞ 1.5708 1.2732 2.4048 1.6021 3.1416 2.0 Catt: Satuan ξ adalah radian

Perpindahan Energi

Besar energi panas yang telah dipindahkan selama waktu tdapat dihitung dengan persamaan berikut:

1 1 * 0 max sin 1 ξ ξ θ − = Q Q (33) Dimana Qmax =ρcpV(Ti−T∞) , dan V adalah volume benda.

Contoh 3

Pada proses manufaktur plat-plat baja, setebal 4cm yang baru diproses didinginkan dengan meniupkan udara lingkungan 30oC hingga koefisien konveksi yang terjadi pada masing-masing sisinya 100 W/m2K. Temperatur awal plat adalah 300oC. Anggap panjang dan lebar plat cukup besar hingga dapat dianalisis sebagai kasus transient 1 dimensi. Sifat fisik yang digunakan k=55W/mK dan

6 10 18× − =

α m2/s. Setelah 20 menit Tentukanlah: (a) temperatur di pusat plat, (b) temperatur permukaan, dan (c) energi yang dikeluarkan dari plat jika volume tiap plat 2m3.

Penyelesaian:

Asumsi konduksi transient 1D dengan sifat fisik konstan. Data soal L=4 2=2×10−2m , waktu pendinginan

1200

=

Gunakan persamaan (32) untuk menghitung temperatur pertengahan plat. Caranya:

1. Hitung Bilngan Fo dan Bi =

= ₂

L t

Fo α 54, karena > 0,2 persamaan pendekatan dapat digunakan. 0364 , 0 = = k hL Bi

2. Hitung ξ dan C₁ dengan menginterpolasi Tabel 1 Interpolasi antara 0,02 dan 0,04

Bi ξ₁ C1

0.02 0.141 1.0033

0.0364 0.188314 1.006006

0.04 0.1987 1.0066

Catatan persamaan (30) dapat juga digunakan untuk menghitung ξ . Tetapi teknik trial and error harus digunakan.

3. Hitung θ₀*dengan menggunakan persamaan (32) 148 , 0 ) 54 1883 , 0 exp( 006 , 1 2 * 0 = − × = θ

4. Hitung temperatur di pertengahan plat 30 300 30 148 , 0 * 0 − − = ⇒ − − = ∞ ∞ T T T T T i θ

Maka jawaban (a) T =70oC.

5. Hitung temperatur permukaan dengan menghitung θ*

146 , 0 ) 1 188 , 0 cos( 148 , 0 ) cos( ₁ * * 0 *_{=θ ξ x = × × =} θ 30 300 30 146 , 0 * − − = ⇒ − − = ∞ ∞ T T T T T i θ Maka jawaban (b) T =69,3oC.

Catatan: perbedaan temperatur di permukaan dan ditengah plat sangat kecil. Hal ini bisa terjadi karena memang konduktivitas plat baja sangat baik.

6. Hitung energi yang dikeluarkan dari plat dengan menggunakan persamaan (33). ) ( ) ( max = − ∞ = V T −T∞ k T T V c Q _{p i i} α ρ =1,65×109J J 10 41 , 1 sin 1 9 1 1 * 0 max × = ⇒ − = Q Q Q ξ ξ θ III.2 Silinder

Penyelesaian pendekatan juga dapat dirumuskan untuk silinder dengan panjang tak terhingga seperti pada Gambar 7. 0 r 0 * r r r = h ∞ T ) , (r t T

Gambar 7 Konveksi transient 1D pada Silinder

Persamaan pendekatan yang dapat digunakan asalkan memenuhu syarat Fo=αt r02 >0,2. ) ( 1 * 0 * 0 * _{θ J ξ r} θ = (34) * 0

θ adalah temperatur pusat silinder, yang dirumuskan dengan: ) exp( 12 1 * 0 C ξ Fo θ = − (35)

Dimana C₁dan ξ₁ merupakan fungsi bilangan Biot yang ditampilkan pada Tabel 1. Dan J₀adalah fungsi Bessel jenis pertama.

Sementara besar perpindahan panas setelah waktu tertentu dapat dihitung dengan persamaan:

) ( 2 1 1 1 1 * 0 max ξ ξ θ J Q Q − = (36)

Dimana J₁adalah fungsi Bessel jenis pertama.

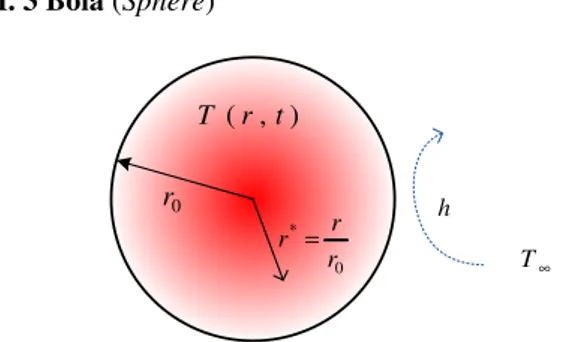
III. 3 Bola (Sphere)

) , (r t T h ∞ T 0 r 0 * r r r =

Gambar 8 Konveksi transient 1D pada Bola Untuk kasus bola seperti yang ditampilkan pada Gambar 7, persamaan menghitung temperaturnya sebagai fungsi waktu ditampilkan pada persamaan berikut:

) sin( 1 * 1 * 1 * 0 * _r r ξ ξ θ θ = (37) * 0

θ adalah temperatur pusat bola, yang dirumuskan dengan: ) exp( 12 1 * 0 C ξ Fo θ = − (38)

Sementara besar perpindahan panas setelah waktu tertentu dapat dihitung dengan persamaan:

[

sin( ) cos( )

]

3 1 3 1 1 1 1 * 0 max ξ ξ ξ ξ θ − − = Q Q (39) Catatan

Penyelesaian secara eksak untuk ketiga bentuk geometri sederhana ini (plat datar, silinder panjang, dan bola) hanya untuk kondisi batas konveksi di permukaan dengan udara luar yang mempunyai temperatur T_∞ . Jawaban dari penyelesaian eksak adalah berupa deret yang akan konvergen pada nilai akhir. Jawaban seperti ini adalah tidak praktis, maka diajukan jawaban pendekatan dengan hanya menggunakan suku pertama dari jawaban yang berbentuk deret tersebut. Hal ini bisa diterima selama bilangan Fourier Fo≥0,2 , kesalahan yang didapat biasanya hanya kurang dari 2%. Diluar dari syarat ini, tidak

disarankan menggunakan penyelesaian pendekatan ini. Harus dicari cara lain untuk menyelesaiakannya.

Masalah kondisi batas di permukaan juga masih terbatas pada kasus dengan konveksi di permukaan. Masih ada dua kemungkinan kasus dengan kondisi batas lain yang tentunya akan memberikan penyelesaiaan yang berbeda. Kedua kasus ini adalah: (a) kasus dengan kondisi batas tempertur permukaan konstan dan (b) kasus dengan kondisi batas flux panas konstan. Untuk kedua kasus ini tidak akan dibahas pada buku ini. Tetapi bagi mahasiswa yang serius ingin mempelajarinya disarankan untuk mengacu pada Referensi I.

Karena penyelesaian eksak dan pendekatan masalah-masalah konduksi transient ini sangat terbatas, maka saya lebih suka menggunakan pendekatan numerik untuk menyelesaiakan masalah konduksi transient ini. Penyelesaian secara numerik ini akan dibahas pada bab berikutnya dari buku ini.

Contoh 4 (Diambil dari Referensi II sebagai pembanding) Sebuah poros berbentuk silinder yang panjang dengan diameter 20cm terbuat dari stainless steel 304 dikeluarkan dari oven produksi dengan temperatur 600oC. Poros didinginkan di ruangan dengan temperatur 200oC dengan koefisien konveksi h=80W/m2K. Tentukan temperatur pusat poros setelah 45 menit dan panas yang dipindahkan per satuan panjang poros.

Penyelesaian:

Asumsi yang digunakan poros mengalami konduksi transient 1 dimensi dan sifat fisik konstan.

Sifat material yang digunakan : k=14,9 W/mK, 7900

=

ρ kg/m3, c_p =477J/kgK, dan α =3,95×10−6 m2/s. Data soal: t=45menit (2700s), r=0,1m, h=80W/m2K,

600

=

i

T oC, dan T_∞ =200 oC. L=1m (persatuan panjang). Gunakan persamaan (35) untuk menghitung temperatur pusat silinder. Tahap penyelesaian soal ini adalah:

1. Hitung bilangan Fo dan Bi

07 , 1 2 = = r t Fo α 537 , 0 = = k hr Bi

Nilai Fo sebenarnya tidak melampaui 0,2 sebagai syarat penggunaan pendekatan. Tetapi kita tidak punya alternatif lain dan memberi asumsi tambahan berlaku pendekatan agar persamaan (35) tetap dapat digunakan. 2. Hitung ξ dan C₁ dengan menginterpolasi Tabel 1

(untuk silinder)

Interpolasi antara 0,5 dan 0,6

Bi _ξ1 C₁

0.50 0.941 1.114

0.537 0.969 1.122

0.60 1.018 1.135

3. Hitung θ₀*dengan menggunakan persamaan (35)

) exp( 12 1 * 0 C ξ Fo θ = − =0,412

4. Hitung temperatu di pusat dengan menjabarkan θ₀*

365 ) , 0 ( ) , 0 ( * 0 ⇒ = − − = ∞ ∞ _{T t} T T T t T i θ o C

Maka temperatur inti akan turun dari 600oC menjadi 365oC setelah 45menit. Jawaban ini berbeda 5oC dengan Referensi II, karena pada buku tersebut soal ini diselesaikan dengan menggunakan grafik.

5. Panas yang dipindahkan persatuan panjang dapat dihitung dengan mengunakan persamaan (36)

2 2 10 14 , 3 × − = = r L V π m3 MJ 378 , 43 ) ( max= c V T −T_∞ = Q ρ _{p i} MJ 30 ) ( 2 1 1 1 1 * 0 max = ⇒ − = J Q Q Q ξ ξ θ

Dimana J₁(0,969)=0,43adalah fungsi Bessel jenis pertama orde pertama. Dapat dilihat pada tabel atau dengan menggunakan fungsi Bessel pada Excell.

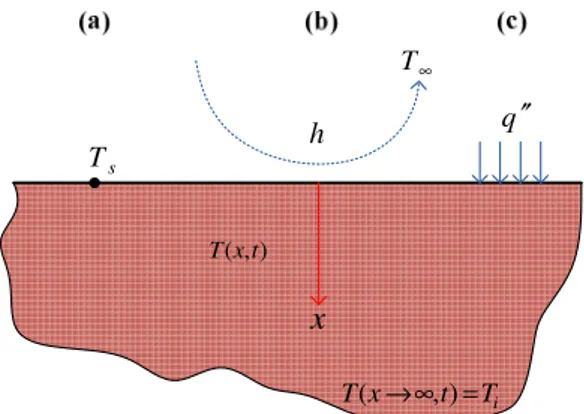
IV. Benda Padat Semi infinite

Di daerah yang beriklim tropis, seperti Indonesia, temperatur tanah (bumi) umumnya lebih redah dari temperatur udara lingkungan. Jika di pagi hari permukaan bumi mendapat penyinaran dari radiasi matahari, maka temperatur permukaan tanah akan naik. Hal ini akan mengakibatkan terjadinya perpindahan panas konduksi dari permukaan tanah ke dalam tanah. Proses perpindahan panas ini dapat dianggap hanya 1 dimensi dan sisi lainnya jauh tak terhingga ke dalam tanah. Kasus semacam ini disebut konduksi transient pada benda padat semi infinite. Artinya pada bagian permukaan bendanya tertentu, sementara pada bagian dalam dimensinya tak terhingga. Diagram perpindahan panasnya ditampilkan pada Gambar 9. Temperatur di dalam benda akan merupakan fungsi jaraknya dari permukaan dan waktu. Tetapi karena bendanya semi infinite, temperatur pada jarak yang menuju tak terhingga akan sama dengan temperatur awal (initial).

x

s T h ∞ T q′′ ) , (xt T i T t x T( →∞, )=

Gambar 9 Konduksi transient pada benda semi-infinite Seperti yang ditunjukkan pada gambar ada tiga kemungkinan kondisi yang mungkin terjadi, yaitu (a) temperatur permukaan konstan Ts, (b) terjadi konveksi dengan udara lingkungan, dan (c) flux panas konstan. Penyelesaian untuk kasus ini akan disesuaikan dengan kondisi batas ini.

a. Temperatur permukaan konstan

Penyelesaian konduksi transient pada benda semi-infinite ini dapat dilakukan dengan menggunakan konsep

similarity variable. Dimisalkan suatu variabel 2 1 ) 4 ( t x α

η = yang harus dimasukkan ke persamaan (21).

t T x T ∂ ∂ = ∂ ∂ α 1 2 2 (21) Dengan menggunakan chain rule akan didapat persamaan-persamaan berikut: η α η η d dT t x d dT x T 4 1 = ∂ ∂ = ∂ ∂ dan ₂ 2 2 2 4 1 η α d T d t x T = ∂ ∂ η α η η d dT t t x t d dT t T 4 2 − = ∂ ∂ = ∂ ∂

Substitusi persamaan-persaman ini ke persamaan (21) akan memberikan: η η η d dT d T d 2 2 2 − = (40)

Nilai batas untuk persamaan ini adalah: s

T

T(η=0)= dan T(η→∞)=T_i (41) Persamaan (40) dapat diubah bentuknya menjadi bentuk yang dapat diintegralkan sekali, yaitu:

(

)

(

η

)

η η η d d dT d dT d 2 − =

Jika diintegralkan, menjadi:

(

dT d

)

=− 2+C ln η η Atau 1exp( η2) η =C − d dT

Integralkan sekali lagi akan memberikan: (agar berbeda, variabelnya akan diganti dengan sebuah variabel dummy

u)

∫

∞ − + = ₀ 2 2 1 exp( u )du C C T

Dengan menggunakan kondisi batas yang pertama di persamaan (41), maka akan di dapat C2 =T_s. Masukkan kondisi batas kedua akan didapat:

∫

∞ − +

= ₀ 2

1 exp( ) s

i C u du T

T

Jika diarrange, bentuknya bisa ditulis menjadi persamaan berikut: π ) ( 2 ) exp( ) ( 0 2 1 s i s i T T du u T T C = − − − =

∫

∞

Dengan menggunakan konstanta ini, maka jawaban untuk persamaan (40) adalah: η π η erf ) exp( 2 0 2 ₌ − = − −

∫

u du T T T T s i s ₍₄₂₎

Dimana bagian yang di sebelah kanan disebut sebagai fungsi error Gauss.

Sementara heat flux perpindahan panas pada permukaan dapat dihitung dengan menggunakan persamaan: 0 0 ) (erf ) ( = = ∂ ∂ − − = ∂ ∂ − = ′′ η η η η x d d T T k x T q _{i s} x s

Jika diselesaiakan akan memberikan:

t T T k q_s s i πα ) ( − = ′′ (43)

b. Permukaan semi infinite dengan konveksi

Untuk kasus dengan kondisi batas konveksi di permukaan, persamaan temperatur dapat dihitung dengan cara yang sama dan hasilnya adalah:

        + −       = − − ∞ 2 2 exp 2 erfc k t h k hx EC t x T T T T i i α α (44) Dimana _       + = k t h t x EC α α 2 erfc (45)

Pada persamaan ini digunakan erfc yang artinya fungsi error tambahan (complement error function). Artinya jika diketahui suatu bilangan sembarang u , maka

u u 1 erf

erfc = − .

c. Flux panas konstan

Untuk kasus dengan flux panas konstan, persamaan temperaturnya adalah:       ′′ −        ₋ ′′ = − t x k x q t x k t q T T s s i α α π α 2 erfc 4 exp 2 2 (46)

Contoh 5 (Diambil dari Referensi II)

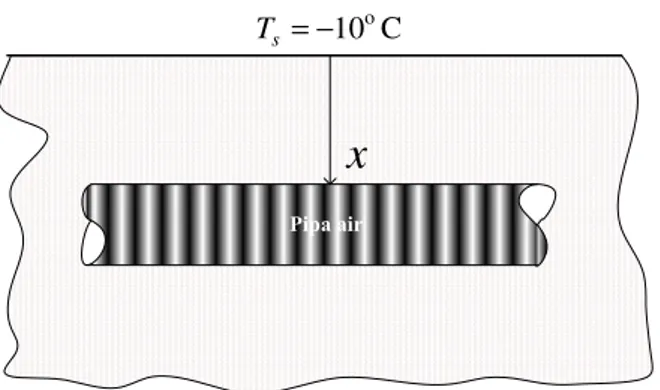
Pada daerah-daerah yang mempunyai musim dingin temperatur udara bisa mencapai temperatur di bawah 0oC hal ini bisa menimbulkan masalah pada pipa aliran air, dimana air akan membeku di dalam pipa yang akan menghentikan aliran air dan dapat juga menyebabkan pipa pecah. Untuk menghindari hal ini terjadinya biasanya pipa ditanam di dalam tanah yang lebih hangat. Masalahnya adalah temperatur permukaan tanah akan berangsur-angsur turun dan jika kedalaman pipa tidak cukup dalam tetap akan terjadi pembekuan. Misalkan suatu pada suatu daerah permukaan tanah tertutup salju selama 3 bulan (lamanya musim dingin) hingga permukaannya sekitar -10oC. Temperatur awal tanah saat memasuki musim dingin adalah 15oC. Jika koefisien konduksi tanah

W/mK 4 , 0 = k dan α =0,15×10−6m2/s tentukan kedalaman minimum pipa air harus ditanam di daerah tersebut untuk menghindari pembekuan air.

Penyelesaian:

C 10o − = s T

x

Pipa air Asumsi yang digunakan: sifat fisik konstan, tempertur permukaan tanah konstant pada -15oC, dan 1 dimensi. Agar air di dalam pipa tidak membeku tempertur paling tidak di atas titik beku, T(x,t) = 0oC. Persamaan yang sesuai untuk soal ini adalah persamaan (39).

1. Hitung lamanya musim dingin dalam detik 6 10 776 , 7 60 60 24 30 3× × × × = × = t s 2. Gunakan persamaan (39)       = − − t x T T T T s i s α 4 erf 4 , 0 ) 10 ( 15 ) 10 ( 0 4 erf = − − − − = − − =       s i s T T T T t x α

Nilai error function yang sesuai adalah jika parameternya 0,371. Nilai ini bisa dilihat di tabel atau dengan menggunakan fungsi Erf (x) pada excell. 3. Hitung x m 8 , 0 10 776 , 7 10 15 , 0 4 371 , 0 371 , 0 4 6 6_{× × =} × × × = = − x t x α

Maka jika pipa ditanam pada kedalaman lebih dari 0,8 m tidak akan membeku meskipun temperatur di permukaan

C 10o

− selama 3 bulan karena tertutup salju.

V. Transient Multi Dimensi

Pada bagian awal kita telah merumuskan konduksi transient tanpa pengaruh posisi dan bagian kedua konduksi transient dengan pengaruh posisi hanya 1 dimensi. Pada bagian ini kita akan membahas kasus transient dengan multi dimensi. Dengan kata lain kita ingin menyelesaian distribusi temperatur T(x,y,z,t). Mungkin anda bertanya: sedangkan hanya kasus 1 dimensi T(x,t)kita sudah hampir menyerah dan minta tolong pada jawaban pendekatan, apakah mungkin menyelesaikan T(x,y,z,t)lagi? Memang benar, untuk saat ini hampir tidak mungkin menyentuh jawaban T(x,y,z,t) secara eksak. Yang akan kita lakukan di bagian ini adalah teknik super posisi. Artinya kita akan menggabung jawaban-jawaban dari kasus-kasus 1 dimensi untuk mendapatkan jawaban multi dimensi. Teknik inilah yang disebut teknik superposisi, yang diperkenalkan oleh Langston 1982.

Teknik Superposisi

0

r

Gambar 10 Teknik superposisi membentuk silinder sepanjang L

Syarat utama menggunakan analisis transient 1 dimensi adalah dimensi benda yang dibahas tak terhingga ke di kedua sisi arah dimensi yang dihilangkan. Misalnya kalau distribusi temperaturnya adalah T(x,t) , karena

ydan z dihilangkan maka panjang benda ke arah ydan

zadalah tak terhingga. Atau kalau kasusnya semi infinite, panjang benda tak terhingga hanya ke satu sisi dari dimensi yang dihilangkan. Sementara jika ukuran benda yang dibahas sudah tertentu, seperti silinder dengan panjang L

dan jari-jari r₀seperti pada Gambar 10(b), kasusnya sudah merupakan multi dimensi, tepatnya T(x,r,t) . Pada Gambar 10(a) ditunjukkan bahwa silinder dengan panjang

L dan jari-jari r₀ merupakan irisan dari plat datar yang panjang dengan tebal W (W =L) dengan silinder sangat panjang dengan yang berjari-jari r₀.

Dengan menggunakan analogi irisan ini, maka distribusi temperatur pada silinder sepanjang L dapat dirumuskan dengan persamaan:

Sil Plat L Sil xt r t t r x, , ) ( , ) ( , ) ( , * * * _{θ θ} θ = × (47)

Dimana θ* adalah temperatur tanpa dimensi yang dirumuskan sebagai berikut:

(

)

) ( ) ) , , ( ( , , _, * ∞ ∞ − − = T T T t r x T t r x i L Sil θ

( )

) ( ) ) , ( ( , * ∞ ∞ − − = T T T t x T t x i plat θ

( )

) ( ) ) , ( ( , * ∞ ∞ − − = T T T t r T t r i Sil θ

Bagaimana menghitung parameter-parameter yang disebelah kanan telah dibahas pada bagian sebelumnya.

Analogi irisan juga dapat digunakan untuk menghitung besar perpindahan panas pada kasus-kasus multi dimensi. Persamaan untuk kasus dua dimensi adalah:

              −       +       =       1 max 2 max 1 max 2 max 1 Q Q Q Q Q Q Q Q D (48) Dan untuk tiga dimensi:

              −               −       +               −       +       =       1 max 1 max 3 max 1 max 2 max 1 max 3 max 1 1 1 Q Q Q Q Q Q Q Q Q Q Q Q Q Q D (49) Contoh 6

Misalkan kelak, anda berminat menjadi pengusaha dengan mendirikan pabrik untuk memproduksi poros yang akan anda pasarkan ke pabrik-pabrik kelapa sawit di Indonesia. Salah satu poros produksi anda berbentuk silinder mempunyai diameter 5cm dan panjang 10cm terbuat dari stainless steel 304. Setelah mengalami proses produksi dengan temperatur awal 500oC, poros-poros tersebut anda dinginkan dengan meniupkan udara lingkungan 30oC hingga terjadi konveksi dengan koefisien 60 W/m2K. Setelah 30 menit, tentukanlah temperatur inti poros dan total panas yang sudah berpindah dari poros

Penyelesaian:

Soal ini tidak dapat lagi diselesaikan dengan mengunakan asumsi silinder sangat panjang (kasus 1D), karena panjang poros sudah tertentu. Soal ini harus diselesaikan dengan menggunakan teknik superposisi antara poros sangat panjang dan plat datar sangat panjang.

Asumsi yang digunakan di sini adalah sifat fisik konstan. Data yang diberikan soal: Poros silinder r=2,5 cm,

15 = L cm, Ti =500 o_C, 30 = ∞ T oC, dan h=60 W/m2K. Sifat material yang digunakan : k=14,9 W/mK,

7900

=

ρ kg/m3, c_p =477J/kgK, dan α =3,95×10−6 m2/s. Cara menyelesaiakan soal ini:

1. Hitung bilangan Fo dan Bi untuk silinder panjang 4 , 11 2 = = r t Fo α 101 , 0 = = k hr Bi

2. Hitung ξ dan C₁ dengan menginterpolasi Tabel 1 (untuk silinder)

Interpolasi antara 0,1 dan 0,2

Bi ξ₁ C₁

0.1 0.4417 1.0246

0.101 0.443 1.025

0.2 0.617 1.0483

3. Hitung θ₀*dengan menggunakan persamaan (35) 11 , 0 ) exp( 12 1 * 0 =C −ξ Fo = θ

4. Hitung Fo dan Bi untuk kasus plat datar panjang Di sini tebal plat sama dengan panjang silinder (perhatikan Gambar 10). Maka L_c =5cm = = ₂ s L t Fo α 2,84 = = k hL Bi c 0,201

5. Hitung ξ dan C₁ dengan menginterpolasi Tabel 1 Interpolasi antara 0,2 dan 0,3

Bi ξ₁ C1

0.02 0.141 1.0033

0.0364 0.188314 1.006006

0.04 0.1987 1.0066

6. Hitung θ₀*dengan menggunakan persamaan (32) 604 , 0 ) exp( 12 1 * 0 =C −ξ Fo = θ

7. Gabungkan kedua parameter ini untuk mendapatkan *

0

θ untuk silinder dengan menggunakan persamaan (47): 11 , 0 604 , 0 ) , 0 ( ) , 0 ( ) , 0 , 0 ( _, * * * _{= × = ×} Sil Plat L Sil t t t θ θ θ Atau

( )

θ₀* _Sil,L =0,0664

8. Hitung temperatur di pusat silinder dengan menjabarkanθ₀*. 2 , 61 30 500 30 0664 , 0 * 0 ⇒ = − − = ⇒ − − = ∞ ∞ T _T T T T T i θ o_C

Angka ini merupakan jawaban untuk soal (a)

9. Panas maksimum yang berpindah dapat dihitung dengan menggunakan persamaan (48)

              −       +       =       1 max 2 max 1 max 2 max 1 Q Q Q Q Q Q Q Q D

10. Hitung

(

Q Q_max

)

₁ dengan menggunakan persamaan (33): 1 1 * 0 1 max sin 1 ξ ξ θ − =       Q Q =0,415

11. Hitung

(

Q Q_max

)

₂ dengan menggunakan persamaan (369: ) ( 2 1 1 1 1 * 0 2 max ξ ξ θ J Q Q − =       =0,893 12. Gabungkan kedua parameter ini:

) 415 , 0 1 ( 893 , 0 415 , 0 , max − + =       L sil Q Q =0,9374 13. Hitung perpindahan panas maksimum

4 2 10 96 , 1 × − = × = r L V π m3 ) ( max= c V T −T∞ Q ρ _{p i} =347,58kJ

14. Hitung perpindahan panas yang telah terjadi:

= ×       = max max Q Q Q Q 325,8kJ

VI. Beberapa bentuk lain multi dimensi

Beberapa bentuk multi dimensi yang merupakan irisan dari bentuk 1 dimensi dapat dilihat pada sub bagian berikut:

VII.Soal –soal Latihan 1. Soal Latihan Menyusul