I PENDAHULUAN II LANDASAN TEORI

I PENDAHULUAN

1.1 Latar Belakang

Semakin tingginya mobilitas penduduk di suatu negara terutama di kota besar tentulah memiliki banyak permasalahan, mulai dari kemacetan yang tak terselesaikan hingga moda transportasi yang efisien. Salah satu moda transportasi yang tepat dalam mengurangi kemacetan adalah kereta api, karena kereta api memiliki daya angkut yang besar dibandingkan angkutan kota pada umumnya.

Jumlah penumpang kereta api yang meningkat akan membuat frekuensi keberangkatan kereta semakin padat. Hal ini tentunya harus ditopang dengan perencanaan yang baik. Perencanaan yang dimaksud adalah perencanaan jadwal perjalanan kereta api yang tepat dan efisien dengan memperhatikan segala kendala semisal ketersediaan rangkaian kereta maupun jalur di setiap stasiun. Tentu

tidak mudah ketika telah mendapatkan jadwal perjalanan kereta api tetapi masih memiliki delay (keterlambatan) kereta yang besar.

Dalam karya ilmiah ini, akan dibahas penentuan jadwal kereta api menggunakan PLI (Pemrograman Linear Integer) yang meminimumkan delay. Solusi yang didapat menggunakan bantuan software LINGO 8.0. Karya ilmiah ini merupakan rekonstruksi dari sebagian artikel yang berjudul A Heuristic for the Train Pathing and Timetabling Problem yang ditulis oleh Yusin Lee dan Chuen-Yih Chen tahun 2009.

1.2 Tujuan

Tujuan penulisan karya ilmiah ini adalah mencari penyelesaian masalah penjadwalan kereta api yang meminimumkan delay (keterlambatan) menggunakan PLI (Pemrograman Linear Integer).

II LANDASAN TEORI

Untuk membuat model penjadwalan kereta api diperlukan pemahaman teori Pemrograman Linear (PL) atau Linear Programming (LP), Pemrograman Linear Integer (PLI) atau Integer Linear Programming (ILP), dan metode branch-and-bound.

Definisi 1 (Fungsi linear)

Suatu fungsi f dalam variabel-variabel 1, 2,..., n

x x x adalah suatu fungsi linear jika dan hanya jika untuk suatu himpunan konstanta c c1, 2,...,c , n fungsi dapat dituliskan sebagai . ... ) ,..., , (x₁ x₂ x_n c₁x₁ c₂x₂ c_nx_n f (Winston 2004) Sebagai contoh, f x x( ,1 2) 2x1 3x 2 merupakan fungsi linear, sementara

2 2

1 2 1 2

( , )

f x x

x x

bukan fungsi linear.

Definisi 2 (Pertidaksamaan dan persamaan linear)

Untuk sembarang fungsi linear )

,..., , (x₁ x₂ x_n

f dan sembarang bilangan b,

pertidaksamaan f(x₁,x₂,...,x_n) b dan b x x x f( ₁, ₂,..., _n) adalah pertidaksamaan linear, sedangkan suatu persamaan

b x x x f( ₁, ₂,..., _n) merupakan persamaan linear. (Winston 2004) 2.1 Pemrograman Linear

Pemrograman Linear (PL) adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan berikut:

a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.

b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.

c) Ada pembatasan tanda untuk setiap variabel dalam masalah ini. Untuk sembarang variabel , pembatasan tanda menentukan harus tak-negatif ( ) atau tidak dibatasi tandanya (unrestricted in sign).

Suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.

Definisi 3 (Bentuk Standar suatu PL)

Suatu pemrograman linear dalam bentuk standar didefinisikan sebagai:

max z = (atau min) s.t. (2.1) Dengan mendefinisikan: A = ,

Maka kendala pada (2.1) dapat ditulis dengan sistem persamaan Ax = b (2.2) (Winston 2004)

2.1.1 Solusi suatu Pemrograman Linear

Suatu masalah PL dapat diselesaikan dalam berbagai teknik, salah satunya adalah metode simpleks. Metode ini dapat menghasilkan suatu solusi optimum bagi masalah PL dan telah dikembangkan oleh Dantzig sejak tahun 1947 (Winston 2004), dan dalam perkembangannya merupakan metode yang paling umum digunakan untuk menyelesaikan PL. Metode ini berupa metode iteratif untuk menyelesaikan PL berbentuk standar.

Pada masalah PL (2.2), vektor x yang memenuhi kendala Ax = b disebut sebagai solusi dari PL (2.2). Misalkan matriks A dapat dinyatakan sebagai A = (B N), dengan B adalah matriks taksingular berukuran m × m yang elemennya berupa koefisien variabel basis dan N merupakan matriks berukuran m × (n – m) yang elemennya berupa koefisien variabel nonbasis pada matriks kendala. Dalam hal ini matriks B disebut matriks basis untuk PL (2.2).

Misalkan x dinyatakan sebagai vektor x = , dengan xB adalah vektor variabel basis

dan xN adalah vektor variabel nonbasis, maka Ax = b dapat dinyatakan sebagai:

Ax =

= BxB + NxN = b (2.3)

Karena matriks B adalah matriks tak singular, maka B memiliki invers, sehingga dari (2.3)

xB dapat dinyatakan sebagai:

xB = B-1b - B-1NxN (2.4)

Kemudian, fungsi objektifnya berubah menjadi:

min z =

(Winston 2004)

Definisi 4 (Daerah Fisibel)

Daerah fisibel suatu PL adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada PL tersebut.

(Winston 2004)

Definisi 5 (Solusi Basis)

Solusi basis adalah solusi pada PL yang didapatkan dengan mengatur variabel n–m sama dengan nol dan nilai untuk penyelesaiannya adalah dari sisa variabel m. Hal ini mengasumsikan bahwa mengatur variabel n–m sama dengan nol sehingga membuat nilai yang unik untuk sisa variabel m atau sejenisnya, dan kolom-kolom untuk sisa dari variabel m adalah bebas linear.

(Winston 2004)

Definisi 6 ( Solusi Fisibel Basis)

Solusi fisibel basis adalah solusi basis pada PL yang semua variabel-variabelnya tak-negatif.

(Winston 2004)

Definisi 7 (Solusi Optimum)

Untuk masalah maksimisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Untuk masalah minimisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil.

(Winston 2004) Ilustrasi untuk solusi basis dan solusi fisibel basis diberikan dalam Contoh 1 di bawah ini.

Contoh 1

Misalkan diberikan PL berikut: minimumkan z = -2 - 3 terhadap -x1 + 2x2 + x3 = 10 -2x1 + x2 + x4 = 2 2x1 + x5 = 3

Dari PL (2.5) didapatkan:

A = , b =

Misalkan dipilih

= T dan = T maka matriks basisnya adalah

B = ,

N = .

.

Dengan menggunakan matriks basis tersebut diperoleh

.

(2.6) .

Solusi (2.6) merupakan solusi basis, karena solusi tersebut memenuhi kendala PL (2.5) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari (2.6) yaitu B adalah bebas linear (kolom yang satu bukan merupakan kelipatan dari kolom yang lain). Solusi (2.6) juga merupakan solusi fisibel basis, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.

2.2 Pemrograman Linear Integer

Pemrograman linear integer (PLI) adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat (integer). Jika semua variabel harus berupa integer, maka masalah tersebut dinamakan pure integer programming. Jika hanya sebagian yang harus berupa integer, maka disebut mixed integer programming (MIP). PLI dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 PLI

(Garfinkel & Nemhauser 1972)

Definisi 8 (Relaksasi Pemrograman Linear)

Relaksasi pemrograman linear atau sering disebut relaksasi-PL merupakan suatu pemrograman linear yang diperoleh dari suatu PLI dengan menghilangkan kendala integer atau kendala 0-1 pada setiap variabelnya.

Untuk masalah maksimisasi, nilai optimum fungsi objektif relaksasi-PL lebih besar atau sama dengan nilai optimum fungsi objektif PLI, sedangkan untuk masalah

minimisasi, nilai optimum fungsi objektif relaksasi-PL lebih kecil atau sama dengan nilai optimum fungsi objektif PLI.

(Winston 2004)

2.3 Metode Branch and Bound

Dalam penulisan karya ilmiah ini, untuk memperoleh solusi optimum dari masalah PLI digunakan software LINGO 8.0, yaitu sebuah program yang dirancang untuk menentukan solusi model linear, nonlinear, dan optimisasi integer. Software LINGO 8.0 ini menggunakan metode branch-and-bound untuk menyelesaikan masalah PLI.

Prinsip dasar metode branch-and-bound adalah memecah daerah fisibel dari masalah relaksasi-PL dengan membuat subproblem-subproblem. Terdapat dua konsep dasar dalam algoritma branch-and-bound.

1. Branch (Cabang)

Branching (pencabangan) adalah proses membagi permasalahan menjadi subproblem-subproblem yang mungkin mengarah ke solusi.

2. Bound (Batas)

Bounding (pembatasan) adalah suatu proses untuk mencari atau menghitung batas atas (dalam masalah minimisasi) dan batas bawah (dalam masalah maksimisasi) untuk solusi optimum pada subproblem yang mengarah ke solusi.

Metode branch-and-bound diawali dari menyelesaikan relaksasi-PL dari suatu pemrograman linear integer. Jika semua nilai variabel keputusan solusi optimum sudah berupa integer, maka solusi tersebut merupakan solusi optimum PLI. Jika tidak, dilakukan pencabangan dan penambahan batasan pada relaksasi-PLnya kemudian diselesaikan.

Winston (2004) menyebutkan bahwa untuk masalah maksimisasi nilai fungsi objektif optimum untuk PLI lebih kecil atau sama dengan nilai fungsi objektif optimum untuk relaksasi-PL, sehingga nilai fungsi objektif optimum relaksasi-PL merupakan batas atas bagi nilai fungsi objektif optimum untuk masalah PLI. Diungkapkan pula oleh Winston (2004) untuk masalah maksimisasi bahwa nilai fungsi objektif optimum untuk suatu kandidat solusi merupakan batas bawah nilai fungsi objektif optimum untuk masalah PLI asalnya. Suatu kandidat solusi diperoleh jika solusi dari suatu subproblem sudah memenuhi kendala integer pada masalah PLI,

artinya fungsi objektif dan semua variabelnya sudah bernilai integer.

Sebelumnya akan dibahas terlebih dahulu pengertian subproblem yang terukur. Menurut Winston (2004), suatu subproblem dikatakan terukur (fathomed) jika salah satu kondisi berikut terpenuhi:

a. Subproblem tersebut takfisibel, sehingga tidak dapat menghasilkan solusi optimum bagi PLI.

b. Subproblem tersebut menghasilkan suatu solusi optimum dengan semua variabelnya bernilai integer. Jika solusi optimum ini mempunyai nilai fungsi objektif yang lebih baik daripada solusi fisibel yang diperoleh sebelumnya, maka solusi ini menjadi kandidat solusi optimum dan nilai fungsi objektifnya menjadi batas bawah (dalam masalah maksimisasi) dan batas atas (dalam masalah minimisasi) nilai fungsi objektif optimum bagi masalah PLI pada saat itu. Bisa jadi subproblem ini menghasilkan solusi optimum untuk masalah PLI.

c. Nilai fungsi objektif optimum untuk subproblem tersebut tidak melebihi batas bawah saat itu (untuk masalah maksimisasi). Suatu subproblem dapat dieliminasi apabila subproblem tersebut takfisibel dan batas bawah kandidat solusi lebih kecil (untuk masalah maksimisasi) dari nilai fungsi objektif optimum untuk subproblem tersebut.

Berikut ini adalah langkah-langkah penyelesaian suatu masalah maksimisasi dengan metode branch-and-bound :

Langkah 0

Didefinisikan z sebagai batas bawah dari solusi PLI yang optimum. Pada awalnya tetapkan z = − dan i = 0.

Langkah 1

Subproblem PL(i) dipilih sebagai bagian masalah berikutnya untuk diteliti. Subproblem PL(i) diselesaikan dan diukur dengan kondisi yang sesuai.

a) Jika PL(i) terukur, maka batas bawah z dapat diperbarui. Batas bawah z dapat diperbaharui jika solusi PLI yang lebih baik telah ditemukan. Jika tidak, maka bagian masalah (subproblem) baru i dipilih dan langkah 1 diulangi. Jika semua subproblem telah diteliti, maka proses dihentikan.

b) Jika PL(i) tidak terukur, lanjutkan ke langkah 2 untuk melakukan pencabangan PL(i).

Langkah 2

Pilih satu variabel xj yang nilai optimumnya, yaitu xj*, tidak memenuhi batasan integer dalam solusi PL(i). Singkirkan bidang [xj*] xj [xj*]+1 dengan membuat dua bagian masalah PL yang berkaitan menjadi dua batasan yang tidak dapat dipenuhi secara bersamaan yaitu:

xj ≤ [xj*] dan xj ≥ [xj*]+1,

dengan [xj*] didefinisikan sebagai integer terbesar yang kurang dari atau sama dengan xj*. Jika PL(i) masih tidak terukur, maka kembali ke Langkah 1.

(Taha 1996) Untuk memudahkan pemahaman mengenai metode branch-and-bound diberikan contoh sebagai berikut:

Contoh 2

Misalkan diberikan PLI sebagai berikut: Maksimumkan z = 5 x1 + 4 x2

terhadap x1 + x2 5 10 x1 + 6 x2

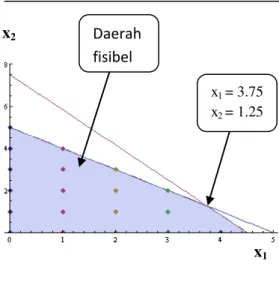
x1, x2 0 dan integer (2.7) Solusi optimal relaksasi-PL dari masalah PLI (2.7) adalah x1=3.75, x2=1.25, dan z =23.75 (lihat Lampiran 1). Jadi batas atas nilai optimal fungsi objektif masalah PLI (2.7) adalah z= 23.75. Daerah fisibel relaksasi-PL masalah (2.7) ditunjukkan pada Gambar 1 (daerah yang diarsir) sedangkan titik-titik merupakan solusi fisibel masalah PLI (2.7).

Gambar 1 Daerah fisibel PLI (2.7) Langkah berikutnya adalah memartisi daerah fisibel relaksasi-PL menjadi dua bagian berdasarkan variabel yang bernilai pecahan (non-integer). Karena x1= 3.75 dan x2=1.25 variabel bernilai pecahan maka dipilih

x

2

x

1

Daerah

fisibel

x1 = 3.75 x2 = 1.25

salah satu variabel, misalkan x1, sebagai dasar pencabangan. Jika masalah relaksasi-PL dari PLI (2.7) diberi nama Subproblem 1 dan Subproblem 1 dicabangkan atas x1, maka pencabangan tersebut menghasilkan 2 subproblem, yaitu:

Subproblem 2: Subproblem 1 ditambah kendala x1 ≥ 4

Subproblem 3: Subproblem 1 ditambah kendala x1 ≤ 3.

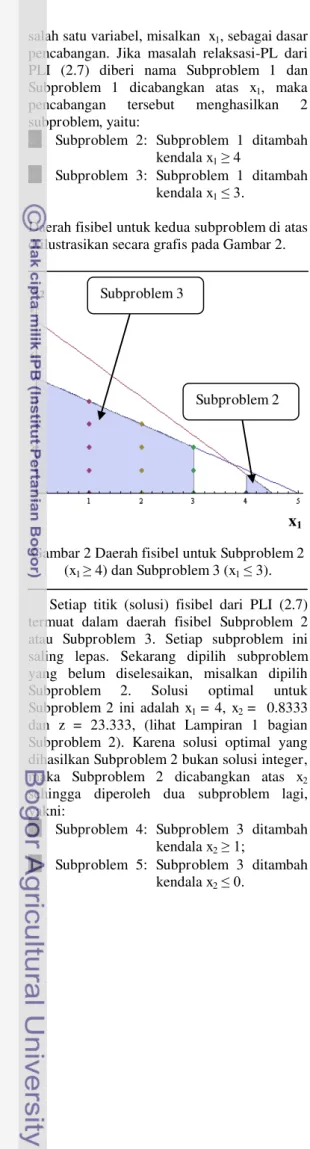
Daerah fisibel untuk kedua subproblem di atas diilustrasikan secara grafis pada Gambar 2.

Gambar 2 Daerah fisibel untuk Subproblem 2 (x1 ≥ 4) dan Subproblem 3 (x1 ≤ 3). Setiap titik (solusi) fisibel dari PLI (2.7) termuat dalam daerah fisibel Subproblem 2 atau Subproblem 3. Setiap subproblem ini saling lepas. Sekarang dipilih subproblem yang belum diselesaikan, misalkan dipilih Subproblem 2. Solusi optimal untuk Subproblem 2 ini adalah x1 = 4, x2 = 0.8333 dan z = 23.333, (lihat Lampiran 1 bagian Subproblem 2). Karena solusi optimal yang dihasilkan Subproblem 2 bukan solusi integer, maka Subproblem 2 dicabangkan atas x2 sehingga diperoleh dua subproblem lagi, yakni:

Subproblem 4: Subproblem 3 ditambah kendala x2 ≥ 1;

Subproblem 5: Subproblem 3 ditambah kendala x2 ≤ 0.

Saat ini subproblem yang belum diselesaikan adalah Subproblem 3, 4 dan 5. Salah satu subproblem dipilih, misalnya dengan aturan LIFO (last in first out). Dengan aturan ini berarti dipilih Subproblem 4 atau Subproblem 5. Subproblem 4 takfisibel (lihat Lampiran 1 bagian Subproblem 4) maka subproblem ini tidak dapat menghasilkan solusi optimal, yang tersisa adalah Subproblem 3 dan Subproblem 5.

Karena aturan LIFO, dipilih Subproblem 5, yang kemudian menghasilkan solusi optimal x1=4.5, x2=0 dan z=22.5 (lihat Lampiran 1 bagian Subproblem 5). Karena x1=4.5 bukan integer, maka dilakukan kembali pencabangan atas x1, sehingga diperoleh:

Subproblem 6: Subproblem 5 ditambah kendala x1≥5;

Subproblem 7: Subproblem 5 ditambah kendala x1≤4.

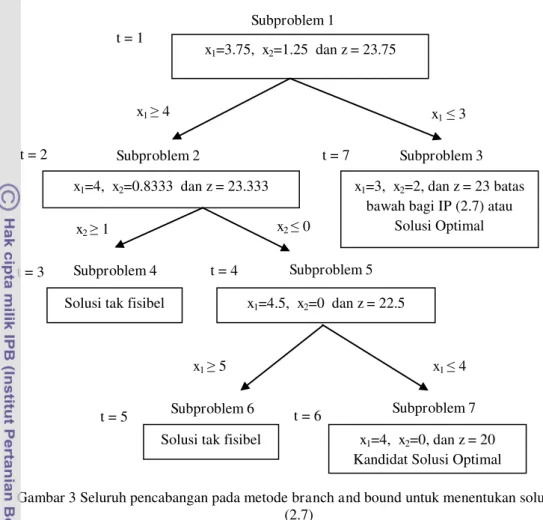
Misalkan dipilih Subproblem 6. Ternyata Subproblem 6 ini juga takfisibel (lihat Lampiran 1 bagian Subproblem 6), sehingga tidak dapat menghasilkan solusi optimal. Dengan demikian subproblem-subproblem yang belum diselesaikan adalah Subproblem 3 dan Subproblem 7. Karena aturan LIFO, dipilih Subproblem 7. Subproblem ini kemudian menghasilkan solusi opimal x1=4, x2= 0, dan z= 20 (lihat Lampiran 1 bagian Subproblem 7). Dapat dilihat bahwa solusi optimal subproblem ini semuanya berupa integer, sehingga merupakan kandidat solusi untuk PLI (2.7). Nilai z pada kandidat solusi ini merupakan batas bawah bagi nilai optimal PLI. Penyelesaian Subproblem 3 menghasilkan solusi optimal x1= 3, x2= 2 dan z= 23 (lihat Lampiran 1 bagian Subproblem 3). Batas bawah yang ditetapkan dari solusi optimal Subproblem 7 tidak lebih baik dari nilai solusi optimal yang dihasilkan Subproblem 3. Dengan demikian, nilai solusi optimal Subproblem 3, yakni z = 23 menjadi batas bawah yang baru. Semua solusi optimal telah berupa integer dan tidak perlu dilakukan pencabangan kembali, sehingga solusi optimal dari Subproblem 3 merupakan solusi optimal PLI (2.7), yakni x1= 3, x2= 2 dan z= 23. Pohon pencabangan yang menunjukkan proses penyelesaian masalah PLI (2.7) secara keseluruhan ditunjukkan pada Gambar 3.

x

1

x

2 Subproblem 3

Gambar 3 Seluruh pencabangan pada metode branch and bound untuk menentukan solusi PLI (2.7)

III DESKRIPSI DAN PEMODELAN MASALAH

3.1 Deskripsi masalah

Untuk mendeskripsikan masalah penjadwalan kereta api di setiap stasiun, hal utama yang harus diketahui adalah banyaknya rangkaian kereta yang ditugaskan di stasiun tersebut. Kemudian dari kereta api yang ditugaskan tadi, seberapa banyak ketersedian jalur yang dapat dilalui. Banyaknya kereta api yang beroperasi juga bergantung pada kebutuhan atau permintaan penumpang.

Dalam memenuhi keinginan penumpang, tersedia dua jenis kereta api yaitu kereta api reguler dan kereta api ekspress. Untuk kereta api regular, waktu tunggu di dalam stasiun lebih lama dibandingkan jenis yang kedua yaitu kereta api ekspress. Selain itu kecepatan kereta api jenis reguler lebih rendah dibandingkan kereta api jenis ekspress.

Berikut ini adalah gambaran dari suatu penjadwalan kereta api. Misalkan terdapat n buah stasiun yang masing-masing stasiun memiliki dua buah jalur pemberhentian dan

dari keseluruhan stasiun tersebut saling dihubungkan oleh jalur tunggal. Stasiun ke-1 dan stasiun ke-n adalah stasiun pemberangkatan, sedangkan stasiun ke-2 hingga stasiun ke−(n-1) adalah stasiun pemberhentian. Andaikan dioperasikan p kereta api ekspress dan q kereta api reguler. Kereta api tersebut ada yang diberangkatkan dari stasiun ke-1 dan juga dari stasiun ke-n. Pengelola stasiun dihadapkan pada masalah penjadwalan kereta sedemikian rupa sehingga dapat meminimumkan delay (keterlambatan), dengan memperhatikan kebutuhan pengguna kereta api.

3.2 Formulai masalah

Model penjadwalan kereta api bergantung pada ketersedian rangkaian kereta api dan jumlah jalur yang dapat dilalui. Selanjutnya, penjadwalan kereta api dapat diformulasikan dalam bentuk PLI.

x1=3.75, x2=1.25 dan z = 23.75

x1=4, x2=0.8333 dan z = 23.333 x1=3, x2=2, dan z = 23 batas bawah bagi IP (2.7) atau

Solusi Optimal

Solusi tak fisibel x1=4.5, x2=0 dan z = 22.5 t = 1

t = 2

x2 ≥ 1 x2 ≤ 0

Solusi tak fisibel x1=4, x2=0, dan z = 20 Kandidat Solusi Optimal

x1 ≤ 4 x1 ≥ 5 t = 5 t = 6 t = 7 t = 3 t = 4 Subproblem 1 Subproblem 3 Subproblem 2 Subproblem 4 Subproblem 5 Subproblem 7 Subproblem 6 x1≤ 3 x1 ≥ 4