Sistem jaringan syaraf kabur.

vii ABSTRAK

viii

ABSTRACT

SISTEM JARINGAN SYARAF KABUR

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh: Sisiria Mardiawati

NIM : 053114006

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii

FUZZY NEURAL NETWORK SYSTEM

Final Assignment

Presented to Fulfill One of the Requirements To Obtain the Sarjana Sains Degree

Mathematics Study Program

By :

Sisiria Mardiawati Student Number : 053114006

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

vi

HALAMAN PERSEMBAHAN

Bersukacitalah senantiasa Tetaplah berdoa

Mengucap syukurlah dalam segala hal, sebab itulah yang dikehendaki Allah di dalam Kristus Yesus bagi kamu (2 Tesalonika 16-18)

Janganlah hendaknya kamu kuatir tentang apa pun juga, tetapi nyatakanlah dalam segala hal keinginanmu kepada Allah dalam doa dan permohonan dengan ucapan syukur (Filipi 4:6)

vii ABSTRAK

viii

ABSTRACT

x

KATA PENGANTAR

Puji dan syukur kepada Tuhan Yang Maha Esa yang telah memberikan berkat dan rahmat-Nya sehingga penulis dapat menyelesaikan skripsi ini.

Penyusunan skripsi ini tidak lepas dari bantuan berbagai pihak yang memberikan dorongan, bimbingan, petunjuk, nasihat serta dukungan dari permulaan sampai selesainya penulisan skripsi ini. Oleh karena itu, pada kesempatan ini dengan segala kerendahan hati penulis ingin menyampaikan ucapan terimakasih kepada: 1. Bapak Yosef Agung Cahyanta S.T., M.T., selaku Dekan Fakultas Sains dan

Teknologi Universitas Sanata Dharma Yogyakarta.

2. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku Ketua Program Studi Matematika Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta sekaligus selaku Dosen Penguji tugas akhir yang selalu memberikan semangat kepada penulis.

3. Romo Prof. Dr. Frans Susilo, SJ, selaku Dosen Pembimbing skripsi dan Dosen Pembimbing akademik yang telah memberikan masukan, bimbingan, nasihat, dorongan serta saran dalam penulisan skripsi ini.

4. Bapak Y. G. Hartono, S.Si, M.Sc, selaku Dosen Penguji tugas akhir yang telah memberikan masukan dan saran.

5. Bapak dan Ibu dosen yang telah memberikan bekal ilmu kepada penulis.

xii DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN JUDUL DALAM BAHASA INGGRIS... ii

HALAMAN PERSETUJUAN PEMBIMBING... iii

HALAMAN PENGESAHAN... iv

HALAMAN PERNYATAAN KEASLIAN KARYA... v

HALAMAN PERSEMBAHAN... vi

ABSTRAK... vii

ABSTRACT... viii

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS... ix

KATA PENGANTAR... x

DAFTAR ISI... xii

BAB I PENDAHULUAN ... 1

A. Latar Belakang ... 1

B. Rumusan Masalah ... 6

C. Pembatasan Masalah ... 7

D. Tujuan Penulisan ... 7

E. Manfaat Penulisan ... 7

xiii

G. Sistematika Penulisan ... 8

BAB II LOGIKA KABUR, DEKOMPOSISI NILAI SINGULAR DAN JARINGAN SYARAF TIRUAN... 11

A. Logika Kabur ... 11

1. Himpunan Kabur ... 11

2. Fungsi Keanggotaan ... 18

3. Operasi Baku pada Himpunan Kabur ... 23

4. Perambatan Operasi Baku pada Himpunan Kabur ... 25

5. Relasi Kabur... 28

6. Variabel Linguistik... 29

7. Proposisi Kabur... 29

8. Implikasi Kabur... 30

9. Model Kabur Takagi Sugeno Kang (TSK)... 34

10. Modus Ponens Rampat... 35

11. Sistem Kendali Kabur... 44

B. Dekomposisi Nilai Singular... 45

C. Jaringan Syaraf Tiruan... 52

1. Konsep Dasar Jaringan Syaraf Tiruan... 52

2. Arsitektur Jaringan Syaraf... 55

3. Proses Pembelajaran... 57

4. Fungsi Aktivasi... 58

xiv

BAB III SISTEM JARINGAN SYARAF KABUR ... 75

A. Jaringan Syaraf dan Logika Kabur... 75

B. Model Kabur dengan Pembelajaran Jaringan Syaraf Terbimbing... 77

1. Arsitektur Jaringan Syaraf Kabur... 77

2. Pembelajaran Rambatan Balik Pada Model Kabur... 80

C. Contoh Model Jaringan Syaraf Kabur... 91

BAB IV PENUTUP... 99

BAB I

PENDAHULUAN

A. Latar Belakang

Dalam kehidupan sehari-hari terdapat banyak hal yang bersifat kompleks dan

rumit untuk dijelaskan secara tepat dan eksak. Sebuah model yang cocok untuk

menggambarkan hal tersebut bisa diperoleh dengan menggunakan himpunan kabur.

Pencapaian dengan menggunakan model tersebut berdasarkan pengamatan bahwa

manusia berpikir menggunakan bahasa yang digunakan seperti “kecil” atau “sangat

besar” dan ungkapan yang lainnya. Oleh karena itu, untuk mendeskripsikan konsep

tersebut ke dalam bahasa yang umum, Zadeh memperkenalkan himpunan kabur

(fuzzy sets) pada tahun 1965. Dalam hal ini Zadeh memperluas konsep “himpunan

klasik” (himpunan tegas, crisp set) menjadi himpunan kabur, dalam arti bahwa

him-punan klasik merupakan kejadian khusus dari himhim-punan kabur itu. Berdasarkan

kon-sep himpunan kabur itu, Zadeh mengembangkan konkon-sep algoritma kabur (1968),

yang merupakan landasan dari logika kabur (fuzzy logic) dan penalaran hampiran (

ap-proximate reasoning), yaitu penalaran yang melibatkan pernyataan-pernyataan

dengan predikat kabur. Inti dari sistem kabur ini sendiri adalah aturan implikasi jika –

maka (if – then rules), yang menggunakan himpunan kabur sebagai syarat dalam

Sejak manusia bisa melakukan banyak hal yang cukup sulit dibandingkan alat

teknologi yang sangat canggih, otak manusia menjadi hal yang sangat menarik bagi

para ahli. Otak manusia memiliki struktur yang sangat kompleks dan memiliki

ke-mampuan yang luar biasa. Otak terdiri dari neuron-neuron dan penghubung yang

disebut sinapsis. Neuron bekerja berdasarkan impuls/sinyal yang diberikan pada

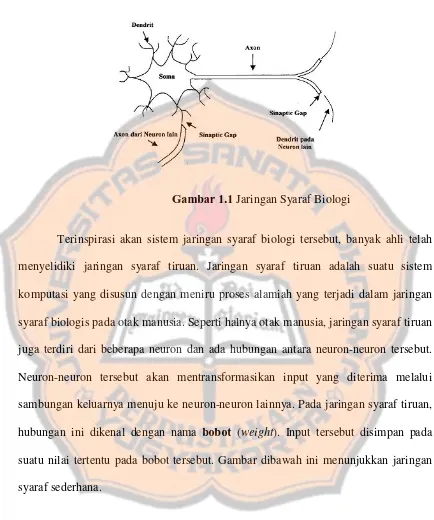
neu-ron. Setiap sel syaraf (neuron) memiliki 3 komponen penting yaitu soma yang

merupakan inti sel dari neuron yang bertugas untuk melakukan pemrosesan

informasi. Informasi yang datang akan diterima oleh dendrit, selain menerima

informasi dendrit juga menyertai axon sebagai keluaran dari suatu pemrosesan

informasi. Informasi hasil olahan ini akan menjadi masukan bagi neuron lain yang

dihubungkan oleh dua dendrit sel yang dipertemukan oleh sinapsis. Informasi yang

dikirimkan antar neuron ini berupa rangsangan yang dilewatkan melalui beberapa

dendrit. Informasi yang datang dan diterima oleh dendrit akan dijumlahkan dan

dikirim melalui axon ke dendrit akhir yang bersentuhan dengan dendrit dari neuron

yang lain. Informasi ini akan diterima oleh neuron lain jika memenuhi batasan

Gambar 1.1 Jaringan Syaraf Biologi

Terinspirasi akan sistem jaringan syaraf biologi tersebut, banyak ahli telah

menyelidiki jaringan syaraf tiruan. Jaringan syaraf tiruan adalah suatu sistem

komputasi yang disusun dengan meniru proses alamiah yang terjadi dalam jaringan

syaraf biologis pada otak manusia. Seperti halnya otak manusia, jaringan syaraf tiruan

juga terdiri dari beberapa neuron dan ada hubungan antara neuron-neuron tersebut.

Neuron-neuron tersebut akan mentransformasikan input yang diterima melalui

sambungan keluarnya menuju ke neuron-neuron lainnya. Pada jaringan syaraf tiruan,

hubungan ini dikenal dengan nama bobot (weight). Input tersebut disimpan pada

suatu nilai tertentu pada bobot tersebut. Gambar dibawah ini menunjukkan jaringan

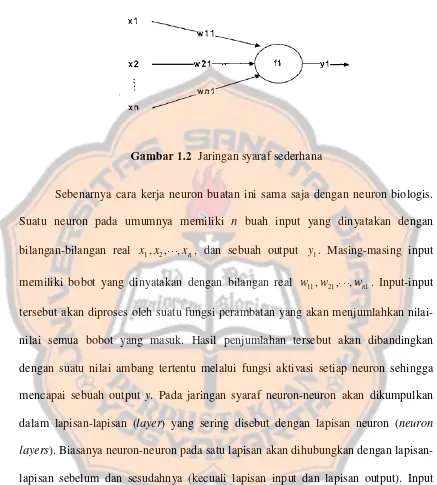
Gambar 1.2 Jaringan syaraf sederhana

Sebenarnya cara kerja neuron buatan ini sama saja dengan neuron biologis.

Suatu neuron pada umumnya memiliki n buah input yang dinyatakan dengan

bilangan-bilangan real x1,x2,⋅ ⋅⋅,xn, dan sebuah output y1. Masing-masing input

memiliki bobot yang dinyatakan dengan bilangan real w11,w21,⋅ ⋅⋅,wn1. Input-input

tersebut akan diproses oleh suatu fungsi perambatan yang akan menjumlahkan

nilai-nilai semua bobot yang masuk. Hasil penjumlahan tersebut akan dibandingkan

dengan suatu nilai ambang tertentu melalui fungsi aktivasi setiap neuron sehingga

mencapai sebuah output y. Pada jaringan syaraf neuron-neuron akan dikumpulkan

dalam lapisan-lapisan (layer) yang sering disebut dengan lapisan neuron (neuron

layers). Biasanya neuron-neuron pada satu lapisan akan dihubungkan dengan

lapisan-lapisan sebelum dan sesudahnya (kecuali lapisan-lapisan input dan lapisan-lapisan output). Input

yang dimasukkan pada jaringan syaraf akan dirambatkan mulai dari lapisan input

sampai ke lapisan output melalui lapisan yang lainnya, yang sering dikenal dengan

Gambar 1.3 Jaringan syaraf tiruan dengan lapisan tersembunyi

Jaringan syaraf dan logika kabur merupakan dua teknologi yang

komplementer. Jaringan syaraf dapat mengenali pola masukan yang diterimanya dan

dengan proses pembelajaran dapat menyesuaikan diri dengan masukan itu. Proses

pembelajaran pada suatu jaringan syaraf adalah proses penyesuaian diri jaringan itu

secara bertahap terhadap masukan yang diterimanya sampai akhirnya menghasilkan

keluaran yang diinginkan. Akan tetapi, memahami proses pembelajaran jaringan

syaraf cukup sulit karena sulit untuk menjelaskan makna setiap neuron dan setiap

bobot yang terkait. Sebaliknya, model berbasis aturan kabur mudah untuk dipahami

karena menggunakan istilah-istilah linguistik dan struktur aturan jika-maka. Akan

tetapi, tidak seperti jaringan syaraf, logika kabur tidak mengenal algoritma

pembelajaran. Penggabungan kedua teknologi tersebut menghasilkan istilah baru,

menggunakan kombinasi logika kabur dan jaringan syaraf. Sistem jaringan syaraf

kabur dirancang untuk merealisasikan proses logika kabur, dimana bobot-bobot yang

terhubung pada jaringan tersebut berhubungan dengan parameter-parameter logika

kabur. Dengan menggunakan algoritma pembelajaran rambatan balik, sistem jaringan

syaraf kabur dapat mengidentifikasi aturan-aturan kabur dan melatih fungsi

keanggotaan dari logika kabur tersebut. Sistem jaringan syaraf kabur dapat

diklasifikasikan ke dalam dua kategori, yaitu:

1. Model berbasis aturan kabur yang dibangun dengan menggunakan teknik

pembelajaran jaringan syaraf terbimbing.

2. Model berbasis aturan kabur yang menggunakan jaringan syaraf untuk

membangun partisi kabur dari ruang masukannya.

Yang akan dibahas dalam skripsi ini adalah sistem jaringan syaraf kabur kategori

pertama.

B. Rumusan Masalah

Pokok permasalahan yang akan dibahas dalam skripsi ini adalah:

1. Bagaimana bentuk model sistem jaringan syaraf kabur?

2. Bagaimana mengimplementasikan pembelajaran rambatan balik pada

C. Pembatasan Masalah

Dalam skripsi ini, penulis membahas tentang sistem jaringan syaraf kabur

yang merupakan interpretasi pembelajaran jaringan syaraf buatan dengan (pada)

model kabur. Pembelajaran yang digunakan adalah pembelajaran rambatan balik, dan

model kabur yang digunakan adalah model kabur Takagi Sugeno Kang (TSK).

D. Tujuan Penulisan

Tujuan dari penulisan skripsi ini adalah:

1. Mengetahui bagaimana bentuk model sistem jaringan syaraf kabur

2. Mengetahui implementasi pembelajaran rambatan balik pada model kabur

E. Manfaat Penulisan

Manfaat dari penulisan skripsi ini adalah dapat mengetahui dan memahami

bagaimana bentuk model sistem jaringan syaraf kabur serta mengetahui implementasi

F. Metode Penulisan

Metode penulisan yang digunakan dalam penulisan skripsi ini adalah metode

studi pustaka, yaitu dengan membaca dan mempelajari materi dari buku-buku acuan

yang berkaitan dengan topik skripsi.

G. Sistematika Penulisan

BAB I : PENDAHULUAN

A. Latar belakang masalah

B. Perumusan masalah

C. Pembatasan masalah

D. Tujuan penulisan

E. Manfaat penulisan

F. Metode penulisan

G. Sistematika penulisan

BAB II : LOGIKA KABUR DAN JARINGAN SYARAF TIRUAN

1. Himpunan Kabur

2. Fungsi Keanggotaan

3. Operasi Baku Pada Himpunan Kabur

4. Perampatan Operasi Baku Pada Himpunan

Kabur

5. Relasi Kabur

6. Variabel Linguistik

7. Proposisi Kabur

8. Implikasi Kabur

9. Prinsip Perluasan

10. Model Kabur Takagi Sugeno Kang

11. Generalisasi Modus Ponens

12. Sistem Kendali Kabur

B. Dekomposisi Nilai Singular (DNS)

C. Jaringan Syaraf Tiruan

2. Arsitektur Jaringan Syaraf

3. Proses Pembelajaran

4. Fungsi Aktivasi

5. Model Rambatan Balik (Backpropagation)

BAB III : SISTEM JARINGAN SYARAF KABUR

A. Jaringan Syaraf dan Logika Kabur

B. Model Kabur dengan Pembelajaran Jaringan Syaraf

Terbimbing

1. Arsitektur Jaringan Syaraf Kabur

2. Pembelajaran Rambatan Balik Pada Model

Kabur

C. Contoh Model Jaringan Syaraf Kabur

BAB II

LOGIKA KABUR, DEKOMPOSISI NILAI SINGULAR DAN JARINGAN SYARAF TIRUAN

A. Logika Kabur 1. Himpunan Kabur

Andaikan A adalah suatu himpunan tegas dalam semesta pembicaraan U,

maka A dapat didefinisikan dengan mendaftarkan semua anggotanya atau dengan

mendefinisikan kaidah yang harus dipenuhi oleh anggota dari himpunan tersebut. Jika

suatu objek x adalah anggota himpunan A, maka ditulis x∈A, dan jika x bukan

anggota A ditulis x∉A. Ada tiga metode untuk mendefinisikan suatu himpunan

dalam suatu semesta pembicaraan U, yaitu:

a. Metode pendaftaran, yaitu metode yang mendefinisikan suatu himpunan dengan

menyebut semua anggotanya. Metode ini digunakan hanya untuk

himpunan-himpunan berhingga. Himpunan A yang anggotanya a1,a2,...,an, ditulis:

A = (a1,a2,...,an)

b. Metode kaidah, yaitu metode yang mendefinisikan suatu himpunan dengan

menyebutkan syarat keanggotaannya. Dalam metode kaidah, himpunan A

=

A {x∈U |p(x)}

di mana p(x)menyatakan bahwa “x mempunyai sifat p”

c. Metode fungsi keanggotaan (fungsi karakteristik), yaitu metode yang

mendefinisikan suatu himpunan dengan sebuah fungsi yang disebut fungsi

karakteristik, untuk menyatakan bahwa anggota-anggota himpunan semesta U

adalah anggota himpunan itu atau bukan. Himpunan A didefinisikan dengan

fungsi karakteristik χ_A:U →{0,1}, sedemikian hingga:

   =

0 1 ) (x A

χ

untuk untuk

A x

A x

∉ ∈

Contoh 2.1 Andaikan U = {1, 2, , 11}. Didefinisikan himpunan A yang

anggota-anggotanya adalah bilangan-bilangan genap dalam himpunan semesta U. Maka

berdasarkan tiga metode di atas, himpunan A dapat dinyatakan sebagai berikut:

1. A= {2, 4, 6, 8, 10}

2. A={x∈U|x bilangan genap}

3.

   =

0 1 ) (x A

χ

jika jika

x x

ganjil bilangan

Fungsi karakteristik dari himpunan tegas menentukan dengan pasti nilai 0 atau

1 untuk setiap anggota U. Fungsi ini dapat diperumum sedemikian sehingga

nilai-nilai yang ditentukan untuk tiap anggota dari himpunan semesta berada dalam

interval tertutup [0,1] dan menunjukkan derajat keanggotaan dari anggota tersebut.

Nilai-nilai yang lebih besar menunjukkan derajat keanggotaan yang lebih tinggi.

Fungsi yang demikian disebut fungsi keanggotaan dan himpunan yang didefinisikan

berdasarkan fungsi tersebut disebut himpunan kabur.

Definisi 2.1 Suatu himpunan kabur A~ dalam semesta U adalah himpunan yang

dilengkapi dengan fungsi keanggotaan µ_A~ yang nilainya berada dalam interval [0,1],

yaitu:

] 1 , 0 [ :

~ U → A

µ

Nilai ~(x)

A

µ disebut derajat keanggotaan dari x dalam himpunan kabur A~.

Secara matematis suatu himpunan kaburA~dalam himpunan semesta U dapat

dinyatakan sebagai himpunan pasangan terurut:

} |

)) ( , {( ~

~ x x U

x

A= µ_A ∈

Apabila semesta U adalah himpunan yang kontinu, maka himpunan kabur A~

x A

U x

A /

~

~

∫

∈

= µ

di mana lambang

∫

di sini bukan lambang integral seperti yang dikenal dalam

kalkulus, tetapi melambangkan keseluruhan unsur-unsur x∈Udengan derajat

keanggotaan ~(x)

A

µ .

Apabila semesta U adalah himpunan yang diskret, maka himpunan kabur A~

seringkali dinyatakan dengan

x x A

U x

A( )/

~

~

∑

∈

= µ

di mana lambang

∑

di sini bukan lambang penjumlahan, tetapi melambangkan

keseluruhan unsur-unsur x∈Udengan derajat keanggotaan ~(x)

A

µ .

Angggota-anggota dari suatu himpunan kaburA~ yang mempunyai derajat

keanggotaan sama dengan 0, yaitu ~(x)=0

A

µ , seringkali tidak ditulis.

Contoh 2.2 Misalkan dalam himpunan semesta semua bilangan real ℝ, A~ adalah

himpunan “bilangan real yang dekat dengan nol”, maka himpunan kabur A~ dapat

x e A x x / ~ R 2

∫

∈ − =

Contoh 2.3 Dalam himpunan semesta U ={-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5},

himpunan kabur A~ dalam Contoh 2.2 di atas dapat dinyatakan sebagai

4 / 1 . 0 3 / 3 . 0 2 / 5 . 0 1 / 7 . 0 0 / 1 1 / 7 . 0 2 / 5 . 0 3 / 3 . 0 4 / 1 . 0 / ) ( ~ ~ = − + − + − + − + + + + + =

∑

∈ x x A U x A µ

Bilangan 5 dan -5 mempunyai derajat keanggotaan 0, sehingga tidak ditulis dalam

penyajian himpunan kabur diskret tersebut.

Berikut akan dibahas beberapa konsep dasar dan istilah-istilah yang

berhubungan dengan himpunan kabur. MisalkanA~ adalah himpunan kabur dalam

himpunan semesta U.

Definisi 2.2 Pendukung (support) dari himpunan kabur A~ adalah himpunan tegas

) ~ (A

P yang memuat semua anggota semesta dengan derajat keanggotaan taknol

dalam A~, yaitu

} 0 ) ( | { ) ~

(A = x∈U ~ x >

P µ_A .

Dari Contoh 2.3 di atas, P(A~)={-4, -3, -2, -1, 0, 1, 2, 3, 4}

Definisi 2.4 Himpunan kabur elemen tunggal adalah himpunan kabur yang

pendukungnya adalah himpunan tegas dengan elemen tunggal (singleton).

Definisi 2.5 Tinggi (height) dari himpunan kaburA~ adalah derajat keanggotaan

terbesar yang dicapai oleh anggota-anggota U, yaitu

)} ( { sup ) ~

(A ~ x

Tinggi _A

U x

µ

∈

= .

Dari Contoh 2.3 di atas, Tinggi(A~)=1.

Definisi 2.6 Himpunan kabur A~ yang memiliki tinggi sama dengan 1 disebut

himpunan kabur normal.

Definisi 2.7 Himpunan kabur A~ yang memiliki tinggi kurang dari 1 disebut

himpunan kabur subnormal.

Definisi 2.8 Titik silang (crossover point) dari himpunan kabur A~ adalah anggota U

yang mempunyai derajat keanggotaan sama dengan 0.5 dalam himpunan kabur A~.

Dalam Contoh 2.3 di atas, titik 2 dan -2 adalah titik silang dari himpunan kabur A~.

Definisi 2.9 Teras (core) dari himpunan kabur A~ adalah himpunan semua anggota U

} 1 ) ( | { ) ~

(A = x∈U ~ x =

Teras µ_A .

Definisi 2.10 Pusat (center) dari himpunan kabur A~ didefinisikan sebagai berikut: jika nilai rata-rata dari semua titik di mana fungsi keanggotaan himpunan kabur itu

mencapai nilai maksimum adalah berhingga, maka pusat himpunan kabur itu adalah

nilai rata-rata tersebut; jika nilai rata-rata itu takhingga positif (negatif), maka pusat

himpunan kabur itu adalah yang terkecil (terbesar) di antara semua titik yang

mencapai nilai fungsi keanggotaan maksimum.

Definisi 2.11 Potongan-α (α-cut) dari himpunan kabur A~ adalah himpunan tegas

α

A yang terdiri dari semua anggota U yang mempunyai derajat keanggotaan dalam

A~ lebih besar dari atau sama dengan α, yaitu:

} ) ( |

{ µ~ α

α = x∈U x ≥

A _A .

Definisi 2.12 Potongan-αkuat dari himpunan kabur A~ adalah himpunan tegas A_α′

yang terdiri dari semua anggota U yang mempunyai derajat keanggotaan dalam A~

lebih besar dari α , yaitu:

} ) ( |

{ µ~ α

α′ = x∈U x >

A _A .

Dari Contoh 2.3 di atas, potongan-

α

dari A~ dengan α = 0.5 adalah A0.5 ={-2, -1, 0,

Definisi 2.13 Dua buah himpunan kabur A~ dan B~ dalam himpunan semesta U

dikatakan sama, dilambangkan dengan A~=B~, bila dan hanya bila

) ( )

( ~

~ x x

B

A µ

µ = , ∀x∈U.

Definisi 2.14 Himpunan kabur A~ dikatakan himpunan bagian darihimpunan kabur

B~, dilambangkan dengan A~⊆B~, bila dan hanya bila

) ( )

( ~

~ x x

B

A µ

µ ≤ , ∀x∈U .

Contoh 2.4 Jika A~ = 0.2/-3 + 0.3/-2 + 0.7/-1 + 1/0 + 0.7/1 + 0.3/2 + 0.2/3 dan B~ =

0.3/-3 + 0.4/-2 + 0.8/-1 + 1/0 + 0.8/1 + 0.4/2 + 0.3/3, maka A~⊆B~.

Definisi 2.15 Himpunan kosong φ dapat dipandang sebagai himpunan kabur dengan

fungsi keanggotaan sama dengan 0, yaitu µ_φ(x)=0 untuk setiap x∈U. Himpunan

semesta U dapat dipandang sebagai himpunan kabur dengan fungsi keanggotaan

sama dengan 1, yaitu µ_u(x)=1 untuk setiap x∈U.

2. Fungsi Keanggotaan

Setiap himpunan kabur dapat dinyatakan dengan fungsi keanggotaan.

Beberapa fungsi keanggotaan himpunan kabur yang dinyatakan dalam bentuk suatu

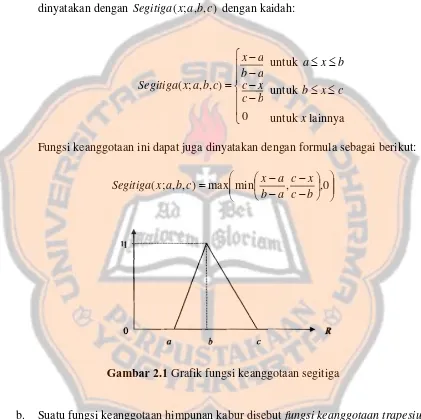
a. Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan segitiga

jika mempunyai tiga buah parameter, yaitu a,b,c∈ℝ dengan a<b<c, dan

dinyatakan dengan Segitiga(x;a,b,c) dengan kaidah:

       − − − − = 0 ) , , ; ( b c x c a b a x c b a x Segitiga

Fungsi keanggotaan ini dapat juga dinyatakan dengan formula sebagai berikut:

            − − − −

=max min , ,0

[image:35.612.97.518.177.597.2]

) , , ; ( b c x c a b a x c b a x Segitiga

Gambar 2.1 Grafik fungsi keanggotaan segitiga

b. Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan trapesium

jika mempunyai empat buah parameter, yaitu a,b,c,d∈ℝ dengan a<b<c<d,

dan dinyatakan dengan Trapesium(x;a,b,c,d) dengan kaidah:

untuk a≤x≤b

untuk b≤x≤c

          − − −− = 0 1 ) , , , ; ( c d x d a b a x d c b a x Trapesium

Fungsi keanggotaan ini dapat juga dinyatakan dengan formula sebagai berikut:

            − − − −

=max min ,1, ,0

[image:36.612.96.524.101.612.2]

) , , , ; ( c d x d a b a x d c b a x Trapesium

Gambar 2.2 Grafik fungsi keanggotaan trapesium

c. Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan Gauss

jika mempunyai dua buah parameter, yaitu a,b∈ℝ, dinyatakan dengan

) , ; (x a b

Gauss dan memenuhi:

2 ) , ; (      − − = b a x e b a x Gauss

untuk a≤ x≤b

untuk b≤x≤c

untuk c≤x≤d

[image:37.612.92.533.109.580.2]

Gambar 2.3 Grafik fungsi keanggotaan Gauss

di mana x=a adalah pusat dan b menentukan lebar dari fungsi keanggotaan

Gauss.

d. Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan Cauchy

jika mempunyai tiga buah parameter, yaitu a,b,c∈ℝ, dinyatakan dengan

) , , ;

(x a b c

Cauchy dan memenuhi:

b

a c x c

b a x

Cauchy ₂

1 1 )

, , ; (

− +

=

di mana x=c adalah pusat, a menentukan lebar, dan b menentukan kemiringan

[image:38.612.95.530.101.609.2]

Gambar 2.4 Grafik fungsi keanggotaan Cauchy

e. Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan Sigmoid

jika mempunyai dua buah parameter, yaitu a,c∈ℝ, dinyatakan dengan

) , ; (x a c

Sigmoid dan memenuhi:

) (

1 1 )

, ;

( _{a x c}

e c

a x

Sigmoid _{− −}

+ =

di mana a menentukan kemiringan fungsi keanggotaan sigmoid di titik silang

c

x= . Untuk a>0 fungsi keanggotaan Sigmoid terbuka ke kanan, dan

[image:39.612.93.530.105.624.2]

Gambar 2.5 Grafik fungsi keanggotaan Sigmoid yang terbuka ke kanan (gambar kiri) dan yang terbuka ke kiri (gambar kanan)

3. Operasi Baku pada Himpunan Kabur

Operasi baku pada himpunan kabur yang akan didefinisikan adalah operasi uner

“komplemen” dan operasi-operasi biner “gabungan” dan “irisan”. Komplemen dari

suatu himpunan kabur A~ adalah himpunan kabur A~′ dengan fungsi keanggotaan

) ( 1 )

( ~

~ x x

A

A µ

µ _′ = −

untuk setiap x∈ X. Gabungan dua buah himpunan kabur A~ dan B~ adalah himpunan

kabur A~∪B~ dengan fungsi keanggotaan

=

∪~( )

~ x

B A

µ max { ~(x), ~(x)}

B

A µ

µ

untuk setiap x∈X. Sedangkan irisan dua buah himpunan kabur A~ dan B~ adalah

=

∩~( )

~ x

B A

µ min { ~(x), ~(x)}

B

A µ

µ

untuk setiap x∈X.

Teorema 2.1 (Teorema Dekomposisi)

Jika A_α adalah potongan-α dari himpunan kabur A~ dalam himpunan semesta U dan

α

A~ adalah himpunan kabur dalam U dengan fungsi keanggotaan ~ _A (x)

Aα αχ α

µ =

untuk setiap x∈U, di mana χA_α adalah fungsi karakteristik dari himpunan Aα,

maka



] 1 , 0 [ ~ ~ ∈ = a A

A _α .

Bukti: Ambil sebarang x∈U dan misalkan µ_A~(x)=r. Untuk setiap α∈[0,r],

α

µ_A~(x)=r≥ , berarti x∈A_α, sehingga µ α

α( )=

~ x

A . Untuk setiap α∈(r,1],

α

µ_A~(x)=r< , berarti x∉A_α, sehingga ~ (x)=0 A_α

µ . Maka

_ ] 1 , 0 [ ~ ∈ α α

µ _A = sup ~ ( )

untuk setiap x∈U. Jadi



] 1 , 0 [

~ ~

∈

=

a A

A _α . ■

4. Perampatan Operasi Baku pada Himpunan Kabur

Di atas telah dibahas definisi operasi-operasi baku komplemen, gabungan dan

irisan untuk himpunan-himpunan kabur. Definisi-definisi tersebut dapat dirampatkan

sedemikian sehingga definisi operasi-operasi baku tersebut merupakan kejadian

khususnya. Perampatan tersebut akan didefinisikan secara aksiomatis, kemudian akan

diperlihatkan macam-macam operasi yang memenuhi aksioma-aksioma tersebut.

a. Operasi Komplemen

Definisi 2.17 Suatu pemetaan k:[0,1]→[0,1] disebut komplemen kabur jika

memenuhi aksioma-aksioma berikut:

K1. k(0)=1dan k(1)=0 (syarat batas)

K2. Jika x< y, maka k(x)≥k(y) untuk semua x,y∈[0,1] (syarat taknaik)

Suatu kelas pemetaan yang merupakan komplemen kabur adalah kelas Sugeno yang

didefinisikan sebagai berikut:

x x x

k

λ

λ ₊

− =

dengan parameter λ∈(−1,∞). Untuk λ=0, diperoleh operasi komplemen baku,

yaitu k₀(x)=1−x, di mana x adalah derajat keanggotaan suatu elemen dalam suatu

himpunan kabur A~ dan k0(x) adalah derajat keanggotaan elemen tersebut dalam

himpunan kabur A~′. Kelas pemetaan lain yang merupakan komplemen kabur adalah

kelas Yager yang didefinisikan sebagai berikut:

w w

w x x

k ( )=(1− )1/

dengan parameter w∈(0,∞). Untuk w=1 diperoleh operasi komplemen baku, yaitu

x x

k1( )=1− .

b. Operasi Gabungan

Definisi 2.18 Suatu pemetaan s:[0,1]×[0,1]→[0,1] disebut gabungan kabur (

norma-s) jika memenuhi aksioma-aksioma berikut:

S1. s(0,x)=s(x,0)=x dan s(1,1)=1 (syarat batas)

S2. s(x,y)=s(y,x) (syarat komutatif)

S3. Jika x≤x′ dan y≤y′, maka s(x,y)≤s(x′,y′), ∀x,y∈[0,1] (syarat takturun)

Contoh-contoh norma-s:

a) Jumlah aljabar: s_ja(x,y)=x+y−xy

b) Jumlah Einstein:

xy y x y x sje

+ + =

1 ) , (

c) Jumlah drastis:

     =

1 ) ,

( y

x

y x s_jd

lainnya 0 0

jika jika jika

= =

x y

c. Operasi Irisan

Definisi 2.19 Suatu pemetaan t:[0,1]×[0,1]→[0,1] disebut irisan kabur (norma-t)

jika memenuhi aksioma-aksioma berikut:

T1. t(x,1)=t(1,x)=x dan t(0,0)=0 (syarat batas)

T2. t(x,y)=t(y,x) (syarat komutatif)

T3. Jika x≤x′ dan y≤y′, maka t(x,y)≤t(x′,y′), ∀x,y∈[0,1] (syarat takturun)

T4. t(t(x,y),z)=t(x,t(y,z)) (syarat asosiatif)

Contoh-contoh norma-t:

b) Darab Einstein:

) (

2 ) , (

xy y x

xy y

x t_de

− + − =

c) Darab drastis:

     =

0 ) ,

( y

x

y x t_dd

lainnya 1 1

jika jika jika

= =

x y

5. Relasi Kabur

Definisi 2.15 Relasi kabur (biner) R~ antara elemen-elemen dalam himpunan U

dengan elemen-elemen dalam himpunan V didefinisikan sebagai himpunan kabur

dengan semesta U×V, yaitu himpunan kabur

} )

, ( | )) , ( ), , {(( ~

~ u v u v U V v

u

R= µ_R ∈ ×

Relasi kabur R~ itu juga disebut relasi kabur pada himpunan semesta U×V. Jika

V

U = , maka R~ disebut relasi kabur pada himpunan U.

Contoh 2.5 Misalnya U = {20, 45, 106}, V = {35, 58, 210} dan R~ adalah relasi

kabur “jauh lebih kecil” antara elemen-elemen dalam U dengan elemen-elemen

dalam V. Maka relasi R~ dapat disajikan sebagai R~ = 0.1/(20,35) + 0.3/(20,58) +

6. Variabel Linguistik

Definisi 2.16 Suatu variabel linguistik adalah suatu rangkap-5 (x, T, U, G, M) di

mana x adalah lambang variabelnya, T adalah himpunan nilai-nilai linguistik yang

dapat menggantikan x, U adalah semesta wacana (numeris) dari nilai-nilai linguistik

dalam T (jadi juga dari variabel x), G adalah himpunan kaidah-kaidah sintaksis yang

mengatur pembentukan istilah-istilah anggota T, dan M adalah himpunan

kaidah-kaidah semantik yang mengaitkan setiap istilah dalam T dengan suatu himpunan

kabur dalam semesta U.

Contoh 2.6 Bila variabel linguistiknya adalah “kecepatan”, maka himpunan

nilai-nilai linguistik dapat diambil himpunan istilah-istilah T = {cepat, sangat cepat, agak

cepat, tidak cepat, lambat, sangat lambat, agak lambat, tidak lambat} dengan semesta

U = [0,100], kaidah sintaksis mengatur pembentukan istilah-istilah dalam T dan

kaidah semantik mengaitkan setiap istilah dalam T dengan suatu himpunan kabur

dalam semesta U.

7. Proposisi Kabur

Definisi 2.17 Proposisi kabur adalah kalimat yang memuat predikat kabur, yaitu predikat yang dapat direpresentasikan dengan suatu himpunan kabur.

Proposisi kabur yang mempunyai nilai kebenaran tertentu disebut pernyataan

real dalam selang [0,1]. Nilai kebenaran itu disebut juga derajat kebenaran dari

pernyataan kabur itu.

Bentuk umum dari suatu proposisi kabur adalah

x adalah A

di mana x adalah suatu variabel linguistik dan predikat A adalah suatu nilai linguistik

dari x.

Bila A~ adalah himpunan kabur yang dikaitkan dengan nilai linguistik A dan

0

x adalah suatu elemen tertentu dalam semesta U dari himpunan kabur A~, maka x₀

mempunyai derajat keanggotaan µA~(x0) dalam himpunan kabur A

~ .

Derajat kebenaran dari pernyataan kabur

0

x adalah A~

didefinisikan sama dengan derajat keanggotaan x₀ dalam himpunan kabur A~, yaitu

) ( 0 ~ x A

µ .

8. Implikasi Kabur

Jika u adalah A, maka v adalah B

di mana A dan B adalah predikat-predikat kabur yang dikaitkan dengan

himpunan-himpunan kabur A~ dan B~ dalam semesta U dan V berturut-turut. Implikasi kabur

dilambangkan dengan →.

Implikasi tegas p→q ekuivalen dengan ¬p∨q. Berdasarkan ekuivalensi

tersebut, implikasi kabur dapat diinterpretasikan sebagai relasi kabur → dalam

V

U× dengan fungsi keanggotaan

)) ( ( )), ( ( ( ) ,

(u v s k ~ u ~ v

B

A µ

µ

µ_→ =

di mana s adalah suatu norma-s dan k adalah suatu komplemen kabur.

Implikasi Dienes-Rescher diperoleh apabila diambil operasi-operasi

gabungan sebagai norma-s dan operasi komplemen baku sebagai komplemen kabur

dengan fungsi keanggotaan

)) ( ), ( 1 max( )

,

(u v ~ u ~ v

B A

dr µ µ

µ_→ = − .

Karena implikasi tegas p→q juga ekuivalen dengan (p∧q)∨¬p, maka

implikasi kabur juga dapat diinterpretasikan sebagai relasi kabur → dalam U×V

dengan fungsi keanggotaan

))) ( ( )), ( ), ( ( ( ) ,

(u v s t ~ u ~ v k ~ u

A B

A µ µ

µ

di mana s adalah suatu norma-s, t adalah suatu norma-t, dan k adalah suatu

komplemen kabur.

Implikasi Zadeh diperoleh apabila diambil operasi-operasi gabungan, irisan,

dan komplemen baku sebagai norma-s, norma-t, dan komplemen kabur dengan fungsi

keanggotaan

)) ( 1 )), ( ), ( max(min( )

,

(u v ~ u ~ v ~ u

A B

A

z µ µ µ

µ_→ = − .

Implikasi Mamdani merupakan salah satu bentuk implikasi kabur yang

digunakan dalam aplikasi sistem kabur. Implikasi ini didasarkan pada asumsi bahwa

implikasi kabur pada dasarnya bersifat lokal, dalam arti bahwa implikasi

Jika u adalah A, maka v adalah B

hanya berbicara mengenai keadaan dimana u adalah A dan v adalah B saja, dan tidak

mengenai keadaan lainnya diluar itu. Berdasarkan asumsi tersebut, implikasi kabur

dapat dipandang sebagai suatu konjungsi kabur, sehingga diperoleh

)) ( ), ( ( ) ,

(u v t ~ u ~ v

B

A µ

µ

µ_→ =

yang disebut implikasi Mamdani. Apabila diambil operasi baku “min” sebagai

norma-t, maka diperoleh

)) ( ), ( min( )

,

(u v ~ u ~ v

B A

mm µ µ

dan bila operasi “darab aljabar” diambil sebagai norma-t, maka diperoleh ) ( ) ( ) ,

(u v ~ u ~ v

B A

md µ µ

µ_→ = .

Contoh 2.7

Misalkan diketahui semesta U = {1, 2, 3, 4} dan V = {60, 70, 80}, dan implikasi

kabur

Jika u banyak, maka v lambat

di mana predikat “banyak” dan “lambat” berturut-turut dikaitkan dengan himpunan

kabur . 80 / 1 70 / 7 . 0 60 / 4 . 0 ~ 4 / 8 . 0 3 / 6 . 0 2 / 4 . 0 1 / 2 . 0 ~ + + = + + + = B A dan

Maka jika digunakan implikasi Dienes-Rescher, diperoleh

) 60 , 3 /( 4 . 0 ) 80 , 2 /( 1 ) 70 , 2 /( 7 . 0 ) 60 , 2 /( 6 . 0 ) 80 , 1 /( 1 ) 70 , 1 /( 8 . 0 ) 60 , 1 /( 8 .

0 + + + + + +

=

→_dr

+0.7/(3,70)+1/(3,80)+0.4/(4,60)+0.7/(4,70)+1/(4,80)

Jika digunakan implikasi Zadeh, maka diperoleh

) 60 , 3 /( 4 . 0 ) 80 , 2 / 6 . 0 ) 70 , 2 /( 6 . 0 ) 60 , 2 /( 6 . 0 ) 80 , 1 /( 8 . 0 ) 70 , 1 /( 8 . 0 ) 60 , 1 /( 8 .

0 + + + + + +

=

→_z

Jika digunakan implikasi Mamdani, maka diperoleh ) 80 , 2 /( 4 . 0 ) 70 , 2 /( 4 . 0 ) 60 , 2 /( 4 . 0 ) 80 , 1 /( 2 . 0 ) 70 , 1 /( 2 . 0 ) 60 , 1 /( 2 .

0 + + + + +

= →_mm ) 80 , 4 /( 8 . 0 ) 70 , 4 /( 7 . 0 ) 60 , 4 /( 4 . 0 ) 80 , 3 /( 6 . 0 ) 70 , 3 /( 6 . 0 ) 60 , 3 /( 4 .

0 + + + + +

+ atau ) 80 , 2 /( 4 . 0 ) 70 , 2 /( 28 . 0 ) 60 , 2 /( 16 . 0 ) 80 , 1 /( 2 . 0 ) 70 , 1 /( 14 . 0 ) 60 , 1 /( 08 .

0 + + + + +

= →_md ). 80 , 4 /( 8 . 0 ) 70 , 4 /( 56 . 0 ) 60 , 4 /( 32 . 0 ) 80 , 3 /( 6 . 0 ) 70 , 3 /( 42 . 0 ) 60 , 3 /( 24 .

0 + + + + +

+

9. Model Kabur Takagi, Sugeno, dan Kang

Model kabur Takagi, Sugeno dan Kang (TSK) dikenal sebagai model kabur

pertama yang dikembangkan untuk menghasilkan kaidah kabur dari himpunan data

masukan-keluaran yang diberikan. Sebuah kaidah kabur yang khas dalam model

tersebut memiliki bentuk sebagai berikut:

Jika x adalah A dan y adalah B, maka z=ax+by+c

di mana a, b, c merupakan konstanta numerik. Secara umum, kaidah dalam model

TSK memiliki bentuk:

di mana A dan B merupakan himpunan kabur dalam anteseden, dan z= f(x,y)

merupakan fungsi tegas dalam konsekuen serta z = f(x,y) merupakan fungsi

polinomial dalam variabel masukan x dan y. Jika f(x,y) adalah fungsi polinomial

ordo satu, hasil sistem inferensi kabur disebut model kabur Takagi Sugeno Kang ordo

satu. Jika f merupakan konstanta, maka disebut model kabur Takagi Sugeno Kang

ordo nol, yang mana merupakan kasus khusus dalam implikasi Mamdani.

10. Modus Ponens Rampat

Untuk melakukan pengambilan keputusan atau penalaran kabur diperlukan

seperangkat implikasi kabur atau suatu fakta yang diketahui (premis). Dalam logika

klasik, pengambilan keputusan didasarkan pada tautologi-tautologi, yaitu

proposisi yang selalu benar, tanpa tergantung pada nilai kebenaran

proposisi-proposisi penyusunnya. Salah satu kaidah pengambilan keputusan yang paling sering

digunakan adalah modus ponens, yang didasarkan pada tautologi:

q p q

p→ )∧ )→

(( .

Bentuk umum penalaran modus ponens adalah sebagai berikut:

1. Bila u adalah A, maka v adalah B (Premis 1 / Kaidah)

2. u adalah A (Premis 2 / Fakta)

Kaidah penalaran tegas dapat dirampatkan menjadi kaidah kabur dengan

premis dan kesimpulannya adalah proposisi-proposisi kabur. Secara umum dapat

dirumuskan dengan skema sebagai berikut:

Premis 1 (kaidah) : Bila u adalah A, maka v adalah B

Premis 2 (fakta) : u adalah A′

Kesimpulan : v adalah B′

Penalaran kabur dengan skema seperti di atas disebut modus ponens rampat.

Berikut ini akan dibahas suatu aturan penarikan kesimpulan yang disebut “kaidah

inferensi komposisional” (compositional rule of inference). Sebelumnya akan dibahas

latar belakang kaidah tersebut dalam kasus pemetaan bernilai selang.

Misalkan diketahui suatu pemetaan kontinu f :U →V dengan U =V =ℝ.

Jika diberikan suatu elemen a∈U, maka akan diperoleh nilai pemetaan f di a, yaitu

V a f

b= ( )∈ . Jika f adalah suatu pemetaan yang bernilai selang, dan diberikan suatu

selang [a,b] di U, maka akan diperoleh nilai pemetaan f di [a,b] yaitu selang

] , [ ]) ,

([a b c d

f = di V. Untuk menggambarkan bagaimana memperoleh selang [c,d]

tersebut, pertama-tama yang dilakukan adalah membuat perluasan silindris dari

selang [a,b] ke bidang U×V , kemudian ditentukan irisan I dari perluasan silindris itu

dengan kurva dari pemetaan f, dan akhirnya irisan I diproyeksikan ke V untuk

[image:53.612.95.530.108.615.2]

Gambar 2.6 Nilai pemetaan f di [a,b], yaitu f([a,b])=[c,d]

Proses di atas dapat dirampatkan lebih lanjut lagi. Misalkan terdapat sebuah

relasi kabur R~ dalam semesta U×V dan himpunan kabur A~ dalam U. Bila

ditentukan perluasan silindris dari A~ ke U×V, namakan APS

~

, dan irisan perluasan

silindris tersebut dengan R~, yaitu APS R

~

~ _∩

, kemudian irisan tersebut diproyeksikan

ke V, maka akan diperoleh himpunan kabur B~ di V. Karena APS

~

adalah perluasan

silindris dari A~ ke U×V , maka

) ( ) ,

( ~

~ u v u

A

A_PS µ

µ =

sehingga

)) , ( ), , ( ( ) ,

( ~ ~

~

~ u v t u v u v

R A

R

APS µ PS µ

µ _∩ =

t( ~(u), ~(u,v))

R

A µ

di mana t adalah suatu norma-t. Kemudian, himpunan kabur B~ di V diperoleh sebagai

proyeksi irisan A~_PS ∩R~ ke V, maka

) , ( sup

)

( ~ _~

~ v u v

R PS

A U u

B _∩

∈

= µ

µ

supt( ~(u), ~(u,v))

R A U u

µ µ

∈

=

Jika himpunan kabur A~ dipandang sebagai relasi dengan satu argumen, maka

komposisi relasi A~ di U dengan relasi R~ di U×V menghasilkan relasi majemuk

R

A~ ~ di V dengan fungsi keanggotaan

)) , ( ), ( ( sup )

( ~ ~

~

~ v t u u v

R A U u R

A µ µ

µ

∈

=



di mana t adalah suatu norma-t. Maka B~= A~R~, yaitu himpunan kabur B~ itu tidak

lain daripada relasi komposit A~R~. Karenanya prosedur untuk memperoleh

himpunan kabur B~ di V dari relasi R~ di U×V dan himpunan kabur A~ di U dengan

cara seperti di atas itu disebut kaidah inferensi komposisional. Kaidah inilah yang

dipakai untuk menarik kesimpulan dalam penalaran kabur.

Dalam modus ponens rampat kaidah tersebut diterapkan sebagai berikut:

Premis 1 : Bila u adalah A, maka v adalah B

(yang merupakan relasi/implikasi kabur → di U×V)

(yang dapat direpresentasikan dengan himpunan kabur A~′ dalam U)

Kesimpulan : v adalah B′

diperoleh dengan menentukan himpunan kabur B~′= A~′ dalam V

dengan fungsi keanggotaan ~(v) supt( ~(u), (u,v))

A U u

B ′ →

∈

′ = µ µ

µ ,

dimana t adalah suatu norma-t.

Bila A′ adalah predikat kabur yang dikaitkan dengan himpunan kabur A~′,

untuk norma-t misalnya diambil operasi baku “min”, dan untuk implikasi kabur

dipakai implikasi Mamdani →mm, maka kesimpulan “v adalah B′” di atas dapat

diperoleh dengan menentukan himpunan kabur B~′ dengan fungsi keanggotaan

))} ( ), ( min( ), ( min{ sup ) ( ~ ~ ~

~ v u u v

B A A

U u

B µ µ µ

µ _′ ∈ ′ = )} ( , min{ )} ( )), ( ), ( min( sup min{ )} ( ), ( ), ( min{ sup ~ ~ ~ ~ ~ ~ ~ v w v u u v u u B B A A U u B A A U u µ µ µ µ µ µ µ = = = ′ ∈ ′ ∈

di mana w supmin{ ~(u), ~(u)} sup(A~ A~)

U u A A U u ∩ ′ = = ∈ ′

∈ µ µ yang menyatakan

derajat

keserasian (degree of compatibility) antara predikat A′ dengan A. Jadi untuk

memperoleh himpunan kabur B~′ tersebut, pertama-tama ditentukan derajat

keserasian w, yaitu supremum dari irisan himpunan kabur A~′ dan A~, dan kemudian

[image:55.612.98.532.182.599.2]

diperoleh B~′ sebagai irisan w dengan himpunan kabur B~, seperti terlihat dalam

[image:56.612.92.572.100.595.2]

Gambar 2.7 Penarikan kesimpulan dalam modus ponens rampat

Modus ponens rampat dapat digeneralisasikan menjadi modus ponens rampat

multikondisional, yang terdiri dari m buah premis kabur berupa kaidah, sebuah

premis kabur berupa fakta, dan sebuah kesimpulan. Skema umumnya adalah sebagai

berikut:

di mana Aij dan A′j adalah predikat kabur yang dikaitkan dengan himpunan kabur

ij

A~ dan Aj

~_′

dalam semesta Uj, dan Bi adalah predikat kabur yang dikaitkan dengan

himpunan kabur Bi

~

dalam semesta V (i = 1, ⋅⋅⋅,m; j = 1, ⋅⋅⋅,n). Masing-masing

premis tersebut dapat dipandang sebagai suatu relasi kabur Ri

~

(i = 1, ⋅⋅⋅,m) dalam Premis 1 : Bila

u

1 adalah

A

11dan

⋅

⋅

⋅

dan

u

n adalah

A

1n, maka v adalah

B

1

Premis 2 : Bila

u

1 adalah

A

21dan

⋅

⋅

⋅

dan

u

n adalah

A

2n, maka v adalah

B

2

… …

Premis m : Bila

u

1 adalah

A

m1dan

⋅

⋅

⋅

dan

u

n adalah

A

mn, maka v adalah

B

m

…

Fakta :

u

₁ adalah

A′

₁dan

⋅

⋅

⋅

dan

u

_n adalah

A

_n

′

V U

U1×⋅ ⋅⋅× n× dan faktanya sebagai himpunan kabur A′= A′×⋅ ⋅⋅×An′

~ ~

~

1 dalam

n U

U₁×⋅ ⋅⋅× . Premis-premis Ri

~

tersebut biasanya diperlakukan secara disjungtif,

sehingga semua premis itu dapat digabung menjadi satu premis R~, yaitu ~ ~.

1



m i i R R = =

Maka kesimpulan “v adalah B′” dapat diperoleh dengan kaidah inferensi

komposisional untuk menentukan himpunan kabur B~′= A~′R~ dalam semesta V

dengan fungsi keanggotaan (dengan mengambil operasi baku “min” untuk norma-t

dan “max” untuk gabungan kabur)

) (

~ v B′

µ ~ ~(v)

R A′

=µ ) ( } ~ ~ { max )} , , , ( ), , , ( min{ sup max )} , , , ( ), , , ( min{ max sup ))} , , , ( ( max ), , , ( min{ sup )} , , , ( ), , , ( min{ sup 1 1 1 ) ~ ~ ( } , , 1 { 1 ~ 1 ~ } , , 1 { 1 ~ 1 ~ } , , 1 { 1 ~ } , , 1 { 1 ~ 1 ~ 1 ~ ) , , ( v R A v u u u u v u u u u v u u u u v u u u u m i i i j j i j j i j j n n R A i m i n R n A U u m i n R n A m i U u n R m i n A U u n R n A U U u u    = ′ ⋅⋅ ⋅ ∈ ′ ∈ ⋅⋅ ⋅ ∈ ′ ⋅⋅ ⋅ ∈ ∈ ⋅⋅ ⋅ ∈ ′ ∈ ′ × ⋅⋅ ⋅ × ∈ ⋅⋅ ⋅ = ′ = ⋅⋅ ⋅ ⋅⋅ ⋅ = ⋅⋅ ⋅ ⋅⋅ ⋅ = ⋅⋅ ⋅ ⋅⋅ ⋅ = ⋅⋅ ⋅ ⋅⋅ ⋅ = µ µ µ µ µ µ µ µ µ

untuk setiap v∈V. Jadi ~ ~ ~ (~ ~) ~,

1

1 1







  m i i m i m i

i A R B

R A B = = = ′ = ′ ′ = ′ =

′ di mana B A Ri

~ ~ ~  ′ = ′ .

Jika untuk implikasi kabur Ri

~

tersebut diambil implikasi Mamdani →mm,

)}, ( ), , , ( min{ ) , , ,

( ₁ ~ ~ ₁ ~

~

1 u u v

v u u i in i

i n A A n B

R µ µ

µ ⋅ ⋅⋅ = _{×⋅⋅⋅×} ⋅ ⋅⋅

maka fungsi keanggotaan B~′ adalah

) ( ~ v B′ µ ( ) 1 ~ ~ v m i i R A   = ′ =µ )} ( , min{ max )} ( )), ( ), ( ( min sup min min{ max ))} ( )), ( ( min )), ( ( min min{ sup max ))} ( ), , , ( min( ), , , ( min{ sup max ~ } , , 1 { ~ ~ ~ } , , 1 { } , , 1 { } , , 1 { ~ ~ } , , 1 { ~ } , , 1 { } , , 1 { ~ 1 ~ ~ 1 ~ ~ } , , 1

{ 1 1

v w v u u v u u v u u u u i i ij j j j i ij j j j i in i n j j B i m i B j A j A n j U u n j m i B j A n j j A n j U u m i B n A A n A A U u m i µ µ µ µ µ µ µ µ µ µ ⋅⋅ ⋅ ∈ ′ ′ ⋅⋅ ⋅ ∈ ∈ ⋅⋅ ⋅ ∈ ⋅⋅ ⋅ ∈ ′ ⋅⋅ ⋅ ∈ ′ ⋅⋅ ⋅ ∈ ∈ ⋅⋅ ⋅ ∈ ′ × ⋅⋅ ⋅ × ′ ′ × ⋅⋅ ⋅ × ′ ∈ ⋅⋅ ⋅ ∈ = = = ⋅⋅ ⋅ ⋅⋅ ⋅ =

di mana ij

n j i w w } , , 1 { min ⋅⋅ ⋅ ∈

= , dan sup min ( ~ ( ), ~ ( ))

} , , 1

{ n A j A j

j U u

ij u u

w ij j j j µ µ _′ ⋅⋅ ⋅ ∈ ∈

= , i = 1, ,⋅⋅⋅ m.

) ~ ~ (

sup j ij

U u

ij A A

w j j ∩ ′ =

∈ merupakan

derajat keserasian (degree of compatibility)

antara fakta A′j

~

dari premis/kaidah Ri

~

, sedangkan wi yang merupakan minimum dari

semua wij untuk j = 1, ⋅⋅⋅, n seringkali disebut daya sulut (firing strength) yang

menyatakan sejauh mana anteseden dari kaidah Ri

~

dipenuhi oleh fakta A~′ yang

diberikan dan menyulut konsekuen dari kaidah tersebut. Dengan demikian

kesimpulan B~′ ditentukan dengan empat langkah sebagai berikut:

Langkah 1 : Tentukan derajat keserasian wij, yaitu supremum dari Aj Aij

~ ~_′∩

untuk

Langkah 2 : Untuk setiap i, tentukan daya sulut wi sebagai minimum dari semua

derajat keserasian wij untuk j = 1, ,⋅⋅⋅ n.

Langkah 3 : Untuk setiap i, tentukan irisan wi dengan Bi

~ .

[image:59.612.101.519.162.612.2]

Langkah 4 : Gabungkanlah semua irisan tersebut untuk memperoleh B~′.

Gambar 2.7 Melukiskan langkah-langkah tersebut untuk m = n = 2.

11. Sistem Kendali Kabur

Sistem kendali kabur berfungsi untuk mengendalikan proses tertentu dengan

mempergunakan kaidah inferensi kabur berdasarkan logika kabur. Pada dasarnya

sistem kendali semacam itu terdiri dari empat unit, yaitu:

a. Unit pengaburan (fuzzification unit)

b. Unit penalaran logika (fuzzy logic reasoning unit)

c. Unit basis pengetahuan (knowledge base unit), yang terdiri dari dua

bagian:

1. Basis data (data base), yang memuat fungsi-fungsi keanggotaan dari

himpunan-himpunan kabur yang terkait dengan nilai dari

variabel-variabel linguistik yang dipakai.

2. Basis kaidah (rule base), yang memuat kaidah-kaidah berupa

implikasi kabur.

d. Unit penegasan (defuzzification unit).

Suatu sistem kendali semacam itu mula-mula mengukur nilai-nilai tegas dari

semua variabel masukan yang terkait dalam proses yang akan dikendalikan.

sesuai. Hasil pengukuran yang telah dikaburkan kemudian diproses oleh unit

penalaran, yang dengan menggunakan unit basis pengetahuan, menghasilkan

himpunan kabur sebagai keluarannya. Langkah terakhir dikerjakan oleh unit

penegasan, yaitu menerjemahkan himpunan kabur keluaran itu ke dalam nilai yang

tegas. Nilai tegas inilah yang kemudian direalisasikan dalan bentuk suatu tindakan

yang dilaksanakan dalam proses pengendalian itu. Gambar 2.6 menunjukkan skema

[image:61.612.100.579.222.608.2]

langkah-langkah tersebut.

Gambar 2.9 Struktur dasar sistem kendali kabur

B. Dekomposisi Nilai Singular (DNS)

Dekomposisi nilai singular (DNS) dari suatu matriks Am×n adalah faktorisasi

dari A menjadi hasil kali dari 3 buah matriks, yaitu =

∑

T

V U

A , di mana mm

R

U∈ ×

dan n n

R

V∈ × adalah matriks-matriks orthogonal, dan

masukan (tegas)

unit basis pengetahuan

keluaran (tegas)

in

y

_

basis data

basis Kaidah

unit penalaran unit

pengaburan

(kabur) (kabur) _unit

(

1, 2, ,

)

R (p min{m,n})

diag ⋅ ⋅⋅ _p ∈ m n =

= ×

∑

σ σ σ adalah matriks diagonal dengan

0

2

1 ≥σ ≥⋅ ⋅⋅≥σp ≥

σ . σi disebut nilai singular dari A dan merupakan akar-akar

positif dari nilai-nilai eigen dari ATA. Kolom-kolom dari U disebut vektor singular

kiri dari A (vektor eigen orthonormal dari T

AA ), sedangkan kolom-kolom dari V

disebut vektorsingular kanan dari A (vektor eigen orthonormal dari ATA).

Untuk mengilustrasikan prinsip dasar penggunaan DNS untuk seleksi kaidah

kabur akan digunakan model kabur dengan konsekuen konstanta sebagai contoh.

Model kabur tersebut adalah model Takagi Sugeno Kang (TSK) yang memiliki

bentuk sebagai berikut:

Jika x₁ adalah A_i1 dan x₂ adalah A dan _i2 ⋅ ⋅⋅dan x_m adalah A_im

maka y adalah c_i , i = 1, 2, ⋅ ⋅⋅, M (2.1)

di mana ci adalah konstanta. Keluaran akhir dari model tersebut dihitung dengan

persamaan berikut:

∑

∑

= =

= _M

i i M

i i i

w c w y

1 1

(2.2)

di mana wi adalah derajat kesesuaian (daya sulut) kaidah ke-i yang didefinisikan

dengan persamaan 2.3 atau 2.4

(

( ), ( ), , ( )

)

min A1 1 A2 2 A m

i a a a

w

im i

i µ µ

µ ⋅ ⋅⋅

atau ) ( ) ( )

( 1 2 2

1 A A m

A

i a a a

w

im i

i µ µ

µ × ×⋅ ⋅⋅×

= (2.4)

Daya sulut kaidah ke-i yang dinormalisasikan adalah :

∑

= = _M i i i i w w N 1 (2.5)

Persamaan 2.2 dapat ditulis kembali menjadi

∑

= = M i i ic N y 1 (2.6)

Persamaan tersebut dapat dipandang sebagai kasus khusus dari model regresi linear:

∑

= + = M i i i e p y 1

θ (2.7)

dengan pi dan θi adalah

i i i

i N c

p ≡ ,θ ≡ (2.8)

di mana pi adalah regresor, θi adalah parameter, dan e adalah sinyal galat yang

diasumsikan tidak berkorelasi dengan regresor pi. Jika diberikan N pasang

masukan-keluaran {x(k),y(k)},k =1,2,⋅ ⋅⋅,N, di mana T

m k x k x k x k

x( )=[ 1( ), 2( ),⋅ ⋅⋅, ( )]



, maka

persamaan 2.7 dapat dinyatakan ke dalam bentuk matriks

e P

y= θ+ (2.9)

di mana [ (1), , ( )]T N,

R N

y y

y= ⋅ ⋅⋅ ∈

 M N m R p p

P=[ 1,⋅ ⋅⋅, ]∈ ×

 

dengan [ (1), , ( )]T N,

i i

i p p N R

, ]

, , [ 1

M T

M ∈R

⋅⋅ ⋅

= θ θ

θ dan

. )]

( , ), 1 (

[ T N

R N

e e

e= ⋅ ⋅⋅ ∈

Masing-masing kolom P berkorespondensi dengan satu kaidah kabur dalam basis

kaidah. Matriks P disebut matriks daya sulut dan Pθ disebut prediktor dari y.

Dalam membangun sebuah model kabur, jumlah data pelatihan biasanya lebih besar

daripada jumlah kaidah kabur dalam basis kaidah. Maka dimensi baris matriks P

lebih besar daripada dimensi kolomnya, yaitu N >M .

Matriks daya sulut P bisa singular (atau mendekati singular) karena adanya

kaidah kabur yang kurang penting atau yang berlebihan dalam basis kaidah. Kaidah

kabur yang kurang penting berarti kontribusi kaidah-kaidah tersebut pada keluaran

akhir adalah kecil, dan kaidah kabur yang berlebihan berarti kontribusi kaidah-kaidah

tersebut dapat digantikan dengan kaidah-kaidah yang lain. Sebuah kaidah yang

kurang penting dapat muncul dalam basis kaidah jika daya sulut yang

dinormalisasikan dari kaidah tersebut adalah nol atau mendekati nol dalam

keseluruhan ruang masukan, sedangkan kaidah yang berlebihan dapat muncul dalam

basis kaidah jika daya sulut yang dinormalisasikan dari kaidah tersebut sama dengan

atau bergantung linear pada satu atau lebih kaidah-kaidah yang lain.

Secara matematis, singularitas dari sebuah matriks ditunjukkan oleh adanya

nilai singular nol atau mendekati nol dalam matriks. Jadi, kaidah kurang penting atau

kaidah berlebihan dalam basis kaidah dapat ditentukan dengan memeriksa nilai-nilai

∑

=

P T P

P V

U

P di mana banyak nilai singular nol atau mendekati nol dalam

∑

_P

mengindikasikan banyaknya kaidah kabur kurang penting atau kaidah kabur

berlebihan dalam basis kaidah. Menghilangkan kaidah kabur kurang penting atau

kaidah kabur berlebihan dari basis kaidah untuk menghasilkan prediktor Pθ, di

mana θ memiliki paling banyak r komponen taknol, dengan r adalah banyaknya

kaidah kabur yang tinggal dalam basis kaidah setelah kaidah kabur kurang penting

atau kaidah kabur berlebihan dihilangkan. Letak dari entri-entri taknol menentukan

kolom-kolom P, yaitu kaidah-kaidah dalam basis kaidah, yang digunakan dalam

membangun model dan mendekati vektor observasi y.

Berikut ini akan diperkenalkan sebuah metode yang digunakan untuk

menyeleksi r kaidah penting (atau M-r kaidah kurang penting atau kaidah berlebihan)

dalam basis kaidah. Metode tersebut diawali dengan menghitung DNS dari P, yaitu:

∑

=

P T P

P V

U

P . (2.10)

Partisikan VP menjadi

r M

r V V

V V VP

−    

  =

22 21

12 11

(2.11)

r M-r

Gunakan algortima QR dengan faktorisasi pivot kolom pada [ 11 21]

T T

V

V untuk

] [

]

[V11 V21 R11 R12

QT T T ∏= (2.12)

r M-r

di mana r r

R

Q∈ × adalah matriks orthogonal, r r

R

R₁₁∈ × adalah matriks segitiga atas,

dan M M

R ×

∈

∏ adalah matriks permutasi. Didefinisikan:

∏ ≡

− P

P

Pr M r]

[ (2.13)

di mana N r

r R

P ∈ × terdiri atas kolom-kolom yang diinginkan dari P yang letak

aslinya dalam P mengindikasikan letak kaidah yang bersesuaian dalam basis kaidah.

Kunci dari metode ini adalah menemukan matriks permutasi ∏ dan

kemudian mendapatkan subset Pr yang diinginkan. Matriks permutasi adalah matriks

identita