Kode, GSR, dan Operasi Pada

Kode, GSR, dan Operasi Pada Graf

2.1 Ruang Vektor Atas F

₂

Ruang vektor V atas lapangan hingga F₂ = {0, 1} adalah suatu himpunan V yang berisi vektor-vektor, termasuk vektor nol, bersama dengan operasi penjumlahan vektor dan perkalian skalar elemen V terhadap elemen dari F2 yang memenuhi kondisi berikut:

1. u + v ∈ V, ∀u, v ∈ V

2. u + v = v + u, ∀u, v ∈ V

3. u + (v + w) = (u + v) + w, ∀u, v, w ∈ V

4. ∃~0 ∈ V 3 ~0 + v = v, ∀v ∈ V

5. ∀u ∈ V ∃ − u ∈ V 3 u + (−u) = (−u) + u = 0

6. rv ∈ V, ∀r ∈ F₂, ∀v ∈ V

8. r(u + v) = ru + rv, ∀r ∈ F₂, ∀u, v ∈ V

9. (r + s)v = rv + sv, ∀r, s ∈ F2, ∀v ∈ V

10. (rs)v = r(sv), ∀r, s ∈ F₂, ∀v ∈ V

Suatu subhimpunan tak kosong U dari ruang vektor V ,U ⊆ V , merupakan subruang dari V jika dan hanya jika

1. untuk setiap u₁, u₂ ∈ U , berlaku u₁+ u₂ ∈ U

2. untuk setiap k ∈ F₂ dan u ∈ U, berlaku ku ∈ U

Misalkan vektor-vektor v1, v2, . . . , vk ∈ F₂ⁿ. Vektor w ∈ F₂ⁿ dikatakan kombi- nasi linier dari v₁, v₂, . . . , v_k jika w dapat dituliskan sebagai berikut:

w = r₁v₁ + r₂v₂+ r₃v₃+ . . . + r_kv_k,

untuk suatu r₁, r₂, . . . , r_k ∈ F₂.

Selanjutnya himpunan semua kombinasi linier dari v₁, v₂, . . . , v_k disebut span dari v₁, v₂, . . . , v_k atau biasa dinotasikan sebagai span {v₁, v₂, . . . v_k}.

Kumpulan vektor v1, v2, . . . , vk dikatakan bebas linier jika kombinasi linier r₁v₁ + r₂v₂ + . . . + r_kv_k = 0 hanya dipenuhi oleh r_i = 0 untuk i = 1, 2, . . . , k.

Jika v₁, v₂, . . . v_k tidak bebas linier maka kita katakan bahwa v₁, v₂, . . . v_k bergan- tung linier.

Himpunan vektor v₁, v₂, . . . , v_k di V disebut basis untuk V jika

1. v₁, v₂, . . . , v_k bebas linier

2. span {v₁, v₂, . . . , v_k} = V

Selanjutnya dimensi dari V adalah banyaknya elemen dari suatu basis V .

2.1.1 Vektor Eigen dan Nilai Eigen

Misalkan A sebuah matriks persegi.

Definisi 2.1.1. vektor tak nol ¯x disebut vektor eigen dari A jika dan hanya jika terdapat bilangan (riil atau kompleks) λ sehingga:

A¯x = λ¯x.

jika bilangan λ tersebut ada, maka λ disebut nilai eigen dari A dan vektor ¯x disebut vektor eigen yang bersesuaian dengan nilai eigen λ.

2.2 Kode atas F

₂

Suatu kode C atas F2 dengan panjang n merupakan subhimpunan tak hampa atas ruang vektor F₂ⁿ, yaitu C = {(c₁, c₂, . . . , c_n)|c_i ∈ F₂, i = 1, 2, . . . , n}. Selanjutnya setiap unsur di kode C yaitu c = (c₁, c₂, . . . , c_n) ∈ C dinamakan katakode dari kode C. Unsur c_i dinamakan koordinat ke-i dari katakode c. Jika setiap unsur pada katakode C bernilai nol, yaitu c = (0, 0, . . . , 0) maka kata tersebut dinamakan katakode nol atau biasa dinotasikan dengan 0_C. Suatu kode C dinamakan kode linier jika kode tersebut merupakan subruang dari F₂ⁿ, dengan kata lain kode C dinamakan kode linier jika kode tersebut tertutup terhadap penjumlahan dan perkalian skalar atas F₂. Contoh sederhana dari kode linier yaitu C = {000, 111}, karena:

000 + 000 = 000, 111 + 111 = 000, 000 + 111 = 111, 111 + 000 = 111 Untuk selanjutnya kode yang akan ditinjau adalah kode linier.

2.3 Bobot dan Jarak Kode

2.3.1 Bobot Katakode dan Bobot Kode

Misalkan c = (c1, c2, . . . , cn) suatu katakode di C. Bobot Hamming dari katakode c adalah banyaknya digit tak nol dari c. Secara formal bobot Hamming katakode dari c yang dinotasikan dengan wt_H(c) didefinisikan sebagai :

wtH(c) = |{i|ci 6= 0, i = 1, 2, . . . , n}|

Selanjutnya bobot dari suatu kode C merupakan bobot terkecil dari katakode tak nol di C, dinotasikan dengan wt_H(C), dan secara formal didefinisikan sebagai:

wt_H(C) = min{wt_H(c)|c 6= 0_c, c ∈ C}

2.3.2 Jarak antar Katakode dan Jarak Kode

Misalkan v = (v₁, v₂, . . . , v_n) dan w = (w₁, w₂, . . . , w_n) merupakan dua buah katakode di C. Jarak Hamming dari v ke w adalah banyaknya posisi di v yang berbeda dengan w. Secara formal dinotasikan dengan d_H(v, w)dan didefinisikan sebagai

d_H(v, w) = |{i|v_i 6= w_i, i = 1, 2, . . . , n}|

Selanjutnya jarak dari kode C dinotasikan dengan d_H(C), dan secara formal didefinisikan sebagai

dH(C) = min{d(v, w)|v, w ∈ C, v 6= w, }

2.3.3 Hubungan Bobot dan Jarak

Jika C merupakan kode linier maka kita memiliki hubungan antara bobot dan jarak yaitu d_H(C) = wt_H(C).

Bukti. misalkan x, y ∈ C maka d_H(x, y) = wt_H(x − y), karena C kode linier maka x − y ∈ C, sehingga d_H(x, y) = wt_H(x − y) = wt_H(c), c ∈ C. Jika d_H(x, y) minimum maka wtH(c) minimum, berdasarkan definisi dari bobot dan jarak kode, jelas bahwa d_H(C) = wt_H(C).

Dengan demikian kita dapat mencari jarak suatu kode linier dari bobotnya.

Selanjutnya kode linier C atas F₂ dengan panjang n, dimensi k, dan jarak d ditulis sebagai kode [n, k, d].

2.3.4 Distribusi Bobot dan Pencacah Bobot

Misalkan C kode atas F₂ dengan panjang n. Distribusi bobot dari kode C dino- tasikan dengan A_t, didefinisikan sebagai

A_t = |{c ∈ C|wt_H(c) = t}|, 0 ≤ t ≤ n

Yaitu banyaknya katakode di C dengan bobot t.

Selanjutnya pencacah bobot dari kode C dinotasikan dengan W_C(x, y), didefi- nisikan sebagai

W_C(x, y) =Pn

i=0A_ixⁿ⁻ⁱyⁱ

2.4 Kode Dual

Misalkan v = (v₁, v₂, . . . , v_n) dan w = (w₁, w₂, . . . , w_n) dua buah katakode (di F₂ⁿ).

Hasil kali dalam antara katakode v dan w dinotasikan dengan v.w, didefinisikan sebagai v.w = Pn

i=1v_iw_i (di F₂). Kemudian kedua katakode tersebut dikatakan (saling) ortogonal jika v.w = 0 (di F2). Selanjutnya katakode u ∈ C⁰ dikatakan ortogonal terhadap kode C jika u.c = 0 (di F2) untuk setiap c ∈ C.

Definisi 2.4.1. Misalkan C kode atas F₂. Kode dual dari kode C, C ⊆ F₂ⁿ, dino-

C^⊥= {v ∈ F₂ⁿ|v.c = 0 untuk setiap c ∈ C}

selanjutnya kode C disebut swa-ortogonal apabila C ⊆ C^⊥, dan disebut swa- dual apabila C = C^⊥.

2.5 Matriks Pembangkit

Misalkan C ∈ F₂ⁿ suatu kode atas F2 dengan panjang n.

Definisi 2.5.1. Suatu matriks G yang memiliki n kolom dengan komponen-komponen atas F₂ dikatakan sebagai matriks pembangkit dari kode C apabila baris baris dari G merupakan basis dari kode C.

2.6 Matriks Cek Paritas

Misalkan C^⊥ merupakan kode dual dari kode C atas F₂ dengan panjang n.

Definisi 2.6.1. Matriks H yang memiliki n baris dengan komponen-komponen atas F₂ dikatakan sebagai matriks cek paritas dari kode C apabila kolom-kolom dari H merupakan basis dari kode C^⊥.

2.7 Graf

Γ disebut graf tak berarah dengan n titik apabila Γ = (V, E) merupakan konfigurasi dari himpunan titik V dan himpunan sisi E, dimana setiap sisi menghubungkan sepasang titik. Dua buah titik dikatakan bertetangga jika terdapat sisi yang meng- hubungkan kedua titik tersebut.

Suatu graf dikatakan sederhana jika graf tersebut tidak memiliki titik yang bertetangga dengan dirinya sendiri dan setiap dua pasang titik dihubungkan tepat oleh satu sisi, atau dengan kata lain graf tersebut tidak memiliki loop dan sisi ganda.

Definisi 2.7.1. Matriks ketetanggaan dari suatu graf sederhana Γ = (V, E) adalah suatu matriks A = (a_ij)ⁿ_(i,j=1) dengan entri sebagai berikut:

aij =







1, jika titik i dan j bertetangga 0, jika titik i dan j tidak bertetangga

2.7.1 Graf Strongly regular

Graf strongly regular dengan parameter (n, k, λ, µ) adalah suatu graf sederhana dan tidak berarah dengan banyaknya titik n, derajat regular k, dengan sifat sebagai berikut:

• setiap dua titik yang bertetangga memiliki tepat λ buah tetangga bersama

• setiap dua titik yang tidak bertetangga memiliki tepat µ buah tetangga bersama

Misalkan A merupakan matriks ketetanggaan dari GSR, maka A memenuhi persamaan berikut:

A² = kI + λA + µ (J − I − A) (2.1)

dengan J merupakan matriks yang semua entrinya 1, (J − I − A) merupakan ma- triks ketetanggaan dari graf komplemennya, dan derajat k merupakan nilai eigen dari A dengan vektor eigen 1 maka A memiliki 2 nilai eigen yang lain yaitu r,s dengan (r ≥ s) dengan multiplisitas berturut-turut f dan g yang memenuhi:

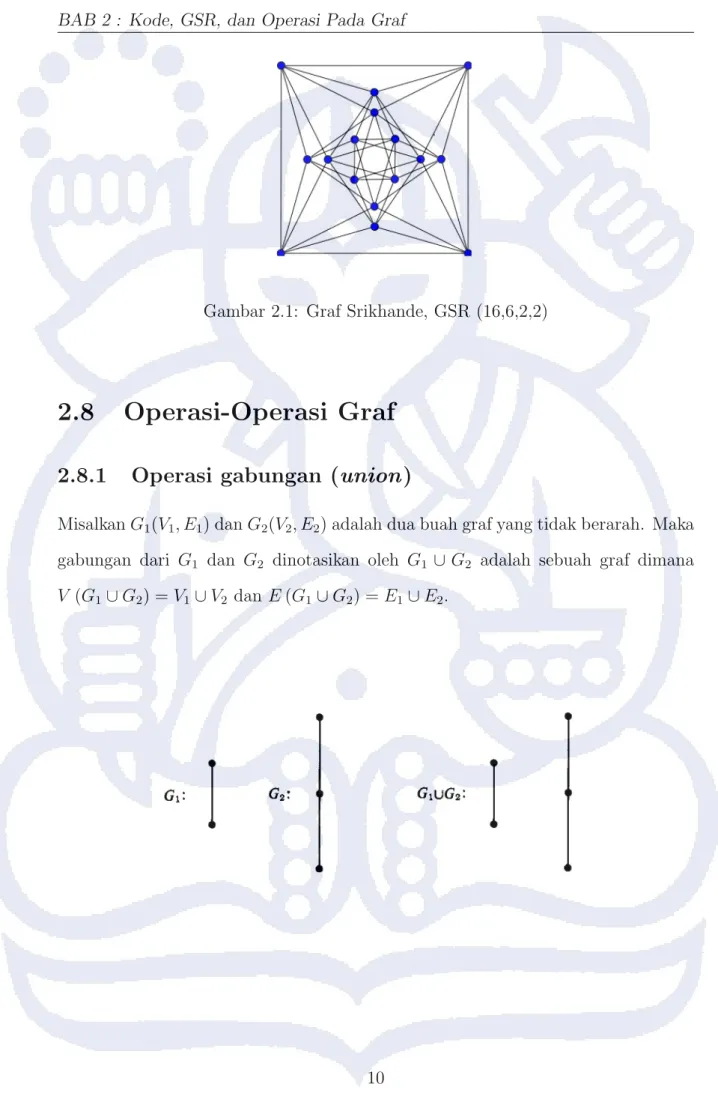
−rs = k −µ, r +s = λ−µ, (k − r) (k − s) = µ+n, n = f +g +1 dan k +f r +gs = 0 salah satu contoh dari graf strongly regular dapat dilihat pada gambar 2.1.

Gambar 2.1: Graf Srikhande, GSR (16,6,2,2)

2.8 Operasi-Operasi Graf

2.8.1 Operasi gabungan (union )

Misalkan G₁(V₁, E₁) dan G₂(V₂, E₂) adalah dua buah graf yang tidak berarah. Maka gabungan dari G₁ dan G₂ dinotasikan oleh G₁ ∪ G₂ adalah sebuah graf dimana V (G₁∪ G₂) = V₁∪ V₂ dan E (G₁∪ G₂) = E₁ ∪ E₂.

2.8.2 Operasi jumlah (join )

Misalkan G₁(V₁, E₁) dan G₂(V₂, E₂) adalah dua buah graf yang tidak berarah. Maka operasi jumlah dari kedua buah graf ini dinotasikan oleh G₁+G₂ adalah graf dengan himpunan titik dari (G₁∪ G₂), dimana setiap titik yang berasal dari G₁ bertetangga dengan semua titik yang berasal dari G₂.

2.8.3 Operasi kali(product )

Misalkan G₁(V₁, E₁) dan G₂(V₂, E₂) adalah dua buah graf yang tidak berarah. Maka operasi kali dari G₁ dan G₂ dinotasikan oleh G₁ × G₂ adalah sebuah graf dengan himpunan titik V₁×V₂dimana dua buah titik (u₁, u₂) dan (v₁, v₂) ∈ V₁×V₂dikatakan bertetangga di G₁× G₂ jika dan hanya jika

1. u₁ = v₁ dan u₂v₂ ∈ E₂

2. u₂ = v₂ dan u₁v₁ ∈ E₁

G₁× G₂ bersifat komutatif.

2.8.4 Line Graf

Diberikan sebuah graf G, maka line graf dari G atau dinotasikan dengan L(G) adalah sebuah graf sehingga

1. Setiap titik di L(G) merepresentasikan sisi di G

2. Dua buah titik di L(G) dikatakan bertetangga jika dan hanya jika sisi sisi di G yang berkorespondensi dengan titik tersebut berinsidensi di G